Как относятся периметры подобных треугольников: Подобные треугольники — урок. Геометрия, 8 класс.

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. 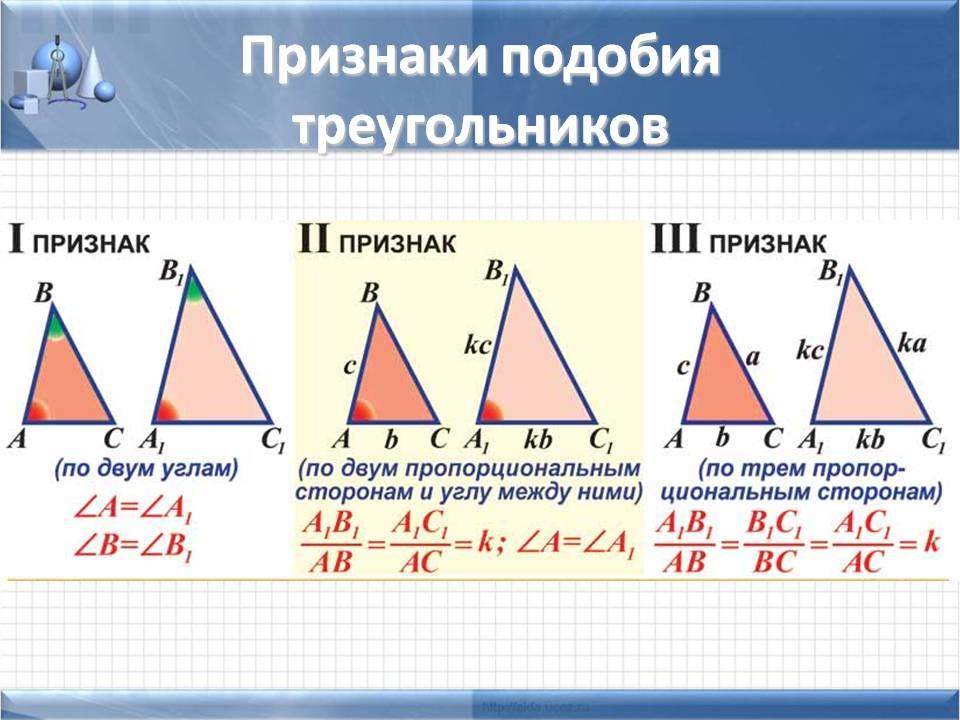Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

Подобные треугольники — презентация онлайн

1. ПОДОБИЕ В ГЕОМЕТРИИ

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

2. Пропорциональные отрезки

• Отношением
отрезков называется
отношение их длин.
• Отрезки AB и CD
пропорциональны
отрезкам A1B1 и
C1D1,, если AB A B
CD
B
A
D
C
AB
CD
A
A1
B
С
D
B1 С1
1 1
C1D1
ПРИМЕР
D1

3. ПРИМЕР

• Даны два прямоугольных треугольника
Стороны ΒC и CA пропорциональны MN и MK,
так как
B
5
3
C
A
4
BC
3
MN 15
AC
4
и
MK 20
т. е.
BC AC 1
MN MK 5
N
?
15
M
K
20
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО
ТРЕУГОЛЬНИКА.

4. Пропорциональность отрезков

• Понятие пропорциональности вводится для
любого числа отрезков.
B
например
5
3
C
A
BC AC AB
MN MK NK
4
N
25
15
M
K
20

5. Подобные фигуры

Предметы одинаковой
формы, но разных
размеров
Фотографии, отпечатанные
с одного негатива, но с
разными увеличениями;
Здание и его макет
Планы,
географические
карты одного и того
же района,
выполненные в
разных масштабах.

6. Подобные фигуры

• В геометрии фигуры одинаковой формы
называют подобными фигурами
Подобными
являются любые
два квадрата
Подобными
являются любые
два круга
два куба
два шара

7. Подобные треугольники

• Даны два треугольника AΒC и A1Β1C1,
у которых A = A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1,
лежащие против равных углов, называют
сходственными
Β1
Β
A
C
A1
C1

8.

Определение• Два треугольника называются подобными,
если их углы соответственно равны и стороны
одного треугольника пропорциональны
сходственным сторонам другого.
Β
ΔAΒC ~ ΔA1Β1C1
A
C
A1
Β1
A = A1, Β = Β1, C = C1.
AB
BC
AC
A1B1 B1C1 A1C1
C1

9. Коэффициент подобия

Β
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
Β1
C
A1
k – коэффициент подобия.
• Число k , равное отношению сходственных
сторон, называется коэффициентом подобия.
C1

10. Дополнительные свойства

Отношение высот подобных треугольников,
проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение медиан подобных треугольников,
проведенных к сходственным сторонам,
равно коэффициенту подобия.
Отношение биссектрис подобных
треугольников, проведенных к сходственным
сторонам, равно коэффициенту подобия.

11. Отношение периметров

Β
Β1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
PABC
k
PA1B1C1
A
C
A1
ДОКАЗАТЕЛЬСТВО
• Отношение периметров подобных
треугольников равно
• коэффициенту подобия.
C1

12. Отношение периметров

ΔAΒC ~ ΔA1Β1C1
Β
Β1
A
AB
BC
AC
k
A1B1 B1C1 A1C1
AB kA1B1
C
A1
C1
BC kB1C1
AC kA1C1
PABC
AB BC AC
kA1B1 kB1C1 kA1C1
PA1B1C1 A1B1 B1C1 A1C1
A1B1 B1C1 A1C1
Выносим общий множитель за скобку и
сокращаем дробь.
PABC
k
PA1B1C1

13. Отношение площадей

Β
Β1
ΔAΒC ~ ΔA1Β1C1
AB
BC
AC
k
A1B1 B1C1 A1C1
A
• Отношение площадей
подобных треугольников
равно квадрату
коэффициента подобия.
C
A1
S ABC
2
k
S A1B1C1
ДОКАЗАТЕЛЬСТВО
C1

14. Отношение площадей

Пусть ΔAΒC ~ ΔA1Β1C1,
коэффициент подобия k
AB
BC
AC
k
A1B1 B1C1 A1C1
Β
Β1
A
A = A1, по теореме об отношении
площадей треугольников, имеющих по
равному углу, имеем
C
A1
SABC
AB AC
AB AC
k k k2
SA1B1C1 A1B1 A1C1 A1B1 A1C1
C1

15. Свойство биссектрисы треугольника

Биссектриса треугольника
делит противоположную
сторону на отрезки,
пропорциональные
прилежащим сторонам
треугольника.
BD DC
или
AB AC
A
ПРИМЕР
B
BD AB
DC AC
ДОКАЗАТЕЛЬСТВО
D
C

16. Свойство биссектрисы треугольника

A
2
1
H
ΔABD и ΔACD имеют
общую высоту AH
S ABD DB
S ACD DC
B
ИМЕЕМ
D
BD AB
DC AC
C
ΔABD и ΔACD имеют
равные углы 1 = 2
S ABD AB AD AB
S ACD AD AC AC

17. Свойство биссектрисы треугольника

Дано: ΔABC
AD – биссектриса
AB = 14 см
BC = 20 см
AC = 21 см
Найти: BD,CD.
Решение:
A
1
B
D
20см
2
C

18. Свойство биссектрисы треугольника

A
1
B
D
20см
2
Решение:
Пусть BD = x см,
тогда CD = (20 – x) см.
По свойству биссектрисы
треугольника BD DC
AB AC
имеем
x
20 x
C
14
21
Решая уравнение, получим х = 8
BD = 8 см, CD = 12 см.

19. Признаки подобия треугольников

Первый признак подобия треугольников.
(по двум углам)
Второй признак подобия треугольников.
(по углу и двум пропорциональным сторонам)
Третий признак подобия треугольников.
(по трем пропорциональным сторонам)

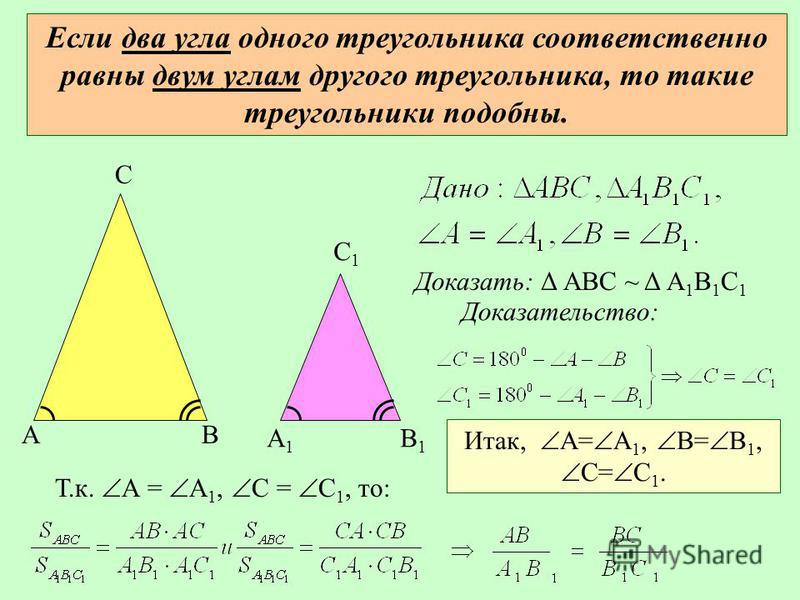
20. Первый признак подобия треугольников.

Если два угла одного треугольника
соответственно равны двум углам
другого треугольника, то такие
треугольники подобны.
C1
C
A
B
A1
B1

21. Первый признак подобия треугольников.

Дано:
ΔABC и ΔA1B1C1,
A = A1,
B = B.
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
C
A
B
C1
A1
B1

22. Первый признак подобия треугольников.

C
A
A1
C1B
Доказательство:
A = A1, B = B1.
C = 180º – A – B,
C1 = 180º – A1 – B1.
C = C1
Таким образом углы
B1 треугольников
соответственно равны.

23. Первый признак подобия треугольников.

Доказательство:
A = A1,
B = B1.
SABC
AB AC
SA1B1C1 A1B1 A1C1
SABC
AB BC
SA1B1C1 A1B1 B1C1
Имеем BC AC
B1C1
A1C1
Аналогично, рассматривая равенство углов
C= C1, A= A1, получим
BC
AB
B1C1 A1B1
Итак, сходственные стороны пропорциональны.

24. Второй признак подобия треугольников.

Если две стороны одного треугольника
пропорциональны двум сторонам
другого треугольника и углы,
заключенные между этими сторонами,
равны, то такие треугольники подобны.
Β
A
Β1
C
A1
AB
AC
A1B1 A1C1
C1

25. Второй признак подобия треугольников.

Дано:
ΔABC и ΔA1B1C1,
A = A1,
Β
Β1
A
AB
AC
A1B1 A1C1
C
A1
C1
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:

26. Второй признак подобия треугольников.

С
Доказательство:
Достаточно доказать, что B = B1.
A
1
2 B
C1
С2
A1
ΔABC2, 1= A1, 2= B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
AB
AC2
(из подобия).
A1B1 A1C1 AB
AC
По условию
A1B1 A1C1
AC=AC2.
B1
ΔABC=ΔABC2, т.е. B = B1.

27. Третий признак подобия треугольников.

Если три стороны одного треугольника
пропорциональны трем сторонам
другого треугольника, то такие Β
1
треугольники подобны.
Β
A1
A
C
AB
BC
AC
A1B1 B1C1 A1C1
C1

28. Третий признак подобия треугольников.

Дано:
ΔABC и ΔA1B1C1,
Β1
A1
C1
Β
A
AB
BC
AC
A1B1 B1C1 A1C1
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
C

29. Третий признак подобия треугольников.

С
A
1
Доказательство:
Достаточно доказать, что A= A1
ΔABC2, 1= A1, 2= B1,
2 B
С2
A1
ΔABC2 ~ ΔA1B1C1 по двум углам.
AB BC2 AC2
Отсюда
Β1
A1B1 B1C1 A1C1
По условию AB BC
AC
A1B1 B1C1 A1C1
ΔABC=ΔABC2 по трем
сторонам, т.е. A = A1
C1

30. Разминка

1
• Отрезки AB и CD пропорциональны
отрезкам MN и PK.
• Найдите MN,
если AB = 3, CD = 4, PK = 2.
AB MN
CD PK
3 MN
4
2
MN = 1,5

31. Разминка

2
• Даны два подобных прямоугольных
треугольника.
• Коэффициент подобия 1,5
• Стороны одного из них 3, 4 и 5.
• Найдите гипотенузу другого.
5 · 1,5 = 7,5
7,5

32. Разминка

3
• По данным на
рисунке найдите х.
х
12
5
х
12
5
4
4
х = 15

33. Разминка

4
• Длины двух окружностей 2π и 8π.
• Найдите отношение их радиусов.
2π : 8π = 1 : 4
0,25

34. Разминка

5
• Отношение площадей двух квадратов
равно 9 : 1.
• Найдите сторону большего их них, если
сторона меньшего равна 2.
k2 = 9, k = 3
Коэффициент подобия
3·2=6
сторона большего квадрата
6

35. Решение задач

Пропорциональные
отрезки
1
2
3
Свойство
биссектрисы
4
5
6
7
8
9
10
11
12
13
14
15
Определение
подобных
треугольников
Отношение
периметров
подобных фигур
Отношение
площадей подобных
фигур

36. 1 задача

Отрезки AB и CD пропорциональны
отрезкам EF и MN.
Найдите EF,
если AB = 5 см, CD = 80 мм, MN = 1 дм.

37.

4 задачаB
В треугольнике АВС
АС = 6 см,
1
2
ВС = 7 см,
AB = 8 см,
A
D
C
BD – биссектриса.
Найдите, AD, CD.

38. 7 задача

Треугольник со сторонами 2 см, 3 см, 4 см
подобен треугольнику
со сторонами 5 мм, 7,5 мм и 1 см.
Найдите коэффициент подобия.

39. 10 задача

Сходственные стороны подобных
треугольников относятся как 1 : 3.
Найдите периметр большего
треугольника, если периметр
меньшего 15 см.

40. 13 задача

ΔABC ~ ΔA1B1C1 ,
AB : A1B1 = k = 4
SΔABC= 48 м2.
Найдите площадь треугольника A1B1C1 .

41. 2 задача

B
C
O
A
10
D
В параллелограмме
ABCD диагонали
пересекаются в точке О,
CD = 10 см.
Найдите периметр
параллелограмма, если
BC
AC
CD OC

42. 5 задача

B
M
12
A
18
C
Основание
равнобедренного
треугольника равно 18 мм,
а биссектриса делит
боковую сторону на
отрезки, из которых
прилежащий к основанию
равен 12 мм. Найдите
периметр треугольника

43. 8 задача

Треугольники KPF и ЕМТ подобны, причем
T
M
40°
E
P
20°
F
K
KP
PF
KF
ME MT ET
F = 20°, E = 40°.
Найдите остальные
углы этих
треугольников.

44. 11 задача

Периметры подобных треугольников
12 мм и 108 мм соответственно.
Стороны одного из них 3 мм, 4 мм и 5 мм.
Найдите стороны другого и
определите его вид.

45. 14 задача

Площади двух подобных треугольников
равны 16 см2 и 25 см2.
Одна из сторон первого треугольника
равна 2 см.
Найдите сходственную ей сторону
второго треугольника.

46. 3 задача

В треугольнике ABC
B
точка K лежит на стороне
10
АС. Площади
треугольников АВK и
KВС относятся
.
A
K
C
как 1 : 3,
ВС = 10 см. Найдите AC ,
BC
AK
если
AC KC

47. 6 задача

B
AD = 4
1
BC = 5
2
AB + DC = 12
Найти AB, DC, AC
4
A
D
C

48.

9 задачаНа рисунке
B
ΔВЕС ~ ΔАВС,
АЕ = 16 см,
A
C
16
E
9
СЕ = 9 см. Углы
ABC и ВЕС тупые.
Найдите ВС.

49. 12 задача

Масштаб плана 1 : 1000.
Какова длина ограды участка,
если на плане размеры
прямоугольника,
изображающего участок 2 см х 5 см.

50. 15 задача

Периметры подобных треугольников
относятся как 2 : 3,
сумма их площадей равна 260 см2.
Найдите площадь каждого
треугольника.

51. ЗАДАЧИ

1.
Диагонали трапеции ABCD пересекаются
в точке O. Площади треугольников BOC
и AOD относятся как 1 : 9. Сумма
оснований BC и AD равна 4,8 см.
Найдите основания трапеции.
Решение:

52. Решение

B
C
2
4
3
O
1
A
D
Рассмотрим ΔAOD и
ΔBOC:
1= 2 (накрест лежащие
при AD || BC, и секущей
AC;
3= 4 (вертикальные)
ΔAOD ~ ΔBOC (по двум
углам)
AO OD AD
=k
OC OB BC

53. Решение

B
C
2
4
3
O
1
D
A
Ответ:
S AOD
9
2
.
k
S BOC
1
k=3
AD + BC =
= 3BC + BC = 4BC
AD + BC = 4,8см
(по условию)
BC = 1,2 см
AD = 3,6 см
BC = 1,2 см AD = 3,6 см

54. ЗАДАЧИ

B
2,5
4
20
A
5
C
D
E
16
10
F
2.
Докажите, что треугольники,
изображенные на рисунке, подобны, и
выясните взаимное положение прямых
CB и DF.
Решение:

55. Решение

B
2,5
4
20
A
5
C
D
E
16
10
Отсюда
BС AC AB
DF DE EF
F
ΔABC~ΔDEF
по трем
пропорциональным
сторонам
Найдем
отношение
сходственных
сторон данных
треугольников
AB 2,5
0,25
EF 10
AC 5
0,25
ED 20
BС 4
0,25
DF 16

56. Решение

B
.
E
1
A
C
D
2
ΔABC~ΔDEF
Соответственно
A = E
B = F
ACB = EDF
F
Рассмотрим
прямые BC и DF,
секущую AE
1 = 2
(внешние накрест
лежащие)
BC || DF.

57. ЗАДАЧИ

3.
Отрезки AB и CD пересекаются
AO DO
в точке O, причем
.
OB OC
Докажите, что CBO = DAO.
Решение:

58. Решение

Рассмотрим ΔAOD и ΔCOB
DOA = COB
(вертикальные).
AO DO .
D
A
O
OB
B
C
OC
ΔAOD ~ ΔCOB по углу и
двум пропорциональным
сторонам.
CBO = DAO (из подобия).

59. ЗАДАЧИ

4.
В треугольнике ABC
AB = 4, BC = 6, AC = 7.
Точка E лежит на стороне AB.
Внутри треугольника взята точка M так,
что MB = 5,25, ME = 4,5, AE = 1.
Прямая BM пересекает AC в точке P.
Докажите, что ΔAPB равнобедренный.
Решение:

60. Решение

.
Рассмотрим ΔBEM и ΔABC
BE = AB − AE = 4 – 1 = 3
BE : AB = 3 : 4 = 0,75
EM : BC = 4,5 : 6 = 0,75
BM : AC = 5,25 : 7 = 0,75,
т.е. стороны треугольников
пропорциональны
A
4 E
1
B
4,5
5,25
M
7
P
6
C
Решение
ΔBEM ~ ΔABC по трем
пропорциональным сторонам.
Следовательно, BME = AСB
EBM = BAC
BEM = ABC.
Рассмотрим треугольник ABP:
EBM = BAC, т.е. ABP = BAP.
ΔABP – равнобедренный, что и
требовалось доказать.

62. ЗАДАЧИ

5.
Диагональ AC параллелограмма ABCD
равна 90.
Середина M стороны AB соединена с
вершиной D.
Отрезок MD пересекает AC в точке O.
Найдите отрезки AО и CО.
Решение:

63. Решение

C
B
M
A
O
D
Рассмотрим
ΔAOM и ΔCОD
AOM = CОD
(вертикальные),
MAO = ОCD
(накрест лежащие при
AB || DC и секущей AC).
Отсюда ΔAOM ~ ΔCОD
по двум углам.

64. Решение

C
B
M
A
O
D
AO OM AM
1
OC OD CD
2
.
AM = ½ AB (по условию)
AB = CD (ABCD параллелограмм),
AM : CD = 1 : 2
ΔAOM ~ ΔCОD
т.е. AO = 0,5CО
AO = ⅓AC = ⅓·90 = 30
CO = ⅔AC = ⅔·90 = 60
Решите задачи, отметьте нужные ячейки
А
1
2
3
4
5
Б
В
Г
1. По данным
рисунка х равен
7
х
А) 7
Б) 14
В) 3,5
Г) 14/3
2) По данным рисунка
периметр ΔABC
равен
В
3
2
А
4
С
А) 9
Б) 27
В) 36
Г) 18
3) По данным рисунка
отрезок BC равен
В
3
3
2,5
А
4
0,5
С
А) 3,75
Б) 7,5
В) 5
Г) 4,5
B
ТЕСТ
E
12
9
3
A
18
C
D
4
6
4) По данным рисунка площади данных
треугольников относятся
А) 3 : 1
Б) 9 : 1
В) 6 : 1
Г) 9 : 4
F
B
E
12
9
3
A
18
C
D
4
6
F
5) По данным рисунка прямые AB и DE
А) нельзя ответить
Б) пересекаются
В) параллельны
ОТВЕТЫ:
А
1
2
3
4
5
Б
В
Г

Отношение периметров двух подобных треугольников равно 1:3.

Площадь большего треугольника равна 27 квадратных футов. Чему равна площадь наименьшего треугольника?

Геометрия

Олдмани Н.

спросил 13.04.20

Коэффициент масштабирования треугольника ABC в треугольник DEF равен 3/5

Подписаться І 2

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Джон С. ответил 13.04.20

Репетитор

5 (6)

Терпеливый и знающий репетитор по математике и английскому языку

См. таких репетиторов

Смотрите таких репетиторов

Если два треугольника подобны, отношение их площадей равно квадрату отношения их периметров, поэтому, если отношение их периметров равно 1:3, отношение их площадей равно 1:9. .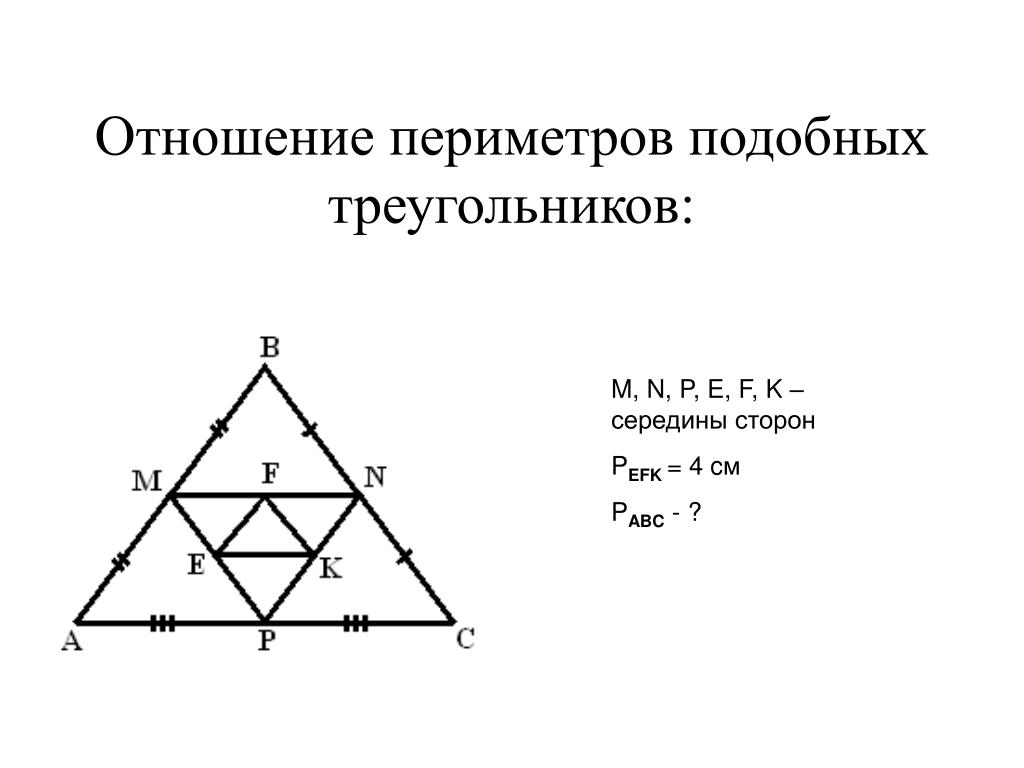

Нам известно, что площадь большего треугольника равна 27 футов, и теперь мы можем использовать отношение их площадей, чтобы найти площадь меньшего треугольника.

Если у вас есть дополнительные вопросы по этой задаче или любой другой геометрической задаче, пожалуйста, свяжитесь со мной.

Голосовать за 0 голос против

Подробнее

Отчет

Артур Д. ответил 13.04.20

Репетитор

4.9 (164)

Сорокалетний педагог: классная комната, летняя школа, заместитель, репетитор

Об этом репетиторе ›

Об этом репетиторе ›

Вот два способа решения проблемы.

В подобных треугольниках отношение их площадей равно квадрату отношения их сторон.

Отношение их периметров равно 1:3, поэтому отношение их сторон и их высот также будет равно 1:3. 92)

Следовательно, 1/9=A/27, где A=площадь меньшего треугольника =3 квадратных фута — это площадь меньшего треугольника

Предположим, что вы этого не знали.

Пусть один треугольник имеет стороны a, b и c.

Пусть другой треугольник будет 3a, 3b и 3c.

Пусть h=высота меньшего треугольника.

3h=высота большего треугольника

пусть b и 3b будут основаниями треугольников

A=(1/2)(b)(h) — площадь меньшего треугольника.

A=(1/2)(3b)(3h) — площадь большего треугольника.

27=(1/2)(9bh)

27=4,5bh

bh=27/4,5

bh=6

подставим это в первую формулу площади меньшего треугольника

A=(1/ 2)(6)

A=3 квадратных фута – площадь меньшего треугольника снова

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Площади двух подобных треугольников равны 50 дм2 и 32 дм2. Сумма их периметров равна 117 дм. Чему равен периметр каждого из этих треугольников?

Геометрия

Джессика К.

спросил 16.03.19

Подписаться І 1

Еще

Отчет

4 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Марк М. ответил 17.03.19

Репетитор

5,0 (265)

Учитель математики — NCLB Высококвалифицированный

Об этом репетиторе ›

Об этом репетиторе ›

Площади двух одинаковых фигур относятся как квадрат масштабного коэффициента.

√50 / √32

5√2 / 4√2

5 / 4

Периметры относятся как 5 : 4

Голосовать за 0 голос против

Подробнее

Отчет

Марк М. ответил 16.03.19

Репетитор

5,0 (265)

Учитель математики — высококвалифицированный специалист NCLB

Об этом репетиторе ›

Об этом репетиторе ›

Площади двух подобных фигур относятся как квадрат масштабного коэффициента. √

√50 / √32 = 5√2 / 4√2 = 5 / 4

Отношение периметров равно 5 : 4

5x + 4x = 117

Можете ли вы найти x и ответить?

Голосовать за 0 голос против

Подробнее

Отчет

Виктория В. ответил 16.03.19

Репетитор

5,0 (402)

Учитель математики: 20 лет преподавания/репетиторства CALC 1, PRECALC, ALG 2, TRIG

См. таких репетиторов

Смотрите таких репетиторов

Если два объекта подобны, то отношения работают следующим образом:

ЛИНЕЙНОЕ отношение длина2 : длина3 или высота1 : высота2 или периметр1 : периметр2

Если вы знаете линейное отношение, отношение ПЛОЩАДЕЙ является линейным отношением КВАДРАТ.

Отношение ОБЪЕМОВ представляет собой линейное отношение КУБ.

Наши ОБЛАСТИ находятся в соотношении 50:32 или 50/32, что сокращается до 25/16.

Это отношение (поскольку это отношение ПЛОЩАДЕЙ) является КВАДРАТОМ линейного отношения.

Итак, если я хочу ЛИНЕЙНОЕ отношение, что я и делаю, потому что это будет отношение ПЕРИМЕТРОВ, мне нужно

взять квадратный корень из 25/16.

Таким образом, ЛИНЕЙНОЕ соотношение равно 5/4.

Итак, если периметр меньшего треугольника равен 4, периметр большего треугольника будет равен 5. Но только 4 + 5 = 9, а не 117, и задача утверждает, что сумма их периметров равна 117 дм.

Сохраняя то же соотношение, если меньший периметр равен 8, больший будет 10. Сумма равна 18, но нам нужно 117.

Продолжая, если меньший периметр равен 12, больший треугольник будет 15. Сумма равна 27 , но нам нужно 117.

Таким образом, мы могли бы делать это, пока не достигнем суммы 117, но с алгеброй было бы проще.

Большой периметр = (5/4) Малый периметр.

Большой периметр + Малый периметр необходимо = 117

Замените «Большой периметр» его эквивалентом «(5/4) Малый периметр»

(5/4) Малый периметр + (1) Малый периметр = 117

(5/4) Малый периметр + (4/4) Малый периметр = 117

(9/4) Малый периметр = 117

Умножить на величину, обратную (9/4), так что левая сторона становится (1) малым периметром, а правая сторона становится (4/9) 117.

(4/9)(9/4) малый периметр = (4/ 9) 117

(1) Малый периметр = 52 дм

Большой периметр = 117 — 52 = 65 дм

Голосовать за 0 Голосовать против

Подробнее

Отчет

Патрик Б. ответил 16.03.19

Репетитор

4.7 (31)

Репетитор/учитель математики и информатики

Смотрите таких репетиторов

Смотрите таких репетиторов

Площадь большего треугольника 50 дм;

(1/2)(ч) = 50 92

4/5 = k

Таким образом, константа пропорциональности равна 4/5

Сумма сторон большего треугольника равна (B+x+y)

Сумма сторон меньшего треугольника равна (B +x+y)*4/5

Итого (9/5)(B+x+y) = 117

B+x+y = 117/9*5 = 13*5 = 65

периметр большего треугольника равен 65.