Как перемножить 3 матрицы: Умножение матриц онлайн

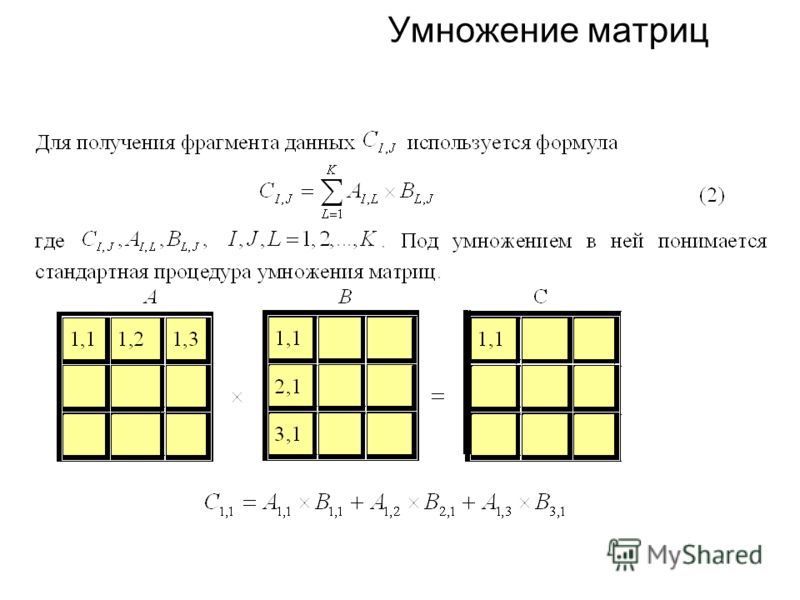
Как находить произведение матриц. Умножение матриц. Скалярное произведение матриц. Произведение трех матриц

С матрицами (таблицами с числовыми элементами) могут проводиться различные вычислительные действия. Одни из них – умножение на число, вектор, другую матрицу, несколько матриц. Произведение иногда получается неверным. Ошибочный результат – итог незнания правил выполнения вычислительных действий. Давайте разберемся, как следует осуществлять умножение.

Матрица и число

Начнем с самого простого – с умножения таблицы с числами на конкретную величину. Например, мы имеем матрицу A с элементами a_ij (i – это номера строк, а j – это номера столбцов) и число e. Произведением матрицы на число e будет матрица B с элементами b_ij, которые находятся по формуле:

b_ij = e × a_ij.

Т. е. для получения элемента b₁₁ нужно взять элемент a₁₁ и умножить его на нужное число, для получения b₁₂ требуется найти произведение элемента a₁₂ и числа e и т. д.

Решим задачу № 1, представленную на картинке. Для получения матрицы B просто умножим элементы из A на 3:

1. a₁₁ × 3 = 18. Это значение записываем в матрицу B в то место, где пересекаются столбец № 1 и строка № 1.
2. a₂₁ × 3 = 15. Мы получили элемент b₂₁.
3. a₁₂ × 3 = –6. Мы получили элемент b₁₂. Записываем его в матрицу B в место, где пересекаются столбец № 2 и строка № 1.
4. a₂₂ × 3 = 9. Данный результат – это элемент b₂₂.
5. a₁₃ × 3 = 12. Данное число вносим в матрицу на место элемента b₁₃.
6. a₂₃ × 3 = –3. Последнее полученное число – это элемент b₂₃.

Таким образом, мы получили прямоугольный массив с числовыми элементами.

18	–6	12
15	9	–3

Векторы и условие существования произведения матриц

В математических дисциплинах существует такое понятие, как «вектор». Под этим термином понимается упорядоченный набор величин от a₁ до a_n. Они называются координатами векторного пространства и записываются в виде столбца. Еще есть термин «транспонированный вектор». Его компоненты располагаются в виде строки.

Векторы можно называть матрицами:

• вектор-столбец – это матрица, построенная из одного столбца;
• вектор-строчка – это матрица, которая включает в себя только одну строку.

При выполнении над матрицами операций умножения важно помнить о том, что есть условие существования произведения. Вычислительное действие A × B может быть выполнено только тогда, когда число столбцов в таблице A равно числу строчек в таблице B. Итоговая матрица, получаемая в результате вычисления, всегда имеет число строк таблицы A и число столбцов таблицы B.

При умножении не рекомендуется переставлять местами матрицы (множители). Их произведение обычно не соответствует коммутативному (переместительному) закону умножения, т. е. результат операции A × B не равен результату операции B × A. Такая особенность именуется некоммутативностью произведения матриц. В некоторых случаях результат умножения A × B равен результату умножения B × A, т. е. произведение коммутативно. Матрицы, при которых равенство A × B = B × A выполняется, называются перестановочными. С примерами таких таблиц можно ознакомиться ниже.

Умножение на вектор-столбец

При выполнении умножения матрицы на вектор-столбец обязательно учитываем условие существования произведения. Число столбцов (n) в таблице должно совпадать с количеством координат, из которых составлен вектор. Результат вычисления – преобразованный вектор. Его количество координат равно числу строчек (m) из таблицы.

Как вычисляются координаты вектора y, если есть матрица A и вектор x? Для расчетов созданы формулы:

y₁ = a₁₁x₁ + a₁₂x₂ + … + a_1nx_n,

y₂ = a₂₁x₁ + a₂₂x₂ + … + a_2nx_n,

…………………………………,

y_m = a_m1x₁ + a_m2x₂ + … + a_mnx_n,

где x₁, …, x_n – координаты из x-вектора, m – число строк в матрице и количество координат в новом y-векторе, n – число столбцов в матрице и количество координат в x-векторе, a₁₁, a₁₂, …, a_mn – элементы матрицы A.

Таким образом, для получения i-й компоненты нового вектора выполняется скалярное произведение. Из матрицы A берется i-я вектор-строка, и она умножается на имеющийся вектор x.

Решим задачу № 2. Произведение матрицы на вектор найти можно, ведь A имеет 3 столбца, и x состоит из 3 координат. В результате мы должны получить вектор-столбец с 4 координатами. Воспользуемся вышеуказанными формулами:

1. Вычислим y₁. 1 × 4 + (–1) × 2 + 0 × (–4). Итоговое значение равно 2.
2. Вычислим y₂. 0 × 4 + 2 × 2 + 1 × (–4). При расчете получим 0.
3. Вычислим y₃. 1 × 4 + 1 × 2 + 0 × (–4). Сумма произведений указанных множителей равна 6.
4. Вычислим y₄. (–1) × 4 + 0 × 2 + 1 × (–4). Координата равна –8.

Умножение вектор-строки на матрицу

Нельзя умножить матрицу, состоящую из нескольких столбцов, на вектор-строку. В таких случаях не выполняется условие существования произведения. А вот умножение вектор-строки на матрицу возможно. Эта вычислительная операция выполняется при совпадении количества координат в векторе и числа строк в таблице. Результат произведения вектора на матрицу – новая вектор-строка. Ее количество координат должно равняться числу столбцов в матрице.

Вычисление первой координаты нового вектора подразумевает умножение вектор-строки и первого вектор-столбца из таблицы. Аналогичным способом производится расчет второй координаты, но вместо первого вектор-столбца берется уже второй вектор-столбец. Вот общая формула для вычисления координат:

y_k = a_1kx₁ + a_2kx₂ + … + a_mkx_m,

где y_k – координата из y-вектора, (k находится в промежутке от 1 до n), m – число строк в матрице и количество координат в x-векторе, n – число столбцов в матрице и количество координат в y-векторе, a с буквенно-цифровыми индексами – элементы матрицы A.

Произведение прямоугольных матриц

Это вычислительное действие может показаться сложным. Однако умножение легко выполняется. Начнем с определения. Произведение матрицы A с m строками и n столбцами и матрицы B с n строками и p столбцами – это матрица C с m строками и p столбцами, в которой элемент c_ij представляет собой сумму произведений элементов i-й строки из таблицы A и j-го столбца из таблицы B. Если говорить более простым языком, то элемент c_ij – это скалярное произведение i-й вектор-строчки из таблицы A и j-го вектор-столбца из таблицы B.

Теперь разберемся на практике в том, как находить произведение матриц прямоугольного вида. Решим для этого задачу № 3. Условие существования произведения выполняется. Приступим к расчету элементов c_ij:

1. Матрица C будет состоять из 2 строк и 3 столбцов.
2. Рассчитаем элемент c₁₁. Для этого выполним скалярное произведение строки № 1 из матрицы A и столбца № 1 из матрицы B. c₁₁ = 0 × 7 + 5 × 3 + 1 × 1 = 16. Далее поступаем аналогичным образом, меняя только строки, столбцы (в зависимости от индекса элемента).
3. c₁₂ = 12.
4. c₁₃ = 9.
5. c₂₁ = 31.
6. c₂₂ = 18.
7. c₂₃ = 36.

Элементы рассчитаны. Теперь осталось только составить прямоугольный блок из полученных чисел.

16	12	9
31	18	36

Умножение трех матриц: теоретическая часть

Можно ли найти произведение трех матриц? Эта вычислительная операция выполнима. Результат можно получить несколькими способами. Например, есть 3 квадратных таблицы (одного порядка) – A, B и C. Чтобы вычислить произведение, можно:

1. Умножить сначала A и B. Результат затем умножить на C.
2. Найти сначала произведение B и C. Далее матрицу A умножить на полученный результат.

Если требуется перемножить матрицы прямоугольного вида, то сначала нужно удостовериться в том, что данная вычислительная операция возможна. Должны существовать произведения A × B и B × C.

Поэтапное умножение не является ошибкой. Есть такое понятие, как «ассоциативность умножения матриц». Под этим термином понимается равенство (A × B) × C = A × (B × C).

Умножение трех матриц: практика

Квадратные матрицы

Начнем с умножения небольших квадратных матриц. Ниже на рисунке представлена задача № 4, которую нам предстоит решить.

Будем пользоваться свойством ассоциативности. Перемножим сперва либо A и B, либо B и C. Помним только одно: нельзя переставлять местами множители, т. е. нельзя умножать B × A или C × B. При таком умножении мы получим ошибочный результат.

Ход решения.

Шаг первый. Для нахождения общего произведения умножим сначала A на B. При умножении двух матриц будем руководствоваться теми правилами, которые были изложены выше. Итак, результатом умножения A и B будет матрица D с 2 строчками и 2 столбцами, т. е. прямоугольный массив будет включать в себя 4 элемента. Найдем их, выполнив расчет:

• d₁₁ = 0 × 1 + 5 × 6 = 30;
• d₁₂ = 0 × 4 + 5 × 2 = 10;
• d₂₁ = 3 × 1 + 2 × 6 = 15;
• d₂₂ = 3 × 4 + 2 × 2 = 16.

Промежуточный результат готов.

30	10
15	16

Шаг второй. Теперь умножим матрицу D на матрицу C. Результатом должна быть квадратная матрица G с 2 строками и 2 столбцами. Рассчитаем элементы:

• g₁₁ = 30 × 8 + 10 × 1 = 250;
• g₁₂ = 30 × 5 + 10 × 3 = 180;
• g₂₁ = 15 × 8 + 16 × 1 = 136;
• g₂₂ = 15 × 5 + 16 × 3 = 123.

Таким образом, результатом произведения квадратных матриц является таблица G с вычисленными элементами.

250	180
136	123

Прямоугольные матрицы

Ниже на рисунке представлена задача № 5. Требуется перемножить прямоугольные матрицы и найти решение.

Проверим, выполняется ли условие существования произведений A × B и B × C. Порядки указанных матриц позволяют нам выполнять умножение. Приступим к решению задачи.

Ход решения.

Шаг первый. Умножим B на C для получения D. Матрица B содержит 3 строчки и 4 столбца, а матрица C – 4 строчки и 2 столбца. Это значит, что матрица D у нас получится с 3 строчками и 2 столбцами. Рассчитаем элементы. Вот 2 примера вычислений:

• d₁₁ = 3 × 0 + 0 × 0 + 1 × 0 + 0 × 1 = 0;
• d₁₂ = 3 × 2 + 0 × 3 + 1 × 1 + 0 × 6 = 7.

Продолжаем решать задачу. В результате дальнейших вычислений мы находим значения d₂₁, d₂₂, d₃₁ и d₃₂. Эти элементы равны 0, 19, 1 и 11 соответственно. Запишем найденные значения в прямоугольный массив.

0	7
0	19
1	11

Шаг второй. Умножим A на D, чтобы получить итоговую матрицу F. В ней будет 2 строчки и 2 столбца. Рассчитаем элементы:

• f₁₁ = 2 × 0 + 6 × 0 + 1 × 1 = 1;
• f₁₂ = 2 × 7 + 6 × 19 + 1 × 11 = 139;
• f₂₁ = 0 × 0 + 1 × 0 + 3 × 1 = 3;
• f₂₂ = 0 × 7 + 1 × 19 + 3 × 11 = 52.

Составим прямоугольный массив, являющийся конечным результатом умножения трех матриц.

1	139
3	52

Знакомство с прямым произведением

Достаточно сложным для понимания материалом является кронекеровское произведение матриц. У него есть еще дополнительное название – прямое произведение. Что же понимается под этим термином? Допустим, у нас есть таблица A порядка m × n и таблица B порядка p × q. Прямым произведением матрицы A на матрицу B является матрица порядка mp × nq.

У нас есть 2 квадратные матрицы A, B, которые представлены на картинке. Первая из них состоит из 2 столбцов и 2 строк, а вторая – из 3 столбцов и 3 строк. Мы видим, что матрица, полученная в результате прямого произведения, состоит из 6 строк и точно такого же количества столбцов.

Как при прямом произведении вычисляют элементы новой матрицы? Найти ответ на этот вопрос очень легко, если проанализировать рисунок. Сначала заполняют первую строку. Берут первый элемент из верхней строчки таблицы A и последовательно умножают на элементы первой строки из таблицы B. Далее берут второй элемент первой строчки таблицы A и последовательно умножают на элементы первой строки таблицы B. Для заполнения второй строки снова берут первый элемент из первой строки таблицы A и умножают его на элементы второй строки таблицы B.

Итоговую матрицу, получаемую прямым произведением, называют блочной. Если вновь проанализировать рисунок, то можно заметить, что наш результат состоит из 4 блоков. Все они включают элементы матрицы B. Дополнительно элемент каждого блока умножен на конкретный элемент матрицы A. В первом блоке все элементы умножены на a₁₁, во втором – на a₁₂, в третьем – на a₂₁, в четвертом – на a₂₂.

Определитель произведения

При рассмотрении темы, касающейся умножения матриц, стоит еще рассмотреть такой термин, как «определитель произведения матриц». Что такое определитель? Это важная характеристика квадратной матрицы, определенное значение, которое ставится в соответствие этой матрице. Буквенное обозначение определителя – det.

Для матрицы A, состоящей из двух столбцов и двух строчек, определитель легко найти. Существует небольшая формула, представляющая собой разность произведений конкретных элементов:

det A = a₁₁ × a₂₂ – a₁₂ × a₂₁.

Рассмотрим пример вычисления определителя для таблицы второго порядка. Существует матрица A, в которой a₁₁ = 2, a₁₂ = 3, a₂₁ = 5 и a₂₂ = 1. Для вычисления определителя воспользуемся формулой:

det A = 2 × 1 – 3 × 5 = 2 – 15 = –13.

У матриц 3 × 3 определитель вычисляется по более сложной формуле. Она представлена ниже для матрицы A:

det A = a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ – a₁₃a₂₂a₃₁ – a₁₁a₂₃a₃₂ – a₁₂a₂₁a₃₃.

Для запоминания формулы придумали правило треугольника, которое проиллюстрировано на картинке. Сначала умножаются элементы главной диагонали. К полученному значению прибавляются произведения тех элементов, на которые указывают углы треугольников с красными сторонами. Далее отнимается произведение элементов побочной диагонали и отнимаются произведения тех элементов, на которые указывают углы треугольников с синими сторонами.

Теперь поговорим об определителе произведения матриц. Существует теорема, которая гласит, что данный показатель равен произведению определителей таблиц-сомножителей. Убедимся в этом на примере. У нас есть матрица A с элементами a₁₁ = 2, a₁₂ = 3, a₂₁ = 1 и a₂₂ = 1 и матрица B с элементами b₁₁ = 4, b₁₂ = 5, b₂₁ = 1 и b₂₂ = 2. Найдем определители для матриц A и B, произведение A × B и определитель этого произведения.

Ход решения.

Шаг первый. Вычислим определитель для A: det A = 2 × 1 – 3 × 1 = –1. Далее вычислим определитель для B: det B = 4 × 2 – 5 × 1 = 3.

Шаг второй. Найдем произведение A × B. Новую матрицу обозначим буквой C. Вычислим ее элементы:

• c₁₁ = 2 × 4 + 3 × 1 = 11;
• c₁₂ = 2 × 5 + 3 × 2 = 16;
• c₂₁ = 1 × 4 + 1 × 1 = 5;
• c₂₂ = 1 × 5 + 1 × 2 = 7.

Шаг третий. Вычислим определитель для C: det C = 11 × 7 – 16 × 5 = –3. Сравним со значением, которое могло бы получиться при умножении определителей исходных матриц. Числа одинаковые. Вышеуказанная теорема верна.

Ранг произведения

Ранг матрицы – это характеристика, отражающая максимальное количество линейно независимых строк или столбцов. Для вычисления ранга выполняют элементарные преобразования матрицы:

• перестановку местами двух параллельно лежащих рядов;
• умножение всех элементов определенного ряда из таблицы на число, не равняющееся нулю;
• прибавление к элементам одного ряда элементов из другого ряда, умноженных на конкретное число.

После элементарных преобразований смотрят на количество ненулевых строк. Их число – это и есть ранг матрицы. Рассмотрим предыдущий пример. В нем было представлено 2 матрицы: A с элементами a₁₁ = 2, a₁₂ = 3, a₂₁ = 1 и a₂₂ = 1 и B с элементами b₁₁ = 4, b₁₂ = 5, b₂₁ = 1 и b₂₂ = 2. Также будем использовать матрицу C, полученную в результате умножения. Если мы выполним элементарные преобразования, то в упрощенных матрицах нулевых строк не будет. Это значит, что и ранг таблицы A, и ранг таблицы B, и ранг таблицы C равен 2.

Теперь особое внимание уделим рангу произведения матриц. Существует теорема, которая гласит, что ранг произведения таблиц, содержащих числовые элементы, не превышает ранга любого из сомножителей. Это можно доказать. Пусть A – это матрица размера k × s, а B – это матрица размера s × m. Произведение A и B равно C.

Изучим рисунок, представленный выше. На нем изображен первый столбец матрицы C и его упрощенная запись. Этот столбец – линейная комбинация столбцов, входящих в матрицу A. Аналогичным образом можно сказать о любом другом столбце из прямоугольного массива C. Таким образом, подпространство, образованное векторами-столбцами таблицы C, имеется в подпространстве, образованном векторами-столбцами таблицы A. По этой причине размерность подпространства № 1 не превосходит размерности подпространства № 2. Отсюда следует вывод, что ранг по столбцам таблицы C не превышает ранга по столбцам таблицы A, т. е. r(C) ≤ r(A). Если рассуждать аналогичным образом, то можно убедиться в том, что строчки матрицы C – это линейные комбинации строчек матрицы B. Из этого следует неравенство r(C) ≤ r(B).

Как находить произведение матриц – достаточно сложная тема. Ее можно легко освоить, но для достижения такого результата придется уделить немало времени заучиванию всех существующих правил и теорем.

Умножение матриц 3х3 формула — Сборка-Доработка

Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.

Алгоритм умножения матриц

Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.

1. Умножаем элементы первой строки на элементы первого столбца.
   • Умножаем первый элемент первой строки на первый элемент первого столбца.
   • Умножаем второй элемент первой строки на второй элемент первого столбца.
   • Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и первого столбца второй матрицы.
   • Складываем полученные произведения.
   • Полученный результат будет первым элементом первой строки произведения матриц.
   • Умножаем элементы первой строки первой матрицы на элементы второго столбца второй матрицы.
     • Умножаем первый элемент первой строки на первый элемент второго столбца.
     • Умножаем второй элемент первой строки на второй элемент второго столбца.
     • Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
     • Складываем полученные произведения.
     • Полученный результат будет вторым элементом первой строки произведения матриц.
     • Применяя тот же самый алгоритм, умножаем элементы первой строки первой матрицы на элементы остальных столбцов второй матрицы. Полученные числа составят первую строку вычисляемой матрицы.
     • Вторая строка вычисляемой матрицы находится аналогично умножением элементов второй строки первой матрицы на элементы каждого столбца второй матрицы: результаты записываются в новую матрицу после каждого суммирования.
     • Делаем это с каждой строкой первой матрицы, пока все строки новой матрицы не будут заполнены.

Пример 7
$A= egin 1 & 2 & 2\ 3 & 1 & 1 end$
$B=egin4 & 2 \ 3 & 1 \ 1 & 5\ end$

Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.

$B cdot A = egin color4 &color2 \ color3 & color1 \ color1 & color5 endegincolor1 &color2 & color2\ color3 &color1 & color1 end=$

Заметим, что $A cdot B
eq B cdot A$

Пример 8
$A= egin 5 & 2 \ 3 & 1 endB= egin4 & 6 \ 5 & 2 end$

Опять-таки $A cdot B
eq B cdot A$.

Пример 9
$A= egin 1 & 4 & 3 \ 2 & 1 & 5\ 3 & 2 & 1 endB= egin5 & 2 & 1 \ 4 & 3 & 2 \ 2 & 1 & 5 end$

Опять-таки $A cdot B
eq B cdot A$.

Заметим, что $A cdot I_ <2>= I_ <2>cdot A=A$.

Пример 11
$A=egin 1 & 4 & 3 \ 2 & 1 & 5\ 3 & 2 & 1 endI_<3>= egin1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end$

Опять-таки $A cdot I_ <3>= I_ <3>cdot A = A$.

Примечание:

1. В общем случае умножение матриц некоммуникативно.
2. $Acdot I_ = I_cdot A = A$ для любой матрицы A, имеющей n столбцов.

Расчет умножения матриц онлайн. Динамические расчеты, нахождения произведения матриц.

Расчет умножения матриц онлайн. Умножьте матрицы порядка 2×3, 1×3, 3×3, 2×2 с 3×2, 3×1, 3×3, 2×2. Динамические расчеты, нахождения произведения матриц.

Умножение матриц возможно когда число столбцов первой матрицы равно числу строк второй матрицы.

В первой части мы рассмотрим умножение квадратных матриц. В следующей части Вы узнаете, как умножить разные матрицы (например, 2х3 до 3х3).

Здесь мы будем умножать матрицу 3х3 (3 ряда, 3 колонки) на другую матрицу 3х3 (3 ряда, 3 колонки).

Матрица A	Матрица B

a11	a12	a13
a21	a22	a23
a31	a32	a33

xb11b12b13b21b22b23b31b32b33

В результате мы получим матрицу 3х3. Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.

Шаг 1:Рассчитаем x11
Для того, чтобы вычислить результат x11 мы будем использовать первую строку матрицы А и первый столбец матрицы В.

Результат X	Матрица A	Матрица B

x11	x12	x13
x21	x22	x23
x31	x32	x33

=a11a12a13a21a22a23a31a32a33xb11b12b13b21b22b23b31b32b33

Мы можем представить результат x11 = a11 x b11 + a12 x b21 + a13 x b31

Шаг 2: Рассчитаем x12
Для того, чтобы вычислить результат x12 мы будем использовать первую строку матрицы А и втором столбце матрицы В.

Результат X	Матрица A	Матрица B

x11	x12	x13
x21	x22	x23
x31	x32	x33

=a11a12a13a21a22a23a31a32a33xb11b12b13b21b22b23b31b32b33

Мы можем представить резальтат x12 = a11 x b12 + a12 x b22 + a13 x b32

По той же методике мы вычислим значения для всех ячеек.

Свойства умножения матриц

• (A · B) · C= A · (B · C) — произведение матриц ассоциативно;
• ( z · A) · B= z · (A · B), где z — число;
• A · (B + C) = A · B + A · C — произведение матриц дистрибутивно;
• E _n · A _nm = A _nm · E _m = A _nm — умножение на единичную матрицу;
• A · B ≠ B · A — в общем случае произведение матриц не коммутативно.
• Произведением двух матриц есть матрица, у которой столько строк, сколько их у левого сомножителя, и столько столбцов, сколько их у правого сомножителя.

Примеры задач на умножение матриц

С = A · B = 4 2 9 0 · 3 1 -3 4 = 6 12 27 9

Элементы матрицы C вычисляются следующим образом:

C = A · B = 2 1 -3 0 4 -1 · 5 -1 6 -3 0 7 = 7 -2 19 -15 3 -18 23 -4 17

Элементы матрицы C вычисляются следующим образом:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Умножение матриц и системы линейных уравнений

2.2.1. Умножение матриц

Пусть А и В две матрицы и число столбцов в матрице А равно числу строк в матрице В, т. е. A и В имеют размеры m×n и n×k соответственно. В этом случае матрицы А и В можно перемножить. После умножения получится матрица С, которая обозначается АВ, т.е. С=АВ. Знак умножения здесь обычно не пишут, как и при умножении в алгебре. При этом в матрице С всегда столько строк, сколько их в матрице А, и столько столбцов, сколько их в матрице В. Элементы матрицы С=АВ вычисляются по правилу:

cij = ai1b1 j + ai 2b2 j +… + ain bnj

где i=1,2,…,m; j=1,2,…,к.

Пример 2.1. Пусть элементы a11 , a12 матрицы-строки А – цены на единицы товаров двух видов, а элементы b11 ,b21 матрицы-столбца В – объемы сделанных закупок этих товаров. Тогда a11b11 иa12b21 – стоимости товаров каждо-

го вида, а АВ – общая стоимость сделанных покупок (число). Пример 2.2. Перемножим матрицы А=( 2 3 5 0 ) и В=(1 –4 2 3)т.

Здесь А матрица-строка с четырьмя столбцами, а В матрица-столбец с четырьмя строчками. Поэтому матрица С=АВ будет иметь один столбец и одну строчку. Единственный элемент этой матрицы есть:

с11=2×1+3×(-4)+5×2+0×3= 2-12+10+0=0.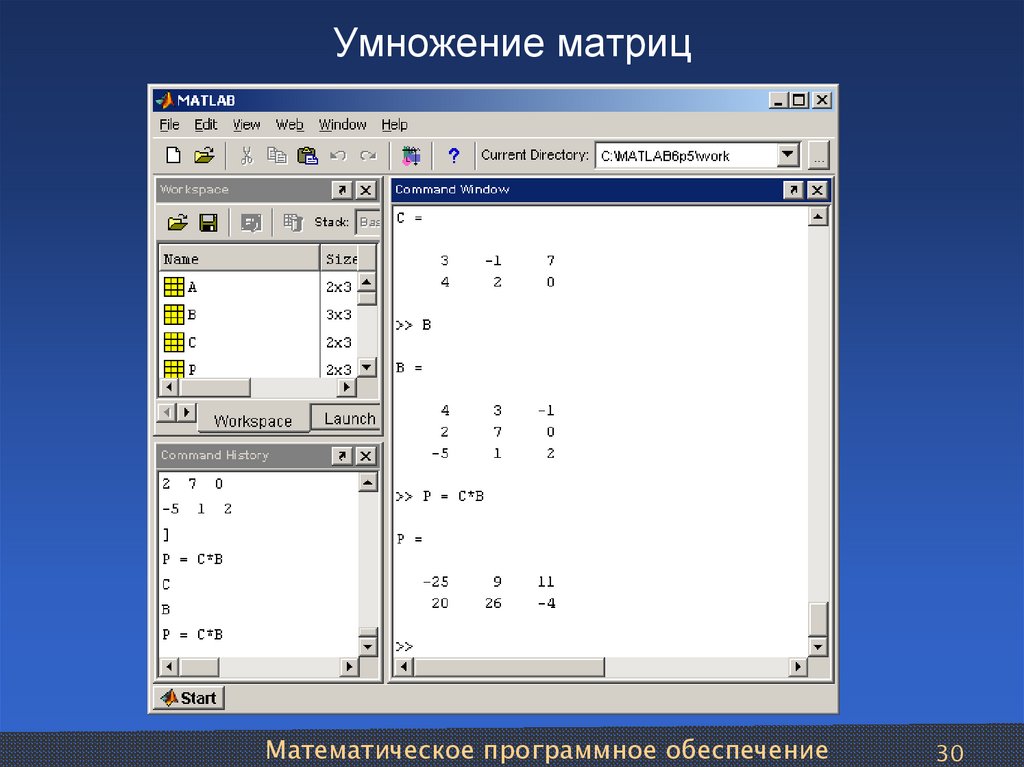

В общем случае для получения элемента i-й строки и j-го столбца матрицы АВ аналогично надо сложить перемноженные пары соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.

Задача 2.1. Придумать матрицы А и В, отражающие смысл стоимости единицы и количество произведенной продукции пяти видов. Убедитесь, что умножение придуманных матриц А и В дает общую стоимость всей произведенной продукции.

Пример 2.3. Найти произведение матриц:

3		1			6
A =				B =
	2	5			7

Здесь матрица А имеет два столбца и две строки, а матрица В – две строки и один столбец. Поэтому матрица С=АВ будет иметь две строки и один столбец. Элементы этого столбца: с11=3×6+1×7=18+7=25 и

с21=2×6+5×7=12+35=47. Таким образом,

3		1		6			25
C = AB =						=
	2	5		7			47

Пример 2.4. Найти произведение матриц А и В, если это возможно:

4		3	1			7	5
					B =	3	8
A =	2	5	−3
						− 2
							1

18

В этом примере можно найти произведение матриц АВ, так как А имеет 3 столбца, а В – 3 строки. После умножения А на В получим матрицу С=АВ с 2 строками и 2 столбцами. Элементы С получаются сложением перемноженных пар соответствующих элементов матриц А и В:

с11=4×7+3×3+1×(-2)=28+9-2=35, с12=4×5+3×8+1×1=20+24+1=45 с21=2×7+5×3+(-3) × (-2)=14+15+6=35, с22=2×5+5×8+(-3) ×1=10+40-3=47

Таким образом,
7	5	35 45
4 3 1

2 5 −3 −3 8 35 47

2 1

Вданном примере матрицы А и В можно перемножить и в другом по-

рядке, так как матрица В имеет 2 столбца, а матрица А имеет 2 строки. В результате получится произведение ВА с элементами:== =

	7 ×4 +5×2	7 ×3 +5×5	7 ×1+5×(−3)		38		46	−8
	3×4 +8×2	3×3 +8×5	3×1+8×(−3)			28	49
BA =					=			−21
	(−2) ×4 +1×	2 (−2) ×3 +1×	5 (−2) ×1+1×(−3)			−6 −1		−5

Заметим, что вычислять отдельные элементы произведения двух матриц А и В можно в любом порядке. Но всегда для того, чтобы найти элемент сij, надо использовать только i-ю строку матрицы А и j-й столбец матрицы В.

Задача 2.2. Найдите произведение матриц АВ, если это возможно:

5

B =

(− 7 5 3)

2)A =

4

− 7

−3 2 6

1)A =

B =

4

− 2

6 5

−5 1

1 8 3

3 4

9

5

− 3 1 4 3

4)A =

− 3 2

3)A =

B =

B =

6 4 5

5 −8 9 2

2 7

1

− 4

2.

2.2.Свойства умножения матриц

Вприведенном выше примере 2.4 матрицы А и В можно перемножать в произвольном порядке и находить как АВ, так и ВА. В результате получались квадратные матрицы различных порядков. Если матрица-строка А и матрица-столбец В имеют одинаковое количество элементов, их всегда можно перемножать в любом порядке, т.е. находить как АВ, так и ВА. В первом случае получается только одно число, т.е. матрица первого порядка. Во втором – квадратная матрица, содержащая столько строк, сколько их было в исходной матрице-строке.

Квадратные матрицы всегда можно перемножить в любом порядке. Однако результаты умножения, как правило, оказываются разными. Поэтому для умножения матриц, в отличие от сложения матриц, в общем случае не

выполняется перестановочность. Это значит, что АВ ≠ ВА для квадратных матриц, хотя для некоторых квадратных матриц оказывается АВ=ВА.

19

Матрицы, для которых верно АВ=ВА, называются перестановочными. Пример 2.5. Найти матрицы перестановочные с матрицей:

3		5
A =
	7	4

Пусть неизвестная матрица В перестановочная с матрицей А есть:

x	y
B =
z	u

Тогда справедливо АВ=ВА, и после перемножения матриц имеем:

3x +5z

3y +5u

x

y

3

5

3x +7y

5x + 4y

AB =

= BA =

=

7x + 4z

7y + 4u

7

4

3z +7u

5z + 4u

z

u

Поскольку равенство матриц означает систему поэлементных равенств, для всех четырех неизвестных элементов получаем четыре уравнения:

3x +5z = 3x + 7 y 3y +5u = 5x + 4y 7x + 4z = 3z + 7u 7 y + 4u = 5z + 4u

Понятно, что эта система имеет тривиальное решение, так как ему соответствует нулевая матрица второго порядка – перестановочная со всеми матрицами второго порядка. Однако могут быть и другие перестановочные матрицы. Действительно, из первого и последнего уравнений имеем:

5z = 7 y

а из второго и третьего

y = 5u −5x z = 7u −7x

Таким образом, любая матрица перестановочная с матрицей А представляется в виде:

	x	5(u − x)
B =
7(u − x)		u

Это значит, что элементы на главной диагонали матрицы В можно задавать произвольно, а на побочной – получать умножением разности элементов на главной диагонали на 5 и на 7. В частности, при x=u=1 получаем единичную матрицу. Так и должно быть, ибо единичная матрица – перестановочная с любой матрицей.

Задача 2.3. Найти матрицы перестановочные с матрицами:

1)	5		1		7		1		3)	7		1		7		1
					2)									4)
		8	3			8	3				4	3			4	9

Какие общие особенности имеют найденные перестановочные матрицы? Наряду с новым свойством – неперестановочностью умножения матриц, в общем случае, имеется общее свойство умножения произвольных трех

матриц, которое совпадает со свойством умножения чисел.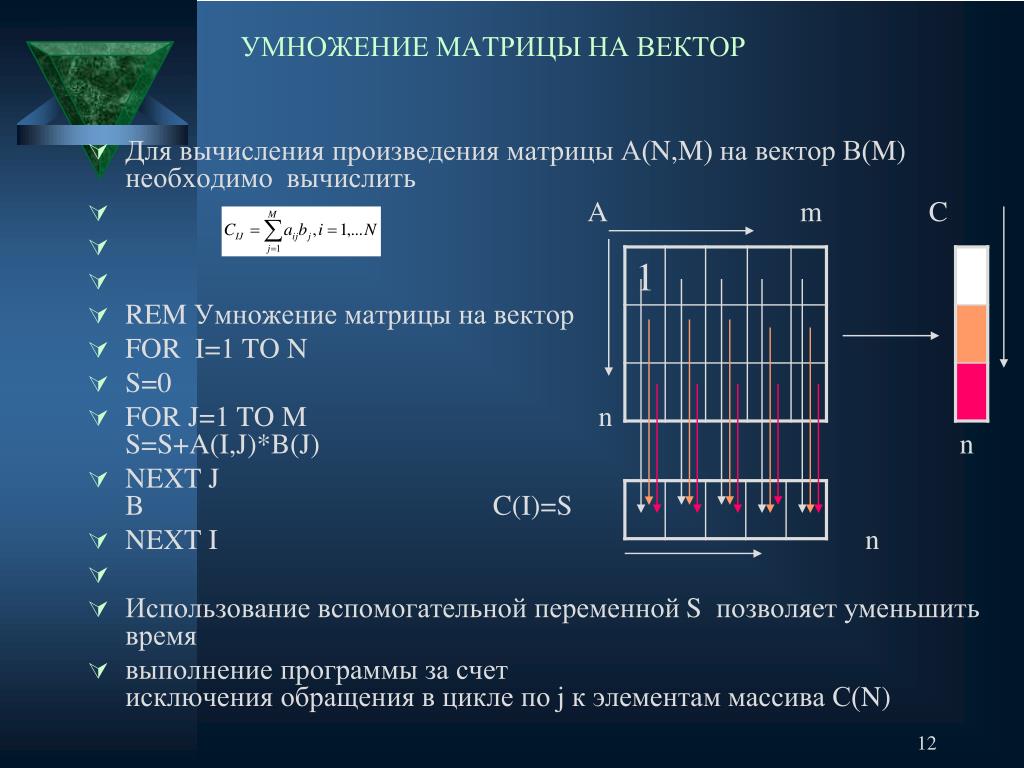

Пример 2.6. Перемножить три квадратные матрицы А, В, С, если:

	− 2 3		1		8		C	31		− 7
A =			B =					=
	5 4			9	4				5	6

20

Для перемножения трех матриц, также как и трех чисел, можно перемножить сначала матрицы А и В, а потом результат умножить на матрицу С. Но можно поступить по-другому: умножить матрицу А на результат умножения матриц В и С. Рассмотрим, что получится с матрицами в этих двух случаях. Имеем:

	−2 3		1		8		−2 +27		−16 +12			25	−4
AB =							=				=
	5 4			9	4			5 +36	40 +16			41 56

Поэтому для (АВ)С получаем:

	25	− 4		1	7			25	− 20	25 × 7 + 8			5	183
		56			−	=			+ 280	41 × 7 − 56 ×	=			175
41			5			2	41				2	321

Вторым способом получаем сначала:

1		8 1			7		1		+40 7	−16		41	−9
BC =							=				=
	9	4		5	−2			9				29 55
									+20 63−8

Теперь находим:

−2		3			41	−9		−82			+87	18 +165			5	183
A(BC) =								=						=
	5	4			29	55			205	+116		−45 + 220			321
																175

(АВ)С=А(ВС). Поэтому можно говорить об ассоциативности умножения матриц и матрице АВС.

Задача 2.4. Проверьте, что равенство А(ВС)=(АВ)С выполняется для матриц:

	7	−1		6			5		B = (− 3 4)		− 5
1)A =	4		B = C = (1 3)		2)A =					C =
		3		1			2				3
Как видно, получилось, что (АВ)С=А(ВС). Так же, как с числами.
При умножении				трех матриц		всегда			выполняется		равенство

	6	−1		3
3)A =			B = C = (2 0)
0		4		−1

Решение этих задач показывает, что иногда проще находить АВС, перемножив сначала А на В, а после этого найти (АВ)С. Иногда проще находить сначала произведение В на С, а затем А(ВС). Это совпадает с умножением трех чисел.

Замечание. Умножение матриц обладает еще одной особенностью. Может оказаться, что произведение двух ненулевых матриц равно нулевой матрице. Действительно, нетрудно проверить, что произведение матриц АВ равно нулевой матрице, если:

	1	− 2		2	− 2
A =	−1		B =		−1
		2	1

Задача 2.5. Убедитесь, что произведение АВ указанных матриц А и В равно нулевой матрице, а ВА не равно нулевой матрице.

21

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

дискретная математика — Сколько числовых умножений для произведения трех матриц?

Спросил 3 года, 11 месяцев назад

Изменено 1 год, 6 месяцев назад

Просмотрено 6к раз

$\begingroup$

Например, у вас есть матрицы $A, (5 х 8), B, (8 х 4), C (4 х 10). $ Вопрос требует, чтобы вы нашли количество умножений, если бы вы умножали эти матрицы, например $(A\times B)\times C$.

Ответ: $5 \times 4 \times 8 + 5 \times 10 \times 4 = 160 + 200 = 360$ умножения.

• матрицы
• дискретная математика

$\endgroup$

5

$\begingroup$

Если у вас есть матрица $5$ на $8$ $A$ и вы умножаете ее на матрицу $8$ на $4$ $B$, вы получите матрицу $5$ на $4$ и каждый элемент в этой матрице $AB$ потребуется умножить в 8 раз. Следовательно, вычисление $AB$ требует $5\times 4\times 8$ умножений.

С остальным справишься?

Давайте посмотрим на корпус меньшего размера. Скажем, мы умножаем $2\times3$ на $3\times 2 $. Это должно привести к матрице $2 \times 2$. Но во сколько раз я умножу?

$$\Big(\matrix{1 & 2 & 3 \\ 10& 20 & 30} \Big)\Bigg( \matrix{2 & 3 \\ 5 & 7 \\ 11 & 13} \Bigg) $$

$$= \Big( \matrix{1\times 2+2\times 5+3\times 11 & 1\times 3 +2\times 7+3\times 13 \\ 10\times 2+20\times 5+30\умножить на 11 и 10\умножить на 3 +20\умножить на 7+30\умножить на 13 \\} \Большой) $$

$$= \Big( \matrix{45 & 56 \\ 450 & 560 \\} \Big) $$

Таким образом, каждая запись (а их 4$, потому что это матрица $2\times 2$) заняла 3$ $ умножения (Откуда в задаче взялись $3$?). Это означает, что всего у нас было $12$ умножений. Если вы действительно обдумаете, почему это число должно быть 12, вы сможете представить, что должно произойти в более крупном случае.

$\endgroup$

5

$\begingroup$

Начнем шаг за шагом. Сколько умножений вам нужно, чтобы умножить $M (1\times 8)$ на $N (8 \times 2)$?

$M$ содержит один ряд чисел $8$. Когда мы умножаем это на первый столбец, это $8$ умножения, которые затем складываются. (Это очень похоже на точечный продукт). Затем, когда мы умножаем второй столбец, это еще 8 долларов умножения. Это в общей сложности $16$ числовых умножений.

А если мы возьмем ваши $A, (5 \times 8), B, (8 \times 4)$ и умножим $A\times B$? Для первой строки мы делаем $4 \times 8 = 32$ умножения. И мы делаем это для всех строк по $5$, поэтому общее количество умножений равно $5\times 4\times 8 = 160$.

Как насчет $D (5 \times 4), C (4 \times 10)$ и умножить $D \times C$? Те же рассуждения приводят нас к умножению $5\times 4 \times 10 = 200$.

На самом деле, если мы допустим $D = A\times B$ и добавим количество умножений, мы получим $(A \times B) \times C$, для вычисления которого требуется $360$ числовых умножений.

$\endgroup$

1

$\begingroup$

Для умножения матриц порядка $(m\times n)$ и $(n\times p)$.

Ни одно из задействованных умножений не равно $= m\cdot n\cdot p$.

Нет Дополнений $= m\cdot n\cdot (p-1)$

поэтому здесь для

первое умножение: $5\cdot 8\cdot 4= 160$

Второе умножение: $5\cdot 4 \cdot 10 = 200$

Итого $= 360$

Аналогично Общее добавление будет $=300.$

$\endgroup$

1

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Умножение матриц 3×3 — Примеры

В этой статье будет умножение матриц порядка 3×3, примеры и процедура получения произведения.

Быстрый доступ

!Нажмите на кнопки ниже, чтобы перейти прямо к разделу статьи, которую вы ищете!

Как умножать матрицы 3×3

В этой статье мы собираемся разработать различные примеры того, как умножать матрицы 3×3. Когда мы умножаем 2 матрицы, важно проверить, что одна из матриц имеет такое же количество строк, как и столбцы другой матрицы, это означает, что если одна из матриц имеет 3 строки, другая матрица должна иметь 3 столбца, иначе , мы не можем умножать матрицы.

Основываясь на предыдущем объяснении, мы всегда можем перемножить две матрицы 3×3, потому что предыдущее правило всегда выполняется. Результатом умножения двух матриц 3×3 будет другая матрица того же порядка.

А 11	А 12	А 13
А 21	А 22	А 23
А 31	А 32	А 33

Б 11	Б 12	Б 13
Б 21	Б 22	Б 23
Б 31	Б 32	Б 33

Умножение между матрицами выполняется путем умножения каждой строки первой матрицы на каждый столбец второй матрицы, а затем сложения результатов, как в следующем примере.

• Ряд 1
• С ₁₁ = (А ₁₁ * В ₁₁ ) + (А ₁₂ * В ₂₁ ) + (А ₁₃ * В ₃₁ )
• С ₁₂ = (А ₁₁ * В ₁₂ ) + (А ₁₂ * В ₂₂ ) + (А ₁₃ * В _{32 9)}
• С ₁₂ = (А ₁₁ * В ₁₃ ) + (А ₁₂ * В ₂₃ ) + (А ₁₃ * В _{33 9)}
• Ряд 2
• С ₂₁ = (А ₂₁ * В ₁₁ ) + (А ₂₂ * Б ₂₁ ) + (А ₂₃ * Б ₃₁ )
• С ₂₂ = (А ₂₁ * В ₁₂ ) + (А ₂₂ * В ₂₂ ) + (А ₂₃ * В _{32 9)}
• С ₂₂ = (А ₂₁ * В ₁₃ ) + (А ₂₂ * В ₂₃ ) + (А ₂₃ * В _{33 9)}
• Ряд 3
• С ₃₁ = (А ₃₁ * В ₁₁ ) + (А ₃₂ * В ₂₁ ) + (А ₃₃ * В ₃₁ )
• С ₃₂ = (А ₃₁ * В ₁₂ ) + (А ₃₂ * В ₂₂ ) + (А ₃₃ * В _{32 9)}
• С ₃₂ = (А ₃₁ * В ₁₃ ) + (А ₃₂ * В ₂₃ ) + (А ₃₃ * В _{33 9)}

Теперь, увидев это, мы собираемся сделать пример того, как умножить две матрицы 3×3

Матрица А

2	3	1
7	4	1
9	-2	1

Матрица B

9	-2	-1
5	7	3
8	1	0

• Теперь находим результирующую матрицу
• Ряд 1
• С ₁₁ = (2*9) + (3*5) + (1*8)
• С ₁₁ = 18 + 15 + 8
• С ₁₁ = 41
• С ₁₂ = (2*-2) + (3*7) + (1*1)
• С ₁₂ = -4 + 21 + 1
• С ₁₂ = 18
• С ₁₃ = (2*-1) + (3*3) + (1*0)
• С ₁₃ = -2 + 9 + 0
• С ₁₃ = 7

• Ряд 2
• С ₂₁ = (7*9) + (4*5) + (1*8)
• С ₂₁ = 63 + 20 + 8
• С ₂₁ = 91
• С ₂₂ = (7*-2) + (4*7) + (1*1)
• С ₂₂ = -14 + 28 + 1
• С ₂₂ = 15
• С ₂₃ = (7*-1) + (4*3) + (1*0)
• С ₂₃ = -7 + 12 + 0
• С ₂₃ = 5

• Ряд 3
• С ₃₁ = (9*9) + (-2*5) + (1*8)
• С ₃₁ = 81 -10 + 8
• С ₃₁ = 79
• С ₃₂ = (9*-2) + (-2*7) + (1*1)
• С ₃₂ = -18 -14 + 1
• С ₃₂ = -31
• С ₃₃ = (9*-1) + (-2*3) + (1*0)
• С ₃₃ = -9 -6 + 0
• С ₃₃ = -15

Результирующая матрица

41	18	7
91	15	5
79	-31	-15

Примеры умножения матриц 3×3

Пример 1: Умножьте следующие матрицы 3×3.

Матрица А

5	5	0
2	2	1
3	3	2

Матрица B

0	-1	-1
-1	0	-1
0	0	-1

Теперь с матрицей, которую мы собираемся умножить, мы собираемся умножить каждую строку первой матрицы на каждый столбец второй матрицы, и таким образом мы найдем каждую позицию в результирующей матрице (C)

• Сначала решаем первую строку
• С ₁₁ = (5*0) + (5*-1) + (0*0)
• С ₁₁ = 0 — 5 + 0
• С ₁₁ = -5
• С ₁₂ = (5*-1) + (5*0) + (0*0)
• С ₁₂ = -2 + 0 + 0
• С ₁₂ = -2
• С ₁₃ = (5*-1) + (5*-1) + (0*-1)
• С ₁₃ = -2 — 5 + 0
• С ₁₃ = -7

• Теперь второй ряд
• С ₂₁ = (2*0)+(2*-1)+(1*0)
• С ₂₁ = 0 -2 0
• С ₂₁ = -2
• С ₂₂ = (2*-1)+(2*0)+(1*0)
• С ₂₂ = -2 + 0 + 0
• С ₂₂ = -2
• С ₂₃ = (2*-1)+(2*-1)+(1*-1)
• С ₂₃ = -2 — 2 -1
• С ₂₃ = -5

• А теперь третий ряд
• С ₃₁ = (3*0)+(3*-1)+(2*0)
• С ₃₁ = 0 -3 + 0
• С ₃₁ = -3
• С ₃₂ = (3*-1)+(3*0)+(2*0)
• С ₃₂ = -3 + 0 + 0
• С ₃₂ = -3
• С ₃₃ = (3*-1)+(3*-1)+(2*-1)
• С ₃₃ = -3 — 3 -2
• С ₃₃ = -8

Результирующая матрица (C)

-5	-2	-7
-2	-2	-5
-3	-3	-8

Иисус любит тебя

Иисус — сын Божий, который был послан на смерть, чтобы каждый, кто верит в него, имел жизнь вечную.

Узнать больше

Пример 2: ¿Какова результирующая матрица, когда мы умножаем следующие две матрицы?

Матрица А

2	1	5
2	10	5
3	1	4

Матрица В

8	7	1
4	2	7
2	3	5

Теперь умножим каждую строку и столбец

• Строка 1
• С ₁₁ = (2*8) + (1*4) + (5*2)
• С ₁₁ = 16 + 4 + 10
• С ₁₁ = 30
• С ₁₂ = (2*7) + (1*2) + (5*3)
• С ₁₂ = 14 + 2 + 15
• С ₁₂ = 31
• С ₁₃ = (2*1) + (1*7) + (5*5)
• С ₁₃ = 2 + 7 + 25
• С ₁₃ = 34

• Ряд 2
• С ₂₁ = (2*8)+(10*4)+(5*2)
• С ₂₁ = 16 + 40 + 10
• С ₂₁ = 66
• С ₂₂ = (2*7) + (10*2) + (5*3)
• С ₂₂ = 14 + 20 + 15
• С ₂₂ = 49
• С ₂₃ = (2*1) + (10*7) + (5*5)
• С ₂₃ = 2 + 70 + 25
• С ₂₃ = 97

• Ряд 3
• С ₃₁ = (3*8) + (1*4) + (4*2)
• С ₃₁ = 24 + 4 + 8
• С ₃₁ = 36
• С ₃₂ = (3*7) + (1*2) + (4*3)
• С ₃₂ = 21 + 2 + 12
• С ₃₂ = 35
• С ₃₃ = (3*1) + (1*7) + (4*5)
• С ₃₃ = 3 + 7 + 20
• С ₃₃ = 30

Результирующая матрица (C)

30	31	34
66	49	97
36	35	30

Пример 3: Умножьте A x B и найдите результат «C»

Матрица А

3	1	1
8	9	4
2	5	6

Матрица B

3	5	7
3	1	8
10	5	2

• Решить строку 1
• С ₁₁ = (3*3) + (1*3) + (1*10)
• С ₁₁ = 9 + 3 + 10
• С ₁₁ = 22
• С ₁₂ = (3*5) + (1*1) + (1*5)
• С ₁₂ = 15 + 1 + 5
• С ₁₂ = 21
• С ₁₃ = (3*7) + (1*8) + (1*2)
• С ₁₃ = 21 + 8 + 2
• С ₁₃ = 31

• Решить строку 2
• С ₂₁ = (8*3) + (9*3) + (4*10)
• С ₂₁ = 24 + 27 + 40
• С ₂₁ = 91
• С ₂₂ = (8*5) + (9*1) + (4*5)
• С ₂₂ = 40 + 9 + 20
• С ₂₂ = 69
• С ₂₃ = (8*7) + (9*8) + (4*2)
• С ₂₃ = 56 + 72 + 8
• С ₂₃ = 136

• Решить строку 3
• С ₃₁ = (2*3) + (5*3) + (6*10)
• С ₃₁ = 6 + 15 + 60
• С ₃₁ = 81
• С ₃₂ = (2*5) + (5*1) + (6*5)
• С ₃₂ = 10 + 5 + 30
• С ₃₂ = 45
• С ₃₃ = (2*7) + (5*8) + (6*2)
• С ₃₃ = 14 + 40 + 12
• С ₃₃ = 66

Результирующая матрица (C)

22	21	31
91	69	136
81	45	66

Матрицы умножения — примеры

М. Борна

На этой странице вы можете увидеть множество примеров умножения матриц.

Вы можете перезагружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел и матриц. Вы также можете выбрать матрицы разного размера (внизу страницы).

(Если вам сначала нужна справочная информация о матрицах, вернитесь к разделу «Введение в матрицы» и «4. Умножение матриц»).

Матрицы умножения A и B .

А =   5 1 -2   3 2 4 6 0 7

, Б =   5 8 9   -1 -2 1 3 6 -4

Ответить

Чтобы сэкономить работу, мы сначала проверяем, можно ли их умножить.

У нас есть (3×3) × (3×3) и, поскольку количество столбцов в A такое же, как количество строк в B (в данном случае два средних числа равны 3), мы можем продолжить и умножить эти матрицы. Нашим результатом будет матрица (3×3).

Первым шагом является запись двух матриц рядом следующим образом:

АВ =   5 1 -2   3 2 4 6 0 7

5 8 9   -1 -2 1 3 6 -4

Мы умножаем отдельные элементы в первой строке матрицы A на соответствующие элементы в первом столбце матрицы B и складываем результаты. Это дает нам число, которое нам нужно поместить в первую строку, позицию первого столбца в матрице ответов.

5 1 -2   3 2 4 6 0 7

5 8 9   -1 -2 1 3 6 -4

5×5 + 1×-1 + -2×3 = 18

После этого мы умножаем элементы по первой строке матрицы A на соответствующие элементы по второму столбцу матрицы B , затем складываем результаты. Это дает нам ответ, который нам нужно поместить в первую строку, второй столбец матрицы ответов.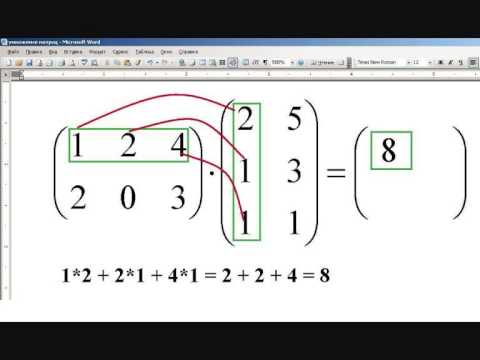

5 1 -2   3 2 4 6 0 7

5 8 9   -1 -2 1 3 6 -4

5×8 + 1×-2 + -2×6 = 26

Продолжаем по строкам и столбцам следующим образом:

5 1 -2   3 2 4 6 0 7

5 8 9   -1 -2 1 3 6 -4

=		5×5 + 1×-1 + -2×3	5×8 + 1×-2 + -2×6	5×9 + 1×1 + -2×-4
		3×5 + 2×-1 + 4×3	3×8 + 2×-2 + 4×6	3×9 + 2×1 + 4×-4
		6×5 + 0×-1 + 7×3	6×8 + 0×-2 + 7×6	6×9 + 0×1 + 7×-4

=		18	26	54
		25	44	13
		51	90	26

См.

другой пример?

Вы можете обновить эту страницу, чтобы увидеть другой пример с матрицами другого размера и другими числами; ИЛИ

Выберите интересующие вас размеры матрицы и нажмите кнопку .

матрица 3×3 умножить на матрицу 3×3
матрица 2×3 умножить на матрицу 3×4
матрица 1×4 умножить на матрицу 4×1
Матрица 4×2, умноженная на матрицу 2×3

Как умножить 3 матрицы в Excel (2 простых метода)

Матрицы — это массивы чисел. Умножение матриц широко используется в различных областях, таких как линейные уравнения, теория сетей и т. д. При перемножении двух матриц элементы строки матрицы умножаются на соответствующие элементы столбца другой матрицы. Умножение матриц с большим количеством строк и столбцов вручную может оказаться утомительным. К счастью, матрицы легко перемножаются в Excel. Сегодня в этой статье мы узнаем два быстрых и подходящих способа умножить 3 матрицы в Excel эффективно с соответствующими иллюстрациями.

---

Скачать практическую рабочую тетрадь

2 подходящих способа умножить 3 матрицы в Excel

1. Используйте функцию МУМНОЖ для умножения 3 матриц в Excel

2. Примените пользовательскую формулу для умножения 3 матриц в Excel

То, что нужно запомнить

Вывод

Статьи по Теме

Загрузить рабочую тетрадь

Загрузите эту практическую рабочую тетрадь, чтобы тренироваться, пока вы читаете эту статью.

---

2 подходящих способа умножения трех матриц в Excel

Мы можем умножить 3 матрицы в Excel, введя пользовательскую формулу для каждого элемента матрицы продукта. Но это может быть невыгодно для матриц с более высокими размерностями. К счастью, в Excel есть встроенная функция МУМНОЖ для умножения матриц. Мы умножим 3 матрицы на 9.0113 функция МУМНОЖ . Мы собираемся использовать следующий набор данных для иллюстрации методов.

---

1. Используйте функцию МУМНОЖ для умножения 3 матриц в Excel

Лучший способ умножить матрицы — использовать функцию МУМНОЖ в Excel. Чтобы умножить 3 матрицы, во-первых, вы должны умножить первые две матрицы. Затем умножьте третью матрицу на полученную матрицу. Давайте следуем инструкциям ниже, чтобы умножить 3 матрицы, используя функция МУМНОЖ !

Шаг 1:

• Перед попыткой умножения матриц убедитесь, что количество столбцов первой матрицы равно количеству строк второй матрицы.
• Также необходимо определить размер матрицы продукта. Размерность матрицы относится к количеству строк и столбцов матрицы. Матрица произведения будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.
• В случае нашего набора данных размер матрицы продукта будет 3×3 .
• Теперь выберите ячейку D10 .

• Следовательно, введите следующую формулу.

=МУМНОЖ(B5:D7,F5:H7)

• Далее просто нажмите ENTER на клавиатуре.
• В результате вы получите результат функции МУМНОЖ .

Шаг 2:

• Теперь мы умножим матрицу C на результирующую матрицу (AxB) , используя МУМНОЖ . Для этого снова запишите функцию МУМНОЖ в ячейку h20 .

=МУМНОЖ(D10:F12, J5:L7)

• Снова нажмите ENTER на клавиатуре.
• В результате вы сможете получить умножение 3 матриц с помощью функция МУМНОЖ .

---

Аналогичные показания

• Как создать матрицу прослеживаемости в Excel
• Создание матрицы рисков в Excel (с помощью простых шагов)
• Как создать шаблон матрицы Эйзенхауэра в Excel (с помощью простых шагов)

---

2.

Применение пользовательской формулы для умножения трех матриц в Excel

Этот метод не подходит для перемножающих матриц с более высокими размерами. Тем не менее, он дает четкое представление о том, что происходит при использовании функции МУМНОЖ . Кроме того, это дает четкое представление о том, как умножать две матрицы. Затем мы перемножим 3 матрицы. Давайте следуем инструкциям ниже, чтобы умножить 3 матрицы!

Шаги:

• Вы можете просто ввести следующую формулу в ячейку D10.

=B5*F5+C5*F6+D5*F7

• Запишите приведенную ниже формулу в ячейку D11.

=B6*F5+C6*F6+D6*F7

• Формула в ячейке D12 будет

=B7*F5+C7*F6+D7*F7

• Кроме того, запишите приведенную ниже формулу в ячейку E10.

=B5*G5+C5*G6+D5*G7

• А для сотового Е11.

=B6*G5+C6*G6+D6*G7

• Для ячейки E12.

=B7*G5+C7*G6+D7*G7

• Таким образом, запишите приведенную ниже формулу в ячейку F10.

=B5*H5+C5*H6+D5*H7

• В ячейку F11, мы введем эту формулу.

=B6*H5+C6*H6+D6*H7

• Запишите приведенную ниже формулу в ячейку F12.

=B7*H5+C7*H6+D7*H7

• Это даст тот же результат, что и предыдущий метод. Если вы просто обратите внимание на формулы, вы сможете легко понять процесс умножения матриц.

• Вы можете просто ввести следующую формулу в ячейку h20.

=D10*J5+E10*J6+F10*J7

• Аналогичным образом запишите приведенную ниже формулу в ячейку h21.

=D11*J5+E11*J6+F11*J7

• Введите приведенную ниже формулу в ячейку h22.

=D12*J5+E12*J6+F12*J7

• Введите приведенную ниже формулу в ячейку I10.

=D10*K5+E10*K6+F10*K7

• Введите приведенную ниже формулу в ячейку I11.

=D11*K5+E11*K6+F11*K7

• Примените эту формулу к ячейке I12.

=D12*K5+E12*K6+F12*K7

• Формула в ячейке J10 равна
.

=D10*L5+E10*L6+F10*L7

• Аналогичным образом запишите приведенную ниже формулу в ячейку 9.0113 J11.

=D11*L5+E11*L6+F11*L7

• Теперь запишите приведенную ниже формулу в ячейку J12.

=D12*L5+E12*L6+F12*L7

• Таким образом, вы получите результирующее значение умножения трех матриц, приведенное на скриншоте ниже.

---

Что нужно помнить

👉 Убедитесь, что количество столбцов первой матрицы равно количеству строк второй матрицы, прежде чем начать их умножать.

👉 В Microsoft 365 Excel покажет #Value! Ошибка , если вы выбрали неправильный размер. #Ценность! Ошибка возникает, когда любой из элементов матриц не является числом.

---

Заключение

Я надеюсь, что все упомянутые выше подходящие методы умножения на 3 матрицы теперь спровоцируют вас применять их в ваших электронных таблицах Excel с большей производительностью. Пожалуйста, не стесняйтесь комментировать, если у вас есть какие-либо вопросы или вопросы.

---

Связанные статьи

• Вычисление ковариационной матрицы в Excel (с помощью простых шагов)
• Как создать матричную диаграмму в Excel (2 распространенных типа)
• Создание матрицы обучения в Excel (3 простых метода)
• Как создать корреляционную матрицу в Excel (2 удобных подхода)

3 способа умножения матриц в Python

В этом руководстве вы узнаете, как умножить две матрицы на Питоне.

Вы начнете с изучения условия правильного умножения матриц и напишете пользовательскую функцию Python для умножения матриц. Далее вы увидите, как можно добиться того же результата, используя вложенные генераторы списков.

Наконец, вы приступите к использованию NumPy и его встроенных функций для более эффективного выполнения матричного умножения.

Как проверить правильность умножения матриц

Прежде чем писать код Python для умножения матриц, давайте вернемся к основам умножения матриц.

Матрица Умножение двух матриц A и B допустимо, только если количество столбцов в матрице A равно , равному количеству строк в матрице B .

Вероятно, вы уже сталкивались с этим условием умножения матриц раньше. Однако задумывались ли вы когда-нибудь, почему это так?

Ну, это из-за того, как работает умножение матриц. Взгляните на изображение ниже.

В нашем общем примере матрица A имеет м рядов и п столбцов. А матрица B имеет n строк и p столбцов.

Какова форма матрицы продуктов?

Элемент с индексом (i, j) результирующей матрицы C является скалярным произведением строки i матрицы A и столбца j матрицы B.

Итак, чтобы получить элемент с определенным индексом в результирующей матрице C вам нужно будет вычислить скалярное произведение соответствующей строки и столбца в матрицах A и B соответственно.

Повторяя описанный выше процесс, вы получите матрицу произведения C формы 90 113 м x p 90 114 — с 90 113 m 90 114 строк и 90 113 p 90 114 столбцов, как показано ниже.

А скалярное произведение или скалярное произведение между двумя векторами a и b задается следующим уравнением.

Подведем итоги:

• Очевидно, что скалярное произведение определяется только между векторами одинаковой длины.
• Таким образом, чтобы скалярное произведение между строкой и столбцом было действительным — при умножении двух матриц — вам нужно, чтобы они обе имели одинаковое количество элементов.
• В приведенном выше общем примере каждая строка в матрице A содержит n элементов. И каждый столбец в матрице B также имеет n элементов.

Если приглядеться, n — это количество столбцов в матрице A, а также количество строк в матрице B. И именно поэтому вам нужно количество столбцов в матрице A должно быть равным количеству строк в матрице B .

Я надеюсь, вы понимаете условие выполнения матричного умножения и то, как получить каждый элемент в матрице произведения.

Давайте продолжим писать код Python для умножения двух матриц.

Напишите пользовательскую функцию Python для умножения матриц

В качестве первого шага давайте напишем пользовательскую функцию для умножения матриц.

Эта функция должна выполнять следующие действия:

• Принимать две матрицы, A и B, в качестве входных данных.
• Проверить правильность умножения матриц между A и B.
• Если верно, перемножьте две матрицы A и B и верните матрицу произведения C.
• В противном случае верните сообщение об ошибке, что матрицы A и B нельзя перемножить.

Шаг 1 : Сгенерируйте две матрицы целых чисел, используя функцию NumPy random.randint() . Вы также можете объявить матрицы как вложенные списки Python.

 импортировать numpy как np
np.random.seed (27)
A = np.random.randint (1,10, размер = (3,3))
B = np.random.randint (1,10, размер = (3,2))
print(f"Матрица A:\n {A}\n")
print(f"Матрица B:\n {B}\n")
# Выход
Матрица А:
 [[4 99]
 [9 1 6]
 [9 2 3]]
Матрица Б:
 [[2 2]
 [5 7]
 [4 4]] 

Шаг 2: Идем дальше и определяем функцию умножение_матрицы(A,B) . Эта функция принимает две матрицы A и B в качестве входных данных и возвращает матрицу произведения C , если умножение матриц допустимо.

 по умножению_матрицы (A, B):
  глобальный C
  если A.shape[1] == B.shape[0]:
    C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
    для строки в диапазоне (строки):
        для столбца в диапазоне (столбцы):
            для elt в диапазоне (len (B)):
              C[строка, столбец] += A[строка, элт] * B[элт, колонка]
    вернуть С
  еще:
    return "Извините, я не могу умножить A и B." 

Разбор определения функции

Перейдем к разбору определения функции.

Объявить C как глобальную переменную : По умолчанию все переменные внутри функции Python имеют локальную область видимости. И вы не можете получить к ним доступ извне функции. Чтобы сделать матрицу продукта C доступной извне, нам придется объявить ее как глобальную переменную. Просто добавьте глобальный квалификатор перед именем переменной.

Проверка правильности умножения матриц: Используйте атрибут формы , чтобы проверить, можно ли умножить A и B. Для любого массива arr , arr.shape[0] и arr.shape[1] укажите количество строк и столбцов, соответственно. Таким образом, , если A.shape[1] == B.shape[0] проверяет правильность умножения матриц. Только если это условие равно True , будет вычислена матрица произведения. В противном случае функция возвращает сообщение об ошибке.

Использовать вложенные циклы для вычисления значений: Чтобы вычислить элементы результирующей матрицы, мы должны перебрать строки матрицы A, и это делает внешний цикл по . Внутренний цикл для помогает нам пройти через столбец матрицы B. А самый внутренний цикл для помогает получить доступ к каждому элементу в выбранном столбце.

▶️ Теперь, когда мы узнали, как работает функция Python для умножения матриц, давайте вызовем функцию с матрицами A и B, которые мы сгенерировали ранее.

 умножить_матрицу (А, В)
# Выход
массив([[ 89, 107],
       [47, 49],
       [ 40, 44]]) 

Поскольку умножение матриц между A и B допустимо, функция multi_matrix() возвращает матрицу произведения C.

Использование понимания вложенных списков Python для умножения матриц написал функцию Python для умножения матриц. Теперь вы увидите, как можно использовать вложенные списки, чтобы сделать то же самое.

Вот понимание вложенного списка для умножения матриц.

Сначала это может показаться сложным. Но мы будем шаг за шагом разбирать понимание вложенного списка.

Давайте сосредоточимся на анализе одного списка и определим, что он делает.

Мы будем использовать следующий общий шаблон для понимания списка:

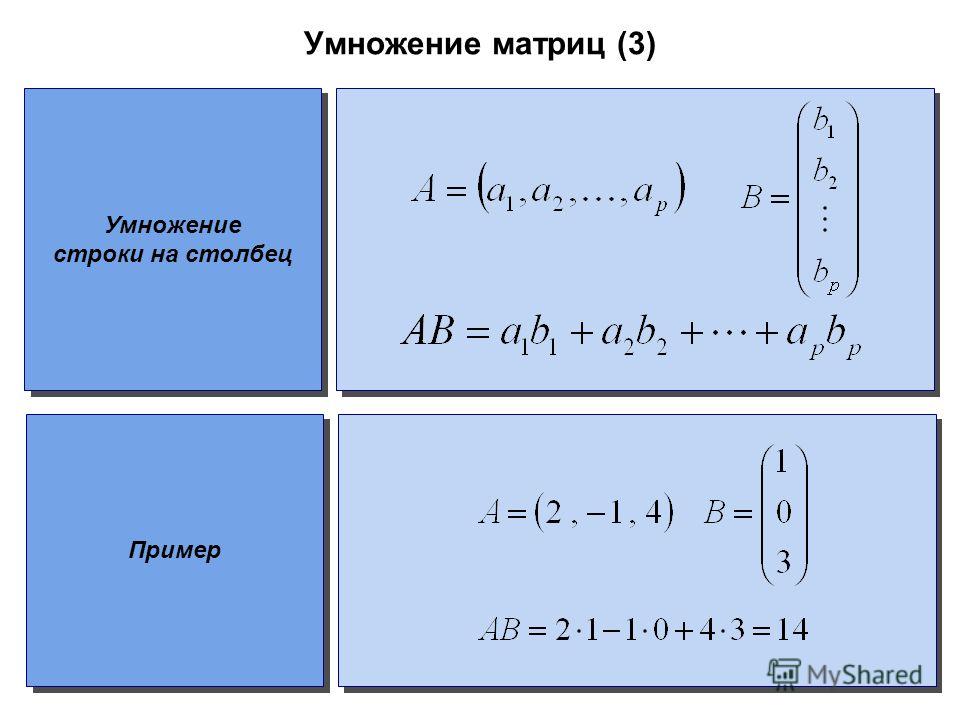
 [ для  в ]
куда,
: что вы хотите сделать — выражение или операцию
: каждый элемент, над которым вы хотите выполнить операцию.
: итерируемый объект (список, кортеж и т.  д.), который вы просматриваете в цикле 

▶️ Ознакомьтесь с нашим руководством «Понимание списков в Python — с примерами», чтобы получить более глубокое понимание.

Прежде чем продолжить, обратите внимание, что мы хотели бы построить результирующую матрицу C по одной строке за раз.

Объяснение понимания вложенного списка

Шаг 1: Вычисление одного значения в матрице C

Для заданной строки i матрицы A и столбца j матрицы B приведенное ниже выражение дает запись с индексом (i, j) в матрице C.

 сумма(a*b для a,b в zip(A_row, B_col)
# zip(A_row, B_col) возвращает итератор кортежей
# Если A_row = [a1, a2, a3] и B_col = [b1, b2, b3]
# zip(A_row, B_col) возвращает (a1, b1), (a2, b2) и т. д. 

Если i = j = 1 , выражение вернет элемент c_11 матрицы C. Таким образом, вы можете получить один элемент в одной строке таким образом.

Шаг 2: Постройте одну строку в матрице C

Наша следующая цель — построить всю строку.

Для строки 1 в матрице A вам нужно перебрать все столбцы в матрице B, чтобы получить одну полную строку в матрице C.

Вернуться к шаблону понимания списка.

• Заменить <сделать это> с выражением из шага 1, потому что это то, что вы хотите сделать.
• Затем замените на B_col — каждый столбец в матрице B.
• Наконец, замените на zip(*B) — список, содержащий все столбцы в матрице B.

А вот и первое понимание списка.

 [сумма (a*b для a, b в zip (A_row, B_col)) для B_col в zip (*B)]
# zip(*B): * оператор распаковки
# zip(*B) возвращает список столбцов матрицы B 

Шаг 3: Постройте все строки и получите матрицу C

Далее вам нужно будет заполнить матрицу произведений C, вычислив остальные строки.

А для этого вам нужно перебрать все строки в матрице A.

Вернуться к пониманию списка еще раз и сделать следующее.

• Замените на понимание списка из шага 2. Вспомните, что мы вычислили целую строку на предыдущем шаге.
• Теперь замените с A_row — каждая строка в матрице A.
• И ваш — это сама матрица A, когда вы перебираете ее строки.

И вот наше окончательное понимание вложенного списка. for A_row in A]

Пришло время проверить результат! ✔

 # преобразование в массив NumPy с помощью np.array()
C = np.array([[sum(a*b для a,b в zip(A_row, B_col)) для B_col в zip(*B)]
    для A_row в A])
# Выход:
[[ 89107]
 [ 47 49]
 [ 40 44]] 

Если вы присмотритесь, это эквивалентно вложенным циклам for, которые мы использовали ранее, только более лаконично.

Вы также можете сделать это более эффективно, используя некоторые встроенные функции. Давайте узнаем о них в следующем разделе.

Использование NumPy matmul() для умножения матриц в Python

np.matmul() принимает две матрицы в качестве входных данных и возвращает произведение, если умножение матриц между входными матрицами равно действительный .

 C = np.matmul(A,B)
печать(С)
# Выход:
[[ 89 107]
 [ 47 49]
 [ 40 44]] 

Обратите внимание, что этот метод проще, чем два метода, которые мы изучали ранее. На самом деле вместо np.matmul() можно использовать эквивалентный оператор @, и мы сразу это увидим.

Как использовать оператор @ в Python для умножения матриц

В Python @ — это бинарный оператор, используемый для умножения матриц.

Он работает с двумя матрицами и, как правило, с N-мерными массивами NumPy и возвращает матрицу произведения.

Примечание: Для использования оператора @ у вас должен быть Python 3.5 и выше.

Вот как вы можете его использовать.

 С = А@В
печать(С)
# Выход
массив([[ 89, 107],
       [47, 49],
       [ 40, 44]]) 

Обратите внимание, что матрица произведения C такая же, как та, которую мы получили ранее.

Можно ли использовать np.dot() для умножения матриц?

Если вы когда-нибудь сталкивались с кодом, который использует np.dot() для умножения двух матриц, вот как это работает.

 C = np.dot(A,B)
печать(С)
# Выход:
[[ 89 107]
 [ 47 49]
 [ 40 44]] 

Вы увидите, что np.dot(A, B) также возвращает ожидаемую матрицу продукта.

Однако, согласно документам NumPy, вы должны использовать np.dot() только для вычисления скалярного произведения двух одномерных векторов, а не для умножения матриц.

Напомним из предыдущего раздела, что элемент с индексом (i, j) матрицы произведения C является скалярным произведением строки i матрицы A и столбца j матрицы B.

Поскольку NumPy неявно передает эту операцию скалярного произведения всем строкам и всем столбцам, вы получаете результирующую матрицу произведения. Но чтобы ваш код был читабельным и чтобы избежать двусмысленности, используйте вместо этого np.matmul() или оператор @ .

Заключение

🎯 В этом уроке вы узнали следующее.

• Условие правильности умножения матриц: количество столбцов в матрице A = количество строк в матрице B .
• Как написать пользовательскую функцию Python, которая проверяет правильность умножения матриц и возвращает матрицу произведения. В теле функции используются вложенные циклы for.
• Далее вы узнали, как использовать вложенные списки для умножения матриц. Они более лаконичны, чем циклы for, но подвержены проблемам с читабельностью.
• Наконец, вы узнали, как использовать встроенную функцию NumPy np.matmul() для умножения матриц и как это наиболее эффективно с точки зрения скорости.
• Вы также узнали об операторе @ для умножения двух матриц в Python.

На этом мы завершаем обсуждение умножения матриц в Python. В качестве следующего шага узнайте, как проверить, является ли число простым в Python. Или решить интересные задачи на строки Python.

Счастливого обучения!🎉

Умножение матриц: (3×3) на (3×2)

---

В этом руководстве показано, как умножить матрицу 3×3 на матрицу 3×2.

Введение

Предположим, у нас есть 3×3 матрица A, которая имеет 3 строки и 3 столбца:

А =	А 11 А 12 А 13   А 21 А 22 А 23 А 31 А 32 А 33

Предположим, у нас также есть 3×2 матрица B, которая имеет 3 строки и 2 столбца:

Б =	Б 11 Б 12   Б 21 Б 22 Б 31 Б 32

Чтобы умножить матрицу A на матрицу B, мы используем следующую формулу:

А х В =

А 11 *В 11 +А 12 *В 21 +А 13 *В 31 A 11 *B 12 +A 12 *B 22 +A 13 *B 32   А 21 *В 11 +А 22 *В 21 +А 23 *В 31 A 21 *B 12 +A 22 *B 22 +A 23 *B 32 А 31 *B 11 +A 32 *B 21 +A 33 *B 31 A 31 *B 12 +A 32 *B 22 +A 33 *B 32

Получается матрица 3×2.

В следующих примерах показано, как умножить матрицу 3×3 на матрицу 3×2, используя действительные числа.

Пример 1

Предположим, у нас есть 3×3 матрица C, которая имеет 3 строки и 3 столбца:

С =	-3 5 4   1 2 3 -1 0 2

Предположим, у нас также есть 3×2 матрица D, состоящая из 3 строк и 2 столбцов:

Д =	2 1   5 1 0 -1

Вот как умножить матрицу C на матрицу D:

С х Г =

-3*2 + 5*5 + 4*0 -3*1 + 5*1 + 4*-1   1*2 + 2*5 + 3*0 1*1 + 2*1 + 3*-1 -1*2 + 0*5 + 2*0 -1*1 + 0*1 + 2*-1

В результате получается следующая матрица 3×2:

С х Г =

19 -2   12 0 -2 -3

Пример 2

Предположим, у нас есть 3×3 матрица E, которая имеет 3 строки и 3 столбца:

Е =	2 8 1   3 3 0 0 1 2

Предположим, у нас также есть 3×2 матрица F, которая имеет 3 строки и 2 столбца:

Ф =	-2 -2   3 1 4 10

Вот как умножить матрицу E на матрицу F:

Е х Ф =

2*-2 + 8*3 + 1*4 2*-2 + 8*1 + 1*10   3*-2 + 3*3 + 0*4 3*-2 + 3*1 + 0*10 0*-2 + 1*3 + 2*4 0*-2 + 1*1 + 2*10

В результате получается следующая матрица 3×2:

Е х Ф =

24 14   3 -3 11 21

Пример 3

Предположим, у нас есть 3×3 матрица G, которая имеет 3 строки и 3 столбца:

Г =	-1 0 0   7 1 0 2 4 6

Предположим, у нас также есть 3×2 матрица H, которая имеет 3 строки и 2 столбца:

Н =	4 5   9 2 0 1

Вот как умножить матрицу G на матрицу H:

Г x В =

-1*4 + 0*9 + 0*0 -1*5 + 0*2 + 0*1   7*4 + 1*9 + 0*0 7*5 + 1*2 + 0*1 2*4 + 4*9 + 6*0 2*5 + 4*2 + 6*1

В результате получается следующая матрица 3×2:

Г x В =

-4 -5   37 37 44 24

Калькулятор матриц

В приведенных выше примерах показано, как умножать матрицы вручную.