Глава 13. Газовые законы
Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).
Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид
(13.1) |
где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.
(13.2) |
Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде
(13.2) |
где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа
(13.3) |
С учетом (13.3) закон (13.2) можно переписать и в таком виде
(13.4) |
Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.
В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.
Для изобарического процесса
Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид
(13.5) |
где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.
Для изохорического процесса
Второй график следует из соотношения
(13. |
где — постоянная при постоянном объеме.
Для изотермического процесса
Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду
(13.7) |
где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.
Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:
(13. |
где — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.
В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :
т.е. давление газа увеличилось в 6 раз (ответ 1).
Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем
где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).
Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает
где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).
Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем
Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).
Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее.
В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее.
Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ  |
В изотермическом процессе давление зависит от объема как ; на диаграмме этот процесс изображается гиперболой. Поэтому изотермическими являются процессы 1 и 3 (задача 13.1.7), но в процессе 1 объем газа убывает. Следовательно, изотермическим расширением является процесс 3 (ответ 3). |
Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева |
получим
(ответ 1).
В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим
Из закона Клапейрона-Менделеева находим
(ответ 1).
Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).
Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим
для гелия |
для азота |
где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда
(ответ 4).
Если бы точки, отвечающие состояниям 1 и 2 в задаче 13. 2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).
Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).
Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.
В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем
(ответ 4).
Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.
Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).
Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).
Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция
т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).
Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 1023 молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).
Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул
(ответ 4). Здесь — масса газа, — масса одной молекулы газа.
Решение задачи
Задача 10
-
Реакция разложения карбоната двухвалентного металла: MCO3 → MO + CO2↑, т.е. потеря массы приходится на CO2. Следовательно, остальные 64,9% – это оксид металла, и M(MO)/M(CO2)=64,9/35,1 ⇒ M(MO)=44,0·64,9/35,1=81,4 а.
 е.м. Отсюда M (M) = 65.4 и М = Zn.
е.м. Отсюда M (M) = 65.4 и М = Zn. -
ZnO+ 2HCl → ZnCl2+ H2O; ZnO+ 2NaOH + H2O → Na2[Zn(OH)4].
-
nH2O: M(Zn(NO3)2·nH2O)/M(Zn(NO3)2) = 100% / 63,7% = (189,4 + 18n) / 189,4; n=6.
-
Процентная концентрация фактически дана в условии задачи: ω=63,7%; смас=63,7/(100/1,4)=0,892г/мл; смол = смас/M(Zn(NO3)2)=0,00471 моль/мл.
-
Zn(NO3)2→ ZnO + 2NO2↑+ ½O2↑. ν(газов)=pV/RT=1·2,76/(0.082·673)=0,05моль=> ν (NO2) = 0.04 моль, ν (O2) = 0.01 моль, ν (Zn(NO3)2) = 0.02 моль, или3,79 г.
Задача 100
Масса смеси составит 3,5*106*0,584 = 2044000 г или 2044 кг. Пропана в смеси 0,58*2044 = 1185,5 кг или 1185,5/44 = 26,94 кмоль. Бутана в смеси 0,42*2044 = 858,5 кг или 858,5/58 = 14,80 кмоль. Мольное отношение пропан/бутан составляет 1,82, общее количество молекул в цистерне газовоза (26,94 + 14,80)*103*6,02*1023 = 2,51*1028, атомов (26,94*11 + 14,80*14)*103*6,02*1023 = 3,03*1029 шт. Объем газообразной смеси при н.у. равен (26,94 + 14,80)*103*22,4 = 935*103 л или 935 м3, что в 935/3,5 = 267 раз больше объема жидкости.
Пропана в смеси 0,58*2044 = 1185,5 кг или 1185,5/44 = 26,94 кмоль. Бутана в смеси 0,42*2044 = 858,5 кг или 858,5/58 = 14,80 кмоль. Мольное отношение пропан/бутан составляет 1,82, общее количество молекул в цистерне газовоза (26,94 + 14,80)*103*6,02*1023 = 2,51*1028, атомов (26,94*11 + 14,80*14)*103*6,02*1023 = 3,03*1029 шт. Объем газообразной смеси при н.у. равен (26,94 + 14,80)*103*22,4 = 935*103 л или 935 м3, что в 935/3,5 = 267 раз больше объема жидкости.
- С3Н8 + 5О2 = 3СО2 + 4Н2О(ж) (DrQ0= 3*393,5 + 4*241,8 – 103,9 = 2043,8 кДж/моль).
С4Н10 + 6,5О2 = 4СО2 + 5Н2О(ж) (DrQ0= 4*393,5 + 5*241,8 – 126,2 = 2656,8 кДж/моль). - При сгорании всей смеси, содержащейся в газовозе, выделится 26,94*103*2043,8 + 14,80*103*2656,8 = (55060 + 39321)*103 кДж = 94,4*106 кДж тепла.

- Масса бензина (октана) 3,5*106*0,703 = 2460500 г или 2460,5 кг. Его количество 2460,5/114 = 21,58 кмоль. Теплота сгорания: С8Н18 + 12,5О2 = 8СО2 + 9Н2О(ж) (DrQ0= 8*393,5 + 9*241,8 – 249,9 = 5074,3 кДж/моль). Количество тепла, которое выделится при сгорании всего бензина 21,58*103*5074,3 = 109,5*106 кДж. Получается, что приобретать пропан-бутановую смесь выгоднее в 94,4*106/3 : 109,5*106/5 = 1,44 раза.
- СН3-СH2-CH(СН3)-CH2-CH2-CH2-CH3(3-метилгептан) – 8 монохлорпроизводных; а) (СН3)3С-С(СН3)3 (2,2,3,3-тетраметилбутан) – 1; б) СН3-CH2-СH2-CH(СН3)-CH2-CH2-CH3(4-метилгептан) – 5.
Задача 101
1. Поскольку при сжигании Х были получены только углекислый газ и вода, Х могло содержать углерод, водород и кислород. Найдем количество образовавшихся при сгорании Х веществ: n(СО2) = 10,08 / 22,4 = 0,45 моль; n(Н2О) = 3,6 /18 = 0,2 моль. Следовательно, количество углерода и водорода, содержащееся в сжигаемой навеске Х равно: n(С) = 0,45 моль; n(Н) = 0,4 моль; n(О) = (6,6 — (0,45 × 12 + 0,4 × 1)) / 16 = 0,05 моль. Установим простейшую формулу соединения Х: С : Н : О = 0,45 : 0,4 : 0,05 = 9 : 8 : 1, т.е. С9Н8О. Поскольку плотность паров соединения Х по воздуху не превышает 5, его молярная масса не должна превышать 5 × 29 = 145 г/моль. Молярная масса вещества, имеющего формулу С9Н8О (совпадающую с простейшей) равна 132 г/моль, следовательно, соединение Х имеет молекулярную формулу С9Н8О.
Поскольку при сжигании Х были получены только углекислый газ и вода, Х могло содержать углерод, водород и кислород. Найдем количество образовавшихся при сгорании Х веществ: n(СО2) = 10,08 / 22,4 = 0,45 моль; n(Н2О) = 3,6 /18 = 0,2 моль. Следовательно, количество углерода и водорода, содержащееся в сжигаемой навеске Х равно: n(С) = 0,45 моль; n(Н) = 0,4 моль; n(О) = (6,6 — (0,45 × 12 + 0,4 × 1)) / 16 = 0,05 моль. Установим простейшую формулу соединения Х: С : Н : О = 0,45 : 0,4 : 0,05 = 9 : 8 : 1, т.е. С9Н8О. Поскольку плотность паров соединения Х по воздуху не превышает 5, его молярная масса не должна превышать 5 × 29 = 145 г/моль. Молярная масса вещества, имеющего формулу С9Н8О (совпадающую с простейшей) равна 132 г/моль, следовательно, соединение Х имеет молекулярную формулу С9Н8О.
2-3. Поскольку соединение содержит один атом кислорода, оно может быть спиртом, альдегидом, кетоном или простым эфиром. Х реагирует с аммиачным раствором оксида серебра(I), при нагревании его с гидроксидом меди(II) наблюдается выпадение красного осадка. Эти реакции указывают на наличие альдегидной группы в составе Х (Х можно отнести к классу альдегидов).
Т.к. вещество Х обесцвечивает бромную воду, оно может содержать в составе молекулы кратные связи (Х можно отнести к непредельным соединениям). Поскольку при окислении перманганатом калия образуется бензойная кислота (Х можно отнести к ароматическим соединениям), единственным соединением, которое удовлетворяет всем условиям, является 3‑фенилпропеналь (коричный альдегид).
3.Уравнения описанных в условии задачи реакций:
4. Коричный альдегид может существовать в виде цис- и транс-изомеров.
Задача 102
1. Рассмотрим схему превращений, основанную на применении этилена в качестве исходного соединения. Этилен при окислении, в присутствии металлического серебра в качестве катализатора окисляется кислородом до этиленоксида (соединение V). Более старым способом его получения является хлорирование этилена в водном растворе, с образованием 2-хлорэтанола (Б), который далее обрабатывают гидроксидом кальция при нагревании. Другим важным мономером, получаемым из этилена, является винилхлорид (III), который образуется при пиролизе 1,2-дихлорэтана (А). Промышленным методом получения 1,2-дихлорэтана является нагревание этилена со смесью хлороводорода и кислорода в присутствии катализатора. При нагревании этилена с уксусной кислотой в присутствии кислорода воздуха образуется винилацетат (IV). Этот процесс имеет сложный многостадийный характер и представляет собой одну из модификаций Вакер-процесса.
Рассмотрим вторую схему превращений. На первой стадии пропилен в условиях кислотного катализа присоединяет воду, образуя изопропиловый спирт (В), который далее превращается в ацетон (Г). Следующая стадия представляет собой реакцию нуклеофильного присоединения синильной кислоты к ацетону с образованием соответствующего циангидрина (Д). При неполном гидролизе нитрильной группы получается амид Е, который при нагревании с метанолом дает метилметакрилат (V).
- Решение задачи 103
- Решение задачи 104
- Решение задачи 105
- Решение задачи 11
Как связаны моль и число авогадро. Атомная единица массы
Инструкция
Чтобы найти моль вещества , нужно запомнить очень простое правило: масса одного моля любого вещества численно равна его молекулярной массе, только выражается в других величинах. А как определяется ? С помощью таблицы Менделеева вы узнаете атомную массу каждого элемента, входящего в молекулы вещества . Далее нужно сложить атомные массы с учетом индекса каждого элемента и получится ответ.
А как определяется ? С помощью таблицы Менделеева вы узнаете атомную массу каждого элемента, входящего в молекулы вещества . Далее нужно сложить атомные массы с учетом индекса каждого элемента и получится ответ.
Посчитайте его молекулярную массу с учетом индекса каждого элемента: 12*2 + 1*4 + 16*3 = 76 а.е.м. (атомных единиц массы). Следовательно, его молярная масса (то есть масса одного моля) также составляет 76, только ее размерность: грамм/моль . Ответ: один моль селитры весит 76 грамм.
Предположим, вам задана такая задача. Известно, что масса 179,2 какого-то газа составляет 352 грамма. Необходимо определить, сколько весит один моль этого газа. Известно, что при нормальных условиях один моль любого газа или смеси газов занимает объем, приблизительно равный 22,4 литра. А у вас 179,2 литра. Произведите вычисление: 179,2/22,4 = 8. Следовательно, в этом объеме содержится 8 молей газа.
Разделив известную по условиям задачи массу на количество молей, получите: 352/8 = 44. Следовательно, один моль этого газа весит 44 грамма — это газ, СО2.
Следовательно, один моль этого газа весит 44 грамма — это газ, СО2.
Если имеется какое-то количество газа массой М, заключенное в объеме V при заданной температуре Т и давлении P. Требуется определить его молярную массу (то есть найти, чему равен его моль ). Решить задачу вам поможет универсальное уравнение Менделеева-Клапейрона: PV = MRT/m, где m – та самая молярная масса, которую нам надо определить, а R – универсальная газовая постоянная, равная 8,31. Преобразуя уравнение, получите: m = MRT/PV. Подставив в формулу известные величины, вы найдете, чему равен моль газа.
Полезный совет
В расчетах обычно используются округленные величины атомных весов элементов. Если требуется более высокая точность, то округление недопустимо.
Различные формулы помогут найти количество вещества, единицей измерения которого является моль . Также количество вещества можно найти по уравнению реакции, данной в задаче.
Инструкция
Если химическое вещество состоит из молекул, в одном моле этого вещества будет содержаться 6,02×10^23 молекул. 23 молекул или атомов. Общее количество вещества (число молей) латинской буквой n или греческой буквой «ню». Его можно найти по отношению общего количества молекул или атомов вещества к числу молекул в 1 моле – числу Авогадро:
23 молекул или атомов. Общее количество вещества (число молей) латинской буквой n или греческой буквой «ню». Его можно найти по отношению общего количества молекул или атомов вещества к числу молекул в 1 моле – числу Авогадро:
n=N/N(A), где n – количество вещества (моль), N – количество частиц вещества, N(A) – число Авогадро.
Отсюда же можно выразить и число частиц в заданном количестве вещества:
Фактическую массу одного моля вещества называют его молярной массой и обозначают букой M. Она выражается в «граммах на моль» (г/моль), но численно равна относительной молекулярной массе вещества Mr (если вещество состоит из молекул) или относительной атомной массе вещества Ar, если вещество состоит из атомов.
Относительные массы элементов можно найти по таблице Менделеева (обычно при расчетах их округляют). Так, для водорода это 1, для лития – 7, для углерода – 12, для кислорода – 16 и т.д. Относительные молекулярные массы складываются из относительных атомных масс составляющих молекулы атомов. К примеру, относительная молекулярная масса воды h3O
К примеру, относительная молекулярная масса воды h3O
Mr(h3O)=2xAr(H)+Ar(O)=2×1+16=18.
Относительные атомные и молекулярные массы – безразмерные величины, поскольку выражают массу атома и молекулы относительно условной единицы – 1/12 массы атома углерода.
В типовых задачах обычно требуется найти, сколько молекул или атомов содержится в заданном количестве вещества, составляет заданное количество вещества, сколько молекул в заданной массе. Важно понимать, что вещества указывает на число молей каждого элемента, входящего в его состав. То есть 1 моль h3SO4 содержит 2 моля атомов водорода H, 1 моль атомов серы S, 4 моля атомов кислорода O.
Вчера обещал объяснить это доступным языком. Вещь важная для понимания химии. Если один раз понять, то потом уже не забудешь.
Химия имеет свой язык, как и любая наука. 2H 2 + O 2 → 2H 2 O — на химическом языке запись реакции образования воды из простых веществ, водорода (H) и кислорода (O). Маленькие цифры относятся к количеству атомов (Они стоят после символа химического элемента), большие — к количеству молекул. Из уравнения видно что две молекулы водорода соединяются с одной молекулой кислорода и в результате выходит две молекулы воды. Внимание — это очень важно понять! Соединяются именно молекулы с молекулами, не «грамм с граммом», а молекула с молекулой.
Из уравнения видно что две молекулы водорода соединяются с одной молекулой кислорода и в результате выходит две молекулы воды. Внимание — это очень важно понять! Соединяются именно молекулы с молекулами, не «грамм с граммом», а молекула с молекулой.
Эта пропорция сохранится всегда:
Всё бы хорошо, но есть две проблемы. Первая — в реальной жизни мы не сможем отмерить один миллион молекул кислорода или водорода. Мы сможем отмерить один грамм или одну тонну реактивов. Вторая — молекулы очень маленькие. В одном стакане воды их 6,7·10 24 штук. Или, в обычной записи 6,7 триллионов триллионов (именно так — почти семь триллионов раз по триллиону молекул). Оперировать такими цифрами неудобно.
Какой же выход? Молекулы ведь тоже имеют массу, пускай очень маленькую. Мы просто берём массу одной молекулы , умножаем на количество молекул и получаем нужную нам массу. Договорились так — берём очень большое количество молекул (600 миллиардов триллионов штук) и изобретаем для этого количества специальную единицу измерения моль . Как для 12 штук чего-либо есть специальное название «дюжина» , и когда говорят о «десяти дюжинах», то имеют в виду 120 штук. 5 дюжин яиц = 60 штук. Так и с молями . 1 моль — это 600 миллиардов триллионов молекул или, в математической нотации, 6,02·10 23 молекул. То есть когда нам говорят «1 моль» водорода, мы знаем что речь идёт о 600 миллиардах триллионов молекул водорода. Когда говорят о 0,2 молях воды, то мы понимаем что речь идёт 120 миллиардах триллионов молекул воды.
Как для 12 штук чего-либо есть специальное название «дюжина» , и когда говорят о «десяти дюжинах», то имеют в виду 120 штук. 5 дюжин яиц = 60 штук. Так и с молями . 1 моль — это 600 миллиардов триллионов молекул или, в математической нотации, 6,02·10 23 молекул. То есть когда нам говорят «1 моль» водорода, мы знаем что речь идёт о 600 миллиардах триллионов молекул водорода. Когда говорят о 0,2 молях воды, то мы понимаем что речь идёт 120 миллиардах триллионов молекул воды.
Ещё раз — моль это просто такая счётная единица, только специально для молекул . Как «десяток», «дюжина» или «миллион», только гораздо больше.
Продолжая таблицу выше, можно написать:
Первую проблему мы решили, писать 1 моль или 2 моля гораздо удобнее чем 600 миллиардов триллионов молекул или 1,2 триллиона триллионов молекул. Но для одного удобства не стоило огород городить. Вторая проблема, как помним, переход от количества молекул (не считать же их поштучно!) к массе вещества , к тому что мы можем отмерить на весах. Такое количество молекул в одном моле (оно ведь немного странное, некруглое — 6,02·10 23 молекул) выбрано неспроста. Один моль молекул углерода весит ровно 12 грамм.
Такое количество молекул в одном моле (оно ведь немного странное, некруглое — 6,02·10 23 молекул) выбрано неспроста. Один моль молекул углерода весит ровно 12 грамм.
Понятно что все молекулы разные. Есть большие и тяжелые — в них может быть много атомов, или не очень много, но зато сами атомы тяжелые. А есть маленькие и легкие молекулы. Для каждого атома и для многих молекул есть в справочниках таблицы с их молярной массой . То есть с весом одного моля таких молекул (если нет, можно легко самим посчитать, сложив молярные массы всех атомов, из которых составлена молекула). Молярная масса измеряется в грамм/моль (сколько грамм весит один моль, то есть сколько грамм весят 6,02·10 23 молекул). Мы помним ведь что моль — просто счётная единица. Ну как если бы в справочнике писали — 1 дюжина куриных яиц весит 600 грамм, а 1 дюжина страусиных весит 19 килограмм. Дюжина — просто количество (12 штук), а сами яйца, куриное или страусиное, весят по-разному. И дюжина таких или других яиц тоже по-разному весит.
Так и с молекулами. 1 моль маленьких и лёгких молекул водорода весит 2 грамма, а 1 моль больших молекул серной кислоты — 98 грамм. 1 моль кислорода весит 32 грамма, 1 моль воды — 18 грамм. Вот картинка для примера, где видны маленькие молекулы водорода и большие молекулы кислорода. Эта картинка — графическое отображение реакции 2H 2 + O 2 → 2H 2 O.
Продолжаем заполнять таблицу:
Видите переход от количества молекул к их массе ? Видите что выполняется закон сохранения вещества? 4 грамма + 32 грамма дали 36 грамм.
Теперь мы можем решать простые задачи по химии. Вот самая примитивная: Было 100 молекул кислорода и 100 молекул водорода. Что произойдёт в результате реакции? Мы знаем что на 1 молекулу кислорода нужно 2 молекулы водорода. Поэтому прореагируют все 100 молекул водорода (и образуется 100 молекул воды), а вот кислород прореагирует не весь, ещё 50 молекул останется. Кислород в избытке.
Молекулы штуками, как я уже сказал выше, никто не считает. Вещества обычно отмеряют граммами. Теперь задача из школьного учебника: есть 10 г. водорода и 64 г. кислорода, что будет если их смешать? Мы для начала должны перевести массы в моли (то есть в количество молекул или количество вещества, как говорят химики). 10 г. водорода — это 5 моль водорода (1 моль водорода весит 2 грамма). 64 г. кислорода — это 2 моля (1 моль весит 32 грамма). Мы знаем что на 1 моль кислорода при реакции уходит 2 моля водорода. Значит, в нашем случае прореагирует весь кислород (2 моля) и 4 моля водорода из пяти. Получится 4 моля воды и ещё останется один моль водорода.
Вещества обычно отмеряют граммами. Теперь задача из школьного учебника: есть 10 г. водорода и 64 г. кислорода, что будет если их смешать? Мы для начала должны перевести массы в моли (то есть в количество молекул или количество вещества, как говорят химики). 10 г. водорода — это 5 моль водорода (1 моль водорода весит 2 грамма). 64 г. кислорода — это 2 моля (1 моль весит 32 грамма). Мы знаем что на 1 моль кислорода при реакции уходит 2 моля водорода. Значит, в нашем случае прореагирует весь кислород (2 моля) и 4 моля водорода из пяти. Получится 4 моля воды и ещё останется один моль водорода.
Переведём ответ снова в граммы. Прореагирует весь кислород (64 грамма) и 8 грамм водорода (4 моля * 2 г/моль). 1 моль водорода останется не прореагировавшим (это 2 грамма) и получится 72 грамма воды (4 моля * 18 г/моль). Закон сохранения вещества опять выполняется — 64 + 10 = 72 + 2.
Думаю что теперь уже всем должно быть понятно. 1 моль — просто количество молекул. Молярная масса — это масса одного моля. Она нужна для того чтобы переходить от массы вещества (с которой мы работаем в реальном мире) к количеству молекул, или количеству вещества, нужному для реакций.
Она нужна для того чтобы переходить от массы вещества (с которой мы работаем в реальном мире) к количеству молекул, или количеству вещества, нужному для реакций.
Снова повторимся:
а) вещества реагирует в соотношении n молекул одного к m молекул другого. Это пропорция будет одинаковой и для 100 молекул исходного вещества, и для ста триллионов, или для ста триллионов триллионов.
б) для удобства, чтобы не считать молекулы штуками, придумали специальную счётную единицу — моль, то есть сразу 6,02·10 23 молекул. Количество этих молей называют обычном «количество вещества»
в) моль каждого вещества весит по-разному, т.к. молекулы и атомы, из которых состоит вещества, сами весят по-разному. Масса одного моля вещества называется его молярной массой. Ещё один пример — обычные и силикатные кирпичи весят по-разному. Если мы проведём аналогию, то «вес тысячи кирпичей» — это «молярная масса» (с тем отличием что молекул не 1000, а больше). Масса этой «тысячи кирпичей» разная для силикатных и обычных кирпичей.
г) весь этот огород городим для того чтобы легко можно было переходить от массы реактивов к количеству вещества (количеству молекул, количеству молей) и обратно. А переходить туда/обратно нужно потому что в реальном мире мы отмеряем реактивы граммами, а химические реакции идут пропорционально не массе, а количеству молекул.
P.S. Химикам и прочим — я здесь специально многое упрощал. Не нужно мне объяснять что 12 грамм весит не 1 моль углерода, а 1 моль молекул изотопа С 12 , или про то что вместо «молекул» нужно было бы писать «структурных единиц» (молекул, ионов, атомов…), специально не упомянул что 1 моль газа занимает одинаковый объём при одинаковых условиях и ещё про многое другое
Что мне не нравилось в учебниках — только формальное определение моля, без указания смысла этого понятия и для чего это нужно.
Моль – количество вещества, которое содержит столько же структурных элементов, сколько атомов содержится в 12 г 12 С, причем структурными элементами обычно являются атомы, молекулы, ионы и др.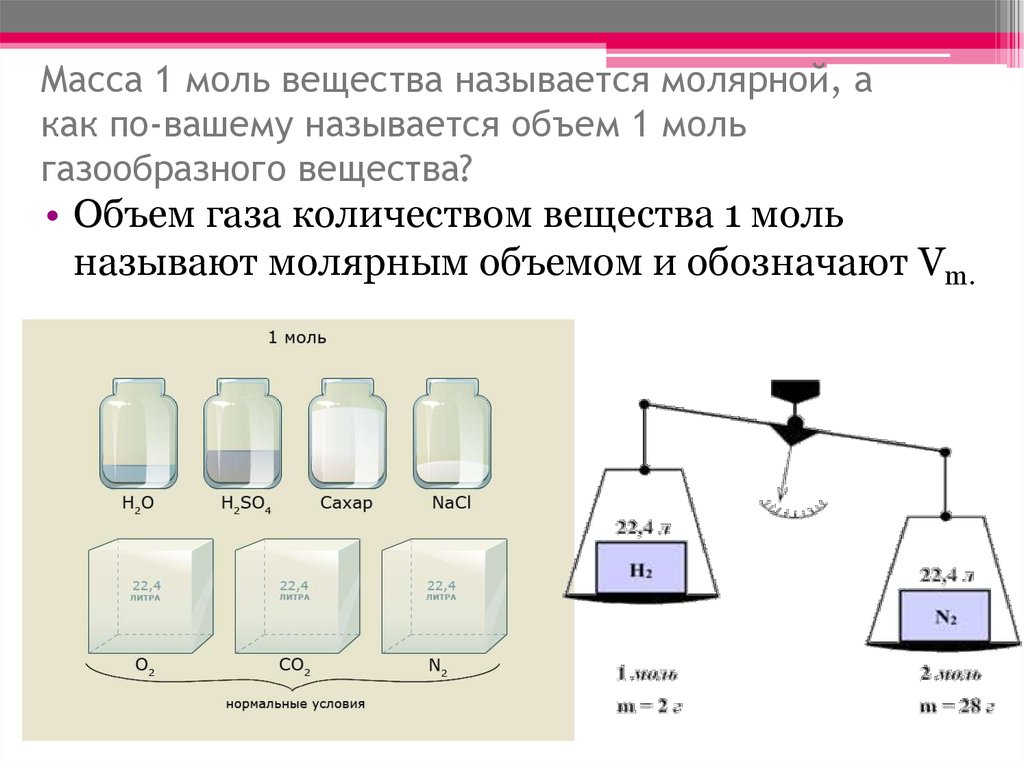 Масса 1 моль вещества, выраженная в граммах, численно равна его мол. массе. Так, 1 моль натрия имеет массу 22,9898 г и содержит 6,02·10 23 атомов; 1 моль фторида кальция CaF 2 имеет массу (40,08 + 2·18,998) = 78,076 г и содержит 6,02·10 23 молекул, как и 1 моль тетрахлорида углерода CCl 4 , масса которого равна (12,011 + 4·35,453) = 153,823 г и т.п.
Масса 1 моль вещества, выраженная в граммах, численно равна его мол. массе. Так, 1 моль натрия имеет массу 22,9898 г и содержит 6,02·10 23 атомов; 1 моль фторида кальция CaF 2 имеет массу (40,08 + 2·18,998) = 78,076 г и содержит 6,02·10 23 молекул, как и 1 моль тетрахлорида углерода CCl 4 , масса которого равна (12,011 + 4·35,453) = 153,823 г и т.п.
Закон Авогадро.
На заре развития атомной теории (1811) А.Авогадро выдвинул гипотезу, согласно которой при одинаковых температуре и давлении в равных объемах идеальных газов содержится одинаковое число молекул. Позже было показано, что эта гипотеза есть необходимое следствие кинетической теории, и сейчас она известна как закон Авогадро. Его можно сформулировать так: один моль любого газа при одинаковых температуре и давлении занимает один и тот же объем, при стандартных температуре и давлении (0° С, 1,01Ч10 5 Па) равный 22,41383 л. Эта величина известна как молярный объем газа.
Сам Авогадро не делал оценок числа молекул в заданном объеме, но понимал, что это очень большая величина. Первую попытку найти число молекул, занимающих данный объем, предпринял в 1865 Й.Лошмидт; было установлено, что в 1 см 3 идеального газа при нормальных (стандартных) условиях содержится 2,68675Ч10 19 молекул. По имени этого ученого указанная величина была названа числом (или постоянной) Лошмидта. С тех пор было разработано большое число независимых методов определения числа Авогадро. Превосходное совпадение полученных значений является убедительным свидетельством реального существования молекул.
Первую попытку найти число молекул, занимающих данный объем, предпринял в 1865 Й.Лошмидт; было установлено, что в 1 см 3 идеального газа при нормальных (стандартных) условиях содержится 2,68675Ч10 19 молекул. По имени этого ученого указанная величина была названа числом (или постоянной) Лошмидта. С тех пор было разработано большое число независимых методов определения числа Авогадро. Превосходное совпадение полученных значений является убедительным свидетельством реального существования молекул.
Метод Лошмидта
представляет только исторический интерес. Он основан на предположении, что сжиженный газ состоит из плотноупакованных сферических молекул. Измеряя объем жидкости, которая образовалась из данного объема газа, и зная приблизительно объем молекул газа (этот объем можно было представить исходя из некоторых свойств газа, например вязкости), Лошмидт получил оценку числа Авогадро ~10 22 .
Определение, основанное на измерении заряда электрона.
Единица количества электричества, известная как число Фарадея F , – это заряд, переносимый одним молем электронов, т. е. F = Ne , где е – заряд электрона, N – число электронов в 1 моль электронов (т.е. число Авогадро). Число Фарадея можно определить, измеряя количество электричества, необходимое для растворения или осаждения 1 моль серебра. Тщательные измерения, выполненные Национальным бюро стандартов США, дали значение F = 96490,0 Кл, а заряд электрона, измеренный разными методами (в частности, в опытах Р.Милликена), равен 1,602Ч10 –19 Кл. Отсюда можно найти N . Этот метод определения числа Авогадро, по-видимому, является одним из самых точных.
е. F = Ne , где е – заряд электрона, N – число электронов в 1 моль электронов (т.е. число Авогадро). Число Фарадея можно определить, измеряя количество электричества, необходимое для растворения или осаждения 1 моль серебра. Тщательные измерения, выполненные Национальным бюро стандартов США, дали значение F = 96490,0 Кл, а заряд электрона, измеренный разными методами (в частности, в опытах Р.Милликена), равен 1,602Ч10 –19 Кл. Отсюда можно найти N . Этот метод определения числа Авогадро, по-видимому, является одним из самых точных.
Эксперименты Перрена.
Исходя из кинетической теории, было получено включающее число Авогадро выражение, описывающее уменьшение плотности газа (например, воздуха) с высотой столба этого газа. Если бы удалось подсчитать число молекул в 1 см 3 газа на двух разных высотах, то, воспользовавшись указанным выражением, мы могли бы найти N . К сожалению, сделать это невозможно, поскольку молекулы невидимы. Однако в 1910 Ж.Перрен показал, что упомянутое выражение справедливо и для суспензий коллоидных частиц, которые видны в микроскопе. Подсчет числа частиц, находящихся на разной высоте в столбе суспензии, дал число Авогадро 6,82Ч10 23 . Из другой серии экспериментов, в которых измерялось среднеквадратичное смещение коллоидных частиц в результате их броуновского движения, Перрен получил значение N = 6,86Ч10 23 . В дальнейшем другие исследователи повторили некоторые из экспериментов Перрена и получили значения, хорошо согласующиеся с ныне принятыми. Следует отметить, что эксперименты Перрена стали поворотным моментом в отношении ученых к атомной теории вещества – ранее некоторые ученые рассматривали ее как гипотезу. В.Оствальд, выдающийся химик того времени, так выразил это изменение во взглядах: «Соответствие броуновского движения требованиям кинетической гипотезы… заставило даже наиболее пессимистично настроенных ученых говорить об экспериментальном доказательстве атомной теории».
Однако в 1910 Ж.Перрен показал, что упомянутое выражение справедливо и для суспензий коллоидных частиц, которые видны в микроскопе. Подсчет числа частиц, находящихся на разной высоте в столбе суспензии, дал число Авогадро 6,82Ч10 23 . Из другой серии экспериментов, в которых измерялось среднеквадратичное смещение коллоидных частиц в результате их броуновского движения, Перрен получил значение N = 6,86Ч10 23 . В дальнейшем другие исследователи повторили некоторые из экспериментов Перрена и получили значения, хорошо согласующиеся с ныне принятыми. Следует отметить, что эксперименты Перрена стали поворотным моментом в отношении ученых к атомной теории вещества – ранее некоторые ученые рассматривали ее как гипотезу. В.Оствальд, выдающийся химик того времени, так выразил это изменение во взглядах: «Соответствие броуновского движения требованиям кинетической гипотезы… заставило даже наиболее пессимистично настроенных ученых говорить об экспериментальном доказательстве атомной теории».
Расчеты с использованием числа Авогадро.
С помощью числа Авогадро были получены точные значения массы атомов и молекул многих веществ: натрия, 3,819Ч10 –23 г (22,9898 г/6,02Ч10 23), тетрахлорида углерода, 25,54Ч10 –23 г и т.д. Можно также показать, что в 1 г натрия должно содержаться примерно 3Ч10 22 атомов этого элемента.
См. также
С понятием «моль» сталкивается каждый школьник, который начинает изучать химию. С более сложными понятиями, такими как концентрация, молярность растворителя, тяжело разобраться, не зная, что такое моль. Можно сделать вывод, что моль — одно из важнейших понятий в химии. Многие задачи нельзя решить, не определив количество молей.
Определение
Так что такое моль в химии? Пояснение дать довольно просто: это единица, в которой выражается количество вещества, одна из единиц СИ. Определение того, что такое моль в химии, можно сформулировать и таким образом: 1 моль эквивалентен содержится структурных частиц в 12 г карбона-12.
Как было установлено, в 12 г этого изотопа содержится количество атомов, численно равное постоянной Авогадро.
Происхождение понятия
Немного разобравшись с тем, что такое моль в химии с помощью определений, обратимся к истории этого понятия. Как принято считать, термин «моль» ввел немецкий химик Вильгельм Освальд, получивший Нобелевскую премию в 1909 году. Слово «моль», очевидно, происходит от слова «молекула».
Интересный факт — гипотеза Авогадро о том, что при одинаковых условиях в одинаковых объемах разных газов содержится одно и то же количество вещества, было выдвинута задолго до Освальда, да и сама константа была подсчитана Авогадро еще в начале XIX века. То есть хоть понятия «моль» и не существовало, само представление о количестве вещества уже было.
Основные формулы
Количество вещества находится по-разному, в зависимости от данных задачи. Такой вид имеет самая распространенная формула, в которой эта величина выражается отношением массы к молярной массе:
Стоит сказать, что количество вещества — величина аддитивная. То есть, чтобы посчитать значение этой величины для смеси, нужно сначала определить количество вещества для каждого ее элемента и сложить их.
То есть, чтобы посчитать значение этой величины для смеси, нужно сначала определить количество вещества для каждого ее элемента и сложить их.
Другая формула применяется, если известно количество частиц:
Если в задаче указано, что процесс происходит при нормальных условиях, можно воспользоваться следующим правилом: при нормальных условиях любой газ занимает инвариантный объем — 22,4 л. Тогда можно воспользоваться следующим выражением:
Количество вещества выражается из уравнения Клапейрона:
Знание того, что такое моль в химии и основных формул для определения количества молей вещества, дает возможность значительно быстрее решать многие задачи. Если известно количество вещества, можно найти массу, объем, плотность и другие параметры.
Закон Авогадро
На заре развития атомной теории () А. Авогадро выдвинул гипотезу, согласно которой при одинаковых температуре и давлении в равных объёмах идеальных газов содержится одинаковое число молекул. Позже было показано, что эта гипотеза есть необходимое следствие кинетической теории, и сейчас она известна как закон Авогадро. Его можно сформулировать так: один моль любого газа при одинаковых температуре и давлении занимает один и тот же объем, при нормальных условиях равный 22,41383 . Эта величина известна как молярный объем газа .
Его можно сформулировать так: один моль любого газа при одинаковых температуре и давлении занимает один и тот же объем, при нормальных условиях равный 22,41383 . Эта величина известна как молярный объем газа .
Сам Авогадро не делал оценок числа молекул в заданном объёме, но понимал, что это очень большая величина. Первую попытку найти число молекул, занимающих данный объем, предпринял в году
Й. Лошмидт
. Из вычислений Лошмидта следовало, что для воздуха количество молекул на единицу объёма составляет 1,81·10 18 см −3
, что примерно в 15 раз
меньше истинного значения. Через 8 лет
Максвелл привёл гораздо более близкую к истине оценку «около 19 миллионов
миллионов миллионов» молекул на кубический сантиметр, или 1,9·10 19 см −3
. В действительности в 1 см³
идеального газа при нормальных условиях содержится 2,68675·10 19 молекул
. Эта величина была названа числом (или постоянной) Лошмидта . С тех пор было разработано большое число независимых методов определения числа Авогадро. Превосходное совпадение полученных значений является убедительным свидетельством реального количества молекул.
Превосходное совпадение полученных значений является убедительным свидетельством реального количества молекул.
Измерение константы
| Данные в этой статье приведены по состоянию на декабрь 2011 года. |
Официально принятое на сегодня значение числа Авогадро было измерено в 2010 году . Для этого использовались две сферы, сделанные из кремния-28 . Сферы были получены в Институте кристаллографии имени Лейбница и отполированы в австралийском Центре высокоточной оптики настолько гладко, что высоты выступов на их поверхности не превышали 98 нм . Для их производства был использован высокочистый кремний-28, выделенный в нижегородском Институте химии высокочистых веществ РАН из высокообогащённого по кремнию-28 тетрафторида кремния, полученного в Центральном конструкторском бюро машиностроения в Санкт-Петербурге.
Располагая такими практически идеальными объектами, можно с высокой точностью подсчитать число атомов кремния в шаре и тем самым определить число Авогадро. Согласно полученным результатам, оно равно 6,02214084(18)×10 23 моль −1
.
Согласно полученным результатам, оно равно 6,02214084(18)×10 23 моль −1
.
Связь между константами
- Через произведение постоянной Больцмана Универсальная газовая постоянная , R =kN A .
- Через произведение элементарного электрического заряда на число Авогадро выражается постоянная Фарадея , F =eN A .
См. также
Примечания
Литература
- Число Авогадро // Большая советская энциклопедия
Wikimedia Foundation . 2010 .
Смотреть что такое «Число Авогадро» в других словарях:
— (постоянная Авогадро, обозначение L), постоянная, равная 6,022231023, соответствует числу атомов или молекул, содержащихся в одном МОЛЕ вещества … Научно-технический энциклопедический словарь
число Авогадро — Avogadro konstanta statusas T sritis chemija apibrėžtis Dalelių (atomų, molekulių, jonų) skaičius viename medžiagos molyje, lygus (6,02204 ± 0,000031)·10²³ mol⁻¹. santrumpa(os) Santrumpą žr. priede. priedas(ai) Grafinis formatas atitikmenys:… … Chemijos terminų aiškinamasis žodynas
santrumpa(os) Santrumpą žr. priede. priedas(ai) Grafinis formatas atitikmenys:… … Chemijos terminų aiškinamasis žodynas
число Авогадро — Avogadro konstanta statusas T sritis fizika atitikmenys: angl. Avogadro’s constant; Avogadro’s number vok. Avogadro Konstante, f; Avogadrosche Konstante, f rus. постоянная Авогадро, f; число Авогадро, n pranc. constante d’Avogadro, f; nombre… … Fizikos terminų žodynas
Авогадро постоянная (число Авогадро) — число частиц (атомов, молекул, ионов) в 1 моле вещества (моль это количество вещества, в котором содержится столько же частиц, сколько атомов содержится точно в 12 граммах изотопа углерода 12), обозначаемое символом N = 6,023 1023. Одна из… … Начала современного естествознания
— (число Авогадро), число структурных элементов (атомов, молекул, ионов или др. ч ц) в ед. кол ва в ва (в одном моле). Названа в честь А. Авогадро, обозна чается NA. А. п. одна из фундаментальных физических констант, существенная для определения мн … Физическая энциклопедия
— (число Авогадро; обозначается NА), число молекул или атомов в 1 моле вещества, NА = 6,022045(31) х 1023моль 1; назв. по имени А. Авогадро … Естествознание. Энциклопедический словарь
по имени А. Авогадро … Естествознание. Энциклопедический словарь
— (число Авогадро), число частиц (атомов, молекул, ионов) в 1 моле в ва. Обозначается NA и равна (6,022045 … Химическая энциклопедия
Na = (6,022045±0,000031)*10 23 число молекул в моле любого вещества или число атомов в моле простого вещества. Одна из фундаментальных постоянных, с помощью которой можно определить такие величины, как, например, массу атома или молекулы (см.… … Энциклопедия Кольера
что это такое в химии, как найти объемные отношения газов, единица измерения
Молярный объем — что это такое в химии
ОпределениеМолярный объем Vm — является отношением объема вещества к его количеству, численно равен объему одного моля вещества.
Термин «молярный объем» применим по отношению к простым веществам, химическим соединениям и смесям. Величина зависит от следующих факторов:
- температура;
- давление;
- агрегатное состояние вещества.
Молярный объем можно находить путем деления молярной массы M вещества на его плотность ρ.
Молярный объем вычисляют по формуле:
Vm=V/n=M/ρ.
Молярный объем является характеристикой плотности упаковки молекул в рассматриваемом веществе. В случае простых веществ в некоторых ситуациях допустимо использовать понятие атомного объема.
Согласно Международной системе единиц (СИ), молярный объем измеряется в кубических метрах на моль (русское обозначение: м3/моль; международное: m3/mol).
Исходя из того, что объем газа определяется температурой и давлением, в процессе расчетов принято использовать объемы газов при нормальных условиях (сокращенно — н. у.). За нормальные условия принимают:
- температура 0 °С;
- давление 101,325 кПа (1 атм.).
Известно, что при нормальных условиях отношение объема любой порции газа к химическому количеству газа есть величина постоянная и равная 22,4дм3/моль.
Молярный объем какого-либо газа при нормальных условиях:
Источник: himi4ka.ru
Таким образом, молярный объем при н. у. равен 22,4дм3 и представляет собой объем, который занимает 1 моль какого-либо газа при нормальных условиях.
Молярный объем смеси
В том случае, когда рассматривается смесь веществ, в процессе вычисления молярного объема за количество вещества принимают сумму количеств всех веществ, входящих в состав смеси. Когда величина плотности смеси ρc, мольные доли компонентов xi и их молярные массы Mi известны, молярный объем смеси допустимо рассчитывать в виде отношения средней молярной массы смеси (суммы молярных масс ее компонентов, умноженных на их мольные доли) к плотности смеси.
ФормулаМолярный объем смеси:
Vm=V∑ni=M¯ρc=∑i=1NxiMiρc.Vm=V∑ni=M¯ρc=∑i=1NxiMiρc.
Молярный объем газов
ОпределениеЗакон Авогадро: одинаковые количества газов при одинаковых условиях занимают одинаковый объем.
Молярный объем идеального газа вычисляют с помощью формулы, которая является выводом из уравнения состояния идеального газа.
ФормулаМолярный объем идеального газа:
Vm=RTPVm=RTP,
где T — является термодинамической температурой;
P — давление;
R — универсальная газовая постоянная.
R = 8,314 Дж/(К·моль) = 0,08205 л·атм/(К·моль).
При нормальных условиях (T = 273,15 K, P = 101 325 Па) молярный объем газов Vm = 22,41396954… л/моль. Молярные объемы в случае реальных газов, так или иначе, не совпадают с молярным объемом идеального газа. С другой стороны, нередко в процессе решения практических задач по химии отклонениями от идеальности допустимо пренебрегать.
Молярный объем кристаллов
Объем Vя элементарной ячейки кристалла вычисляют с помощью характеристик кристаллической структуры, которые определяют на основании результатов рентгеноструктурного анализа.
ФормулаЗависимость между объемом ячейки и молярным объемом:
Vm=VяNA/Z
где Z — определяет, сколько формульных единиц в элементарной ячейке.
Значения молярного объема химических элементов
Уточнить величину молярного (атомного) объема, характерного для простых веществ, в см3/моль(10−6м3/моль, 10−3 л/моль) при нормальных условиях (для газообразных простых веществ), либо при температуре конденсации и нормальном давлении, можно в таблице:
Источник: ru. wikipedia.org
wikipedia.org
Вычисление химического количества газа по его объему
Объем газа можно рассчитать по его химическому количеству. В этом случае необходимо преобразовать формулу молярного объема путем выражения из нее V:
Источник: www.yaklass.ru
Таким образом, объем газа равен произведению его химического количества на молярный объем. Продемонстрировать данное утверждение можно на примере. Допустим, что необходимо определить объем (н. у.) метана с химическим количеством 1,5 моль. Используя уравнение, записанное ранее, проведем вычисления:
Источник: www.yaklass.ru
При известном объеме газообразного вещества можно определить химическое количество рассматриваемого газа. В этом случае следует выразить из уравнения молярного объема n:
Источник: www.yaklass.ru
Таким образом, химическое количество газообразного вещества допустимо рассчитывать, как отношение его объема к молярному объему. Данное утверждение можно применить на практическом примере. Предположим, что необходимо вычислить химическое количество водорода, соответствующее при н. у. его объему 11,2 дм3. Выполним расчеты:
Предположим, что необходимо вычислить химическое количество водорода, соответствующее при н. у. его объему 11,2 дм3. Выполним расчеты:
Источник: www.yaklass.ru
Определение объема веществ при химических реакциях
Перед тем, как приступить к расчетам объема веществ, следует ввести понятие плотности. Данный показатель определяется отношением массы вещества к его объему. Плотность измеряют в кг/м3 (или г/л, г/мл). В случае газообразных веществ плотность принимает очень маленькие значения. Упростить расчеты химических реакций можно, если рассматривать отношение плотностей газов.
ОпределениеОтносительной плотностью газа В по газу А называют величину, равную отношению плотностей рассматриваемых веществ или отношению молярных масс этих газов.
Данный параметр обозначают DA(B) и определяют по формуле:
Источник: uahistory.co
В связи с тем, что в расчете относительной плотности используют величины одинаковой размерности, данный параметр является безразмерной величиной. Определить относительную плотность газообразных веществ по некому газу можно с помощью отношения молярных масс этих газов. Например, относительная плотность кислорода по водороду составляет:
Определить относительную плотность газообразных веществ по некому газу можно с помощью отношения молярных масс этих газов. Например, относительная плотность кислорода по водороду составляет:
Источник: uahistory.co
Согласно закону Авогадро, в равных объемах различных газов, которые существуют при одинаковых температурах и давлениях, содержится одно и то же количество молекул. Данная гипотеза была представлена в 1811 году в Турине профессором физики Амедео Авогадро.
Подтверждение теория нашла во множестве экспериментальных опытах. Закон получил название закона Авогадро и стал в дальнейшем количественной основой современной химии. Закон Авогадро в точности реализуем в случае идеального газа. С увеличением разреженности газообразного вещества повышается точность расчетов по этому закону применительно к данному реальному газу.
ОпределениеПервое следствие из закона Авогадро: один моль (одинаковое количество молей) любого газа при одинаковых условиях занимает одинаковый объем.
Исходя из закона Авогадро, одинаковое число молекул какого-либо газа занимает при одинаковых условиях один и тот же объем. Наряду с тем, 1 моль какого-то вещества включает в себя (согласно определению) одинаковое количество частиц (к примеру, молекул). Таким образом, при определенных температуре и давлении 1 моль любого вещества в газообразном состоянии занимает один и тот же объем.
Если условия соответствуют нормальным, то есть температура равна 0 °C (273,15 К), и давление составляет 101,325 кПа, объем 1 моль газа соответствует 22,413 962(13) л. Данная физическая константа является молярным объемом идеального газа и обозначается Vm.
ФормулаВычислить молярный объем при температуре и давлении, отличных от нормальных условий, можно с помощью уравнения Клапейрона:
Vm=RTpVm=RTp,
где R≈8,314Дж/(моль·К) — является универсальной газовой постоянной.
ОпределениеВторое следствие из закона Авогадро: молярная масса первого газа равна произведению молярной массы второго газа на относительную плотность первого газа ко второму.
Благодаря данному положению, наука химия получила активное развитие. Причиной этому является открытие возможности для расчета молекулярной массы веществ, которые обладают способностью к переходу в газообразное или парообразное состояние. В том случае, когда молекулярная масса вещества равна μ, а ρ, является его относительной плотностью в газообразном состоянии по другому газу, отношение μ/ρ, должно быть постоянным для всех веществ, его значение зависит только от вида газа, по которому определяют относительную плотность данного вещества. Из результатов практического опыта можно сделать вывод о том, что для любых известных веществ, которые способны переходить в газообразное состояние без разложения, рассматриваемая постоянная составляет 28,9 а.е.м. (атомных единицы массы), если при определять относительную плотность по воздуху. С другой стороны, данная постоянная будет равна 2 а.е.м. в том случае, когда относительную плотность определяют по водороду.
Как найти объемные отношения газов в смеси
В процессе вычисления объемных отношений газов, участвующих в химических реакциях, используют закон Гей-Люссака (химический закон объемных отношений). В англоязычной литературе данный закон можно встретить под названием закона Шарля.
В англоязычной литературе данный закон можно встретить под названием закона Шарля.
Закон Гей-Люссака — закон, демонстрирующий пропорциональную зависимость между объемом газообразного вещества и абсолютной температурой при постоянном давлении (то есть в изобарном процессе).
Закон получил название в честь французского физика и химика Жозефа Луи Гей-Люссака.
ФормулаМатематическое выражение закона Гей-Люссака:
V~T или V/T = const, P = const,
где V — объем газа;
T — температура;
P — давление.
В том случае, когда известно состояние газа при постоянном давлении и двух разных температурах, закон допустимо записывать таким образом:
V1 : T1 = V2 : T2 или V1T2 = V2T1.
По итогам химических реакций атомы не исчезают и не возникают. В результате таких процессов происходит их перегруппировка. Количество атомов до реакции и после ее протекания не меняется, что отличает их от молекул. Данное условие учитывают, расставляя стехиометрические коэффициенты в уравнениях химических реакций.
Коэффициенты в уравнениях реакций демонстрируют числа объемов газов, которые реагируют и образовываются. К примеру, 2 объема водорода и 1 объем кислорода дают 2 объема пара воды:
2h3+O2=2h3O
В процессе, записанном в виде уравнения 3Н2+N2=2Nh4, объемы азота и водорода, между которыми протекает реакция, и объем образовавшегося аммиака связаны между собой, что можно выразить с помощью следующего соотношения:
V(Н2):V(N2):V(Nh4)=3:2:1
С другой стороны, данные соотношения справедливы лишь в случае веществ, которые участвуют в одной и той же химической реакции. Когда реагент принимает участие в двух параллельных реакциях, его химические количества в данных процессах не связаны и могут принимать любые значения.
Согласно первому следствию из закона Авогадро, при одинаковых условиях 1 моль любого газа занимает одинаковый объем. Объем газа количеством 1 моль в нормальных условиях носит название молярного объема и обозначается Vm. Таким образом:
n = V : Vm,
где V — объем газа,
n — количество газа.
Выразить молярный объем газов можно в л/моль:
Vm = 22,4 л/моль.
Источник: uchitel.pro
В данной таблице использованы следующие обозначения:
- V — объем;
- Р — давление;
- Т — температура;
- n — количество вещества;
- m — масса вещества;
- М — молярная масса вещества;
- R — универсальная газовая постоянная.
R=8,314Дж/(К·моль)=0,08205л·атм/(К·моль).
Нормальные условия: 0°Си1,013·105Па.
Нормальное давление: 1,013·105Па=1атм=760ммрт.ст.
АВОГАДРО ЧИСЛО | Энциклопедия Кругосвет
Содержание статьи- Закон Авогадро.
- Метод Лошмидта
- Определение, основанное на измерении заряда электрона.
- Эксперименты Перрена.
- Расчеты с использованием числа Авогадро.
АВОГАДРО ЧИСЛО, NA = (6,022045±0,000031)·1023, число молекул в моле любого вещества или число атомов в моле простого вещества. Одна из фундаментальных постоянных, с помощью которой можно определить такие величины, как, например, массу атома или молекулы (см. ниже), заряд электрона и т.д.
ниже), заряд электрона и т.д.
Моль – количество вещества, которое содержит столько же структурных элементов, сколько атомов содержится в 12 г 12С, причем структурными элементами обычно являются атомы, молекулы, ионы и др. Масса 1 моль вещества, выраженная в граммах, численно равна его мол. массе. Так, 1 моль натрия имеет массу 22,9898 г и содержит 6,02·1023 атомов; 1 моль фторида кальция CaF2 имеет массу (40,08 + 2·18,998) = 78,076 г и содержит 6,02·1023 молекул, как и 1 моль тетрахлорида углерода CCl4, масса которого равна (12,011 + 4·35,453) = 153,823 г и т.п.
Закон Авогадро.
На заре развития атомной теории (1811) А.Авогадро выдвинул гипотезу, согласно которой при одинаковых температуре и давлении в равных объемах идеальных газов содержится одинаковое число молекул. Позже было показано, что эта гипотеза есть необходимое следствие кинетической теории, и сейчас она известна как закон Авогадро. Его можно сформулировать так: один моль любого газа при одинаковых температуре и давлении занимает один и тот же объем, при стандартных температуре и давлении (0° С, 1,01Ч105 Па) равный 22,41383 л. Эта величина известна как молярный объем газа.
Эта величина известна как молярный объем газа.
Сам Авогадро не делал оценок числа молекул в заданном объеме, но понимал, что это очень большая величина. Первую попытку найти число молекул, занимающих данный объем, предпринял в 1865 Й.Лошмидт; было установлено, что в 1 см3 идеального газа при нормальных (стандартных) условиях содержится 2,68675Ч1019 молекул. По имени этого ученого указанная величина была названа числом (или постоянной) Лошмидта. С тех пор было разработано большое число независимых методов определения числа Авогадро. Превосходное совпадение полученных значений является убедительным свидетельством реального существования молекул.
Метод Лошмидта
представляет только исторический интерес. Он основан на предположении, что сжиженный газ состоит из плотноупакованных сферических молекул. Измеряя объем жидкости, которая образовалась из данного объема газа, и зная приблизительно объем молекул газа (этот объем можно было представить исходя из некоторых свойств газа, например вязкости), Лошмидт получил оценку числа Авогадро ~1022.
Определение, основанное на измерении заряда электрона.
Единица количества электричества, известная как число Фарадея F, – это заряд, переносимый одним молем электронов, т.е. F = Ne, где е – заряд электрона, N – число электронов в 1 моль электронов (т.е. число Авогадро). Число Фарадея можно определить, измеряя количество электричества, необходимое для растворения или осаждения 1 моль серебра. Тщательные измерения, выполненные Национальным бюро стандартов США, дали значение F = 96490,0 Кл, а заряд электрона, измеренный разными методами (в частности, в опытах Р.Милликена), равен 1,602Ч10–19 Кл. Отсюда можно найти N. Этот метод определения числа Авогадро, по-видимому, является одним из самых точных.
Эксперименты Перрена.
Исходя из кинетической теории, было получено включающее число Авогадро выражение, описывающее уменьшение плотности газа (например, воздуха) с высотой столба этого газа. Если бы удалось подсчитать число молекул в 1 см3 газа на двух разных высотах, то, воспользовавшись указанным выражением, мы могли бы найти N. К сожалению, сделать это невозможно, поскольку молекулы невидимы. Однако в 1910 Ж.Перрен показал, что упомянутое выражение справедливо и для суспензий коллоидных частиц, которые видны в микроскопе. Подсчет числа частиц, находящихся на разной высоте в столбе суспензии, дал число Авогадро 6,82Ч1023. Из другой серии экспериментов, в которых измерялось среднеквадратичное смещение коллоидных частиц в результате их броуновского движения, Перрен получил значение N = 6,86Ч1023. В дальнейшем другие исследователи повторили некоторые из экспериментов Перрена и получили значения, хорошо согласующиеся с ныне принятыми. Следует отметить, что эксперименты Перрена стали поворотным моментом в отношении ученых к атомной теории вещества – ранее некоторые ученые рассматривали ее как гипотезу. В.Оствальд, выдающийся химик того времени, так выразил это изменение во взглядах: «Соответствие броуновского движения требованиям кинетической гипотезы… заставило даже наиболее пессимистично настроенных ученых говорить об экспериментальном доказательстве атомной теории».
К сожалению, сделать это невозможно, поскольку молекулы невидимы. Однако в 1910 Ж.Перрен показал, что упомянутое выражение справедливо и для суспензий коллоидных частиц, которые видны в микроскопе. Подсчет числа частиц, находящихся на разной высоте в столбе суспензии, дал число Авогадро 6,82Ч1023. Из другой серии экспериментов, в которых измерялось среднеквадратичное смещение коллоидных частиц в результате их броуновского движения, Перрен получил значение N = 6,86Ч1023. В дальнейшем другие исследователи повторили некоторые из экспериментов Перрена и получили значения, хорошо согласующиеся с ныне принятыми. Следует отметить, что эксперименты Перрена стали поворотным моментом в отношении ученых к атомной теории вещества – ранее некоторые ученые рассматривали ее как гипотезу. В.Оствальд, выдающийся химик того времени, так выразил это изменение во взглядах: «Соответствие броуновского движения требованиям кинетической гипотезы… заставило даже наиболее пессимистично настроенных ученых говорить об экспериментальном доказательстве атомной теории».
Расчеты с использованием числа Авогадро.
С помощью числа Авогадро были получены точные значения массы атомов и молекул многих веществ: натрия, 3,819Ч10–23 г (22,9898 г/6,02Ч1023), тетрахлорида углерода, 25,54Ч10–23 г и т.д. Можно также показать, что в 1 г натрия должно содержаться примерно 3Ч1022 атомов этого элемента.
См. также АТОМНАЯ МАССА.
Проверь себя!
Ответь на вопросы викторины «Неизвестные подробности»
Какой музыкальный инструмент не может звучать в закрытом помещении?
Пройти тест
Объем газа при нормальных условиях
Урок 9. Молярная масса и молярный объем – HIMI4KA
Архив уроков › Химия 8 класс
В уроке 9 «Молярная масса и молярный объем» из курса «Химия для чайников» выясним, что подразумевается под молярной массой и молярным объемом; приведем формулы для их вычисления. Напоминаю, что в прошлом уроке «Химическое количество вещества и моль» мы выяснили, что такое химическое количество вещества; рассмотрели моль в качестве единицы количества вещества, а также познакомились с постоянной Авогадро.
Молярная масса
Вы знаете, что одинаковое химическое количество любых веществ содержит одно и то же число структурных единиц. Но у каждого вещества его структурная единица имеет собственную массу. Поэтому и массы одинаковых химических количеств различных веществ тоже будут различны.
Молярная масса — это масса порции вещества химическим количеством 1 моль.
Молярная масса вещества Х обозначается символом M(Х). Она равна отношению массы данной порции вещества m(Х) (в г или кг) к его химическому количеству n(Х) (в моль):
В Международной системе единиц молярная масса выражается в кг/моль. В химии чаще используется дольная единица — г/моль.
Обратите внимание
Определим молярную массу углерода. Масса углерода химическим количеством 1 моль равна 0,012 кг, или 12 г. Отсюда:
Молярная масса любого вещества, если она выражена в г/моль, численно равна его относительной молекулярной (формульной) массе.
Например:
На рисунке 47 показаны образцы веществ (h3O, CaCO3, Zn), химическое количество которых одно и то же — 1 моль. Как видите, массы разных веществ химическим количеством 1 моль различны.
Молярная масса является важной характеристикой каждого отдельного вещества. Она отражает зависимость между массой и химическим количеством вещества. Зная одну из этих величин, можно определить вторую — массу по химическому количеству:
и, наоборот, химическое количество по массе:
а также число структурных единиц:
Взаимосвязь между этими тремя характеристиками вещества в любом его агрегатном состоянии можно выразить простой схемой:
В отличие от твердых и жидких веществ все газообразные вещества химическим количеством 1 моль занимают одинаковый объем (при одинаковых условиях). Эта величина называется молярным объемом и обозначается Vm.
Подобно молярной массе, молярный объем газа равен отношению объема данного газообразного вещества V(Х) к его химическому количеству n(Х):
Так как объем газа зависит от температуры и давления, то при проведении различных расчетов берутся обычно объемы газов при нормальных условиях (сокращенно — н. у.). За нормальные условия принимаются температура 0 °С и давление 101,325 кПа.
у.). За нормальные условия принимаются температура 0 °С и давление 101,325 кПа.
Важно
Установлено, что при нормальных условиях отношение объема любой порции газа к химическому количеству газа есть величина постоянная и равная 22,4 дм3/моль. Другими словами, молярный объем любого газа при нормальных условиях:
Молярный объем — это объем, равный 22,4 дм3, который занимает 1 моль любого газа при нормальных условиях.
Пример 1. Вычислите химическое количество SiO2, масса которого равна 240 г.
Спойлер
[свернуть]
Пример 2. Определите массу серной кислоты h3SO4, химическое количество которой 2,5 моль.
Спойлер
[свернуть]
Пример 3. Сколько молекул CO2 и сколько атомов кислорода содержится в углекислом газе массой 110 г?
Спойлер
[свернуть]
Пример 4. Какой объем занимает кислород химическим количеством 5 моль при нормальных условиях?
Какой объем занимает кислород химическим количеством 5 моль при нормальных условиях?
Спойлер
[свернуть]
Краткие выводы урока:
- Масса вещества химическим количеством 1 моль называется его молярной массой. Она равна отношению массы данной порции вещества к его химическому количеству.
- Объем газообразных веществ химическим количеством 1 моль при нормальных условиях одинаков и равен 22,4 дм3.
- Величина, равная 22,4 дм3/моль, называется молярным объемом газов.
Надеюсь урок 9 «Молярная масса и молярный объем» был понятным и познавательным. Если у вас возникли вопросы, пишите их в комментарии. Данный урок был заключительным в главе «Основные химические понятия».
Источник: https://himi4ka.ru/arhiv-urokov/urok-9-moljarnaja-massa-i-moljarnyj-obem.html
молярный объём газа
Лианата Просветленный (24284) 10 лет назадЗакон АвогадроАмадео Авогадро в 1811г.
выдвинул гипотезу, которая в дальнейшем была подтверждена опытными данными и потому стала называться законом Авогадро: 4Одинаковые объемы различных газов при одинаковых условиях (температуре и давлении) содержат одинаковое число молекул.
Таким образом, Авогадро указал, что противоречие между законом объемных отношений Гей-Люссака и учением Дальтона легко устраняется, если ввести представление о молекуле и атоме как о различных формах материи. Закон Гей-Люссака есть закон о числе молекул, а не атомов, находящихся в объеме газа.
Авогадро предположил, что молекулы простых газов состоят из двух одинаковых атомов. Таким образом, при соединени водорода с хлором их молекулы хлористого водорода. Из одной молекулы водорода и одной молекулы хлора образуются две молекулы хлористого водорода.
Совет
h3+Cl2=2HClИз закона Авогадро вытекает важное следствие: при одинаковых условиях 1 моль газа занимает одинаковый объем. Этот объем легко вычислить, если известна масса 1л газа.
Экспериментально установлено, что масса 1л кислорода при нормальных условиях (при температуре 273?К (0?С) и давлении 1 атм. ) равна 1,429г.
Следовательно, объем, занимаемый 1 молем при этих условиях, равен:Объем одного моля газа называется молярным объемом (VM) и равен отношению объема газа к количеству вещества:VM = V/ν.Молярный объем любого газа при н. у. (нормальный уровень) равен 22,4 л.VM = 22,4 л.Если Mr(h3O) = 18, a p(h3O) = 1 г/мл, то Vm(Н2О) = 18 мл.
На основе закона Авогадро определяют молекулярные массы газообразных веществ по их плотности.
Источник:
Александр Самардакевич Профи (929) 2 года назадЗакон АвогадроАмадео Авогадро в 1811г. выдвинул гипотезу, которая в дальнейшем была подтверждена опытными данными и потому стала называться законом Авогадро: 4Одинаковые объемы различных газов при одинаковых условиях (температуре и давлении) содержат одинаковое число молекул.
Таким образом, Авогадро указал, что противоречие между законом объемных отношений Гей-Люссака и учением Дальтона легко устраняется, если ввести представление о молекуле и атоме как о различных формах материи. Закон Гей-Люссака есть закон о числе молекул, а не атомов, находящихся в объеме газа.
Закон Гей-Люссака есть закон о числе молекул, а не атомов, находящихся в объеме газа.
Авогадро предположил, что молекулы простых газов состоят из двух одинаковых атомов. Таким образом, при соединени водорода с хлором их молекулы хлористого водорода. Из одной молекулы водорода и одной молекулы хлора образуются две молекулы хлористого водорода.
Совет
h3+Cl2=2HClИз закона Авогадро вытекает важное следствие: при одинаковых условиях 1 моль газа занимает одинаковый объем. Этот объем легко вычислить, если известна масса 1л газа.Экспериментально установлено, что масса 1л кислорода при нормальных условиях (при температуре 273?К (0?С) и давлении 1 атм. ) равна 1,429г.
Следовательно, объем, занимаемый 1 молем при этих условиях, равен:Объем одного моля газа называется молярным объемом (VM) и равен отношению объема газа к количеству вещества:VM = V/ν.Молярный объем любого газа при н. у. (нормальный уровень) равен 22,4 л.VM = 22,4 л.Если Mr(h3O) = 18, a p(h3O) = 1 г/мл, то Vm(Н2О) = 18 мл.
На основе закона Авогадро определяют молекулярные массы газообразных веществ по их плотности.
Никита Кузнецов Ученик (131) 11 месяцев назадЗакон АвогадроАмадео Авогадро в 1811г. выдвинул гипотезу, которая в дальнейшем была подтверждена опытными данными и потому стала называться законом Авогадро: 4Одинаковые объемы различных газов при одинаковых условиях (температуре и давлении) содержат одинаковое число молекул.
Таким образом, Авогадро указал, что противоречие между законом объемных отношений Гей-Люссака и учением Дальтона легко устраняется, если ввести представление о молекуле и атоме как о различных формах материи. Закон Гей-Люссака есть закон о числе молекул, а не атомов, находящихся в объеме газа.
Авогадро предположил, что молекулы простых газов состоят из двух одинаковых атомов. Таким образом, при соединени водорода с хлором их молекулы хлористого водорода. Из одной молекулы водорода и одной молекулы хлора образуются две молекулы хлористого водорода.
Совет
h3+Cl2=2HClИз закона Авогадро вытекает важное следствие: при одинаковых условиях 1 моль газа занимает одинаковый объем. Этот объем легко вычислить, если известна масса 1л газа.Экспериментально установлено, что масса 1л кислорода при нормальных условиях (при температуре 273?К (0?С) и давлении 1 атм. ) равна 1,429г.
Следовательно, объем, занимаемый 1 молем при этих условиях, равен:Объем одного моля газа называется молярным объемом (VM) и равен отношению объема газа к количеству вещества:VM = V/ν.Молярный объем любого газа при н. у. (нормальный уровень) равен 22,4 л.VM = 22,4 л.Если Mr(h3O) = 18, a p(h3O) = 1 г/мл, то Vm(Н2О) = 18 мл.
На основе закона Авогадро определяют молекулярные массы газообразных веществ по их плотности.
Источник: https://otvet.mail.ru/question/20339456
Большая Энциклопедия Нефти и Газа
Cтраница 1
Молярный объем идеальных газов определяют, экстраполируя до р О молярные объемы, измеренные при нескольких давлениях. Идеальными газами называются газы, строго подчиняющиеся газовым законам. Каждый реальный газ ведет себя как идеальный газ при достаточно высокой температуре и достаточно низком давлении. [1]
Идеальными газами называются газы, строго подчиняющиеся газовым законам. Каждый реальный газ ведет себя как идеальный газ при достаточно высокой температуре и достаточно низком давлении. [1]
Величинамолярного объема идеальных газов в нормальных физических условиях равна г 22 4 мг / кмоль. [2]
Принятое значениемолярного объема идеального газа при нормальных условиях ( 22 412 л) основано на результатах многочисленных экспериментальных измерений плотности различных газов. [3]
Обратите внимание
При нормальных условияхмолярный объем идеального газа равен 22 414 л / моль, или 22 414 м3 / кмоль. [4]
Произведение vp (1.12) представляетсобой молярный объем идеального газа и обозначается У. Из (1.12) следует, что при одинаковых р и Т молярные объемы различных газов одинаковы. [5]
К ( 0 С), при которыхмолярный объем идеального газа равен 2 241383 10 — 2 м3 / моль. [6]
Если с этой же точки зрения проанализировать значения входящих в табл.
1 некоторых других величин, например молярного объема идеального газа Fm, определенного при нормальных условиях ( 1 атм; 273 15 К), и скорости света с, то нетрудно заметить справочный характер константы Vm и фундаментальное значение для всей науки скорости света, как максимально возможной скорости передачи любых взаимодействий в природе. Сведение этих констант в одну таблицу является грубейшей физической ошибкой. [7]
Сведение этих констант в одну таблицу является грубейшей физической ошибкой. [7]
Новое базисное значение единицы массы привело к некоторому изменению числа Авогадро Л / А и связанных с ним величин, таких, как число Фарадея, универсальная газовая постоянная имолярный объем идеального газа. Согласно последним данным ( см. также разд. [8]
При рассмотрении газовой фазы СНГ, которая несколько отличается от идеального газа, в уравнение равновесного состояния вводится коэффициент сжимаемости z, учитывающий, что молярный объем газовой фазы V при повышении давления уменьшается по сравнению смолярным объемом идеального газа. [9]
В этих уравнениях: К-Дж / ( кг — К) и Лц 8314 ДжДкмоль К) — удельная и универсальная газовые постоянные соответственно, причем R Яц / ц, где ц — молярная масса идеального газа; V 22 4 мэ / кмоль — молярный объем идеального газа при нормальных условиях. [10]
Наибольшее отклонение от величины 22 4 л обнаруживают газы ( С12, SO2), которые при комнатной температуре находятся в состоянии, не слишком удаленном от критического.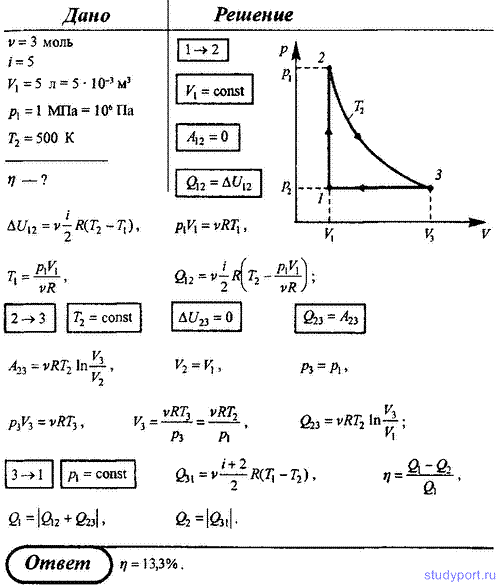
Для трудно сжижаемых газов ( Но, Не, N2, O2 и др.
) отклонения отмолярного объема идеального газа в нормальных условиях незначительны; это позволяет при расчетах для них пользоваться законами и уравнениями состояния идеальных газов. [11]
Важно
NA — Авогадро число, моль — , V t — молярный объем идеального газа при норм, условиях, М3 / моль. [12]
Решите сначала уравнение Ван-дер — Ваальса относительно молярного объема V, входящего в член ( V — Ь), подставив в знаменатель члена a / V2 значениемолярного объема идеального газа.
Затем, если вас не удовлетворит полученное решение, повторите вычисления, подставив найденное решение в знаменатель члена а / V2, и продолжайте поступать так до тех пор, пока при последовательных циклах вычислений ваши ответы не перестанут отличаться друг от друга. [13]
Страницы: 1
Источник: https://www.ngpedia.ru/id204501p1.html
ПОИСК
Распространенной ошибкой абитуриентов является использование молярного объема газов при нормальных условиях (22,4 л/моль) для решения задач, в условиях которых не говорится, что объемы газов измерены при н. у.
у.
[c.213]
Один моль любого газа при данных условиях занимает один и тот же объем. Этот объем называется молярным объемом газа. Он равен отношению объема газа к его количеству вещества [c.
90]
Объем, занимаемый данной массой газа. Если газ находится при 0°С и нормальном атмосферном давлении, то расчет можно произвести, исходя из молярного объема газа (22,4 л/моль). Если же газ находится при иных давлении и температуре, то вычисление объема производят по уравнению Клапейрона— Менделеева [c.35]
Этот объем часто называют молярным объемом газа. [c.132]
По мере уменьшения молярного объема газа оба допущения, положенные в основу представления об идеальном газе, становятся все менее верными.
Для описания газа в более щироком диапазоне давлений Ван-дер-Ваальсом было предложено уравнение, носящее его имя.
В уравнении Ван-дер-Ваальса учитывается, во-первых, что молекулы газа занимают некоторый конечный объем и в уравнение (8. 1) вместо молярного объема вводится свободный от молекул [c.123]
1) вместо молярного объема вводится свободный от молекул [c.123]
Из гипотезы Авогадро следует, что если равные объемы газов содержат равные числа молекул, то объемы, занимаемые 1 моль газа, должны быть одинаковыми для всех газов. Этот объем, называемый молярным объемом газа, равен 22,414 дм при СТД , i i i (О °С и 1 атм) или 24,056 дм при КТД (20 °С и [c.154]
В частности, при нормальных условиях (и.у.)-при температуре Т= 273,15 К (0°С) и давлении /7 = 1,01325 10 Па (1 атм, 760 мм рт. ст.)-любой газ (близкий по свойствам к идеальному газу), количество которого равно 1 моль, занимает объем 22,4 л. Эта физическая постоянная называется молярным объемом газа при нормальных условиях. [c.13]
Молярный объем эквивалента газа X связан с молярным объемом газа X соотношением [c.11]
Следовательно, при нормальных условиях 1 моль любого газа занимает объем, разный 22,4 л. Этот объем называется молярным объемом газа и обозначается V,,,. [c.12]
[c.12]
Совет
Следовательно, при нормальных условиях моль любого газа занимает объем, равный 22,4 л. Этот объем называют молярным объемом газа (обозначают Ут) - [c.23]
При нормальных условиях (и. у.), т. е. давлении р, равном 101 325 Па, и температуре 7 = 273,15 К (О °С), I моль различных газов занимает объем 22,4 л (точнее, 22,41383 л). Такой объем называется молярным объемом газа и имеет размерность литр на моль (л/моль).
По аналогии эквивалентный объем — объем, который занимает при данных условиях 1 моль эквивалента газооб разного вещества. Например, эквивалентный объем молекулярного водорода при нормальных условиях раве 22,4/2= 11,2 л/моль молекулярного кислорода — 22,4/4 = = 5,6 л/моль.
[c.12]
При этом содержании в пределах достигаемой обычно точности наблюдается постоянство кажущегося молярного объема газа в воде, и он принимается за парциальный молярный объем при бесконечном разведении. Очевидно, что это утверждение имеет условный характер и определяется точностью эксперимента.
Очевидно, что это утверждение имеет условный характер и определяется точностью эксперимента.
В ряде случаев измерения объемов растворов проводились при таких содержаниях растворенных газов, при которых кажущиеся молярные объемы могут заметно отличаться от парциальных молярных объемов при предельном разведении.
Тогда кажущиеся молярные объемы соответствуют изменению объема растворителя при растворении в нем веществ в области тех концентраций, при которых эти объемы были определены.
Учитывая низкую относительную точность определений кажущихся молярных объемов малорастворимых веществ эти величины в качестве более или менее точного приближения могут быть приняты за парциальные молярные объемы при предельном разведении. [c.93]
Кажущиеся молярные объемы газов, растворенных в воде [c.94]
Анализ данных, приведённых в табл. 55, показал, что парциальные молярные объемы газов, растворенных в воде, полученные различными исследователями и различными методами как правило расходятся на 3—10 . Это объясняется прежде всего значительными трудностями при проведении экспериментов.
Это объясняется прежде всего значительными трудностями при проведении экспериментов.
Обратите внимание
Большинство исследований проводилось при 25 °С и в условиях насыщения воды газом при атмосферном давлении.
Из сопоставления результатов, полученных по методам определения плотности [47] и измерения приращения давления газа, находящегося в равновесии с водным раствором газа, который подвергнут гидростатическому давлению [35], можно заключить, что погрешность обоих методов не более 3 %. [c.95]
ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ ГАЗОВ (ЖИДКОСТЕЙ) [c.98]
Так как Л/ > Л/ , а парциальные молярные объемы газов в неводных жидкостях больше, чем в воде (см. табл. 56), 2 (ЪМ»/Ър)
Так как в критической точке двойной системы (Ъц.»/ЪМ») = О, то при приближении к конечной критической точке (см. гл. О значение (ЪЫ»/Ър) резко возрастает, оставаясь отрицательным по знаку. Эту особенность подтверждают данные, приведенные на рис.
55 [11]. [c.160]
При нормальных условиях — давлении 101,325 кПа и температуре О или 273 К 1 моль любого газа занимает объем, примерно равный 22,4 л. Он называется молярным объемом газа при нормальных условиях и обозначается V». Единицы измерения — л/моль или мкмоль. [c.17]
При нормальных условиях 1 моль различных газов занимает объем, равный 22,4 л. Этот объем называется молярным объемом газа = 22,4 л). [c.48]
Значение молярного объема газа при нормальных условиях является коэффициентом пропорциональности между постоянными Авогадро и Лошмидта Нд (см. 2.5) [c.47]
Из закона Авогадро вытекают два важных следствия 1) моль любого газа при одинаковых условиях занимает один и тот же объем 2) при нормальных условиях (н. у.), т. е. при температуре 0°С и давлении 1,013-105 -[з ахм), моль любого газа занимает объем около 22,4 л.
Важно
Этот объем называют молярным объемом газа (Ум), единица измерения его — л/. моль. Таким образом, молярный объем представляет собой частное от деления объема газа в литрах на его количество в молях Ум=У1п.
моль. Таким образом, молярный объем представляет собой частное от деления объема газа в литрах на его количество в молях Ум=У1п.
Молярная масса и молярный объем данного газа связаны соотношением М=Умр, где р — плотность газа, г/л. [c.24]
E jui в реакции участвуют газы, то мой.но использовать молярные объемы газов. Прежде чем разбирагь дальнейшие примеры, приведем общий алгоритм расчетов по уравнению химической реакции. [c.250]
В блоке Состав вещества отражена и количественная сторона. Ее объем различен в разных учебниках.
Кроме обязательного понятия об относительной атомной массе и относительной молекулярной массе многими авторами вводятся понятия о количестве вещества и о единице количества вещества — моле, о молярной массе и молярном объеме газов при нормальных условиях, о законе Авогадро, относительной плотности газов понятия о тепловом эффекте химических реакций и расчеты как по формулам, так и по уравнениям реакций. Именно на этом этапе учащиеся знакомятся с принципами решения химических задач разных типов, что в дальнейшем явится базой для развития этих умений. Одновременно получает развитие и использование химической символики. [c.262]
Именно на этом этапе учащиеся знакомятся с принципами решения химических задач разных типов, что в дальнейшем явится базой для развития этих умений. Одновременно получает развитие и использование химической символики. [c.262]
В частности, нормальных условиях (н.у.) — при температуре Т = 273 К (О °С) и давлении Р = 101,325 кПа (1 атм, или 760 мм рт.ст.) — любой газ, количество которого равно 1 моль, занимает объем 22,4 л. Этот объем называется молярным объемом газа при н.у. [c.8]
Значение молярного объема газа, равное 22,4 л/моль (см. 2.9), относится к нормальным физическим условиям, под которыми понимаются давление, равное 1,01325-10 Па, или 1 атм, и термодинамическая температура, равная 273,15 К (или температура Цельсия, равная О «С). [c.49]
Следует отметить, что для большинства исследованных бинарных газовых смесей, состоящих из газов, находящихся при температурах более высоких, чем критическая, различия между молярным объемом газа в смеси и объемом газа, тссчптапиым по уравнению состояния чистого газа, относительно не велики и пе могут оказывать существепного влияния на результаты расчета по уравнению (40). [c.164]
[c.164]
Совет
В полученном выражении отношение aVlVm — это изменение объема системы, выраженное числом молярных объемов газа, т. е. изменение числа моль газа [c.70]
Уаювия, Ш1да Р=101,ЗкПа=1агм., Т=273,15К (0 С), называют нормальными. Объем, который занимает 1 моль любого газа при заданных условиях, назьшают молярным объемом газа при этих условиях. [c.247]
Уравнение Мснделссва-Клайперона обычно изучается в курсс физики, однако для решения многих химических задач необходимо уметь пользоваться молярными объемами газов и относительной плотностью газов. И для этого часто приходится находить молярный объем при заданных (не нормальных) условиях. Поэтому мы сочли необходимым включить это уравнение. [c.247]
Следует отметить, что закон Авогадро справедлив для идеальных газов . Для реальных газов наблюдаются отклонения от закона молярный объем некоторых газов при нормальных условиях несколько меньше 22,4 л/моль.
Например, для хлороводорода он составляет 22,2 л/моль, для хлора — 22,0 л/моль. В настоящей книге значение молярного объема газов при нормальных условиях считается постоянной величиной, и возможные отклонения не учиты ваются.
[c.24]
Постоянство молярного объема газов при нормальных условиях — это одно из важнейших следствий из закона Авогадро. В объеме газообразного вещества (н. у.) 22,4140 л/моль, как и в любой другой системе количеством вещества в 1 моль, число стру)
Источник: https://www.chem21.info/info/463228/
Моль. Закон Авогадро. Молярный объем газа
Моль (n) — кол-во вещества, содержащее столько структурных единиц (молекул, атомов, ионов и др.), сколько атомов содержится в 12 г (0,012 кг) изотопа углерода 12С 1моль вещества содержит 6,02*1023 структурных единиц (число Авогадро , NА)
Формулы, отражающие взаимосвязь объема вещества, его массы и молекулярной массы.
Где m-масса,M-молярная масса, V- объем.
4. Закон Авогадро. Установлен итальянским физиком Авогадро в 1811 г. Одинаковые объемы любых газов, отобранные при одной температуре и одинаковом давлении, содержат одно и тоже число молекул.
Таким образом, можно сформулировать понятие количества вещества: 1 моль вещества содержит число частиц, равное 6,02*1023 (называемое постоянной Авогадро)
Следствием этого закона является то, что 1 моль любого газа занимает при нормальных условиях (Р0 =101,3кПа и Т0=298К) объём, равный 22,4л.
5. Закон Бойля-Мариотта
При постоянной температуре объем данного количества газа обратно пропорционален давлению, под которым он находится:
PV = const.
6. Закон Гей-Люссака
При постоянном давлении изменение объема газа прямо пропорционально температуре:
V/T = const.
7. Зависимость между объемом газа, давлением и температурой можно выразить объединенным законом Бойля-Мариотта и Гей-Люссака, которым пользуются для приведения объемов газа от одних условий к другим :
Обратите внимание
P0, V0 ,T0-давление объема и температуры при нормальных условиях: P0=760 мм рт. ст. или 101,3 кПа ; T0=273 К (00С)
ст. или 101,3 кПа ; T0=273 К (00С)
8. Независимая оценка значения молекулярноймассы М может быть выполнена с использованием так называемого уравнения состояния идеального газа или уравнения Клапейрона-Менделеева:
pV=(m/M)*RT=vRT.(1.1)
где р — давление газа в замкнутой системе, V — объем системы, т — масса газа, Т — абсолютная температура, R —универсальная газовая постоянная.
Отметим, что значение постоянной R может быть получено подстановкой величин, характеризующих один моль газа при н.у., в уравнение (1.1):
r = (р V)/( Т)=(101,325кПа 22.4л)/(1 моль 273К)=8.31Дж/моль.К)
Примеры решения задач
Пример 1. Приведение объема газа к нормальным условиям.
Какой объем (н.у.) займут 0,4×10-3 м3 газа, находящиеся при 500С и давлении 0,954×105 Па?
Решение.
Для приведения объема газа к нормальным условиям пользуются общей формулой, объединяющей законы Бойля-Мариотта и Гей-Люссака:
pV/T = p0V0/T0.
Объем газа (н.у.) равен, где Т0 = 273 К; р0 = 1,013×105 Па; Т = 273 + 50 = 323 К;
м3 = 0,32×10-3 м3.
При (н.у.) газ занимает объем, равный 0,32×10-3 м3.
Пример 2. Вычисление относительной плотности газа по его молекулярной массе.
Вычислите плотность этана С2Н6 по водороду и воздуху.
Решение.
Из закона Авогадро вытекает, что относительная плотность одного газа по другому равна отношению молекулярных масс (Мч) этих газов, т.е. D=М1/М2. Если М1 С2Н6 = 30, М2 Н2 = 2, средняя молекулярная масса воздуха равна 29, то относительная плотность этана по водороду равна DН2 = 30/2 =15.
Относительная плотность этана по воздуху: Dвозд = 30/29 = 1,03, т.е. этан в 15 раз тяжелее водорода и в 1,03 раза тяжелее воздуха.
Пример 3. Определение средней молекулярной массы смеси газов по относительной плотности.
Определение средней молекулярной массы смеси газов по относительной плотности.
Вычислите среднюю молекулярную массу смеси газов, состоящей из 80 % метана и 20 % кислорода (по объему), используя значения относительной плотности этих газов по водороду.
Решение.
Часто вычисления производят по правилу смешения, которое заключается в том, что отношение объемов газов в двухкомпонентной газовой смеси обратно пропорционально разностям между плотностью смеси и плотностями газов, составляющих эту смесь. Обозначим относительную плотность газовой смеси по водороду через DН2. она будет больше плотности метана, но меньше плотности кислорода:
;;
80DН2 – 640 = 320 – 20DН2 ; DН2 = 9,6.
Плотность этой смеси газов по водороду равна 9,6. средняя молекулярная масса газовой смеси МН2 = 2DН2 = 9,6×2 = 19,2.
Пример 4. Вычисление молярной массы газа.
Важно
Масса0,327×10-3 м3 газа при 130С и давлении 1,040×105 Па равна 0,828×10-3 кг. Вычислите молярную массу газа.
Вычислите молярную массу газа.
Решение.
Вычислить молярную массу газа можно, используя уравнение Менделеева-Клапейрона:
,
где m – масса газа; М – молярная масса газа; R – молярная (универсальная) газовая постоянная, значение которой определяется принятыми единицами измерения.
Если давление измерять в Па, а объем в м3, то R=8,3144×103 Дж/(кмоль×К).
Источник: https://megaobuchalka.ru/4/43254.html
Формулы для вычисления массы и объема газа
2.1. Относительная плотность газа d равна отношению плотностей (ρ1 и ρ2) газов (при одинаковых давлении и температуре):
d = ρ1: ρ2 ≈ М1 :М2 (2.1)
где М1 и М2 – молекулярные массы газов.
Относительная плотность газа:
по отношению к воздуху: d ≈ М/29
по отношению к водороду: d ≈ М/2
где М, 29 и 2 – соответствующие молекулярные массы данного газа, воздуха и водорода.
2.2. Весовое количество а (в г ) газа в данном объеме V (в дм3):
- а =М *1.
 293 *р *273 * V /28.98 (273 +t) *760 =0.01605 * р *М * V/273 +t (2.2)
293 *р *273 * V /28.98 (273 +t) *760 =0.01605 * р *М * V/273 +t (2.2)
где М – молекулярная масса газа, р – давление газа, мм РТ.ст., t – температура газа, 0С.
Количество газа в г на 1 дм3 при нормальных условиях
а =1.293 : d
где d – относительная плотность газа по отношению к воздуху.
2.3. Объем V, занимаемый данным весовым количеством а газа:
V = а*22.4 *760*(273 +t) /М*р (2.4)
2.5. Газовые смеси
Масса (в г) смеси n образных компонентов, имеющих объемы V1, V2 … Vn и молекулярные массы М1, М2 … Мn, равна
где 22,4 – объем 1 моль вещества в газообразном состоянии при 273 К и 101,32 кПа (0°С и 760мм. рт. ст.)
Так как объем смеси V= V1 + V2 + … + Vn, то 1 дм3 ее имеет массу:
Средняя молекулярная масса М газовой смеси (при аддитивности ее свойств) равна:
Концентрацию компонентов газовых смесей выражают чаще всего в объемных процентах. Объемная концентрация (V1/V·100) численно совпадает с долей парциального давления компонента (р1/р·100) и с его мольной концентрацией (М1/М·100).
Доли отдельных компонентов i в газовой смеси равны, %
массовыеобъемные
где qi – массовое содержание i-го компонента в смеси.
В равных объемах различных газов при одинаковых условиях содержится одинаковое число молекул, поэтому
р1:р2: … = V1:V2: … = М1:М2:…
где М – число молей.
Число молей компонента:
и т.д.
Если газ находится при одних условиях (Р, Т) и необходимо определить его объем или массу при других условиях (Р´, Т´), то используют формулы:
для пересчета объема
для пересчета массы
При Т = const парциальное давление Рнас насыщенного пара в газовой смеси вне зависимости от общего давления постоянно. При 101,32 кПа и Т К 1 моль газа или пара занимает объем 22,4 (Т/273)дм3. Если давление пара при этой температуре равно Рнас, то объем 1 моль равен:
Таким образом, масса 1м3 пара молекулярной массы М при температуре Т и давлении Рнас равна, в г/м3
Зная массовое содержание насыщенного пара в 1м3 смеси, можно вычислить его давление:
Объем сухого газа вычисляют по формуле:
где Рнас. ,Т – давление насыщенного водяного пара при температуре Т.
,Т – давление насыщенного водяного пара при температуре Т.
Приведение объемов сухого V(Т,Р)сух. и влажного V(Т,Р)вл. газов к нормальным условиям (н.у.) (273 К и 101,32 кПа) производят по формулам:
Формулой
пользуются для пересчета объема влажного газа, находящегося при Р и Т, к другим Р´, Т´, при условии, что с изменением температуры меняется и равновесное давление водяного пара. Выражения для пересчета объемов газа в разных условиях аналогичны:
Совет
Если давление водяного пара насыщенного пара при какой-либо температуре равно Рнас., а необходимо вычислить Gн.у. – содержание его в 1 м3 газа при н.у., то используют уравнение (1.2), но в этом случае Т не есть температура насыщения, а равна 273 К.
Отсюда следует, что:
Gн.у. = 4,396·10-7 Мрнас..
Давление насыщенного водяного пара, если известно его содержание в 1м3 при н.у. вычисляют по формуле:
Источник: https://homework.net.ua/formuly-dlya-vychisleniya-massy-i-obema-gaza/
10.
 6: Гипотеза Авогадро и молярный объем
6: Гипотеза Авогадро и молярный объем- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 53770
Как аквалангисты узнают, кончится ли у них бензин?
Знание количества газа, доступного для погружения, имеет решающее значение для выживания дайвера. Баллон на спине дайвера оснащен датчиками, показывающими, сколько газа присутствует и какое давление. Базовые знания о поведении газа позволяют дайверу оценить, как долго он может оставаться под водой без возникновения проблем.
Гипотеза Авогадро и молярный объем
Объем — это третий способ измерения количества материи после подсчета предметов и массы. У жидкостей и твердых тел объем сильно различается в зависимости от плотности вещества. Это связано с тем, что твердые и жидкие частицы упакованы близко друг к другу с очень небольшим пространством между частицами. Однако газы в основном состоят из пустых пространств между реальными частицами газа (см. рисунок ниже).
Рисунок \(\PageIndex{2}\): Частицы газа очень малы по сравнению с большим количеством пустого пространства между ними. (Источник: Christopher Auyeung; Источник: CK-12 Foundation; Лицензия: CC BY-NC 3.0 (opens in new window)) В 1811 году Амадео Авогадро объяснил, что объемы всех газов можно легко определить. Гипотеза Авогадро утверждает, что равные объемы всех газов при одинаковых температуре и давлении содержат равное количество частиц. Поскольку общий объем, который занимает газ, состоит в основном из пустого пространства между частицами, фактический размер самих частиц почти незначителен. Заданный объем газа с небольшими легкими частицами, такими как водород \(\left( \ce{H_2} \right)\), содержит такое же количество частиц, как и такой же объем тяжелого газа с крупными частицами, такими как гексафторид серы, \(\ce{SF_6}\).
Заданный объем газа с небольшими легкими частицами, такими как водород \(\left( \ce{H_2} \right)\), содержит такое же количество частиц, как и такой же объем тяжелого газа с крупными частицами, такими как гексафторид серы, \(\ce{SF_6}\).
Газы сжимаемы, а это означает, что под высоким давлением частицы сближаются. Это уменьшает количество пустого пространства и уменьшает объем газа. Объем газа также зависит от температуры. Когда газ нагревается, его молекулы движутся быстрее, и газ расширяется. Из-за изменения объема газа из-за изменений давления и температуры сравнение объемов газа необходимо проводить при стандартной температуре и давлении. Стандартная температура и давление (СТП) 9{23}\) частиц. Однако масса каждого газа различна и соответствует молярной массе этого газа: \(4,00 \: \text{г/моль}\) для \(\ce{He}\), \(28,0 \:\ text{г/моль}\) для \(\ce{N_2}\) и \(16,0 \: \text{г/моль}\) для \(\ce{CH_4}\).
Рисунок \(\PageIndex{4}\): Гипотеза Авогадро утверждает, что равные объемы любого газа при одинаковых температуре и давлении содержат одинаковое количество частиц. При стандартной температуре и давлении 1 моль любого газа занимает \(22,4 \: \text{L}\). (Источник: Christopher Auyeung; Источник: CK-12 Foundation; Лицензия: CC BY-NC 3.0 (откроется в новом окне))
При стандартной температуре и давлении 1 моль любого газа занимает \(22,4 \: \text{L}\). (Источник: Christopher Auyeung; Источник: CK-12 Foundation; Лицензия: CC BY-NC 3.0 (откроется в новом окне)) Резюме
- Равные объемы газов при одинаковых условиях содержат одинаковое количество частиц.
- Стандартная температура и давление сокращенно (STP).
- Стандартная температура 0°C (273,15 K), стандартное давление 1 атм.
- При нормальных условиях один моль любого газа занимает объем 22,4 л
Обзор
- Контейнер заполнен газом, что мы знаем о пространстве, фактически занимаемом газом?
- Почему мы должны проводить все наши сравнения при одной и той же температуре и давлении?
- При стандартной температуре и давлении 1 моль газа всегда равен количеству литров?
Эта страница под названием 10. 6: Гипотеза и молярный объем Авогадро распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
6: Гипотеза и молярный объем Авогадро распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
ЛИЦЕНЗИЯ ПОД
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Фонд СК-12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать страницу TOC
- № на стр.

- Теги
- источник@https://flexbooks.ck12.org/cbook/ck-12-chemistry-flexbook-2.0/
Закон идеального газа
Закон идеального газаИдеальный газ определяется как газ, в котором все столкновения между атомами или молекулами абсолютно упругие и в котором нет сил межмолекулярного притяжения. Можно представить себе это как набор совершенно твердых сфер, которые сталкиваются, но в остальном не взаимодействуют друг с другом. В таком газе вся внутренняя энергия находится в виде кинетической энергии, и любое изменение внутренней энергии сопровождается изменением температуры. Идеальный газ можно охарактеризовать тремя переменными состояния: абсолютным давлением (P), объемом (V) и абсолютной температурой (T).
Закон идеального газа можно рассматривать как результат кинетического давления молекул газа, сталкивающихся со стенками сосуда в соответствии с законами Ньютона. Но есть и статистический элемент в определении средней кинетической энергии этих молекул. Температура считается пропорциональной этой средней кинетической энергии; это вызывает идею кинетической температуры. Один моль идеального газа при СТП занимает 22,4 литра.
| Индекс Концепции газового закона Концепции кинетической теории | ||
|
В кинетической теории газов существуют определенные константы, ограничивающие непрекращающуюся молекулярную активность. Свойства газа описываются в терминах переменных состояния. Свойства газа описываются в терминах переменных состояния.
| Индекс Концепции кинетической теории | ||
| Назад |
Переменная состояния — это точно измеримое физическое свойство, которое
характеризует состояние системы независимо от того, как система
довели до такого состояния. Типичными примерами переменных состояния являются давление P, объем V и температуры T. В законе идеального газа состояние n молей газа точно определяется этими тремя переменными состояния. Если свойство, например, энтальпия H, определяется как комбинация других переменных состояния, то это тоже состояние переменная. Энтальпия является одним из четырех «термодинамических потенциалов», а остальные три, внутренняя энергия U, свободная энергия Гельмгольца F и свободная энергия Гиббса G, также являются переменными состояния. Энтропия S также является переменной состояния. В некоторых текстах используется термин «термодинамическая переменная» вместо описания «переменная состояния». | Индекс Концепции кинетической теории | ||||||||||||||||||||||
| Назад |
10.7: Преобразование молей в объем газа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 53771
Как узнать, сколько газа в этих контейнерах?
Небольшие газовые баллоны часто используются для подачи газов для химических реакций. Газометр даст некоторую информацию о том, сколько газа в баке, но нужны количественные оценки, чтобы реакция могла протекать до конца. Знание того, как рассчитать необходимые параметры для газов, очень полезно, чтобы избежать их исчерпания раньше, чем хотелось бы.
Газометр даст некоторую информацию о том, сколько газа в баке, но нужны количественные оценки, чтобы реакция могла протекать до конца. Знание того, как рассчитать необходимые параметры для газов, очень полезно, чтобы избежать их исчерпания раньше, чем хотелось бы.
Преобразование между молями и объемом газа
Молярный объем при нормальных условиях можно использовать для преобразования молей в объем газа и из объема газа в моли. Равенство \(1 \: \text{mol} = 22,4 \: \text{L}\) является основой для коэффициента преобразования.
Пример \(\PageIndex{1}\): преобразование объема газа в моли
Многие металлы реагируют с кислотами с образованием газообразного водорода. В ходе определенной реакции образуется \(86,5 \: \text{L}\) газообразного водорода при нормальных условиях. Сколько молей водорода было получено?
Решение
Шаг 1: Перечислите известные количества и спланируйте задачу. Известно- \(86.
 5 \: \text{L} \: \ce{H_2}\)
5 \: \text{L} \: \ce{H_2}\) - \(1 \: \text{моль} = 22,4 \: \text{L}\)
- моль H 2
Примените коэффициент преобразования литров в моли.
Шаг 2: Расчет.\[86,5 \: \text{L} \: \ce{H_2} \times \frac{1 \: \text{моль} \: \ce{H_2}}{22,4 \: \text{L} \: \ce{H_2}} = 3,86 \: \text{mol} \: \ce{H_2}\nonumber \]
Шаг 3: Подумайте о своем результате.Объем произведенного газа почти в четыре раза превышает молярный объем. Тот факт, что газ является водородом, не играет никакой роли в расчетах.
Пример \(\PageIndex{2}\): преобразование молей в объем газа
Какой объем \(4,96 \: \text{моль}\) из \(\ce{O_2}\) занимает при STP?
Решение
Шаг 1: Перечислите известные количества и спланируйте задачу .
Известно- \(4.96 \: \text{моль} \: \ce{O_2}\)
- \(1 \: \text{моль} = 22,4 \: \text{L}\)
- Объем O 2

\[4,96 \: \text{моль} \times 22,4 \: \text{л/моль} = 111,1 \: \text{л}\номер \]
Шаг 3: Подумайте о своем результате.Объем кажется правильным, учитывая количество молей.
Пример \(\PageIndex{3}\): Преобразование объема в массу
Если мы знаем объем пробы газа на STP, мы можем определить, сколько массы присутствует. Предположим, у нас есть \(867 \: \text{L}\) из \(\ce{N_2}\) в STP. Какова масса газообразного азота?
Решение
Шаг 1: Перечислите известные количества и спланируйте задачу. Известно- \(867 \: \text{L} \: \ce{N_2}\)
- \(1 \: \text{моль} = 22,4 \: \text{L}\)
- Молярная масса \(\ce{N_2} = 28,02 \: \text{г/моль}\)
- Масса N 2
Начнем с определения количества молей присутствующего газа. Мы знаем, что 22,4 литра газа при нормальных условиях равны одному молю, поэтому:
\[867 \: \text{L} \times \frac{1 \: \text{mol}}{22,4 \: \text{L}} = 38,7 \: \text{mol}\nonumber \]
Мы также знаем молекулярную массу \(\ce{N_2}\) \(\left( 28,0 \: \text{г/моль} \right)\), поэтому мы можем вычислить вес газообразного азота в 867 литры:
\[38,7 \: \text{моль} \times \frac{28 \: \text{г}}{1 \: \text{моль}} = 1083,6 \: \text{г} \: \ ce{N_2}\nonumber \]
Шаг 3: Подумайте о своем результате.
В многошаговой задаче убедитесь, что единицы проверены.
Резюме
- Показаны преобразования между молями и объемом газа.
Обзор
- Почему в приведенных выше задачах газ всегда имел нормальную температуру и давление?
- Контейнер содержит 45,2 л газа N 2 при нормальных условиях. Сколько молей газа N 2 в сосуде?
- Если в предыдущей задаче газом был CH 4 газ при СТП вместо N 2 газ, то сколько молей CH 4 газ будет?
Эта страница под названием 10.7: Conversions Between Moles and Gas Volume используется в соответствии с лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
Платформа; подробная история редактирования доступна по запросу.
ЛИЦЕНЗИЯ ПОД
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Фонд СК-12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать страницу TOC
- № на стр.
- Теги
- источник@https://flexbooks.
 ck12.org/cbook/ck-12-chemistry-flexbook-2.0/
ck12.org/cbook/ck-12-chemistry-flexbook-2.0/
- источник@https://flexbooks.
Определение родинки Учебное пособие по химии
Пожалуйста, не блокируйте рекламу на этом сайте.
Нет рекламы = нет денег для нас = нет бесплатных вещей для вас!
Концепции крота
Номер Авогадро, N
A| Справа на схеме 1 дюжина яиц, каждое яйцо представлено как 0 . «Дюжина» — это термин, используемый для обозначения определенного числа, на самом деле 12. 1 дюжина яиц = 12 яиц |
|
Если бы у вас было 12 коробок с дюжиной яиц, у вас было бы огромное количество яиц.
«Гросс» — это термин, используемый для обозначения 12 дюжин чего-то.
Термин «число Авогадро» — это просто название, данное определенному числу.
Число Авогадро чрезвычайно велико: 602 200 000 000 000 000 000 000
, поэтому мы обычно записываем его в экспоненциальном представлении: 6,022 × 10 23
Крот, n
| Справа на схеме 1 дюжина яиц, каждое яйцо представлено как 0 , и каждое яйцо находится на своем месте в коробке. 1 коробка яиц содержит 1 дюжину яиц 1 коробка яиц = 1 дюжина яиц Слово «картон» относится к набору из 1 дюжины яиц. 1 коробка яиц = 1 дюжина яиц = 12 яиц |
|
Если у вас есть коллекция из 6,022 × 10 23 вещей, эта коллекция называется кротом.
1 моль любого вещества содержит число Авогадро:
1 моль яиц = N A яиц = 6,022 × 10 23 яиц
1 моль частиц пыли = N A частиц пыли = 6,022 × 10 23 частиц пыли
1 моль песчинок = N A песчинок = 6,022 × 10 23 песчинок
1 моль капель воды = N A капель воды = 6,022 × 10 23 капель воды
1 моль молекул воды = N A молекул воды = 6,022 × 10 23 молекул воды
1 моль атомов водорода = N A атомов водорода = 6,022 × 10 23 атомов водорода
Молярная масса, М
| Справа на схеме 1 дюжина очень больших яиц, каждое очень большое яйцо представлено как 0 , и каждое яйцо находится в своем собственном месте в коробке. Масса каждого очень большого яйца составляет 55 грамм. масс яиц в 1 коробке особо крупных яиц = 1 дюжина яиц × масса каждого очень большого яйца = 12 × 55 г = 660 г |
|
Справа на схеме 1 дюжина маленьких яиц, каждое маленькое яйцо представлено как 0 и каждое яйцо сидит на своем месте в коробке. Каждое маленькое яйцо имеет массу 25 грамм. масс яиц в 1 коробке мелких яиц = 1 дюжина яиц × масса каждого маленького яйца = 12 × 25 г = 300 г |
|
В коробке всегда содержится 1 дюжина яиц.
1 дюжина яиц всегда равна 12 яйцам.
Но масса коробки из 1 дюжины яиц зависит от «идентичности» яиц, то есть маленькие яйца имеют меньшую массу, чем очень большие яйца.
То же самое верно для молей атомов и молекул.
Моль атомов всегда содержит 6,022 × 10 23 атомов, но масса этого моля зависит от массы атомов.
Атомы разных элементов имеют разную массу, поэтому масса моля атомов одного элемента будет отличаться от массы моля атомов другого элемента.
Молярная масса атомов
молей атомов элемента аналогичны приведенной выше аналогии с коробкой яиц:
1 моль атомов всегда содержит число атомов Авогадро
1 моль атомов всегда содержит N A атомов
1 моль атомов всегда содержит 6,022 × 10 23 атомов
Но масса 1 моля атомов будет зависеть от «идентичности» атомов.
«Идентичность» атома определяется тем, к какому элементу принадлежат атомы.
Атомы разных элементов имеют разные относительные атомные массы (атомные веса).
Можно найти относительную атомную массу (или атомный вес), M r , для атома любого элемента Периодической таблицы элементов.
Масса 1 моля атомов элемента – это относительная атомная масса (атомный вес) элемента, выраженная в граммах.
Масса 1 моля атомов элемента называется молярной массой элемента и выражается в граммах на моль, г-моль -1
Ниже приведена таблица некоторых элементов, с которыми вы столкнетесь на курсе химии:
| Наименование элемента | Символ элемента | Относительная атомная масса (атомный вес) | Количество атомов в 1 моле (N A ) | Масса 1 моля атомов (г) | Молярная масса атомов (г моль -1 ) |
|---|---|---|---|---|---|
| водород | Х | 1. 008 008 | 6,022 × 10 23 атомов Н | 1,008 г | 1,008 г моль -1 |
| уголь | С | 12.01 | 6,022 × 10 23 атомов C | 12,01 г | 12,01 г моль -1 |
| азот | Н | 14.01 | 6,022 × 10 23 Атомы N | 14,01 г | 14,01 г моль -1 |
| кислород | О | 16.00 | 6,022 × 10 23 атомов О | 16,00 г | 16,00 г моль -1 |
Молярная масса молекул
(8)Молекула состоит из 2 или более атомов, химически соединенных (связанных) вместе.
1 моль молекул всегда содержит число молекул Авогадро
1 моль молекул всегда содержит N A молекул
1 моль молекул всегда содержит 6,022 × 10 23 молекул
Но масса 1 моля молекул будет зависеть от «идентичности» молекул.
«Идентичность» молекулы определяется количеством атомов каждого элемента, из которых состоит молекула.
Для каждой молекулы можно написать молекулярную формулу.
Для каждой молекулярной формулы, которую мы можем написать, мы можем определить относительную молекулярную массу молекулы.
И точно так же, как мы сделали для примеров атомов элементов выше, 1 моль молекул будет иметь массу, равную его относительной молекулярной массе, выраженной в граммах.
Относительная молекулярная масса, выраженная в граммах, известна как молярная масса молекулы.
Ниже приведена таблица некоторых молекул, с которыми вы столкнетесь на курсе химии:
| Название Молекула | Молекулярная Формула | Относительный Молекулярный Массовый | Количество молекул в 1 моле (N A ) | Масса 1 моль молекул (г) | Молярная масса молекулы (г моль -1 ) |
|---|---|---|---|---|---|
| кислород | О 2 | 32,00 | 6,022 × 10 23 O 2 молекулы | 32,00 г | 32,00 г моль -1 |
| азот | Н 2 | 28. 02 02 | 6,022 × 10 23 N 2 молекулы | 28,02 г | 28,02 г моль -1 |
| вода | Н 2 О | 18.016 | 6,022 × 10 23 H 2 Молекулы O | 18,016 г | 18,016 г моль -1 |
| аммиак | НХ 3 | 17.034 | 6,022 × 10 23 NH 3 молекулы | 17,034 г | 17,034 г моль -1 |
Молярный объем газа, V
мВы наверняка видели, как воздушный шар наполняется гелием из газового баллона.
Чем больше гелия попадает в воздушный шар, тем больше объем воздушного шара.
Это происходит потому, что атомы гелия, составляющие газообразный гелий, занимают как можно больший объем.
И этот объем определяется количеством атомов гелия в воздушном шаре, а также температурой и давлением воздуха.
Если бы вы одновременно наполнили один шарик 1 молем атомов гелия, а другой шарик 1 молем атомов аргона, вы бы обнаружили, что оба шарика наполнятся и займут один и тот же объем.
Объем 1 моля газа зависит от окружающей температуры и давления, а не от «идентичности» атомов или молекул, составляющих газ! (9)
Объем 1 моля газа называется его молярным объемом и обозначается символом V м .
Молярный объем газа является полезным термином, ТОЛЬКО если вы знаете преобладающие условия температуры и давления.
Молярный объем газа, V
м , при стандартной температуре и давлении Стандартная температураопределяется как 0°C (примерно 273,15 K).
Стандартное давление определяется как 100 кПа (или 0,987 атм)
Следовательно, условия стандартной температуры и давления составляют 0°C (273,15 K) и 100 кПа (0,987 атм).
Стандартная температура и давление обычно обозначаются аббревиатурой STP.
Объем 1 моля любого идеального газа при температуре 0°С и давлении 100 кПа равен 22,71 л.
Объем 1 моля любого идеального газа при стандартной температуре и давлении равен 22,71 л.
Объем 1 моля любого идеального газа при нормальных условиях составляет 22,71 л.
Для идеального газа при 0°C и 100 кПа молярный объем газа V м равен 22,71 л.
Для идеального газа при стандартной температуре и давлении молярный объем газа V м составляет 22,71 л.
Для идеального газа при СТП молярный объем газа, V м , составляет 22,71 л.
Ниже приведена таблица молярного объема некоторых газов, с которыми вы столкнетесь на курсе химии:
| Название газа | Молекулярная формула | Относительная молекулярная масса | Молярная масса газа (г моль -1 ) | Количество молекул газа в 1 моле (N A ) | Молярный объем газа при нормальных условиях (л) |
|---|---|---|---|---|---|
| гелий | Он | 4.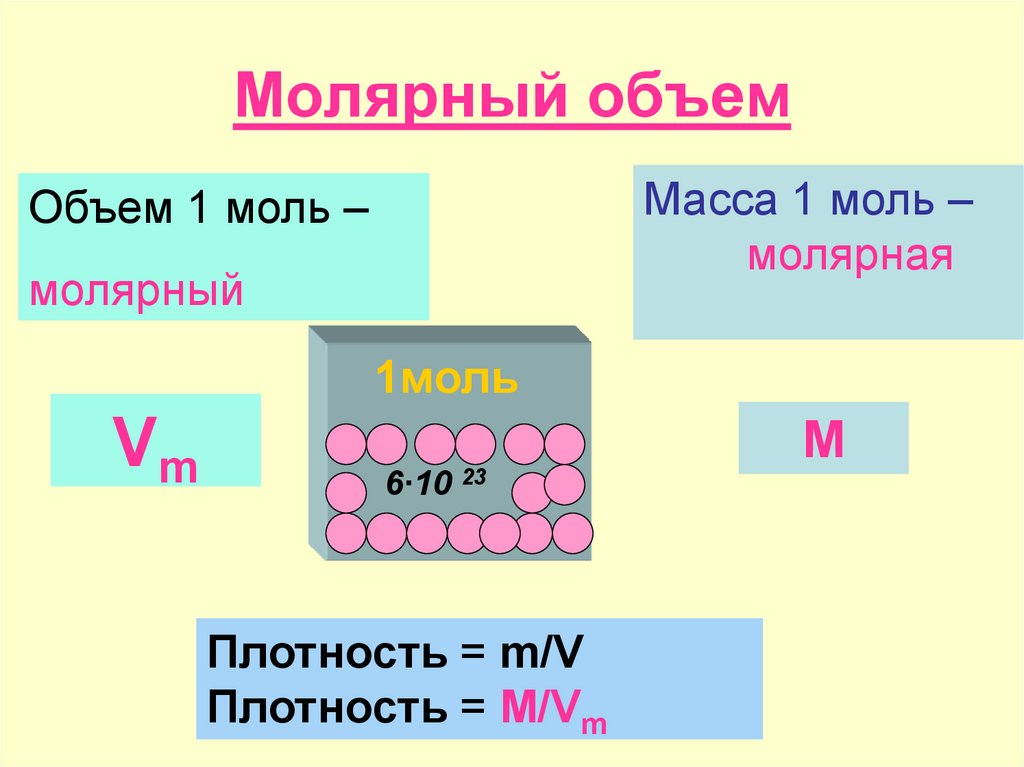 003 003 | 4,003 г моль -1 | 6,022 × 10 23 Атомы He | 22,71 л |
| азот | Н 2 | 28.02 | 28,02 г моль -1 | 6,022 × 10 23 N 2 молекулы | 22,71 л |
| окись углерода | СО | 28.01 | 28,01 г моль -1 | 6,022 × 10 23 Молекулы CO | 22,71 л |
| двуокись углерода | СО 2 | 44.01 | 44,01 г моль -1 | 6,022 × 10 23 CO 2 молекулы | 22,71 л |
Молярный объем газа, V
м , при 25°C и 100 кПа Хотя 0°C является очень удобным стандартом температуры, на самом деле это не та температура, которую вы хотели бы поддерживать в лаборатории во время работы.
Таким образом, химики определяют в качестве стандарта полезную температуру и давление в зависимости от вида выполняемой ими работы.
В некоторых случаях 25°C (298,15 K) и 100 кПа (0,987 атм) используется для определения стандарта и затем упоминается как стандартные лабораторные условия (сокращенно SLC) или стандартные температура и давление окружающей среды (сокращенно SATP).
1 моль любого идеального газа при 25°C и 100 кПа имеет объем 24,79 л.
Молярный объем, V м , любого идеального газа при 25°C и 100 кПа равен 24,79 л.
Ниже приведена таблица молярного объема некоторых газов, с которыми вы столкнетесь на курсе химии:
| Название газа | Молекулярная формула | Относительная молекулярная масса | Молярная масса газа (г моль -1 ) | Количество молекул газа в 1 моле (N A ) | Молярный объем газа при SLC (л) |
|---|---|---|---|---|---|
| гелий | Он | 4. 003 003 | 4,003 г моль -1 | 6,022 × 10 23 Атомы He | 24,79 л |
| азот | Н 2 | 28.02 | 28,02 г моль -1 | 6,022 × 10 23 N 2 молекулы | 24,79 л |
| окись углерода | СО | 28.01 | 28,01 г моль -1 | 6,022 × 10 23 Молекулы CO | 24,79 л |
| двуокись углерода | СО 2 | 44.01 | 44,01 г моль -1 | 6,022 × 10 23 CO 2 молекулы | 24,79 л |
Рабочие примеры с использованием определения крота
Рабочий пример определения крота: число Авогадро (N
A )Вопрос: Сколько молекул хлора Cl 2 содержится в 1 моле газообразного хлора Cl 2 (г)?
Решение:
- Какой вопрос просит вас сделать?
Рассчитайте количество молекул хлора в 1 моле газообразного хлора.

- Какая информация (данные) была дана в вопросе? Молекулярная формула
для молекул хлора: Cl 2
количество газообразного хлора = 1 моль
- Какая связь существует между молями и количеством присутствующих молекул?
1 моль молекул = N A молекул = 6,022 × 10 23 молекул
- Замените слово «молекулы» выше на конкретную молекулу, указанную в вопросе, «Cl 2 молекулы»:
1 моль Cl 2 молекул = N A Cl 2 молекул = 6,022 × 10 23 Cl 2 молекул
- Укажите свой ответ:
1 моль газообразного хлора содержит 6,022 × 10 23 молекул хлора.
Рабочий пример определения молей: Молярная масса (M)
Вопрос: Какова масса 1 моля метана, CH 4 , молекул?
Решение:
- Какой вопрос просит вас сделать?
Рассчитайте массу 1 моля молекул метана.

- Какая информация (данные) была дана в вопросе? Молекулярная формула
для молекул метана: CH 4
количество метана = 1 моль
- Какая связь существует между молями и массой молекул?
масс 1 моль молекул = относительная молекулярная масса, выраженная в граммах
- Расчет относительной молекулярной массы метана, M r (CH 4 )
Используйте периодическую таблицу, чтобы найти относительную атомную массу (атомный вес) углерода, M r (C), и водорода, M r (H):
М р (С) = 12,01
М r (Н) = 1,008
CH 4 содержит 1 атом углерода и 4 атома водорода, поэтому
M r (CH 4 ) = 1 × M r (C) + 4 × M r (H) = 1 x 12,01 + 4 × 1,008 = 16,042
- Рассчитайте массу 1 моля CH 4 :
масса 1 моля CH 4 = M r (CH 4 ), выраженная в граммах
масса 1 моля CH 4 = 16,042 г
- Укажите свой ответ:
Масса 1 моля метана, CH 4 , составляет 16,042 г.

Рабочий пример определения молей: молярный объем газа (V
м )Вопрос: Какой объем занимают 32,00 г газообразного кислорода O 2 (g) при температуре 0°C и давлении 100 кПа?
Решение:
- Что за вопрос просит вас сделать?
Рассчитайте объем газообразного кислорода.
- Какая информация (данные) была дана в вопросе? Молекулярная формула
газообразного кислорода: O 2 (г)
масса газообразного кислорода = m(O 2(г) ) = 32,00 г
условий проведения эксперимента: температура = 0°С, давление = 100 кПа
Напомним: 0°C и 100 кПа = стандартная температура и давление (STP)
- Какая связь существует между массой газа и его объемом при СТП?
При нормальных условиях 1 моль газа имеет объем 22,71 л.
1 моль газа имеет массу, равную его относительной молекулярной массе, выраженной в граммах.

- Расчет относительной молекулярной массы газообразного кислорода, M р (О 2(г) ):
Используйте периодическую таблицу, чтобы найти относительную атомную массу (атомный вес) для атомов кислорода, M r (O):
М р (О) = 16,00
Каждая молекула кислорода O 2 содержит 2 атома кислорода (O), поэтому
M r (O 2 ) = 2 × M r (O) = 2 × 16,00 = 32,00
- Рассчитайте массу 1 моля молекул кислорода, m(O 2(g) )
масса 1 моля O 2 молекул = m(O 2 ) = M r (O 2 ) в граммах = 32,00 г
Обратите внимание, что масса O 2 (г), указанная в вопросе, составляет 32,00 г, поэтому вопрос касается объема 1 моля O 2 (г).
- Рассчитайте объем 1 моля O 2 (г):
При нормальных условиях 1 моль газа имеет объем 22,71 л.

При STP 1 моль O 2 (g) имеет объем 22,71 л.
- Укажите свой ответ:
32,00 г газообразного кислорода имеет объем 22,71 л при 0°C и 100 кПа.
ИДЕАЛЬНЫЕ ГАЗЫ И ЗАКОН ИДЕАЛЬНЫХ ГАЗОВ На этой странице рассматриваются предположения, сделанные в кинетической теории об идеальных газах, и вводный обзор закона идеального газа: pV = nRT. Это предназначено только как введение, подходящее для студентов-химиков примерно на стандартном уровне Великобритании (для 16–18 лет), и поэтому здесь нет попытки вывести закон идеального газа с использованием расчетов в физическом стиле. Предположения кинетической теории об идеальных газах Конечно, идеального газа не существует, но многие газы ведут себя примерно так, как если бы они были идеальными при обычных рабочих температурах и давлениях. Предположения:
И затем два абсолютно ключевых предположения, потому что это два самых важных отличия реальных газов от идеальных: Уравнение идеального газа Уравнение идеального газа: пВ = нРТ В целом, это уравнение легко запомнить и использовать. Проблемы кроются почти полностью в агрегатах. Изучение различных терминов Давление, стр. Давление измеряется в паскалях, Па — иногда выражается в ньютонах на квадратный метр, Н·м -2 . Эти слова означают одно и то же. Будьте осторожны, если давление указано в кПа (килопаскалях). Например, 150 кПа — это 150 000 Па. Вы должны сделать это преобразование, прежде чем использовать уравнение идеального газа. Если вы хотите преобразовать другие измерения давления: Объем, В Наиболее вероятно, что вы ошибетесь при использовании этого уравнения. Это потому, что единицей объема в системе СИ является кубический метр, м 3 — , а не см 3 или дм 3 . 1 м 3 = 1000 дм 3 = 1 000 000 см 3 Таким образом, если вы вводите значения объема в уравнение, вам сначала нужно преобразовать их в кубические метры. Вам придется разделить объем в дм 3 на 1000, или в см 3 на миллион. Точно так же, если вы вычисляете объем с помощью уравнения, не забудьте преобразовать ответ в кубических метрах в дм 3 или см 3 , если вам нужно — на этот раз умножив на 1000 или миллион. Если вы сделаете это неправильно, вы получите глупый ответ, отличающийся в тысячу или миллион раз. Так что обычно довольно очевидно, если вы сделали что-то не так, и вы можете проверить еще раз. Число молей, n Это, конечно, просто — это просто число. Вы уже знаете, что вычисляете это путем деления массы в граммах на массу одного моля в граммах. Чаще всего вы будете использовать уравнение идеального газа, сначала сделав замену, чтобы получить: Я не рекомендую вам запоминать уравнение идеального газа в этой форме, но вы должны быть уверены, что сможете преобразовать его в эту форму. Газовая постоянная, Р Значение для R будет предоставлено вам, если оно вам нужно, или вы можете найти его в источнике данных. Значение СИ для R составляет 8,31441 Дж К -1 моль -1 . | ||
Примечание: Вы можете встретить другие значения для этого с другими единицами измерения. Обычно используемый в прошлом был 82,053 см 3 атм K -1 моль -1 . Единицы говорят вам, что объем будет в кубических сантиметрах, а давление в атмосферах. К сожалению, единицы измерения в версии СИ не столь очевидны. | ||
Температура, Т Температура должна быть в кельвинах. Не забудьте добавить 273, если вам дана температура в градусах Цельсия. Использование уравнения идеального газа Расчеты по уравнению идеального газа включены в мою книгу расчетов (см. Молярный объем при ст. Если вы производили простые расчеты по уравнениям, вы, вероятно, использовали молярный объем газа. 1 моль любого газа занимает 22,4 дм 3 при ст. ст. (стандартные температура и давление, принятые за 0°С и давление в 1 атмосферу). Возможно, вы также использовали значение 24,0 дм 3 при комнатной температуре и давлении (примерно 20°C и 1 атмосфера). На самом деле эти цифры верны только для идеального газа, и мы посмотрим, откуда они взялись. Мы можем использовать уравнение идеального газа для расчета объема 1 моля идеального газа при 0°C и давлении в 1 атмосферу. Во-первых, мы должны правильно подобрать единицы измерения. 0°C составляет 273 K. 1 атмосфера = 101325 Па p = 101325 Па Мы знаем, что n = 1, потому что пытаемся рассчитать объем 1 моля газа. И, наконец, R = 8,31441 Дж К -1 моль -1 . Вписывая все это в уравнение идеального газа, а затем переставляя его, мы получаем: И, наконец, поскольку нас интересует объем в кубических дециметрах, вам нужно не забыть умножить его на 1000, чтобы перевести кубические метры в кубические дециметры. Таким образом, молярный объем идеального газа равен 22,4 дм 3 при ст. И, конечно же, вы можете переделать это вычисление, чтобы найти объем 1 моля идеального газа при комнатной температуре и давлении — или при любой другой температуре и давлении. Нахождение относительной формулы массы газа по его плотности Это так же сложно, как и при использовании уравнения идеального газа. Плотность этана 1,264 г дм -3 при 20°С и 1 атмосфере. Значение плотности означает, что 1 дм 3 этана весит 1,264 г. Опять же, прежде чем мы займемся чем-то еще, разберитесь с неудобными юнитами. Давление в 1 атмосферу равно 101325 Па. Объем 1 дм 3 необходимо перевести в кубические метры, разделив на 1000. У нас есть объем 0,001 м 3 . Температура 293 К. Теперь поместите все числа в форму уравнения идеального газа, которое позволяет вам работать с массами, и измените его так, чтобы вычислить массу 1 моля. Масса 1 моля чего-либо — это просто относительная формула массы в граммах. Таким образом, относительная формула массы этана равна 30,4, т. е. 3 сиг. Теперь, если вы сложите относительную формулу массы этана, C 2 H 6 , используя точные значения относительных атомных масс, вы получите ответ 30,07 с точностью до 4 значащих цифр. Есть две возможности.
Если вам нужно узнать о реальных газах, сейчас самое время прочитать о них.
Для исследования реальных газов. . . В меню кинетической теории. . . В меню «Физическая химия» . . . В главное меню . . . © Джим Кларк, 2010 г. (последнее изменение: июль 2017 г.) | ||
Закон идеального газа и некоторые приложения
Цели обучения
- Изучить закон идеального газа.
- Применить закон идеального газа к любому набору условий газа.
- Применение закона идеального газа к молярным объемам, плотности и стехиометрии.
До сих пор все газовые законы, которые мы рассматривали, требовали, чтобы газ менял свои условия; затем мы предсказываем результирующее изменение одного из его свойств. Существуют ли газовые законы, связывающие физические свойства газа в любой момент времени?
Существуют ли газовые законы, связывающие физические свойства газа в любой момент времени?
Рассмотреть возможность дальнейшего расширения комбинированного закона о газах, включив в него n . По аналогии с законом Авогадро n располагаются в знаменателе дроби напротив объема. Итак,
Поскольку давление, объем, температура и количество являются единственными четырьмя независимыми физическими свойствами газа, константа в приведенном выше уравнении действительно является константой; действительно, поскольку нам не нужно указывать идентичность газа, чтобы применить газовые законы, эта константа одинакова для всех газов. Определим эту константу символом R , поэтому предыдущее уравнение записывается как
, которое обычно преобразуется в
PV = nRT
Это уравнение называется законом идеального газа. Он связывает четыре независимых свойства газа в любой момент времени. Константа R называется постоянной закона идеального газа. Его значение зависит от единиц, используемых для выражения давления и объема. В таблице 6.1 «Значения постоянной закона идеального газа R » перечислены числовые значения Р .
Его значение зависит от единиц, используемых для выражения давления и объема. В таблице 6.1 «Значения постоянной закона идеального газа R » перечислены числовые значения Р .
Таблица 6.1 Значения постоянной закона идеального газа R
| Числовое значение | Единицы |
|---|---|
| 0,08205 | л·атм/моль·K |
| 62,36 | л·торр/моль·К = л·мм рт.ст./моль·К |
| 8.314 | Дж/моль·К |
Закон для идеального газа используется так же, как и любой другой закон для газа, с уделением особого внимания единицам измерения и обязательному выражению температуры в градусах Кельвина. Однако закон идеального газа не требует изменения условий газовой пробы . Закон идеального газа подразумевает, что если вы знаете любые три физических свойства газа, вы можете вычислить четвертое свойство.
Пример 9
Образец 4,22 моль Ar имеет давление 1,21 атм и температуру 34°C. Каков его объем?
Каков его объем?
Решение
Первым шагом является преобразование температуры в кельвины:
34 + 273 = 307 K
Теперь мы можем подставить условия в закон идеального газа:
Единица атм находится в числителе обеих сторон, поэтому она отменяется. В правой части уравнения единицы моль и К появляются в числителе и знаменателе, поэтому они также сокращаются. Единственная оставшаяся единица — это L, которая является единицей объема, которую мы ищем. Мы изолируем переменную объема, разделив обе части уравнения на 1,21:
Затем, решая объем, получаем
V = 87,9 л
Проверь себя
Образец O 9 0,0997 моль0160 2 имеет давление 0,692 атм и температуру 333 К. Каков его объем? Пример 10
Решение
Нам не дано количество молей Hg напрямую, но нам дан вес. Мы можем использовать молярную массу Hg для преобразования в число молей.
Давление указано в миллиметрах ртутного столба. Мы можем либо преобразовать это в атмосферу, либо использовать значение постоянной идеального газа, которое включает единицу измерения в мм рт. ст. Мы возьмем второй вариант. Подставляя в закон идеального газа,
ст. Мы возьмем второй вариант. Подставляя в закон идеального газа,
Единицы мм рт.ст., л и моль сокращаются, оставляя единицу К, единицу измерения температуры. Выделив T отдельно с одной стороны, мы получим
Затем, решив K, мы получим
T = 507 K
Проверь себя
Для образца 0,00554 моль H 2 , P = 23,44 торр и T = 557 К. Каков его объем?
Ответ
8,21 л
Закон идеального газа можно также использовать в задачах стехиометрии.
Пример 11
Какой объем H 2 образуется при 299 К и 1,07 атм, когда 55,8 г металлического Zn реагируют с избытком HCl?
Zn(т) + 2 HCl(водн.) → ZnCl 2 (водн.) + H 2 (г)
Решение
Здесь у нас есть задача на стехиометрию, где нам нужно найти количество молей произведенного H 2 . Затем мы можем использовать закон об идеальном газе при заданных температуре и давлении, чтобы определить объем произведенного газа. Сначала вычисляется количество молей H 2 :
Сначала вычисляется количество молей H 2 :
Теперь, когда мы знаем количество молей газа, мы можем использовать закон идеального газа для определения объема, учитывая другие условия:
Все единицы сокращаются. кроме L, для объема, что означает
В = 19,6 л
Проверь себя
Какое давление HCl образуется, если 3,44 г Cl 2 прореагируют в 4,55 л при 455 К?
H 2 (г) + Cl 2 (г) → 2HCl(г)
Ответ
0,796 атм
К настоящему времени должно быть очевидно, что некоторые физические свойства газов сильно зависят . Что нам нужно, так это набор стандартных условий, чтобы свойства газов можно было правильно сравнивать друг с другом. Стандартная температура и давление (STP) определяется как точное давление 100 кПа (0,986 атм) и 273 К (0°С). Для простоты мы будем использовать 1 атм в качестве стандартного давления. Определение STP позволяет нам более непосредственно сравнивать свойства газов, которые отличаются друг от друга.
Одним из общих свойств газов является молярный объем. Молярный объем – это объем 1 моля газа. В STP молярный объем газа можно легко определить, используя закон идеального газа:
Все единицы сокращаются, кроме L, единицы объема. Итак,
В = 22,4 л
Обратите внимание, что мы не указали идентичность газа; мы указали только, что давление равно 1 атм, а температура 273 К. Это дает очень полезное приближение: объем любого газа на СТП составляет 22,4 л на моль газа ; то есть молярный объем при нормальных условиях составляет 22,4 л/моль (рис. 6.3 «Молярный объем»). Этот молярный объем является полезным коэффициентом преобразования в задачах стехиометрии, если условия находятся на уровне STP. Если условия не соответствуют STP, молярный объем 22,4 л/моль неприменим. Однако, если условия не соответствуют STP, можно использовать комбинированный газовый закон для расчета объема газа при STP; тогда можно использовать молярный объем 22,4 л/моль.
Рис. 6.3 Молярный объем
6.3 Молярный объем
Моль газа при нормальных условиях занимает 22,4 л, объем куба со стороной 28,2 см.
Пример 12
Сколько молей Ar содержится в 38,7 л при нормальных условиях?
Решение
Мы можем использовать молярный объем, 22,4 л/моль, в качестве коэффициента пересчета, но нам нужно обратить дробь так, чтобы единицы L сокращались, а единицы моля вводились. Это одношаговое преобразование:
Проверь себя
Какой объем имеет 4,87 моль Kr при СТП?
Ответ
109 л
Пример 13
Какой объем H 2 образуется на СТП, когда 55,8 г металлического Zn реагируют с избытком HCl?
Zn(т) + 2 HCl(водн.) → ZnCl 2 (водн.) + H 2 (г)
Раствор
Это стехиометрическая задача с изюминкой: нам нужно использовать молярный объем газа на STP, чтобы определить окончательный ответ. Первая часть расчета такая же, как и в предыдущем примере:
Теперь мы можем использовать молярный объем, 22,4 л/моль, потому что газ находится в STP:
В качестве альтернативы, мы могли бы применить молярный объем в качестве третьего коэффициента преобразования в первоначальном расчете стехиометрии.
Проверь себя
Какой объем HCl образуется, если 3,44 г Cl 2 прореагируют при нормальных условиях?
H 2 (г) + Cl 2 (г) → 2 HCl(г)
Ответ
2,17 L
Закон идеального газа также можно использовать для определения плотности. Напомним, что плотность определяется как масса вещества, деленная на его объем:
Предположим, что у вас есть ровно 1 моль газа. Если вы знаете идентичность газа, вы можете определить молярную массу вещества. Используя закон идеального газа, вы также можете определить объем этого моля газа, используя любые условия температуры и давления. Затем вы можете рассчитать плотность газа, используя
Пример 14
Какова плотность N 2 при 25°C и 0,955 атм?
Решение
Сначала мы должны перевести температуру в кельвины:
25 + 273 = 298 К
Если принять ровно 1 моль N 2 , то мы знаем его массу: 28,0 г. Используя закон об идеальном газе, мы можем вычислить объем:
Используя закон об идеальном газе, мы можем вычислить объем:
Все единицы сокращаются, кроме L, единицы объема. Итак,
V = 25,6 л
Зная молярную массу и молярный объем, мы можем определить плотность N 2 при этих условиях: при давлении 0,0079 атм и 227 К? (Это приблизительные атмосферные условия на Марсе). легкие, чтобы наши тела могли поглощать кислород из воздуха. Применим газовые законы к дыханию.
Начните с учета давления. Мы втягиваем воздух в легкие, потому что диафрагма, мышца под легкими, движется вниз, чтобы уменьшить давление в легких, заставляя внешний воздух устремляться внутрь, чтобы заполнить объем с более низким давлением. Мы выталкиваем воздух за счет того, что диафрагма давит на легкие, увеличивая давление внутри легких и вытесняя воздух под высоким давлением наружу. О каких изменениях давления идет речь? Четверть атмосферы? Десятая часть атмосферы? На самом деле в нормальных условиях разница давлений всего в 1 или 2 Торр заставляет нас вдыхать и выдыхать.
Рисунок 6.4 Механика дыхания
Дыхание связано с перепадом давления между внутренней частью легких и воздухом снаружи. Разница давлений составляет всего несколько торр.
Нормальный вдох составляет около 0,50 л. Если комнатная температура составляет около 22 °C, то температура воздуха составляет около 295 K. При нормальном давлении 1,0 атм сколько молей воздуха мы вдыхаем при каждом вдохе? Закон идеального газа дает нам ответ:
Решая количество молей, получаем
n = 0,021 моль воздуха
Получается около 0,6 г воздуха на вдох — немного, но достаточно, чтобы поддерживать нашу жизнь.
Ключевые выводы
- Закон идеального газа связывает четыре независимых физических свойства газа в любой момент времени.
- Закон идеального газа можно использовать в задачах стехиометрии, в которых в химических реакциях участвуют газы.
- Стандартная температура и давление (STP) — полезный набор эталонных условий для сравнения других свойств газов.


 6)
6) 8)
8) е.м. Отсюда M (M) = 65.4 и М = Zn.
е.м. Отсюда M (M) = 65.4 и М = Zn.
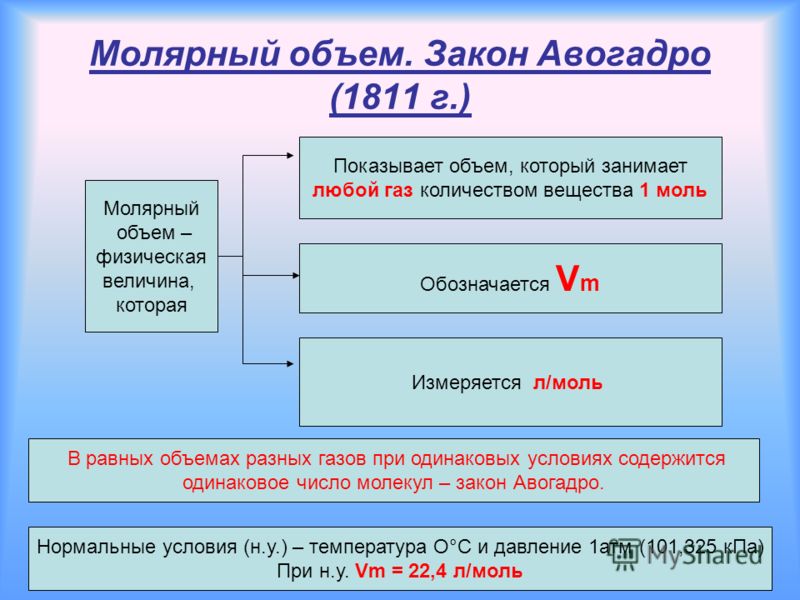 Экспериментально установлено, что масса 1л кислорода при нормальных условиях (при температуре 273?К (0?С) и давлении 1 атм. ) равна 1,429г.
Экспериментально установлено, что масса 1л кислорода при нормальных условиях (при температуре 273?К (0?С) и давлении 1 атм. ) равна 1,429г. 293 *р *273 * V /28.98 (273 +t) *760 =0.01605 * р *М * V/273 +t (2.2)
293 *р *273 * V /28.98 (273 +t) *760 =0.01605 * р *М * V/273 +t (2.2)
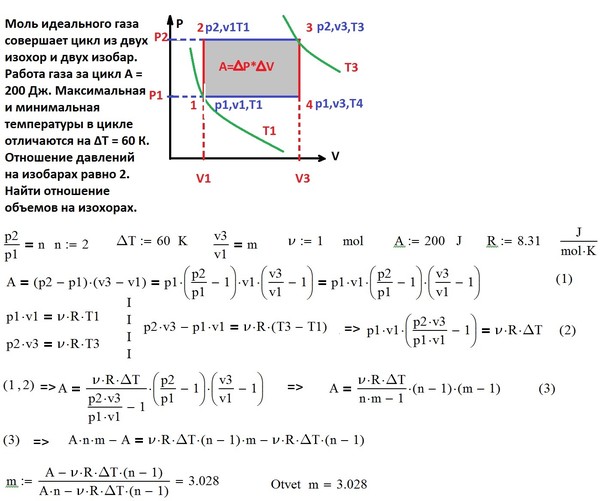 Отношение
между ними может быть выведено из кинетической теории и называется
Отношение
между ними может быть выведено из кинетической теории и называется Оно должно быть однозначно однозначным, чтобы характеризовать состояние. Например, в примере с тепловой работой конечное состояние
характеризуется определенной температурой (переменной состояния) независимо от
было ли оно доведено до этого состояния нагреванием или совершением работы над
это, или оба.
Оно должно быть однозначно однозначным, чтобы характеризовать состояние. Например, в примере с тепловой работой конечное состояние
характеризуется определенной температурой (переменной состояния) независимо от
было ли оно доведено до этого состояния нагреванием или совершением работы над
это, или оба.
 Стандартная температура – это точка замерзания воды, а стандартное давление – одна стандартная атмосфера. Их можно количественно оценить следующим образом:
Стандартная температура – это точка замерзания воды, а стандартное давление – одна стандартная атмосфера. Их можно количественно оценить следующим образом: Хотя это полезное измерение для многих практических целей, оно должно быть преобразовано в абсолютное давление для таких приложений, как закон идеального газа.
Хотя это полезное измерение для многих практических целей, оно должно быть преобразовано в абсолютное давление для таких приложений, как закон идеального газа. На правом изображении система закрыта, а поршень нажат до тех пор, пока давление не станет около 15 фунтов/дюйм 2 . Это означает, что абсолютное давление увеличилось примерно вдвое за счет сжатия газа до половины его объема (закон идеального газа). Стандартное атмосферное давление в этих общепринятых единицах измерения США составляет 14,7 фунта/дюйм 9 .0154 2 , поэтому его необходимо добавить к указанному выше манометрическому давлению, чтобы получить абсолютное давление.
На правом изображении система закрыта, а поршень нажат до тех пор, пока давление не станет около 15 фунтов/дюйм 2 . Это означает, что абсолютное давление увеличилось примерно вдвое за счет сжатия газа до половины его объема (закон идеального газа). Стандартное атмосферное давление в этих общепринятых единицах измерения США составляет 14,7 фунта/дюйм 9 .0154 2 , поэтому его необходимо добавить к указанному выше манометрическому давлению, чтобы получить абсолютное давление. Если температура должна быть постоянной, это становится:
Если температура должна быть постоянной, это становится:  5 \: \text{L} \: \ce{H_2}\)
5 \: \text{L} \: \ce{H_2}\) ck12.org/cbook/ck-12-chemistry-flexbook-2.0/
ck12.org/cbook/ck-12-chemistry-flexbook-2.0/