INGELRII Попытаюсь повторить ваше рассуждение, как я его вижу. — 18.12.2017, 02:48 — arseniiv в сообщении #1274664 писал(а): Да. Только если «координаты», это о декартовых координатах, и про полярные вообще можно было не говорить, а только о том, что центры кругов совпадают с началом координат; если же о полярных, умножается только . И ещё условие Sdy в сообщении #1274662 писал(а): a < b лишнее, как и условие Sdy в сообщении #1274662 писал(а): a, b — real numbers раз уж вещественная и мы, к тому же, с ней сравниваем — на комплексные числа этот порядок не переносится. Понял упущения, спасибо. — 18.12.2017, 02:50 — Dan B-Yallay в сообщении #1274668 писал(а):Sdy в сообщении #1274123 писал(а): Да мне главное «увидеть», то есть полностью понять. Ну, если Вам нужно обязательно видеть , то графическая подсказка под оффтопом. Биекцию между полученным треугольником и произвольным предлагается построить самостоятельно. (Оффтоп) Вложение: rect4886.jpg Спасибо за рисунки, они мне понятны. Неясно лишь то что указал выше, то есть самая суть. — 18.12.2017, 02:54 — arseniiv в сообщении #1274109 писал(а): Имеется в виду, равномощность квадрата и круга и равномощность круга и треугольника? Тогда в чём проблема взять композицию двух соответствующих биекций? Вы предлагаете установить биекцию квадрат -> круг, треугольник -> круг и далее воспользоваться транзитивностью? |
Postroenie_biektsiy
До сих пор мы рассматривали лишь счётные множества. Но оказывается, что большая часть множеств на числовой прямой вообще не являются счётными. Мы начнём с того, что рассмотрим некоторые примеры несчётных множеств и сделаем пару комментариев по поводу доказательства существования таких множеств. Далее ближайшей нашей задачей будет построить биекцию, которую мы так и не построили в первом материале.
Несчётные множества
Как уже было сказано, несчётные множества – это множества, которые не являются счётными.
Мы много привели примеров счётных множеств. А вот какие можно привести примеры несчётных?
Пока
что лишь примем без доказательства, что
отрезок являет собой типичный пример таких
множеств. Но обоснование этого очень
полезно для понимания многих вещей,
поэтому сделаю кое-какие комментарии(само
же доказательство можно найти в
литературе).
Что мы должны сделать, чтобы доказать несчётность этого отрезка? Попробовать предположить, что это счётное множество. Дальше мы строим такое число, которое гарантированно не войдёт ни в одно из построенных счётных множеств. То есть, как бы мы ни старались, но мы не сможем этим счётным множеством исчерпать весь отрезок – всегда найдётся какое-нибудь число отрезка(в доказательстве мы лишь определяем его формат), которое не будет содержаться в этом множестве.
Уже из сделанного комментария следует, что несчётное множество гораздо больше счётного. Причём, даже не на счётное множество(иначе мы всё равно получили бы счётное множество). Вот это и имелось в виду, когда я говорил, что счётное множество – самое “маленькое” среди всех бесконечных. Более того, соответствующий факт теории множеств говорит: любое бесконечное множество содержит счётное подмножество. То есть, счётное множество – лишь часть несчётных.
Таким
образом, один пример мы уже нашли. Можно
назвать второй – множество всех
действительных чисел R. Однако, нами это пока не доказано. Чтобы
доказать, нам нужно установить биекцию
между R
и заведомо несчётным(тогда мы покажем
их эквивалентность).
Однако, нами это пока не доказано. Чтобы
доказать, нам нужно установить биекцию
между R
и заведомо несчётным(тогда мы покажем
их эквивалентность).
Мы хотели установить биекцию . Второе множество здесь несчётно. Следовательно, если это получится сделать, то автоматически и R будет несчётным. Перейдём теперь к этой задаче.
Установление биекции
Эта задача предложена как тренировочная для подготовки к экзамену. Раньше мы уже устанавливали биекцию, просто предъявив нужную функцию. В этот раз мы тоже построим функцию, но несколько более сложным образом. Более того, это отображение уже не будет непрерывным. В случае отображения всех чисел на интервал (0,1) мы ещё могли им обойтись. А вот биекция интервала на отрезок уже не может быть описана без точек разрыва.
Я уже говорил ранее, что мы намереваемся строить биекцию так:
Первый
пункт этой программы уже выполнен,
осталось лишь найти взаимно однозначное
отображение интервала на отрезок. Вот
здесь-то и начинаются сложности, потому
что непосредственно это сделать не
удастся.
Вот
здесь-то и начинаются сложности, потому
что непосредственно это сделать не
удастся.
Начнём с того, что вспомним: всякое бесконечное множество содержит счётное подмножество. Значит, и интервал (0,1) должен содержать такое подмножество. Сейчас мы хотим сделать следующее: построить пока биекцию между счётной частью интервала и счётной частью отрезка [0,1]. Поэтому начнём с того, что выделим счётные подмножества.
На интервале (0,1) рассмотрим, например, такую последовательность точек: . Очевидно, что это множество счётно, так как соответствие с натуральными числами есть(это даже на глаз видно). А теперь рассмотрим счётную часть отрезка [0,1]. Выделим там такое же подмножество, плюс точки 0 и 1, которых не было в интервале.
Это
множество тоже счётно, поскольку, как
уже мы говорили ранее, добавка конечного
числа точек не влияет на счётность(здесь
мы добавили к предыдущему множеству
две точки: 0 и 1). Следовательно, в силу
счётности обоих множеств, между ними
существует биекция.
А теперь ясно, как установить между ними биекцию.
Теперь можно это соответствие задать аналитически:
Здесь x, понятное дело, пробегает интервал (0,1)
Но это ещё не всё. Мы только установили биекцию между счётными частями интервала и отрезка. Надо затем продолжить эту биекцию до соответствия целых множеств. Для этого достаточно заметить, что остальная часть их одинакова(отрезок и интервал различаются лишь наличием точек 0 и 1, которые мы уже “воткнули” в биекцию). Следовательно, все остальные точки интервала должны перейти в те же точки отрезка: то есть, это тождественная биекция. Тогда в итоге получаем :
Советую запомнить эту идею: сначала построение биекции между счётными подмножествами, а затем расширение её на всё множество. Это может потребоваться на экзамене.
Теперь
у нас есть две половинки искомой биекции.
Построим их композицию(совмещение). Тут
надо быть осторожным, поскольку при
неправильном совмещении двух биекций
искомое соответствие уже потеряет
биективность.
– это первая половина биекции(её мы построили ранее)
Искомое отображение будет кусочно-заданным. Для его построения учтём, что в указанном только что отображении (0,1) в [0,1] x не сам по себе уже, а это результат отображения из R в (0,1), то есть наш арккотангенс. Подставим его:
Теперь выразим везде x и вернём его во множество R:
На арккотангенсы навесим котангенсы, чтобы вернуться к x. Кроме того,
, откуда
Работаем с первым равенством:
, откуда (это можно сделать в силу биективности арккотангенса в области своего определения).
Работаем со вторым равенством, выполняя то же самое(это возможно в силу биективности):
откуда
В силу биективности и монотонности арккотангенса последняя строка будет выполняться при остальных x.
Таким образом, искомая биекция будет иметь вид:
Рассмотрим ещё одну экзаменационную задачу.
Задача. Установить биекцию .
Здесь
я использовал следующую последовательность
биекций .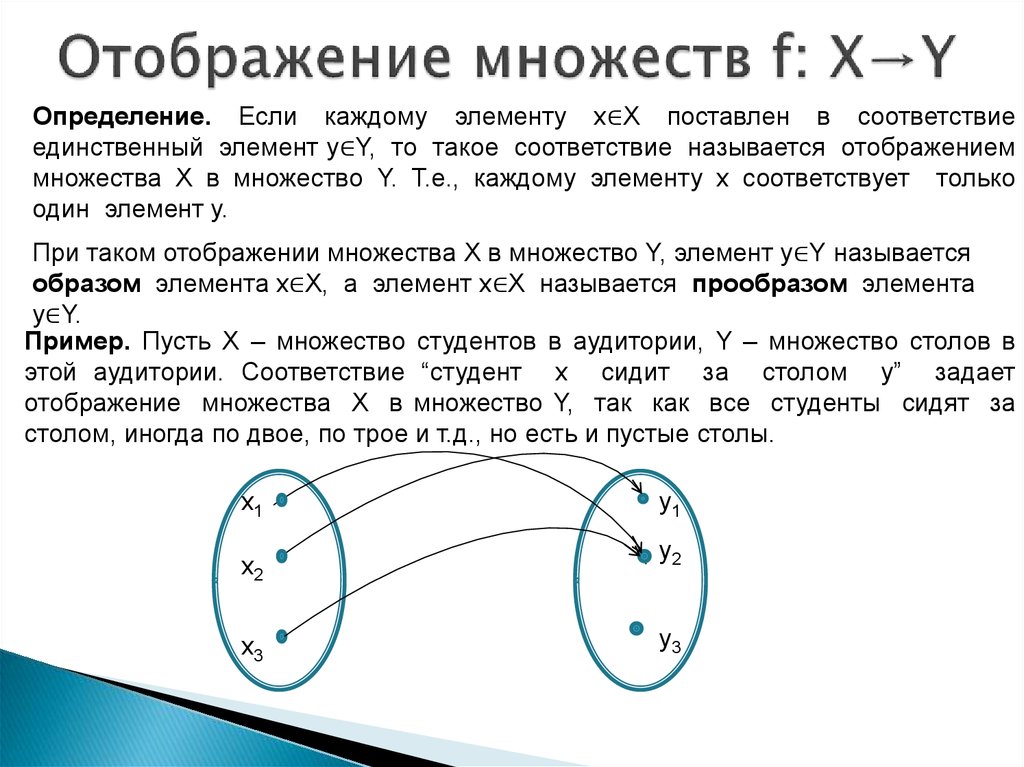
Трудность здесь составит построение биекции .
Первое отображение у нас уже давно есть.
Биекцию построить очень легко. Например, . Это легко объяснить, поняв, что после растяжения линейным преобразованием из полуинтервала [0,1) получается полуинтервал , на котором тангенс монотонно возрастает(а значит, биективен), и принимает все неотрицательные значения(в этом можно убедиться по кругу).
Следовательно, нужно построить лишь биекцию – это самое сложное здесь. Идея такая же. Выделяем счётные подмножества. В следующем файле я пришлю верный вариант.
А дальше нужно составить из них композицию так, как мы это делали.
Как доказать, что функция биективна?
Изменено 3 года, 10 месяцев назад
Просмотрено 217 тысяч раз
$\begingroup$
У меня возникли проблемы с формальной демонстрацией того, является ли функция биективной (и, следовательно, сюръективной и инъективной). Вот пример:
Вот пример:
Как доказать, что $g(x)$ биективна?
\begin{align} f &: \mathbb R \to\mathbb R \\ g &: \mathbb R \to\mathbb R \\ г(х) &= 2f(х) + 3 \end{align}
Однако, боюсь, я действительно не знаю, как это сделать. Я понимаю, что приведенный выше пример подразумевает композицию (что немного усложняет задачу?). Во всяком случае, я не понимаю, как это доказать (будь то композиция или нет).
Для инъективного, я считаю, мне нужно доказать, что различных элементов домена кода имеют разные прообразы в домене . Хорошо, но как?
Что касается сюръективности, я думаю, мне нужно доказать, что все элементы кодомена имеют один и только один прообраз в домене , верно? Я тоже не знаю, как это доказать!
РЕДАКТИРОВАТЬ
f является биекцией. Извините, я забыл сказать это.
- функции
$\endgroup$
4
$\begingroup$
Чтобы проверить что-то подобное, нужно проверить определения одно за другим и посмотреть, удовлетворяет ли $g(x)$ необходимым свойствам.
Напомним, что $F\colon A\to B$ является биекцией тогда и только тогда, когда $F$ является:
- инъективным : $F(x)=F(y)\имеет x=y$, и
- сюръектив : для всех $b\in B$ существует некоторое $a\in A$ такое, что $F(a)=b$.
Предполагая, что $R$ обозначает действительные числа, мы проверяем.
Является ли $g$ инъективным?
Возьмем $x,y\in R$ и предположим, что $g(x)=g(y)$. Поэтому $2f(x)+3=2f(y)+3$. Мы можем сократить $3$ и разделить на $2$, тогда мы получим $f(x)=f(y)$. Так как $f$ биекция, то она инъективна, и мы имеем, что $x=y$.
Является ли $g$ сюръективным?
Возьмем некоторое число $y\in R$, мы хотим показать, что $y=g(x)$, то есть $y=2f(x)+3$. Вычтем $3$ и разделим на $2$, снова получим $\frac{y-3}2=f(x)$. Как и раньше, если $f$ было сюръективным, то мы почти закончили, просто обозначим $w=\frac{y-3}2$, поскольку $f$ сюръективно, существует некоторый $x$ такой, что $f(x)= ш$. Покажите теперь, что $g(x)=y$, как и требовалось.
Покажите теперь, что $g(x)=y$, как и требовалось.
В качестве альтернативы вы можете использовать теоремы. Какие теоремы? Композиция биекций есть биекция. Если $f$ — биекция, покажите, что $h_1(x)=2x$ — биекция, и покажите, что $h_2(x)=x+2$ — тоже биекция. Теперь у нас есть $g=h_2\circ h_1\circ f$ и, следовательно, биекция.
Конечно, это снова в предположении, что $f$ биекция.
$\endgroup$
4
$\begingroup$
Сначала покажите, что $g$ инъективно ($1$-$1$), показав, что если $g(x)=g(y)$, то $x=y$. Это несложно: если $g(x)=g(y)$, то $2f(x)+3=2f(y)+3$, поэтому по элементарной алгебре $f(x)=f(y) $. По условию $f$ является биекцией и, следовательно, инъективной, поэтому $x=y$.
Теперь покажите, что $g$ сюръективно. Для этого нужно показать, что для каждого $y\in\Bbb R$ существует такой $x\in\Bbb R$, что $g(x)=y$. Для этого нужно найти такое $x\in\Bbb R$, что $2f(x)+3=y$ или, что то же самое, такое, что $f(x)=\frac{y-3}2$. Но известно, что $f$ является биекцией и, следовательно, сюръекцией, так что вы знаете, что существует 9{-1}\большой(е(х)\большой)\\
&=х\;,
\end{align*}$$
Для этого нужно найти такое $x\in\Bbb R$, что $2f(x)+3=y$ или, что то же самое, такое, что $f(x)=\frac{y-3}2$. Но известно, что $f$ является биекцией и, следовательно, сюръекцией, так что вы знаете, что существует 9{-1}\большой(е(х)\большой)\\
&=х\;,
\end{align*}$$
, так как $f$ биекция.
$\endgroup$
2
$\begingroup$
Чтобы доказать, что функция биективна, вам нужно доказать, что она инъективна, а также сюръективна.
«Инъективный» означает, что никакие два элемента в домене функции не могут быть сопоставлены с одним и тем же изображением.
«Сюръективный» означает, что функция затрагивает любой элемент в диапазоне функции.
Сначала докажем, что $g(x)$ инъективно. Если $g(x_1) = g(x_2)$, то мы получаем, что $2f(x_1) + 3 = 2f(x_2) +3 \имеет f(x_1) = f(x_2)$. Поскольку $f(x)$ биективен, он также инъективен, и, следовательно, мы получаем, что $x_1 = x_2$.
Теперь докажем, что $g(x)$ сюръективно. Рассмотрим $y \in \mathbb{R}$ и посмотрим на число $\dfrac{y-3}2$. Поскольку $f(x)$ сюръективен, существует $\hat{x}$ такое, что $f(\hat{x}) = \dfrac{y-3}2$. Это означает, что $g(\hat{x}) = 2f(\hat{x}) +3 = y$. Следовательно, для любого $y \in \mathbb{R}$ существует $\hat{x} \in \mathbb{R}$ такое, что $g(\hat{x}) = y$. Следовательно, $g$ также сюръективен.
Следовательно, $g(x)$ биективна.
В общем случае, если $g(x) = h(f(x))$ и если $f(x) : A \to B$ и $h(x): B \to C$ взаимно биективны, то $ g(x): A \to C$ также биективен.
В вашем случае $f(x)$ было биективно из $\mathbb{R} \ в \mathbb{R}$ и $h(x) = 2x+3$ также биективно из $\mathbb{R} \to \mathbb{R}$.
$\endgroup$
$\begingroup$
Вы недостаточно рассказали о функции $f$, чтобы сказать, биективна ли $g$.
«Инъективный» означает, что разные элементы домена всегда сопоставляются с разными элементами кодового домена.
«Сюръективный» означает, что каждый элемент кодового домена имеет по крайней мере один прообраз в домене.
Позднее редактирование: То, что вы сейчас добавили — что $f$ является биекцией — подводит нас к тому моменту, когда мы можем ответить на вопрос. Однако, возможно, вам стоит взглянуть на то, что я написал выше. Поскольку оба определения, которые я дал, противоречат тому, что вы написали, этого может быть достаточно, чтобы вы поняли.
$\endgroup$
1
Биективные функции | Brilliant Math & Science Wiki
Содержание
- Краткое изложение техники
- Биномиальные коэффициенты
- Фи-функция Эйлера
- Перегородки
- Каталонские номера
- Смотрите также
Для данной формулы вида a=b a = b a=b, где a a a и b b b — конечные положительные целые величины, зависящие от некоторых переменных, вот как доказать формулу:
- Найдите множество S S S такое, что ∣S∣ =а |S| = a ∣S∣=a, и множество T T T такое, что ∣T∣=b |T| = б ∣Т∣=б.
 Эти множества в общем случае не будут экзотическими: иногда они будут ясны из задачи, а иногда будут хорошо известны как множества, подсчитываемые по величинам в формуле. Например, если a a a — биномиальный коэффициент или сумма биномиальных коэффициентов, то S S S будет набором подмножеств большего множества или способами выбора определенных объектов из множества.
Эти множества в общем случае не будут экзотическими: иногда они будут ясны из задачи, а иногда будут хорошо известны как множества, подсчитываемые по величинам в формуле. Например, если a a a — биномиальный коэффициент или сумма биномиальных коэффициентов, то S S S будет набором подмножеств большего множества или способами выбора определенных объектов из множества. - Придумайте способ связать элементы T T T с элементами SSS или наоборот. Иногда один из них изначально легче, чем другой. Используйте это, чтобы построить функцию f :S→T f \ двоеточие S \to Tf:S→T (((или T→S). T \to S). T→S).
- (необязательно) Убедитесь, что ff f является биекцией для малых значений переменных, записав ее явно.
- Докажите, что ff f является биекцией, либо показав, что она взаимно однозначна и на, либо (часто проще), построив обратную ff f.
Докажите, что биномиальные коэффициенты симметричны: (nk)=(nn−k).{n\выбрать k} = {n\выбрать n-k}.(kn)=(n−kn).
Мы можем доказать, что биномиальные коэффициенты симметричны: (nk)=(nn−k){n\выбрать k} = {n\выбрать n-k}(kn)=(n−kn) через биекцию. Поскольку (nk) n \choose k (kn) подсчитывает kkk-элементные подмножества множества nnn-элементов S S S, а (nn−k) n\choose n-k(n−kn) подсчитывает (n−k)(n-k) (n−k)-элементных подмножеств S S S, доказательство состоит в нахождении однозначного соответствия между этими двумя типами подмножеств.
Самый естественный способ получить (n−k) (n−k)(n−k)-элементное подмножество из kkk-элементного подмножества — взять дополнение. Итак, пусть Si S_i Si будет набором i i i-элементных подмножеств S S S и определите fk : Sk→Sn−kfk(X)=S−X.\begin{выровнено} f_k \ двоеточие & S_k \ to S_ {n-k} \\ f_k(X) = &S — X. \end{align}fk:fk(X)=Sk→Sn−kS−X. Легко доказать, что это биекция: действительно, fn−k f_{n-k} fn−k является обратным к fk f_k fk, так как S−(S−X)=X S — (S — X) = X S-(S-X)=X. Итак, Sk S_k Sk и Sn−k S_{n-k} Sn−k имеют одинаковое количество элементов; то есть (nk)=(nn−k) {n\выбрать k} = {n \выбрать n-k}(kn)=(n−kn).
□_\квадрат □
Для иллюстрации приведем биекцию f2 f_2f2 при n=5 n = 5 n=5 и k=2: k = 2:k=2: {1,2}↦{3,4,5}{1,3}↦{2,4,5}{1,4}↦{2,3,5}{1,5}↦{2,3, 4}{2,3}↦{1,4,5}{2,4}↦{1,3,5}{2,5}↦{1,3,4}{3,4}↦{1, 2,5}{3,5}↦{1,2,4}{4,5}↦{1,2,3}.\begin{выровнено} \{1,2\} &\mapsto \{3,4,5\} \\ \{1,3\} &\mapsto \{2,4,5\} \\ \{1,4\} &\mapsto \{2,3,5\} \\ \{1,5\} &\mapsto \{2,3,4\} \\ \{2,3\} &\mapsto \{1,4,5\} \\ \{2,4\} &\mapsto \{1,3,5\} \\ \{2,5\} &\mapsto \{1,3,4\} \\ \{3,4\} &\mapsto \{1,2,5\} \\ \{3,5\} &\mapsto \{1,2,4\} \\ \{4,5\} &\mapsto \{1,2,3\}. \end{выровнено} {1,2} {1,3} {1,4} {1,5} {2,3} {2,4} {2,5} {3,4} {3,5} {4,5}↦{3,4,5}↦{2,4,5}↦{2,3,5}↦{2,3,4}↦{1,4,5}↦{1, 3,5}↦{1,3,4}↦{1,2,5}↦{1,2,4}↦{1,2,3}. Поскольку это дает однозначное соответствие между 2 подмножествами по 22 элемента и 3 подмножествами по 33 элемента набора из 5 55 элементов, это показывает, что (52) = (53) {5 \ выберите 2} = {5 \ выберите 3} (25)=(35).
Ключевой результат фи-функции Эйлера:
∑d∣nϕ(d)=n. \sum_{d|n} \phi(d) = n.
d∣n∑ϕ(d)=n.
Вот доказательство с использованием биекций:
\sum_{d|n} \phi(d) = n.
d∣n∑ϕ(d)=n.
Вот доказательство с использованием биекций:
Пусть S={(a,d):d∣n,1≤a≤d,gcd(a,d)=1} S = \{ (a,d) : d \big|n, 1\le a \le d, \text{gcd}(a,d) = 1 \} S={(a,d):d∣∣n,1≤a≤d,gcd( а,г)=1}. Тогда число элементов S S S равно просто ∑d∣nϕ(d) \sum_{d|n} \phi(d) ∑d∣nϕ(d). Пусть теперь T={1,2,…,n} T = \{ 1,2,\ldots,n \} T={1,2,…,n}. Чтобы завершить доказательство, мы должны построить биекцию между S S S и T T T.
Определите f :S→T f \colon S \to T f:S→T как f((a,d))=и f\big((a,d)\big) = \frac{an}d f ((а,г))=дан. Определим g :T→S g \colon T \to S g:T→S следующим образом: g(b) g(b) g(b) — упорядоченная пара (bgcd(b,n),ngcd( б,н)). \left(\frac{b}{\gcd (b,n)}, \frac{n}{\gcd (b,n)}\right). (НОД(b,n)b, НОД(b,n)n). Затем обычно проверяется, что ff f и g g g обратны друг другу, поэтому они являются биекциями. □_\квадрат □
Это элегантное доказательство, но оно может быть неочевидным для студента, который может не сразу понять, откуда взялись функции f f f и g g g. Первоначальная идея состоит в том, чтобы рассмотреть дроби
1н,2н,…,нн
\frac1{n}, \frac2{n}, \ldots, \frac{n}{n}
n1,n2,…,nn
и сократить их до минимума. Все они будут иметь вид ad \frac{a}{d} da для единственного (a,d)∈S (a,d) \in S (a,d)∈S. Множество T T T есть множество числителей несократимых дробей. Функции f f f и g g g в доказательстве получаются путем преобразования редуцированной дроби обратно в нередуцированную дробь и наоборот соответственно.
Первоначальная идея состоит в том, чтобы рассмотреть дроби
1н,2н,…,нн
\frac1{n}, \frac2{n}, \ldots, \frac{n}{n}
n1,n2,…,nn
и сократить их до минимума. Все они будут иметь вид ad \frac{a}{d} da для единственного (a,d)∈S (a,d) \in S (a,d)∈S. Множество T T T есть множество числителей несократимых дробей. Функции f f f и g g g в доказательстве получаются путем преобразования редуцированной дроби обратно в нередуцированную дробь и наоборот соответственно.
Некоторые классические результаты о разбиениях имеют естественные доказательства, включающие биекции. Раздел целого числа представляет собой выражение целого числа как суммы положительных целых чисел, называемых «частями». Порядок не имеет значения; два выражения, состоящие из одних и тех же частей, написанных в разном порядке, считаются одним и тем же разделом.
Покажите, что количество разбиений nn n на нечетные части равно количеству разбиений n n n на разные части. Например, 5+1=3+3=3+1+1+1=1+1+1+1+1+1 5+1 = 3+3 = 3+1+1+1 = 1+1+ 1+1+1+1 5+1=3+3=3+1+1+1=1+1+1+1+1+1 и 6=5+1=4+2=3+2+1 6 = 5 + 1 = 4 + 2 = 3 + 2 + 1 6 = 5 + 1 = 4 + 2 = 3 + 2 + 1, поэтому для n = 6 n = 6 n = 6 имеется по четыре каждого типа.
Цель состоит в том, чтобы дать рецепт превращения одного вида разбиения в другой, а затем показать, что этот рецепт дает однозначное соответствие (биекцию). Вероятно, более естественно начать с разбиения на отдельные части и «разбить его» на нечетные части. Самое очевидное, что нужно сделать, это взять четную часть и переписать ее в виде суммы нечетных частей, а для простоты лучше всего использовать нечетные части, равные друг другу.
9a 2a частей, равных b b b. Например, для n=6 n = 6 n=6, 6=3+35+1=5+14+2=(1+1+1+1)+(1+1)3+2+1=3+(1+1)+1.\begin{выровнено} 6 &= 3+3 \\ 5+1 &= 5+1 \\ 4+2 &= (1+1+1+1)+(1+1) \\ 3+2+1 &= 3+(1+1)+1. \end{align}65+14+23+2+1=3+3=5+1=(1+1+1+1)+(1+1)=3+(1+1)+1. Чтобы показать, что это соответствие взаимно однозначно и на, проще всего построить его обратное. Учитывая разбиение n n n на нечетные части, соберите части одинакового размера в группы. Предположим, что имеется d dd частей размера r r r. Затем запишите d dd в двоичном виде как 2a1+2a2+⋯+2ak, 2^{a_1} + 2^{a_2} + \cdots + 2^{a_k},2a1+2a2+⋯+2ak, где ai a_i ай различны.{a_k}r 2a1r+2a2r+⋯+2akr. Например, 3+3=2⋅3=65+1=5+11+1+1+1+1+1=6⋅1=(4+2)⋅1=4+23+1+1+1=3+ 3⋅1=3+(2+1)⋅1=3+2+1.\begin{выровнено} 3+3 &= 2\cdot 3 = 6 \\ 5+1 &= 5+1 \\ 1+1+1+1+1+1 &= 6 \cdot 1 = (4+2) \cdot 1 = 4+2 \\ 3+1+1+1 &= 3+ 3\cdot 1 = 3+(2+1)\cdot 1 = 3+2+1. \end{выровнено}3+35+11+1+1+1+1+13+1+1+1=2⋅3=6=5+1=6⋅1=(4+2)⋅1= 4+2=3+3⋅1=3+(2+1)⋅1=3+2+1. Несложно проверить, что это дает разбиение на отдельные части и что эти два преобразования обратны друг другу. □_\квадрат□
Пусть p(n) p(n) p(n) будет количеством разделов n nn. Пусть q(n)q(n) q(n) — количество разбиений 2n 2n 2n ровно на nn n частей. Например, q(3)=3q(3) = 3 q(3)=3, потому что 6=4+1+1=3+2+1=2+2+2. 6 = 4+1+1 = 3+2+1 = 2+2+2. 6=4+1+1=3+2+1=2+2+2. Вычислите p(12)−q(12). р(12)-q(12). р(12)−q(12).
Определение : Разделение целого числа — это выражение целого числа как суммы одного или нескольких положительных целых чисел, называемых частями. Два выражения, состоящие из одних и тех же частей, написанных в разном порядке, считаются одним и тем же разделом («порядок не имеет значения»).
Каталонские числа Cn=1n+1(2nn) C_n = \frac1{n+1}\binom{2n}{n} Cn=n+11(n2n) считают множество различных объектов; в частности, каталонское число Cn C_n Cn – это размер множества последовательностей (a1,a2,…,a2n) (a_1,a_2,\ldots,a_{2n}) (a1,a2,…,a2n ) где ai=±1 a_i = \pm 1 ai=±1 и частичные суммы a1+a2+⋯+ak a_1 + a_2 + \cdots + a_k a1+a2+⋯+ak всегда неотрицательны. Часто лучший способ показать, что каталонские числа учитывают определенный набор, — это поставить биекцию между этим набором и другим набором, который, как известно, считается с каталонскими числами.
Возьмите 2n2n 2n равноотстоящих друг от друга точек по кругу. Сколькими способами можно соединить эти точки с n n n отрезками, не пересекающимися друг с другом?
Для этого есть Cn C_n Cn способы. Пронумеруйте точки 1,2,…,2n 1,2,\lddots,2n 1,2,…,2n по порядку по окружности. Пусть ak=1 a_k = 1 ak=1, если точка k k k соединена с точкой с более высоким номером, и −1 −1 −1, если нет.
Тогда нетрудно проверить, что частичные суммы этой последовательности всегда неотрицательны. Это дает функцию, посылающую набор Sn S_n Sn способов соединения набора точек с набором Tn T_n Tn последовательностей 2n 2n 2n копий ±1 \pm 1 ±1 с неотрицательными частичными суммами.
Обратную функцию построить несложно; учитывая последовательность в Tn T_nTn, найдите часть последовательности, которая идет 1,−1 1,-1 1,−1. Соедините эти две точки. Теперь забудьте эту часть последовательности, найдите другую копию 1,−11,-11,−1 и повторите. Опять же, обычно проверяется, являются ли эти две функции обратными друг другу.
Например, для данной последовательности 1,1,−1,−1,1,−11,1,−1,−1,1,−11,1,−1,−1,1,−1 соединить точки 2 2 2 и 33 3, затем проигнорируйте их, чтобы получить 1,−1,1,−1 1,-1,1,-1 1,−1,1,−1. Затем соединяем точки 1 1 1 и 4 4 4 (первая пара 1,−1 1,-11,−1) и 5 5 5 и 6 6 6 (вторая пара).
Так как Tn T_n Tn имеет элементы Cn C_n Cn, то же самое имеет и Sn S_n Sn.


 Обычно без биекции не вижу.
Обычно без биекции не вижу.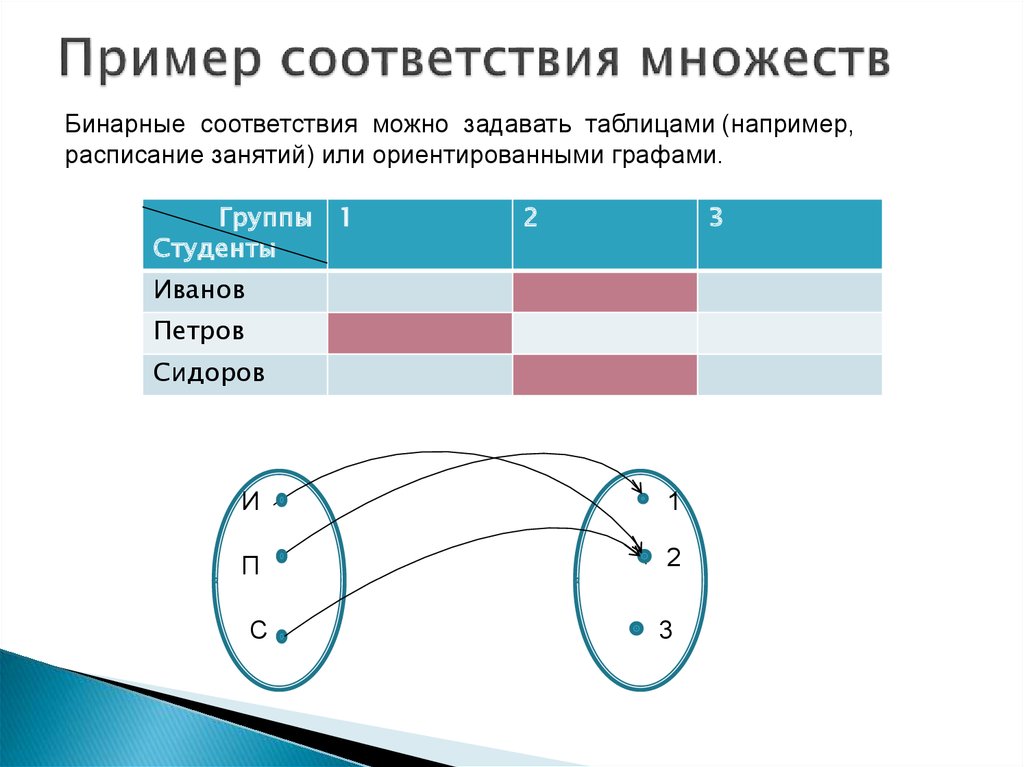
 Эти множества в общем случае не будут экзотическими: иногда они будут ясны из задачи, а иногда будут хорошо известны как множества, подсчитываемые по величинам в формуле. Например, если a a a — биномиальный коэффициент или сумма биномиальных коэффициентов, то S S S будет набором подмножеств большего множества или способами выбора определенных объектов из множества.
Эти множества в общем случае не будут экзотическими: иногда они будут ясны из задачи, а иногда будут хорошо известны как множества, подсчитываемые по величинам в формуле. Например, если a a a — биномиальный коэффициент или сумма биномиальных коэффициентов, то S S S будет набором подмножеств большего множества или способами выбора определенных объектов из множества.
 □_\квадрат □
□_\квадрат □
 {a_k}r 2a1r+2a2r+⋯+2akr. Например,
3+3=2⋅3=65+1=5+11+1+1+1+1+1=6⋅1=(4+2)⋅1=4+23+1+1+1=3+ 3⋅1=3+(2+1)⋅1=3+2+1.\begin{выровнено}
3+3 &= 2\cdot 3 = 6 \\
5+1 &= 5+1 \\
1+1+1+1+1+1 &= 6 \cdot 1 = (4+2) \cdot 1 = 4+2 \\
3+1+1+1 &= 3+ 3\cdot 1 = 3+(2+1)\cdot 1 = 3+2+1.
\end{выровнено}3+35+11+1+1+1+1+13+1+1+1=2⋅3=6=5+1=6⋅1=(4+2)⋅1= 4+2=3+3⋅1=3+(2+1)⋅1=3+2+1.
Несложно проверить, что это дает разбиение на отдельные части и что эти два преобразования обратны друг другу. □_\квадрат□
{a_k}r 2a1r+2a2r+⋯+2akr. Например,
3+3=2⋅3=65+1=5+11+1+1+1+1+1=6⋅1=(4+2)⋅1=4+23+1+1+1=3+ 3⋅1=3+(2+1)⋅1=3+2+1.\begin{выровнено}
3+3 &= 2\cdot 3 = 6 \\
5+1 &= 5+1 \\
1+1+1+1+1+1 &= 6 \cdot 1 = (4+2) \cdot 1 = 4+2 \\
3+1+1+1 &= 3+ 3\cdot 1 = 3+(2+1)\cdot 1 = 3+2+1.
\end{выровнено}3+35+11+1+1+1+1+13+1+1+1=2⋅3=6=5+1=6⋅1=(4+2)⋅1= 4+2=3+3⋅1=3+(2+1)⋅1=3+2+1.
Несложно проверить, что это дает разбиение на отдельные части и что эти два преобразования обратны друг другу. □_\квадрат□ Тогда нетрудно проверить, что частичные суммы этой последовательности всегда неотрицательны. Это дает функцию, посылающую набор Sn S_n Sn способов соединения набора точек с набором Tn T_n Tn последовательностей 2n 2n 2n копий ±1 \pm 1 ±1 с неотрицательными частичными суммами.
Тогда нетрудно проверить, что частичные суммы этой последовательности всегда неотрицательны. Это дает функцию, посылающую набор Sn S_n Sn способов соединения набора точек с набором Tn T_n Tn последовательностей 2n 2n 2n копий ±1 \pm 1 ±1 с неотрицательными частичными суммами.