Как посчитать экспоненту: Посчитать экспоненту — онлайн калькулятор

alexxlab / / Разное

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения
  

Федорюк М. В. Обыкновенные дифференциальные уравнения:— 2-е изд., перераб. и доп.— М.: Наука. Главная редакция физико-математической литературы, 1985. — 448 с.

Книга содержит изложение основ теории обыкновенных дифференциальных уравнении, включая теорию устойчивости, и вариационное, исчисление. Значительное место уделено уравнениям с частными производными первого порядка, аналитической теории дифференциальных уравнений и асимптотике решений линейных уравнений второго порядка. В новом издании (первое издание выходило в 1980 г.) добавлены методы теории возмущений при исследовании нелинейных дифференциальных уравнений с малым параметром.

Для студентов втузов, а также для инженеров-исследователей.


Оглавление

ПРЕДИСЛОВИЕ
ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 2. Дифференциальные уравнения первого порядка
2. Уравнения с разделяющимися переменными.
3. Однородные уравнения.
4. Линейные уравнения.
5. Уравнения в полных дифференциалах.
6. Интегрирующий множитель.
7. Уравнение Бернулли.
8. Уравнение Риккати.
§ 3. Линейные дифференциальные уравнения. Принцип суперпозиции
2. Принцип суперпозиции.
§ 4. Линейное уравнепие первого порядка с постоянными коэффициентами
2. Комплексные функции вещественного аргумента. Комплексная экспонента.
§ 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
2. Случай простых корней.
3. Случай кратных корней.
4. Уравнение Эйлера.
5. Выделение вещественных решений.
§ 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
2. Ангармонические колебания.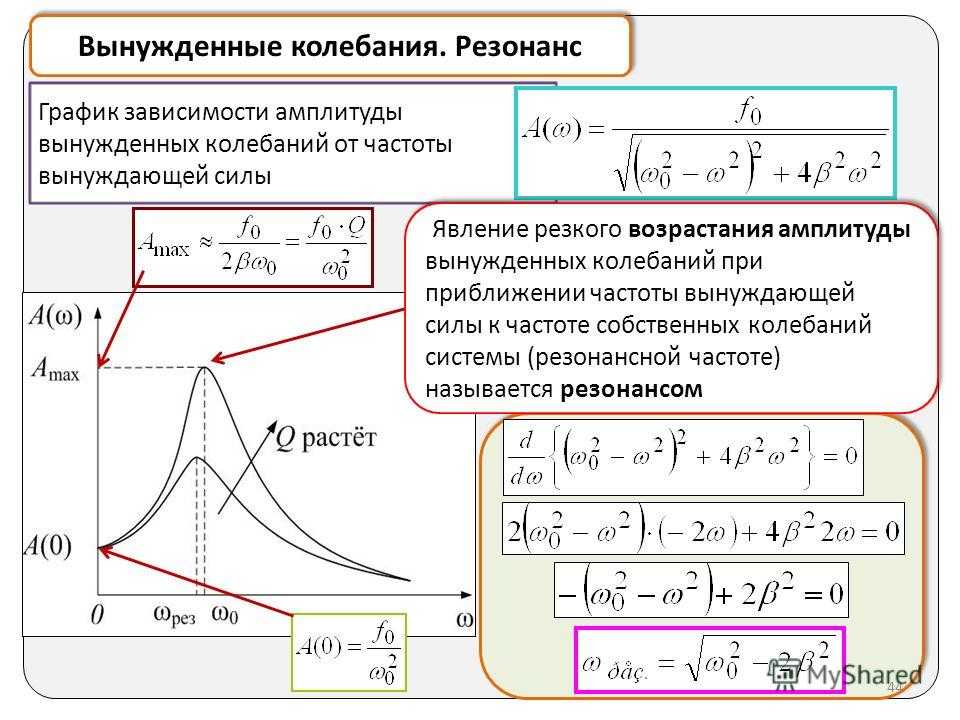
§ 7. Линейные уравнения с правой частью — квазимногочленом
§ 8. Линейные системы с постоянными коэффициентами. Случай простых корней
§ 9. Фазовая плоскость линейной системы
2. Комплексные корни.
3. Уравнение второго порядка.
§ 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
§ 11. Операционное исчисление
§ 12. Линейные разностные уравнения
ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2. Доказательство основной теоремы при n = 1.
3. Теорема Коши.
§ 2. Линейные нормированные пространства
§ 3. Принцип сжатых отображений
§ 4. Лемма Адамара
§ 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
2. Дифференциальные уравнения n-го порядка.
3. Комментарии к основной теореме.
4. Продолжение решений.
§ 6. Гладкость решений
§ 7. Зависимость решений от параметров и начальных условий
§ 8. Обратные и неявные функции
2. Теорема о неявной функции.
3. Дифференцирование сложных функций.
§ 9. Зависимые и независимые функции. Криволинейные координаты
2. Кривые и поверхности.
3. Криволинейные координаты.
§ 10. Уравнения первого порядка, не разрешенные относительно производной
2. Особые решения. Огибающая.
3. Интегрирование уравнений вида (1).
ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
2. Доказательство теоремы.
3. Линейное уравнение n-го порядка.
§ 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
2. Вычисление матричной экспоненты.
3. Функции от матриц.
4. Малые колебания механических систем.
§ 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
2. Определитель Вронского.
§ 4. Формула Лиувилля
§ 5. Фундаментальные системы решений
§ 6. Неоднородные линейные системы с переменными коэффициентами
§ 7. Линейные дифференциальные уравнения n-го порядка
2. Уравнения второго порядка.
§ 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
§ 9. Нули решений однородных линейных уравнений второго порядка
2. Теорема сравнения.
§ 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
2. Регулярные особые точки.
3. Уравнение Бесселя.
§ 11. Уравнения с периодическими коэффициентами
2. Зоны устойчивости и неустойчивости.
§ 12. Дельта-функция и ее применения
2. Толчки. Принцип Дюамеля.
3. Периодические толчки в системах с трением.
ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
2. Векторные поля. Механическая интерпретация фазовых траекторий.
§ 2. Структура решений автономной системы в окрестности неособой точки
§ 3. Изменение фазового объема
2. Замечания о системах в трехмерном пространстве.
§ 4. Производная в силу системы. Первые интегралы
2. Первые интегралы.
§ 5. Одномерное движение частицы в потенциальном поле
2. Колебания маятника.
3. Эллиптические функции.
4. Движение частицы в поле с кубическим потенциалом.
§ 6. Устойчивость. Функция Ляпунова
§ 7. Устойчивость положения равновесия линейной системы
§ 8. Устойчивость по линейному приближению
2. Устойчивость по линейному приближению.
3. Неустойчивость по линейному приближению.
4. Устойчивость неавтономных систем.
5. Устойчивые многообразия решений (условная устойчивость).
§ 9. Двумерные автономные системы (элементы качественной теории)
2. Предельное поведение траекторий.
3. Функция последования. Автоколебания.
ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
2. Другие примеры.
3. Классификация уравнений с частными производными 1-го порядка.
§ 2. Интегрирование линейных и квазилинейных уравнений
2. Квазилинейные уравнения.
3. Характеристики и интегральные поверхности.
§ 3. Задача Коши для линейных и квазилинейных уравнений
2. Область зависимости от начальных данных.
3. Линейные уравнения со многими переменными.
4. Квазилинейные уравнения.
§ 4. Линейные и нелинейные волны
§ 5. Нелинейные уравнения
2. Задача Коши.
ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
§ 2. Функционалы в линейных нормированных пространствах
2. Линейные функционалы.
3. Первая вариация.
4. Необходимое условие экстремума.
§ 3. Простейшие задачи вариационного исчисления
2. Задача с одним закрепленным и с одним подвижным концом.
3. Примеры.
§ 4. Функционалы, зависящие от высших производных
§ 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
2. Принцип наименьшего действия.
§ 6. Условный экстремум
§ 7. Задача Лагранжа
§ 8. Функционалы от функций многих переменных
2. Уравнение колебаний мембраны.
§ 9. Достаточные условия слабого экстремума
2. Квадратичные функционалы.
3. Достаточные условия слабого экстремума.
§ 10. Дополнительные сведения из вариационного исчисления
2. Гамильтонова форма уравнений механики.
3. Задача с подвижными концами.
§ 11. Принцип максимума Понтрягина
2. Необходимые условия экстремума.
ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 2. Основные оценки
2. Оценка решений.
§ 3. Асимптотика решений при больших значениях аргумента
2. Неосциллирующие решения.
3. Уравнения с комплексными коэффициентами.
§ 4. Асимптотика решений при больших значениях параметра
2. Неосциллирующие решения.
3. Двойные асимптотики.
4. Асимптотические разложения решений.
§ 5. Элементы теории возмущений
2. Метод Линдштедта — Пуанкаре.
3. Метод Крылова — Боголюбова.
4. Метдд осреднения.
5. Пограничный слой и метод сращивания асимптотических разложений.
6. Метод ВКБ для нелинейных уравнений.
СПИСОК ЛИТЕРАТУРЫ

Время разряда аккумулятора в зависимости от тока нагрузки

Я, в общем, дилетант в электротехнике, поэтому прощу прощения за неточности, если они есть, а ниже изложено то, что я могу сказать по поводу времени разряда аккумулятора, потратив на это несколько часов чтения материалов из Интернета. Итак,

Емкость аккумулятора довольно часто указывают в амперчасах, ну или в миллиампер часах.
Казалось бы, все просто — есть, у тебя скажем аккумулятор емкостью (C) 800 миллиамперчасов и устройство с током потребления (I) в 100 миллиампер, значит, по формуле
,
он может обеспечить работу этого устройства на протяжении восьми часов. Так?

Конечно же, не совсем так. Количество электроэнергии, которое можно извлечь из аккумулятора, зависит от тока разряда аккумулятора. То есть при слишком большом токе разряда аккумулятор разряжается очень быстро и отдает меньше электроэнергии. Эффект этот был замечен довольно давно, но первым, кто попробовал учесть его количественно, был Пекерт (Peukert), который модифицировал формулу, внеся показатель, который теперь называют экспонента Пекерта (Peukert’s exponent).

По Пекерту, время разряда аккумулятора равно
,
где n — экспонента Пекерта.
Сp — емкость Пекерта, то есть емкость аккумулятора, измеренная при токе разряда в 1 ампер.
I — ток разряда, для которого делается расчет.

Значение экспоненты Пекерта определяется экспериментально. Оно зависит от типа аккумулятора и даже от его возраста. Обычно значение экспоненты Пекерта лежит в диапазоне от 1.1 до 1.3. Чем она меньше, тем лучше, конечно же.
Для некоторых аккумуляторов производитель его указывает, но это бывает довольно редко. Чаще можно встретить в спецификации данные по емкости аккумулятора для разного времени разряда. Этого в принципе достаточно, чтобы вычислить значение экспоненты Пекерта самому. Калькулятор ниже делает это.

Экспонента Пекерта

Номинальная емкость 1, Ач

Номинальное время 1, ч

Номинальная емкость 2, Ач

Номинальное время 2, ч

Точность вычисления

Знаков после запятой: 2

Экспонента Пекерта

 

Разберемся теперь с емкостью Пекерта; как уже сказано выше, это емкость, или количество электроэнергии, которое может отдать этот аккумулятор при токе разряда в 1 ампер.
Емкость, указанная на аккумуляторе, это, конечно же, не оно. Это емкость, полученная при токе разряда, соответствующем какому-либо значению C-рейтинга (C-Rate).
Емкость с рейтингом 1С, это емкость, получаемая от аккумулятора при разряде его током, соответствующим этой же емкости. То есть 1000 миллиапмерчасов с рейтингом 1С означает, что данный аккумулятор способен обеспечивать ток в 1000 миллиампер в течении 1 часа. Емкость с рейтингом 0.05С это емкость, получаемая от аккумулятора при разряде его током, соответствующим 0.05 емкости. То есть 1000 миллиамперчасов с рейтингом 0.05С означает, что данный аккумулятор способен обеспечивать ток 50 миллиампер в течении 20 часов. Как уже можно догадаться, из-за эффекта Пекерта такой аккумулятор не сможет обеспечить 1000 миллиампер в течении часа. Время будет меньше.
Так вот, некоторые производители указывают C-рейтинг своего аккумулятора. Иногда как C-рейтинг, например, 0.05C или , иногда как «100 Амперчасов за 20 часов». А некоторые производители — не указывают. Наиболее частым значением в этом случае является рейтинг 0.05С () или «за 20 часов». То есть можно смело рассчитывать на 20 часов работы, но при токе в 20 раз меньше тока, соответствующего указанной емкости.

Зная этот рейтинг, можно перейти от емкости, указанной на аккумуляторе, к емкости Пекерта, и использовать ее для расчета.
Емкость Пекерта в этом случае равна
, где
С — емкость аккумулятора
R — рейтинг выраженный в часах, соответсвующий данной емкости, например, 20.
n — экспонента Пекерта
Подробнее можно почитать здесь. Там еще много интересного про формулу Пекерта есть.

Зная емкость, рейтинг в часах, ток нагрузки и экспоненту Пекерта можно рассчитать время разряда. Калькулятор ниже делает это для разного процента разряда.

Зачем нужен процент разряда? Дело в том, что для многих типов аккумуляторов невозможно извлечь всю запасенную энергию, не повредив фатально при этом сам аккумулятор. Это зависит от химии аккумулятора. Поэтому обычно производители указывают допустимую глубину разряда (Depth of Discharge, DOD). Например, если указана глубина разряда 20% (это верно для большинства автомобильных аккумуляторов, кстати), то сильно не рекомендуется использовать более 20% мощности батареи. Иногда даже указывают допустимую дневную норму разряда.

Время разряда батареи в зависимости от тока нагрузки

Ток потребления, А

Емкость батареи, А/ч

Номинальная емкость батареи, Ампер час

Время, ч.

Время работы для номинальной емкости, часы

Экспонента Пекерта

Точность вычисления

Знаков после запятой: 3

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Емкость Пекерта, Ач

 

Номинальный ток разряда, А

 

Из всего вышеизложенного понятно, что при малых токах потребления аккумулятор может обеспечить большее время работы.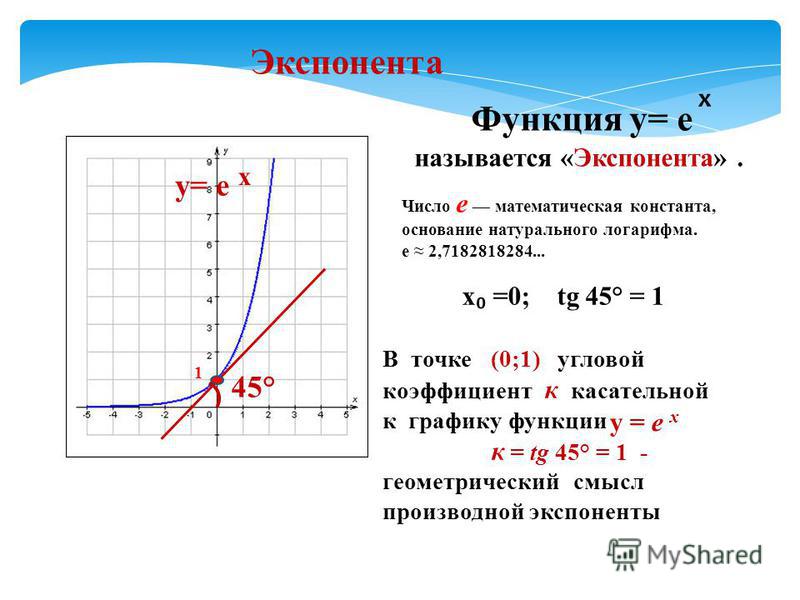 Это, в принципе так. Но не стоит доводить до крайностей — нельзя взять аккумулятор большой емкости, подключить к нему небольшую нагрузку и рассчитывать, что он сможет работать практически вечно 🙂
Тут в дело вступают уже другие эффекты, например, эффект саморазряда аккумулятора. NiMH аккумуляторы теряют саморазрядом до 30% заряда за месяц.

Поиграться с зависимостью времени работы от тока можно с калькулятором ниже.

Время разряда батареи в зависимости от тока нагрузки

Емкость батареи, А/ч

Номинальная емкость батареи, Ампер час

Время, ч.

Время работы для номинальной емкости, часы

Экспонента Пекерта

Точность вычисления

Знаков после запятой: 3

Номинальный ток разряда, А

 

Емкость Пекерта, Ач

 

Зависимость времени разряда от тока нагрузки

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

 аккумулятор батарея емкость заряд Пекерт разряд ток Физика экспонента электричество

Вычисление экспоненциального значения в Python

Обзор

В математике экспоненциальное значение числа получается в результате умножения этого числа на себя определенное количество раз. Основание — это целое число, умноженное само на себя, а показатель степени — это количество раз, которое оно будет умножено.

Область применения статьи

  • В этой статье мы узнаем о вычислении экспоненциального значения в Python различными способами.
  • Мы увидим, как вычислить экспоненциальное значение в python, используя циклы, оператор возведения в степень и т. д. 93 = 5 * 5 * 5 = 125

    В этом примере 5 — базовое значение, а 3 — показатель степени, поэтому мы умножили 5 три раза.

    Существует несколько способов вычисления экспоненциального значения в Python. Итак, давайте пройдемся по ним один за другим.

    Использование циклов

    Первый метод вычисления экспоненциального значения в Python — использование циклов.

    Циклы помогут нам выполнять блок кода снова и снова, чтобы воспользоваться его преимуществами для вычисления экспоненциального значения в Python.

     
     # инициализация значений основания и степени
база = 5
показатель = 3
 
# Берем переменную ans и инициализируем ее базовым значением
результат = база
 
если показатель != 0:
#Использование цикла для вычисления экспоненциального значения
для i в диапазоне (показатель степени - 1):
       результат = результат * база
 
еще:
  результат == 1
 
# Печать ответа
print("Экспоненциальное значение: ", результат) # 125

    Здесь мы взяли базовое значение 5 и показатель степени 3.

    Мы взяли результирующую переменную и инициализировали ее базовым значением для создания логики.

    Здесь диапазон цикла for установлен от 0 до 2 (т.е. показатель степени – 1) для повторения цикла два раза.

    Таким образом, временная сложность для приведенного выше примера становится O(n), а пространственная сложность — O(1).

    Здесь мы повторяем цикл много раз, чтобы вычислить окончательное значение. Но у нас есть более простые методы вычисления экспоненциального значения в Python.

    Оператор возведения в степень (**)

    В Python у нас есть оператор возведения в степень, который является одним из способов вычисления экспоненциального значения заданных базовых и экспоненциальных значений.

    Мы используем (**) двойную звездочку/оператор возведения в степень между базовым и экспоненциальным значениями.

     
     # инициализация значений основания и степени
база = 2
показатель степени = 16
 
# Использование оператора возведения в степень
print("Экспоненциальное значение: ", основание ** экспоненты)
 
# Выход:
# Экспоненциальное значение: 65536

    В приведенном выше примере мы взяли основание 2 и показатель степени равным 16. Здесь 2 умножается 16 раз.

    Это самый простой метод вычисления экспоненциального значения в Python.

    Мы также можем использовать значения с плавающей запятой при вычислении экспоненциальных значений.

    Использование оператора возведения в степень

    Когда мы используем любой операнд в качестве числа с плавающей запятой, мы получаем результат в виде числа с плавающей запятой, как показано в следующем фрагменте кода.

     
     # с использованием оператора возведения в степень
печать (5.6 ** 2.3) # 52.581438372010965
печать (5.6 ** 2) # 31.359999999999996
печать(5 ** 2.3) # 40.51641491731905

    Вот некоторые методы вычисления экспоненциальных значений в Python. Существуют различные плюсы и минусы для различных методов, описанных выше, поэтому используйте их в соответствии с вашими требованиями.

    Функция pow()

    У нас есть огромное количество встроенных функций в Python, и pow() — одна из них, которая помогает нам вычислять экспоненциальное значение.

    В функцию pow() мы можем передавать значения основания и экспоненты. Эти значения могут относиться к разным типам данных, включая целые числа, числа с плавающей запятой и комплексные значения.

    pow(base, exponent) эквивалентно основанию ** степени.

     
     база = 2
показатель = 8
 
# использование функции pow() для вычисления экспоненциального значения
результат = pow (база, экспонента)
 
print("Экспоненциальное значение: ", результат)
 # Выход:
 # Экспоненциальное значение: 256
# Мы также можем рассчитать значения с плавающей запятой
напечатать (pow (2.3, 4)) # 27.98409999999999

    Но в этой функции pow() разрешены также три параметра. Первые два аргумента — это основание и показатель степени, но мы можем указать третий аргумент, который будет вычислять модуль вычисляемого экспоненциального значения.

    Временная сложность вычисления экспоненциального значения путем возведения в квадрат составляет O(Log(экспонента)).

    Хотя Python не использует метод возведения в квадрат, но по-прежнему показывает сложность из-за экспоненциального увеличения при больших значениях.

    Рассмотрим несколько примеров с 3 параметрами.

     
     # pow(x,y,z) с 3 аргументами оценивается как ((x**y)%z)
print("Пример 1 : ", pow(5, 3, 2)) # Пример 1 : 1
print("Пример 2 : ", pow(2, 16, 2)) # Пример 2 : 0
print("Пример 3 : ", pow(10, 5, 6)) # Пример 3 : 4
 
print("Пример 4 : ", pow(3, 6)) # Пример 4 : 729

    В приведенных выше примерах первые три примера имеют три аргумента, а четвертый только два аргумента.

    Рекомендуется использовать pow(5,3,2) вместо pow(5,3)%2, потому что здесь больше эффективности для вычисления модуля экспоненциального значения.

    Мы можем выполнять эти операции и для отрицательных чисел:

    При использовании отрицательного числа в функции pow() мы должны позаботиться о некоторых вещах при использовании отрицательного числа.

    Поскольку функция pow() сначала преобразует свой аргумент в число с плавающей запятой, а затем вычисляет степень, мы видим некоторые различия в типах возвращаемого значения.

    Основание Экспонента Возвращаемое значение
    Неотрицательное Non-Negative Integer
    Non-Negative Negative Float
    Negative Non-Negative Integer
    Negative Negative Float
      
     # основание и показатель степени положительны
print(pow(5, 3)) # 125
 
# основание отрицательное, показатель положительный
print(pow(-5, 3)) # -125
 
# основание положительное, показатель отрицательный
print(pow(5, -3)) # 0. 008
 
# основание и показатель степени отрицательны
print(pow(-5, -3)) # -0.008

    Функция pow() может выдавать разные ошибки в разных ситуациях, например.

     
     # Если мы попытаемся взять модуль комплексных чисел.
распечатать (pow (4 + 3j, 5, 3))
# ValueError: сложный модуль
 
 
# Если мы возьмем 1-й или 2-й аргумент как число с плавающей запятой, то 3-й аргумент не разрешен
печать (печать (pow (6.4, 2, 3)))
# TypeError: третий аргумент pow() не разрешен, если все аргументы не являются целыми числами
 
# Мы не можем принять 3-й аргумент, если 2-й аргумент отрицательный
распечатать (pow (2, -16, 4))
# ValueError: основание не обратимо для заданного модуля
 
# Если мы передадим какой-либо аргумент в виде строки, это выдаст ошибку типа.
распечатать (pow ('2', 4, 3))
# TypeError: неподдерживаемые типы операндов для pow(): 'str', 'int', 'int'

    Функция math.pow()

    Помимо встроенной функции pow(), у нас есть функция math.pow() из математического модуля Python, содержащего некоторые полезные математические функции.

    Эта функция math.pow() также может вычислять экспоненциальное значение в Python.

    Функция math.pow() показывает временную сложность O(1) из-за возведения в степень с плавающей запятой, что лучше, чем встроенная функция pow(), но из-за этого она жертвует точностью результата .

    Функция math.pow() может принимать только два аргумента, в отличие от трех аргументов встроенной функции pow().

    Функция math.pow() всегда возвращает значение с плавающей запятой, тогда как в функции pow() большую часть времени мы получаем значения типа int.

     
     # встроенная функция pow возвращает результат в int
print(pow(5, 2)) # 125
 
# те же входные данные в math.pow() возвращают результат в формате с плавающей запятой
print(math.pow(5, 2)) # 125.0

    Функция math.exp()

    У нас есть функция exp() в математическом модуле, которая использует значение e в качестве основы.

    Значение e в математике приблизительно равно 2,71828.

    Значение e в Python равно 2,718281828459045

     
     # Проверка значения e в python
print(math.e) # 2.718281828459045

    Это значение e используется в качестве базового значения, а значение показателя степени задается в качестве аргумента.

    Чтобы реализовать это, мы должны импортировать математический модуль.

     
     # импорт математического модуля для использования math.pow()
импортировать математику
 
# присвоение значения экспоненты
показатель = 5
 
# Значение e принимается за базовое значение
результат = math.exp(показатель степени)
 
# результат
print("Экспоненциальное значение: ", результат) # 148.4131591025766

    Эти разные методы имеют разную временную сложность наряду со своими плюсами и минусами.

    .
    Метод Сложность времени Сложность пространства
    O(1)
    функция pow() O(Log(expponent)) O(1)
    функция math. pow() O(1) O(1)

    Заключение

    В этой статье мы рассмотрели экспоненциальные значения и способы их вычисления с использованием различных методов в Python.

    1. Экспоненциальное значение — это произведение экспоненты базового значения на время.
    2. В методе циклов нам нужно написать так много кода и продумать логику.
    3. Оператор возведения в степень, который обозначается **, является одним из самых простых способов найти экспоненциальное значение.
    4. pow() — одна из встроенных функций, которая принимает от 2 до 3 аргументов. Это помогает нам найти экспоненциальное значение при передаче двух аргументов, а если мы передаем третий аргумент, то вычисляется модуль экспоненциального значения.
    5. Функция math.pow() исходит из модуля math, и это самый быстрый способ вычисления экспоненциального значения с временной сложностью O(1).
    6. Функция exp() находит экспоненциальное значение с основанием e и показателем степени, которые мы передали в качестве аргумента.

    Как вычислить экспоненту в Python?

    Вы здесь: Домашняя страница / Python / Как вычислить экспоненту в Python?

    Последнее обновление By Maryam Anwar

    Возведение в степень — это процесс в математике, в котором число умножается на себя заданное количество раз. Мы назвали операцию « a в степени n-й ». Число, умноженное на определенное количество раз, называется основанием, т. е. 9.0289 a , а число, указывающее, сколько раз оно должно быть умножено, называется показателем степени, т.е. n Python предлагает несколько различных способов вычисления степени или степени значения. Python имеет следующие методы для выполнения.

    1. Двойная звездочка **
    2. Функция Pow()
    3. Функция Math. pow()
    4. Exp( ) Функция
    5. Numpy.ny()

    В этой статье мы обсудим пять упомянутых способов вычисления показателя степени в Питон . Существует пример фрагмента кода для каждого метода вместе с выводом для лучшего понимания. Примечание: Python также предлагает методы для округления числа.

    Содержание

    1. Двойная звездочка **

    Вы можете использовать оператор Python asterisk ** . Этот оператор принимает два значения точно так же, как мы делаем простое умножение. Это ярлык для вычисления экспоненты. Давайте посмотрим на следующие примеры.

     exp1 = 6**5
print("Показатель степени 6**5 = ",exp1)
 
float_exp2 = 2,6**3
print("Показатель 2.6**3 = ",float_exp2)
 
float_exp3 = 5**2,5
print("Показатель степени 5**2.5 = ",float_exp3)
 
отрицательное_выражение4 = 25**-4
print("Показатель степени 25**-4 = ",negative_exp4)

    Вывод:

    2.

    Функция Pow()

    Pow() — это встроенная степенная функция для вычисления значения экспоненты в Python. Он принимает два значения в качестве аргументов. Если есть еще один параметр, то он возвращает модуль. Синтаксис имеет следующий вид:

     pow (основание, экспонента)

    Вот пример кода:

     pow1 = pow(6, 5)
print("Для pow(6, 5) = ",pow1)
 
pow2 = pow(2.6, 3)
print("Для pow(2.6, 3) = " ,pow2)
 
pow3 = pow(5, 2.5)
print("Для pow(5, 2.5) = " ,pow3)
 
pow3 = pow(-6, 3)
print("Для pow(-6, 3) = " ,pow3)
 
pow4 = pow(25, -4)
print("Для pow(25, -4) = " ,pow4)

    Вывод:

    Модуль с третьим параметром: 

     pow1 = pow(6, 5, 8)
print("Для pow(6, 5, 8) = " ,pow1)
 
pow2 = pow(10, 3, 2)
print("Для pow(10, 3, 2) = " ,pow2)

    Вывод:

    3. Math. Функция pow()

    Библиотека math в Python предлагает собственную реализацию pow() для вычисления экспоненты в Python. В функцию передаются два аргумента, один для основания, а другой для показателя степени. Давайте посмотрим на пример:

     импорт математики
 
math_pow1 = math.pow(5, 4)
print("5 в степени 4 = ",math_pow1)
 
math_pow2 = math.pow(2.5, 3)
print("2.5 в степени 3 = " ,math_pow2)
 
math_pow3 = math.pow(6, 5.5)
print("6 в степени 5.5 = " ,math_pow3)

    Вывод:

    4. Функция Exp( )

    Эта функция используется для вычисления экспоненты с основанием ‘e’ .

    e — математическая константа. Сначала мы импортируем математический модуль. Синтаксис:

     импортировать математику
math.exp (экспонента)

    И код примера:

     import math
 
math_exponent1 = math.exp(4)
print("Результат возведения e в степень 4 = " ,math_exponent1)
 
math_exponent2 = math.exp(16)
print("Результат возведения e в степень 16 = " ,math_exponent2)

    Вывод:

    5.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *