тренажеры по теме Вычисление производных
Тренажеры по теме «Вычисление производных».
1. Ефремов Дмитрий Борисович.
2. Средняя школа при Посольстве России в Швеции.
3. Учитель математики.
Рассмотренная ниже система тренировочных заданий помогает осуществить поэтапную отработку умения вычислять производную функции, что является основой для успешного изучения темы «Применение производной», которая, в свою очередь, представлена на экзамене по математике.
Распределение блоков заданий по принципу «от простого к сложному» создает ситуацию успеха для слабоуспевающих учеников.
10 тренажеров позволят каждому десятикласснику отработать изучаемые формулы и правила дифференцирования.
Каждый из тренажеров 1-3 направлен на отработку одной формулы:
1 – производная линейной функции,
2 – производная степенной функции с натуральным показателем,
3- производная степенной функции с целым отрицательным показателем.
В тренажере 4 требуется применить все формулы, изучаемые до рассмотрения правил дифференцирования.
Тренажеры 5-9 направлены на отработку правил дифференцирования:
5- «производная суммы функций»,
6- «постоянный множитель выносится за знак производной»,
7- комбинация правил из пунктов 5 и 6,
8 – «производная произведения двух функций»,
9 – «производная частного двух функций».
Последний тренажер 10 помогает на примере тригонометрических функций еще раз повторить все правила дифференцирования.
Вычисление производных.
Тренажер 1.Тренажер 2.
№ | y=kx+b | y‘ =k | ||||
1 | y= 3x-2 | y‘ = | ||||
2 | y=5x+1 | y‘ = | ||||
3 | y=2+7x | y‘ = | ||||
4 | y=4-6x | y‘ = | ||||
5 | y=8x | y‘ = | ||||
6 | y= — 4x | y‘ = | ||||
7 | y= x | y‘ = | ||||
8 | y= | y‘ = | ||||
9 | y=5+x | y‘ = | ||||
10 | y=x-7 | y‘ = | ||||
11 | y= -0,5x | y‘ = | ||||
12 | y=x-4 | y‘ = | ||||
13 | y=6x-1 | y‘ = | ||||
14 | y=3-11x | y‘ = | ||||
15 | y=8+7x | y‘ = | ||||
№ | y=xn | y‘ = n· xn-1, n>0 |
1 | y= x2 | y‘ = |
2 | y= x3 | y‘ = |
3 | y= x4 | y‘ = |
4 | y= x5 | y‘ = |
5 | y= x6 | y‘ = |
6 | y= x7 | y‘ = |
7 | y= x15 | y‘ = |
8 | y= x100 | y‘ = |
9 | y= x311 | y‘ = |
10 | y= x201 | y‘ = |
Тренажер 3.
Тренажер 4.
y=xn | y‘ = n· xn-1, n<0 | |
1 | y= x -2 | y‘ = |
2 | y= x -3 | y‘ = |
3 | y= x -4 | y‘ = |
4 | y= x -5 | y‘ = |
5 | y= x -6 | y‘ = |
6 | y= x -7 | y‘ = |
7 | y= x -100 | y‘ = |
8 | y= x -15 | y‘ = |
9 | y= x -150 | y‘ = |
10 | y= x -1000 | y‘ = |
функция | производная | |
1 | y= | y‘ = |
2 | y= | y‘ = |
3 | y= π | y‘ = |
4 | y= 6x+3 | y‘ = |
5 | y= 4 | y‘ = |
6 | y= x2 | y‘ = |
7 | y= x | y‘ = |
8 | y= 1024 x | y‘ = |
9 | y= | y‘ = |
10 | y= sin2x + cos2x | y‘ = |
Тренажер 5.
Тренажер 6.
Правило 1 (u + v)’ = u‘ + v‘ | ||
1 | y=x7+x | y‘ = |
2 | y=x-2 + | y‘ = |
3 | y= -4x+x4 | y‘ = |
4 | y= x9 + | y‘ = |
5 | y=x-1–x2+1 | y‘ = |
6 | y=6x-3+x5 | y‘ = |
7 | y=4+ π+ | y‘ = |
8 | y=x10+x-3 | y‘ = |
9 | y=x7-3x+2 | y‘ = |
10 | y=x-5+ — π | y‘ = |
Правило 2 (c ∙u)’=c ∙ u‘ | ||
1 | y=3x4 | y‘ = |
2 | y= -2x7 | y‘ = |
3 | y= -7x-3 | y‘ = |
4 | y=1,5x4 | y‘ = |
5 | y=6 | y‘ = |
6 | y= | y‘ = |
7 | y= -2 | y‘ = |
8 | y=3x -5 | y‘ = |
9 | y= | y‘ = |
10 | y= | y‘ = |
Тренажер7.
Тренажер 8.
Правила 1 и 2 (u + v)’ = u‘ + v‘ (c ∙u)’=c ∙ u‘ | ||
1 | y=4x3 +8x2 | |
2 | y=6x3-4 | |
3 | y=+4x-2 | |
4 | y=6x3-5x2+2х-4 | |
5 | y=2x-2+4x-1+7 | |
6 | y=3x3 +x-9 π | |
7 | y=2х+ +1 | |
8 | y= x6+12 | |
9 | y=-5x-2 +2x-5 | |
10 | y=х4+9x2+8 |
Правило 3 (u∙v)’ = u‘∙v+u ∙ v‘ | ||
1 | y= x· | y‘ = |
2 | y= x4·(x6+3x+4) | y‘ = |
3 | y=·(3x-7) | y‘ = |
4 | y= (x-3π)· | y‘ = |
5 | y= (5x3+2x4)·(3-x) | y‘ = |
Тренажер 9.
Правило 4 | ||
1 | y= | y‘ = |
2 | y= | y‘ = |
3 | y= | y‘ = |
4 | y‘ = | |
5 | y‘ = | |
Тренажер10.
тригонометрические функции | ||
1 | y=sin x | y‘ = |
2 | y=cos x | y‘ = |
3 | y=tg x | y‘ = |
4 | y=ctg x | y‘ = |
5 | y=2sinx | y‘ = |
6 | y=-3cosx | y‘ = |
7 | y=tgx | y‘ = |
8 | y= | y‘ = |
9 | y= (3x-1)·tgx | y‘ = |
10 | y= (x-4+1)·ctgx | y‘ = |
11 | y= (2x3+4x2-6)·cosx | y‘ = |
12 | y= x2·cosx | y‘ = |
13 | y= x4·sinx | y‘ = |
14 | y= | y‘ = |
15 | y= | y‘ = |
Адрес публикации: https://www.
prodlenka.org/metodicheskie-razrabotki/171850-trenazhery-po-teme-vychislenie-proizvodnyh
Добавить код BF к соответствующим номерам […] заказов муфт и ниппелей. staubli.com staubli.com |
Add the code BF to the concerned part-numbers […] of the sockets and the plugs. staubli.com staubli.com |
Она весит 13 т и может перевозить до 2 т […] груза с помощью установленного
[…]
дизельного двигателя Deutz BF 6L 913 мощностью 160 [. л.с. или GM 4-53T мощностью 175 л.с. Колеса амфибии имеют диаметр 2.96 м и ширину 1.5 м. Скорость на суше 8 км/ч, на воде — 5 км/ч. На палубу амфибии может приземляться небольшой вертолет, а чтобы амфибия не перевернулась от воздушных потоков, создаваемых лопастями вертолета, предусмотрена система 4х якорей, фиксирующих VARF. trucksplanet.com trucksplanet.com |
Weighing a total of 13 t, 2 t payload, it was powered by a […] Deutz BF 6L 913 160 hp or GM 4-53T 175 hp engine […] with wheels of 2.96 m diameter and […] 1.5 m wide. Speed of 8 km / h on land and 5 in water. trucksplanet.com trucksplanet.com |
Эта опция меню будет доступна после установки CD/DVD/BD— ROM-привода в NMT, или при подключении внешнего USB-привода CD/DVD/BD—ROM. popcornhour.es popcornhour.es |
This option will only be accessible when a CD/DVD/BD-ROM drive has been installed into or attached to your NMT. popcornhour.es popcornhour.es |
В 2000 году, проработав около года на должности начальника отдела обслуживания и продаж в подразделении Olympus France, он вернулся в компанию Olympus Medical Systems Europa GmbH в Гамбурге, заняв пост начальника отдела GI/EUS/BF и подразделения маркетинга услуг. olympus.com.ru olympus.com.ru |
In 2000, after spending about a year as Department Manager, Service & Sales Management with Olympus France, he returned to Olympus Medical Systems Europa GmbH in Hamburg to take on the role of Department Manager GI/EUS/BF and Service Marketing Division. olympus.it olympus.it |
BD выпускается в строгом соответствии с техническими условиями, все аудио могут быть расшифрованы вывода см. в разделе BD RIP, BD ISO треков были совершенны следующего поколения выходе источника macbook-covers.net macbook-covers.net |
BD produced in strict accordance with specifications, all the audio can be decoded output, see BD RIP, BD ISO tracks were perfect the next generation of source output macbook-covers.net macbook-covers.net |
Выполнен проект по изготовлению пилотных […] образцов портативного мультимедийного проигрывателя, использующего разнообразные
[. promwad.com promwad.com |
The project for the pilot samples production of the portable […] […] are based on Blackfin BF548 processor was successfully […] completed. promwad.com promwad.com |
SF1605x400 обработанной винт мяч […] шариковинтовая SF типа обрабатываемой в соответствии с BK12 и BF/FF12 опор ШВП. zappautomation.co.uk zappautomation.co.uk |
The SF1605x400 machined ball screw is
[. zappautomation.co.uk zappautomation.co.uk |
Во-вторых, […] использовать VAV BF типа низкого шума […] ветра шасси используется в основном для различных кондиционеры, воздушные […] завесы, отопления и охлаждения, вентилятор и т.д., также могут быть использованы в промышленных и горнодобывающих предприятий, общественных мест, крытый вентиляции. ru.shyngda.com ru.shyngda.com |
Second, use VAV BF type low-noise wind […] chassis is mainly used for a variety of air conditioning units, air curtain, heating
[. and cooling fan, etc., can also be used in industrial and mining enterprises, public places, indoor ventilation. en.shyngda.com en.shyngda.com |
Чтобы привести автомобиль в боевую готовность и показать силу были использованы 3-дюймовые навесы и особые […] колеса матового черного цвета, а также […] грязевые шины М/Т BF Goodrich, был добавлен […] большой передний кенгурятник, ограничительная […] планка и багажник на крыше. ms-auto.co.jp ms-auto.co.jp |
To be fully armed and show the impact, 3 inch lift ups and […] special mat black wheel and BF Goodrich […] mud terrain tires, large front grill guard [. ..]
and tail guard and roof racks are added. ms-auto.co.jp ms-auto.co.jp |
Мы также добавили черные боковые пороги, 2-дюймовый […] навес, эксклюзивные колеса черного цвета и всесезонные […] грязевые шины BF Goodrich для придания […] более неустрашимого вида. ms-auto.co.jp ms-auto.co.jp |
We also added black side tube step, 2 inch lift up, exclusive black color […] wheel and BF Goodrich mud ter to make it with a look of fearless determination. ms-auto.co.jp ms-auto.co.jp |
Поскольку пропорциональная
[…]
счетная трубка BF3 будет реагировать [. только на термальные нейтроны, полиэтиленовый модератор, […] который замедляет случайные быстрые нейтроны до термальных энергий, окружает нейтронно чувствительную трубу. ru.flukebiomedical.com ru.flukebiomedical.com |
Since the BF3 proportional counter […] tube will only respond to thermal neutrons, a polyethylene moderator, which slows the […]incident fast neutrons to thermal energies, surrounds the neutron sensitive tube. flukebiomedical.com flukebiomedical.com |
В настоящий момент компания
[…]
[…]
Promwad работает над системой видео наблюдения и регистрации с использованием стандарта сжатия изображения JPEG2000 на базе кодека ADV212/202 и двухъядерного процессора Blackfin BF561. promwad.com promwad.com |
Currently Promwad Company develops a video surveillance and recording system using JPEG2000 image compression standard based on ADV212/202 codec and Blackfin BF561 duo core processor. promwad.com promwad.com |
На грузовики могут устанавливаться зарубежные […] дизели Perkins мощностью 65 л.с. (базовый […] двигатель) и Deutz BF 04L 2011 мощностью […] 79 л.с. или отечественный владимирский […] ВМТЗ Д-130Т мощностью 65 л.с. Приводы от валов отбора мощности спереди и сзади позволяют навешивать различное дополнительное оборудование. trucksplanet.com trucksplanet.com |
The trucks can be equipped with foreign
[. Perkins 65 hp diesel (Base engine) and Deutz BF 04L 2011 with […] an output of 79 hp or domestic VMTZ D-130T […] developes 65 hp. trucksplanet.com trucksplanet.com |
Если заготовка имеет важное значение в стране, то […] составителям кадастров рекомендуется использовать национальные […] данные по заготовкам или вывести значение BF по конкретной стране. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp |
If logging is significant in the […] country, the inventory compilers are encouraged to use national […] harvest data or derive country-specific BF values. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp |
I. Общие сведения о Шанхае должен достичь Фан-Ко, […] дизайн и производство BF VAV низким шасси шум […] ветра предназначены для вентилятора выхлопных […] устройств для удовлетворения оперативных потребностей различных рабочих условиях, он имеет небольшой размер, легкий вес, красивый внешний вид, низкий уровень шума, простота в обслуживании. ru.shyngda.com ru.shyngda.com |
I. Overview of Shanghai should reach a Fan Co., the design and […] production of the BF VAV low noise wind chassis […] designed for the blower exhaust devices
[. to meet the operational requirements of different working conditions, it has a small size, light weight, beautiful appearance, low noise, easy maintenance. en.shyngda.com en.shyngda.com |
Наряду со страхованием кредита на инвестиции мы наше предложение расширили на два следующих страховых продукта для страхования […] просроченных задолженностей по экспортным […] поставочным кредитам (вид Bf и Cf), которые позволяют […] банкам откупать экспортные задолженности […] без регресса на экспортера. egap.cz egap.cz |
Simultaneously with insurance of a credit for the financing of investments, we extended our offer by two other insurance products for
[. insurance of ceded receivables from export […] supplier credits (types Bf and Cf) which enable […] banks to purchase export receivables […] without recourse against the exporter. egap.cz egap.cz |
Параметр “bf” содержит файл, который […] клиент должен получить по TFTP; подробности смотрите в Разд. 4.5.4. debian.org debian.org |
The “bf” option specifies the […] file a client should retrieve via TFTP; see Section 4.5.4 for more details. debian.org debian.org |
Оборот
[. только на подъемных машинах, превысил миллиард евро (более 15 миллиардов […] эстонских крон) в год. intrac.ee intrac.ee |
The turnover of Manitou BF, who is focused […] only on lifting machines, is over one milliard euro (more than 15 milliard Estonian kroons ) a year. intrac.ee intrac.ee |
Для учета коры в изымаемой при заготовке древесине необходимо использовать «долю коры в заготовленной древесине» (BF). ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp |
Bark fraction in harvested wood (BF) should be 4. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp |
Если бы Володя Малахов, до этого очень здорово […] игравший ту партию, пошел Bf5 c Ефименко, то мы […] бы выиграли тот матч, вышли на чистое первое […] место, и, что очень важно, поменялись бы с украинцами местами психологически. crestbook.com crestbook.com |
If Volodya Malakhov, who had played that game extremely well until […] then, had gone for Bf5 against Efimenko […] then we’d have won the match, moved into […] clear first place and, very importantly, switched places with the Ukrainians psychologically. crestbook.com crestbook.com |
Изъятие древесины (L древ.-изъятия ) рассчитывается с помощью уравнения 2.12 из главы 2, товарные круглые лесоматериалы с корой (H), коэффициент преобразования и […] разрастания биомассы (BCEF ), доля […] коры в заготовленной древесине (BF), отношение подземной биомассы […] к надземной биомассе (R), доля […] углерода в сухом веществе (CF) и табличные данные по умолчанию, раздел 4.5. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp |
Wood removal (L wood-removals ) is calculated with Equation 2.12, Chapter 2, merchantable round wood over bark (H), biomass conversion expansion factor (BCEF ), bark […] fraction in harvested wood
[. fraction of dry matter (CF) […] and default tables, Section 4.5. ipcc-nggip.iges.or.jp ipcc-nggip.iges.or.jp |
В Институте агротехники и животноводства Баварского земельного управления сельского хозяйства вот уже много лет […] используются инкубаторы с принудительной […] циркуляцией воздуха серии BF от BINDER, благодаря […] которым качество исследований остается […] неизменном высоким. binder-world.com binder-world.com |
At the Institute for Agricultural Engineering and Animal Husbandry at the Bavarian State Research Center for Agriculture,
[. incubators with mechanical convection of the BF […] series from BINDER have supported the consistently […] high quality of research for many years. binder-world.com binder-world.com |
влажность,W; —коэффициент биоразложения отходов на стадии […] полного метаногенеза Bf (зависит от морфологического […] состава биоразлагаемой части ТБО). ogbus.com ogbus.com |
factor of biodecomposition of waste products at the stage of complete […] formation of methane Bf (depends on morphological […] structure of biodecomposing part of MSW). ogbus.ru ogbus. |
Хотя […] Me.410 превосходил Bf.110 по лётно-техническим […] характеристикам, прежде всего по скорости и дальности полёта, но всё […] же уступал ему в универсальности применения. warthunder.com warthunder.com |
Although the Me.410 was […] superior to the Bf 110 in its performance […] characteristics, most of all in its speed and flight range, […] it was inferior as far as versatility was concerned. warthunder.com warthunder.com |
Светодиоды «R», «BF«, «FDO» и «FS» не являются [. элементами системы обеспечения безопасности и не должны использоваться в […] качестве таковых. download.sew-eurodrive.com download.sew-eurodrive.com |
The «R«, «BF», «FDO» and «FS» LEDs are not safety-oriented […] and may not be used as a safety device. download.sew-eurodrive.com download.sew-eurodrive.com |
Страхование типа «Bf« и «Cf» подготовила EGAP […] при тесном сотрудничестве с банковским сектором с целью позволить банкам оперативно […] реагировать на потребности своих клиентов, а экспортёрам позволить получить от продажи экспортных дебиторских задолженностей финансовые средства для реализации последующих контрактов. egap.cz egap.cz |
The insurance of the types «Bf» and «Cf» has been prepared […] by EGAP in close cooperation with the banking sector with aim […] of enabling banks to react flexibly to needs of their clients and helping exporters to acquire financial funds for realization of further contracts by selling of their export receivables. egap.cz egap.cz |
ELSR—M—BF/AF облегченная версия […] саморегулирующийся нагревательный кабель, включающий внешнюю оболочку, которая безопасна […] для использования с пищевыми продуктами и питьевой водой. eltherm.com eltherm.com |
ELSR-M-BF/AF is the light version [. of a self-regulating heating cable featuring an outer jacket which is KTW-proofed and […] suitable for use in potable water. eltherm.com eltherm.com |
BFC продолжает тесно сотрудничать с BFМ для обеспечения максимальной координации деятельности […] с подразделениями на местах. unesdoc.unesco.org unesdoc.unesco.org |
BFC continue to work closely with BFM to ensure maximum coordination with the field offices. unesdoc.unesco.org unesdoc.unesco.org |
..]
..]
аудиоинтерфейсы, на процессоре Blackfin BF548.
..]
the SF type ballscrew machined to fit the BK12 and BF/FF12 ballscrew supports.
..]
..]
..]
..]
..]
компании Manitou BF, специализирующейся […]
33 applied to account for bark in wood removals with harvest.
..]
(BF), below-ground biomass to above-ground biomass ratio (R), carbon […]
..]
ru
..]
..]
Получение производной функции в Python
спросил
Изменено 6 лет, 10 месяцев назад
Просмотрено 7к раз
Я написал простой код, который принимает производные, но не принимает производные от тригонометрии.
из math import sin, радианы
определение синуса (х):
вернуть грех (радианы (х))
производная по определению (функция, х):
ч = 0,0000000001
возврат (функция (x+h)-функция (x))/ч
защита f(x):
вернуть 2*х**2+х
печать (производная (f, 5))
печать (производная (синус, 60))
Поскольку производная синуса равна косинусу, а косинус (60) равен 0,5, вывод должен быть
21.000... 0,5
, но вместо этого выводит
21.0000195011 0,00872746319658
Я делаю что-то не так или это только из-за функции math.sin() ?
- питон
- производная
1
Что касается небольшой разницы в производной от f() , это происходит из-за того, что ваша формула не является точной. Этот общий разностный коэффициент дает точный ответ только для бесконечно малого значения ч . Компьютер явно не может справиться с бесконечно малым значением, поэтому вы использовали «обычное», но несколько маленькое значение ч и получили приблизительный ответ.
Если вы используете очень маленькое значение ч , вы получите другие проблемы из-за того, что компьютер работает только с конечной точностью. Эта точность настолько хороша, насколько вы можете получить с числами с плавающей запятой двойной точности. Есть более сложные формулы, которые дают лучшие ответы: выполните поиск «числовой производной».
2
Часто при численных вычислениях нежелательно выполнять вычислительную задачу так, как вы это делаете на бумаге. В первую очередь потому, что вам нужно беспокоиться об ошибках с плавающей запятой. Таким образом, лучшая реализация производной находится следующим образом:
def производная(func, x, h = None):
если h равно None:
# Обратите внимание, что найденное здесь жестко закодированное значение представляет собой квадратный корень из
# точность с плавающей запятой, которую можно узнать из функции
# вызов np.sqrt(np.finfo(float).
eps).
ч = 1,411938477e-08
хф = х + ч
дх = хф - х
возврат (функция (xph) - функция (х)) / dx
eps).
ч = 1,411938477e-08
хф = х + ч
дх = хф - х
возврат (функция (xph) - функция (х)) / dx
Глядя на это, вы можете возразить и сказать, что dx = h , так как xph - x = x + h - x = h , однако, если вы действительно произведете вычисления на компьютере, вы обнаружите, что это неверно из-за округления. Также обратите внимание, что важно выбрать правильное значение для ч , чтобы получить наилучший результат. Прямо сейчас по умолчанию установлен квадратный корень машинной точности для числа с плавающей запятой в python.
3
Нет, вы не ошиблись в коде.
‘d/dx sin(радианы(x))’ равно 1/180 π cos((π x)/180)
http://www.wolframalpha.com/input/?i=d%2Fdx +sin(radians(x))
, а при 60 ~ 0,00872746319658
Синусоидальная производная работает не так, как ожидалось, потому что sinus преобразует часть +h в радианы, а знаменатель оставляет ее в градусах.
Вы заметите, что следующая функция правильно вычисляет производную.
# рассматривать h как градусы
производная по определению (функция, х):
ч = 0,0000000001
return (func(x + h) - func(x)) / радианы(h)
производная(синус, 60) # 0.5000468070196941
Или, в качестве альтернативы, значение ч может быть преобразовано в градусы перед передачей его в синус .
# рассматривать h как радианы
производная по определению (функция, х):
ч = 0,0000000001
return (функция (х + градусы (ч)) - функция (х)) / ч
производная(синус, 60) # 0,5000000413701855
Обратите внимание, что последняя функция дает более точное значение, поскольку значение в радианах 0,00…01 меньше, чем соответствующее значение в градусах. Однако оба эти подхода не будут работать для функций, которые не ожидают аргумента в градусах.
Единственный способ решить эту проблему — указать, вводятся ли входные данные в градусах, и даже это может не сработать для более сложных тригонометрических уравнений (поскольку степени π/180 появляются при дифференцировании уравнений, выраженных в градусах).
производная по определению (функция, х, транс = лямбда х: х):
ч = 0,0000000001
return (func(x + trans(h)) - func(x)) / h
производная(синус, 60, градусы) # 0,5000000413701855
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Math Tutor — Производные — Обзор методов
Math Tutor — Производные — Методы Обзор — Производные Если вы хотите одновременно следовать другому тексту о деривативах в
отдельное окно, нажмите здесь, чтобы
Теория и здесь для решения проблем.
Здесь мы покажем алгоритм вычисления производных. Дифференциация является основой для большинства расчетов в реальном анализе, поэтому вам следует освоить его хорошо. Желаемый уровень мастерства прост: вы должны быть уверены, что вы может найти (не долго думая) производную любой функции, которая придет к вам, предполагая, что он собран с использованием элементарных функций и алгебраические операции/композиции. Алгоритм, изложенный ниже, способен именно это.
Чтобы уметь различать, нужно знать наизусть два основных
вещи:
Словарь , то есть
элементарные производные.
Грамматика , что означает пять основных правил операций:
Также удобно помнить, что производная линейна, т. е. когда дифференцируя суммы, дифференцируем каждое слагаемое в отдельности; более того, мультипликативные константы могут быть извлечены из производной.
Есть две возможности для производных. Иногда мы можем использовать элементарный
производные и сразу напишите результат.
Однако обратите внимание, что мы можем использовать
формулы для элементарных производных только в точности так, как указано, любые
модификация означает, что формулы больше не работают, и мы должны использовать правила.
Например, хотя мы можем написать эту производную от
грех( х ) это потому что ( х ),
это правило не распространяется на модификации типа
sin(2 x ), sin( x 2 ), sin 2 ( x ) и т. д. Например,
производная sin(2 x ) точно не
cos(2 х ).
Вторая возможность заключается в том, что у нас есть выражение, которого нет в списке. элементарных производных. Затем мы должны использовать правила, чтобы разбить его на строительные блоки, которые, наконец, сделаны с использованием элементарных производных. алгоритм для этого ниже, но прежде чем мы перейдем к нему, одно замечание относительно обозначение.
У новичков иногда возникают проблемы с применением производной
символ, например, их может запутать обозначение цепи
правило выше.
На самом деле это просто. Начнем с примера. Рассмотрим
функция f ( x ) = x 2 .
Когда мы пишем f ′(5), то символ f ′ представляет конкретную функцию, а именно
функция f ′( x ) = 2 x , в
который мы подставляем 5: f ′(5) = 10.
С другой стороны, обозначение [ f (5)]′ означает, что мы
сначала подставьте 5 и только потом дифференцируйте. С f (5) — константа, получаем
[ f (5)]′ = [25]′ = 0. Если это делает
смысле, то два обозначения из цепного правила также должны быть понятны.
[ g ( f )]′ означает, что мы сначала оцениваем
состав, а затем дифференцировать составленную функцию. С другой стороны, g ′( f ) означает, что мы сначала
дифференцировать г как независимую функцию и затем заменить f в полученную производную (то есть составляем производную от г с внутренней функцией f ).
Производная выражения
Алгоритм для производной.
Шаг 1. Посмотрите на выражение, которое предполагается дифференцировать
и определить операцию, которая выполняется последней. Это может быть алгебраический
операция или внешняя функция в композиции. Если вам нужно освежить в памяти
это, проверьте
примечание к заказу
оценка.
Шаг 2. В зависимости от «последней операции» применить соответствующую
правило грамматики. Правило разбивает дифференцированное выражение на более простое
выражения, некоторые из них необходимо различать.
Шаг 3. Проверьте производные, полученные из правила из шага
2. Если все они элементарные, воспользуйтесь словарем. Вы сделали. Если некоторые
производные более сложные, для каждой из них повторяем процесс
начиная с шага 1.
Обратите внимание, что ни одно из приведенных выше правил или элементарных производных не применимо к общие полномочия . Их следует различать по их каноническому
форма
.
Также нет правила дифференцирования абсолютного значения.
Функции, которые
функция должна быть переписана как разделенная функция, см. ниже.
Внимание! Результаты, которые мы получаем с помощью этой процедуры, дают производную только в таких точках, что данное выражение существует в их окрестностях. Это означает, что мы можем использовать этот алгоритм для нахождения производной функции только в точках, в окрестностях которых функция определяется одной формулой. Что произойдет, если это не так, например, если ф дается одним формула слева и другая формула справа от точки, где мы хотим получить производную? правильная процедура описана ниже.
Производная как интуитивная процедура. Хотя есть и другие способы
запоминать и применять правила, у меня были лучшие результаты с интуитивным
подход «различить и забыть». Дифференциация немного похожа на чистку
лук. Вы всегда видите только самый внешний слой, операцию, которая выполняется
последний. Все остальное, как бы сложно оно ни было, в данный момент не имеет значения.
за исключением того, что он как целое участвует в самой внешней операции. Ты
не нужно беспокоиться об этом, так как он «скрыт» внешним слоем. Когда вы подаете заявку
соответствующее правило для внешней операции, эта конкретная операция
сделано, и вам больше не нужно об этом беспокоиться (кроме необходимости
копировать то, что выходит из него), как только оно дифференцировано (путем применения
правила), вы забываете об этом и переходите к следующему слою; так как мы закончили
с наружным слоем обнажается следующий.
Лучше всего это видно в цепном правиле. Например, когда мы различаем cos( g ( x )), это правило говорит
[cos( г ( x ))]’ = -sin( г ( x ))⋅[ г ( x )]’.
Как это согласуется с вышесказанным? Самая внешняя операция косинус, и мы делаем
неважно, что внутри косинуса, косинус скрывает это от нас. Итак, мы
дифференцировать косинус, цепное правило говорит, что мы должны заменить
внутри выражения в производную от косинуса, а затем сделать «раз».
В
с этим косинусом покончено, проблема ушла, мы наконец видим
что было внутри него и настало время его дифференцировать.
Точно так же мы можем интерпретировать, например, правило произведения. Когда мы хотим дифференцировать f ⋅ g , нам в данный момент все равно каковы индивидуальные факторы, мы сосредоточимся только на внешнем действии. Правило гласит, что для дифференцирования этой операции мы должны перейти к выражение ж ′⋅ г + ж ⋅ г ′. Таким образом, продукт вышел из проблемы, ушел от дифференциации, мы переходим на следующий слой и посмотрите на факторы ф и г , которые были скрыто от нас. Затем эта процедура пилинга повторяется до тех пор, пока мы не сможем применить элементарные производные.
Как мы уже говорили ранее, это всего лишь один из возможных подходов к деривативам.
Некоторые люди предпочитают другие способы, например, чисто формальные (они
на каждом шаге записывайте, какие части f , а какие g и
применять правила буквально).
Выбирайте тот способ, который вам больше подходит.
Пример: Найдите производную от
Решение: Последней выполненной операцией является умножение, данное функция является произведением члена в скобках и дроби. Поэтому мы применить правило произведения.
Мы получили два слагаемых с производными, ни одно из них не является элементарным функция. Таким образом, мы рассматриваем каждую производную как новую задачу.
Выражение в квадратных скобках (первое) имело сложение в качестве последней операции. Это непонятно, какое из двух добавлений последнее, но нам все равно, т.к. линейность говорит нам, что мы просто различаем каждый термин отдельно.
Второй дифференцированный член — это четкая дробь, мы используем частное правило.
Теперь у нас много производных, берем слева. Логарифм – это
элементарная функция, производная которой находится в словаре.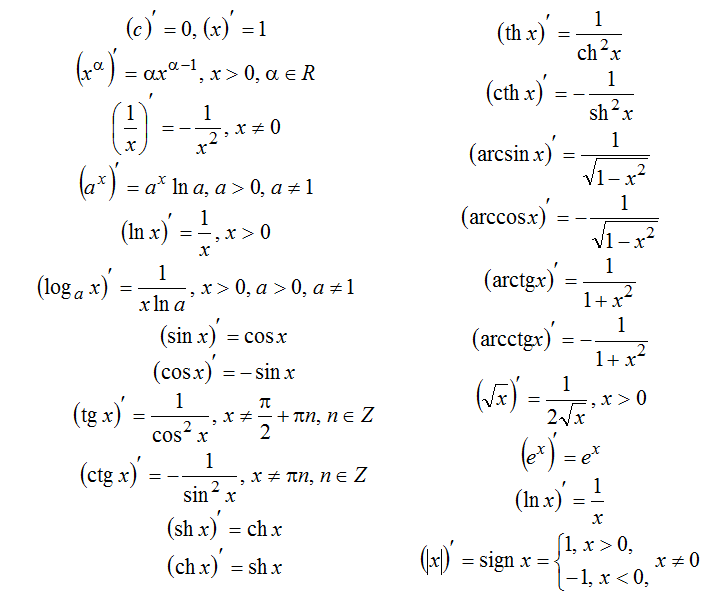
Второй срок
сложнее. Последняя операция, которую мы делаем, — экспоненциальная, поэтому
композиция, и мы должны использовать цепное правило, например, в форме
[ e y ]′ = e г г ′.
Следующий член тоже выглядит как нечто более сложное, а именно дробь,
и в самом деле, частное правило помогло бы нам. Тем не менее, опытный
дифференциатор знает, что такие выражения легче обрабатывать при изменении
во власть.
До последней фракции. Первый член сверху представляет собой линейную комбинацию, поэтому мы используем тот факт, что производная является линейной. Другими словами, мы знаем, что должны принять производную каждого слагаемого в отдельности, а в первом мы можем вытащить вывести мультипликативную постоянную из производной. Второй дифференцированный термин (в конце) представляет собой составное выражение, в качестве последнего мы делаем квадратный корень, поэтому мы применяем цепное правило.
Почти там, снова берем его слева.
Производные синуса и x −3 есть в словаре. В последней дроби мы снова
имеют элементарные производные от x 2 и 2 x .
Последняя производная представляет собой сумму, поэтому мы дифференцируем каждый член отдельно.
Осталось немного его отшлифовать и найти домен. Мы переписываем негатив мощность в виде дроби, поскольку так она выглядит лучше. Кроме того, большая фракция немного упрощается, если мы вытащим корень во втором члене числитель из числителя.
Обратите внимание, что размер домена составляет всего 90 132 x 90 133 > 0, хотя само выражение имеет смысл также для всех отрицательных x . Тем не менее, домен производная ограничена прежде всего областью определения данной функции.
Некоторые примечания:
1. Если не преобразовывать 1/ x 3 в отрицательную степень, а применить
частное правило к нему, мы получаем тот же ответ, это просто немного больше
сложный.
2. Что произойдет, если мы забудем, что мультипликативные константы могут быть вытащили из производной? Вместо простого расчета [13 x 2 ]′ = 13[ x 2 ]’ мы используем правило произведения, чтобы получить тот же вывод:
3. Опытный дифференцирующий не стал бы писать все шаги. Когда
применяя правила к заданному выражению, выражение постепенно «расцветает»
или «растет ветками», усложняется с каждым шагом. Однако есть
логика к этому, и если у вас есть опыт, вы можете сохранить немного этого в
твоя голова. Таким образом, ответ часто пишут прямо, строя его по частям.
кусок. Когда данное выражение более сложное, это может быть опасно,
так как при различении одной части легко забыть, что другая должна
сделать также, можно также перепутать брекетинг. Хорошей мерой безопасности является
идти средним путем. Делайте в голове ровно столько, сколько сможете безопасно удержать и
упростить общую картину, оставив некоторые части «на потом» с помощью []′
обозначение.
Например, приведенный выше пример может быть выполнен в два этапа, например
этот:
Односторонние производные
Вопрос: Найдите f ′ + ( a ).
Лучший случай: Если функция f задана некоторым выражение на некоторой окрестности a , мы можем найти (обе стороны) производная с использованием вышеуказанного алгоритма и односторонняя должны быть одинаковыми.
Типичный случай: Функция f задается определенным выражение о некоторой правой окрестности [ a , a + b ) из a и это выражение непрерывно там. Тогда мы можем использовать удобный теорема:
другими словами, мы находим производную выражения, используя приведенное выше
алгоритм для x > a а затем взять предел этой производной
для x → a + .
Пример смотрите в разделе
Производная и предел в
Теория — МВТ.
Другие случаи: Довольно много вещей может пойти не так, это невозможно охватывают все возможные случаи. В общем, если мы не можем использовать вышеуказанные приемы, мы обычно возвращаются к определению и пытаются разобраться.
Вопрос: Найти f ′′ — ( a ).
Очевидно, мы используем соответствующие модификации описанных выше процедур.
Функции разделения и производные
Функции разделения — это функции, которые определяются разными выражениями на различные наборы (см. Введение в Функции — Теория — Реальные функции). Мы будем игнорировать монстров и сосредоточимся на разумные функции расщепления, те, определения которых основаны на интервалах которые идут друг за другом, и их конечное число (некоторые интервалы могут быть вырожденными, т. е. одной точкой).
Процедура: Рассмотрим «разумную» функцию разделения f .
Шаг 1. Для каждого невырожденного интервала в определении f находим производную соответствующего выражения, которая дает функцию
там.
Этот результат затем также дает производную f на салон этого интервала.
Шаг 2. Если область f покрыта внутренностями из Шага 1,
мы сделали. В противном случае есть точки в области ф не являющиеся
покрыты внутренними частями, указанными выше, и нам нужно исследовать f ′ в
эти точки. Рассмотрим одну такую точку a .
а) Если эта точка является конечной точкой интервала из определения и
также конечная точка домена, это означает, что f определен на каком-то
справа или слева от и , но не с другой стороны. Поэтому
производной нет, но может быть односторонняя производная. Мы
исследовать его, как описано выше. Обратите внимание, что если f не является непрерывным
справа/слева на a , то у него не может быть соответствующего одностороннего
производная там, так что нам не нужно утруждать себя ее поиском.
b) Другой интересный случай состоит в том, что a находится внутри
области, но не внутри любого из интервалов из
определение f .
Тогда f скорее всего определяется разными
формулы справа и слева от a . Таким образом, несмотря на наличие
шанс для обычной двусторонней производной, мы не можем использовать алгоритм выше
(см. Предупреждение там). Опять же, если функция не является непрерывной в точке a , мы сразу знаем, что производной нет.
Поэтому предположим, что f непрерывна в точках a и определяется двумя разные выражения справа и слева от и . Тогда мы можем найдите односторонние производные, используя предельный трюк, как описано выше, и Сравните их. Если односторонние производные совпадают, они также дают производная от f по a .
Пример: Находим производную от абсолютного значения f ( x ) = | х |.
Поскольку нет правила для абсолютного значения, начнем с того, что избавимся от него:
Поскольку f определяется выражением x на открытом интервале
(0,∞), находим f ′ , применяя обычный алгоритм к выражению x .