Как построить функцию квадратичную: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

Квадратичная функция и ее график

На уроках математики в школе Вы уже познакомились с простейшими свойствами и графиком функции y = x². Давайте расширим знания по квадратичной функции.

Задание 1.

Построить график функции y = x². Масштаб: 1 = 2 см. Отметьте на оси Oy точку F(0; 1/4). Циркулем или полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1). Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?

Результат: какую бы точку на параболе y = x² вы не взяли, расстояние от этой точки до точки F(0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.

Можно сказать иначе: расстояние от любой точки параболы до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = -1/4. Эта замечательная точка F(0; 1/4) называется фокусом параболы y = x², а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.

Интересные свойства параболы:

1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.

2. Если вращать параболу вокруг оси симметрии (например, параболу y = x² вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.

Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.

3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе (рис. 2).

4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола (рис. 3).

5. В парках развлечений иногда устраивают забавный аттракцион «Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.

6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.

7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.

Построение графика квадратичной функции

На уроках математики вы изучали получение из графика функции y = x² графиков функций вида:

1) y = ax² – растяжение графика y = x² вдоль оси Oy в |a| раз (при |a| < 0 – это сжатие в 1/|a| раз, рис.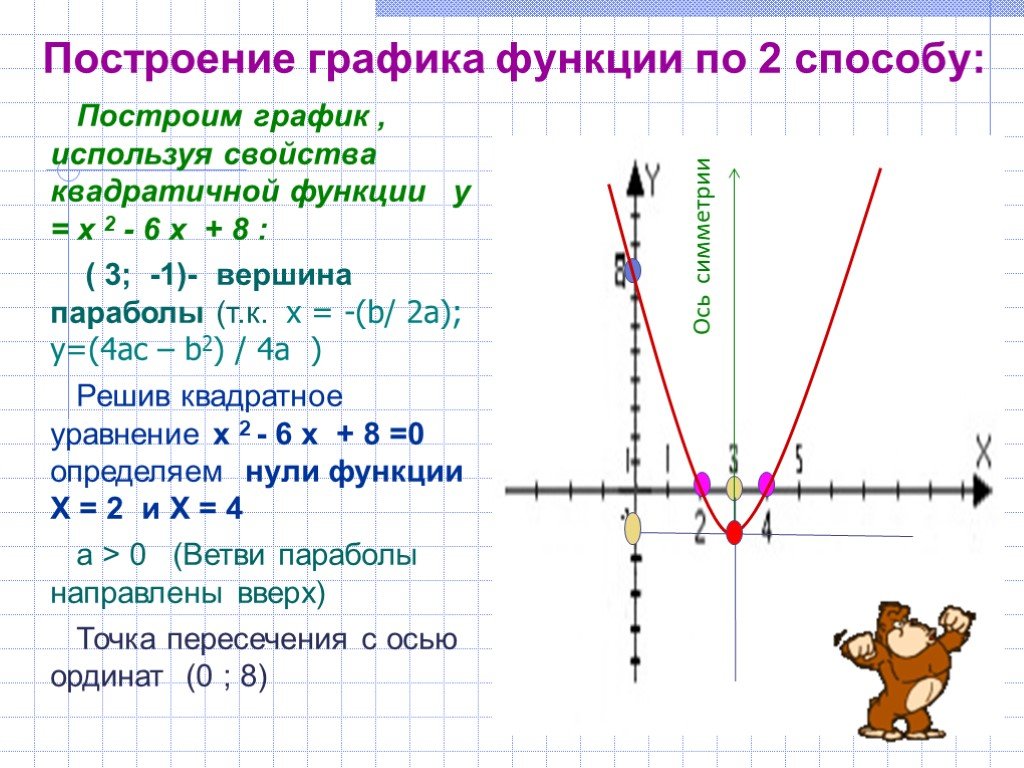 4).

2) y = x² + n – сдвиг графика на n единиц вдоль оси Oy, причем,  если n > 0, то сдвиг вверх, а если n < 0, то вниз, (или же можно переносить ось абсцисс).

3) y = (x + m)²  – сдвиг графика на m единиц вдоль оси Ox: если m < 0, то вправо, а если m > 0, то влево, (рис. 5).

4) y = -x²  – симметричное отображение относительно оси Ox графика  y = x².

Подробнее остановимся на построении графика функции

y = a(x – m)² + n.

Квадратичную функцию вида y = ax² + bx + c всегда можно привести к виду

y = a(x – m)² + n, где m = -b/(2a), n = -(b² – 4ac)/(4a).

Докажем это.

Действительно,

y = ax² + bx + c = a(x² + (b/a) x + c/a) =

= a(x² + 2x · (b/a) +  b²/(4a²) – b²/(4a²) + c/a) =

= a((x + b/2a) ² – (b² – 4ac)/(4a²)) = a(x + b/2a) ² – (b² – 4ac)/(4a).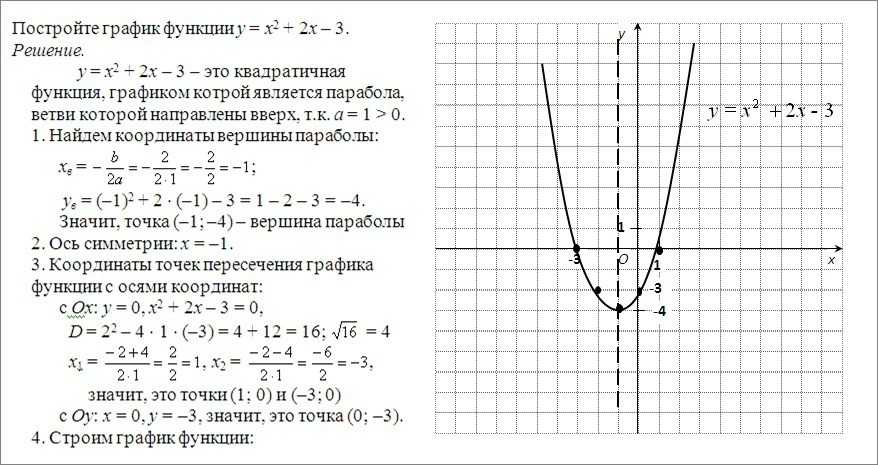

Введем новые обозначения.

Пусть m = -b/(2a), а n = -(b² – 4ac)/(4a),

тогда получим y = a(x – m)² + n или y – n = a(x – m)².

Сделаем еще замены: пусть y – n = Y, x – m = X (*).

Тогда получим функцию Y = aX², графиком которой является парабола.

Вершина параболы находится в начале координат. X = 0; Y = 0.

Подставив координаты вершины в (*), получаем координаты вершины графика y = a(x – m)² + n: x = m, y = n.

Таким образом, для того, чтобы построить график квадратичной функции, представленной в виде

y = a(x – m)² + n

путем преобразований, можно действовать следующим образом:

a) построить график функции y = x²;

б) путем параллельного переноса вдоль оси Ox на m единиц и вдоль оси Oy на n единиц – вершину параболы из начала координат перевести в точку с координатами (m; n) (рис.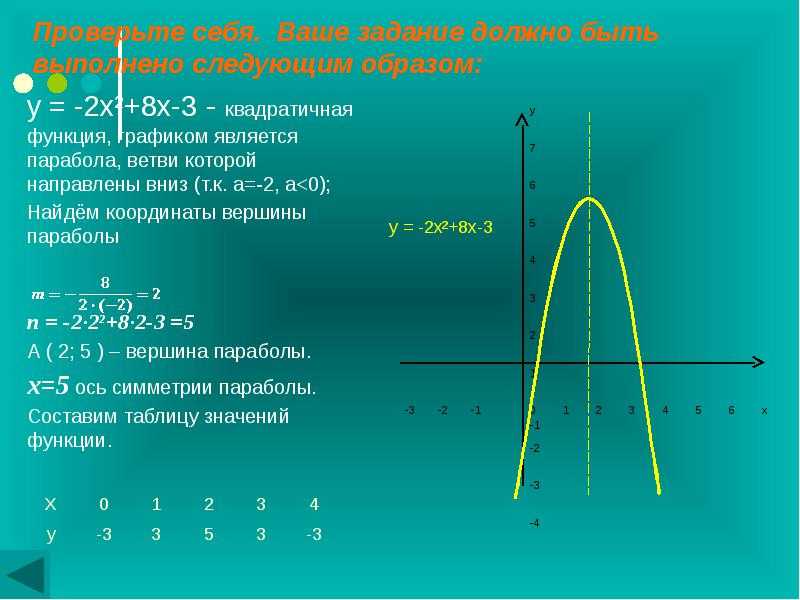 6).

Запись преобразований:

y = x² → y = (x – m)² → y = a(x – m)² → y = a(x – m)

2 + n.

Пример.

С помощью преобразований построить в декартовой системе координат график функции y = 2(x – 3)²– 2.

Решение.

Цепочка преобразований:

y = x²(1) → y = (x – 3)²(2) → y = 2(x – 3)²(3) → y = 2(x – 3)² – 2 (4).

Построение графика изображено на рис. 7.

Вы можете практиковаться в построении графиков квадратичной функции самостоятельно. Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3)² + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации.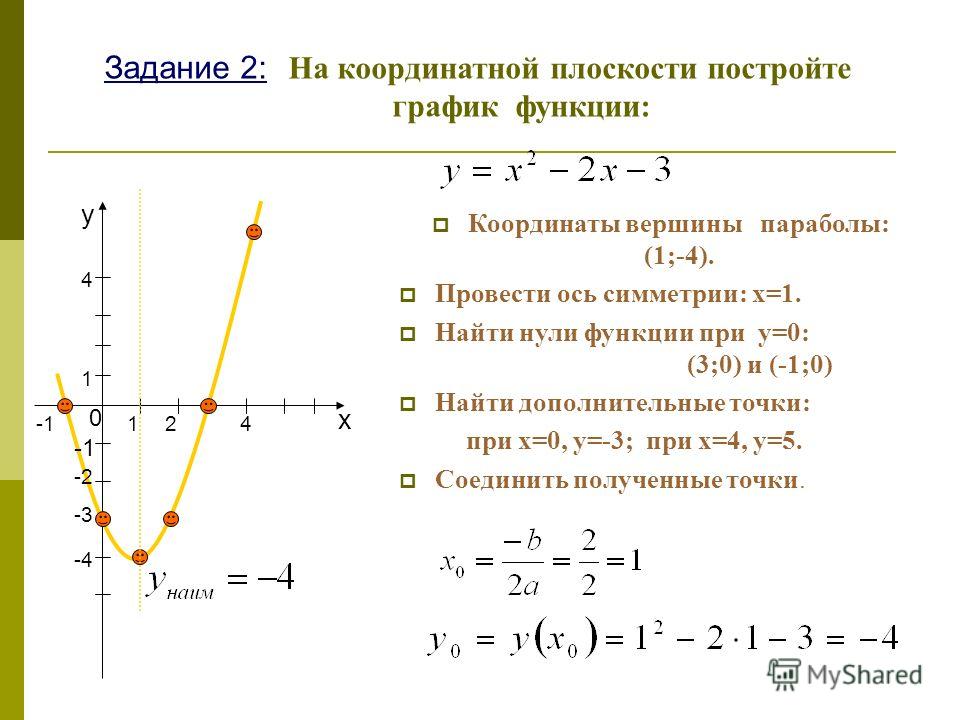

Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.

 Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

квадратичной функции

В уравнении квадратичной функции:

a – старший коэффициент

b – второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.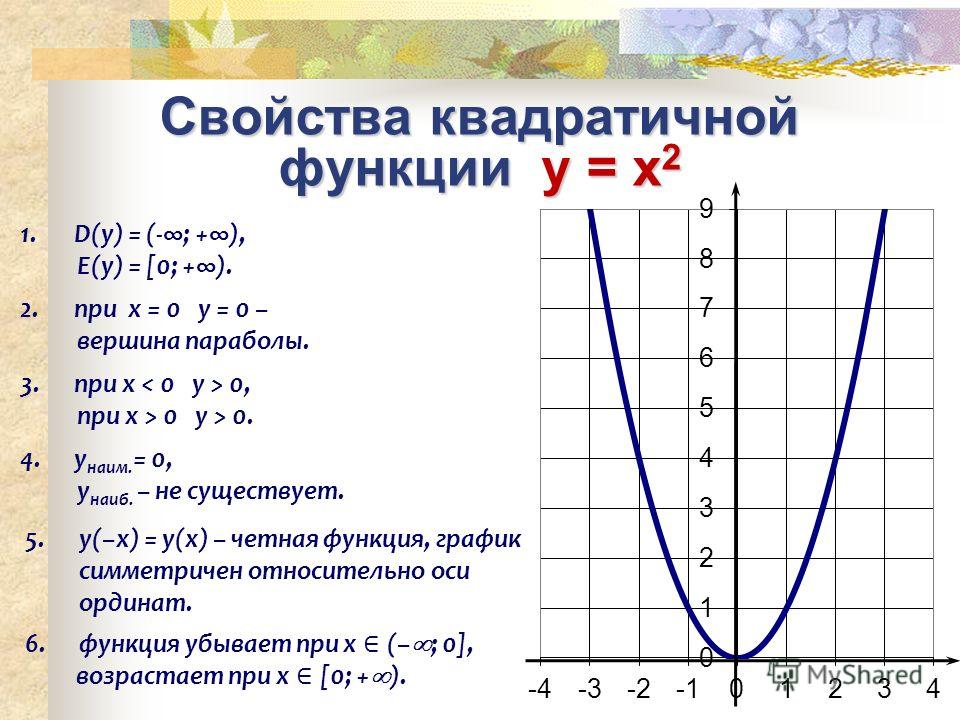

График  функции  имеет вид:

Для нахождения координат базовых точек составим таблицу:

 

Обратите внимание, что график функции  симметричен графику функции  относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвленывверх.

Если старший коэффициент a<0, то ветви параболы напрaвленывниз.

Второй параметр для построения графика  функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции  с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю,

чтобы найти координаты  точек  пересечения графика функции  с осью ОХ, нужно решить уравнение .

В случае квадратичной функции  нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.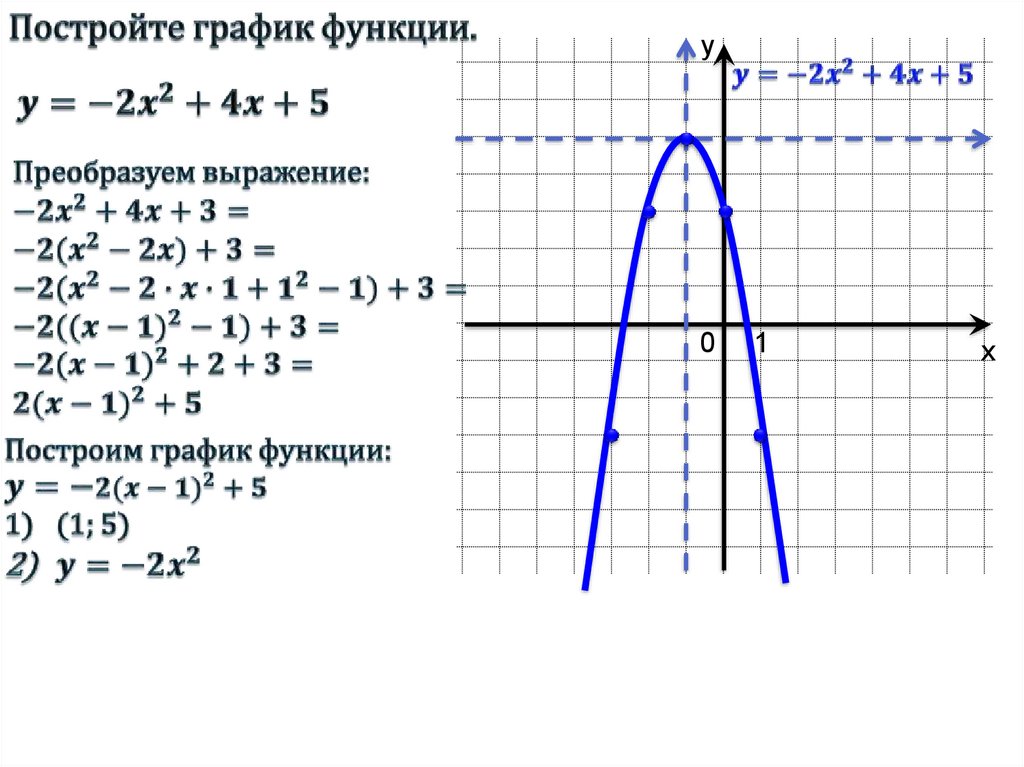

И здесь возможны три случая:

1. Если ,то уравнение  не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

2. Если ,то уравнение   имеет одно решение, и, следовательно, квадратичная парабола   имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

3.  Если ,то уравнение   имеет два решения, и, следовательно, квадратичная парабола   имеет две точки пересечения с осью ОХ:

,  

Если ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции –координаты вершины параболы:

 

Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.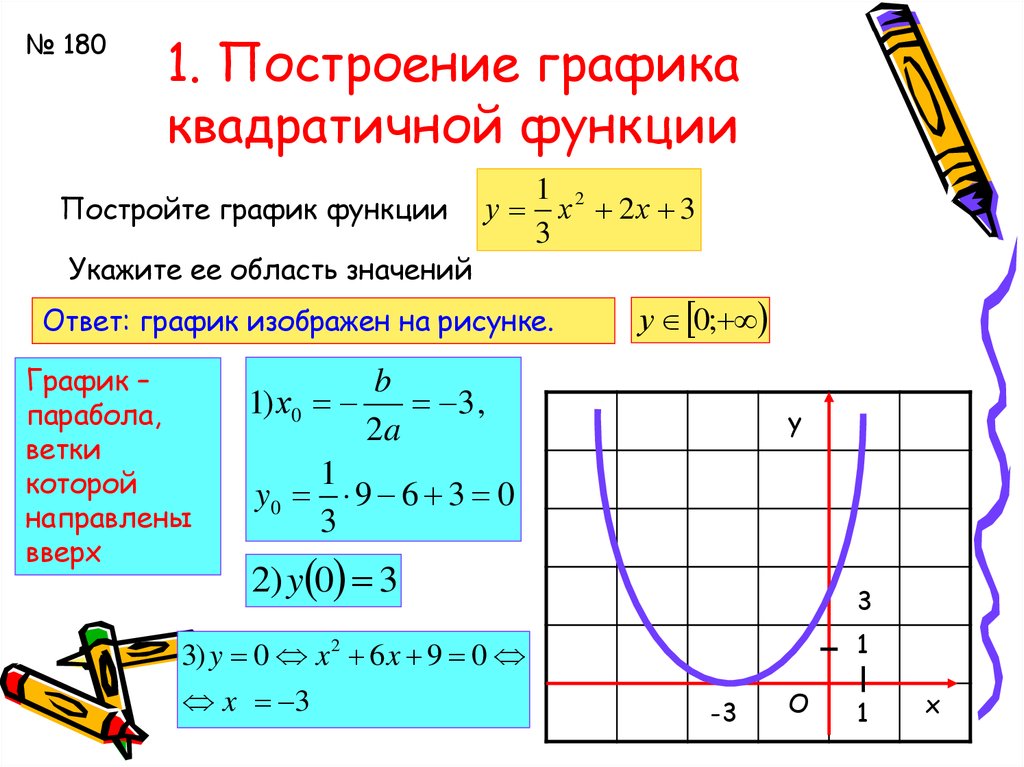

И еще один параметр, полезный при построении графика функции –точка пересечения параболы  с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны  на рисунке:

Рассмотрим несколько способов построения квдартичной параболы.В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 

1. Направление ветвей параболы.

Так как ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена 

  

Дискримнант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.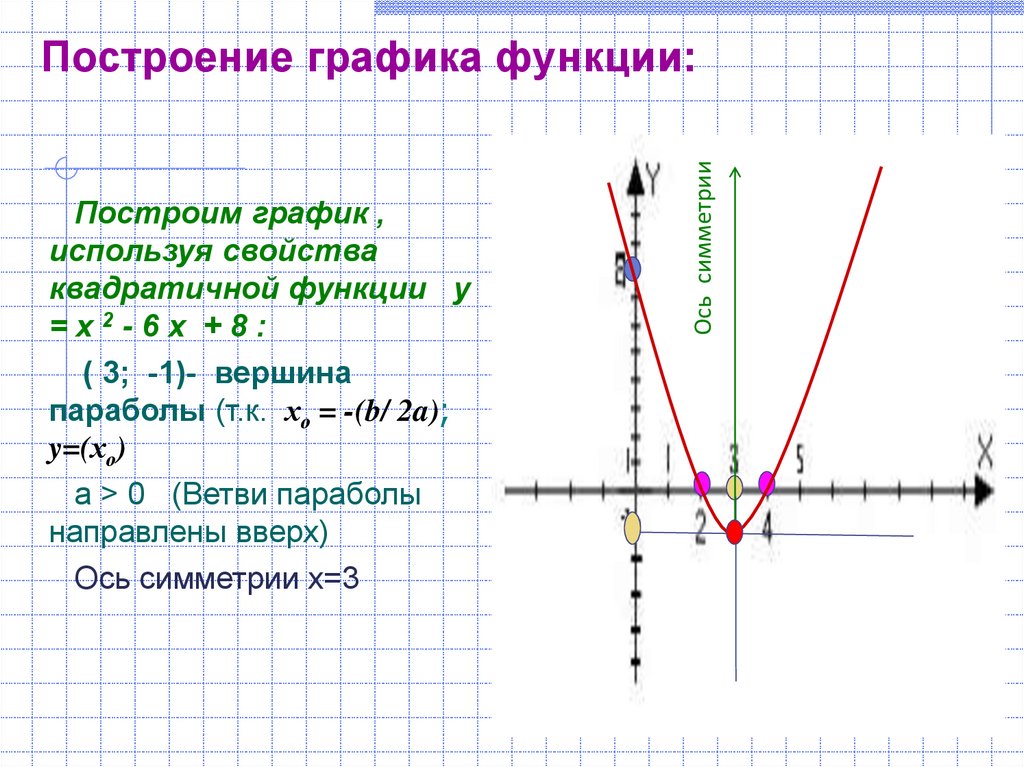

Для того, чтобы найти их координаты, решим уравнение: 

,  

3.   Координаты  вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем коодинаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные  слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы  соответственно 0;1;2

Подствим значения х в уравнение функции, найдем ординаты этих точек и занесем их  в таблицу:

Нанесем эти точки на кординатную плоскость и соединим плавной линией:

2.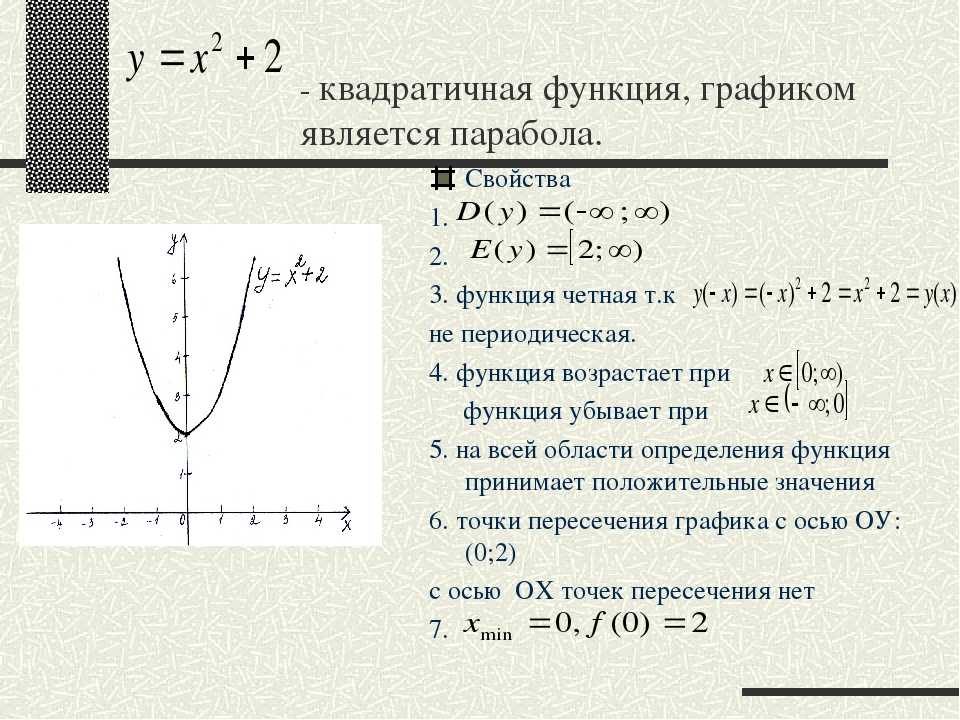  Уравнение квадратичной функции имеет вид  – в этом уравнении  – координаты вершины параболы

или в уравнении квадратичной функции  , и второй коэффициент – четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,

• затем одинаты всех точек графика умножить на 2,

• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,

• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение  графика функции . В уравнении этой функции , и второй коэффициент – четное число.

Выделим в уравнении функции полный квадрат: 

Следовательно,  координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3.  Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции – точки пересечения графика функции с осью ОХ:

(х-2)(х+4)=0, отсюда 

2. Координаты вершины параболы: 

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на  координатную плоскость и построим график:

Квадратичные функции в стандартной форме

Квадратичные функции определяются как полиномиальное уравнение второй степени, что означает, что оно имеет по крайней мере один член со степенью двойки. Квадратичные функции названы так потому, что Quad означает «четыре» (в квадрате), а наибольшая степень квадратичной функции должна быть равна 2.

Квадратичные функции могут быть представлены в трех формах:  

• Стандартная форма: ax² + bx + с = 0
• Форма вершины:  a(x – h)² + k = 0
• Форма перехвата: a(x – p)(x – q) = 0

Как записать квадратичную функцию в стандартной форме?

Вот как можно записать квадратичную функцию в стандартной форме:

f(x) = ax² + bx + c = 0

неизвестная переменная с наивысшей степенью 2, a никогда не равна нулю, что делает f (x) квадратичной функцией. Старший коэффициент всегда является ненулевым действительным числом и обозначается буквой «а». В противном случае функция не будет квадратичной, поскольку наибольшей степени 2 не существует. Стандартная форма квадратичной функции также называется общей формой квадратичной функции.

Примеры стандартной формы квадратного уравнения:

• 4x² + 3x + 10 = 0
• -x² + 5x = 0
• 7 3 x² + 7x + 3 = 0
• 9x² – 1 = 0

Преобразование квадратного уравнения из стандартной формы в вершинную

Вершинная форма квадратичной функции: ,k) — вершина квадратичной функции f(x).

и, a — коэффициент x².

Следовательно, приравнивая стандартную квадратичную функцию и квадратичную функцию вершины

Мы получаем,

AX ² + BX + C = A (x — H) ² + K

AX ² + bx + c = a (x ² – 2xh + h ² ) + k

ax ² + bx + c = ax ² – 2ah x + (ah ² + k)

3

х с обеих сторон,

b = -2ah или h = (-b)/ 2a

Теперь, сравнивая константы с обеих сторон, получаем, /2а) ² + k (Из (1))

c = b ² /(4a) + k

k = c – (b ² /4a)

k =

4 90 – b²

4a

Теперь мы можем переписать форму вершины в стандартную форму следующим образом:

f(x) = a(x – (-b) 2a )² + 4ac – b² 4a = 0

Например, для стандартной квадратичной функции f(x) = 4x² + 90tex + 100 = 0

A = 4

H = (-B) 2A = (-3) 2 × 4 = -38

K = 4AC-B² 4A 4A = 4x4x10 – 3² 4×4 = 160 – 9 16 = 151 16

Следовательно, 2a)² + 4ac – b² 4a= 0

= 4(x – (-3)8)² + 151 16 = 0

= 4(x + 3

50

)² + 151 16 = 0     

Практический вопрос: Q.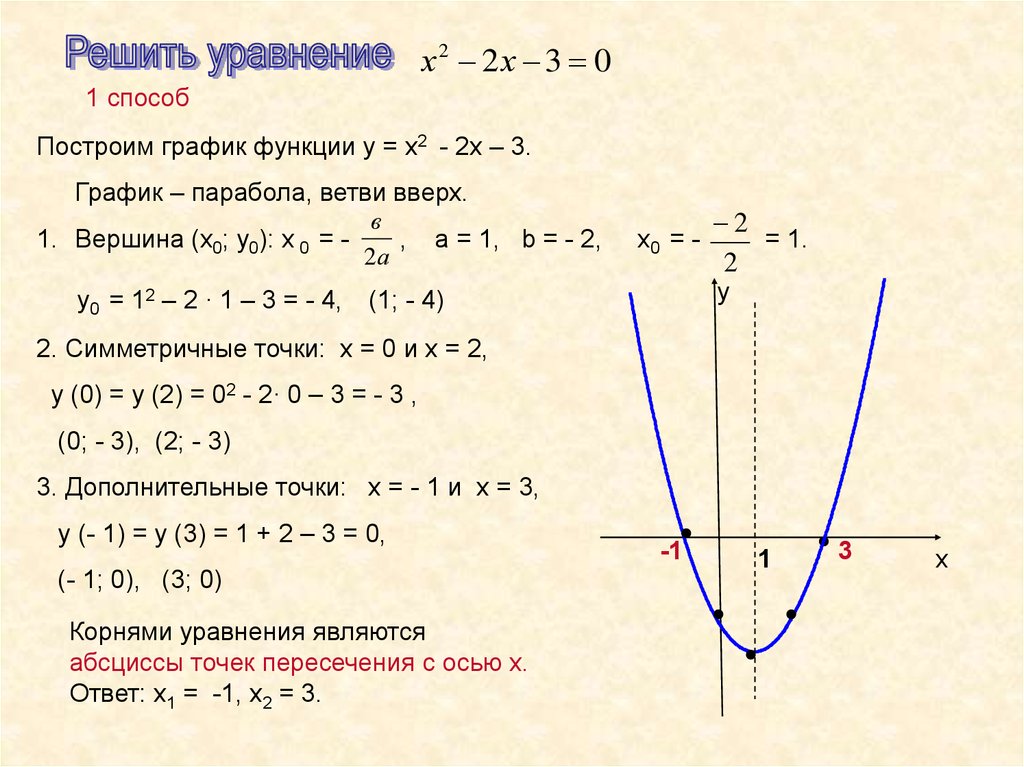 Перепишите квадратичную функцию в стандартной форме: 2 (x ² – 2x + 1) + 1 = 0

Переход от формы вершины к стандартной форме

Путем вычисления и упрощения (x – h) ² = (x – h) (x – h), a квадратное уравнение может быть преобразовано из вершинной формы в стандартную:

Например,

3 (x – 1) ² + 11 = 0 находится в вершинной форме

Следовательно, подставив (x – h) ² = (x – h) (x – h),

3 (x – 1) (x – 1) + 11 = 0

3 (x ² – х – х + 1) + 11 = 0

3 (х ² – 2х + 1) + 11 = 0

3х ² – 4х + 2 + 11 = 0

3 х 0 2 – 4x + 13 = 0 , что в стандартной форме.

Преобразование стандартного квадратного уравнения в форму пересечения

A (x – p)(x – q) = 0 используется для преобразования стандартной формы квадратного уравнения в вершинную форму.

Точки пересечения по оси x квадратичной функции f(x) = ax² + bx + c = 0 равны (p, 0) и (q, 0) соответственно, поэтому p и q являются корнями квадратного уравнения.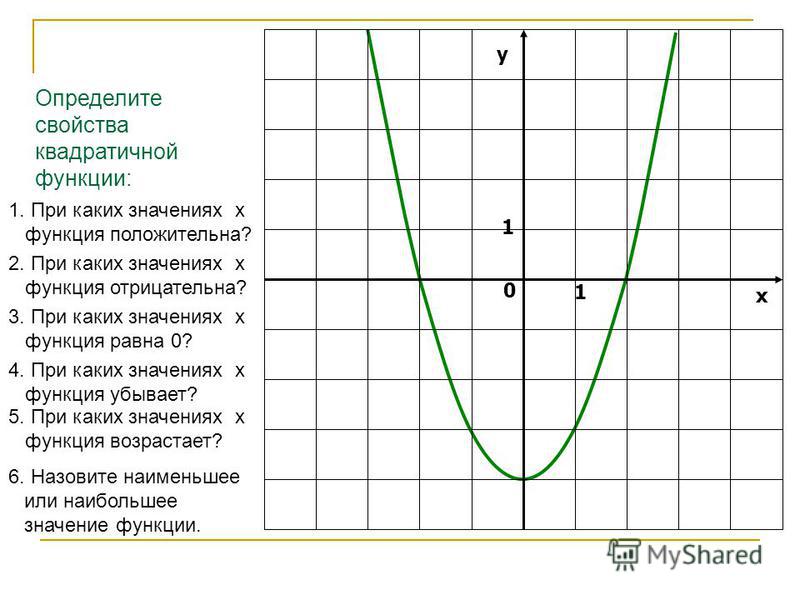

Чтобы найти p и q, мы просто используем любой из методов решения квадратного уравнения.

Например,  

Для квадратного уравнения 4x ² + 6x – 18 = 0. 

Теперь мы разложим квадратное уравнение на множители, чтобы решить его.

4x ² + 6x – 18 = 0

2(2x ² + 3x – 9) = 0

2(2x – 3) (x + 3) = 0

0x – 2 2 х + 3 = 0

2х = 3; х + 3 = 0

Следовательно, а = 4 , p = 3/2 и q = -3

Таким образом,

a (x – p)(x – q) = 0

2 (x – 3/2) (x – (-3)) = 0

2 (x – 3/2) (x + 3) = 0

(2x – 3) (2x + 6) = 0

Изменение формы перехвата на стандартную Форма

Квадратное уравнение может быть преобразовано из формы с прямой точкой в ​​стандартную форму путем умножения и упрощения (x – p) (x – q):

Например,

(2x — 3) (2x + 6) = 0 находится в форме перехвата

4x ² + 12x — 6x — 18 = 0

4x ² + 6x — 18 = 0, который находится в стандартной форме.

Графики квадратичных функций в стандартной форме

Квадратичная функция определяется как f(x) = ax2 + bx + c, где a, b и c — ненулевые значения. Парабола — это кривая, представляющая график квадратичной функции.

Различные типы парабол могут иметь разную ширину и наклон, но базовая U-образная структура всегда остается неизменной. Ось симметрии параболы пересекает вершину параболы. Все параболы симметричны из-за этой линии, известной как ось симметрии.

Говорят, что квадратичная функция f(x) = ax² + bx + c = 0 имеет стандартную форму, в которой a (коэффициент x²) не равен нулю. Если a положительно, парабола графика будет открываться вверх, а если отрицательное, то вниз.

Применение квадратичной функции

Квадратичные уравнения и параболы используются в различных сценариях реальной жизни. Случаи касаются самой высокой или самой низкой точки (вершины параболы), и все они связаны с понятием квадратичной функции. Квадратные уравнения включают движение снаряда, скорость, ускорение, геометрию и т. д.

Ниже приведены некоторые примеры таких ситуаций:

• Архитектура: Многие проекты показывают использование параболических фигур для формирования фундамента зданий, мостов, парков развлечений и т. д.
• Стрельба из пушки: пушки используются для стрельбы тяжелой взрывчаткой, а для определения угла снаряда (параболы) можно использовать квадратичные уравнения.
• Движение: В задачах, связанных со скоростью, перемещением, ускорением и т. д., широко используются квадратичные формулы.
• Геометрия: Задачи, связанные с определением площади различных фигур, таких как прямоугольники, параллелограммы и т. д., являются основными приложениями квадратных уравнений.
• Симметрия: Симметрия параболических фигур помогает развивать знания о симметрии других форм. Использование квадратичных уравнений для вывода уравнения также может помочь в понимании симметрии.

  Вы можете найти вершину, если знаете уравнение для функции, моделирующей ситуацию. Если

функция такова: f(x) = ax² + bx + c = 0

Мы знаем, что координата x вершины будет (-b) 2a , а координата y вершины можно найти, подставив координату x в функцию.

Квадратичная функция — это полиномиальное уравнение с максимальной степенью два. Степень переменной всегда представляет собой положительное целое число, меньшее или равное двум. Стандартная форма, форма вершины и форма пересечения — это три способа выражения квадратичной функции.

При построении графика стандартная форма уравнения всегда дает параболу. Значение коэффициента переменной старшей степени влияет на форму этой параболы. Квадратные уравнения могут ответить на широкий круг реальных проблем. Некоторые приложения с квадратными уравнениями могут быть основаны на задачах на скорость и вопросах из области геометрии. Работа с вопросами, связанными с четырехугольниками, такими как расстояние, скорость, время и т. д.

Часто задаваемые вопросы

Q1. Что такое квадратичные функции?

Полиномиальное уравнение второй степени содержит по крайней мере один член степени двойки, то есть квадратичные функции. Квадратичные функции названы так потому, что Quad означает «четыре» (в квадрате), а наибольшая степень квадратичной функции должна быть 2.

Q2. Как записать квадратичную функцию в стандартной форме?

Вот как можно записать квадратичную функцию в стандартной форме:

f(x) = ax² + bx + c = 0

f(x) — квадратичная функция, где a, b и c равны постоянные коэффициенты, а x — неизвестная переменная с наибольшей степенью 2, а a не может быть равно нулю. Старший коэффициент, представленный буквой «а», всегда является ненулевым действительным числом. В противном случае, если максимальной степени 2 не существует, функция не будет квадратичной.

Q3. Сколько существует форм для представления квадратичной функции?

Квадратичные функции могут быть выражены тремя различными способами: 

• Стандартная форма: ax² + bx + c = 0
• Форма вершины:  a(x – h)² + k = 0
• Форма перехвата: a(x – p)(x – q) = 0

Q4. Какой график получается при построении квадратичной функции?

Парабола — это кривая, изображающая график квадратичной функции.

Ширина и наклон различных типов парабол могут различаться, но базовая U-образная структура всегда одинакова. Ось симметрии параболы пересекается в вершине параболы. Благодаря этой линии, известной как ось симметрии, все параболы симметричны.

Q5. Какое влияние оказывает коэффициент при x² на параболу?

Различные формы парабол имеют разную ширину и наклон, но основная U-образная структура остается неизменной. Когда a (коэффициент x2) не равен нулю, говорят, что квадратичная функция f(x) = ax2 + bx + c = 0 имеет стандартную форму. Если a положительно, парабола графика развернется вверх; если он отрицательный, парабола графика разомкнется вниз.

4.4 Построение квадратичных моделей из словесных описаний и данных

4.2 Применение и моделирование квадратичных функций, 4.4 Построение квадратичных моделей из словесных описаний и данных

7 марта 2020 г. админ

4. 2 Приложения и моделирование квадратичных функций, 4.4 Построение квадратичных моделей на основе словесных описаний и данных

2 июля 2018 г. админ

Проблема:

Необходимо обрезать 28-дюймовый провод. Один кусок нужно согнуть в форме квадрата, а другой кусок согнуть в форме прямоугольника, длина которого в два раза больше ширины. Найдите ширину прямоугольника, площадь которого будет наименьшей.

Решение:

Сначала нарисуйте фигуры, которые получится из проволоки, и обозначьте стороны.

Стороны квадрата равны. Обозначьте сторону как неизвестную величину x.

Периметр квадрата равен , а площадь квадрата равна .

Прямоугольник, длина которого в два раза больше ширины. Обозначьте стороны как y и 2y.

Периметр прямоугольника и площадь прямоугольника .

 

Поскольку 28-дюймовый кусок проволоки будет отрезан и использован для формирования квадрата и прямоугольника, общий периметр двух фигур составит 28 дюймов.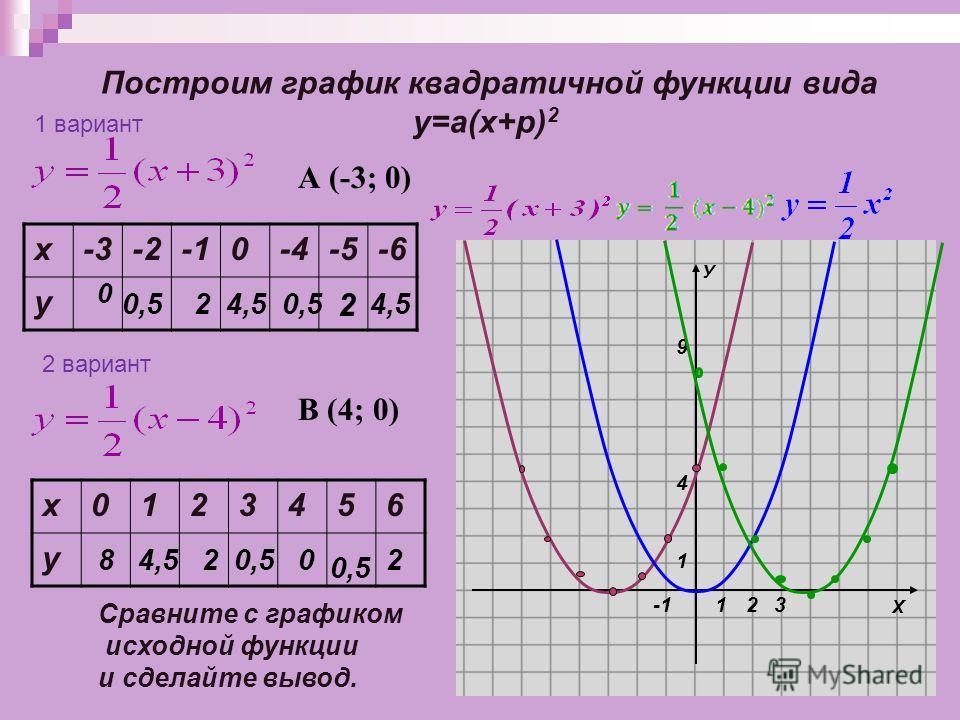

Общая площадь должна быть минимизирована.

Чтобы минимизировать площадь, в выражении должна быть только одна переменная. Используйте уравнение периметра, чтобы уменьшить количество переменных.

Уравнение периметра
Найдите одну из переменных. В этом примере найдите x, сначала вычитая 6y с обеих сторон. Упрощать.
Продолжайте находить x, разделив обе части на 4 и упростив.

Замените в выражении области, чтобы уменьшить две переменные до одной переменной.

Выражение площади
Заменяет x.
Упростите, применив показатель степени и упростив.

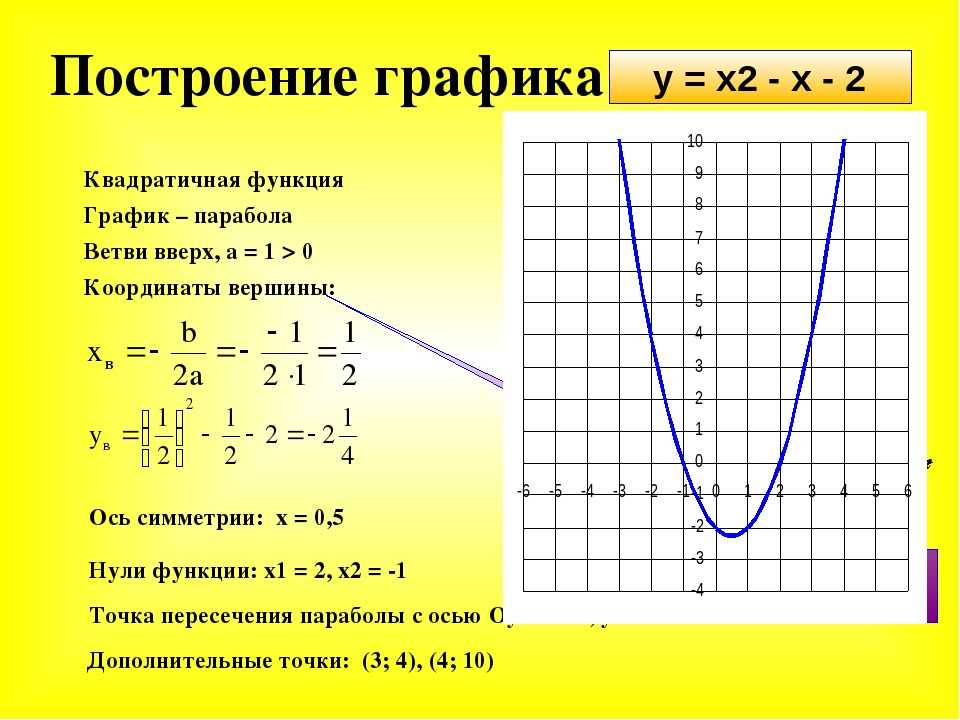имеет вид квадратичной функции. График квадратичной функции представляет собой параболу. Эта квадратичная функция имеет старший коэффициент и, поскольку она положительна, означает, что парабола раскрывается.

Найдите вершину, чтобы найти минимальное значение.

Формула координаты x вершины
Для квадратичной функции a – это коэффициент квадратного члена, b – коэффициент линейного члена, а c – константа
Подставьте значения a и b в формулу
Упростите с помощью калькулятора

Округлить до десятых и .

Суммарная площадь квадрата и прямоугольника минимизируется, если ширина прямоугольника составляет 2,5 дюйма.

4.2 Приложения и моделирование квадратичных функций, 4.4 Построение квадратичных моделей на основе словесных описаний и данных

17 ноября 2017 г. админ

Пример:

Бейсболист замахивается и бьет поп-мушку прямо в воздух в ловушку. Высота бейсбольного мяча в метрах через t секунд после удара определяется квадратичной функцией . За какое время бейсбольный мяч достигнет максимальной высоты? Какой максимальной высоты достигает бейсбольный мяч?

Решение:

определяется как квадратичная функция. График квадратичной функции представляет собой параболу. Эта квадратичная функция имеет старший коэффициент -4,9, и поскольку он отрицателен, это означает, что парабола раскрывается вниз.

Найдите вершину, чтобы найти максимальное значение.

Формула координаты x вершины
Для квадратичной функции a — это коэффициент квадратного члена, b — коэффициент линейного члена, а c — константа
Подставьте значения a и b в формулу
Упростите с помощью калькулятора

Мяч достигает максимальной высоты через 1,5 секунды после удара по мячу.