Как построить параболу? Что такое парабола? Как решаются квадратные уравнения? ГИА. Квадратичная функция Как строить график функции y ax2
Вывод о симметричности графиков функций y=ax 2 и y=-ax2 (при ≠0) относительно оси абсцисс отдельно выделен на слайде 12 для запоминания и наглядно отображен на соответствующем графике. Далее понятие о графике квадратичной функции y=x 2 распространяется на более общий случай функции y=ax 2 , утверждая, что такой график также будет называться параболой.
На слайде 14 рассматриваются свойства квадратичной функции y=ax 2 при положительном. Отмечается, что ее график проходит через начало координат, а все точки, кроме, лежат в верхней полуплоскости. Отмечена симметричность графика относительно оси ординат, уточняя, что противоположным значениям аргумента соответствуют одинаковые значения функции. Указано, что промежуток убывания данной функции (-∞;0], а возрастание функции выполняется на промежутке. Значения данной функции охватывают всю положительную часть действительной оси, нулю она равна в точке, а наибольшего значения не имеет.
Значения данной функции охватывают всю положительную часть действительной оси, нулю она равна в точке, а наибольшего значения не имеет.
На слайде 15 описываются свойства функции y=ax 2 , если отрицательный. Отмечается, что ее график также проходит через начало координат, но все его точки, кроме, лежат в нижней полуплоскости. Отмечена симметричность графика относительно оси, и противоположным значениям аргумента соответствуют равные значения функции. Возрастает функция на промежутке, убывает на. Значения данной функции лежат в промежутке, нулю она равна в точке, а наименьшего значения не имеет.
Обобщая рассмотренные характеристики, на слайде 16 выводится, что ветви параболы направлены вниз при, а вверх — при. Парабола симметрична относительно оси, а вершина параболы располагается в точке ее пересечения с осью. У параболы y=ax 2 вершина — начало координат.
Также важный вывод о преобразованиях параболы отображается на слайде 17. На нем представлены варианты преобразований графика квадратичной функции.
Автор данного видеоурока позаботился о том, чтобы помочь учителям при подготовке к урокам по этой теме. Он разработал видеоурок с учетом всех требований. Материал подобран по возрасту школьников. Он не перегружен, но достаточно емок. Автор подробно рассказывает материал, останавливаясь на более важных моментах. Каждый теоретический пункт сопровождается примером, чтобы восприятие учебного материала было гораздо эффективнее и качественнее.
Урок может быть использован учителем на обычном уроке алгебры в 9 классе в качестве определенного этапа урока — объяснение нового материала. Учителю не придется в этот период ничего говорить или рассказывать. Ему достаточно включить этот видеоурок и следить за тем, чтобы обучающиеся внимательно слушали и записывали важные моменты.
Затем из свойств выводятся следствия. Их четыре. Среди них появляется новое понятие — вершины параболы. Далее следует замечание, где говорится, какие преобразования возможны для графика данной функции. После этого говорится о том, как получается график функции y=-f(x) из графика функции y=f(x), а также y=af(x) из y=f(x).
На этом урок, содержащий учебный материал заканчивается. Остается его закрепить, подобрав соответствующие задания в зависимости от способностей обучающихся.
Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса «вымучивают» свойства параболы и строят ее графики для различных параметров.
Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на «чтение» графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика. На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.
Не будем требовать от школьников невозможного и просто предложим один из алгоритмов решения подобных задач.
Итак, функция вида y = ax 2 + bx + c называется квадратичной, графиком ее является парабола. Как следует из названия, главным слагаемым является ax 2 . То есть
Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.
Самая простая зависимость для коэффициента а . Большинство школьников уверенно отвечает: » если а > 0, то ветви параболы направлены вверх, а если а а > 0.
y = 0,5x 2 — 3x + 1
В данном случае а = 0,5
А теперь для а
y = — 0,5×2 — 3x + 1
В данном случае а = — 0,5
Влияние коэффициента с тоже достаточно легко проследить. Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу:
Представим, что мы хотим найти значение функции в точке х = 0. Подставим ноль в формулу:
y = a 0 2 + b 0 + c = c . Получается, что у = с . То есть с — это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с > 0 или с
с > 0:
y = x 2 + 4x + 3
с
y = x 2 + 4x — 3
Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат:
y = x 2 + 4x
Сложнее с параметром b . Точка, по которой мы будем его находить, зависит не только от b но и от а . Это вершина параболы. Ее абсцисса (координата по оси х ) находится по формуле х в = — b/(2а) . Таким образом, b = — 2ах в . То есть, действуем следующим образом: на графике находим вершину параболы, определяем знак ее абсциссы, то есть смотрим правее нуля (х в > 0) или левее (х в
Однако это не все.
- Заполняем таблицу значениями x от -10 до 10 с шагом 1. Это можно сделать вручную, но легче для указанных целей воспользоваться инструментами прогрессии. Для этого в первую ячейку столбца «X» заносим значение «-10». Затем, не снимая выделения с данной ячейки, переходим во вкладку «Главная». Там щелкаем по кнопке «Прогрессия», которая размещена в группе «Редактирование». В активировавшемся списке выбираем позицию «Прогрессия…».
Только вместо значения x подставляем адрес первой ячейки столбца «X», который мы только что заполнили. Поэтому в нашем случае выражение примет вид:
На этом формирования таблицы можно считать законченным и переходить непосредственно к построению графика.
Построение графика
Как уже было сказано выше, теперь нам предстоит построить сам график.
- Выделяем таблицу курсором, зажав левую кнопку мыши.
 Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.
Перемещаемся во вкладку «Вставка». На ленте в блоке «Диаграммы» щелкаем по кнопке «Точечная», так как именно данный вид графика больше всего подходит для построения параболы. Но и это ещё не все. После нажатия на вышеуказанную кнопку открывается список типов точечных диаграмм. Выбираем точечную диаграмму с маркерами.Редактирование диаграммы
Теперь можно немного отредактировать полученный график.
- Если вы не хотите, чтобы парабола отображалась в виде точек, а имела более привычный вид кривой линии, которая соединяет эти точки, кликните по любой из них правой кнопкой мыши. Открывается контекстное меню. В нем нужно выбрать пункт «Изменить тип диаграммы для ряда…».
Кроме того, можно совершать любые другие виды редактирования полученной параболы, включая изменение её названия и наименований осей. Данные приёмы редактирования не выходят за границы действий по работе в Эксель с диаграммами других видов.
Как видим, построение параболы в Эксель ничем принципиально не отличается от построения другого вида графика или диаграммы в этой же программе. Все действия производятся на основе заранее сформированной таблицы. Кроме того, нужно учесть, что для построения параболы более всего подходит точечный вид диаграммы.
Мы рады, что смогли помочь Вам в решении проблемы.
Как построить параболу в excel?
Для добавления вопроса на сайт, блог или форум просто скопируйте и вставьте в html код:
Если ваша работа или учеба связана с построением различных графиков, диаграмм, составлением таблиц, отчетов и вычислениями различной сложности, то программа Excel станет для этого отличным помощником.
1. В ней удобно работать с электронными таблицами, а еще в ней содержится множество шаблонов графиков и диаграмм. Данную программу еще называют большим и мощным калькулятором с множеством возможностей и функций, и если у вас возникла необходимость построения параболы именно в этой офисной программе, и вы не знаете как этого сделать, то наша статья вам в этом поможет.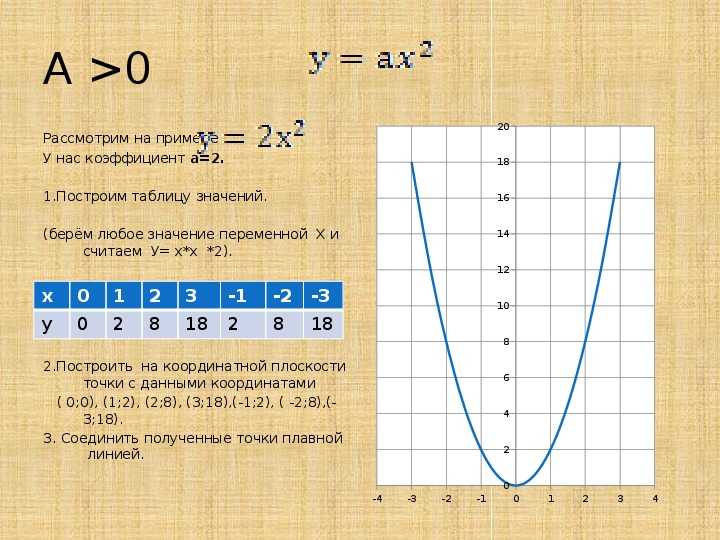 2-2. С помощью маркера автозаполнения приступаем к рассчитыванию значений Y для оси X.
2-2. С помощью маркера автозаполнения приступаем к рассчитыванию значений Y для оси X.
Заходим в меню Вставка. Выбираем Точечная, затем переходим во вкладку Точечная с гладкими кривыми и маркерами.
Как построить в экселе параболу?
В программе эксель можно строить разнообразные графики: гистограммы, круговые диаграммы, параболы, гиперболы и т.п. Давайте разберемся, как можно построить в экселе параболу.
Первый этап. Построим простую параболу по функции: y=x 2 . Для этого в программе эксель сделаем таблицу из двух столбцов: «Значение X» и «Значение Y». В столбце «А» напишем значения от -5 до 5 с шагом 1. Чтобы посчитать значение Y, в ячейке «В2» пропишем формулу =СТЕПЕНЬ(A2;2), где «A2» значение первой точке, 2 – степень, в которую мы будем возводить. В итоге мы получим первое значение.
Второй этап. Нужно рассчитать оставшиеся значения, для этого мы выделяем ячейку «В2», нажимаем на правую кнопку мыши, чтобы появилось меню, в котором выбираем строчку «Копировать».
Третий этап. Выделяем диапазон ячеек с «В3» по «В12» и нажимаем на клавиатуре клавишу «Enter», в итоге у нас должны посчитаться все значения функции параболы.
Четвертый этап. Выделим теперь полностью область со значениями. После нужно перевести взгляд на верхнюю панель настроек, где отыщите вкладку «Вставка» и активируйте её. В ней есть блок «Диаграммы», в которой ищем иконку с надписью «Точечная», нажмите на неё. На экране отобразиться дополнительное меню, среди представленного выбора, выберем в первой строке вторую иконку.
Пятый этап. На экране появиться график параболы. Осталось его немного оформить, сначала подпишем оси. Для этого в верхней панели настроек снова заходим во вкладку «Вставка», где слева есть блок «Текст», следует нажать на иконку с надписью «Надпись». После на экране появится крести, нажмите им рядом с одной из оси, напишите «Y» и поставьте рядом с осью, тоже самое нужно сделать с ось «Х».
Шестой этап. Подпишем линию, для этого выделяем квадрат с надписью «Ряд1» и жмем на правую кнопку мыши, в появившемся меню выбираем «Выбрать» данные.
Седьмой этап. Появиться новое меню «Выбор источника данных», выделяем в нем запись «Ряд1» и нажимаем на кнопку «Изменить». В небольшой таблице, в строке «Имя радя» даем новое название, после закрываем все меню.
Парабола — уравнение, свойства, примеры
Парабола — это график квадратичной функции. Паскаль утверждал, что парабола — это проекция окружности. Галилей объяснил, что снаряды, падающие под действием силы тяжести, следуют по траектории, называемой параболической траекторией. Многие физические движения тел следуют криволинейной траектории, имеющей форму параболы. Параболой в математике называют любую плоскую кривую, которая является зеркально-симметричной и обычно имеет приблизительно U-образную форму. Здесь мы будем стремиться понять вывод стандартной формулы параболы, различные стандартные формы параболы и свойства параболы.
| 1. | Что такое парабола? |
2. | Стандартные уравнения параболы |
| 3. | Парабола Формула |
| 4. | График параболы |
| 5. | Вывод уравнения параболы |
| 6. | Свойства параболы |
| 7. | Часто задаваемые вопросы о Parabola |
Что такое парабола?
Парабола относится к уравнению кривой, так что точка на кривой равноудалена от фиксированной точки и фиксированной линии. Неподвижная точка называется фокусом параболы, а неподвижная линия — направляющей параболы. Также важно отметить, что фиксированная точка не лежит на фиксированной линии. Геометрическое место любой точки, равноудаленной от данной точки (фокуса) и данной прямой (направляющей), называется параболой. Парабола — важная кривая конических сечений координатной геометрии.
Уравнение параболы
Общее уравнение параболы: y = a(x-h) 2 + k или x = a(y-k) 2 +h, где (h,k) обозначает вершину.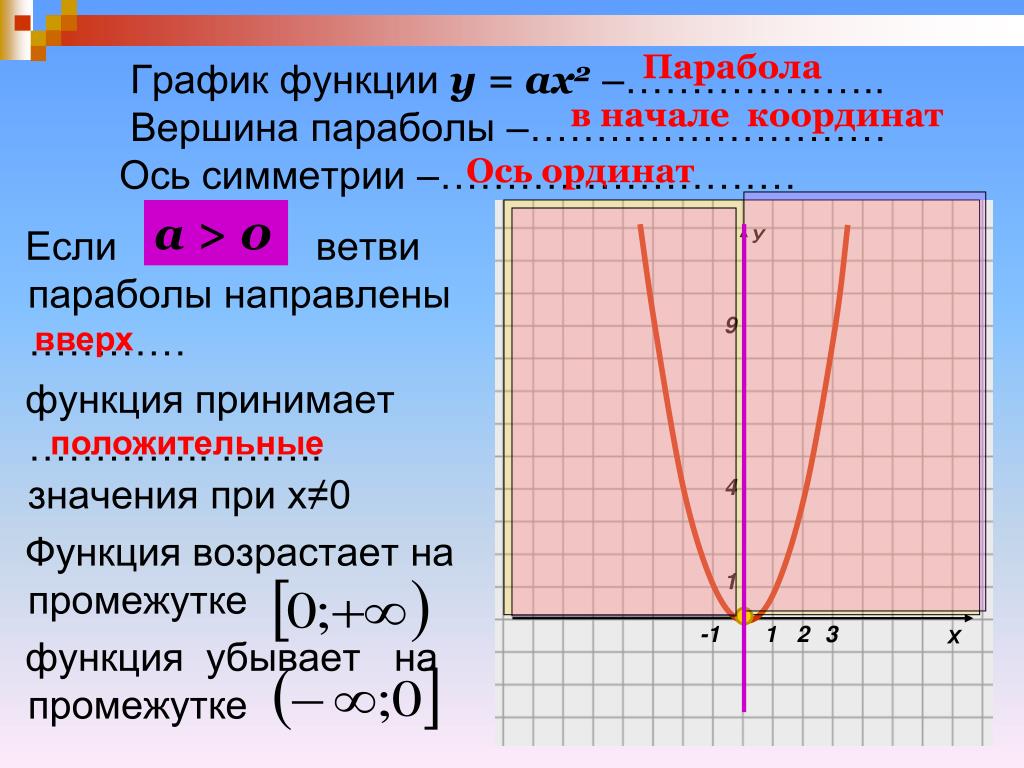 Стандартное уравнение правильной параболы: y 2 = 4ax.
Стандартное уравнение правильной параболы: y 2 = 4ax.
Некоторые важные термины, приведенные ниже, помогут понять особенности и части параболы.
- Фокус: Точка (a, 0) является фокусом параболы
- Направляющая: Линия, проведенная параллельно оси Y и проходящая через точку (-a, 0), является направляющей параболы. Директриса перпендикулярна оси параболы.
- Фокусная хорда: Фокусная хорда параболы — это хорда, проходящая через фокус параболы. Фокальная хорда пересекает параболу в двух различных точках.
- Фокусное расстояние: Расстояние точки \((x_1, y_1)\) на параболе от фокуса является фокусным расстоянием. Фокусное расстояние также равно перпендикулярному расстоянию этой точки от директрисы.
- Latus Rectum: Это фокальная хорда, перпендикулярная оси параболы и проходящая через фокус параболы. Длину широкой прямой кишки принимают LL’ = 4а.
 Концы широкой прямой кишки: (а, 2а), (а, -2а).
Концы широкой прямой кишки: (а, 2а), (а, -2а). - Эксцентриситет:
Стандартные уравнения параболы
Есть четыре стандартных уравнения параболы. Четыре стандартные формы основаны на оси и ориентации параболы. Поперечная ось и сопряженная ось каждой из этих парабол различны. На изображении ниже представлены четыре стандартных уравнения и формы параболы.
Следующие наблюдения сделаны из стандартной формы уравнений:
- Парабола симметрична относительно своей оси. Если в уравнении есть член с y 2 , то ось симметрии проходит по оси x, а если в уравнении есть член с x 2 , то ось симметрии проходит по оси y.
- Когда ось симметрии проходит вдоль оси x, парабола открывается вправо, если коэффициент x положительный, и открывается влево, если коэффициент x отрицателен.

- Когда ось симметрии проходит вдоль оси y, парабола открывается вверх, если коэффициент y положительный, и открывается вниз, если коэффициент y отрицателен.
Формула параболы
Формула параболы помогает представить общую форму параболического пути на плоскости. Ниже приведены формулы, которые используются для получения параметров параболы.
- Направление параболы определяется значением a.
- Вершина = (h,k), где h = -b/2a и k = f(h)
- Широкая прямая кишка = 4a
- Фокус: (h, k+ (1/4a))
- Директриса: y = k — 1/4a
График параболы
Рассмотрим уравнение y = 3x 2 — 6x + 5. Для этой параболы a = 3, b = -6 и c = 5. Вот график данного квадратного уравнения, которое является параболой.
Направление: Здесь а положительно, поэтому парабола раскрывается.
Вершина: (h,k)
h = -b/2a
= 6/(2 × 3) = 1
k = f(h)
= f(1) = 3(1) 2 — 6 (1) + 5 = 2
Таким образом, вершина равна (1,2)
Широкая прямая кишка = 4a = 4 × 3 =12
Фокус: (h, k+ 1/4a) = (1,25 /12)
Ось симметрии x =1
Директриса: y = k-1/4a
y = 2 — 1/12 ⇒ y — 23/12 = 0
Вывод уравнения параболы
Рассмотрим точку P с координатами (x, y) на параболе.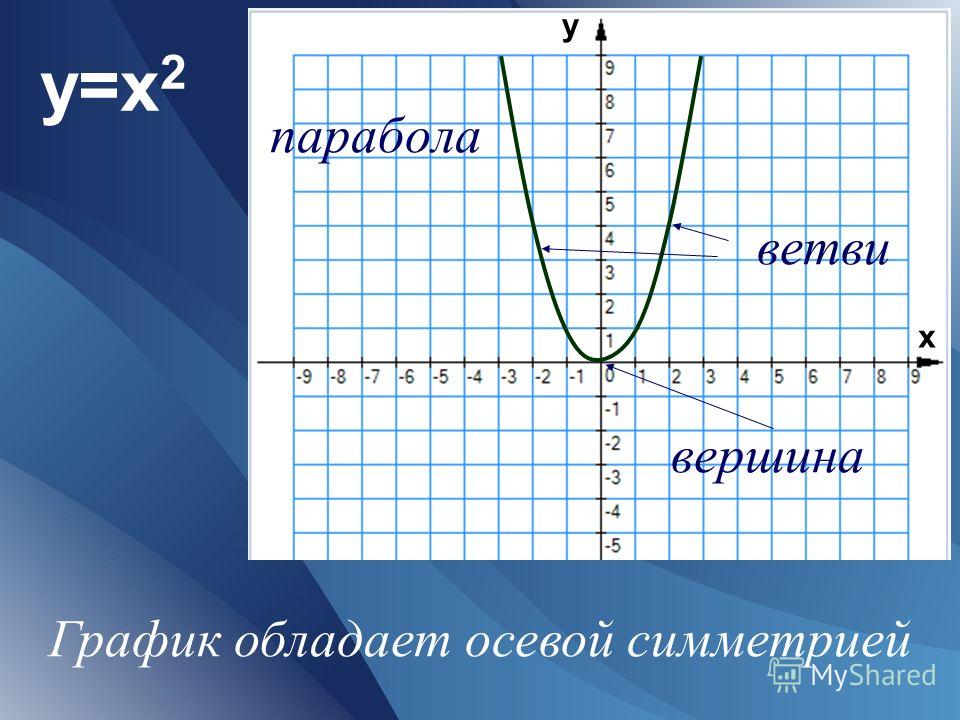 По определению параболы расстояние этой точки от фокуса F равно расстоянию этой точки P от директрисы. Здесь мы рассматриваем точку B на директрисе, а для расчетов берется перпендикулярное расстояние PB. 92}\)
По определению параболы расстояние этой точки от фокуса F равно расстоянию этой точки P от директрисы. Здесь мы рассматриваем точку B на директрисе, а для расчетов берется перпендикулярное расстояние PB. 92}\)
Возведение уравнения в квадрат в обе стороны,
(х — а) 2 + у 2 = (х + а) 2
х 2 ах 2 5 9 + y 2 = x 2 + a 2 + 2ax
y 2 — 2ax = 2ax
y 2 = 4ax
3.
Точно так же мы можем вывести уравнения парабол как:
- (б): у 2 = – 4акс,
- (с): х 2 = 4ay,
- (г): х 2 = – 4ау.
Приведенные выше четыре уравнения являются стандартными уравнениями парабол.
Свойства параболы
Здесь мы постараемся понять некоторые важные свойства и термины, связанные с параболой.
Касательная: Касательная — это линия, касающаяся параболы. Уравнение касательной к параболе y 2 = 4ax в точке контакта \((x_1, y_1)\) равно \(yy_1 = 2a(x + x_1)\).
Уравнение касательной к параболе y 2 = 4ax в точке контакта \((x_1, y_1)\) равно \(yy_1 = 2a(x + x_1)\).
Нормаль: Линия, проведенная перпендикулярно касательной и проходящая через точку касания и фокус параболы, называется нормалью. Для параболы y 2 = 4ax уравнение нормали, проходящей через точку \((x_1, y_1)\) и имеющей наклон m = -y1/2a, уравнение нормали имеет вид \((y — y_1) = \dfrac{-y_1}{2a}(x — x_1)\)
Хорда контакта: Хорда, соединяющая точку касания касательных, проведенных из внешней точки к параболе, называется хордой касания. Для точки \((x_1, y_1)\) вне параболы уравнение хорды контакта имеет вид \(yy_1 = 2x(x + x_1)\).
Полюс и поляра: Для точки, лежащей вне параболы, геометрическое место точек пересечения касательных, проведенных на концах хорд, проведенных из этой точки, называется полярой. И эта упомянутая точка называется полюсом. Для полюса с координатами \((x_1, y_1)\), для параболы y 2 =4ax, уравнение поляры: \(yy_1 = 2x(x + x_1)\).
Параметрические координаты: Параметрические координаты уравнения параболы y 2 = 4ax (at 2 , 2at). Параметрические координаты представляют собой все точки параболы.
☛ Также проверьте:
- Эллипс
- Гипербола
Примеры параболы
Пример 1: Уравнение параболы: y 2 = 24x. Найдите длину широкой прямой кишки, фокуса и вершины.
Решение:
Найти: Длину широкой прямой кишки, фокус и вершину параболы
Дано: Уравнение параболы: y 2 = 24x
Следовательно, 29 900/24 4 = 6
Формула параболы для широкой прямой кишки:
Длина широкой прямой кишки = 4a
= 4(6) = 24
Теперь фокус = (a,0) = (6,0)
Теперь вершина = (0,0)
Ответ: Длина широкой прямой кишки = 24, фокус = (6,0), вершина = (0,0)
Пример 2: Уравнение параболы: 2(y-3) 2 + 24 = x.
 Найдите длину широкой прямой кишки, фокуса и вершины.
Найдите длину широкой прямой кишки, фокуса и вершины. Решение: Найти: длину широкой прямой кишки, фокус и вершину параболы
Дано: уравнение параболы: 2(y-3) 2 + 24 = x
Сравнивая его с общим уравнением параболы x = a(y-k) 2 + h, получаем
a = 2
(h, k) = (24, 3)
Теперь формула параболы для широкой прямой кишки: длина прямой кишки = 4a
= 4(2) = 8
Ответ: Длина широкой прямой кишки = 8, фокус = (0, 2), вершина = (24,3)
Пример 3. Какое уравнение описывает параболу с фокусом (0, 0) и направляющей y = 4?
Решение:
Учитывая, что Focus = (0, 0) и директриса y = 4
Предположим, что на параболе есть точка (x, y).
Его расстояние от точки фокусировки (0, 0) равно √((x − 0) 2 + (y — 0) 2 )
Его расстояние от направляющей y = 4 равно |y — 4|
Следовательно, уравнение будет таким:
√[(x − 0) 2 + (y — 0) 2 ] = |y — 4|
Квадрат с обеих сторон.

(x — 0) 2 + (y — 0) 2 = (Y — 4) 2
x 2 + Y 2 = Y 2 — 8y + 16
x 2 + 8y — 16 = 0
Ответ: Следовательно, уравнение параболы с фокусом в точке (0, 0) и направляющей y = 4 равно x 2 + 8y — 16 = 0.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по параболе
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Parabola
Что такое парабола в коническом сечении?
Парабола — важная кривая конического сечения. Это геометрическое место точки, равноудаленной от фиксированной точки, называемой фокусом, а фиксированная линия называется направляющей. Многие движения в физическом мире следуют параболическим траекториям. Следовательно, изучение свойств и приложений параболы является основой для физиков.
Многие движения в физическом мире следуют параболическим траекториям. Следовательно, изучение свойств и приложений параболы является основой для физиков.
Что такое уравнение параболы?
Стандартное уравнение параболы: y 2 = 4ax. Осью параболы является ось x, которая также является поперечной осью параболы. Фокус параболы есть F(a, 0), а уравнение директрисы этой параболы есть x + a = 0.
Что такое вершина параболы?
Вершина параболы — это точка пересечения параболы с осью. Вершина параболы, имеющей уравнение y 2 = 4ax равно (0,0), так как он разрезает ось в начале координат.
Как найти уравнение параболы?
Уравнение параболы можно вывести из основного определения параболы. Парабола — это геометрическое место точки, равноудаленной от фиксированной точки, называемой фокусом (F), а фиксированная линия называется директрисой (x + a = 0). Рассмотрим точку P(x, y) на параболе, и по формуле PF = PM можно найти уравнение параболы. Здесь точка «М» является основанием перпендикуляра из точки Р на директрисе. Следовательно, полученное стандартное уравнение параболы имеет вид y 2 = 4 оси.
Здесь точка «М» является основанием перпендикуляра из точки Р на директрисе. Следовательно, полученное стандартное уравнение параболы имеет вид y 2 = 4 оси.
Что такое эксцентриситет параболы?
Эксцентриситет параболы равен 1 (e = 1). Эксцентриситет параболы – это отношение расстояния точки от фокуса к расстоянию этой точки от директрисы параболы.
Что такое фокусы параболы?
Парабола имеет только один фокус. Для стандартного уравнения параболы y 2 = 4ax фокус параболы равен F(a, 0). Это точка, лежащая на оси абсцисс и на поперечной оси параболы.
Что такое сопряженная ось параболы?
Линия, перпендикулярная поперечной оси параболы и проходящая через вершину параболы, называется сопряженной осью параболы. Для параболы y 2 = 4ax сопряженной осью является ось y.
Что такое вершины параболы?
Точка на оси, где парабола пересекает ось, является вершиной параболы. Вершина параболы для стандартного уравнения параболы y 2 = 4ax равно (0, 0). Парабола пересекает ось x в начале координат.
Парабола пересекает ось x в начале координат.
Что такое стандартное уравнение параболы?
Стандартное уравнение параболы используется для алгебраического представления параболы в координатной плоскости. Общее уравнение параболы можно записать в виде y = a(x-h) 2 + k или x = a(y-k) 2 +h, где (h,k) обозначает вершину. Стандартное уравнение правильной параболы: y 2 = 4ax.
Как найти поперечную ось параболы?
Линия, проходящая через вершину и фокус параболы, является поперечной осью параболы. Стандартное уравнение параболы y 2 = 4ax имеет ось x в качестве оси параболы.
Общее уравнение параболы:
y = a(x — h) 2 + k (обычное)
x = a(y — k) 2 + h (боковое)
где,
(h,k) = вершина параболы
Где формула параболы используется в реальной жизни?
Параболы используются в физике и технике для траекторий баллистических ракет, конструкции отражателей автомобильных фар и т. д.
д.
Как вы решаете задачи, используя формулу параболы?
Для решения задач на параболы используется общее уравнение параболы, оно имеет общий вид y = ax 2 + bx + c (вершинная форма y = a(x — h) 2 + k), где, (h,k) = вершина параболы.
Все ли формулы парабол представляют функцию?
Все параболы не обязательно являются функциями. Параболы, открывающиеся вверх или вниз, считаются функциями.
Форма вершины — Как найти уравнение параболы
RadfordMathematics.com
Онлайн-книга по математике
(нахождение уравнения параболы)
Узнаем как найти уравнение параболы записав его в вершинной форме 92+к\] куда:
- \(h\): горизонтальная координата вершины
- \(k\): вертикальная координата вершины.
Это проиллюстрировано здесь:
Мы можем использовать формы вершины , чтобы найти уравнение параболы . Идея состоит в том, чтобы использовать координаты его вершины ( максимальная точка , или минимальная точка 92+k\) (при условии, что мы можем прочитать координаты \(\begin{pmatrix}h,k\end{pmatrix}\) из графика), а затем найти значение коэффициента \(a\).
Идея состоит в том, чтобы использовать координаты его вершины ( максимальная точка , или минимальная точка 92+k\) (при условии, что мы можем прочитать координаты \(\begin{pmatrix}h,k\end{pmatrix}\) из графика), а затем найти значение коэффициента \(a\).
Это объясняется в пошаговом методе ниже, а также в руководствах .
Как найти уравнение параболы, используя ее форму вершины
Учитывая график параболы , для которой мы даны или можем ясно видеть:
- координаты вершины , \(\begin{pmatrix}h,k\end{pmatrix}\), и:
- координаты другой точки \(P\), через которую проходит парабола .
мы можем найти уравнение параболы в вершинной форме после двух шагов :
- Шаг 1: используйте (известные) координаты 92+к\]
теперь проблема состоит только в том, чтобы найти значение коэффициента \(а\).

- Шаг 2: Найдите значение коэффициента \(a\), подставив координаты точки \(P\) в уравнение, записанное на шаге 1, и решив \(a\).
Этот двухэтапный метод лучше/дополнительно объясняется в следующем учебнике , найдите время, чтобы посмотреть его сейчас.
Учебник 1
В следующем уроке мы узнаем , как найти параболы, используя координаты ее вершины , а также координаты ее \(y\)-перехвата .
Упражнение 1
Используя двухэтапный метод , который мы только что изучили, найдите уравнение каждой из следующих парабол в следующих двух формах:
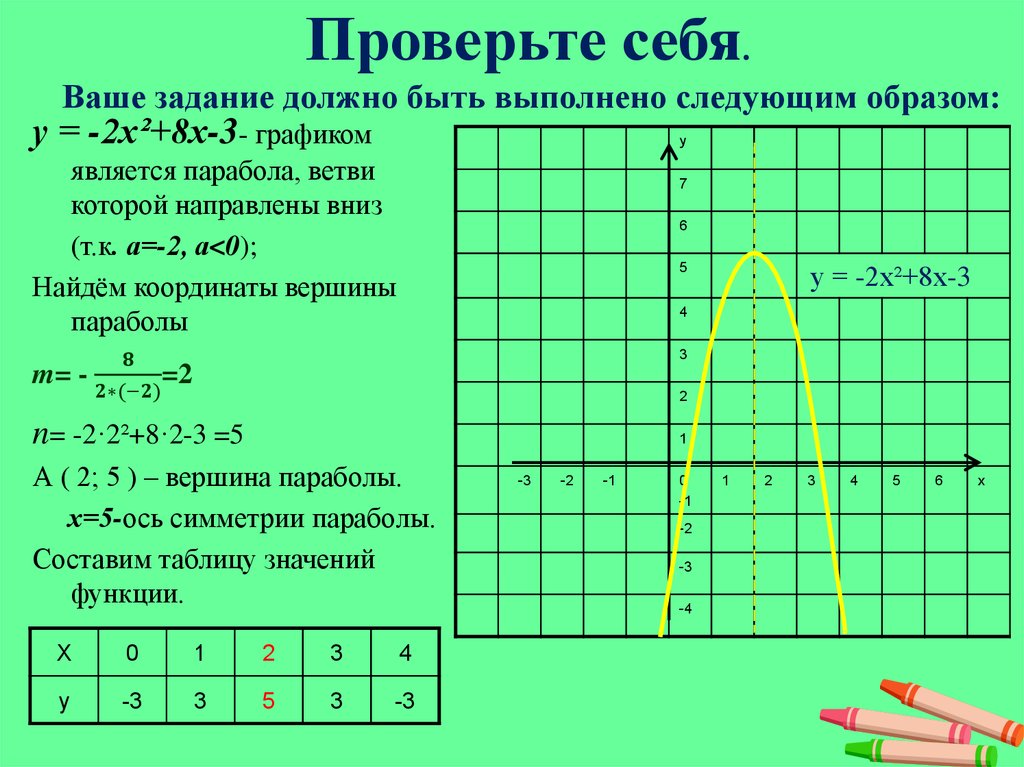
92+4х+3\) Выберите номер вопроса, по которому вы хотите увидеть работу: В следующем уроке мы узнаем , как найти параболы, используя координаты ее вершины , а также координаты другой точки вдоль ее длины (это не точка пересечения \(y\)). Коники К концу этого раздела вы сможете: Прежде чем начать, пройдите этот тест на готовность. Следующим коническим сечением, которое мы рассмотрим, является парабола. Мы определяем параболу как все точки плоскости, находящиеся на одинаковом расстоянии от фиксированной точки и фиксированной прямой. Парабола Парабола — это все точки на плоскости, находящиеся на одинаковом расстоянии от фиксированной точки и фиксированной линии. Неподвижная точка называется фокусом , , а фиксированная линия называется направляющей параболы. Ранее мы научились строить вертикальные параболы из общей формы или стандартной формы с помощью свойств. Эти методы также будут работать здесь. Здесь мы подведем итог свойствам. Графики показывают, как выглядят параболы, когда они открываются вверх или вниз. Их положение относительно оси x или y является просто примером. Чтобы построить параболу из этих форм, мы использовали следующие шаги. График вертикальных парабол с использованием свойств. В следующем примере рассматривается метод построения графика параболы из общей формы ее уравнения. График с использованием свойств. График с использованием свойств. График с использованием свойств. В следующем примере рассматривается метод построения графика параболы из стандартной формы ее уравнения, Запишите в стандартной форме, а затем используйте свойства стандартной формы для построения графика уравнения. ⓐ Напишите в стандартной форме и ⓑ используйте свойства стандартной формы для построения графика уравнения. ⓐ ⓐ Напишите в стандартной форме и ⓑ используйте свойства стандартной формы для построения графика уравнения. ⓐ До сих пор наша работа касалась только парабол, которые открываются вверх или вниз. Графики показывают, как выглядят параболы, когда они смещены влево или вправо. Их положение относительно оси x или y является просто примером. Глядя на эти параболы, представляют ли их графики функцию? Поскольку оба графика не прошли тест на вертикальную линию, они не представляют функцию. График параболы, открывающейся влево или вправо, в основном аналогичен тому, что мы делали для парабол, открывающихся вверх или вниз, с разворотом x и y переменных. График горизонтальных парабол с использованием свойств. График с использованием свойств. Так как вершина имеет размеры x и y , пересечения являются точкой. Нарисуйте параболу. График с использованием свойств. График с использованием свойств. В следующем примере вершина не является исходной точкой. График с использованием свойств. График с использованием свойств. График с использованием свойств. На (Рисунок) мы видим связь между уравнением в стандартной форме и свойствами параболы. В поле How To перечислены шаги для построения графика параболы в стандартной форме. Мы будем использовать эту процедуру в следующем примере. График с использованием свойств. График с использованием свойств. График с использованием свойств. В следующем примере мы замечаем, что а отрицательно, поэтому парабола открывается влево. График с использованием свойств. График с использованием свойств. График с использованием свойств. Следующий пример требует, чтобы мы сначала привели уравнение в стандартную форму, а затем использовали свойства. Напишите в стандартной форме, а затем используйте свойства стандартной формы для построения графика уравнения. Пусть ⓐ Напишите в стандартной форме и ⓑ используйте свойства стандартной формы для построения графика уравнения. ⓐ ⓐ Напишите в стандартной форме и ⓑ используйте свойства стандартной формы для построения графика уравнения. ⓐ Параболы используются во многих архитектурных проектах. Мосты нередко строятся с использованием парабол, как мы увидим в следующем примере. Найдите уравнение параболической арки, образованной в основании показанного моста. Запишите уравнение в стандартной форме. Сначала создадим систему координат и нарисуем параболу. График даст нам информацию, необходимую для написания уравнения графика в стандартной форме Значение a пока неизвестно. Чтобы найти Найдите уравнение параболической арки, образованной в основании показанного моста. Запишите уравнение в стандартной форме. Найдите уравнение параболической арки, образованной в основании показанного моста. Запишите уравнение в стандартной форме. Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с квадратичными функциями и параболами. График вертикальных парабол В следующих упражнениях нарисуйте график каждого уравнения, используя свойства. В следующих упражнениях ⓐ запишите уравнение в стандартной форме и ⓑ используйте свойства стандартной формы для построения графика уравнения. График горизонтальных парабол В следующих упражнениях постройте график каждого уравнения, используя свойства. In the following exercises, ⓐ write the уравнение в стандартной форме и ⓑ использовать свойства стандартной формы для построения графика уравнения. Смешанная практика В следующих упражнениях сопоставьте каждый график с одним из следующих уравнений: ⓐ x 2 + Y 2 = 643333333. Учебник 2

Параболы – Промежуточная алгебра
Цели обучения
Если вы пропустили эту проблему, просмотрите (рисунок).
Если вы пропустили эту задачу, просмотрите (рисунок).
Если вы пропустили эту проблему, просмотрите (Рисунок). Вертикальные параболы графика
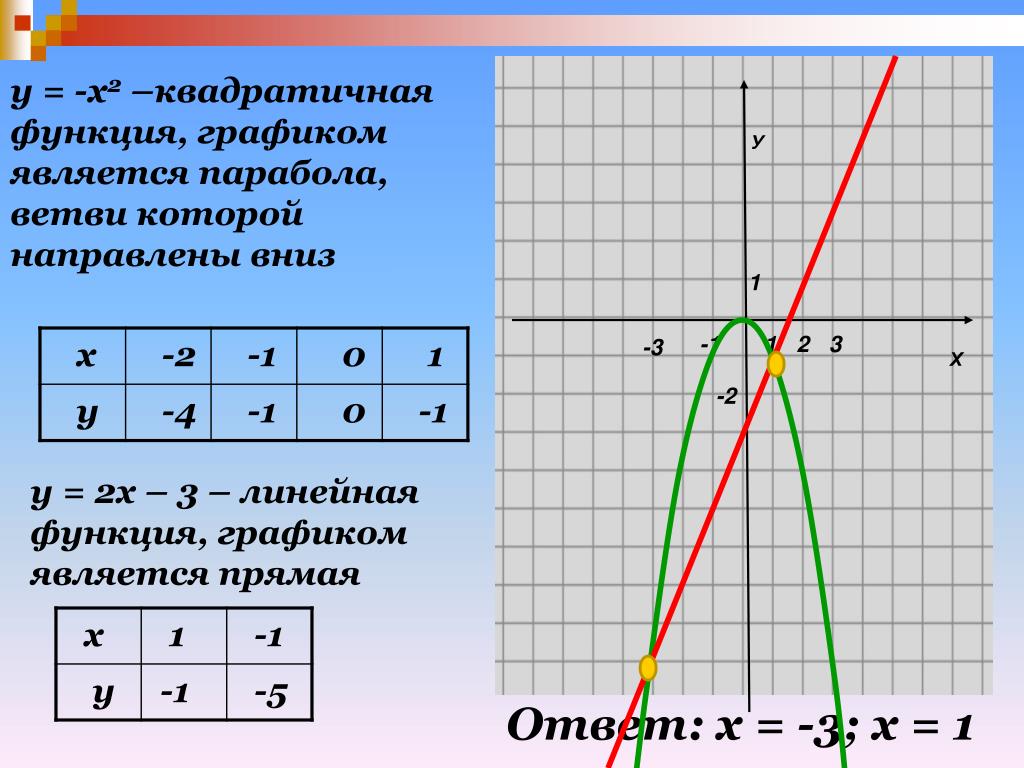 Фиксированная точка называется фокусом , , а фиксированная линия называется директрисой 9.0073 параболы.
Фиксированная точка называется фокусом , , а фиксированная линия называется директрисой 9.0073 параболы. Row one: orientation: general form is a greater than 0, up and a less than 0 down. Standard form is the same. Row 2: Axis of symmetry: general form is x equals minus b upon 2a and standard form is x equals h. Row 3: vertex: general form, substitute x equals minus b upon 2a and solve for y; standard form is point h, k. Row 4: y intercept: general and standard forms, let x be 0. Row 5: x intercept: general and standard forms, let y be 0.» data-label=»»>
Вертикальные параболы Общая форма Стандартная форма Ориентация вверх; вниз вверх; вниз Ось симметрии Вершина Подставьте и
найдите y .
y -перехват Пусть Пусть x -пересечения Пусть Пусть 
The y intercept occurs when x equals 0. Substituting in the equation and simplifying, we get y equals minus 8. The point 0, 8 is three units to the left of the line of symmetry. The point three units to the right of the line of symmetry is 6, negative 8. The x intercept occurs when y equals 0. We substitute this in the original equation and factor the trinomial. We get x intercepts 4, 0 and 2, 0. Graph the parabola.» data-label=»»>
Начиная с и парабола открывается вниз. Чтобы найти ось симметрии, найдите Ось симметрии Вершина находится на прямой Лет Вершина Перехват y происходит, когда Заменитель Упрощение. 
y -перехват равен Точка находится на три единицы левее .
линия симметрии. Точка на три единицы правее
от линии симметрии равна Точка, симметричная y — точка пересечения равна Перехват x происходит, когда Пусть Фактор GCF. 
Фактор трехчлена. Найти x . x — перехваты равны Постройте параболу. 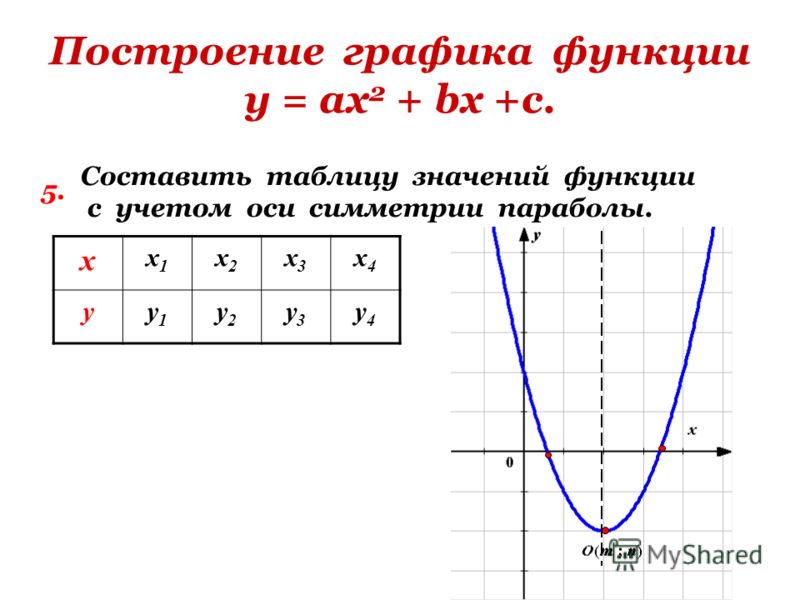
Перепишите функцию в форме
, заполнив квадрат.
Определите константы a, h, k . , , Так как парабола открывается вверх. Ось симметрии Ось симметрии Вершина Вершина Найдите y -перехват, подставив y — перехват Найдите точку, симметричную относительно оси симметрии. 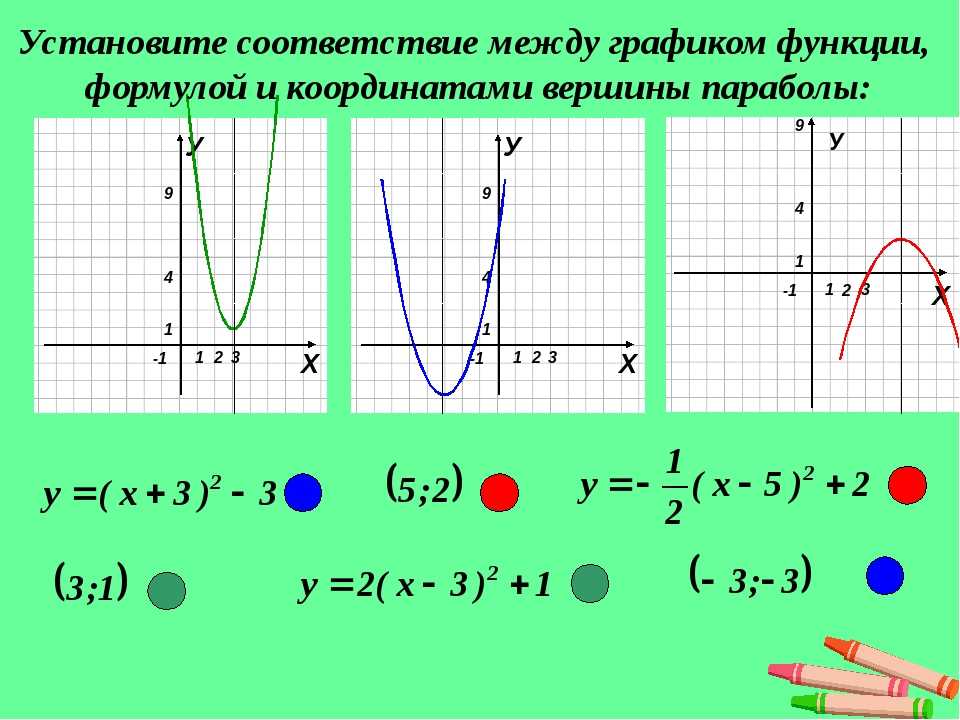
Найдите пересечения x . Квадратный корень из отрицательного числа
говорит нам, что решения представляют собой комплексные числа
. Так что нет x -перехватов. Постройте параболу.
ⓑ
ⓑ График горизонтальных парабол
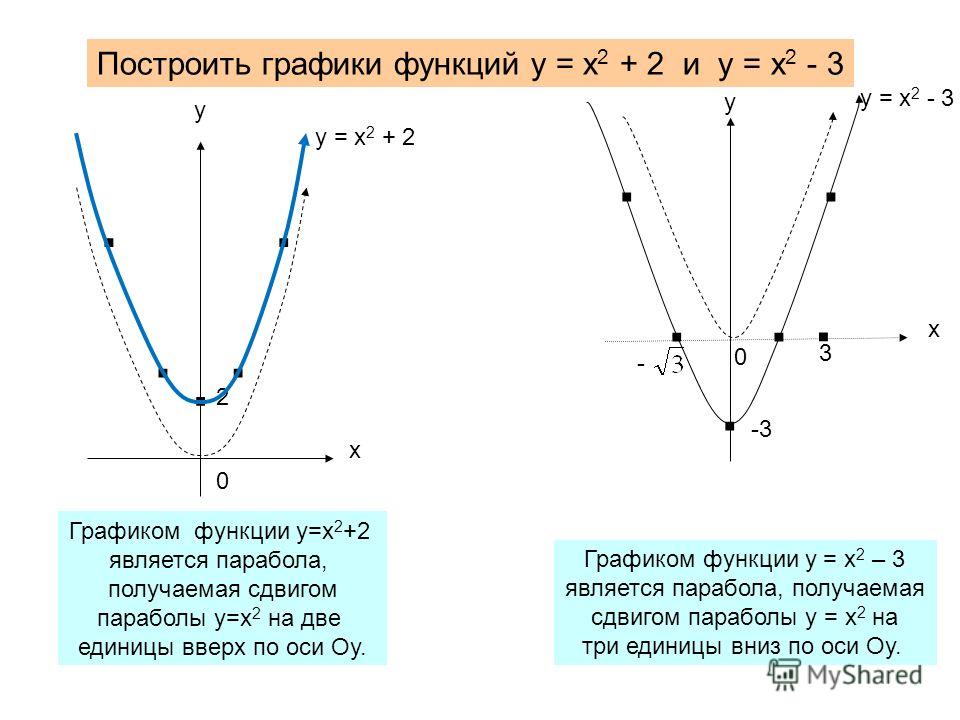 Теперь мы рассмотрим горизонтальные параболы. Эти параболы открываются либо влево, либо вправо. Если мы поменяем местами x и y в наших предыдущих уравнениях для парабол, мы получим уравнения для парабол, которые открываются влево или вправо.
Теперь мы рассмотрим горизонтальные параболы. Эти параболы открываются либо влево, либо вправо. Если мы поменяем местами x и y в наших предыдущих уравнениях для парабол, мы получим уравнения для парабол, которые открываются влево или вправо. Row 5: x intercept: general and standard forms, let y be 0.»>
Горизонтальные параболы Общая форма Стандартная форма Ориентация правый; оставил правый; оставил Ось симметрии Вершина Заменить и
решить для x .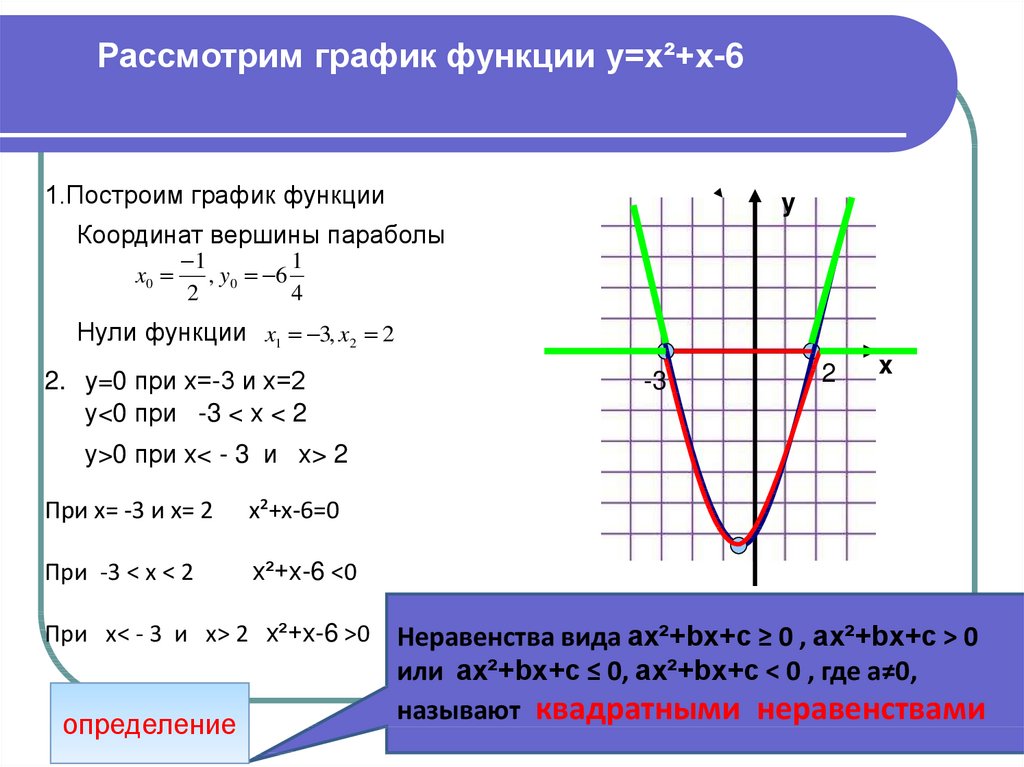
y -перехваты Пусть Пусть x — перехват Пусть Пусть 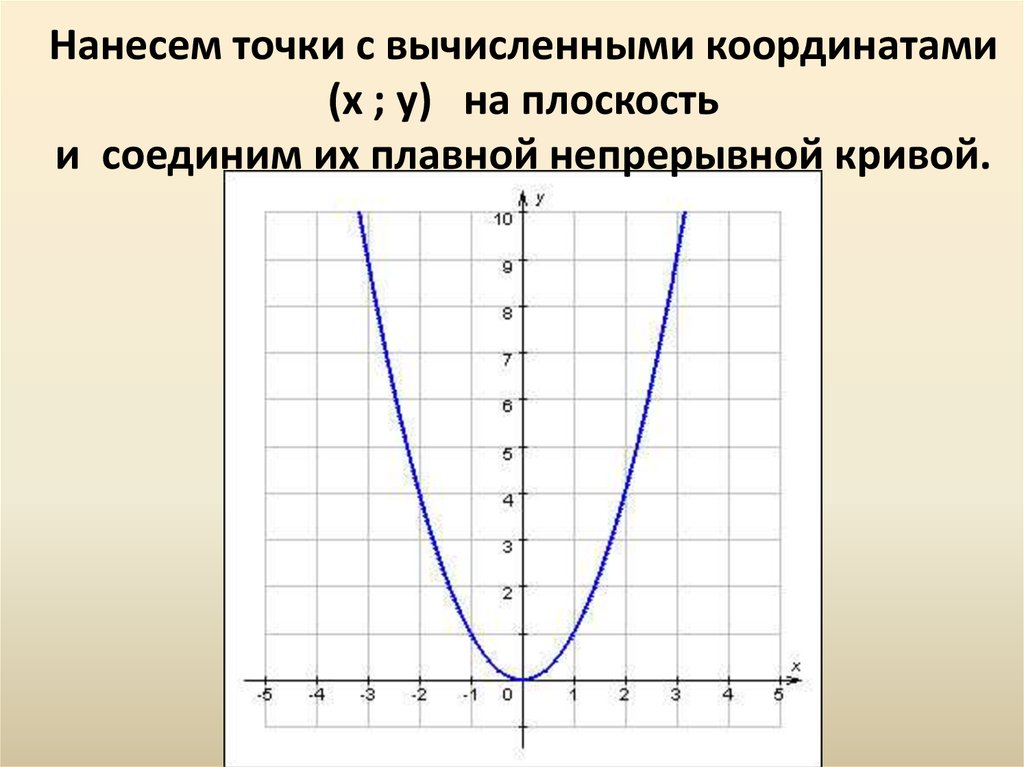
Hence y is 0. This is the axis of symmetry. The vertex is on this line. Let y be 0. Substituting in equation, we get x equals 0. The vertex is (0, 0). Since the vertex is (0, 0) both the x- and y-intercepts are the point (0, 0). To graph the parabola we need more points. In this case it is easiest to choose values of y.» data-label=»»>
Так как парабола открывается вправо. Чтобы найти ось симметрии, найдите Ось симметрии Вершина находится на прямой Пусть Вершина  Чтобы построить параболу, нам нужно больше точек. В этом случае проще всего выбрать значения и .
Чтобы построить параболу, нам нужно больше точек. В этом случае проще всего выбрать значения и .
Мы также нанесем точки, симметричные относительно оси y и поперек нее, точки Connect the points to graph the parabola.» data-label=»»>
Так как парабола открывается влево. Чтобы найти ось симметрии, найдите Ось симметрии Вершина находится на прямой Пусть Вершина Перехват x происходит, когда Пересечение x равно Точка на единицу ниже линии .
симметрия. Симметричная точка на единицу
Симметричная точка на единицу
выше линии симметрии равна Симметричная точка Перехват y происходит, когда Заменитель Решить. и — перехваты и Соедините точки, чтобы построить параболу. 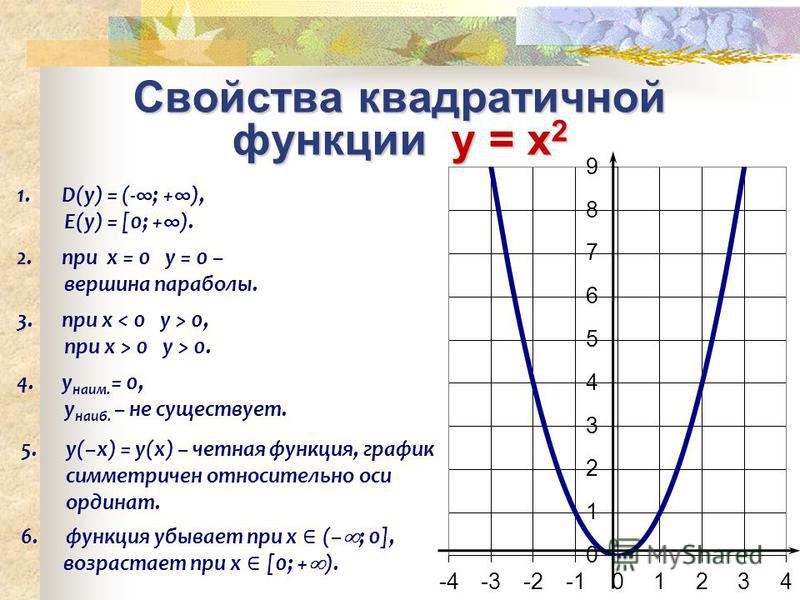
So there are no y-intercepts. Graph the parabola.» data-label=»»>
Определение констант а, з, к . Так как парабола открывается вправо. Ось симметрии Ось симметрии Вершина Вершина Найдите точку пересечения x , подставив Пересечение x равно Найдите точку, симметричную относительно оси симметрии
.
Найдите и -перехваты. Пусть Квадрат не может быть отрицательным, поэтому реального решения
не существует. Так что нет и -перехватов. Постройте параболу. Since a is negative 4, the parabola opens to the left. The axis of symmetry is y equals negative 1 and vertex is (4, negative 1). Substituting y equals 0, we get x intercept (0, 0). The symmetric point across the axis is (0, negative 2). Substituting x equals 0, we get y intercepts (0, 0) and (0, negative 2). Graph the parabola.» data-label=»»>
Определите константы a, h, k . Так как парабола открывается влево. Ось симметрии Ось симметрии Вершина Вершина Найдите точку пересечения x , подставив Пересечение x равно Найдите точку, симметричную относительно оси симметрии
.
Найдите и -перехваты. Пусть y — перехваты и Постройте параболу. 
Перепишите функцию в форме
, заполнив
квадрат.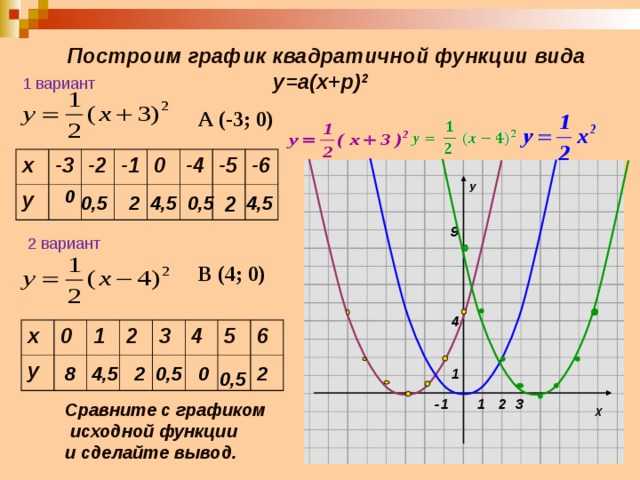
Определите константы a, h, k . Так как парабола открывается на
направо. Ось симметрии Ось симметрии Вершина Вершина Найдите x — перехват, подставив Пересечение x равно Найдите точку, симметричную
относительно оси симметрии.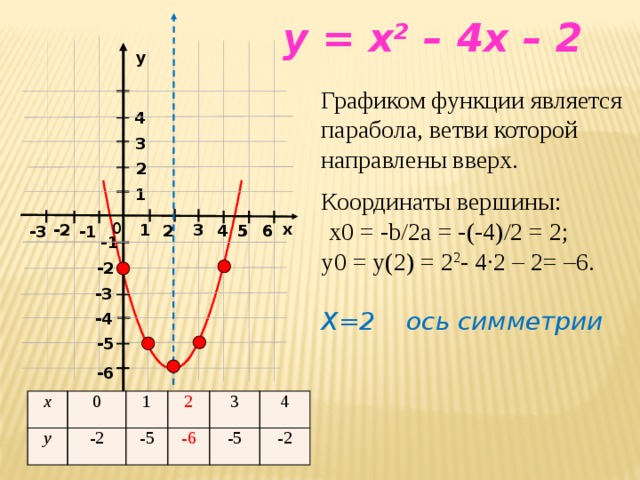
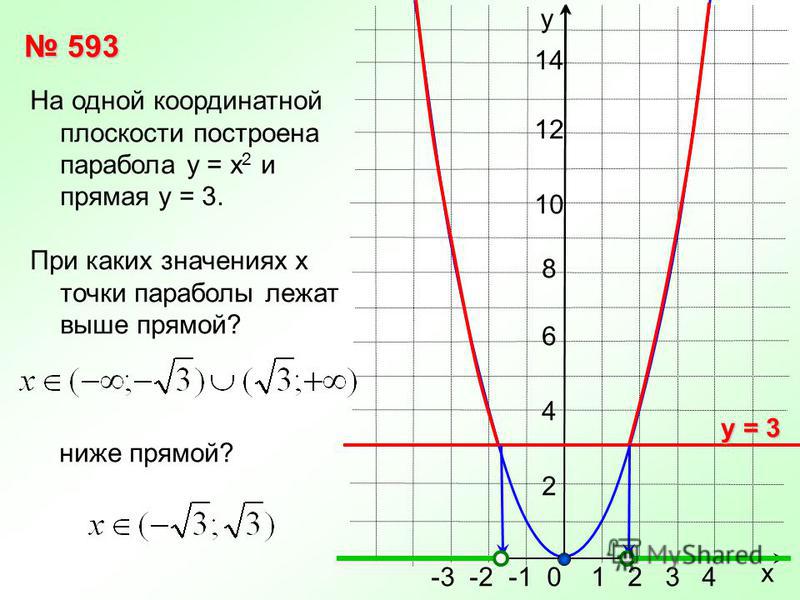
Найдите и -перехваты. и — перехваты равны Постройте параболу.
ⓑ 
ⓑ Решение задач с помощью парабол
From this we know that the x coordinate of the vertex will also be 10. The vertex is 10, 10. So h is 10 and k is 10. Substitute the values into the standard form y equals a open parentheses x minus h close parentheses squared plus k. The value of a is still unknown. To find the value of a use one of the other points on the parabola, point (0, 0). Substituting the values into the equation, we get a equal to minus 1 by 10. Substitute the value for a into the equation. We get y equals minus 1 upon 10 open parentheses x minus 10 close parentheses squared plus 10.» data-label=»»>
Пусть нижняя левая сторона моста будет
началом координатной сетки в точке
Так как основание 20 футов в ширину точка
представляет нижнюю правую сторону.
Высота моста 10 футов в самой высокой точке
. Самая высокая точка является вершиной параболы
, поэтому координата y вершины
будет равна 10.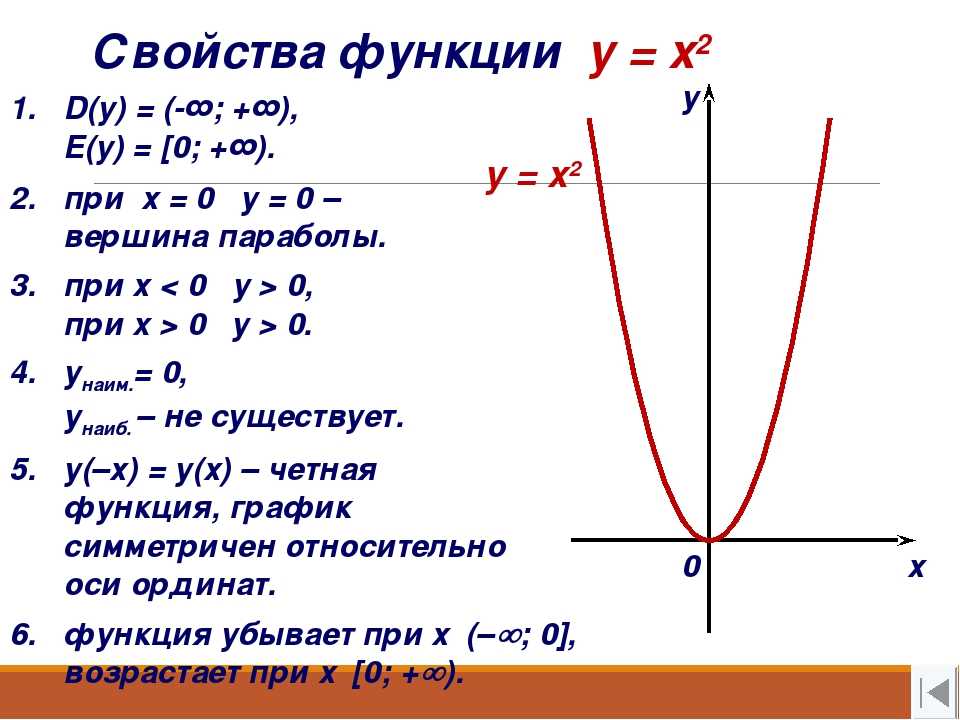
Поскольку мост симметричен, вершина
должна находиться на полпути между крайней левой точкой
и самой правой точкой
. Отсюда мы знаем, что
x -координата вершины тоже будет 10. Определите вершину, Подставьте значения в стандартную форму.
значение и , используйте одну из других точек
на параболе. Подставьте значения другой точки
в уравнение.
Найдите и . Подставьте значение на в уравнение
. Основные понятия
Практика ведет к совершенству
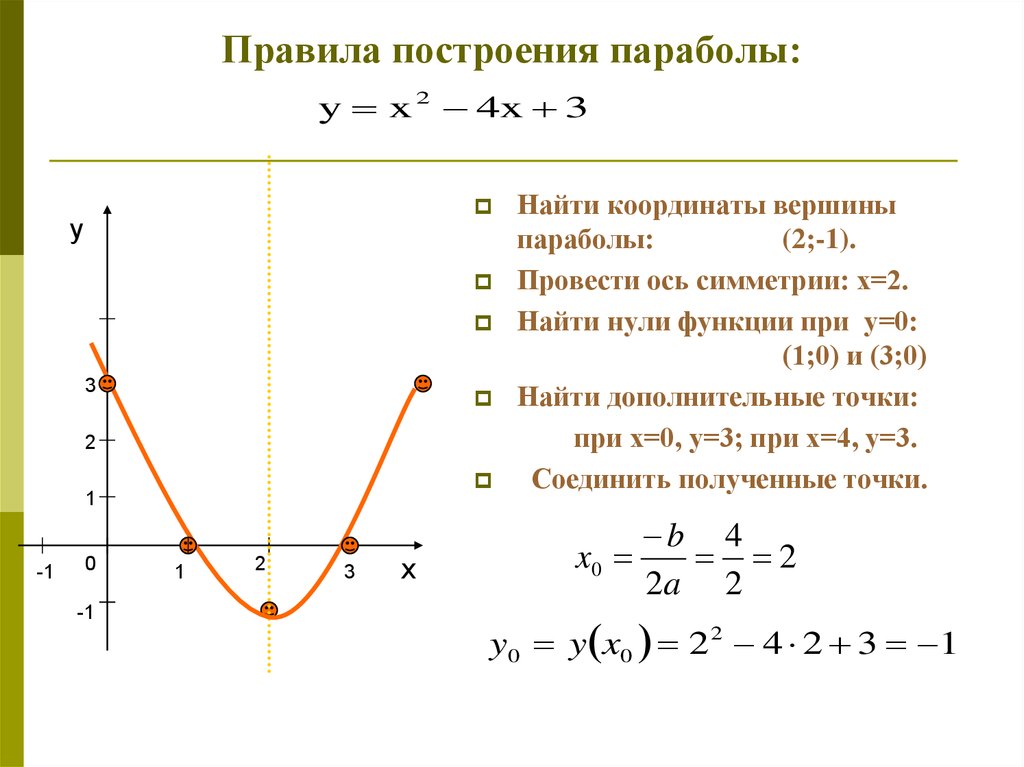

ⓒ ( x + 5) 2 + ( Y + 2) 2 = 4 ⓓ ( x — 2) 2 = 4 ⓓ ( x — 2) 2 + ( x — 2) 2 + + ( x — 2) 2 . − 3) 2 = 9 ⓔ y = − х 2 + 8 x − 15 ⓕ y = 6 x 2 + 2 x − 1
ⓐ
ⓑ
ⓓ
Solve Applications with Parabolas
Write уравнение в стандартной форме параболической арки, образованной в основании показанного моста.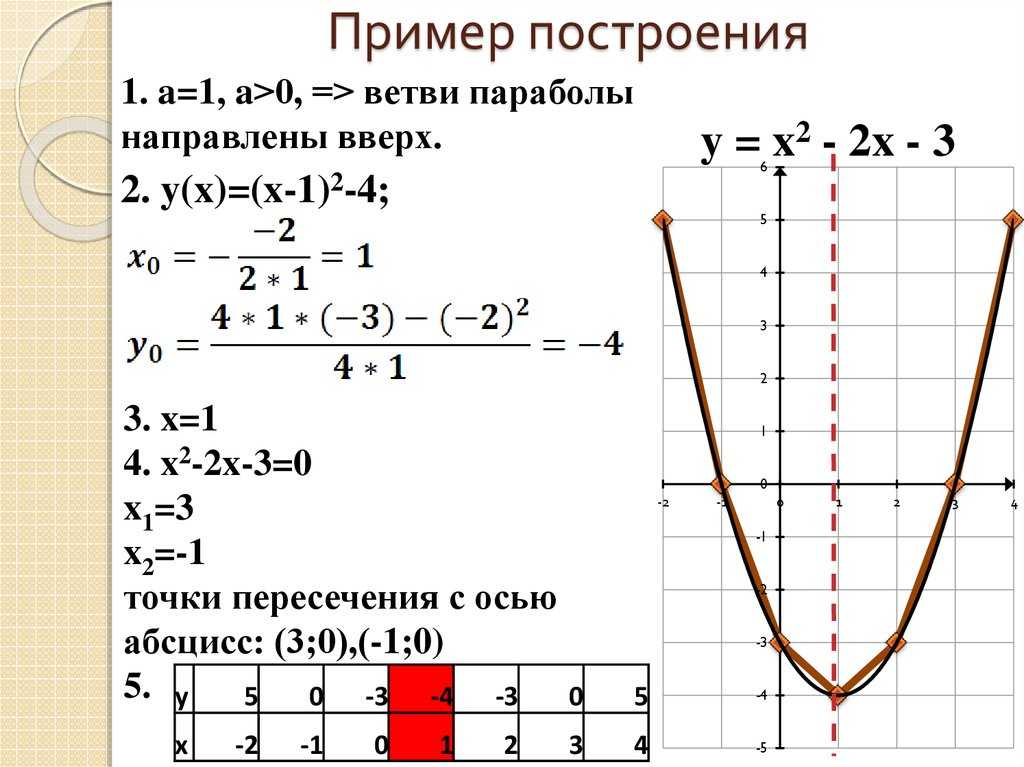 Используйте нижнюю левую сторону моста в качестве начала координат (0, 0).
Используйте нижнюю левую сторону моста в качестве начала координат (0, 0).
Запишите в стандартной форме уравнение параболической арки, образованной в основании показанного моста. Используйте нижнюю левую сторону моста в качестве начала координат (0, 0).
Напишите уравнение в стандартной форме для параболической арки, образованной в основании показанного моста. Используйте нижнюю левую сторону моста в качестве начала координат (0, 0).
Запишите в стандартной форме уравнение параболической арки, образованной в основании показанного моста. Используйте нижнюю левую сторону моста в качестве начала координат (0, 0).
Письменные упражнения
Своими словами дайте определение параболе.
Ответы будут разными.
Является ли парабола функцией? Является ли парабола функцией? Объясните, почему да или почему нет.
Напишите уравнение параболы, выходящей вверх или вниз в стандартной форме, и уравнение параболы, выходящей влево или вправо в стандартной форме.

 Концы широкой прямой кишки: (а, 2а), (а, -2а).
Концы широкой прямой кишки: (а, 2а), (а, -2а).
 Найдите длину широкой прямой кишки, фокуса и вершины.
Найдите длину широкой прямой кишки, фокуса и вершины.