Построение диаграмм на Python с помощью Matplotlib
Бывает, что нужно по-быстрому визуализировать какие-то данные — построить графики для презентации или вроде того. Есть много способов сделать это. Например, можно открыть CSV-файл в LibreOffice или Google Docs и построить графики в нем. Но что, если диаграммы нужно строить регулярно, а значит предпочтительнее делать это автоматически? Вот тут-то на помощь и приходит Python с его потрясающей библиотекой Matplotlib.
Примечание: Для решения той же задачи в свое время мне доводилось использовать Scala Chart. Однако, как вы сами сейчас убедитесь, Matplotlib куда гибче, да и графики у него получаются намного красивее. Если вас интересует тема визуализации данных, вам стоит обратить внимание на мои стары посты, посвященные Graphviz, а также JavaScript-библиотекам Flot и Dracula.
Не будем ходить вокруг да около, лучше сразу перейдем к примерам. Пожалуй, простейший график, который можно построить в Matplotlib, это график синуса и косинуса:
#!/usr/bin/env python3
# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib. pyplot as plt
pyplot as plt
import math
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 10})
plt.axis([0, 10, -1.5, 1.5])
plt.title(‘Sine & Cosine’)
plt.xlabel(‘x’)
plt.ylabel(‘F(x)’)
xs = []
sin_vals = []
cos_vals = []
x = 0.0
while x < 10.0:
sin_vals += [ math.sin(x) ]
cos_vals += [ math.cos(x) ]
xs += [x]
x += 0.1
plt.plot(xs, sin_vals, color = ‘blue’, linestyle = ‘solid’,
label = ‘sin(x)’)
plt.plot(xs, cos_vals, color = ‘red’, linestyle = ‘dashed’,
label = ‘cos(x)’)
plt.legend(loc = ‘upper right’)
fig.savefig(‘trigan.png’)
Я думаю, что код не нуждается в пояснениях. В крайнем случае, вы можете полистать официальную документацию или почитать вывод help() в REPL’е.
Получившийся график:
Однако на практике часто нужно построить график функции не от абстрактного вещественного числа, а от вполне конкретного времени.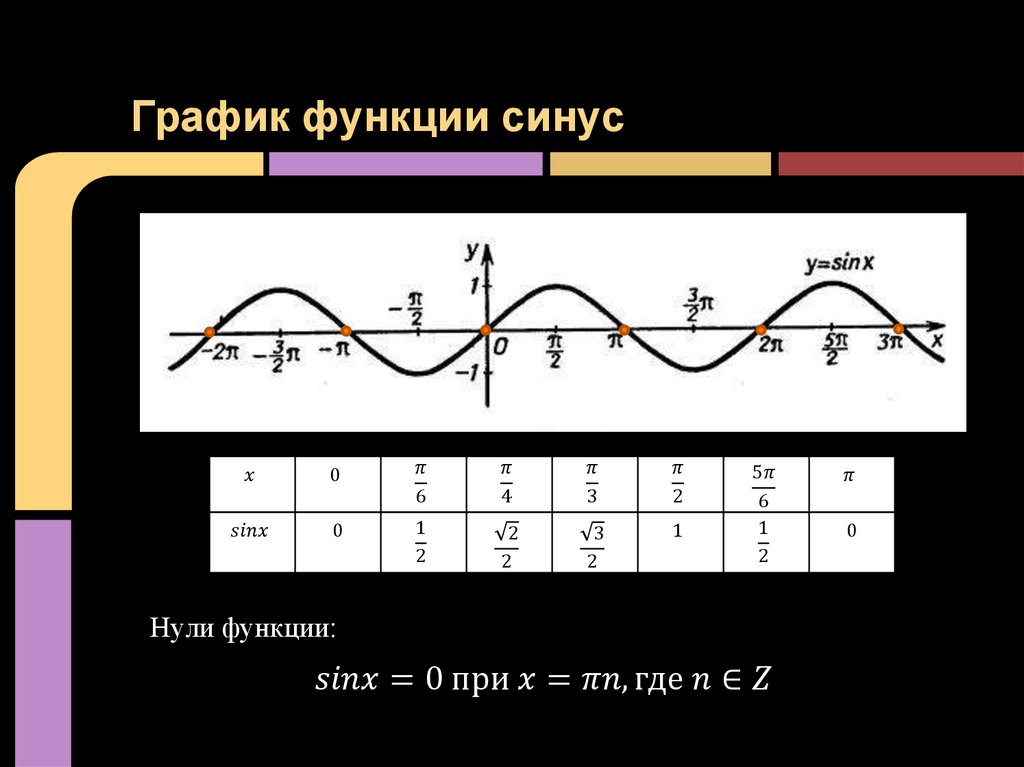 И в этом случае хочется, чтобы по оси OX были подписаны не абстрактные 1, 2, 3, а вполне конкретные временные метки. Для примера рассмотрим построение графика регистрации новых доменов в зоне RU за разное время с разбивкой по регистраторам:
И в этом случае хочется, чтобы по оси OX были подписаны не абстрактные 1, 2, 3, а вполне конкретные временные метки. Для примера рассмотрим построение графика регистрации новых доменов в зоне RU за разное время с разбивкой по регистраторам:
#!/usr/bin/env python3
# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
dates = []
values = {}
with open(‘ru-newreg.csv’, newline = ») as f:
for row in csv.reader(f, delimiter = ‘,’, quotechar = ‘»‘):
if dates == []:
dates = [
dt.datetime.strptime(
«{}-01».format(d),
‘%Y-%m-%d’
).date()
for d in row[1:]
]
continue
values[ row[0] ] = row[1:]
dpi = 80
fig = plt.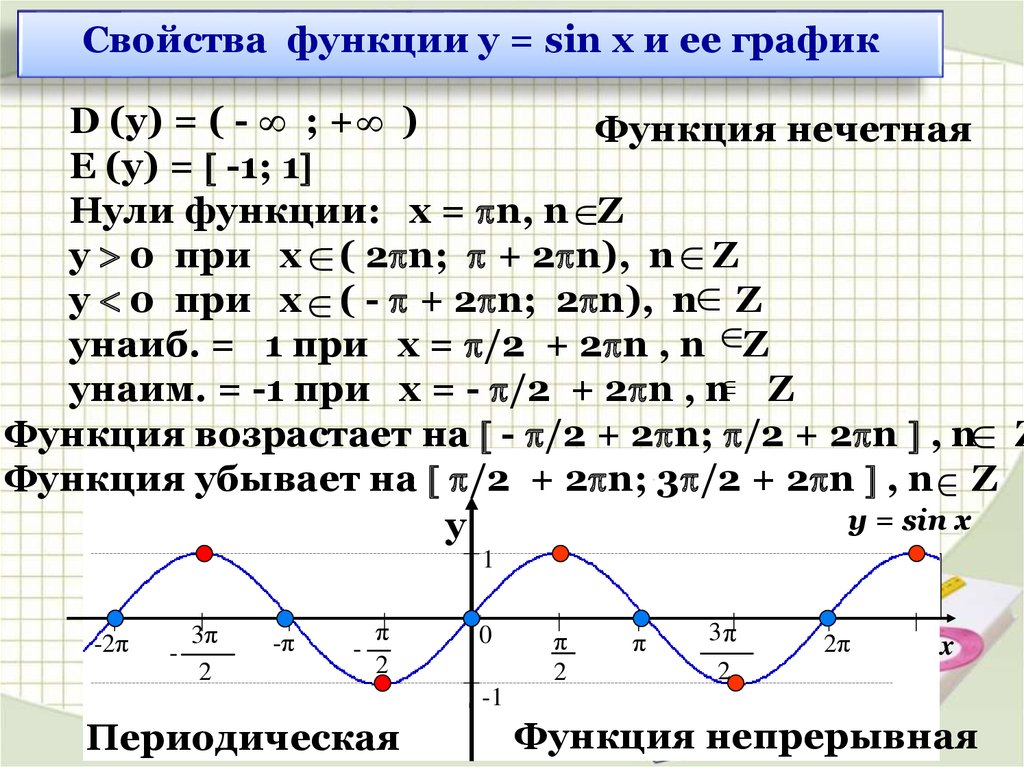 figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 10})
plt.title(‘RU New Domain Names Registration’)
plt.xlabel(‘Year’)
plt.ylabel(‘Domains’)
ax = plt.axes()
ax.yaxis.grid(True)
ax.xaxis.set_major_formatter(mdates.DateFormatter(‘%Y’))
ax.xaxis.set_major_locator(mdates.YearLocator())
for reg in values.keys():
plt.plot(dates, values[reg], linestyle = ‘solid’, label = reg)
plt.legend(loc=’upper left’, frameon = False)
fig.savefig(‘domains.png’)
Данные были получены с ныне уже закрытого сайта stat.nic.ru, который, впрочем, все еще доступен на web.archive.org. Результирующий график:
Что еще часто строят, это столбчатые диаграммы. В качестве примера возьмем данные из заметки Поиск по географическим данным при помощи PostGIS и построим диаграмму, отображающую сколько точек на карте к какому типу (заправка, кафе и так далее) относятся. Чтобы было чуть интереснее, сделаем вид, что в прошлом году точек каждого вида было на 10% меньше, и попытаемся отразить это изменение:
#!/usr/bin/env python3
# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.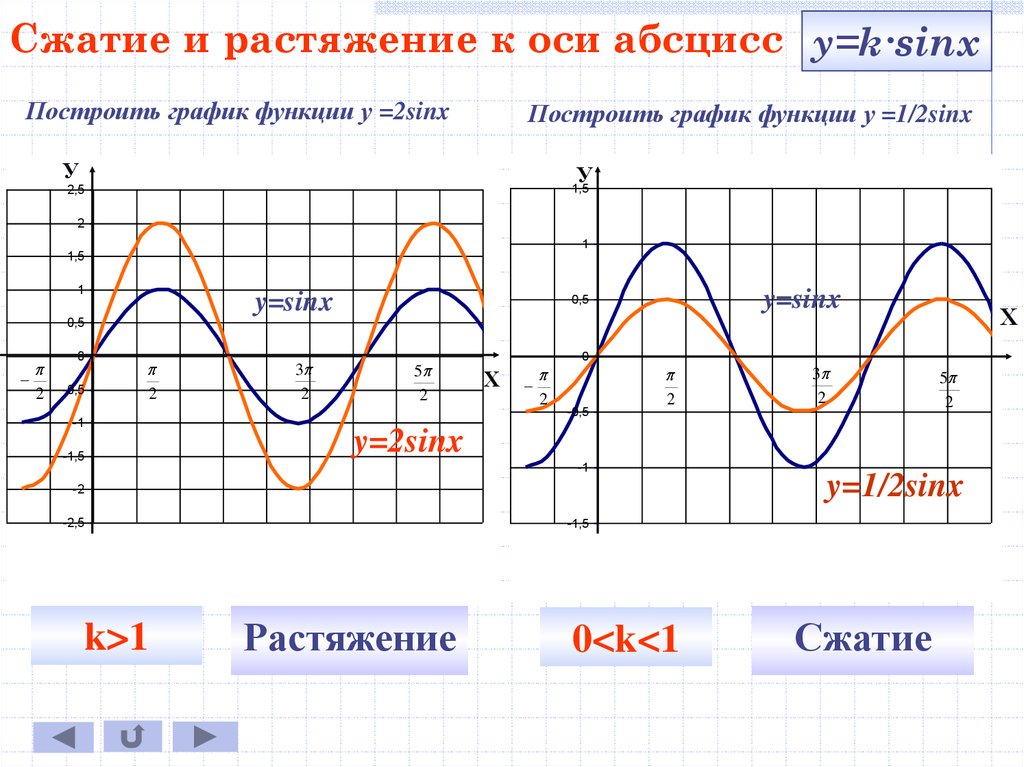 pyplot as plt
pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
data_names = [‘cafe’, ‘pharmacy’, ‘fuel’, ‘bank’, ‘waste_disposal’,
‘atm’, ‘bench’, ‘parking’, ‘restaurant’,
‘place_of_worship’]
data_values = [9124, 8652, 7592, 7515, 7041, 6487, 6374, 6277,
5092, 3629]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 10})
plt.title(‘OpenStreetMap Point Types’)
ax = plt.axes()
ax.yaxis.grid(True, zorder = 1)
xs = range(len(data_names))
plt.bar([x + 0.05 for x in xs], [ d * 0.9 for d in data_values],
width = 0.2, color = ‘red’, alpha = 0.7, label = ‘2016’,
zorder = 2)
plt.bar([x + 0.3 for x in xs], data_values,
width = 0.2, color = ‘blue’, alpha = 0.7, label = ‘2017’,
zorder = 2)
plt.xticks(xs, data_names)
fig.autofmt_xdate(rotation = 25)
plt.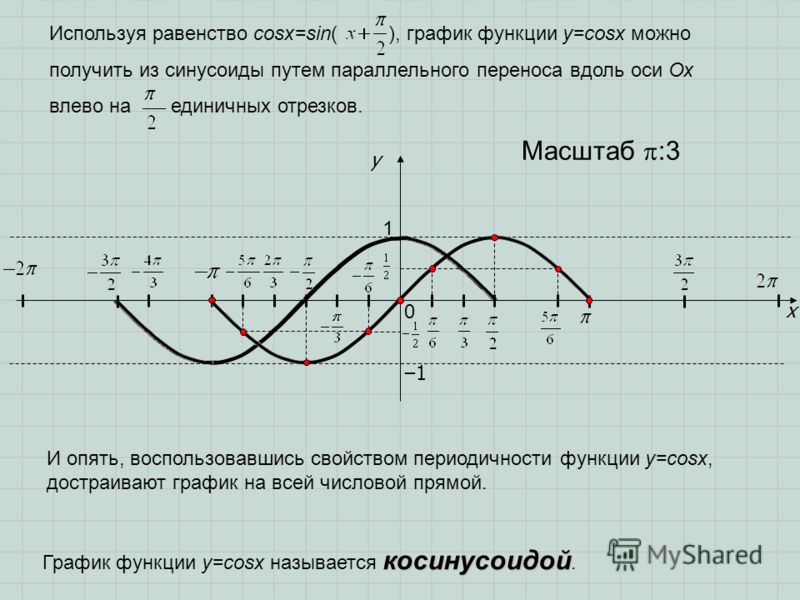 legend(loc=’upper right’)
legend(loc=’upper right’)
fig.savefig(‘bars.png’)
Результат:
Те же данные можно отобразить, расположив столбики горизонтально:
#!/usr/bin/env python3
# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
data_names = [‘cafe’, ‘pharmacy’, ‘fuel’, ‘bank’, ‘w.d.’, ‘atm’,
‘bench’, ‘parking’, ‘restaurant’, ‘p.o.w.’]
data_values = [9124, 8652, 7592, 7515, 7041, 6487, 6374, 6277,
5092, 3629]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 9})
plt.title(‘OpenStreetMap Point Types’)
ax = plt.axes()
ax.xaxis.grid(True, zorder = 1)
xs = range(len(data_names))
plt.barh([x + 0.3 for x in xs], [ d * 0.9 for d in data_values],
height = 0.2, color = ‘red’, alpha = 0.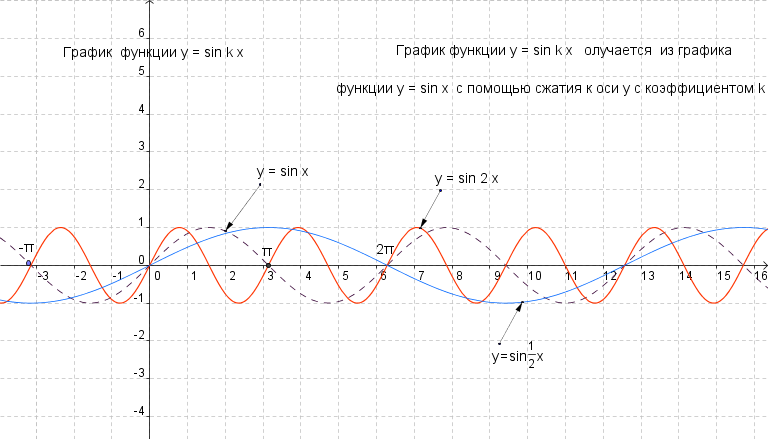 7, label = ‘2016’,
7, label = ‘2016’,
zorder = 2)
plt.barh([x + 0.05 for x in xs], data_values,
height = 0.2, color = ‘blue’, alpha = 0.7, label = ‘2017’,
zorder = 2)
plt.yticks(xs, data_names, rotation = 10)
plt.legend(loc=’upper right’)
fig.savefig(‘barshoris.png’)
Соответствующая диаграмма:
И последний на сегодня вид диаграмм — круговая диаграмма, или «пирог». Для примера попробуем визуализировать распределение кафе по различным городам России:
#!/usr/bin/env python3
# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
data_names = [‘Москва’, ‘Санкт-Петербург’, ‘Сочи’, ‘Архангельск’,
‘Владимир’, ‘Краснодар’, ‘Курск’, ‘Воронеж’,
‘Ставрополь’, ‘Мурманск’]
data_values = [1076, 979, 222, 189, 137, 134, 124, 124, 91, 79]
dpi = 80
fig = plt.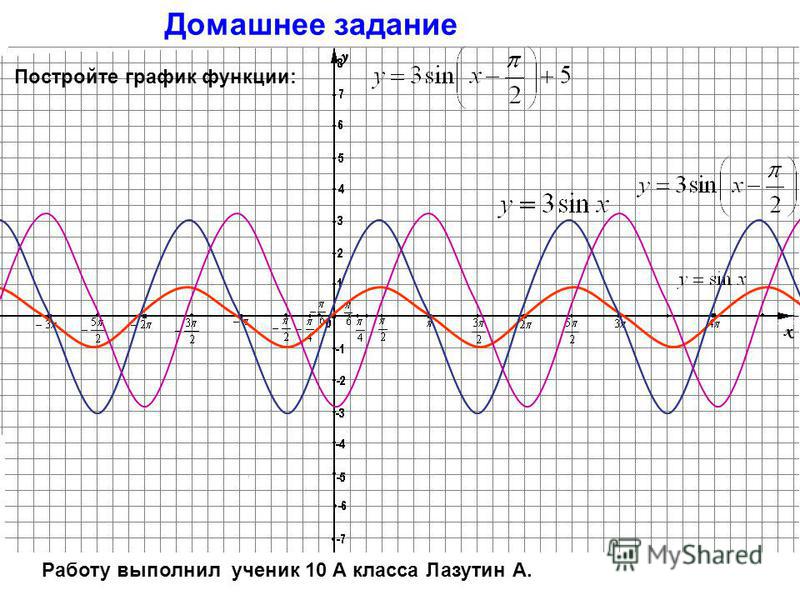 figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 9})
plt.title(‘Распределение кафе по городам России (%)’)
xs = range(len(data_names))
plt.pie(
data_values, autopct=’%.1f’, radius = 1.1,
explode = [0.15] + [0 for _ in range(len(data_names) — 1)] )
plt.legend(
bbox_to_anchor = (-0.16, 0.45, 0.25, 0.25),
loc = ‘lower left’, labels = data_names )
fig.savefig(‘pie.png’)
Полученная круговая диаграмма:
Выше была рассмотрена лишь малая часть возможностей Matplotlib. Чтобы получить более полное представление о всей мощи этой библиотеки, советую заглянуть в галерею построенных с ее помощью графиков на официальном сайте. Что же до исходников к этому посту, как обычно, вы найдете их на GitHub.
А чем вы строите диаграммы и, если не секрет, как они при этом выглядят?
Дополнение: См также заметки Примеры использования Python-библиотеки NumPy, Визуализация проведенных радиосвязей с помощью Matplotlib и Basemap, Рисуем диаграммы Вольперта-Смита на Python и Моделирование антенн на Python при помощи PyNEC.
Метки: Python.
Как построить график в Gnuplot, основы
2019.08.15Viktar HaurylavetsОсвоить основные принципы работы в Gnuplot легко:
Gnuplot является консольной программой, что позволяет автоматизировать работу в построении сотен графиков. Так же он распространяется под лицензией подразумевающей свободное распространение и использование, т.е. вы можете использовать Гнуплот совершенно бесплатно и это не нарушает никаких прав.
Где скачать Gnuplot?
Скачать можно с официального сайта http://gnuplot.info.
Linux
В большинстве дистрибутивов Gnuplot находится в официальных репозиториях, т.е. его нужно просто установить. В Ubuntu можно установить командойsudo apt-get install gnuplot
Windows
Для виндовс на странице скачивания доступные скомпилированые сборкиcygwin и MinGW. Должны в принципе работать они двое, лучше может использовать вторую, MinGW.OS X
Для macbook ссылки можно найти под заголовком 3rd party OS/X binaries.
Запуск Gnuplot
В консоли запускаем Gnuplot командой
gnuplot
И увидим приветствие программы
Вывод Gnuplot при запускеЭто интерактивный режим работы — когда мы пишем команды и Gnuplot их сразу выполняет.
Построить график функции
Для построения графика функции используем команду
plot sin(x)
И получим такой график
График функцииSin(x) построенный в GnuplotРазберем подробнее команду
plot- — команда для построения или отрисовки графика,
sin(x)- — функция для отрисовки, синус. По умолчанию
xиграет роль переменной.
Так как мы еще не настраивали вид графиков, то по умолчанию ось OX или x у нас в интервале от -10 до 10. Ось OY или y подстраивается автоматически от минимума до максимума, за исключением особых точек на графике, например — бесконечность.
Построить график из файла данных
Что бы построить график из файла данных"data. txt"
txt" воспользуемся командойplot "data.txt" u 1:2 w l
И получим такой рисунок
График построенный из файла данных в GnuplotРазберем команду
plot- — команда построить график
"data.txt"- — файл данных, пример файла здесь, подробнее о том какого он должен быть формата и чего там не должно быть будет изложено в другой статье.
И разумеется, Gnuplot не телепат, не знает где лежат ваши файлы, по умолчанию он берет файлы из директории или папки в которой он запущен. Ее вы можете узнать командой
pwd
Можно также указать полное имя от корневой директории "/", например "/home/black/програмирование/Сайт/dev.asifmoda.com/текста/скрипты/data.txt"
u- — сокращение от
using, то есть использовать. В файле находится две колонки цифр разделенные пробелами, 1 означает для
В файле находится две колонки цифр разделенные пробелами, 1 означает для xиспользовать первую колонку, далее двоеточие, и 2 — использовать вторую колонку дляy. Если указано 0, то используется порядок цифр или другими словами номер строки начиная с нуля. Разумеется, можно в качествеxиспользовать разные колонки цифр. w- — сокращение от
with, и вместе с l- — сокращение от
line, линия означает построить график линиями.
Таким образом мы задали следующую команду: построить график из файла «data.txt» используя первую колону цифр как x, вторую колонку цифр как y с помощью линий.
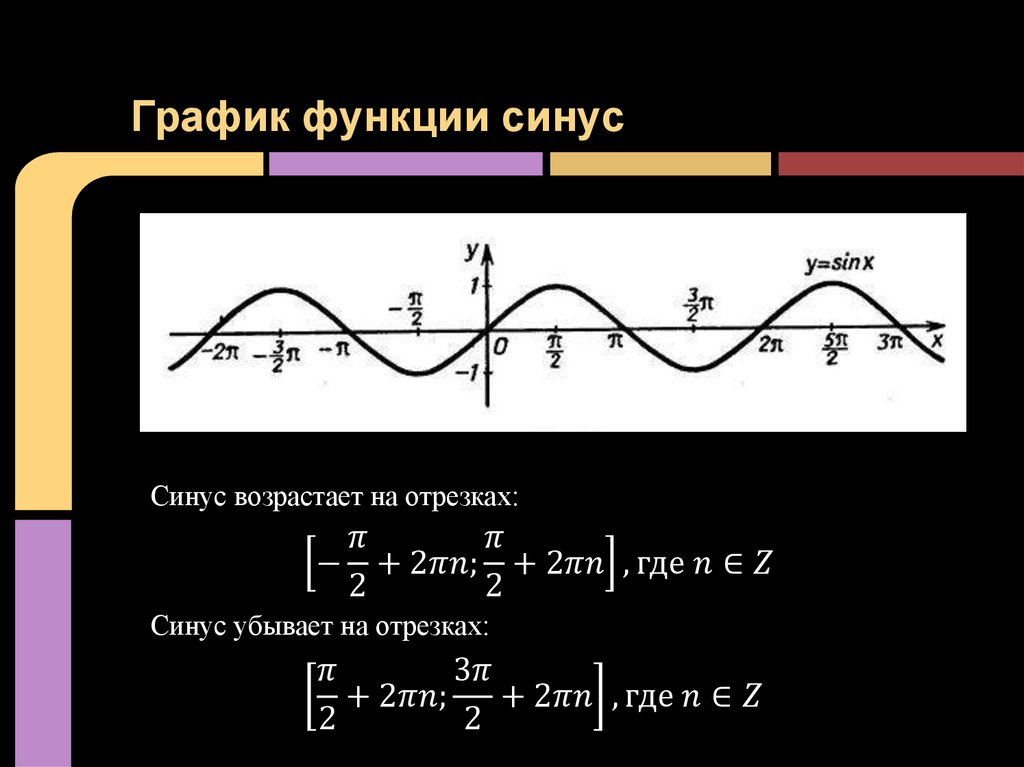
Синусоидальный график
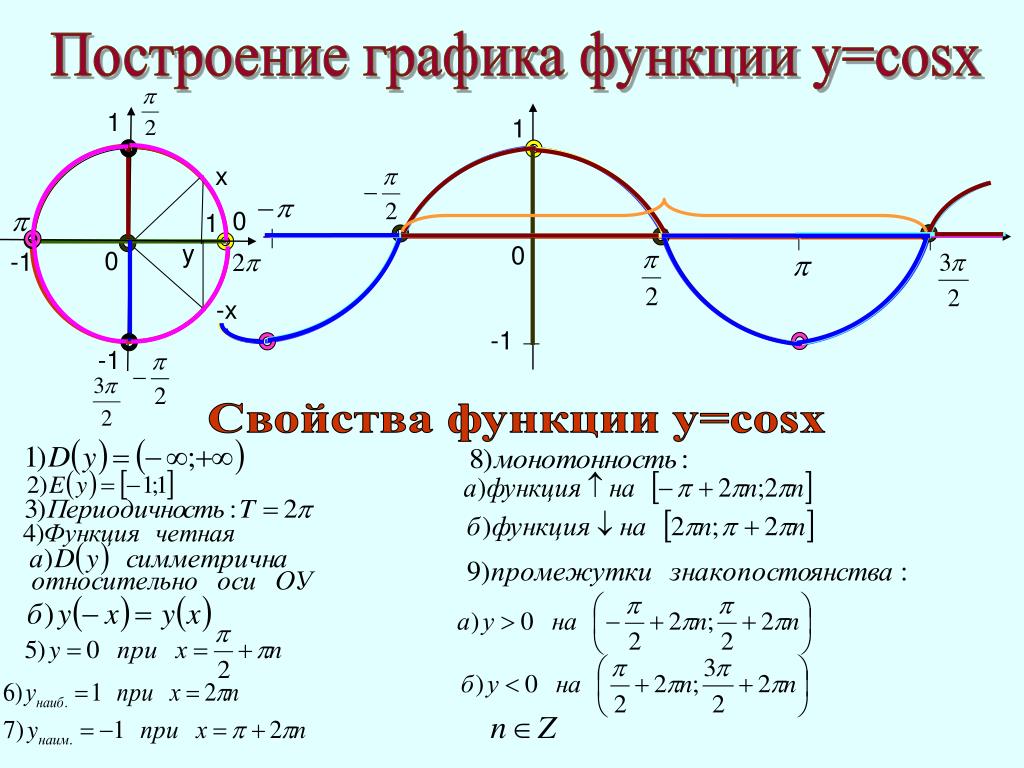
Синусоидальный график Графики функций, определяемые соотношением y = sin x , называются синусоидальными волнами.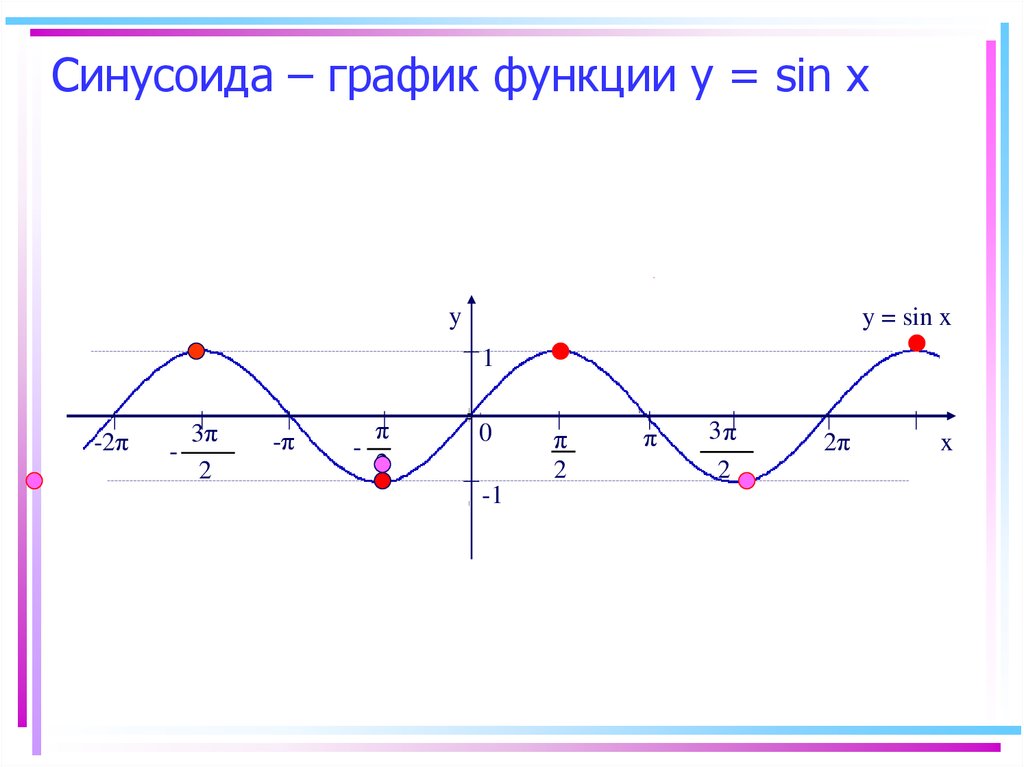 или синусоидальные волны. Обратите внимание, что график повторяется по мере движения
ось х. Циклы этого регулярного повторения называются периодами. Этот
график повторяется каждые 6,28 единиц или 2 пи радиана. Он колеблется от -1 до 1;
половина этого расстояния называется амплитудой. Таким образом, график ниже имеет период
6,28 и амплитудой 1,
или синусоидальные волны. Обратите внимание, что график повторяется по мере движения
ось х. Циклы этого регулярного повторения называются периодами. Этот
график повторяется каждые 6,28 единиц или 2 пи радиана. Он колеблется от -1 до 1;
половина этого расстояния называется амплитудой. Таким образом, график ниже имеет период
6,28 и амплитудой 1,
Мы также исследуем различные значения амплитуды и периода. как фазовый сдвиг, который, кажется, устанавливает график в другом месте на ось х.
Давайте посмотрим, что происходит с графиком при разных значениях а. Включено
слева внизу x = 2 sin x и y = 6 sin x на том же графике
с у = грех х . Обратите внимание, как высоко и как низко идет график; этот
называется диапазоном. Как вы думаете, что произойдет, когда знак на меняется на минус? Посмотрите на график справа ниже, чтобы увидеть лет.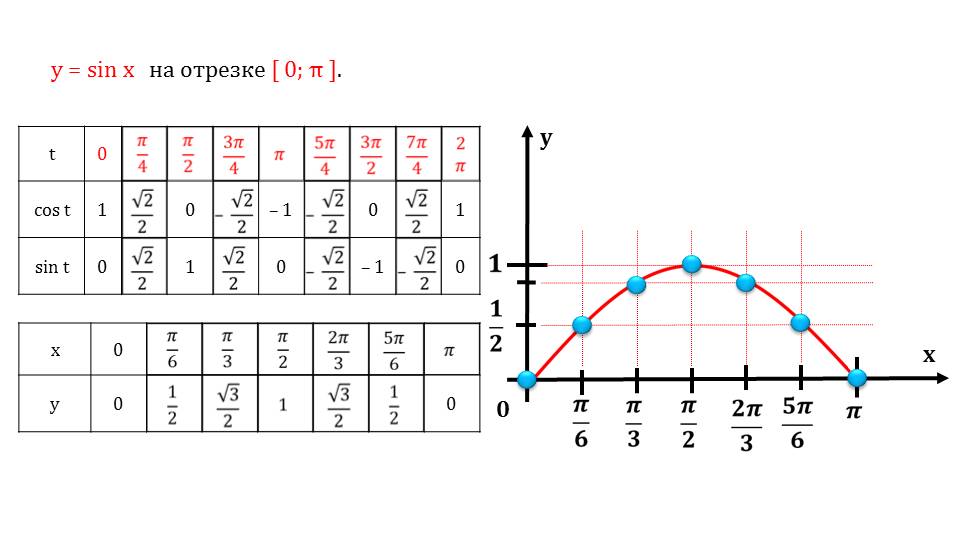 = -3 sin x и y = -5 sin x на том же графике с y = sin
х . Что происходит с графиком при изменении на ?
= -3 sin x и y = -5 sin x на том же графике с y = sin
х . Что происходит с графиком при изменении на ?
.
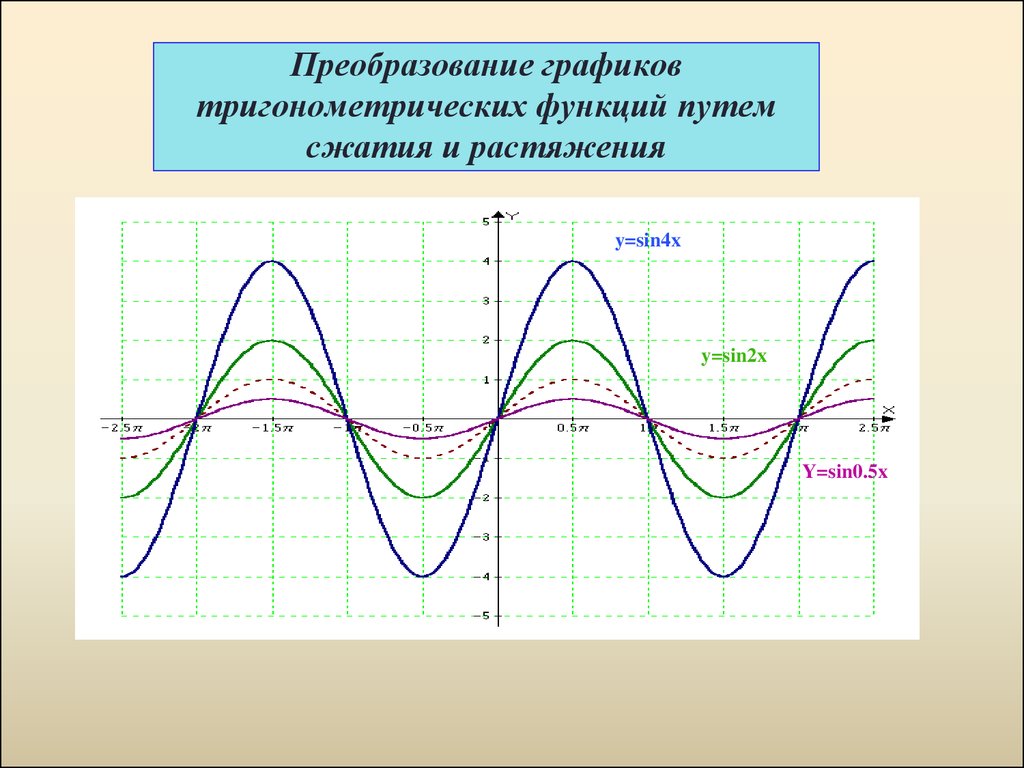
Период
Теперь давайте посмотрим на период. Посмотрите, как цикл повторяется каждые 6,28 ед. (2 пи). Глядя на левый график, обратите внимание, что происходит г = sin (1)x заменяется на y = sin 2x . выделяют два периода в пространство, где он был. Это означает, что месячные происходят в два раза чаще, или мы говорят, что они вдвое короче. А этот выглядит так, как будто это может быть 3.14? или пи.? Теперь посмотрите на график справа внизу. Здесь у = грех х накладывается на y = sin 1/2 x . Что здесь происходит? Сделать предположение о том, что происходит с графиком y = sin bx при изменении b .
Фазовый сдвиг
Посмотрите еще раз на уравнение y = a sin (bx + c) .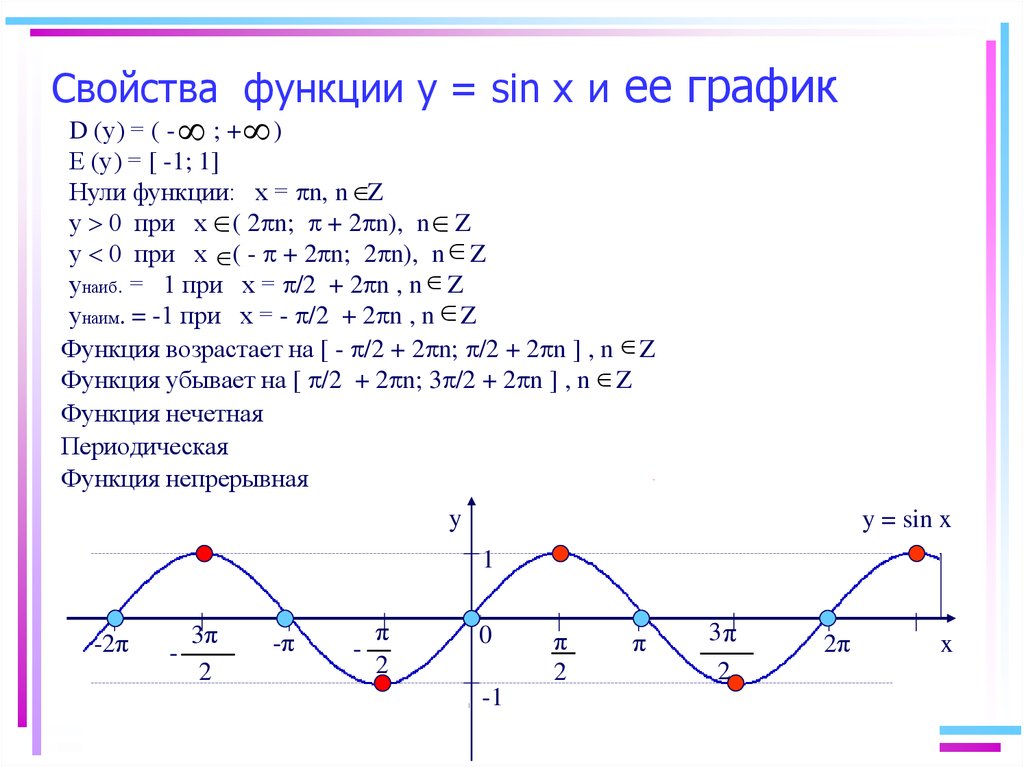 Обратите внимание, что мы
варьировались a , амплитуда, и b , период. Последний
вариация в этом уравнении будет c . В первом уравнении лет
= sin x , c равно нулю. Посмотрите на график слева, чтобы
см. эту кривую, а также кривую уравнения y = sin (x + 2)
Обратите внимание, что мы
варьировались a , амплитуда, и b , период. Последний
вариация в этом уравнении будет c . В первом уравнении лет
= sin x , c равно нулю. Посмотрите на график слева, чтобы
см. эту кривую, а также кривую уравнения y = sin (x + 2)
Что произойдет, если все три константы будут варьироваться в в то же время? Посмотрите внизу слева на графике
y = sin x и наложите на него y = 4 sin (2x +1) . Заметить, что новый график имеет амплитуду 4, период 3,14 или пи, а фазу сдвиг на 1 единицу влево.
 Что произойдет, если все коэффициенты
отрицательный? Посмотрите на график справа, чтобы увидеть y = -3 sin (-1/2 x -1) .
Объясните, что здесь происходит. Теперь вы можете посмотреть на уравнения вида y= a sin (bx + c) и предсказать, как будет выглядеть кривая?
Что произойдет, если все коэффициенты
отрицательный? Посмотрите на график справа, чтобы увидеть y = -3 sin (-1/2 x -1) .
Объясните, что здесь происходит. Теперь вы можете посмотреть на уравнения вида y= a sin (bx + c) и предсказать, как будет выглядеть кривая?Синусоидальная волна/функция Python Plot sin(x) (с Matplotlib)
В декартовой системе координат тригонометрическая функция синуса $\text{sin}(x)$ порождает правильную волнообразную кривую, проходящую через начало координат. Его значения варьируются от $-1$ до $1$ для всех реальных значений $x$.
В этом уроке мы узнаем, как построить синусоиду в Python с Matplotlib. Мы будем рисовать $\text{sin}(x)$ вместе с его кратными и дольными углами между интервалами $-\pi$ и $\pi$.
Так как значения $y=\text{sin}(x)$ могут упасть ниже $-1$, ось $x$ устанавливается в центр.
Вот код для генерации синусоиды в Matplotlib.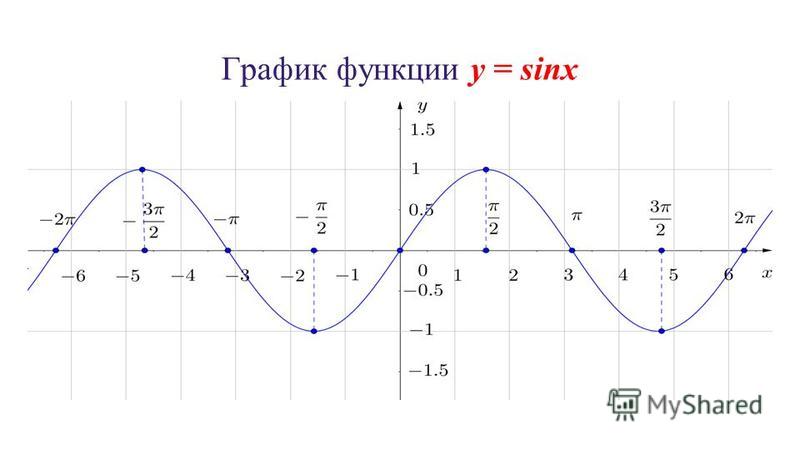 График $y=\text{sin}(x)$ для $x$ между $-\pi$ и $\pi$.
График $y=\text{sin}(x)$ для $x$ между $-\pi$ и $\pi$.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 линейно расположенных чисел
х = np.linspace(-np.pi, np.pi, 100)
# функция, которая здесь y = sin(x)
у = np.sin (х)
# установка осей в центре
рис = plt.figure()
топор = fig.add_subplot (1, 1, 1)
ax.spines['слева'].set_position('центр')
ax.spines['нижний'].set_position('центр')
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('внизу')
ax.yaxis.set_ticks_position('слева')
# построить функцию
plt.plot(x,y, 'b-')
# показать сюжет
plt.show()
Несколько углов
В этом разделе мы вместе построим графики множественных углов $y=\text{sin}(x)$, $y=\text{sin}(2x)$ и $y=\text{sin}(3x) $.
импортировать matplotlib.pyplot как plt импортировать numpy как np # 100 линейно расположенных чисел х = np.linspace(-np.pi, np.pi, 100) p = np.sin(x) # y = sin(x) q = np.sin(2*x) # y = sin(2x) r = np.sin(3*x) # y = sin(3x) # установка осей в центре рис = plt.figure() топор = fig.add_subplot (1, 1, 1) ax.spines['слева'].set_position('центр') ax.spines['нижний'].set_position('центр') ax.spines['право'].set_color('нет') ax.spines['top'].set_color('none') ax.xaxis.set_ticks_position('внизу') ax.yaxis.set_ticks_position('слева') # построить функции с метками plt.plot(x,p, 'b-', метка='y=sin(x)') plt.plot(x,q, 'c-', метка='y=sin(2x)') plt.plot(x,r, 'm-', метка='y=sin(3x)') plt.legend(loc='верхний левый') # показать сюжет plt.show()
Дольный угол
И здесь мы наносим вместе дробный угол $y=\text{sin}(\frac{x}{2})$ вместе с $y=2\text{sin}(x)$ и $y=\text{sin }(х)$.
импортировать matplotlib.pyplot как plt импортировать numpy как np # 100 линейно расположенных чисел х = np.linspace(-np.pi, np.pi, 100) p = 2*np.sin(x) # y = 2sin(x) q = np.sin(x) # y = sin(x) r = np.sin(x/2) # y = sin(x/2) # установка осей в центре рис = plt.figure() топор = fig.add_subplot (1, 1, 1) ax.spines['слева'].set_position('центр') ax.spines['нижний'].set_position('ноль') ax.spines['право'].set_color('нет') ax.spines['top'].set_color('none') ax.xaxis.set_ticks_position('внизу') ax.yaxis.set_ticks_position('слева') # построить функции с метками plt.plot(x,p, 'b-', метка='y=2sin(x)') plt.plot(x,q, 'c-', метка='y=sin(x)') plt.plot(x,r, 'm-', метка='y=sin(x/2)') plt.legend(loc='верхний левый') # показать сюжет plt.show()
грех(х)/х
И, наконец, иллюстрация $\text{lim}_{x \to 0} \frac{\text{sin}(x)}{x} = 1$.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 линейно расположенных чисел
х = np.linspace(-20,20,500)
y = np.sin(x)/x # y = sin(x)/x
# установка осей в центре
рис = plt.figure()
топор = fig.add_subplot (1, 1, 1)
ax.spines['слева'].set_position('центр')
ax.spines['нижний'].set_position('ноль')
ax.spines['право'].set_color('нет')
ax.spines['top'].

 txt"
txt" В файле находится две колонки цифр разделенные пробелами, 1 означает для
В файле находится две колонки цифр разделенные пробелами, 1 означает для 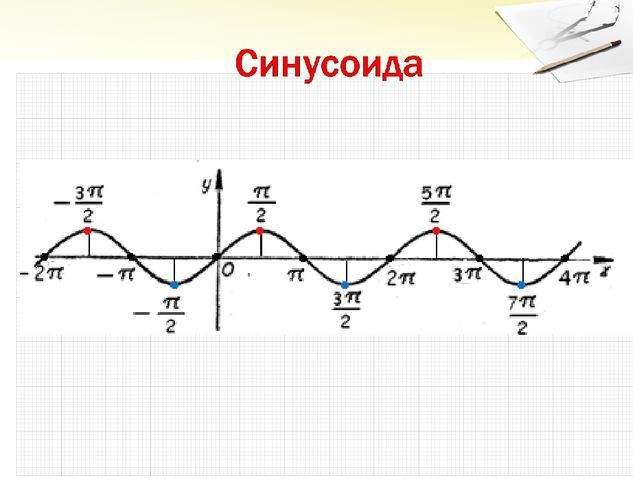 sin(2*x) # y = sin(2x)
r = np.sin(3*x) # y = sin(3x)
# установка осей в центре
рис = plt.figure()
топор = fig.add_subplot (1, 1, 1)
ax.spines['слева'].set_position('центр')
ax.spines['нижний'].set_position('центр')
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('внизу')
ax.yaxis.set_ticks_position('слева')
# построить функции с метками
plt.plot(x,p, 'b-', метка='y=sin(x)')
plt.plot(x,q, 'c-', метка='y=sin(2x)')
plt.plot(x,r, 'm-', метка='y=sin(3x)')
plt.legend(loc='верхний левый')
# показать сюжет
plt.show()
sin(2*x) # y = sin(2x)
r = np.sin(3*x) # y = sin(3x)
# установка осей в центре
рис = plt.figure()
топор = fig.add_subplot (1, 1, 1)
ax.spines['слева'].set_position('центр')
ax.spines['нижний'].set_position('центр')
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('внизу')
ax.yaxis.set_ticks_position('слева')
# построить функции с метками
plt.plot(x,p, 'b-', метка='y=sin(x)')
plt.plot(x,q, 'c-', метка='y=sin(2x)')
plt.plot(x,r, 'm-', метка='y=sin(3x)')
plt.legend(loc='верхний левый')
# показать сюжет
plt.show()