построение, гистограмма, выборочная дисперсия и СКО
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
| Интервалы, \(\left.\left[a_{i-1},a_i\right.\right)\) | \(\left.\left[a_{0},a_1\right.\right)\) | \(\left. \left[a_{1},a_2\right.\right)\) \left[a_{1},a_2\right.\right)\) | … | \(\left.\left[a_{k-1},a_k\right.\right)\) |
| Частоты, \(f_i\) | \(f_1\) | \(f_2\) | … | \(f_k\) |
Здесь k — число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+\lfloor\log_2 N\rfloor $$ или, через десятичный логарифм: $$ k=1+\lfloor 3,322\cdot\lg N\rfloor $$
Скобка \(\lfloor\ \rfloor\) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=\left\lceil\frac Rk\right\rceil $$
Скобка \(\lceil\ \rceil\) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака \(\left\{x_j\right\},\ j=\overline{1,N}\)
Шаг 1. Найти размах вариации \(R=x_{max}-x_{min}\)
Шаг 2. Найти оптимальное количество интервалов \(k=1+\lfloor\log_2 N\rfloor\)
Шаг 3. Найти шаг интервального ряда \(h=\left\lceil\frac{R}{k}\right\rceil\)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min},\ \ a_i=1_0+ih,\ \ i=\overline{1,k} $$ Шаг 5. Найти частоты \(f_i\) – число попаданий значений признака в каждый из интервалов \(\left.\left[a_{i-1},a_i\right.\right)\).
На выходе: интервальный ряд с интервалами \(\left.\left[a_{i-1},a_i\right.\right)\) и частотами \(f_i,\ i=\overline{1,k}\)
Заметим, что поскольку шаг h находится с округлением вверх, последний узел \(a_k\geq x_{max}\).
Например:
Проведено 100 измерений роста учеников старших классов.
Найдем узлы для построения соответствующего интервального ряда.
По условию: \(N=100,\ x_{min}=142\ см,\ x_{max}=197\ см\).
Размах вариации: \(R=197-142=55\) (см)
Оптимальное число интервалов: \(k=1+\lfloor 3,322\cdot\lg 100\rfloor=1+\lfloor 6,644\rfloor=1+6=7\)
Шаг интервального ряда: \(h=\lceil\frac{55}{5}\rceil=\lceil 7,85\rceil=8\) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142,\ a_i=142+i\cdot 8,\ i=\overline{1,7} $$
| \(\left.\left[a_{i-1},a_i\right.\right)\) cм | \(\left.\left[142;150\right.\right)\) | \(\left.\left[150;158\right.\right)\) | \(\left.\left[158;166\right.\right)\) | \(\left.\left[166;174\right.\right)\) | \(\left.\left[174;182\right.\right)\) | \(\left.\left[182;190\right.\right)\) | \(\left[190;198\right]\) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала \(\left.\left[a_{i-1},a_i\right.\right)\) — это отношение частоты \(f_i\) к общему количеству исходов: $$ w_i=\frac{f_i}{N},\ i=\overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки \((x_i,w_i)\), где \(x_i\) — середины интервалов: \(x_i=\frac{a_{i-1}+a_i}{2},\ i=\overline{1,k}\).
Накопленные относительные частоты – это суммы: $$ S_1=w_1,\ S_i=S_{i-1}+w_i,\ i=\overline{2,k} $$ Ступенчатая кривая \(F(x)\), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является
Кумулята – это ломаная, которая соединяет точки \((x_i,S_i)\), где \(x_i\) — середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
\(\left. \left[a_{i-1},a_i\right.\right)\) cм \left[a_{i-1},a_i\right.\right)\) cм | \(\left.\left[142;150\right.\right)\) | \(\left.\left[150;158\right.\right)\) | \(\left.\left[158;166\right.\right)\) | \(\left.\left[166;174\right.\right)\) | \(\left.\left[174;182\right.\right)\) | \(\left.\left[182;190\right.\right)\) | \(\left[190;198\right]\) |
| \(f_i\) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| \(x_i\) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| \(w_i\) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| \(S_i\) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= \begin{cases} 0,\ x\leq 146\\ 0,04,\ 146\lt x\leq 154\\ 0,11,\ 154\lt x\leq 162\\ 0,22,\ 162\lt x\leq 170\\ 0,56,\ 170\lt x\leq 178\\ 0,89,\ 178\lt x\leq 186\\ 0,97,\ 186\lt x\leq 194\\ 1,\ x\gt 194 \end{cases} $$
п.
 k x_iw_i $$
k x_iw_i $$Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+\frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
\(h\) – шаг интервального ряда;
\(x_o\) — нижняя граница модального интервала;
\(f_m,f_{m-1},f_{m+1}\) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+\frac{0,5-S_{me-1}}{w_{me}}h $$ где
\(h\) – шаг интервального ряда;
\(x_o\) — нижняя граница медианного интервала;
\(S_{me-1}\) накопленная относительная частота для интервала слева от медианного;
\(w_{me}\) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. k x_iw_i=171,68\approx 171,7\ \text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
k x_iw_i=171,68\approx 171,7\ \text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: \begin{gather*} x_o=166,\ f_m=34,\ f_{m-1}=11,\ f_{m+1}=33,\ h=8\\ M_o=x_o+\frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\\ =166+\frac{34-11}{(34-11)+(34-33)}\cdot 8\approx 173,7\ \text{(см)} \end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: \begin{gather*} x_o=166,\ w_m=0,34,\ S_{me-1}=0,22,\ h=8\\ \\ M_e=x_o+\frac{0,5-S_{me-1}}{w_me}h=166+\frac{0,5-0,22}{0,34}\cdot 8\approx 172,6\ \text{(см)} \end{gather*} \begin{gather*} \\ X_{cp}=171,7;\ M_o=173,7;\ M_e=172,6\\ X_{cp}\lt M_e\lt M_o \end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом \(\frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=\frac{2,0}{0,9}\approx 2,2\lt 3\), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: \begin{gather*} D=\frac1N\sum_{i=1}^k(x_i-X_{cp})^2 f_i=\frac1N\sum_{i=1}^k x_i^2 f_i-X_{cp}^2 \end{gather*} где \(x_i\) — середины интервалов: \(x_i=\frac{a_{i-1}+a_i}{2},\ i=\overline{1,k}\). 2w_i\)
2w_i\)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18,\ \ x_{max}=38,\ \ N=30 $$ Размах вариации: \(R=38-18=20\)
Оптимальное число интервалов: \(k=1+\lfloor\log_2 30\rfloor=1+4=5\)
Шаг интервального ряда: \(h=\lceil\frac{20}{5}\rceil=4\)
Получаем узлы ряда: $$ a_0=x_{min}=18,\ \ a_i=18+i\cdot 4,\ \ i=\overline{1,5} $$
\(\left. \left[a_{i-1},a_i\right.\right)\) лет \left[a_{i-1},a_i\right.\right)\) лет | \(\left.\left[18;22\right.\right)\) | \(\left.\left[22;26\right.\right)\) | \(\left.\left[26;30\right.\right)\) | \(\left.\left[30;34\right.\right)\) | \(\left.\left[34;38\right.\right)\) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| \(\left.\left[a_{i-1},a_i\right.\right)\) лет | \(\left.\left[18;22\right.\right)\) | \(\left.\left[22;26\right.\right)\) | \(\left.\left[26;30\right.\right)\) | \(\left.\left[30;34\right.\right)\) | \(\left.\left[34;38\right.\right)\) |
| \(f_i\) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| \(x_i\) | 20 | 24 | 28 | 32 | 36 | ∑ |
| \(f_i\) | 1 | 7 | 12 | 6 | 4 | 30 |
| \(w_i\) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| \(S_i\) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | — |
| \(x_iw_i\) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| \(x_i^2w_i\) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= \begin{cases} 0,\ x\leq 20\\ 0,033,\ 20\lt x\leq 24\\ 0,267,\ 24\lt x\leq 28\\ 0,667,\ 28\lt x\leq 32\\ 0,867,\ 32\lt x\leq 36\\ 1,\ x\gt 36 \end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=\sum_{i=1}^k x_iw_i\approx 28,7\ \text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка). 2}\approx 4,2\)
2}\approx 4,2\)
Коэффициент вариации: \(V=\frac{4,2}{28,7}\cdot 100\text{%}\approx 14,7\text{%}\lt 33\text{%}\)
Выборка однородна. Найденное значение среднего возраста \(X_{cp}=28,7\) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Как построить вариационный ряд в excel
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, – генеральной совокупностью.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.
Рисунок 2.13. Полигон распределения частот
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» – «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
Пример 2.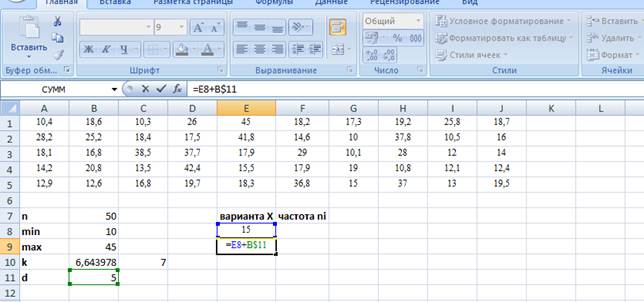 2.
2.
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
Воспользуемся функцией ЧАСТОТА.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
Рисунок 2.22. Построение гистограммы
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Дата добавления: 2018-11-12 ; просмотров: 1065 | Нарушение авторских прав
Вариационный ряд может быть:
– дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
– интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение .
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа – в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).
Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).
Размахом вариации называется число
где хтах — наибольший вариант;
x min — наименьший вариант.
Сумма всех частот равна определенному числу л, которое называется объемом совокупности:
Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:
Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.
Построить дискретный вариационный ряд.
Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.
В результате получим дискретный вариационный ряд (табл. 3.10).
Ранжированный ряд успеваемости
Число студентов, л,
Относительная частота, А
В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).
Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).
Рис. 3.13. Контекстное меню строки состояния
Рассмотрим два варианта подсчета частот:
- 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см.
 рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты; - 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.
Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»
В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).
Рис. 3.15. Результаты применения инструмента «Гистограмма)
Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).
В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.
Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.
3. Интервальный вариационный ряд
При большом объеме выборки работа с вариационными рядами представляет определенные неудобства, и тогда наблюдаемые данные группируют.
Группировка должна наиболее полно выявлять существенные свойства распределения. Существуют формулы для определения оптимального количества интервалов, но в психологии считается, что следует брать от 5 до 15 интервалов.
Первый способ построения интервального ряда.
Если
у исследователя нет предварительной
информации о характере распределения
признака, то лучше задавать равные
интервалы,
при этом длина
интервала определяется по формуле
,
где- количество выбранных интервалов (числоокругляется до целого значения).
Начало первого интервала равно , а конец(это будет одновременно и началом второго интервала). Условимся все интервалы считать соткрытым правым концом: . Построение интервалов заканчивается, если в интервал попало наибольшее значение признака.
Далее подсчитывают число значений признака, попавших в каждый интервал (с учетом открытого правого конца). Получается таблица, называемаяинтервальным вариационным рядом.
Интервалы
…
Сумма
Частоты,
…
Относительные частоты,
1
Второй
способ построения интервального ряда.
Весь диапазон значений признака от доразбивается на равныеинтервалы, называемые также классами. Затем все варианты совокупности распределяются по этим интервалам. Порядок действий:
Определяется число классов по формуле Стэрджеса .
Затем определяется размах выборки .
Находим ширину интервала по формуле.
Находим нижнюю границу первого интервала: .
Начальные и конечные значения всех последующих интервалов можно вычислить путем последовательного прибавления величины интервала к значениям конца предыдущего интервала: ,и так далее.
Пример построения интервального вариационного ряда.
Пусть измерен некоторый показатель для 30 испытуемых:
23, 29, 35, 7, 11, 18, 23, 30, 36, 18, 11, 8, 13, 20, 25,
27,
14, 30, 20, 20, 24, 19, 21, 26, 22, 16, 26, 25, 33, 27.
Это статистический ряд.
Расставим экспериментальные данные в возрастающем порядке, то есть построим вариационный ряд:
7, 8, 11, 11, 13, 14, 16, 18, 18, 19, 20, 20, 20, 21, 22,
23, 23, 24, 25, 25, 26, 26, 27, 27, 29, 30, 30, 33, 35, 36.
Число классов (интервалов) для :
.
Минимальное и максимальное значения: ,.
Вариационный размах: .
Величина интервала: .
Находим границы интервалов:
;
; ;
; ;
; .
Построим интервальный вариационный ряд.
Номера интервалов
Интервалы
Серединные значения интервалов
Частоты
1
4 – 10
7
2
2
10 – 16
13
4
3
16 – 22
19
8
4
22 – 28
25
10
5
28 – 34
31
4
6
34 – 40
37
2
Вариационные
ряды изображают графически с помощью
полигона и гистограммы.
с1с2с3с4 с5с6с7с8с9
Гистограммой называется графическое изображение интервального вариационного ряда. На оси абсцисс откладываются отрезки, изображающие интервалы значений варьирующего признака, а затем на этих отрезках, как на основаниях, строятся прямоугольники, площади которых пропорциональны частотам (или относительным частотам).
Полигон частот для дискретного вариационного ряда — это ломаная, отрезки которой соединяют точки с координатами .
Полигон частот признака
Построение вариационного ряда
Министерство образования и науки РФ
Государственное образовательное учреждение
Высшего профессионального образования
«Алтайская государственная педагогическая академия»
Институт физико-математического образования
«Построение вариационного ряда»
Реферат
Выполнил: студент
4 курса, 372группы
Сорокин А. Б.
Б.
Барнаул 2010
Оглавление:
Вариационным ряд. 3
Дискретный вариационный ряд. 3
Интервальный вариационный ряд. 3
Частота. 3
Формула Стерджеса. 3
Обобщающие количественные показатели. 3
Средняя арифметическая. 4
Медиана. 4
Мода. 4
Размах вариации. 4
Дисперсия. 5
Стандартное отклонение. 5
Коэффициент
вариации. 5
5
Пример 1. 6
Пример 2. 6
Пример 3. 6
Пример 4. 7
Пример 5. 8
Пример 6. 8
Пример 7. 10
Пример 8. 11
Пример 9. 12
Пример 10. 13
Список используемых источников: 15
Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им частотами или частостями
В зависимости от вида вариации может быть дискретным или интервальным. Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и интервальным, если варианты могут отличаться один от другого на сколь угодно малую величину. Интервалы в ряду могут быть как равными, так и неравными. Это зависит от характера статистических данных и задач исследования.
Определение числа интервалов (m) проводится согласно формуле Стерджеса m=1+3,322
lg n, а величина интервала xmax,xmin-наибольшее
и наименьшее значение признака соответственно.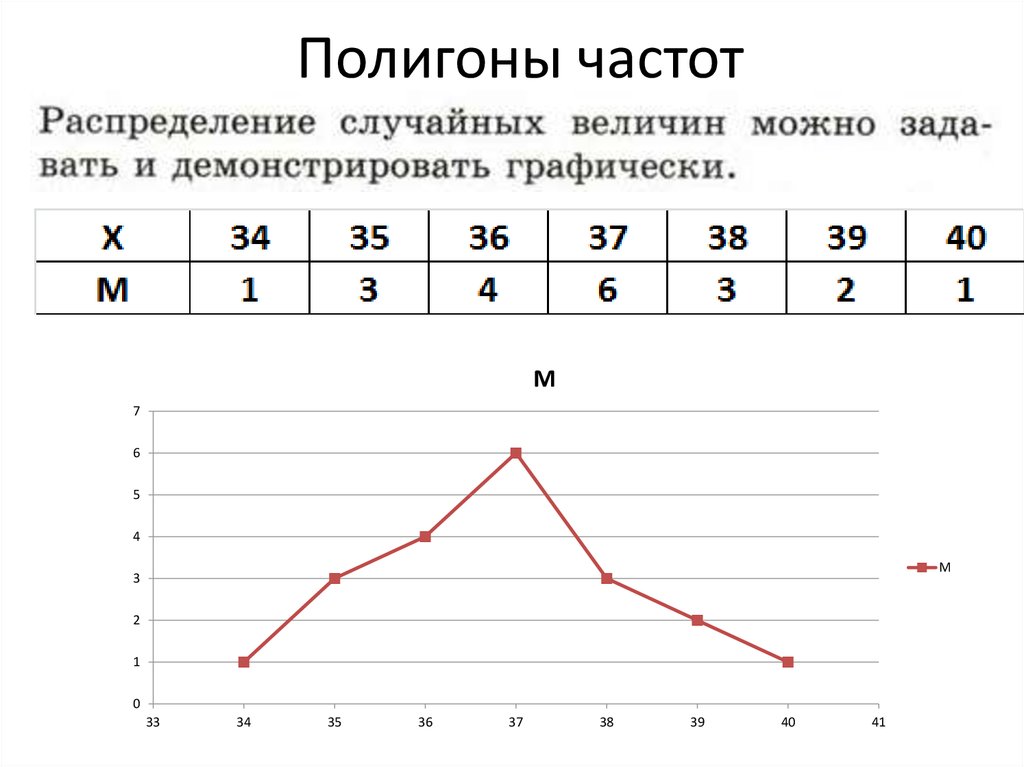
Каждой варианте Xi соответствует частота Ni, т.е. величина, показывающая сколько раз данное значение варианты встречается в ряду. При построении вариационного ряда можно использовать не частоты, а частости Qi, которые вычисляются как отношения соответствующих частот к объему всей совокупности.
Qi = Ni/Сумма (Ni). Частости могут быть выражены в относительных числах (дроби) или в процентах.
Обобщающие количественные показатели (характеристики) в исследовании: вскрывают общие свойства имеющейся совокупности статистических данных; показывают тенденцию развития явления или процесса; нивелируют случайные индивидуальные отклонения изучаемого признака у некоторых объектов; позволяют сравнивать вариационные ряды; используются во всех разделах математической статистики при более сложном и полном анализе данных.
Средняя арифметическая: ,
где — объем совокупности значений в ряду
ni – частота варианты в ряду
xi – варианты с порядковым номером i
k – число вариант в ряду
При расчете средней арифметической в интервальном ряду за
значение варианты принимается середина интервала.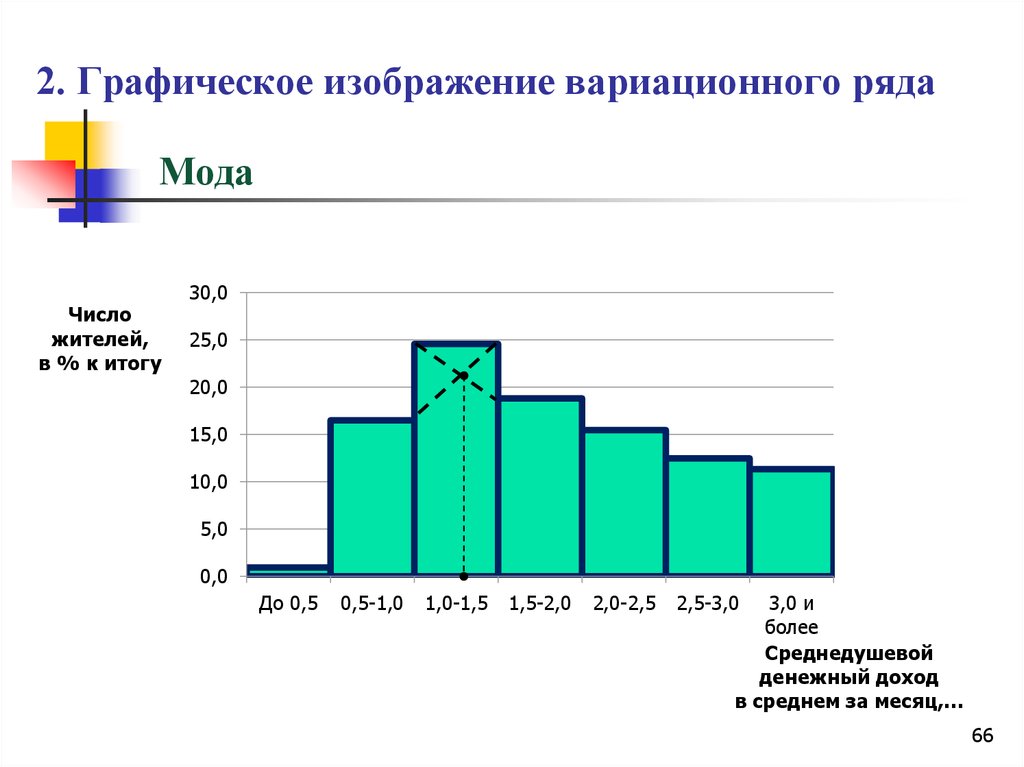 Середина интервала вычисляется как среднее арифметическое его границ.
Середина интервала вычисляется как среднее арифметическое его границ.
Медиана (Ме) Срединное значение варьирующего признака в упорядоченном (ранжированном) ряду. Применяется в случаях, когда совокупность статистических данных неоднородна (асимметрична), поскольку Ме менее чувствительна к средним значениям ряда, чем средняя арифметическая.
Мода (Мо) Наиболее часто встречающаяся в ряду варианта. В интервальном вариационном ряду определяется модальный интервал. Мо используется для характеристики среднего уровня в неоднородных совокупностях, как и медиана.
Размах вариации (R) — разность максимального и минимального значений периода в вариационном ряду.
R=xmax-xmin
Зависит от случайных колебаний выборки, т.е. для вычисления R используются лишь крайние значения варианты.
Дисперсия — представляет собой среднюю
арифметическую квадратов отклонений всех вариант от их средней арифметической.
где
xi – варианты с порядковым номером i
– среднее арифметическое
k – число вариант в ряду
ni – частость ( частота) с порядковым номером i
Стандартное отклонение (среднее квадратическое отклонение) — квадратный корень из дисперсии. Используется исследователями чаще, чем дисперсия, так как вычисляется в тех же единицах измерения, что и варианты.
Коэффициент вариации (V) Относительный показатель рассеяния значений варианты. Достоинства: позволяет сравнивать вариацию одного и того же признака в разных совокупностях; позволяет выявить степень различия одного и того же признака у одной и той же группы объектов в разное время; сопоставить вариацию значений разных признаков у одной и той же группы объектов.
()
Если коэффициент вариации
признака, принимающего только положительные значения, высок ( например, более
100%), то, как правило, это свидетельствует о неоднородности значений признака.
Пример 1: α частицы, достигающие счетчика в некотором опыте, образуют следующую выборку:
|
хi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
mi |
21 |
81 |
156 |
200 |
195 |
152 |
97 |
54 |
26 |
11 |
7 |
Найдите выборочную
среднюю, моду и медиану для числа α — частиц, достигающих
счетчика.
=
Mo=3
Me=5
Пример 2:Измерение веса (в кг.) 100 телят совхоза «Луч» дало следующие результаты:
|
Вес |
154-158 |
158-162 |
162-166 |
166-170 |
170-174 |
174-178 |
178-182 |
|
Число телят |
10 |
14 |
26 |
28 |
12 |
8 |
2 |
Найдите выборочную среднюю и выборочное среднее квадратическое
отклонение веса телят.
Решение. В качестве хi примем середины интервалов и найдем выборочную среднюю веса телят.
=0,01·(156∙10+160∙14+164∙26+168∙28+172·12+176·8+180·2)=166 (кг.)
Вычислим теперь выборочную дисперсию:
S2=0,01·((-10)2·10+(-6)2·14+(-2)2·26+22·28+62·12+102·8+142·2)=33,44
и, извлекая из полученного числа корень квадратный, находим среднее квадратическое отклонение:
S=5,78 (кг.)
Пример 3: Имеются данные о количестве студентов в 30 группах физико-математического факультета:
|
26 |
25 |
25 |
26 |
25 |
23 |
|
23 |
24 |
19 |
23 |
20 |
19 |
|
22 |
24 |
24 |
23 |
20 |
23 |
|
24 |
19 |
21 |
18 |
21 |
18 |
|
20 |
18 |
18 |
21 |
15 |
15 |
Найти вариационный ряд количества студентов в
группах и размах варьирования. Построить полигон частот.
Построить полигон частот.
Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:
|
хi |
15 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
mi |
2 |
4 |
2 |
4 |
3 |
1 |
5 |
4 |
3 |
2 |
Размах варьирования R=xmax-xmin=26-15=11
Для построения полигона частот
обозначим на оси абсцисс возможные значения признака, а на оси ординат
соответствующие частоты mi и полученные точки соединим
отрезками.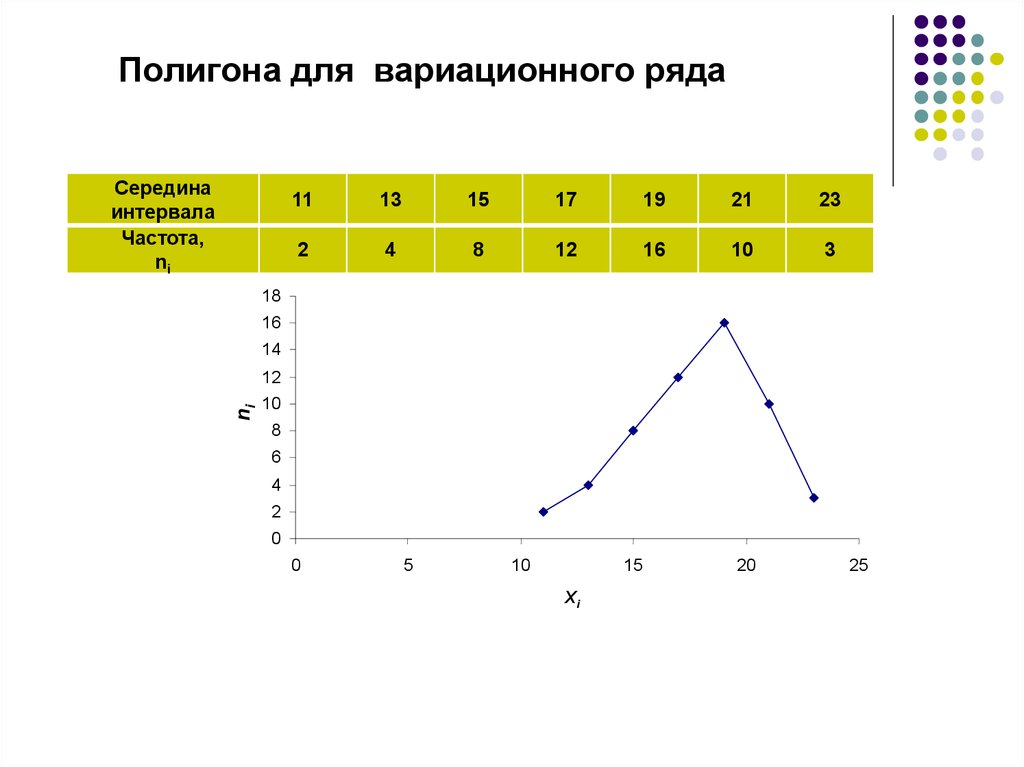
Пример 4: Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающие числа. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
|
Кол-во баллов |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Кол-во школьников |
2 |
3 |
2 |
4 |
12 |
10 |
8 |
9 |
Составить статистическое
распределение количества школьников по количеству набранных баллов и построить
полигон относительных частот.
Решение. Пусть Х={количество набранных баллов}, a f = {относительные частоты}. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
|
X |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
f |
0,04 |
0,06 |
0,04 |
0,08 |
0,24 |
0,2 |
0,16 |
0,18 |
Чтобы построить полигон относительных частот,
отложим на оси абсцисс значения X, а
на оси ординат — относительные частоты f. После этого
последовательно соединим полученные точки отрезками.
После этого
последовательно соединим полученные точки отрезками.
Пример 5: Распределение рабочих цеха по проценту выполнения норм выработки выглядит следующим образом:
|
% выполнения норм |
50 — 70 |
70 — 90 |
90 — 110 |
110 — 130 |
130 — 150 |
150 — 170 |
|
Число рабочих |
20 |
25 |
35 |
30 |
20 |
10 |
Найдите средний процент выполнения норм выработки
рабочими цеха.
Решение.
Пример 6: Над случайной величиной X проведено 100 независимых испытаний, в результате чего получена выборка.
|
1.49 |
1.44 |
1.68 |
1.19 |
3,93 |
2,34 |
7,08 |
1,56 |
0,46 |
1,14 |
|
0,60 |
3,58 |
1,32 |
2. |
4,32 |
0,78 |
1,63 |
2,13 |
2,22 |
3,36 |
|
1.26 |
0,89 |
2,35 |
1,59 |
2,38 |
0,80 |
1,23 |
0,78 |
1,65 |
0,95 |
|
0,34 |
0,64 |
0,26 |
3,05 |
0,68 |
0,96 |
0,69 |
1,77 |
1,02 |
1,07 |
|
0,69 |
2,02 |
3,42 |
4,35 |
2,66 |
1 |
1,85 |
3,25 |
0,93 |
1,44 |
|
1,63 |
3. |
1,16 |
1,44 |
0.45 |
2,41 |
0,87 |
0,81 |
2,85 |
1.94 |
|
1,25 |
1,90 |
0,72 |
2.05 |
2,38 |
1.80 |
2,88 |
2,02 |
1,26 |
1,11 |
|
0,54 |
0,94 |
1,71 . |
1,52 |
1,38 |
1,32 |
1,01 |
0,79 |
1,71 |
0,99 |
|
0.78 |
0,99 |
1,60 |
2.07 |
2,11 |
1.47 |
0.84 |
1,95 |
0,28 |
2,36 |
|
2,01 |
1,51 |
0,95 |
3,17 |
1,08 |
1,09 |
2. |
1,88 |
2,64 |
4,80. |
Требуется составить интервальный вариационный ряд и построить гистограмму относительных частот.
Решение. Количество интервалов разбиения считаем по формуле Стерджесса
m=1+3,322·lg n=1+6,664≈8
Минимальное значение элемента выборки 0,26. Максимальное 7,08. Для удобства разбиения выберем интервал (0; 7,2) с шагом разбиения
|
Интервал |
Абсолютная частота |
Относительная частота |
Середина интервала |
|
(0;0. |
21 |
0.21 |
0.45 |
|
(0.9; 1.8) |
41.5 |
0.415 |
1.35 |
|
(1.8; 2.7) |
23.5 |
0.235 |
2.25 |
|
(2.7; 3.6) |
9 |
0. |
3.15 |
|
(3.6; 4.5) |
3 |
0.03 |
4.05 |
|
(4.5; 5.4) |
1 |
0.01 |
4.95 |
|
(5.4; 6.3) |
0 |
0.00 |
5.85 |
|
(6. |
1 |
0.01 |
6.75 |
Пример 7: Суммарное число набранных баллов в соревнованиях:
|
Кол-во баллов |
49-52 |
52-55 |
55-58 |
58-61 |
61-64 |
64-67 |
67-70 |
|
Кол-во участников |
3 |
6 |
11 |
19 |
30 |
21 |
10 |
Построить гистограмму относительных
частот.
Решение. Пусть Х={количество набранных баллов}, a f = {относительные частоты}. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
|
X |
49-52 |
52-55 |
55-58 |
58-61 |
61-64 |
64-67 |
67-70 |
|
f |
0,03 |
0,06 |
0,11 |
0,19 |
0,3 |
0,21 |
0,1 |
Пример 8: Горизонтальное отклонение от цели (м) для 200 испытаний ракет:
|
Границы интервалов |
-40– -30 |
-30– -20 |
-20– -10 |
-10– 0 |
0 – 10 |
|
Частоты |
7 |
11 |
15 |
24 |
49 |
|
Границы интервалов |
10–20 |
20–30 |
30–40 |
40–50 |
50–60 |
|
Частоты |
41 |
26 |
17 |
7 |
3 |
Найдите выборочную
среднюю и выборочное среднее квадратическое отклонение от цели.
Решение. В качестве хi примем середины интервалов и найдем выборочную среднее отклонение пули.
=8,6
Вычислим теперь выборочную дисперсию:
377,04
и, извлекая из полученного числа корень квадратный, находим среднее квадратическое отклонение:
S=19,42
Пример 9:Дан дискретный ряд распределения 50 рабочих механического цеха по тарифному разряду
|
Тарифный разряд хi |
1 |
2 |
3 |
4 |
5 |
6 |
|
Частота(кол-во рабочих) ni |
2 |
3 |
6 |
8 |
22 |
9 |
Построить полигон распределения по
данным таблицы и найти выборочную
среднюю.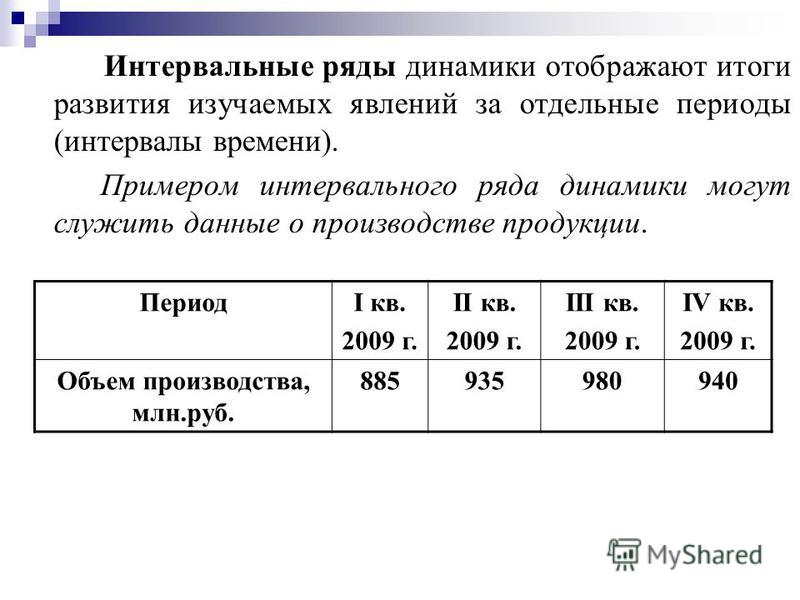
Решение. Пусть Х={количество тарифных разрядов}, a f = {относительные частоты}. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
f |
0,04 |
0,06 |
0,12 |
0,16 |
0,44 |
0,18 |
Чтобы построить полигон относительных частот,
отложим на оси абсцисс значения X, а
на оси ординат — относительные частоты f.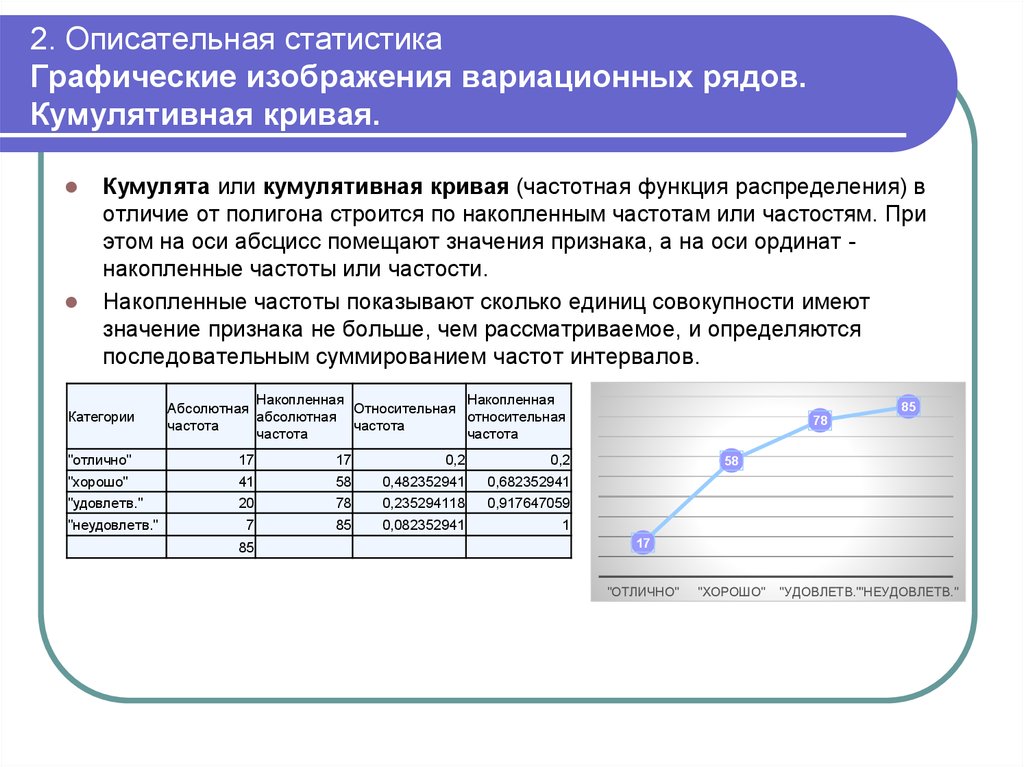 После этого
последовательно соединим полученные точки отрезками.
После этого
последовательно соединим полученные точки отрезками.
Пример 10: X-число сделок на фондовой бирже за квартал; N=400 (инвесторов)
|
xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ni |
146 |
97 |
73 |
34 |
23 |
10 |
6 |
3 |
4 |
2 |
2 |
1) Построить полигон
2) Найти числовые характеристики вариационного ряда
а) Среднюю арифметическую
б) Дисперсию
в) Среднее квадратическое отклонение
г) Коэффициент вариации
Решение. 1)
1)
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
f |
0,365 |
0,2425 |
0,1825 |
0,085 |
0,0575 |
0,025 |
0,015 |
0,0075 |
0,01 |
0,005 |
0,005 |
3) а)
4) б)
в)
г)
1. Борисенко О. В.
Теория вероятностей и математическая статистика: Учебное – методическое
пособие. – Барнаул: Изд-во БГПУ. – 50 с.
Борисенко О. В.
Теория вероятностей и математическая статистика: Учебное – методическое
пособие. – Барнаул: Изд-во БГПУ. – 50 с.
2. Вуколов Э. А. Сборник задач по математике для вузов. В 4 частях. Ч. 4: Учебное пособие для вузов / Под общ. Ред. А. В. Ефимома и А. С. Поспелова. – 3-е изд. Перераб. И доп. – М.: Издательство Физико-математической литературы, 2003. – 432 с.
4.2. Вариационный ряд. Полигон частот и гистограмма эмпирическая функция распределения
Пусть Х — некоторый признак изучаемого объекта или явления (срок службы электролампы, вес студента, диаметр шарика для подшипника и т. п.). Генеральной совокупностью является множество всех возможных значений этого признака, а результаты N наблюдений над признаком Х дадут нам выборку объема N — первоначальные статистические данные, значения (простая выборка, не сгруппированные данные)
При этом значение получено при первом наблюдении случайной величины Х, – при втором наблюдении той же случайной величины и т. д.
д.
Выборку преобразуют в Вариационный ряд, располагая результаты наблюдений в порядке возрастания: Каждый член Вариационного ряда называется Вариантой.
Пример 4.1.
1. Измерена масса тела 10-ти детей 6-ти лет. Полученные данные образуют простой статистический ряд: 24 22 23 28 24 23 25 27 25 25.
2. Из 10000 выпущенных на конвейере электрических лампочек отобрано 300 штук для проверки качества всей партии. Здесь а
Отдельные значения статистического ряда называются Вариантами. Если варианта ХI появилась M раз, то число M называют Частотой, а ее отношение к объему выборки M/N – Относительной частотой.
Последовательность вариант, записанная в возрастающем (убывающем) порядке, называется Ранжированным рядом.
Пример 4.2. Для ранжированного ряда: 23 23 24 24 25 25 25 27 28 в нижеприведенной таблице в первой строке записаны все значения величины (варианты), во второй – соответствующие им частоты (безынтервальный вариационный ряд), в третьей – накопленные частоты, в четвертой – относительные частоты (табл. 4.1).
4.1).
Таблица 4.1. Значения вариант и их частот
|
Х |
22 |
23 |
24 |
25 |
27 |
28 |
|
Ni |
1 |
2 |
2 |
3 |
1 |
1 |
|
NН |
1 |
3 |
5 |
8 |
9 |
10 |
|
|
0.1 |
0.2 |
0.2 |
0.3 |
0.1 |
0. |
Полигоном частот называют ломаную линию, отрезки которой соединяют точки с координатами (ХI; Ni) (рис. 4.1).
Отметим, что сумма частот статистического ряда равна объему выборки. Часто статистический ряд составляют, используя относительные частоты вариант: (M — количество различных вариант). Сумма относительных частот равна единице.
Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки с координатами (ХI; Hi).
|
А) |
Б) |
Рисунок 4.1. Полигон частот а), кумулятивная кривая б)
Эмпирическим аналогом графика интегральной функции распределения является Кумулятивная кривая (Кумулята). Для ее построения на оси ОХ откладывают значения вариант, на оси ОY – накопленные частоты или относительные частоты.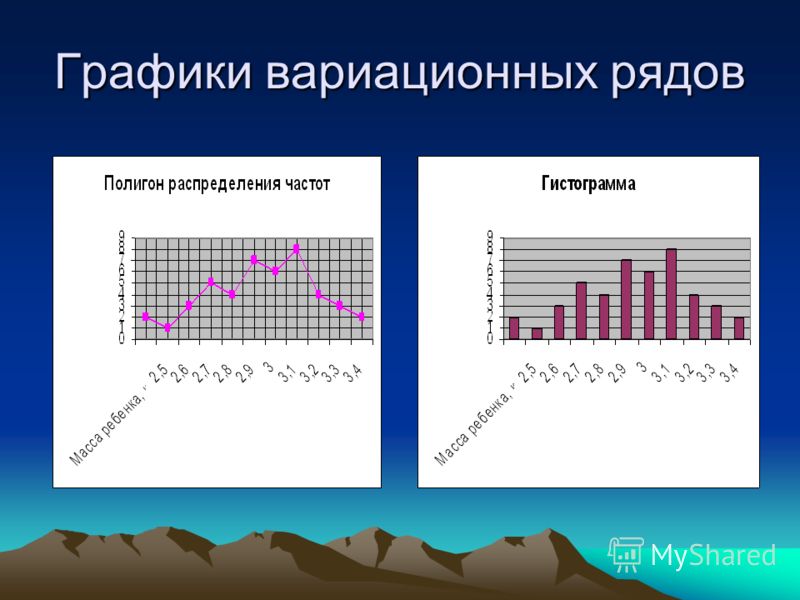 Полученная плавная кривая называется кумулятой.
Полученная плавная кривая называется кумулятой.
В том случае, если выборка представлена большим количеством различных значений непрерывной случайной величины, то группировку данных проводят в виде интервального вариационного ряда (ИВР). Для этого диапазон варьирования признака разбивают на несколько (5–10) равных интервалов и указывают количество вариант, попавших в каждый интервал.
Алгоритм построения интервального вариационного ряда.
1. Исходя из объема выборки (N), определить количество интервалов (K) (см. табл. 4.2).
Таблица 4.2.Рекомендуемое соотношение Объем выборки-число интервалов
|
N |
25–40 |
40–60 |
60–100 |
100–200 |
>200 |
|
K |
5–6 |
6–8 |
7–10 |
8–12 |
10–15 |
2. Вычислить размах ряда: R=Xmax – Xmin
Вычислить размах ряда: R=Xmax – Xmin
3. Определить ширину интервала: H=R/(K–1)
4. Найти начало первого интервала X0 = Xmin – H/2
5. Составить интервальный вариационный ряд.
Графическим изображением ИВР является Гистограмма. Для ее построения на оси ОХ откладывают интервалы шириной H, на каждом интервале строят прямоугольник высотой M/H. Величина M/H называется Плотностью частоты. Гистограмма является эмпирическим аналогом графика дифференциальной функции распределения.
Пример 4.3. Измерена масса тела 100 женщин 30 лет, получены значения от 60 до 90 кг. Построить интервальный вариационный ряд (табл. 4.3) и гистограмму.
Таблица 4.3. Интервальный вариационный ряд
|
Интервал |
Середина интервала |
M |
M/H |
|
60–65 |
62. |
14 |
2.8 |
|
65–70 |
67.5 |
32 |
6.4 |
|
70–75 |
72.5 |
28 |
5.6 |
|
75–80 |
77.5 |
14 |
2.8 |
|
80–85 |
82.5 |
7 |
1.4 |
|
85–90 |
87.5 |
2 |
0.4 |
Рисунок 4.2. Гистограмма
Эмпирическая функция распределения находится по следующей формуле (отношение накопленных частот к объему выборки):
(4.1)
| < Предыдущая | Следующая > |
|---|
|
⇐ ПредыдущаяСтр 2 из 6Следующая ⇒ Если число значений в выборке велико или признак имеет непрерывную природу, то строится интервальный вариационный ряд. Алгоритм построения интервального вариационного ряда 1) Находим размах выборки (диапазон варьирования): 2) Определяем число k интервалов группировки, которое определяется условиями задачи исходя из требований исследователя или (если признак Х ГС имеет нормальное распределение) по формуле Стёрджеса: (4) где n объем выборки. Число интервалов следует брать не очень большим, чтобы после группировки ряд не был громоздким, и не очень маленьким, чтобы не потерять особенности распределения признака. 3) Определяем длину (шаг варьирования) частичного интервала . Если получаемое число – дробное, то в качестве длины интервала рассматривают ближайшее целое число или простую дробь (обыкновенную или десятичную). 4) Строим интервалы Ii=[yi-1;yi], где , или , 5) Находим интервальные частоты, т.е. число вариант в ранжированном ряду, попавших в данный интервал. Число вариант, попавших в i-ый интервал, будем также обозначать . При подсчёте частот в интервал включают варианты, большие или равные нижней границы и меньшие верхней границы интервала. Иногда поступают наоборот: включают варианты, большие нижней границы и меньшие или равные верхней границы интервала.
Интервальное распределение выборки Таблица 4
Интервальные вариационные ряды графически можно представить с помощью гистограммы частот или относительных частот. Гистограммой частот (относительных частот) называют столбчатую диаграмму, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны Из определения следует, что площадь гистограммы относительных частот равна единице, а площадь Si каждого i-го прямоугольника равна wi. Гистограмма относительных частот даёт приближённое представление о виде кривой распределения ГС. По ее форме можно выдвинуть предположение о виде распределения ГС. Соответственно, площадь гистограммы частот равна объему выборки n, а площадь Si каждого i-го прямоугольника равна ni. Для интервального вариационного ряда построение кумуляты начинают с точки, абсцисса которой равна началу первого интервала, а ординату принимают равной нулю. Для дальнейших вычислений интервальный ряд условно заменяют дискретным: в качестве варианты такого ряда берутся серединные значения интервалов разбиения [yi-1;yi], а соответствующую интервальную частоту принимают за частоту этой варианты. Пример 2. Имеются данные о возрастном составе служащих фирмы (лет): 18; 38; 28; 29; 26; 38; 34; 22; 28; 30; 22; 23; 35; 33; 27; 24; 30; 32; 28; 25; 29; 26; 31; 24; 29; 27; 32; 25; 29; 29. Требуется построить интервальный вариационный ряд и изобразить его графически: построить гистограмму частот и частостей и кумулятивную кривую. Р е ш е н и е. Ранжируем ряд — наблюдаемые значения признака расположим в неубывающем порядке: 18; 22; 22; 23; 24; 24; 25; 25; 26; 26; 27; 27; 28; 28; 28; 29; 29; 29; 29; 29; 30; 30 ;31; 32; 32; 33; 34; 35; 38; 38. Объем выборки равен 30. По формуле Стёрджеса находим число интервалов группировки: Размах выборки равен , то для удобства возьмем 7 интервалов с шагом . Строим интервальный вариационный ряд: в первой строке – интервалы, а во второй и третьей интервальные частоты и частости. Кроме того, поместим в таблицу строки накопленных частот и частостей и абсолютной и относительной плотности частоты ( и ).
Таблица 5.
Строим гистограммы частот и относительных частот, используя две последние строки таблицы 5:
Для построения кумуляты, используем строку накопленных частостей (третья снизу).
Самостоятельная работа №2. Задача 2.1. Построить гистограмму частот и относительных частот по заданному распределению выборки. Составить эмпирическую функцию распределения, построить ее график.
Задача 2.2. Из генеральной совокупности извлечена выборка объёма 200, гистограмма относительных частот которой имеет вид. Найти значение параметра а. Построить интервальный ряд распределения данной выборки с указанием частот и относительных частот.
Задача 2.3. Из генеральной совокупности извлечена выборка объёма 150, гистограмма частот которой имеет вид.
⇐ Предыдущая123456Следующая ⇒ |
CV доверительный интервал | Реальная статистика с использованием Excel
Основные понятияКак показано в разделе «Показатели изменчивости», коэффициент вариации определяется как
, где формула слева — версия выборки, а формула справа — версия генеральной совокупности .
Если V является коэффициентом вариации выборки, то это V является смещенной оценкой коэффициента вариации генеральной совокупности. В этом случае несмещенная оценка коэффициента вариации населения дается формулой
, где n = размер выборки. Однако также обычно используется более короткая версия, а именно
Для данной выборки мы хотим оценить доверительный интервал для коэффициента вариации генеральной совокупности на основе выборочной корреляции вариации и размера выборки. Оказывается, существует множество способов создания такой оценки. Мы рассмотрим четыре таких подхода.
Оказывается, существует множество способов создания такой оценки. Мы рассмотрим четыре таких подхода.
В этом подходе используется нецентральное t-распределение.
Сначала мы определим
Достоверное интервал Келли составляет
Наичная оценкаСначала мы определяем
. Доверительный интервал Маккея составляет
. Оценка Маккея верна для больших значений n (по крайней мере, n ≥ 10). Маккей рекомендует эту оценку только тогда, когда коэффициент вариации меньше 0,33. В противном случае приближение Маккея может оказаться неверным.
Оценка ВангеляМодификация Вангелем оценки Маккея дает лучшие результаты для небольших выборок, но все же не рекомендуется для V ≥ 0,33.
Функция рабочего листа Функция реальной статистики : Ресурсный пакет реальной статистики предоставляет следующую функцию рабочего листа.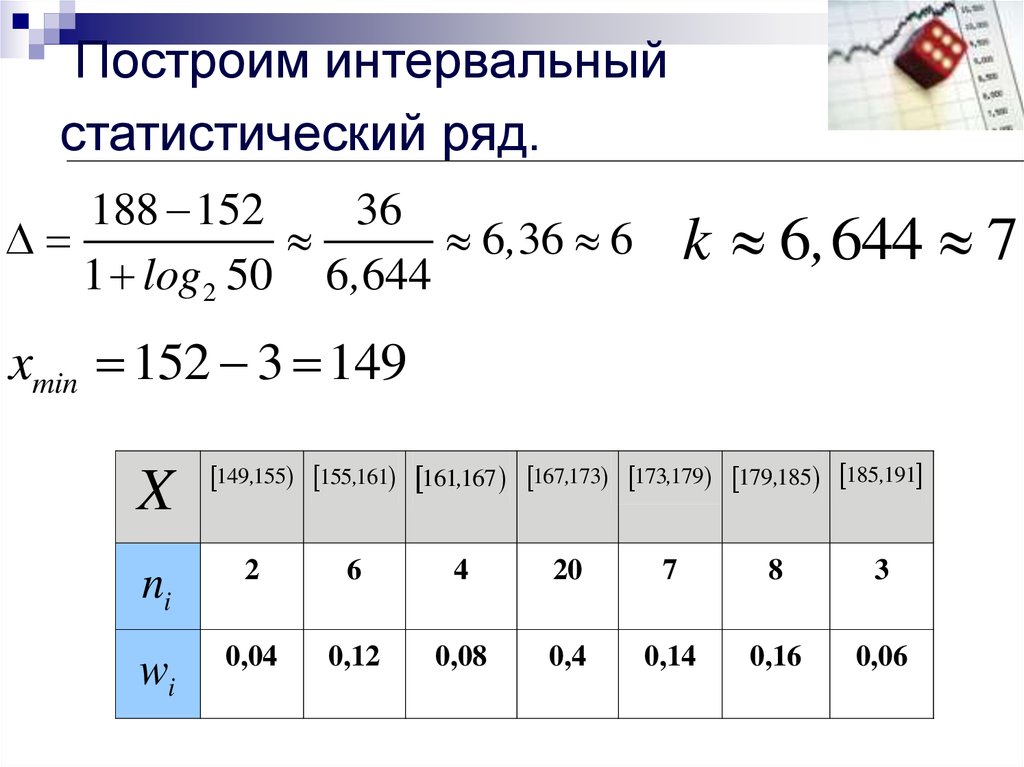
CV_CONF (R1, lab, ctype, short, tails, alpha ): возвращает массив столбцов 4 × 1 со значениями: CV данных в R1, исправленная версия CV и 1- alpha (по умолчанию для alpha .05) доверительный интервал для CV.
Если lab = TRUE (по умолчанию FALSE), к выходным данным добавляется столбец меток. Если short = TRUE (по умолчанию), то краткая версия исправленного CV; в противном случае сообщается длинная версия.
Какой доверительный интервал сообщается, зависит от выбора ctype со значениями 1 (Келли, по умолчанию), 2 (Наивный), 3 (Маккей) или 4 (Вангел). Это интервалы вокруг выборки В . Вы также можете использовать отрицательные значения этих значений, и в этом случае интервалы будут соответствовать исправленной версии V (короткие или длинные, в зависимости от значения short ).
Если хвостов = 2 (по умолчанию), возвращается двусторонний доверительный интервал ( нижний, верхний ). 2)).
2)).
Используя функцию CV_CONF, мы получаем оценки доверительного интервала, показанные на рисунке 2.
диапазон L7:M10 содержит формулу массива =CV_CONF(A4:A9,TRUE), которая является сокращением от =CV_CONF(A4:A9,TRUE,1,TRUE, 2,.05). Если бы мы хотели использовать доверительный интервал вокруг длинной версии скорректированного V , мы использовали бы формулу =CV_CONF(A4:A9,TRUE,-1,FALSE).
Если мы вычислим доверительный интервал вручную, используя оценку Келли, мы вставим формулу =SQRT(D4)/NT_NCP(I4/2,D4-1,I7) в ячейку M92+I6/(D4-1)) в ячейке P10. Мы также можем использовать формулу массива реальной статистики =CV_CONF(A4:A9,4) в диапазоне P7:P10.
Ссылки График данных NIST (2017) Доверительный интервал коэффициента вариации
https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/coefvari.htm777 7 Sokal , R.R. и Braumann, C.A. (1980) Тесты значимости для коэффициентов вариации и профилей изменчивости
https://academic.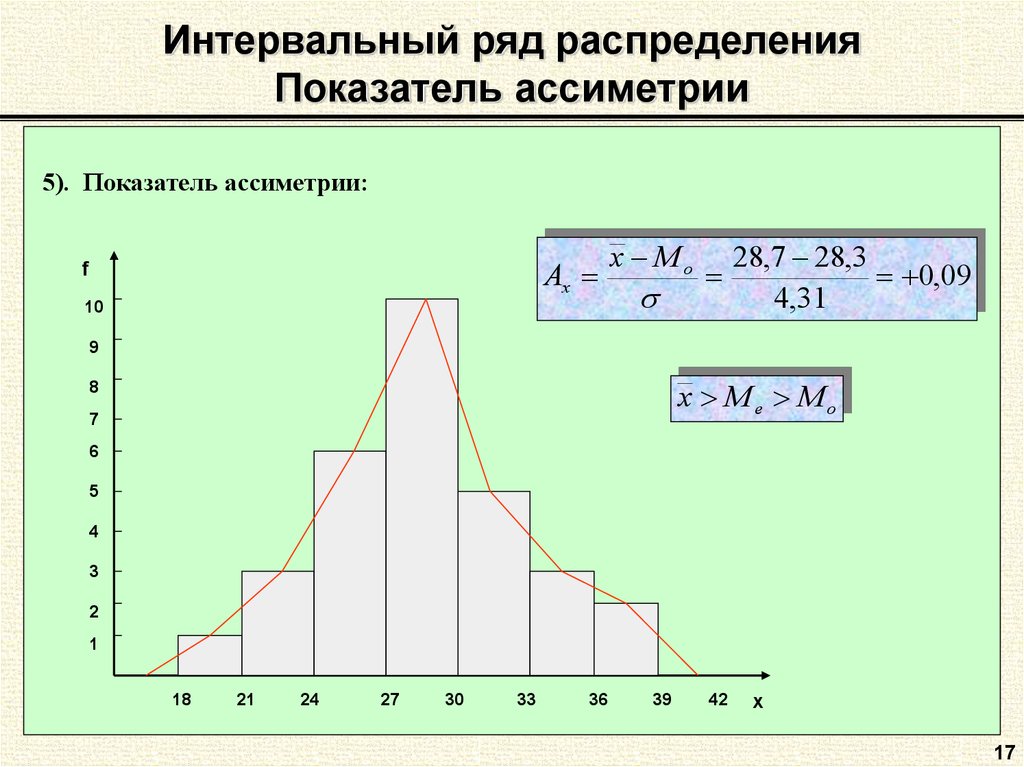 oup.com/sysbio/article-pdf/29/1/50/4659819/29-1-50.pdf
oup.com/sysbio/article-pdf/29/1/50/4659819/29-1-50.pdf
Beigy, M. (2019) Коэффициент вариации
https://cran.r-project.org/web/packages/cvcqv/vignettes/cv_versatile .html
McKay, AT (1932) Распределения коэффициента вариации и расширенное t-распределение. Журнал Королевского статистического общества, Vol. 95, стр. 695-698.
https://www.jstor.org/stable/2342041
Вангель, М. (1996) Доверительные интервалы для нормального коэффициента вариации . Американский статистик, Vol. 15, № 1, стр. 21-26.
https://www.jstor.org/stable/2685039
Расчет диапазона, IQR, дисперсии, стандартного отклонения
Изменчивость описывает, насколько далеко точки данных расположены друг от друга и от центра распределения. Наряду с мерами центральной тенденции меры изменчивости дают вам описательную статистику, которая обобщает ваши данные.
Изменчивость также называется разбросом, разбросом или дисперсией. Чаще всего измеряется следующим образом:
Чаще всего измеряется следующим образом:
- Диапазон: разница между самым высоким и самым низким значением
- Межквартильный диапазон: диапазон средней половины распределения
- Стандартное отклонение: среднее расстояние от среднего
- Дисперсия: среднее квадратов расстояний от среднего
Содержание
- Почему важна изменчивость?
- Диапазон
- Межквартильный диапазон
- Стандартное отклонение
- Дисперсия
- Что является наилучшей мерой изменчивости?
- Часто задаваемые вопросы об изменчивости
Почему важна изменчивость?
В то время как центральная тенденция, или среднее, говорит вам, где находится большинство ваших точек, изменчивость суммирует, насколько далеко они друг от друга. Это важно, потому что степень изменчивости определяет, насколько хорошо вы можете обобщить результаты выборки на вашу совокупность.
Низкая изменчивость идеальна, потому что это означает, что вы можете лучше прогнозировать информацию о генеральной совокупности на основе выборочных данных. Высокая изменчивость означает, что значения менее постоянны, поэтому делать прогнозы сложнее.
Наборы данных могут иметь одну и ту же центральную тенденцию, но разные уровни изменчивости или наоборот. Если вы знаете только центральную тенденцию или изменчивость, вы ничего не можете сказать о другом аспекте. Оба они вместе дают вам полную картину ваших данных.
Пример: изменчивость в нормальном распределении. Вы исследуете количество времени, ежедневно проводимого разными группами людей за телефоном.Используя простые случайные выборки, вы собираете данные из 3 групп:
- Образец A: старшеклассники,
- Образец B: студенты колледжа,
- Образец C: взрослые штатные сотрудники.
Все три ваших образца имеют одинаковое среднее время использования телефона: 195 минут или 3 часа 15 минут. Это значение по оси x, где находятся пики кривых.
Это значение по оси x, где находятся пики кривых.
Хотя данные имеют нормальное распределение, каждая выборка имеет различный разброс. Образец А имеет наибольшую изменчивость, тогда как образец С имеет наименьшую изменчивость.
Диапазон
Диапазон показывает разброс ваших данных от самого низкого до самого высокого значения в распределении. Это самая простая мера изменчивости для расчета.
Чтобы найти диапазон, просто вычтите наименьшее значение из наибольшего значения в наборе данных.
Пример диапазона У вас есть 8 точек данных из образца A.| Данные (минуты) | 72 | 110 | 134 | 190 | 238 | 287 | 305 | 324 |
|---|
Наибольшее значение ( H ) равно 324 , а наименьшее ( L ) равно 72 .
П = В – Д
Ч = 324 – 72 = 252
Диапазон ваших данных: 252 минуты .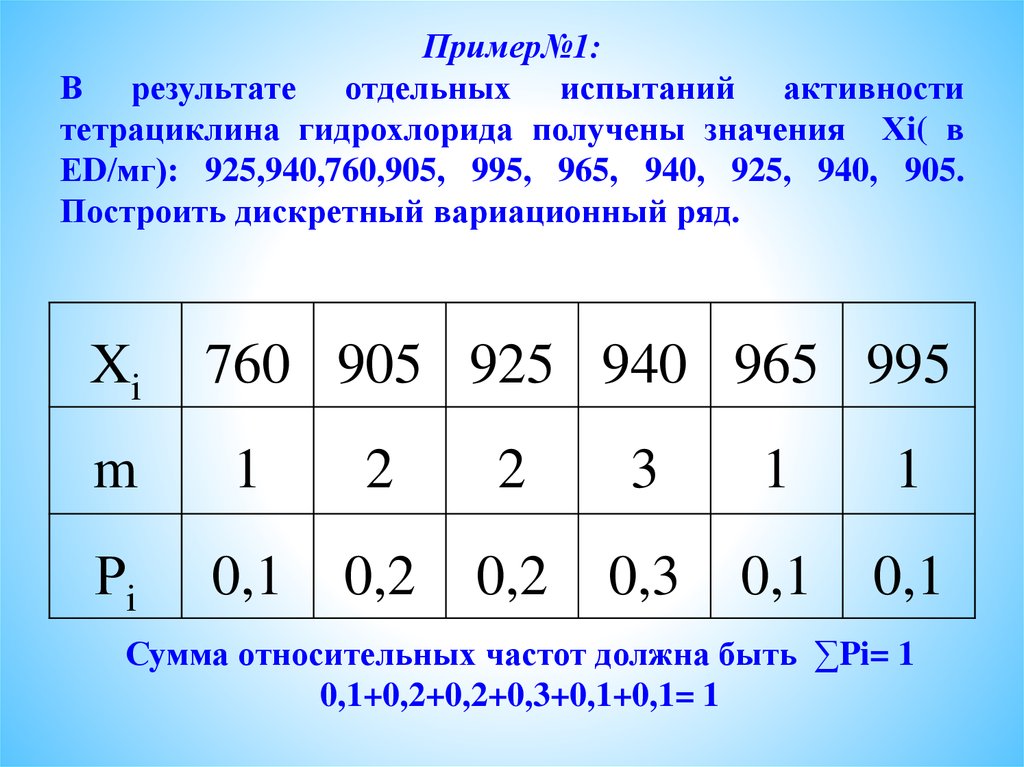
Поскольку используются только 2 числа, диапазон зависит от выбросов и не дает никакой информации о распределении значений. Лучше всего использовать его в сочетании с другими мерами.
Получение отзывов о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
- Академический стиль
- Расплывчатые предложения
- Грамматика
- Согласованность стиля
См. пример
Межквартильный диапазон
Межквартильный диапазон дает вам разброс середины вашего распределения.
Для любого распределения, упорядоченного от низкого к высокому, межквартильный диапазон содержит половину значений. В то время как первый квартиль (Q1) содержит первые 25% значений, четвертый квартиль (Q4) содержит последние 25% значений.
Межквартильный диапазон равен третьему квартилю (Q3) минус первый квартиль (Q1). Это дает нам диапазон средней половины набора данных.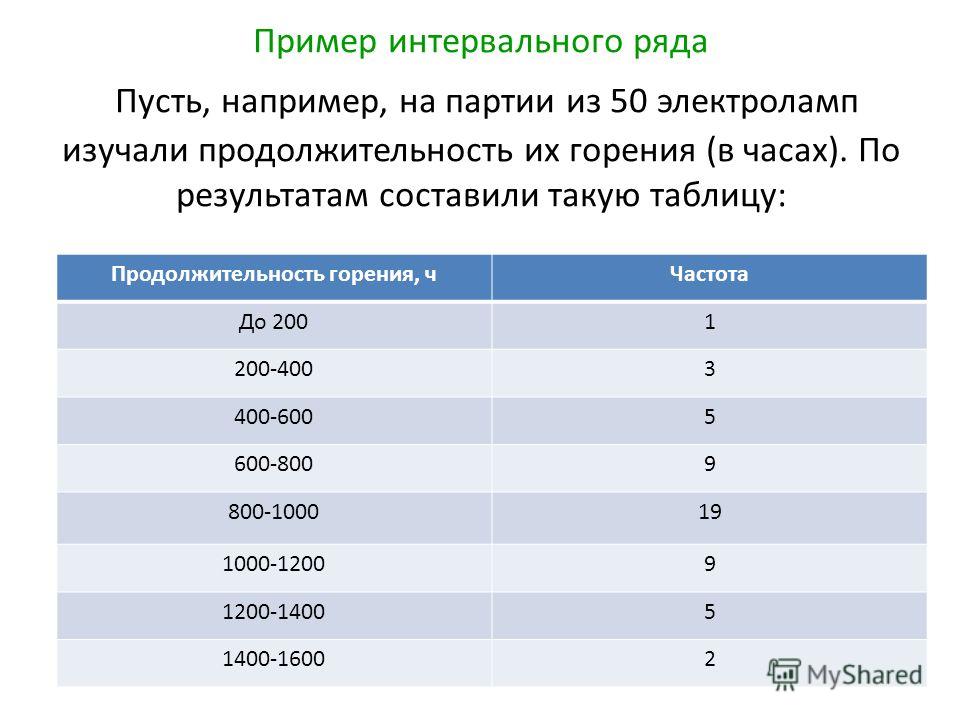
Умножьте количество значений в наборе данных (8) на 0,25 для 25-го процентиля (Q1) и на 0,75 для 75-го процентиля (Q3).
Позиция Q1: 0,25 x 8 = 2
Позиция Q3: 0,75 x 8 = 6
Q1 — это значение во 2-й позиции, равное 110 . Q3 — это значение на 6-й позиции, равное 287 .
IQR = Q3 – Q1
IQR = 287 – 110 = 177
Межквартильный диапазон ваших данных составляет 177 минут .
Как и диапазон, межквартильный диапазон использует при расчете только 2 значения. Но выбросы меньше влияют на IQR: два значения взяты из средней половины набора данных, поэтому вряд ли они будут крайними значениями.
IQR дает последовательную меру изменчивости как для асимметричных, так и для нормальных распределений.
Итог из пяти чисел
Каждое распределение может быть организовано с использованием сводки из пяти чисел : :
- Наименьшее значение
- Q1: 25-й процентиль
- Q2: медиана
- Q3: 75-й процентиль
- Максимальное значение (Q4)
Эти сводки из пяти чисел можно легко визуализировать с помощью диаграмм с ячейками и усами.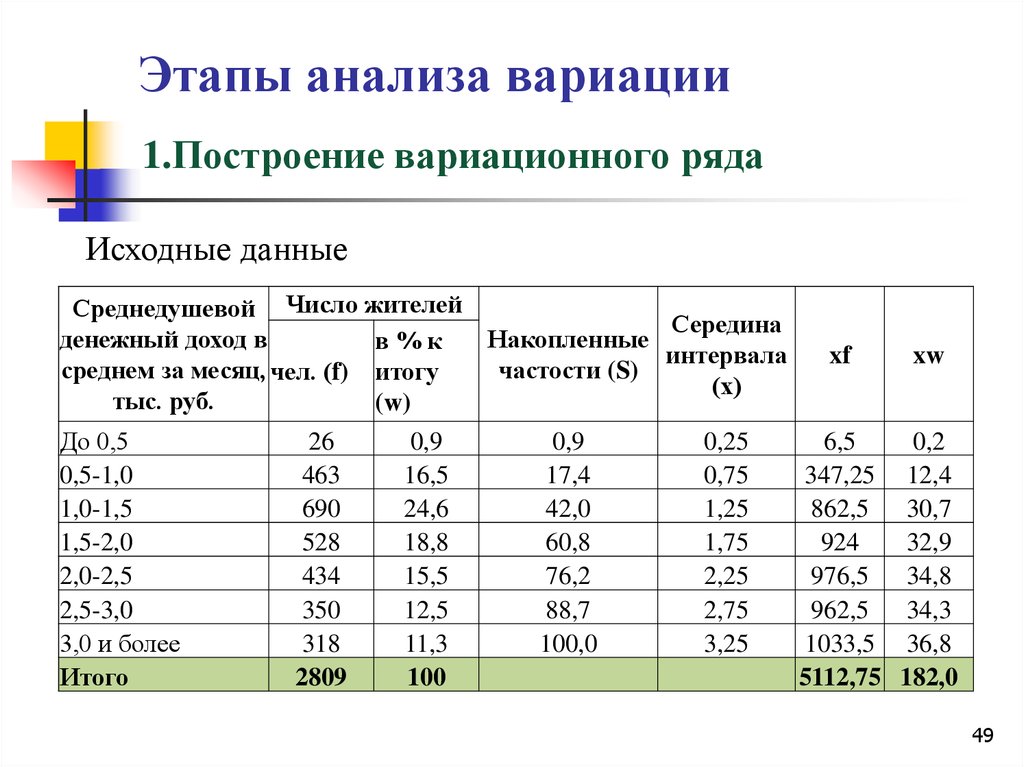
Стандартное отклонение
Стандартное отклонение — это средняя величина изменчивости в вашем наборе данных.
Сообщает вам, в среднем, насколько каждый результат отличается от среднего. Чем больше стандартное отклонение, тем более изменчив набор данных.
Существует шесть шагов для нахождения стандартного отклонения вручную:
- Перечислите все баллы и найдите их среднее значение.
- Вычтите среднее из каждой оценки, чтобы получить отклонение от среднего.
- Возведите в квадрат каждое из этих отклонений.
- Сложите все квадраты отклонений.
- Разделить сумму квадратов отклонений на n – 1 (для выборки) или N (для генеральной совокупности).
- Найдите квадратный корень из найденного числа.

Пример стандартного отклонения
| Шаг 1: Данные (минуты) | Шаг 2: отклонение от среднего | Шаги 3 + 4: Квадрат отклонения |
|---|---|---|
| 72 | 72 – 207,5 = -135,5 | 18360.25 |
| 110 | 110 – 207,5 = -97,5 | 9506.25 |
| 134 | 134 – 207,5 = -73,5 | 5402.25 |
| 190 | 190 – 207,5 = -17,5 | 306,25 |
| 238 | 238 – 207,5 = 30,5 | 930,25 |
| 287 | 287 – 207,5 = 79,5 | 6320.25 |
| 305 | 305 – 207,5 = 97,5 | 9506.25 |
| 324 | 324 – 207,5 = 116,5 | 13572.25 |
| Среднее = 207,5 | Сумма = 0 | Сумма квадратов = 63904 |

п – 1 = 7
63904 / 7 = 9129,14
Пример стандартного отклоненияс = √9129,14 = 95,54
Стандартное отклонение ваших данных составляет 95,54 . Это означает, что в среднем каждая оценка отклоняется от среднего значения на 95,54 балла.
Формула стандартного отклонения для совокупностей
Если у вас есть данные по всей совокупности, используйте формулу стандартного отклонения совокупности:
| Формула | Объяснение |
|---|---|
|
Формула стандартного отклонения для проб
Если у вас есть данные из выборки, используйте формулу стандартного отклонения выборки:
| Формула | Объяснение |
|---|---|
|
Зачем использовать
n – 1 для стандартного отклонения выборки? Выборки используются для статистических выводов о населении, из которого они получены.
Когда у вас есть данные о населении, вы можете получить точное значение стандартного отклонения населенности. Поскольку вы собираете данные от каждого члена совокупности, стандартное отклонение отражает точную величину изменчивости в вашем распределении, совокупности.
Но когда вы используете данные выборки, стандартное отклонение вашей выборки всегда используется в качестве оценки стандартного отклонения генеральной совокупности. Использование n в этой формуле может дать вам необъективную оценку, которая последовательно занижает изменчивость.
При уменьшении выборки n до n – 1 стандартное отклонение искусственно увеличивается, что дает вам консервативную оценку изменчивости.
Хотя это и не беспристрастная оценка, это менее предвзятая оценка стандартного отклонения: лучше переоценить, чем недооценить изменчивость в выборках.
Разница между предвзятыми и консервативными оценками стандартного отклонения становится намного меньше, когда у вас большой размер выборки.
Дисперсия
Дисперсия — это среднее квадратов отклонений от среднего значения. Отклонение от среднего — это то, насколько далеко результат находится от среднего.
Дисперсия — это квадрат стандартного отклонения. Это означает, что единицы дисперсии намного больше, чем единицы типичного значения набора данных.
Хотя интуитивно интерпретировать число дисперсии сложнее, важно рассчитать дисперсию для сравнения различных наборов данных в статистических тестах, таких как ANOVA.
Дисперсия отражает степень разброса в наборе данных. Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению.
Пример дисперсии Чтобы получить дисперсию, возведите стандартное отклонение в квадрат.с = 95,5
с 2 = 95,5 х 95,5 = 9129,14
Дисперсия ваших данных составляет 9129,14.
Чтобы найти дисперсию вручную, выполните все шаги для стандартного отклонения, кроме последнего шага.
Формула дисперсии для совокупностей
| Формула | Объяснение |
|---|---|
|
Формула дисперсии для проб
| Формула | Объяснение |
|---|---|
|
Смещенные и несмещенные оценки дисперсии
Беспристрастная оценка в статистике — это оценка, которая не всегда дает вам ни высокие, ни низкие значения — она не имеет систематической погрешности.
Как и для стандартного отклонения, существуют разные формулы для генеральной совокупности и выборочной дисперсии. Но хотя не существует объективной оценки стандартного отклонения, она есть для выборочной дисперсии.
Но хотя не существует объективной оценки стандартного отклонения, она есть для выборочной дисперсии.
Если бы формула выборочной дисперсии использовала выборку n , выборочная дисперсия была бы смещена в сторону меньших чисел, чем ожидалось. Уменьшение выборки n до n – 1 искусственно увеличивает дисперсию.
В этом случае смещение не только снижается, но и полностью устраняется. Формула выборочной дисперсии дает полностью объективные оценки дисперсии.
Так почему же стандартное отклонение выборки не является также объективной оценкой?
Это потому, что стандартное отклонение выборки получается из нахождения квадратного корня выборочной дисперсии. Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.
Что является лучшей мерой изменчивости?
Лучшая мера изменчивости зависит от вашего уровня измерения и распределения.
Уровень измерения
Для данных, измеренных на порядковом уровне, диапазон и межквартильный диапазон являются единственными подходящими показателями изменчивости.
Для более сложных уровней интервалов и отношений также применимы стандартное отклонение и дисперсия.
Распределение
Для нормальных распределений можно использовать все меры. Стандартное отклонение и дисперсия предпочтительнее, потому что они учитывают весь ваш набор данных, но это также означает, что на них легко влияют выбросы.
Для асимметричных распределений или наборов данных с выбросами наилучшим показателем является межквартильный диапазон. На него меньше всего влияют экстремальные значения, поскольку он фокусируется на разбросе в середине набора данных.
Часто задаваемые вопросы об изменчивости
- Что такое изменчивость? org/Answer»>
Изменчивость говорит вам, как далеко точки находятся друг от друга и от центра распределения или набора данных.
Изменчивость также называется распространением, разбросом или дисперсией.
Интервальный вариационный ряд и его характеристики являются примерами. Библиотека сообщений МЕДСТАТИСТИКА об анализе медицинских данных
вариативных называемых рядами распределения, построенными на количественной основе. Значения количественных признаков у отдельных единиц совокупности непостоянны, более или менее отличаются друг от друга.
Вариация — колебание, изменчивость значения признака в единицах совокупности. Отдельные числовые значения признака, встречающиеся в изучаемой популяции, называются вариантами значений. Недостаточность среднего значения для полной характеристики совокупности заставляет дополнять средние значения показателями, позволяющими оценить типичность этих средних путем измерения флуктуации (изменчивости) изучаемого признака.
Наличие изменчивости обусловлено влиянием большого количества факторов на формирование уровня признака. Эти факторы действуют с неодинаковой силой и в разных направлениях. Индикаторы вариации используются для описания меры изменчивости признаков.
Задачи статистического изучения вариации:
- 1) изучение характера и степени вариации признаков у отдельных единиц совокупности;
- 2) определение роли отдельных факторов или их групп в изменчивости тех или иных признаков совокупности.
В статистике используются специальные методы исследования вариации, основанные на использовании оценочной карты, С , с помощью которой измеряется вариация.
Изучение вариаций имеет важное значение. Измерение вариаций необходимо при проведении выборочного наблюдения, корреляционного и дисперсионного анализа и т. д. Ермолаев О.Ю. Математическая статистика для психологов: Учебник [Текст] / О.Ю. Ермолаев. — М.: Флинт, издательство Московского психолого-социального института, 2012. — 335с.
— 335с.
По степени изменчивости можно судить об однородности совокупности, стабильности отдельных значений признаков и типичности среднего. На их основе разрабатываются показатели тесноты связи между признаками, показатели оценки точности выборочного наблюдения.
Существует изменение в пространстве и изменение во времени.
Под изменчивостью в пространстве понимают колебание значений признака в единицах совокупности, представляющих отдельные территории. Под вариацией во времени понимается изменение значений признака в разные периоды времени.
Для изучения вариации в ряду распределения все варианты значений атрибута располагаются в порядке возрастания или убывания. Этот процесс называется ранжированием серий.
Простейшими признаками изменчивости являются минимум и максимум — наименьшее и наибольшее значение признака в совокупности. Количество повторений отдельных вариантов значений признака называется частотой повторения (fi). Удобно заменить частоты на частоты — wi. Частота — относительный показатель частоты, который может быть выражен в долях единицы или процентах и позволяет сравнивать вариационные ряды при различном количестве наблюдений. Выражается формулой:
Частота — относительный показатель частоты, который может быть выражен в долях единицы или процентах и позволяет сравнивать вариационные ряды при различном количестве наблюдений. Выражается формулой:
где Xmax, Xmin — максимальное и минимальное значения признака в совокупности; n — количество групп.
Для измерения изменчивости признака используются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия, стандартное отклонение. К относительным показателям флуктуации относятся коэффициент колебательности, относительное линейное отклонение, коэффициент вариации.
Пример нахождения вариационного ряда
Упражнение. Для этого образца:
- а) Найдите вариационный ряд;
- б) Построить функцию распределения;
№=42. Примеры позиций:
1 5 1 8 1 3 9 4 7 3 7 8 7 3 2 3 5 3 8 3 5 2 8 3 7 9 5 8 8 1 2 2 5 1 6 1 7 6 7 7 6 2
Решение.
- а) построение ранжированного вариационного ряда:
- 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 4 5 5 5 5 5 6 6 6 7 7 7 7 7 7 7 8 8 8 8 8 8 99
- б) построение дискретного вариационного ряда.
Рассчитаем количество групп в вариационном ряду по формуле Стерджесса:
Примем количество групп равным 7.
Зная количество групп, вычислим значение интервала:
Для удобства построения таблицы количество групп возьмем равным 8, интервал будет равен 1.
Рис. 1 Объем реализации товаров магазином за определенный период времени
В результате освоения данной главы студент должен: знать
- показатели вариации и их взаимосвязь;
- основных закона распределения признаков;
- сущность критериев согласия; уметь
- рассчитать коэффициенты вариации и точность соответствия;
- определить характеристики дистрибутивов;
- оценивают основные числовые характеристики рядов статистического распределения;
собственные
- методы статистического анализа ранги распределения;
- основы дисперсионного анализа;
- методы проверки рядов статистического распределения на соответствие основным законам распределения.

При статистическом изучении признаков различных статистических совокупностей большой интерес представляет изучение вариации признака отдельных статистических единиц совокупности, а также характера распределения единиц по этому признаку. Вариация — это различия индивидуальных значений признака между единицами изучаемой совокупности. Изучение вариации имеет большое практическое значение. По степени варьирования можно судить о границах варьирования признака, об однородности совокупности по этому признаку, о типичности среднего, о соотношении факторов, определяющих варьирование. Индикаторы вариации используются для характеристики и упорядочения статистической совокупности.
Результаты обобщения и группировки материалов статистического наблюдения, оформленные в виде статистических рядов распределения, представляют собой упорядоченное распределение единиц изучаемой совокупности на группы по группирующему (переменном) признаку. Если за основу группировки берется качественный признак, то такой ряд распределения называется атрибутивным (распределение по профессиям, полу, цвету кожи и т. д.). Если ряд распределения построен на количественной основе, то такой ряд называется вариационный (распределение по росту, весу, заработной плате и др.). Построить вариационный ряд — значит упорядочить количественное распределение единиц совокупности по значениям признака, подсчитать количество единиц совокупности с этими значениями (частотность), оформить результаты в виде таблицы.
д.). Если ряд распределения построен на количественной основе, то такой ряд называется вариационный (распределение по росту, весу, заработной плате и др.). Построить вариационный ряд — значит упорядочить количественное распределение единиц совокупности по значениям признака, подсчитать количество единиц совокупности с этими значениями (частотность), оформить результаты в виде таблицы.
Вместо частоты варианта можно использовать его отношение к общему объему наблюдений, которое называется частотой (относительной частотой).
Существует два типа вариационного ряда: дискретный и интервальный. Дискретная серия — это такой вариационный ряд, построение которого основано на признаках с прерывистым изменением (дискретных признаках). К последним относятся численность занятых на предприятии, разряд заработной платы, количество детей в семье и т. д. Дискретный вариационный ряд представляет собой таблицу, состоящую из двух столбцов. В первом столбце указано конкретное значение атрибута, а во втором — количество единиц совокупности с конкретным значением атрибута. Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных средств предприятия и т. д., которые в определенных пределах могут принимать любые значения), то для этого признака можно построить серия интервальных вариаций. Таблица при построении интервального вариационного ряда также имеет два столбца. В первом указывается значение признака в интервале «от – до» (варианты), во втором – количество единиц, входящих в интервал (частота). Частота (частота повторения) — количество повторений того или иного варианта значения атрибута. Интервалы могут быть закрытыми и открытыми. Замкнутые промежутки ограничены с обеих сторон, т.е. имеют границу как нижнюю («от»), так и верхнюю («до»). Открытые интервалы имеют какую-то одну границу: либо верхнюю, либо нижнюю. Если варианты расположены в порядке возрастания или убывания, то строки называются рейтинг.
Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных средств предприятия и т. д., которые в определенных пределах могут принимать любые значения), то для этого признака можно построить серия интервальных вариаций. Таблица при построении интервального вариационного ряда также имеет два столбца. В первом указывается значение признака в интервале «от – до» (варианты), во втором – количество единиц, входящих в интервал (частота). Частота (частота повторения) — количество повторений того или иного варианта значения атрибута. Интервалы могут быть закрытыми и открытыми. Замкнутые промежутки ограничены с обеих сторон, т.е. имеют границу как нижнюю («от»), так и верхнюю («до»). Открытые интервалы имеют какую-то одну границу: либо верхнюю, либо нижнюю. Если варианты расположены в порядке возрастания или убывания, то строки называются рейтинг.
Для вариационных серий существует два типа вариантов частотной характеристики: кумулятивная частота и кумулятивная частота.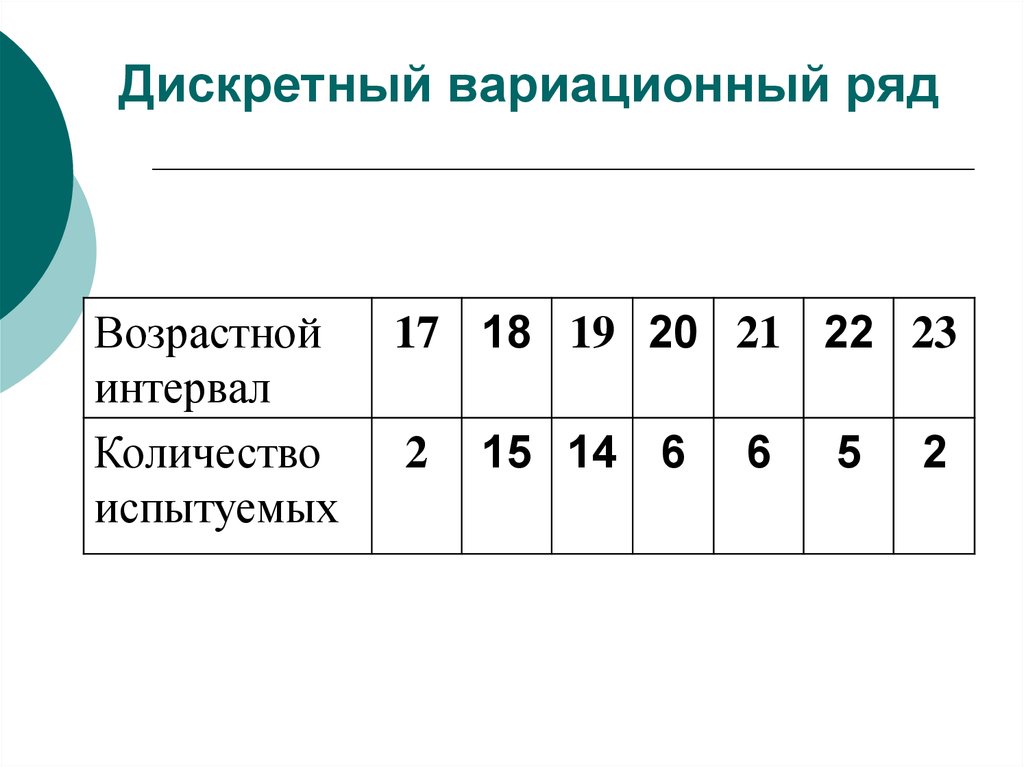 Кумулятивная частота показывает, сколько наблюдений значение признака приняло за значения меньше указанного значения. Суммарная частота определяется суммированием значений характеристической частоты для данной группы со всеми частотами предыдущих групп. Накопленная частота характеризует долю единиц наблюдения, в которых значения признака не превышают верхнюю границу дневной группы. Таким образом, накопленная частота показывает удельный вес варианта в совокупности, имеющего значение не выше заданного. Частота, частота, абсолютная и относительная плотность, кумулятивная частота и частота являются характеристиками величины варианта.
Кумулятивная частота показывает, сколько наблюдений значение признака приняло за значения меньше указанного значения. Суммарная частота определяется суммированием значений характеристической частоты для данной группы со всеми частотами предыдущих групп. Накопленная частота характеризует долю единиц наблюдения, в которых значения признака не превышают верхнюю границу дневной группы. Таким образом, накопленная частота показывает удельный вес варианта в совокупности, имеющего значение не выше заданного. Частота, частота, абсолютная и относительная плотность, кумулятивная частота и частота являются характеристиками величины варианта.
Вариации знака статистических единиц совокупности, а также характер распределения изучают с помощью показателей и характеристик вариационного ряда, к которым относятся средний уровень ряда, среднее линейное отклонение, стандартное отклонение , дисперсия, коэффициенты колебаний, вариация, асимметрия, эксцесс и др.
Средние значения используются для характеристики центра распределения. Среднее является обобщающей статистической характеристикой, в которой получает количественное выражение типичный уровень признака, которым обладают представители изучаемой совокупности. Однако возможны случаи, когда средние арифметические совпадают при различном характере распределения, поэтому в качестве вариационных рядов статистических характеристик рассчитываются так называемые структурные средние — мода, медиана, а также квантили, которые делят ряды распределения. на равные части (квартили, децили, процентили и т. д.).
Среднее является обобщающей статистической характеристикой, в которой получает количественное выражение типичный уровень признака, которым обладают представители изучаемой совокупности. Однако возможны случаи, когда средние арифметические совпадают при различном характере распределения, поэтому в качестве вариационных рядов статистических характеристик рассчитываются так называемые структурные средние — мода, медиана, а также квантили, которые делят ряды распределения. на равные части (квартили, децили, процентили и т. д.).
Мода — это значение признака, который чаще встречается в ряду распределения, чем другие его значения. Для дискретных серий это вариант с наибольшей частотой. В интервальных вариационных рядах для определения моды необходимо прежде всего определить интервал, в котором она находится, так называемый модальный интервал. В вариационном ряду с равными интервалами модальный интервал определяется наибольшей частотой, в рядах с неравными интервалами — но наибольшей плотностью распределения.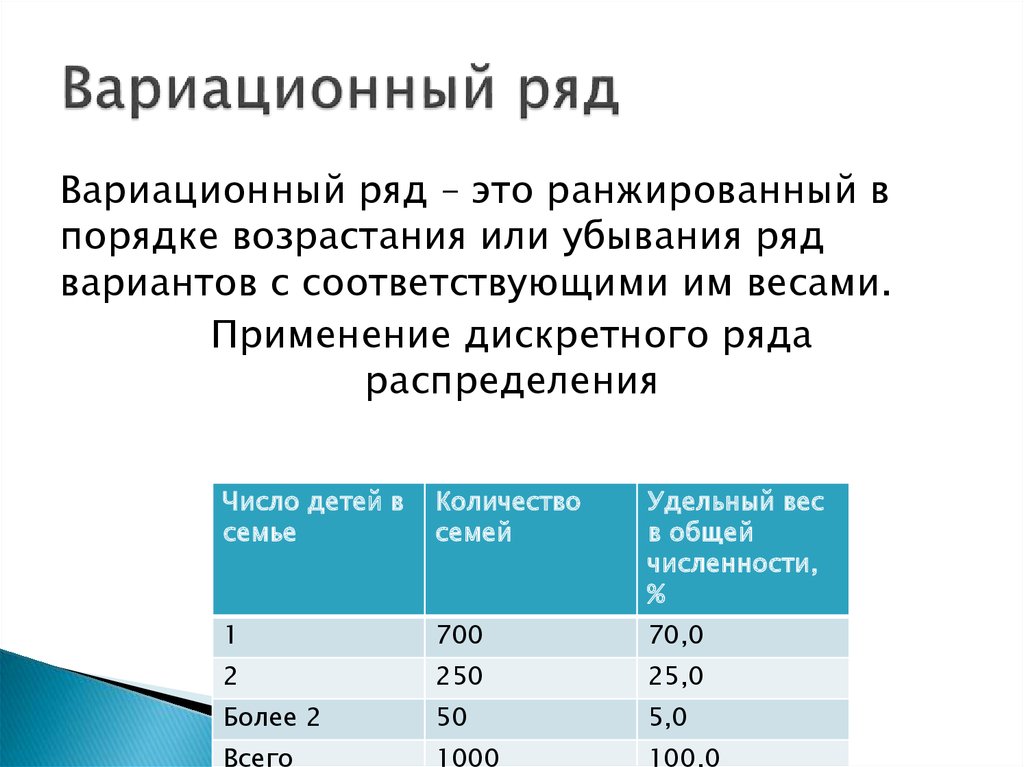 Затем для определения режима в рядах с равными интервалами применяют формулу
Затем для определения режима в рядах с равными интервалами применяют формулу
где Мо — стоимость моды; х Мо — нижняя граница модального интервала; ч — ширина модального интервала ; /Mo — частота модального интервала; /Mo j — частота премодального интервала; / Мо+1 — частота постмодального интервала, и для ряда с неравными интервалами в этой расчетной формуле вместо частот / Мо, / Мо, / Мо следует использовать плотности распределения Ум 0 _| , Ум 0> УМО+»
Если имеется одна мода, то распределение вероятностей случайной величины называется одномодальным; если мод больше одной, оно называется полимодальным (полимодальным, многомодальным), в случай двух мод — бимодальность.Как правило, многомодальность свидетельствует о том, что исследуемое распределение не подчиняется нормальному закону распределения.Однородные совокупности, как правило, характеризуются одномодальными распределениями.Многовершинность также свидетельствует о неоднородности изучаемой совокупности.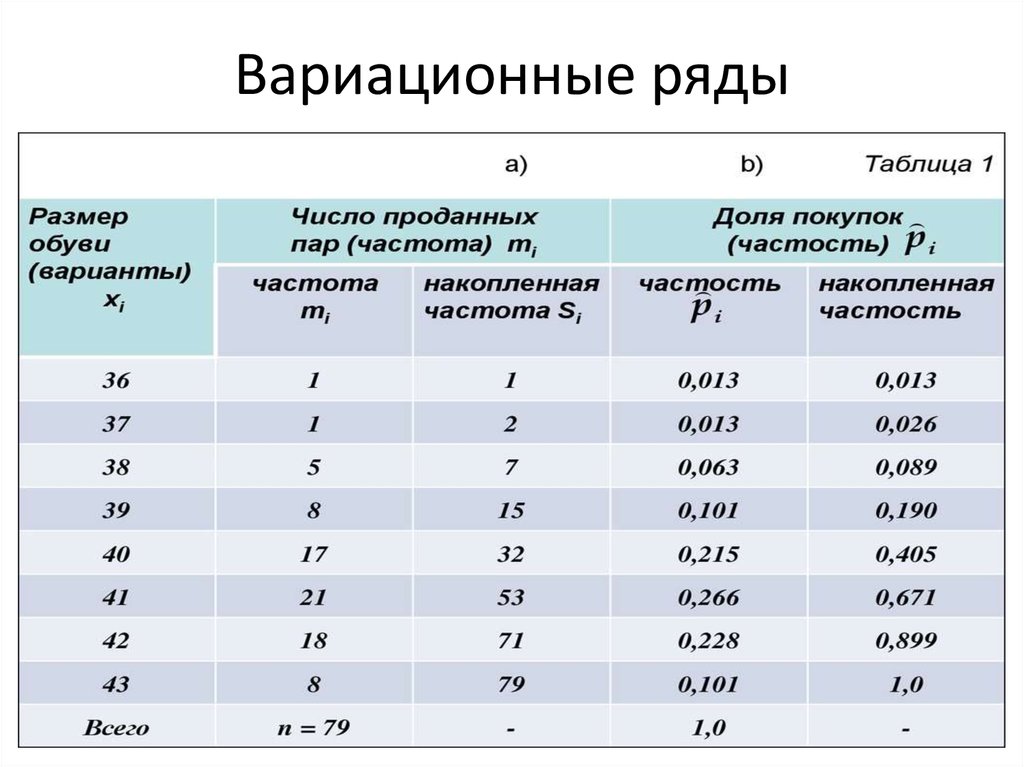 Появление двух и более вершин вызывает необходимость перегруппировки данных для выделения более однородных групп9.0007
Появление двух и более вершин вызывает необходимость перегруппировки данных для выделения более однородных групп9.0007
В интервальном вариационном ряду мода может быть определена графически с помощью гистограммы. Для этого проводятся две пересекающиеся линии от верхних точек самого высокого столбца гистограммы к верхним точкам двух соседних столбцов. Затем из точки их пересечения опускается перпендикуляр к оси абсцисс. Значение признака на оси абсцисс, соответствующей перпендикуляру, является модой. Во многих случаях при характеристике населения как обобщенного показателя предпочтение отдается моде, а не среднему арифметическому.
Медиана — это центральное значение признака; им обладает центральный член ранжированного ряда распределения. В дискретных рядах для нахождения значения медианы сначала определяется ее порядковый номер. Для этого при нечетном числе единиц к сумме всех частот добавляется единица, число делится на два. Если имеется четное количество единиц, в ряду будет 2 срединных единицы, поэтому в этом случае медиана определяется как среднее значение двух срединных единиц.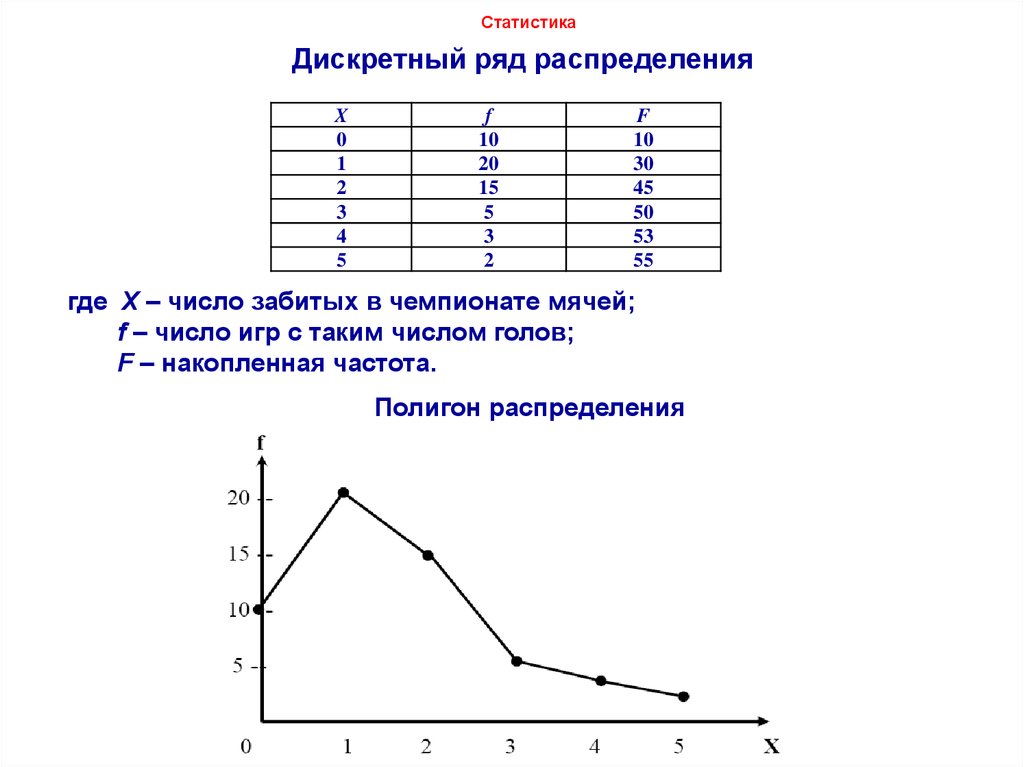 Таким образом, медиана в дискретном вариационном ряду — это значение, которое делит ряд на две части, содержащие одинаковое количество вариантов.
Таким образом, медиана в дискретном вариационном ряду — это значение, которое делит ряд на две части, содержащие одинаковое количество вариантов.
В интервальном ряду после определения порядкового номера медианы находят медианный интервал по накопленным частотам (частотам), а затем по формуле расчета медианы определяют значение самой медианы:
, где Me — значение медианы; х Ме — нижняя граница срединного интервала; ч — ширина медианного интервала ; — сумма частот ряда распределения; /D — накопленная частота предмедианного интервала; /Me — частота срединного интервала.
Медиана может быть найдена графически с помощью кумулята. Для этого на шкале накопленных частот (частот) кумулята от точки, соответствующей порядковому номеру медианы, проводят прямую, параллельную оси абсцисс, до пересечения с кумулятом. Далее из точки пересечения указанной прямой с кумулятом опускается перпендикуляр к оси абсцисс. Значение признака на оси X, соответствующее нарисованной ординате (перпендикуляру), является медианой.
Медиана характеризуется следующими свойствами.
- 1. Не зависит от тех значений атрибута, которые расположены по обе стороны от него.
- 2. Обладает свойством минимальности, означающим, что сумма абсолютных отклонений значений атрибута от медианы является минимальным значением по сравнению с отклонением значений атрибута от любого другого значения.
- 3. При объединении двух распределений с известными медианами невозможно заранее предсказать значение медианы нового распределения.
Эти свойства медианы широко используются при проектировании расположения пунктов бытового обслуживания — школ, поликлиник, АЗС, водокачек и т. д. Например, если в определенном квартале города планируется построить поликлинику, тогда целесообразнее расположить его в такой точке квартала, которая делит пополам не длину квартала, а число жителей.
Соотношение моды, медианы и среднего арифметического указывает на характер распределения признака в совокупности, позволяет оценить симметричность распределения. Если х Ме то имеет место правосторонняя асимметрия ряда. При нормальном распределении X — Me — Mo.
Если х Ме то имеет место правосторонняя асимметрия ряда. При нормальном распределении X — Me — Mo.
К. Пирсон на основании совмещения различных типов кривых определил, что для умеренно асимметричных распределений справедливы следующие приближенные соотношения между средним арифметическим, медианой и модой :
где Me — значение медианы; Мо — значение моды; x arithm — значение среднего арифметического.
Если есть необходимость более подробно изучить структуру вариационного ряда, то рассчитываются характеристические значения, аналогичные медиане. Такие значения признаков делят все единицы распределения на равные числа, их называют квантилями или градиентами. Квантиль подразделяется на квартили, децили, процентили и т. д. 9- нижняя граница первого квартильного интервала; h — ширина первого квартального интервала; /, — частоты интервального ряда;
Накопленная частота в интервале, предшествующем интервалу первого квартиля; Jq ( — частота интервала первого квартиля.
Первый квартиль показывает, что 25% единиц совокупности меньше его значения, а 75% больше. Второй квартиль равен медиане, т.е. Q2 = Me
По аналогии вычисляется третий квартиль, предварительно найдя третий квартальный интервал:
где – нижняя граница третьего квартильного интервала; h — ширина третьего квартильного интервала; /, — частоты интервального ряда; /X»- накопленная частота в интервале, предшествующем
G
интервал третьего квартиля; Jq — частота третьего квартильного интервала.
Третий квартиль показывает, что 75% единиц совокупности меньше ее значения, а 25% больше.
Разница между третьим и первым квартилями составляет межквартильный размах:
где Aq — значение межквартильного интервала; Q 3 — значение третьего квартиля; Q, — значение первого квартиля.
Децили делят население на 10 равных частей. Дециль — это значение признака в ряду распределения, которое соответствует десятым долям населения.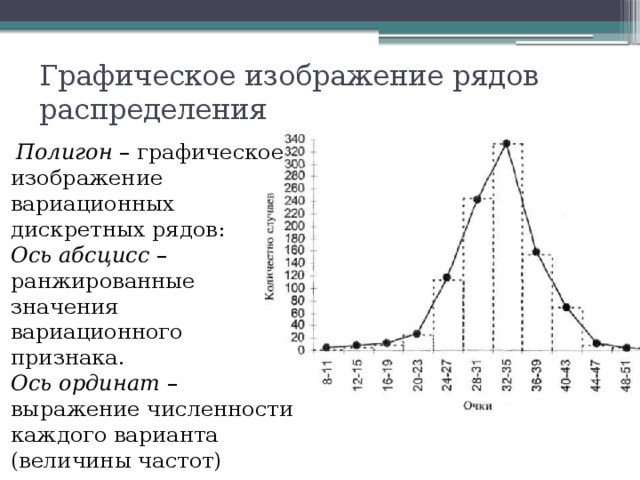 По аналогии с квартилями первый дециль показывает, что 10 % единиц совокупности меньше ее значения, а 90 % больше, а девятая дециль показывает, что 90 % единиц совокупности меньше ее значения, а 10 % больше ее значения. более. Соотношение девятого и первого децилей, т. е. децильный коэффициент, широко используется при изучении дифференциации доходов для измерения соотношения уровней доходов 10% наиболее обеспеченного и 10% наименее обеспеченного населения. Процентили делят ранжированное население на 100 равных частей. Расчет, значение и использование процентилей аналогичны децилям.
По аналогии с квартилями первый дециль показывает, что 10 % единиц совокупности меньше ее значения, а 90 % больше, а девятая дециль показывает, что 90 % единиц совокупности меньше ее значения, а 10 % больше ее значения. более. Соотношение девятого и первого децилей, т. е. децильный коэффициент, широко используется при изучении дифференциации доходов для измерения соотношения уровней доходов 10% наиболее обеспеченного и 10% наименее обеспеченного населения. Процентили делят ранжированное население на 100 равных частей. Расчет, значение и использование процентилей аналогичны децилям.
Квартили, децили и другие структурные характеристики можно определить графически по аналогии с медианой с помощью кумулята.
Для измерения размера вариации используются следующие показатели: диапазон вариации, среднее линейное отклонение, стандартное отклонение и дисперсия. Величина размаха вариации целиком зависит от случайности распределения крайних членов ряда. Этот показатель представляет интерес в тех случаях, когда важно знать, какова амплитуда колебаний значений признака:
где R- значение диапазона варьирования; x max — максимальное значение признака; x tt — минимальное значение признака.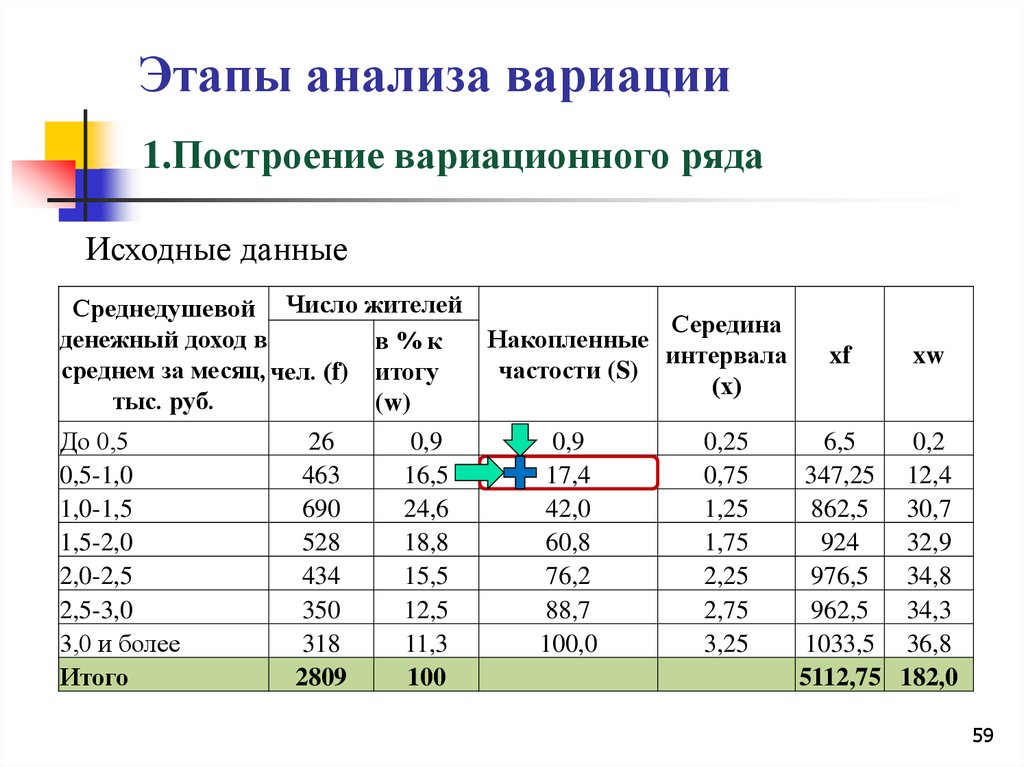
При расчете диапазона варьирования не учитывается значение подавляющего большинства членов ряда, а изменение связано с каждым значением члена ряда. Этого недостатка лишены показатели, представляющие собой средние значения, полученные из отклонений отдельных значений признака от их среднего значения: среднее линейное отклонение и стандартное отклонение. Между индивидуальными отклонениями от среднего и колебаниями того или иного признака существует прямая зависимость. Чем сильнее волатильность, тем больше абсолютный размер отклонений от среднего.
Среднее линейное отклонение представляет собой среднее арифметическое абсолютных значений отклонений отдельных вариантов от их среднего значения.
Среднее линейное отклонение для несгруппированных данных
где / пр — значение среднего линейного отклонения; х, — — значение признака; X — P — количество единиц населения.
Среднее линейное отклонение сгруппированного ряда
где / vz — значение среднего линейного отклонения; х, — значение признака; X — среднее значение признака для изучаемой популяции; / — количество единиц населения в отдельной группе.
Признаки отклонения в этом случае не учитываются, иначе сумма всех отклонений будет равна нулю. Среднее линейное отклонение в зависимости от группировки анализируемых данных рассчитывается по разным формулам: для сгруппированных и не сгруппированных данных. Среднее линейное отклонение в силу своей условности отдельно от других показателей вариации на практике используется относительно редко (в частности, для характеристики выполнения договорных обязательств в части равномерности поставок; при анализе внешнеторгового оборота, состав работников, ритм производства, качество продукции с учетом технологических особенностей производства и др.).
Стандартное отклонение характеризует, насколько отдельные значения изучаемого признака в среднем отклоняются от среднего значения по совокупности, и выражается в единицах изучаемого признака. Стандартное отклонение, являясь одной из основных мер вариации, широко используется при оценке границ вариации признака в однородной популяции, при определении значений ординат кривой нормального распределения, а также в расчеты, связанные с организацией наблюдения за пробами и установлением точности характеристик проб.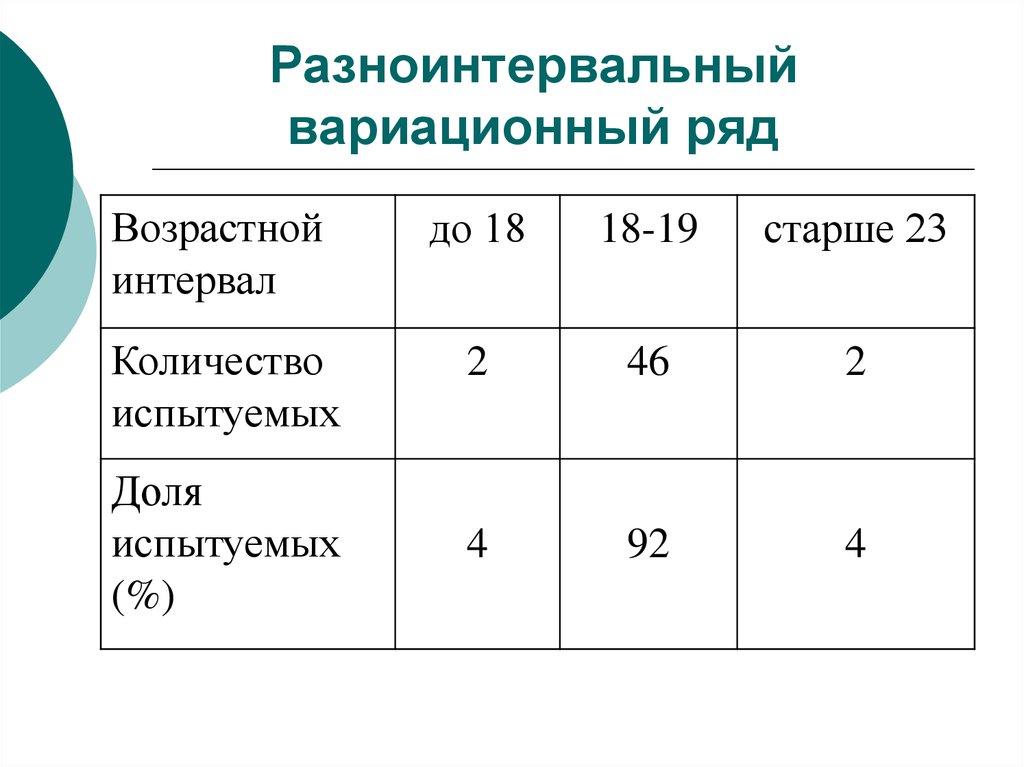 Стандартное отклонение для разгруппированных данных рассчитывается по следующему алгоритму: каждое отклонение от среднего возводится в квадрат, все квадраты суммируются, после чего сумма квадратов делится на количество членов ряда и из него извлекается квадратный корень. частное:
Стандартное отклонение для разгруппированных данных рассчитывается по следующему алгоритму: каждое отклонение от среднего возводится в квадрат, все квадраты суммируются, после чего сумма квадратов делится на количество членов ряда и из него извлекается квадратный корень. частное:
где Iip — значение стандартного отклонения; Xj- значение признака ; X — среднее значение признака для изучаемой совокупности; P — количество единиц населения.
Для сгруппированных проанализированных данных стандартное отклонение данных рассчитывается по взвешенной формуле
где — значение стандартного отклонения; Xj- значение признака ; X — среднее значение признака для изучаемой популяции; fx- количество единиц населения в определенной группе.
Выражение под корнем в обоих случаях называется дисперсией. Таким образом, дисперсия рассчитывается как средний квадрат отклонений значений признака от их среднего значения. Для невзвешенных (простых) значений признаков дисперсия определяется следующим образом:
Для значений взвешенных признаков
Существует также специальный упрощенный способ расчета дисперсии: в общем виде
для невзвешенных (простых) значений признаков для значений взвешенных признаков
с использованием метода отсчета от условного нуля
где 2 — значение дисперсии; х, — — значение признака; X — среднее значение признака, h — значение группового интервала, t 1 — вес (A =
Дисперсия имеет самостоятельное выражение в статистике и является одним из важнейших показателей вариации.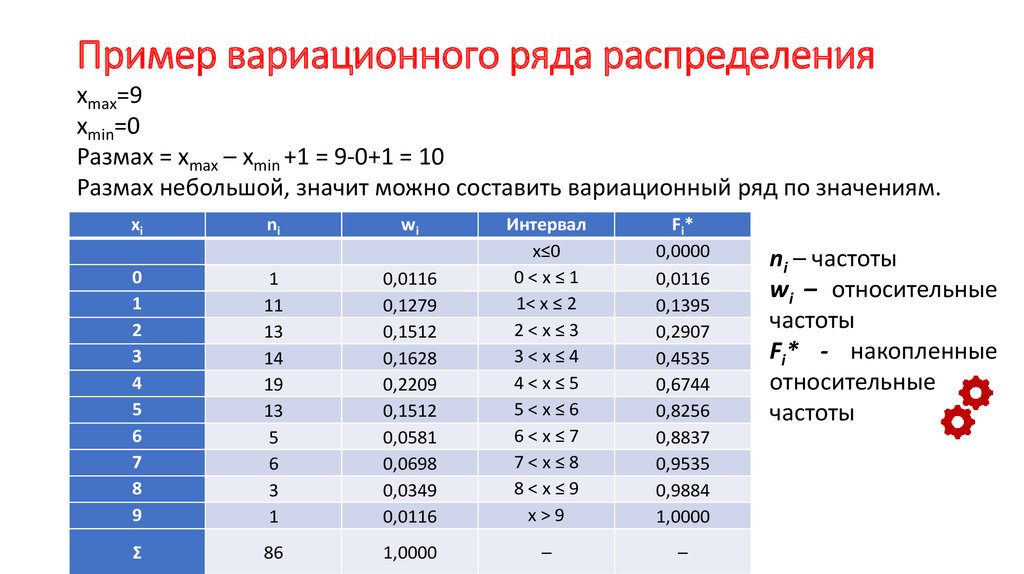 измеряется в единицах, соответствующих квадрату единиц измерения изучаемого признака.
измеряется в единицах, соответствующих квадрату единиц измерения изучаемого признака.
Дисперсия обладает следующими свойствами.
- 1. Дисперсия постоянной величины равна нулю.
- 2. Уменьшение всех значений признака на одно и то же значение А не меняет значение дисперсии. Это означает, что средний квадрат отклонений можно вычислить не от заданных значений признака, а от их отклонений от некоторого постоянного числа.
- 3. Уменьшение всех значений признака в к раз уменьшает дисперсию в к в 2 раза, а стандартное отклонение — в к раз, т.е. все значения атрибута можно разделить на некоторое постоянное число (скажем, на значение интервала ряда), можно вычислить стандартное отклонение, и затем умножается на постоянное число.
- 4. Если вычислить средний квадрат отклонений от какого-либо значения А при в какой-то мере отличается от среднего арифметического, то он всегда будет больше среднего квадрата отклонений, вычисленного от среднего арифметического.
 В этом случае средний квадрат отклонений будет больше на вполне определенную величину — на квадрат разницы между средним и этим условно принятым значением.
В этом случае средний квадрат отклонений будет больше на вполне определенную величину — на квадрат разницы между средним и этим условно принятым значением.
Вариативность Альтернативный признак состоит в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие изучаемого свойства у единицы обозначается единицей (1), а его отсутствие обозначается нулем (0). Долю единиц, обладающих изучаемым свойством, обозначим через P, а долю единиц, не обладающих этим свойством, обозначим через G. Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (P), на долю единиц, не обладающих этим свойством (Г). Наибольшая изменчивость совокупности достигается в тех случаях, когда часть совокупности, составляющая 50 % от общего объема совокупности, имеет признак, а другая часть совокупности, также равная 50 %, не имеет обладают этой особенностью, при этом дисперсия достигает максимального значения 0,25, м.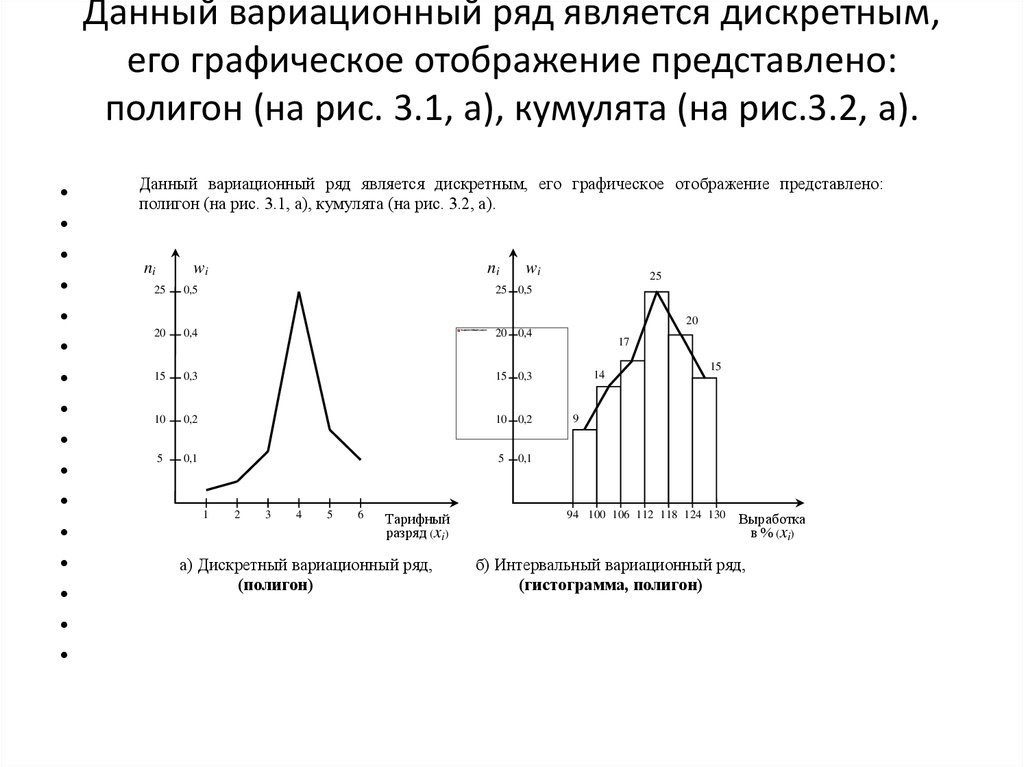 э. Р = 0,5, G = 1 — Р = 1 — 0,5 = 0,5 и о 2 = 0,5·0,5 = 0,25. Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой вариация агрегата отсутствует. Практическое применение дисперсии альтернативного признака состоит в построении доверительных интервалов при выборке.
э. Р = 0,5, G = 1 — Р = 1 — 0,5 = 0,5 и о 2 = 0,5·0,5 = 0,25. Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой вариация агрегата отсутствует. Практическое применение дисперсии альтернативного признака состоит в построении доверительных интервалов при выборке.
Чем меньше значение дисперсии и стандартного отклонения, тем однороднее и типичнее будет совокупность. Средняя стоимость. В практике статистики часто возникает необходимость сравнивать вариации различных признаков. Например, интересно сопоставить вариации возраста рабочих и их квалификации, стажа и заработной платы, себестоимости и прибыли, стажа и производительности труда и т. д. Для таких сравнений непригодны показатели абсолютной изменчивости характеристик. : нельзя сравнивать изменчивость стажа, выраженного в годах, с изменчивостью заработной платы, выраженной в рублях. Для проведения таких сравнений, а также сравнений колебаний одного и того же признака в нескольких популяциях с разными средними арифметическими используют показатели вариации — коэффициент осцилляции, линейный коэффициент вариации и коэффициент вариации, которые показывают меру колебания крайних значений вокруг средних.
Коэффициент колебаний :
где V R — значение коэффициента колебаний; R — значение диапазона варьирования; X —
Линейный коэффициент вариации».
где vj- значение линейного коэффициента вариации; значение признака для изучаемой популяции
Коэффициент вариации :
где Va- значение коэффициента вариации; а — значение стандартного отклонения; X — среднее значение признака для изучаемой популяции.
Коэффициент осцилляции представляет собой процент размаха изменчивости к среднему значению изучаемого признака, а линейный коэффициент вариации представляет собой отношение среднего линейного отклонения к среднему значению изучаемого признака, выраженное как процент. Коэффициент вариации представляет собой процент стандартного отклонения от среднего значения изучаемого признака. Как относительная величина, выраженная в процентах, коэффициент вариации используется для сравнения степени изменчивости различных признаков.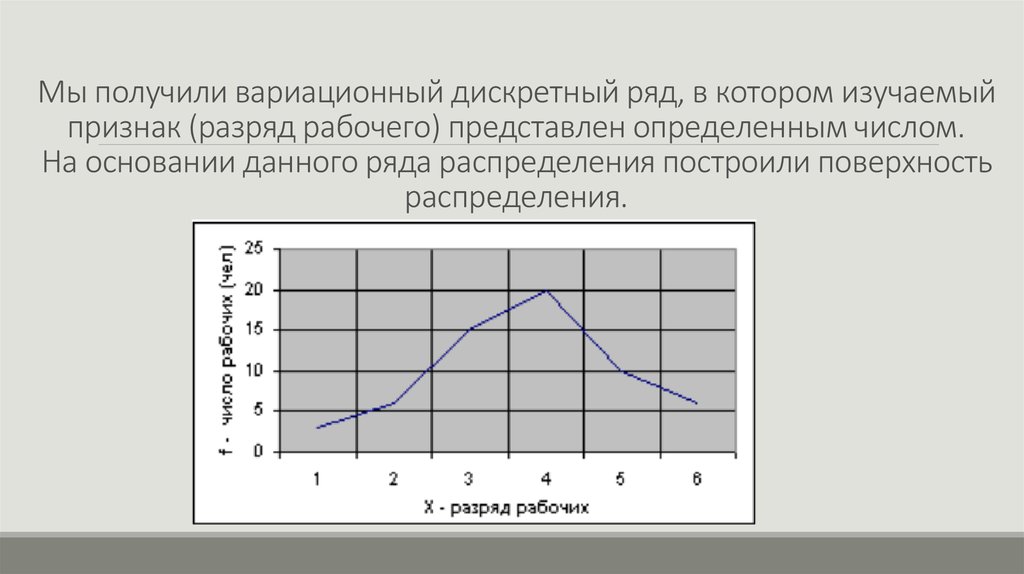 С помощью коэффициента вариации оценивается однородность статистической совокупности. Если коэффициент вариации меньше 33%, то изучаемая совокупность однородна, а вариация слабая. Если коэффициент вариации больше 33%, то изучаемая популяция неоднородна, вариация сильная, а среднее значение нетипично и не может быть использовано в качестве обобщающего показателя данной популяции. Кроме того, коэффициенты вариации используются для сравнения колебаний одного признака в разных популяциях. Например, оценить разброс стажа рабочих на двух предприятиях. Чем больше значение коэффициента, тем значительнее изменение признака.
С помощью коэффициента вариации оценивается однородность статистической совокупности. Если коэффициент вариации меньше 33%, то изучаемая совокупность однородна, а вариация слабая. Если коэффициент вариации больше 33%, то изучаемая популяция неоднородна, вариация сильная, а среднее значение нетипично и не может быть использовано в качестве обобщающего показателя данной популяции. Кроме того, коэффициенты вариации используются для сравнения колебаний одного признака в разных популяциях. Например, оценить разброс стажа рабочих на двух предприятиях. Чем больше значение коэффициента, тем значительнее изменение признака.
На основании рассчитанных квартилей можно также рассчитать относительный показатель квартальной вариации по формуле
где Q 2 и
Межквартильный размах определяется по формуле также рассчитывается. Он определяется как отношение соответствующей частоты или частоты к значению интервала. В неравноинтервальных рядах используются абсолютная и относительная плотности распределения. Абсолютная плотность распределения – это частота, приходящаяся на единицу длины интервала. Относительная плотность распределения — частота на единицу длины интервала.
Абсолютная плотность распределения – это частота, приходящаяся на единицу длины интервала. Относительная плотность распределения — частота на единицу длины интервала.
Все сказанное справедливо для рядов распределения, закон распределения которых хорошо описывается нормальным законом распределения или близок к нему.
При обработке больших объемов информации, что особенно важно при проведении современных научных разработок, перед исследователем стоит серьезная задача правильной группировки исходных данных. Если данные дискретные, то, как мы видели, проблем нет — нужно просто вычислить частоту каждого признака. Если изучаемый признак имеет непрерывный символ (что чаще встречается на практике), то выбор оптимального количества интервалов для группировки признака — задача отнюдь не тривиальная.
Для группировки непрерывных случайных величин весь диапазон изменения признака разбивается на определенное количество интервалов от до.
Сгруппированный интервал ( непрерывный ) вариационный ряд называют интервалами, ранжированными по значению признака (), где указано вместе с соответствующими частотами () число наблюдений, попавших в r»-й интервал, или относительные частоты ():
Интервалы значений характеристики | ||||||
миль частота |
Гистограмма и кумулятивная (ожива), уже подробно рассмотренная нами, являются прекрасным инструментом визуализации данных, позволяющим получить первичное представление о структуре данных.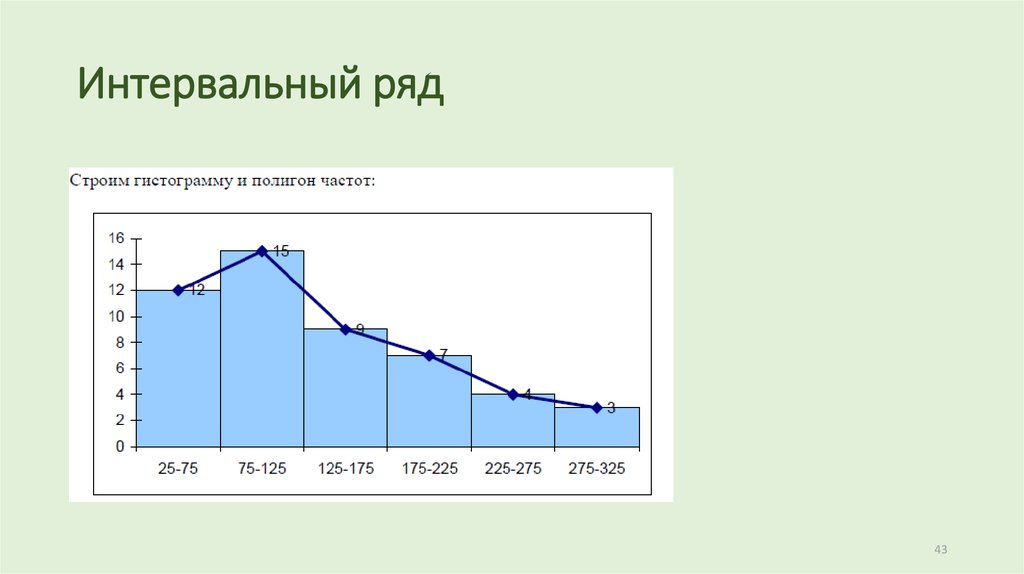 Такие графики (рис. 1.15) строятся для непрерывных данных так же, как и для дискретных данных, только с учетом того, что непрерывные данные полностью заполняют область своих возможных значений, принимая любые значения.
Такие графики (рис. 1.15) строятся для непрерывных данных так же, как и для дискретных данных, только с учетом того, что непрерывные данные полностью заполняют область своих возможных значений, принимая любые значения.
Рис. 1.15.
Поэтому столбцы на гистограмме и кумуляте должны соприкасаться, не иметь областей, где значения атрибута не попадают во все возможные (т.е. гистограмма и кумулят не должны иметь «дыр» по ось абсцисс, в которую не попадают значения исследуемой переменной, как на рис. 1.16). Высота столбца соответствует частоте — количеству наблюдений, попадающих в заданный интервал, или относительной частоте — доле наблюдений. Интервалы не должны пересекаться с и обычно имеют одинаковую ширину.
Рис. 1.16.
Гистограмма и многоугольник представляют собой аппроксимации кривой плотности вероятности (дифференциальной функции) f(x) теоретического распределения, рассматриваемого в курсе теории вероятностей. Поэтому их построение имеет такое значение при первичной статистической обработке количественных непрерывных данных — по их виду можно судить о гипотетическом законе распределения.
Поэтому их построение имеет такое значение при первичной статистической обработке количественных непрерывных данных — по их виду можно судить о гипотетическом законе распределения.
Кумулировать — кривая накопленных частот (частот) интервального вариационного ряда. График интегральной функции распределения сравнивается с кумулятом F(x) , также рассматриваемым в курсе теории вероятностей.
В основном понятия гистограммы и кумулята связаны именно с непрерывными данными и их интервальными вариационными рядами, поскольку их графики представляют собой эмпирические оценки функции плотности вероятности и функции распределения соответственно.
Построение интервального вариационного ряда начинается с определения количества интервалов k. И эта задача, пожалуй, самая сложная, важная и дискуссионная в изучаемом вопросе.
Количество интервалов не должно быть слишком маленьким, так как гистограмма будет слишком гладкой ( пересглаженной), теряет все черты изменчивости исходных данных — на рис. 1.17 видно, как одни и те же данные, на которых графики рис. 1.15 используются для построения гистограммы с меньшим числом интервалов (левый график).
1.17 видно, как одни и те же данные, на которых графики рис. 1.15 используются для построения гистограммы с меньшим числом интервалов (левый график).
При этом количество интервалов не должно быть слишком большим — иначе мы не сможем оценить плотность распределения исследуемых данных по числовой оси: гистограмма получится недосглаженной (недосглаженной) с незаполненными интервалами, неровный (см. рис. 1.17, правый график).
Рис. 1.17.
Как определить наиболее предпочтительное количество интервалов?
Еще в 1926 году Герберт Стерджес предложил формулу для расчета количества интервалов, на которые необходимо разделить исходный набор значений изучаемого признака. Эта формула действительно стала суперпопулярной — ее предлагают большинство учебников по статистике, и многие статистические пакеты используют ее по умолчанию. Оправданно ли это и во всех ли случаях — очень серьезный вопрос.
Так на чем основана формула Стерджеса?
Рассмотрите биномиальное распределение }
python — Вычисление доверительного интервала на основе выборочных данных
На основе оригинала, но с некоторыми конкретными примерами:
import numpy as np def mean_confidence_interval (данные, достоверность: float = 0,95) -> tuple [float, np.ndarray]: """ Возвращает (кортеж) среднее значение и доверительный интервал для заданных данных. Данные представляют собой итерацию np.arrayable. ссылка: - https://stackoverflow.com/a/15034143/1601580 - https://github.com/WangYueFt/rfs/blob/f8c837ba93c62dd0ac68a2f4019c619aa86b8421/eval/meta_eval.py#L19 """ импортировать scipy.stats импортировать numpy как np а: np.ndarray = 1,0 * np.array (данные) n: интервал = длина (а) если п == 1: журнал импорта logging.warning('Первое измерение ваших данных равно 1, возможно, вы хотели перенести свои данные? Или удалить' 'одноэлементное измерение?') m, se = a.mean(), scipy.stats.sem(a) tp = scipy.stats.t.ppf((1 + достоверность) / 2., n - 1) ч = се * тп возврат м, ч определение ci_test_float(): импортировать numpy как np # - один НЕПРАВИЛЬНЫЙ набор данных размера 1 на N data = np.random.randn(1, 30) # выдает ошибку, потому что len устанавливает n=1, так что не эта форма! m, ci = средний_доверительный_интервал (данные) print('-- вы должны получить среднее значение и список nan ci (поскольку данные в неправильном формате, он считает, что это 30 наборов данных ' 'длина 1.
') печать (м, ки) # правильные данные как N на 1 данные = np.random.randn (30, 1) m, ci = средний_доверительный_интервал (данные) print('-- дает среднее значение и список длины 1 для одного ЭК (поскольку он думает, что у вас есть один набор данных)') печать (м, ки) # несколько наборов данных (7) размера N (=30) данные = np.random.randn (30, 7) print('-- дает 7 CI для 7 наборов данных длиной 30. 30 - это число, которое нужно увеличить, если вы использовали z(p)' «из-за CLT».) m, ci = средний_доверительный_интервал (данные) печать (м, ки) ci_test_float()
вывод:
-- вы должны получить среднее значение и список nan ci (поскольку данные имеют неправильный формат, он считает, что это 30 наборов данных длины 1. 0.1431623130952463 [нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан нан] -- дает среднее значение и список длины 1 для одного ЭК (поскольку он думает, что у вас есть один набор данных) 0,04947206018132864 [0,40627264] -- дает 7 CI для 7 наборов данных длиной 30.30 - это число, которое нужно увеличить, если вы использовали z(p) из-за CLT. -0,03585104402718902 [0,31867309 0,35619134 0,34860011 0,3812853 0,44334033 0,35841138 0,40739732]
Я думаю, что Num_samples от Num_datasets правильный, но если это не так, дайте мне знать в разделе комментариев.
Я думаю, что его можно использовать для любых данных из-за следующего:
Я считаю, что это нормально, поскольку среднее значение и стандартное значение рассчитываются для общих числовых данных, а значение z_p/t_p принимает только доверительный интервал и размер данных, поэтому оно не зависит от предположений о распределении данных.
Думаю, его можно использовать для регрессии и классификации.
В качестве бонуса реализация факела, который почти использует только факел:
def torch_compute_confidence_interval(data: Tensor,
уверенность: поплавок = 0,95
) -> Тензор:
"""
Вычисляет доверительный интервал для заданного опроса набора данных. """
n: интервал = длина (данные)
означает: Tensor = data.mean()
# se: Tensor = scipy.stats.sem(data) # вычислить стандартную ошибку
# se, mean: Tensor = torch.std_mean(data, unbiased=True) # вычислить стандартную ошибку
se: Tensor = data.std(unbiased=True) / (n ** 0,5)
t_p: float = float(scipy.stats.t.ppf((1 + достоверность)/2., n - 1))
ci = t_p * se
среднее значение возврата, ci
9* Вам не нужно будет оценивать это. Этот анализ предполагает
что оценщик/значение, которое вы оцениваете, является истинным средним значением с использованием среднего значения выборки (оценщика). Поскольку обычно используется
t.val или z.val (второе для стандартизированной с.в. нормали), то это означает приближение, что mu_n ~ гауссовское
должен держать. Это, скорее всего, верно, если n >= 0. Обратите внимание, что это похоже на статистическую теорию обучения, где мы используем
оценщик MLE/ERM для выбора функции с дельта-, гамма-рассуждениями и т. д. Обратите внимание, что если вы занимаетесь алгеброй, вы также можете
скажите, что среднее значение выборки находится в этом интервале, но относительно mu^* но это рождается, никого не волнует, так как вы не знаете mu^*
так что это не полезно.
"""
n: интервал = длина (данные)
означает: Tensor = data.mean()
# se: Tensor = scipy.stats.sem(data) # вычислить стандартную ошибку
# se, mean: Tensor = torch.std_mean(data, unbiased=True) # вычислить стандартную ошибку
se: Tensor = data.std(unbiased=True) / (n ** 0,5)
t_p: float = float(scipy.stats.t.ppf((1 + достоверность)/2., n - 1))
ci = t_p * se
среднее значение возврата, ci
9* Вам не нужно будет оценивать это. Этот анализ предполагает
что оценщик/значение, которое вы оцениваете, является истинным средним значением с использованием среднего значения выборки (оценщика). Поскольку обычно используется
t.val или z.val (второе для стандартизированной с.в. нормали), то это означает приближение, что mu_n ~ гауссовское
должен держать. Это, скорее всего, верно, если n >= 0. Обратите внимание, что это похоже на статистическую теорию обучения, где мы используем
оценщик MLE/ERM для выбора функции с дельта-, гамма-рассуждениями и т. д. Обратите внимание, что если вы занимаетесь алгеброй, вы также можете
скажите, что среднее значение выборки находится в этом интервале, но относительно mu^* но это рождается, никого не волнует, так как вы не знаете mu^*
так что это не полезно. *(х) — ид.
Std_n против t_p*std_n/ sqrt(n)
- std_n = var(x) более пессимистичен, но выполняется всегда. Никогда не сжимается как n->infinity
- но если n мало, то pCI может быть слишком маленьким, и вы «лжете себе». Итак, если у вас очень мало данных
возможно, лучше использовать std_n для CI. Это относится к проблеме 99,9%. Надеюсь, стандартный размер не слишком велик для вашего
эксперименты признать недействительными.
ссылка:
- https://stats.stackexchange.com/questions/554332/confidence-interval-given-the-population-mean-and-standard-deviation?noredirect=1&lq=1
- https://stackoverflow.com/questions/70356922/what-is-the-proper-way-to-compute-95-confidence-intervals-with-pytorch-for-clas
- https://www.youtube.com/watch?v=MzvRQFYUEFU&list=PLUl4u3cNGP60hI9ATjSFgLZpbNJ7myAg6&index=205
"""
*(х) — ид.
Std_n против t_p*std_n/ sqrt(n)
- std_n = var(x) более пессимистичен, но выполняется всегда. Никогда не сжимается как n->infinity
- но если n мало, то pCI может быть слишком маленьким, и вы «лжете себе». Итак, если у вас очень мало данных
возможно, лучше использовать std_n для CI. Это относится к проблеме 99,9%. Надеюсь, стандартный размер не слишком велик для вашего
эксперименты признать недействительными.
ссылка:
- https://stats.stackexchange.com/questions/554332/confidence-interval-given-the-population-mean-and-standard-deviation?noredirect=1&lq=1
- https://stackoverflow.com/questions/70356922/what-is-the-proper-way-to-compute-95-confidence-intervals-with-pytorch-for-clas
- https://www.youtube.com/watch?v=MzvRQFYUEFU&list=PLUl4u3cNGP60hI9ATjSFgLZpbNJ7myAg6&index=205
"""
Оценки с уверенностью
Оценки с уверенностьюЧтобы получить односторонний (верхний или нижний) доверительный интервал с уровнем значимости, введите 1-2a в качестве уровня достоверности.Этот сайт является частью учебных объектов JavaScript E-labs для принятия решений. Другие JavaScript из этой серии относятся к разным областям применения в разделе МЕНЮ на этой странице.
Профессор Хоссейн Аршам
На практике доверительный интервал используется для выражения неопределенности оцениваемой величины. Следующий JavaScript, который вычисляет доверительный интервал для стандартного отклонения, доверительный интервал для дисперсии и доверительный интервал для ожидаемого значения совокупности на основе набора случайных наблюдений. Поскольку доверительные интервалы (ДИ) являются двойственными проверками гипотез, можно использовать ДИ и для проверки.
В то время как доверительный интервал для среднего применим к любой популяции даже с дискретными случайными величинами, такими как доля, два других доверительных интервала требуют проверки на нормальность, чтобы быть действительными.
Допустим, вы вычисляете 95% доверительный интервал для среднего значения (или дисперсии) генеральной совокупности.
Способ интерпретировать это состоит в том, чтобы представить бесконечное количество выборок из одной и той же совокупности, по крайней мере, 95% вычисленных интервалов будут содержать среднее значение совокупности (или дисперсию), а не более 5% — нет. Однако неверно утверждать: «Мне 95% уверены, что параметр популяции попадает в интервал».
Обратите внимание, что необходимо соблюдать осторожность при округлении доверительных интервалов до желаемого числа цифр: нижний предел должен быть округлен в большую сторону, а верхний предел должен быть округлен в меньшую сторону. Знайте, что доверительный интервал, рассчитанный по одной выборке, будет отличаться от доверительного интервала, рассчитанного по другой выборке.
Односторонний доверительный интервал:
Проверка гипотез по доверительному интервалу: В качестве альтернативы прямой проверке гипотезы для среднего значения и дисперсии можно использовать двусторонний или односторонний доверительный интервал для проверки гипотезы с двусторонней или односторонней альтернативной гипотезой.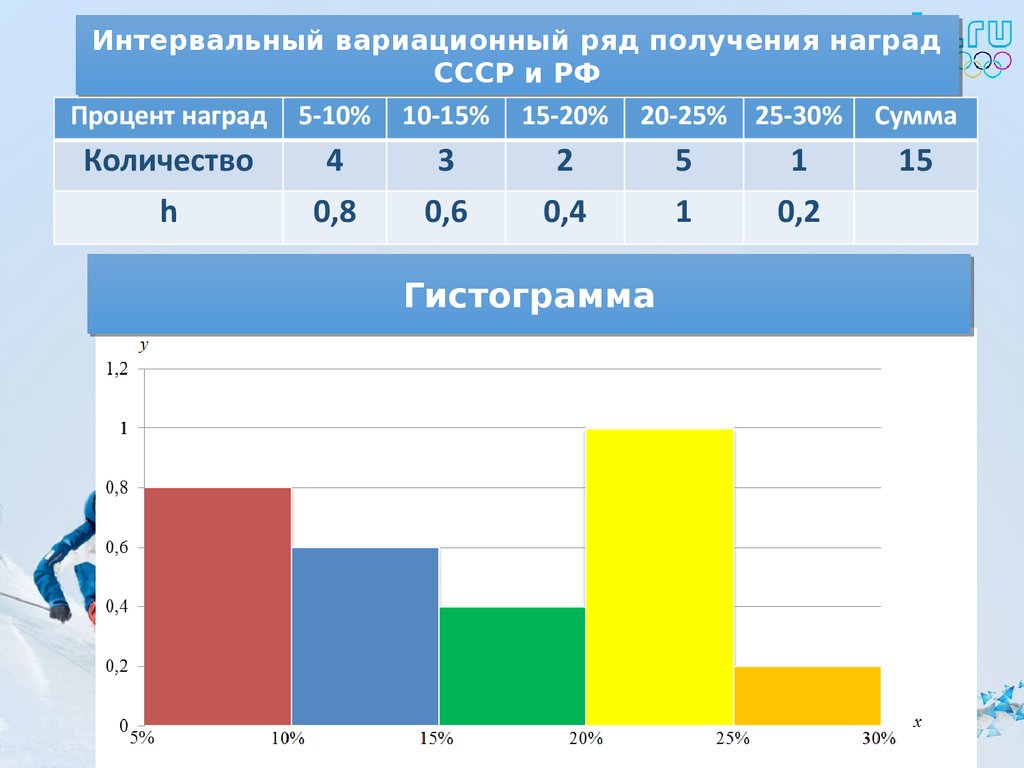 , соответственно. При таком подходе, если доверительный интервал с желаемым уровнем достоверности содержит значение нулевой гипотезы, то нулевую гипотезу можно не отвергать.
, соответственно. При таком подходе, если доверительный интервал с желаемым уровнем достоверности содержит значение нулевой гипотезы, то нулевую гипотезу можно не отвергать.
Введите до 80 образцов данных и Желаемый уровень достоверности , а затем нажмите кнопку Вычислить . Пустые квадраты не учитываются при расчетах, а нули учитываются.
При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab , а не клавиши со стрелками или клавиши ввода.
Для редактирования ваших данных, включая добавление/изменение/удаление, вам не нужно нажимать на кнопку «очистить», а заново вводить свои данные заново. Вы можете просто добавить число в любую пустую ячейку, изменить число на другое в той же ячейке или удалить число из ячейки. После редактирования нажмите кнопку «Рассчитать».
Для расширенного редактирования или использования JavaScript для нового набора данных используйте кнопку «очистить».
Статистическое мышление для принятия решений
Пожалуйста, отправьте ваши комментарии по адресу:
Профессор Хоссейн Аршам
|
|
Заявление об авторских правах.
Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Руководством по добросовестному использованию образовательных мультимедиа от 1996 г. разрешено только в некоммерческих целях и в учебных целях.
Этот сайт может быть переведен и/или зеркально отображен в неизменном виде (включая эти уведомления) на любом сервере с общедоступным доступом. Все файлы доступны по адресу http://home.ubalt.edu/ntsbarsh/Business-stat для зеркалирования.Пожалуйста, пришлите мне по электронной почте ваши комментарии, предложения и проблемы. Спасибо.
Профессор Хоссейн Аршам
Вернуться к: Домашняя страница доктора Аршама
ЕОФ: 1994-2015 гг.
2.11. Доверительные интервалы — улучшение процесса с использованием данных
До сих пор мы вычисляли точечные оценки параметров, называемых статистикой. В последнем разделе в \(t\)-распределении мы уже вычислили доверительный интервал. В этом разделе мы формализуем идею, начиная с примера.
В этом разделе мы формализуем идею, начиная с примера.
Пример : новый клиент оценивает ваш продукт, ему нужен доверительный интервал для уровня примесей в вашей серной кислоте. Вы можете сказать им: « диапазон от 429 ppm до 673 ppm содержит истинный уровень примеси с достоверностью 95% ». Это компактное представление уровня примесей. Вы могли бы сказать своему потенциальному клиенту, что
среднее значение выборки за последний год данных составляет 551 ppm
стандартное отклонение выборки от данных за последний год составляет 102 ppm
данные за последний год нормально распределены
Но доверительный интервал передает аналогичную концепцию полезным образом. Он дает оценку местоположения, разброса и неопределенности, связанной с этим параметром (например, в данном случае уровень примеси).
Вернемся к предыдущему примеру с вязкостью, где у нас было 9 измерений вязкости 23, 19, 17, 18, 24, 26, 21, 14, 18 .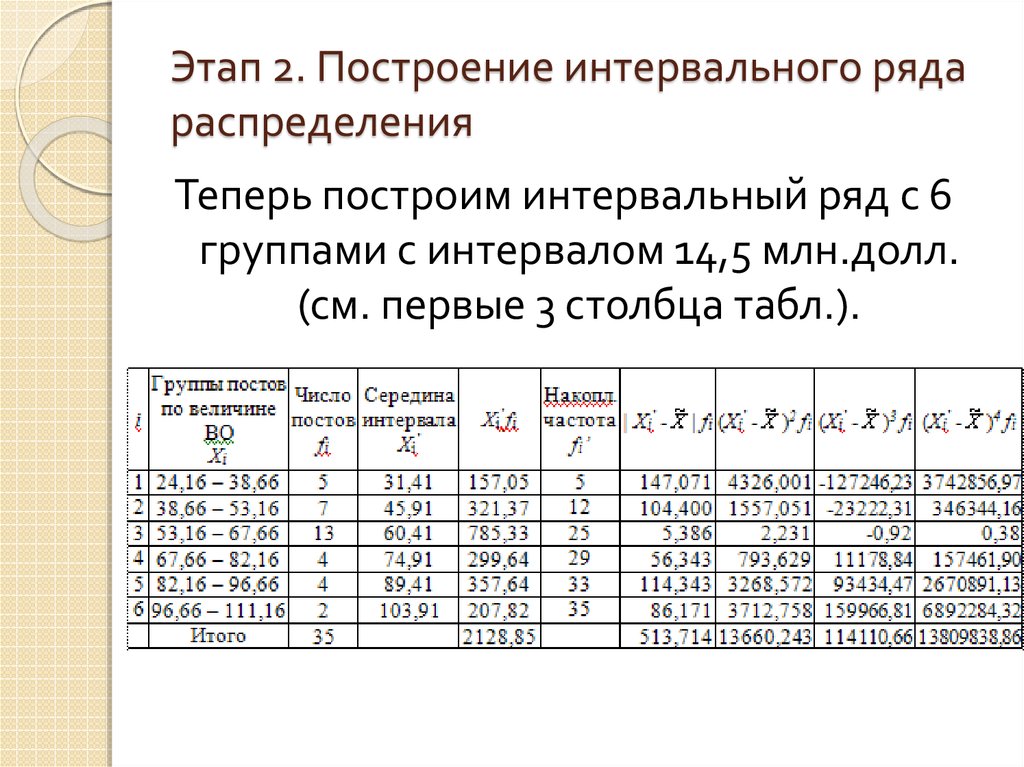 Среднее значение выборки было \(\overline{x} = 20,0\), а стандартное отклонение было \(s = 3,81\). Значение \(z\) равно: \(z = \dfrac{\overline{x} — \mu}{s/\sqrt{n}}\). И мы показали, что это было распределено согласно \(t\)-распределению с 8 степенями свободы.
Среднее значение выборки было \(\overline{x} = 20,0\), а стандартное отклонение было \(s = 3,81\). Значение \(z\) равно: \(z = \dfrac{\overline{x} — \mu}{s/\sqrt{n}}\). И мы показали, что это было распределено согласно \(t\)-распределению с 8 степенями свободы.
Для расчета доверительного интервала необходимо найти диапазон, в котором встречается это значение \(z\). Чаще всего нас интересуют симметричные доверительные интервалы, поэтому процедура такова:
(1)\[\begin{split} \begin{массив}{rcccl} — c_t &\leq& z &\leq & +c_t\\ — c_t &\leq& \displaystyle \frac{\overline{x} — \mu}{s/\sqrt{n}} &\leq & +c_t\\ \overline{x} — c_t \dfrac{s}{\sqrt{n}} &\leq& \mu &\leq& \overline{x} + c_t\dfrac{s}{\sqrt{n}} \\ \text{LB} &\leq& \mu &\leq& \text{UB} \конец{массив}\конец{разделить}\]
Критические значения \(c_t\) равны qt(1 - 0,05/2, df=8) = 2,306004 при использовании 95% доверительного интервала (2,5% в каждом хвосте). Мы подсчитали, что LB = 20,0 — 2,92 = 17,1 и что UB = 20,0 + 2,92 = 22,9.
Мы подсчитали, что LB = 20,0 — 2,92 = 17,1 и что UB = 20,0 + 2,92 = 22,9.
2.11.1. Интерпретация доверительного интервала
Выражение в (1) не следует интерпретировать как означающее, что вязкость составляет 20 единиц и находится в диапазоне от LB (нижняя граница) до UB (верхняя граница) от 17,1 до 22,9 с 95% вероятность. На самом деле выборочное среднее лежит точно в середине диапазона со 100% уверенностью — именно так был рассчитан диапазон.
Выражение в (1) подразумевает , так это то, что \(\mu\) лежит в этом интервале. Доверительный интервал — это диапазон возможных значений для \(\mu\), а не для \(\overline{x}\). Доверительные интервалы предназначены для параметров, а не для статистики.
Обратите внимание, что верхняя и нижняя границы являются функцией выборки данных, используемой для вычисления \(\overline{x}\) и количества точек, \(n\).
 Если мы возьмем другую выборку данных, мы получим разные верхние и нижние границы.
Если мы возьмем другую выборку данных, мы получим разные верхние и нижние границы.Что означает уровень достоверности?
Вероятность того, что истинная вязкость населения \(\mu\) находится в заданном диапазоне. При достоверности 95% это означает, что 5% времени интервал не будет содержать истинного среднего. Таким образом, если мы собрали 20 наборов \(n\) выборок, в 19 случаях из 20 диапазон доверительных интервалов будет содержать истинное среднее значение, но ожидается, что один из этих 20 доверительных интервалов не будет содержать истинное среднее значение.
Что произойдет, если уровень достоверности изменится? Рассчитайте доверительные интервалы вязкости для 90%, 95%, 99%.
Уверенность
фунтов
УБ
90%
17,6
22,4
95%
17,1
22,9
99%
15,7
24,2
Поскольку уровень достоверности увеличивается , наш интервал расширяется, указывая на то, что у нас есть более надежный регион, но он менее точен.
 Чем шире интервал, тем больше уверенность в том, что истинный параметр будет внутри этой области.
Чем шире интервал, тем больше уверенность в том, что истинный параметр будет внутри этой области.Попробуйте:
# Попробуйте изменить это значение: конф.уровень
Что произойдет, если уровень достоверности равен 100 %?
Тогда доверительный интервал становится бесконечным. Мы на 100% уверены, что этот бесконечный диапазон содержит среднее значение генеральной совокупности, однако это бесполезный интервал. Проверьте это в приведенном выше коде; также попробуйте создать интервал с достоверностью 99,9 %, а затем с достоверностью 99,99 %.
Что произойдет, если мы увеличим значение \(n\)?
Как и следовало ожидать, при увеличении значения \(n\) ширина доверительного интервала уменьшается.
Возвращаясь к приведенному выше случаю, где на уровне 95% мы нашли доверительный интервал \([17,1; 22,9]\) для вязкости тюка.
 Что, если бы мы тщательно проанализировали тюк и обнаружили, что вязкость населения равна 23,2. Какова вероятность того, что это произойдет?
Что, если бы мы тщательно проанализировали тюк и обнаружили, что вязкость населения равна 23,2. Какова вероятность того, что это произойдет?Менее 5% времени.
2.11.2. Доверительный интервал для среднего нормального распределения
Цель состоит в том, чтобы формализовать расчеты доверительного интервала \(\overline{x}\) для выборки \(n\)
независимых точек, взятых из
нормальное распределение.
Обязательно проверьте эти два предположения, прежде чем двигаться дальше.
Возможны 2 случая: в одном известно стандартное отклонение генеральной совокупности (маловероятно), а в другом нет (обычный случай). Безопаснее использовать доверительный интервал для случая, когда стандартное отклонение неизвестно, так как это более консервативный (т. е. более широкий) интервал.
е. более широкий) интервал.
Детальный вывод для двух случаев был рассмотрен в предыдущих разделах.
2.11.2.1. Случай A. Дисперсия известна
Когда дисперсия известна, доверительный интервал определяется формулой (2) ниже, полученной из этого \(z\)-отклонения: \(z = \dfrac{\overline{x} - \mu}{\sigma/\ sqrt{n}}\) обратно в раздел о нормальном распределении.
(2)\[\begin{split}\begin{массив}{rcccl} - c_n &\leq& z &\leq & +c_n\\ - c_n &\leq& \displaystyle \frac{\overline{x} - \mu}{\sigma/\sqrt{n}} &\leq & +c_n\\ \overline{x} - c_n \dfrac{\sigma}{\sqrt{n}} &\leq& \mu &\leq& \overline{x} + c_n\dfrac{\sigma}{\sqrt{n}} \\ \text{LB} &\leq& \mu &\leq& \text{UB} \конец{массив}\конец{разделить}\]
Значения \(c_n\) составляют qnorm(1 - 0,05/2) = 1,96 , когда мы используем 95% доверительный интервал (2,5% в каждом хвосте).
2.11.2.2. Случай B. Дисперсия неизвестна
В более реалистичном случае, когда дисперсия неизвестна, мы используем уравнение, полученное в разделе о t-распределении и повторенное здесь ниже.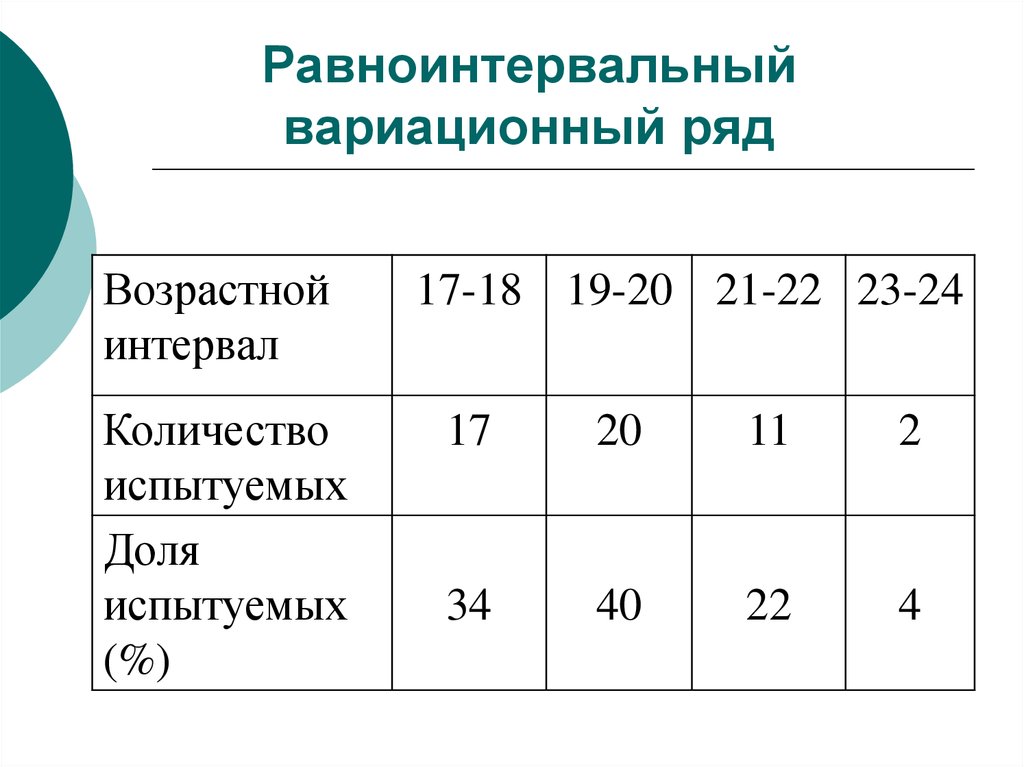 Это получено из \(z\)-отклонения: \(z = \dfrac{\overline{x} - \mu}{s/\sqrt{n}}\):
Это получено из \(z\)-отклонения: \(z = \dfrac{\overline{x} - \mu}{s/\sqrt{n}}\):
(3)\[\begin{split}\begin{массив}{rcccl} - c_t &\leq& z &\leq & +c_t\\ - c_t &\leq& \displaystyle \frac{\overline{x} - \mu}{s/\sqrt{n}} &\leq & +c_t\\ \overline{x} - c_t \dfrac{s}{\sqrt{n}} &\leq& \mu &\leq& \overline{x} + c_t\dfrac{s}{\sqrt{n}} \\ \text{LB} &\leq& \mu &\leq& \text{UB} \конец{массив}\конец{разделить}\] 92\), то мы можем сравнить 2 интервала в уравнениях (2) и (3). Единственная разница будет заключаться в значении \(c_n\) из нормального распределения и \(c_t\) из \(t\)-распределения. Для типичных значений, используемых в качестве уровней достоверности, от 90% до 99,9%, значения \(c_t > c_n\) для любых степеней свободы.
Это означает, что доверительные интервалы шире для случая, когда стандартное отклонение неизвестно, что приводит к более консервативным результатам, отражающим нашу неопределенность параметра стандартного отклонения, \(\сигма\).

 рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты; 45
45 45
45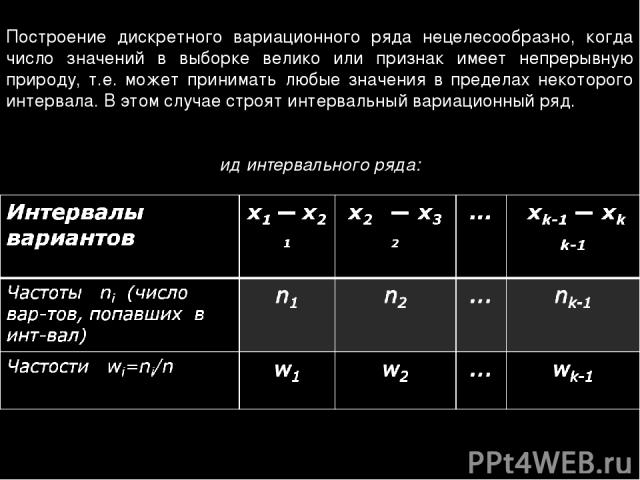
 43
43 9)
9) 09
09 3;
7.2)
3;
7.2) 1
1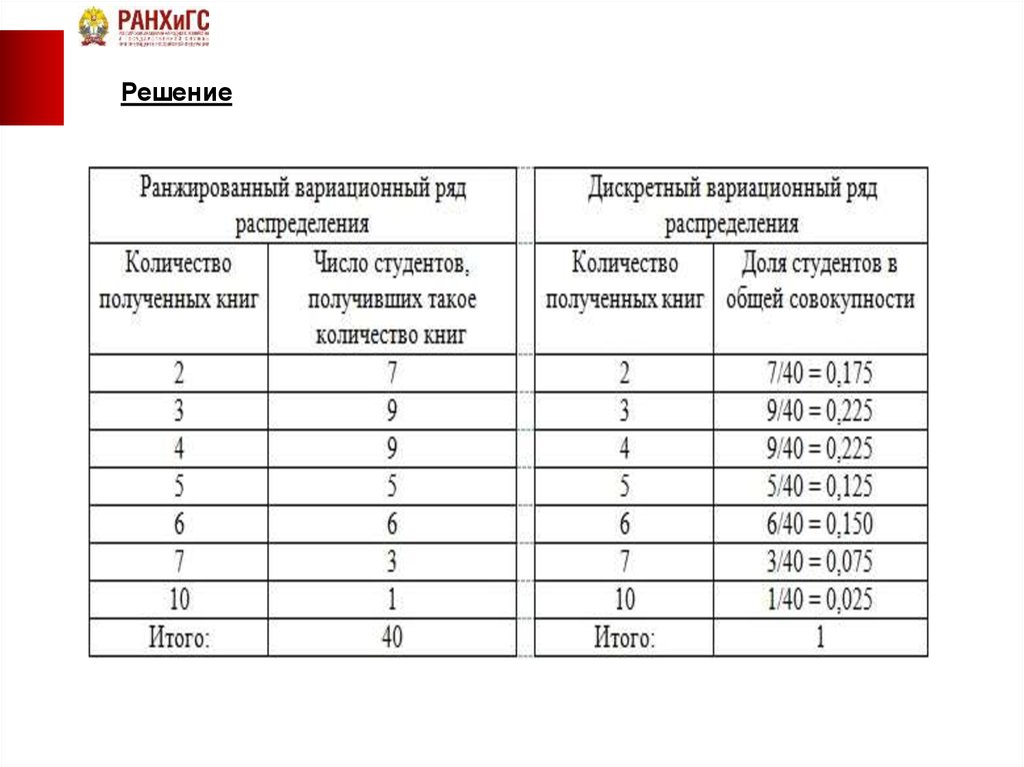 5
5 Для этого диапозон варьирования признака разбивают на несколько равных частей и указывают число вариант, попадающих в каждый частичный интервал (интервальная частота).
Для этого диапозон варьирования признака разбивают на несколько равных частей и указывают число вариант, попадающих в каждый частичный интервал (интервальная частота).

 Абсциссы следующих точек этой ломаной будут соответствовать концам интервалов, а ординаты – соответствующим накопленным частотам или частостям.
Абсциссы следующих точек этой ломаной будут соответствовать концам интервалов, а ординаты – соответствующим накопленным частотам или частостям.
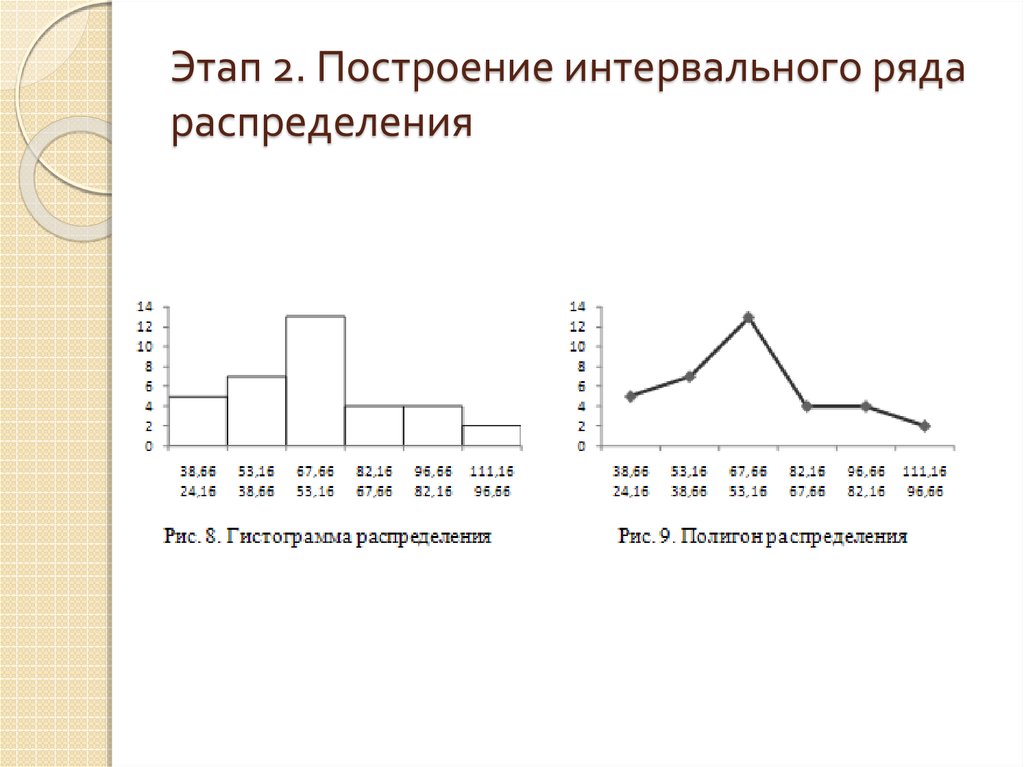
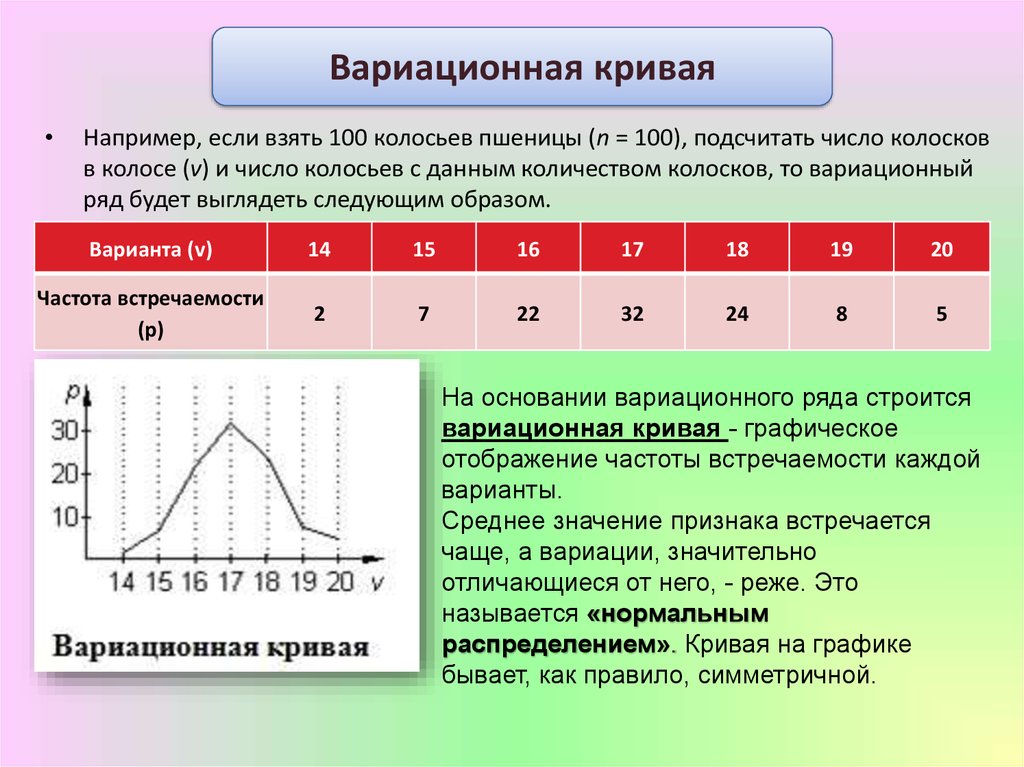 Найти значение параметра а. Построить интервальный ряд распределения данной выборки с указанием частот и относительных частот.
Найти значение параметра а. Построить интервальный ряд распределения данной выборки с указанием частот и относительных частот.

 В этом случае средний квадрат отклонений будет больше на вполне определенную величину — на квадрат разницы между средним и этим условно принятым значением.
В этом случае средний квадрат отклонений будет больше на вполне определенную величину — на квадрат разницы между средним и этим условно принятым значением. ndarray]:
"""
Возвращает (кортеж) среднее значение и доверительный интервал для заданных данных.
Данные представляют собой итерацию np.arrayable.
ссылка:
- https://stackoverflow.com/a/15034143/1601580
- https://github.com/WangYueFt/rfs/blob/f8c837ba93c62dd0ac68a2f4019c619aa86b8421/eval/meta_eval.py#L19
"""
импортировать scipy.stats
импортировать numpy как np
а: np.ndarray = 1,0 * np.array (данные)
n: интервал = длина (а)
если п == 1:
журнал импорта
logging.warning('Первое измерение ваших данных равно 1, возможно, вы хотели перенести свои данные? Или удалить'
'одноэлементное измерение?')
m, se = a.mean(), scipy.stats.sem(a)
tp = scipy.stats.t.ppf((1 + достоверность) / 2., n - 1)
ч = се * тп
возврат м, ч
определение ci_test_float():
импортировать numpy как np
# - один НЕПРАВИЛЬНЫЙ набор данных размера 1 на N
data = np.random.randn(1, 30) # выдает ошибку, потому что len устанавливает n=1, так что не эта форма!
m, ci = средний_доверительный_интервал (данные)
print('-- вы должны получить среднее значение и список nan ci (поскольку данные в неправильном формате, он считает, что это 30 наборов данных '
'длина 1.
ndarray]:
"""
Возвращает (кортеж) среднее значение и доверительный интервал для заданных данных.
Данные представляют собой итерацию np.arrayable.
ссылка:
- https://stackoverflow.com/a/15034143/1601580
- https://github.com/WangYueFt/rfs/blob/f8c837ba93c62dd0ac68a2f4019c619aa86b8421/eval/meta_eval.py#L19
"""
импортировать scipy.stats
импортировать numpy как np
а: np.ndarray = 1,0 * np.array (данные)
n: интервал = длина (а)
если п == 1:
журнал импорта
logging.warning('Первое измерение ваших данных равно 1, возможно, вы хотели перенести свои данные? Или удалить'
'одноэлементное измерение?')
m, se = a.mean(), scipy.stats.sem(a)
tp = scipy.stats.t.ppf((1 + достоверность) / 2., n - 1)
ч = се * тп
возврат м, ч
определение ci_test_float():
импортировать numpy как np
# - один НЕПРАВИЛЬНЫЙ набор данных размера 1 на N
data = np.random.randn(1, 30) # выдает ошибку, потому что len устанавливает n=1, так что не эта форма!
m, ci = средний_доверительный_интервал (данные)
print('-- вы должны получить среднее значение и список nan ci (поскольку данные в неправильном формате, он считает, что это 30 наборов данных '
'длина 1.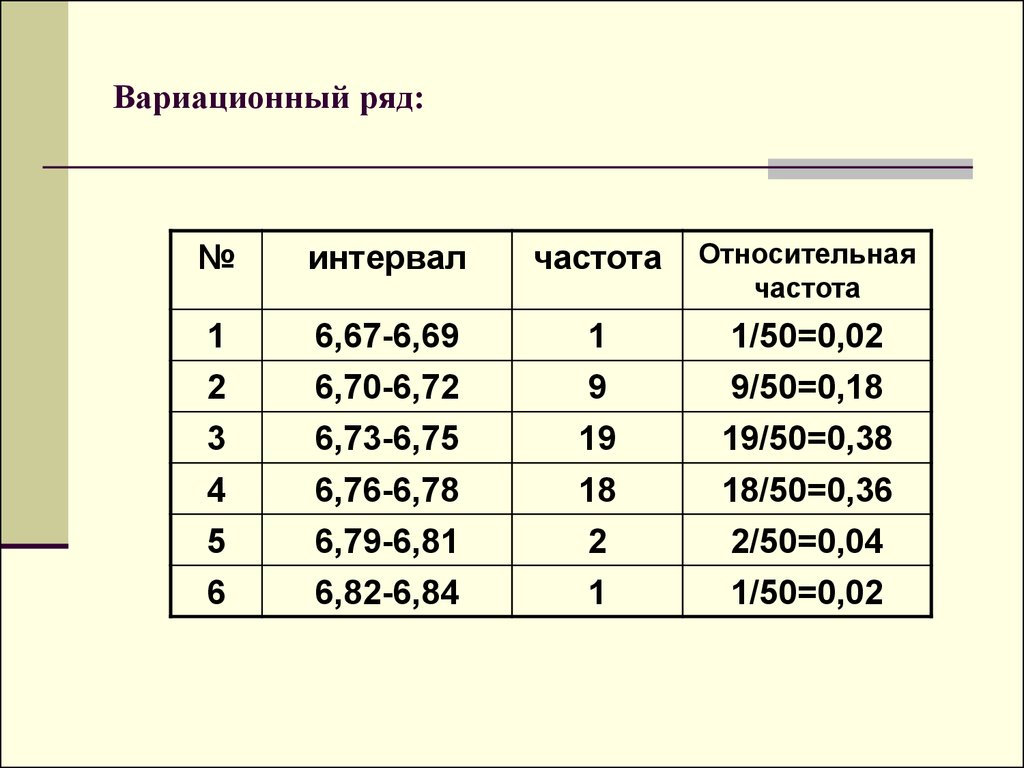 ')
печать (м, ки)
# правильные данные как N на 1
данные = np.random.randn (30, 1)
m, ci = средний_доверительный_интервал (данные)
print('-- дает среднее значение и список длины 1 для одного ЭК (поскольку он думает, что у вас есть один набор данных)')
печать (м, ки)
# несколько наборов данных (7) размера N (=30)
данные = np.random.randn (30, 7)
print('-- дает 7 CI для 7 наборов данных длиной 30. 30 - это число, которое нужно увеличить, если вы использовали z(p)'
«из-за CLT».)
m, ci = средний_доверительный_интервал (данные)
печать (м, ки)
ci_test_float()
')
печать (м, ки)
# правильные данные как N на 1
данные = np.random.randn (30, 1)
m, ci = средний_доверительный_интервал (данные)
print('-- дает среднее значение и список длины 1 для одного ЭК (поскольку он думает, что у вас есть один набор данных)')
печать (м, ки)
# несколько наборов данных (7) размера N (=30)
данные = np.random.randn (30, 7)
print('-- дает 7 CI для 7 наборов данных длиной 30. 30 - это число, которое нужно увеличить, если вы использовали z(p)'
«из-за CLT».)
m, ci = средний_доверительный_интервал (данные)
печать (м, ки)
ci_test_float()
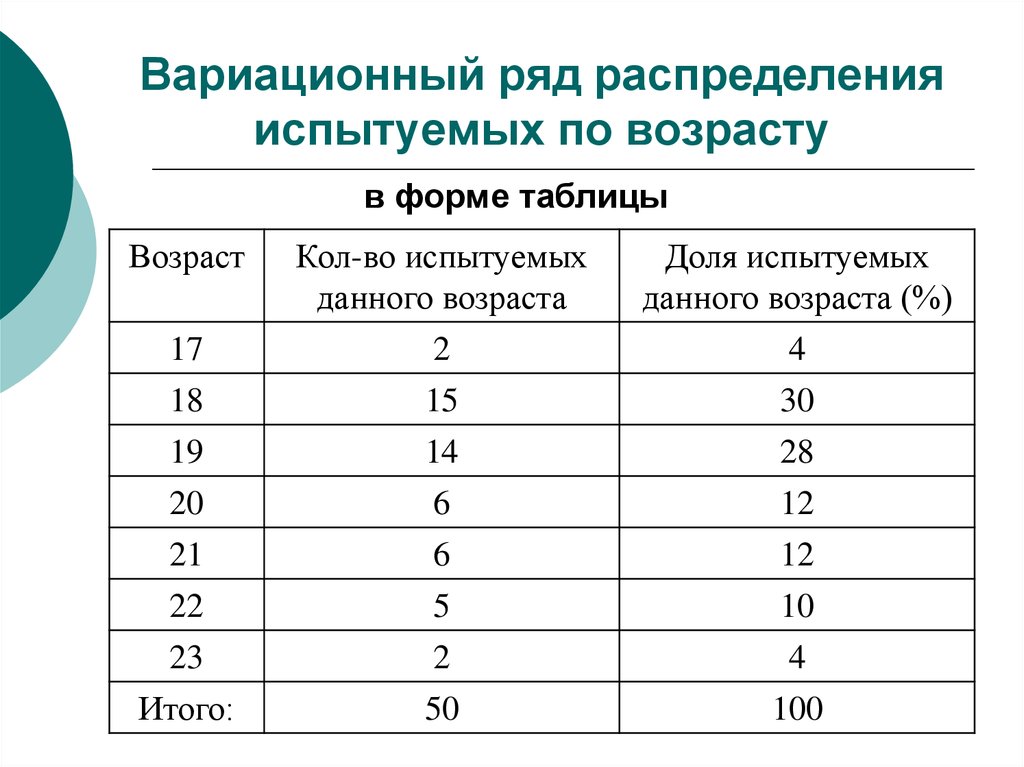 30 - это число, которое нужно увеличить, если вы использовали z(p) из-за CLT.
-0,03585104402718902 [0,31867309 0,35619134 0,34860011 0,3812853 0,44334033 0,35841138
0,40739732]
30 - это число, которое нужно увеличить, если вы использовали z(p) из-за CLT.
-0,03585104402718902 [0,31867309 0,35619134 0,34860011 0,3812853 0,44334033 0,35841138
0,40739732]
 """
n: интервал = длина (данные)
означает: Tensor = data.mean()
# se: Tensor = scipy.stats.sem(data) # вычислить стандартную ошибку
# se, mean: Tensor = torch.std_mean(data, unbiased=True) # вычислить стандартную ошибку
se: Tensor = data.std(unbiased=True) / (n ** 0,5)
t_p: float = float(scipy.stats.t.ppf((1 + достоверность)/2., n - 1))
ci = t_p * se
среднее значение возврата, ci
9* Вам не нужно будет оценивать это. Этот анализ предполагает
что оценщик/значение, которое вы оцениваете, является истинным средним значением с использованием среднего значения выборки (оценщика). Поскольку обычно используется
t.val или z.val (второе для стандартизированной с.в. нормали), то это означает приближение, что mu_n ~ гауссовское
должен держать. Это, скорее всего, верно, если n >= 0. Обратите внимание, что это похоже на статистическую теорию обучения, где мы используем
оценщик MLE/ERM для выбора функции с дельта-, гамма-рассуждениями и т. д. Обратите внимание, что если вы занимаетесь алгеброй, вы также можете
скажите, что среднее значение выборки находится в этом интервале, но относительно mu^* но это рождается, никого не волнует, так как вы не знаете mu^*
так что это не полезно.
"""
n: интервал = длина (данные)
означает: Tensor = data.mean()
# se: Tensor = scipy.stats.sem(data) # вычислить стандартную ошибку
# se, mean: Tensor = torch.std_mean(data, unbiased=True) # вычислить стандартную ошибку
se: Tensor = data.std(unbiased=True) / (n ** 0,5)
t_p: float = float(scipy.stats.t.ppf((1 + достоверность)/2., n - 1))
ci = t_p * se
среднее значение возврата, ci
9* Вам не нужно будет оценивать это. Этот анализ предполагает
что оценщик/значение, которое вы оцениваете, является истинным средним значением с использованием среднего значения выборки (оценщика). Поскольку обычно используется
t.val или z.val (второе для стандартизированной с.в. нормали), то это означает приближение, что mu_n ~ гауссовское
должен держать. Это, скорее всего, верно, если n >= 0. Обратите внимание, что это похоже на статистическую теорию обучения, где мы используем
оценщик MLE/ERM для выбора функции с дельта-, гамма-рассуждениями и т. д. Обратите внимание, что если вы занимаетесь алгеброй, вы также можете
скажите, что среднее значение выборки находится в этом интервале, но относительно mu^* но это рождается, никого не волнует, так как вы не знаете mu^*
так что это не полезно. *(х) — ид.
Std_n против t_p*std_n/ sqrt(n)
- std_n = var(x) более пессимистичен, но выполняется всегда. Никогда не сжимается как n->infinity
- но если n мало, то pCI может быть слишком маленьким, и вы «лжете себе». Итак, если у вас очень мало данных
возможно, лучше использовать std_n для CI. Это относится к проблеме 99,9%. Надеюсь, стандартный размер не слишком велик для вашего
эксперименты признать недействительными.
ссылка:
- https://stats.stackexchange.com/questions/554332/confidence-interval-given-the-population-mean-and-standard-deviation?noredirect=1&lq=1
- https://stackoverflow.com/questions/70356922/what-is-the-proper-way-to-compute-95-confidence-intervals-with-pytorch-for-clas
- https://www.youtube.com/watch?v=MzvRQFYUEFU&list=PLUl4u3cNGP60hI9ATjSFgLZpbNJ7myAg6&index=205
"""
*(х) — ид.
Std_n против t_p*std_n/ sqrt(n)
- std_n = var(x) более пессимистичен, но выполняется всегда. Никогда не сжимается как n->infinity
- но если n мало, то pCI может быть слишком маленьким, и вы «лжете себе». Итак, если у вас очень мало данных
возможно, лучше использовать std_n для CI. Это относится к проблеме 99,9%. Надеюсь, стандартный размер не слишком велик для вашего
эксперименты признать недействительными.
ссылка:
- https://stats.stackexchange.com/questions/554332/confidence-interval-given-the-population-mean-and-standard-deviation?noredirect=1&lq=1
- https://stackoverflow.com/questions/70356922/what-is-the-proper-way-to-compute-95-confidence-intervals-with-pytorch-for-clas
- https://www.youtube.com/watch?v=MzvRQFYUEFU&list=PLUl4u3cNGP60hI9ATjSFgLZpbNJ7myAg6&index=205
"""
 Другие JavaScript из этой серии относятся к разным областям применения в разделе МЕНЮ на этой странице.
Другие JavaScript из этой серии относятся к разным областям применения в разделе МЕНЮ на этой странице. Способ интерпретировать это состоит в том, чтобы представить бесконечное количество выборок из одной и той же совокупности, по крайней мере, 95% вычисленных интервалов будут содержать среднее значение совокупности (или дисперсию), а не более 5% — нет. Однако неверно утверждать: «Мне 95% уверены, что параметр популяции попадает в интервал».
Способ интерпретировать это состоит в том, чтобы представить бесконечное количество выборок из одной и той же совокупности, по крайней мере, 95% вычисленных интервалов будут содержать среднее значение совокупности (или дисперсию), а не более 5% — нет. Однако неверно утверждать: «Мне 95% уверены, что параметр популяции попадает в интервал». Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Руководством по добросовестному использованию образовательных мультимедиа от 1996 г. разрешено только в некоммерческих целях и в учебных целях.
Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Руководством по добросовестному использованию образовательных мультимедиа от 1996 г. разрешено только в некоммерческих целях и в учебных целях. 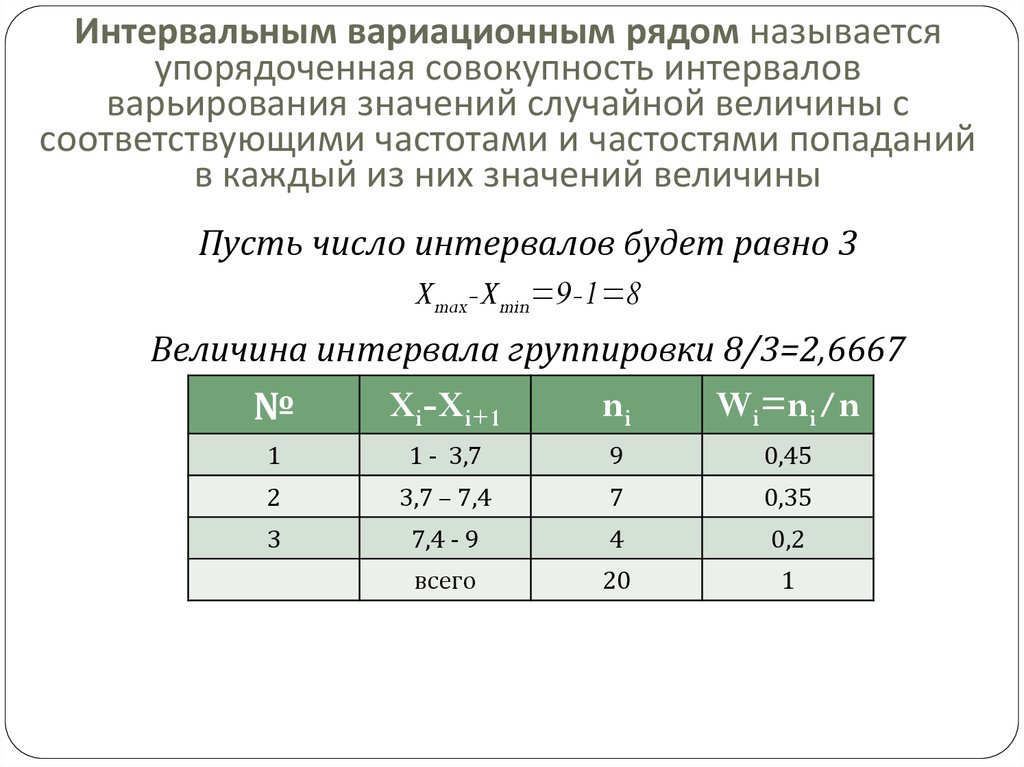 Если мы возьмем другую выборку данных, мы получим разные верхние и нижние границы.
Если мы возьмем другую выборку данных, мы получим разные верхние и нижние границы.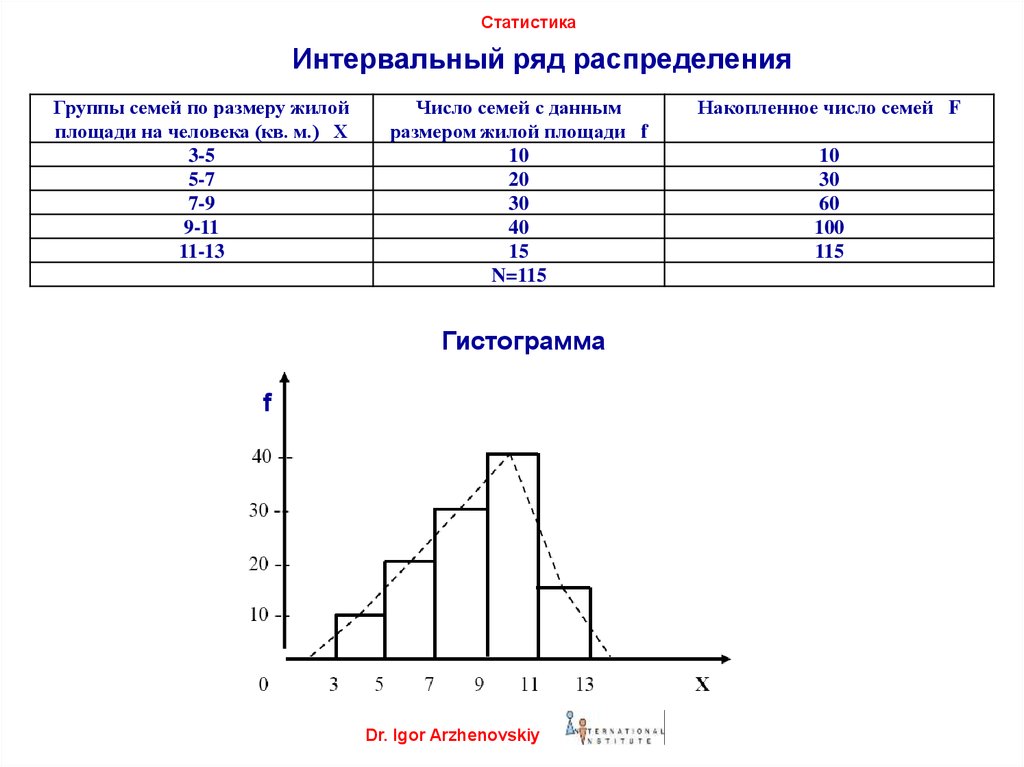 Чем шире интервал, тем больше уверенность в том, что истинный параметр будет внутри этой области.
Чем шире интервал, тем больше уверенность в том, что истинный параметр будет внутри этой области.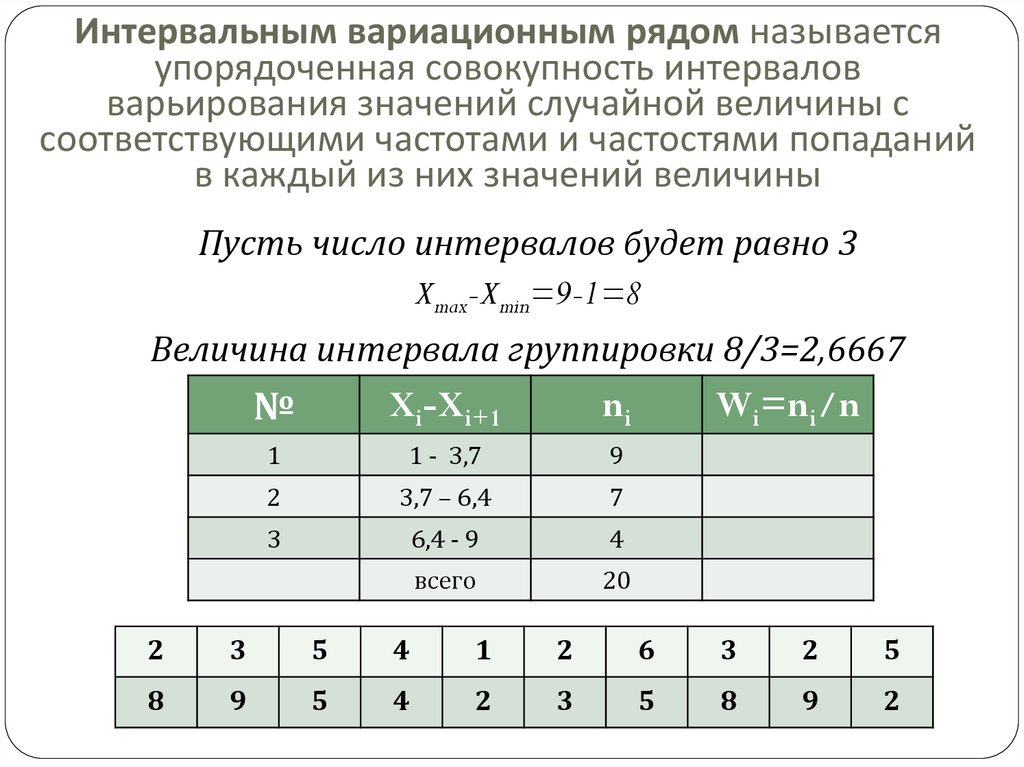 Что, если бы мы тщательно проанализировали тюк и обнаружили, что вязкость населения равна 23,2. Какова вероятность того, что это произойдет?
Что, если бы мы тщательно проанализировали тюк и обнаружили, что вязкость населения равна 23,2. Какова вероятность того, что это произойдет?