Как быстро найти уравнение регрессии в Excel
Редакция Кодкампа
читать 2 мин
Вы можете использовать функцию ЛИНЕЙН , чтобы быстро найти уравнение регрессии в Excel.
Эта функция использует следующий базовый синтаксис:
LINEST(known_y's, known_x's)
куда:
- known_y’s : столбец значений для переменной ответа.
- known_x’s : один или несколько столбцов значений для переменных-предикторов.
В следующих примерах показано, как использовать эту функцию для поиска уравнения регрессии для простой модели линейной регрессии и модели множественной линейной регрессии .
Пример 1: Найдите уравнение для простой линейной регрессииПредположим, у нас есть следующий набор данных, который содержит одну предикторную переменную (x) и одну переменную ответа (y):
Мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить простое уравнение линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:B15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для простой модели линейной регрессии:
Вот как интерпретировать вывод:
- Коэффициент на перехват 3,115589.
- Коэффициент наклона равен 0,479072.
Используя эти значения, мы можем написать уравнение для этой простой модели регрессии:
у = 3,115589 + 0,478072 (х)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
Пример 2: найти уравнение для множественной линейной регрессииПредположим, у нас есть следующий набор данных, который содержит две переменные-предикторы (x1 и x2) и одну переменную ответа (y):
Мы можем ввести следующую формулу в ячейку E1 , чтобы вычислить уравнение множественной линейной регрессии для этого набора данных:
=LINEST( A2:A15 , B2:C15 )
Как только мы нажмем ENTER , будут показаны коэффициенты для модели множественной линейной регрессии:
Вот как интерпретировать вывод:
- Коэффициент на перехват 1. 471205
- Коэффициент для x1 равен 0,047243.
- Коэффициент для x2 равен 0,406344.
471205Используя эти значения, мы можем написать уравнение для этой модели множественной регрессии:
у = 1,471205 + 0,047243 (х1) + 0,406344 (х2)
Примечание.Чтобы найти p-значения для коэффициентов, значение r-квадрата модели и другие показатели для модели множественной линейной регрессии в Excel, следует использовать функцию регрессии из пакета анализа данных. В этом руководстве объясняется, как это сделать.
В следующих руководствах представлена дополнительная информация о регрессии в Excel:
Как интерпретировать вывод регрессии в Excel
Как добавить линию регрессии на диаграмму рассеяния в Excel
Как выполнить полиномиальную регрессию в Excel
Как выполнить простую линейную регрессию в Excel
Простая линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между объясняющей переменной x и переменной отклика y.
В этом руководстве объясняется, как выполнить простую линейную регрессию в Excel.
Пример: простая линейная регрессия в ExcelПредположим, нас интересует взаимосвязь между количеством часов, которое студент тратит на подготовку к экзамену, и полученной им экзаменационной оценкой.
Чтобы исследовать эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя часы обучения в качестве независимой переменной и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести простую линейную регрессию.
Шаг 1: Введите данные.
Введите следующие данные о количестве часов обучения и экзаменационном балле, полученном для 20 студентов:
Шаг 2: Визуализируйте данные.
Прежде чем мы выполним простую линейную регрессию, полезно создать диаграмму рассеяния данных, чтобы убедиться, что действительно существует линейная зависимость между отработанными часами и экзаменационным баллом.
Выделите данные в столбцах A и B. В верхней ленте Excel перейдите на вкладку « Вставка ». В группе « Диаграммы » нажмите « Вставить разброс» (X, Y) и выберите первый вариант под названием « Разброс ». Это автоматически создаст следующую диаграмму рассеяния:
Количество часов обучения показано на оси x, а баллы за экзамены показаны на оси y. Мы видим, что между двумя переменными существует линейная зависимость: большее количество часов обучения связано с более высокими баллами на экзаменах.
Чтобы количественно оценить взаимосвязь между этими двумя переменными, мы можем выполнить простую линейную регрессию.
Шаг 3: Выполните простую линейную регрессию.
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .
Как только вы нажмете « Анализ данных», появится новое окно.
Выберите «Регрессия» и нажмите «ОК».
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для независимой переменной.
Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны.
В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии.
Затем нажмите ОК .
Автоматически появится следующий вывод:
Шаг 4: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,7273.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющей переменной. В этом примере 72,73 % различий в баллах за экзамены можно объяснить количеством часов обучения.
Стандартная ошибка: 5.
2805.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,2805 единиц.
Ф: 47,9952.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель статистически значимой. Другими словами, он говорит нам, имеет ли независимая переменная статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на наличие статистически значимой связи между отработанными часами и полученными экзаменационными баллами.
Коэффициенты: коэффициенты дают нам числа, необходимые для написания оценочного уравнения регрессии. В этом примере оцененное уравнение регрессии:
экзаменационный балл = 67,16 + 5,2503*(часов)
Мы интерпретируем коэффициент для часов как означающий, что за каждый дополнительный час обучения ожидается увеличение экзаменационного балла в среднем на 5,2503.
Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится без часов, составляет 67,16 .
Мы можем использовать это оценочное уравнение регрессии для расчета ожидаемого экзаменационного балла для учащегося на основе количества часов, которые он изучает.
Например, ожидается, что студент, который занимается три часа, получит на экзамене 82,91 балла:
экзаменационный балл = 67,16 + 5,2503*(3) = 82,91
Дополнительные ресурсыВ следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как создать остаточный график в Excel
Как построить интервал прогнозирования в Excel
Как создать график QQ в Excel
Линейная регрессия Excel: пошаговые инструкции
Что такое линейная регрессия?
Линейная регрессия — это тип анализа данных, который рассматривает линейную связь между зависимой переменной и одной или несколькими независимыми переменными.
Обычно он используется для визуального отображения силы взаимосвязи или корреляции между различными факторами и разбросом результатов — и все это с целью объяснения поведения зависимой переменной. Целью модели линейной регрессии является оценка величины взаимосвязи между переменными и ее статистической значимости.
Скажем, мы хотели проверить силу связи между количеством съеденного мороженого и ожирением. Мы возьмем независимую переменную, количество мороженого, и свяжем ее с зависимой переменной, ожирением, чтобы увидеть, есть ли связь. Учитывая, что регрессия является графическим отображением этой взаимосвязи, чем ниже изменчивость данных, тем сильнее взаимосвязь и тем точнее соответствие линии регрессии.
В финансах линейная регрессия используется для определения взаимосвязей между ценами на активы и экономическими данными в ряде приложений. Например, он используется для определения весов факторов в модели Фамы-Френча и является основой для определения коэффициента бета акций в модели ценообразования капитальных активов (CAPM).
Здесь мы рассмотрим, как использовать данные, импортированные в Microsoft Excel, для выполнения линейной регрессии и как интерпретировать результаты.
Ключевые выводы
- Линейная регрессия моделирует взаимосвязь между зависимой и независимой переменной (переменными).
- Линейная регрессия, также известная как метод наименьших квадратов (OLS), по существу оценивает линию наилучшего соответствия среди всех переменных в модели.
- Регрессионный анализ можно считать устойчивым, если переменные независимы, отсутствует гетероскедастичность и члены ошибок переменных не коррелированы.
- Моделирование линейной регрессии в Excel упрощается с помощью пакета инструментов анализа данных.
- Выходные данные регрессии можно интерпретировать как по размеру, так и по силе корреляции между одной или несколькими переменными зависимой переменной.
Важные соображения
Есть несколько критических предположений о вашем наборе данных, которые должны быть верными, чтобы продолжить регрессионный анализ.
В противном случае результаты будут интерпретированы неправильно или в них будет систематическая ошибка:
- Переменные должны быть действительно независимыми (используя критерий хи-квадрат).
- Данные не должны иметь разные дисперсии ошибок (это называется гетероскедастичностью (также пишется как гетероскедастичность)).
- Члены ошибок каждой переменной не должны быть коррелированы. Если нет, это означает, что переменные последовательно коррелированы.
Если эти три пункта кажутся сложными, они могут быть такими. Но эффект того, что одно из этих соображений не соответствует действительности, является предвзятой оценкой. По сути, вы исказили бы отношения, которые вы измеряете.
Вывод регрессии в Excel
Первым шагом при выполнении регрессионного анализа в Excel является повторная проверка того, установлен ли бесплатный подключаемый модуль Excel Data Analysis ToolPak. Этот плагин позволяет очень легко рассчитать ряд статистических данных.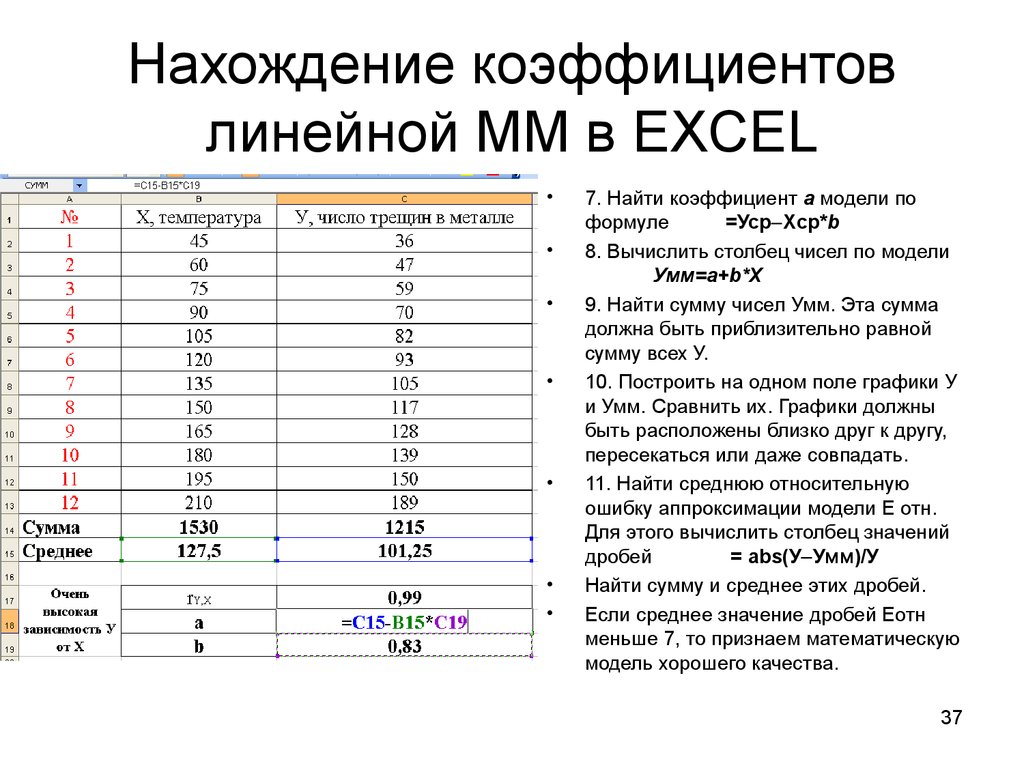
Для построения графика линейной регрессии требуется , а не , но это упрощает создание статистических таблиц. Чтобы проверить, установлено ли оно, выберите «Данные» на панели инструментов. Если «Анализ данных» является опцией, функция установлена и готова к использованию. Если он не установлен, вы можете запросить этот параметр, нажав кнопку «Офис» и выбрав «Параметры Excel».
С помощью Data Analysis ToolPak создание выходных данных регрессии выполняется всего несколькими щелчками мыши.
Независимая переменная в Excel находится в диапазоне X.
Скажем, учитывая доходность S&P 500, мы хотим знать, можем ли мы оценить силу и взаимосвязь доходности акций Visa (V). Данные о возврате акций Visa (V) заполняют столбец 1 в качестве зависимой переменной. S&P 500 возвращает данные, заполняющие столбец 2 в качестве независимой переменной.
- Выберите «Данные» на панели инструментов. Появится меню «Данные».
- Выберите «Анализ данных». Отобразится диалоговое окно Анализ данных — Инструменты анализа.
- В меню выберите «Регрессия» и нажмите «ОК».
- В диалоговом окне «Регрессия» щелкните поле «Входной диапазон Y» и выберите данные зависимой переменной (доходность акций Visa (V)).
- Щелкните поле «Входной диапазон X» и выберите данные независимой переменной (возврат S&P 500).
- Нажмите «ОК», чтобы просмотреть результаты.
[Примечание. Если таблица кажется маленькой, щелкните изображение правой кнопкой мыши и откройте в новой вкладке для более высокого разрешения.]
Интерпретация результатов
Используя эти данные (то же самое из нашей статьи о R-квадрате), мы получаем следующую таблицу:
Значение R 2 , также известное как коэффициент детерминации, измеряет долю вариации зависимой переменной, объясняемую независимой переменной, или насколько хорошо регрессионная модель соответствует данным. Значение R 2 находится в диапазоне от 0 до 1, и более высокое значение указывает на лучшее соответствие.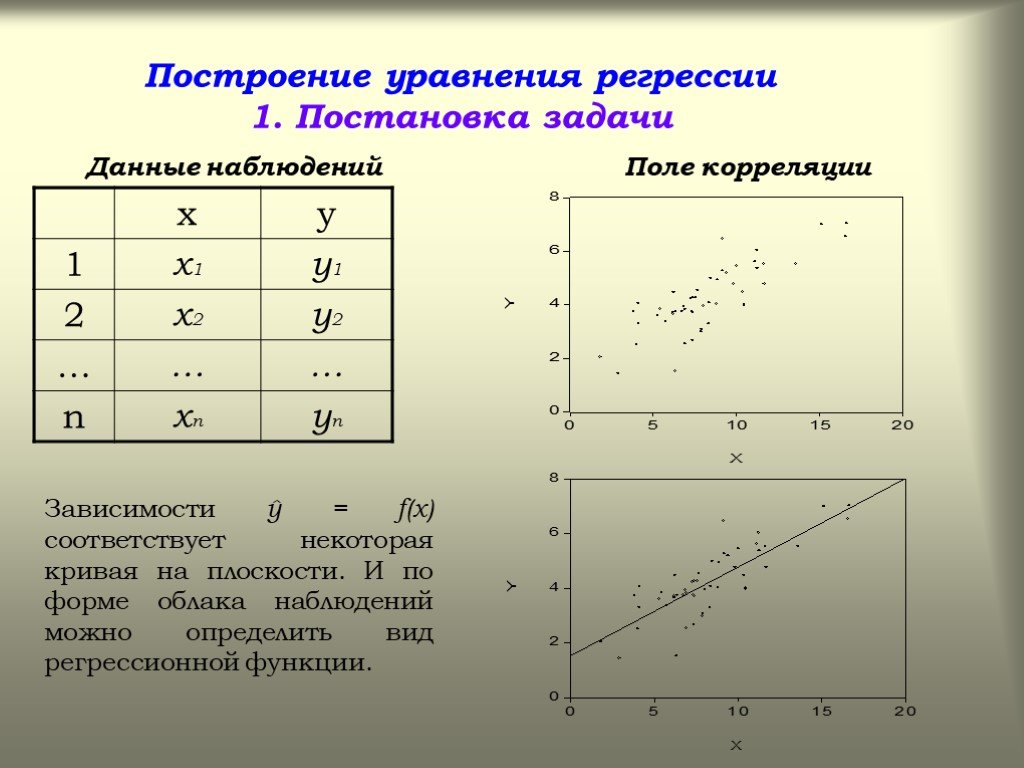
Интерпретация результатов
Суть в том, что изменения в акциях Visa, похоже, сильно коррелируют с S&P 500. соответствующее изменение S&P 500 на 1,36 пункта.
Однако в этот момент аналитик может принять во внимание некоторую осторожность по следующим причинам:
- При наличии только одной переменной в модели неясно, влияет ли V на цены S&P 500, если S&P 500 влияет на цены V, или если какая-то ненаблюдаемая третья переменная влияет на обе цены.
- Visa является компонентом S&P 500, поэтому здесь может быть корреляция между переменными.
- Есть только 20 наблюдений, которых может быть недостаточно, чтобы сделать правильный вывод.
- Данные представляют собой временной ряд, поэтому также может быть автокорреляция.
- Исследуемый период времени может не быть репрезентативным для других периодов времени.
График регрессии в Excel
Мы можем наметить регрессию в Excel, выделив данные и отобразив их в виде точечной диаграммы. Чтобы добавить линию регрессии, выберите «Добавить элемент диаграммы» в меню «Дизайн диаграммы». В диалоговом окне выберите «Линия тренда», а затем «Линейная линия тренда». Чтобы добавить R
Как интерпретировать линейную регрессию?
Выходные данные регрессионной модели будут давать различные числовые результаты.
Коэффициенты (или бета) говорят вам об ассоциации между независимой переменной и зависимой переменной, сохраняя все остальное постоянным. Если коэффициент равен, скажем, +0,12, это говорит о том, что каждое изменение этой переменной на 1 пункт соответствует изменению зависимой переменной на 0,12 в том же направлении. Если бы вместо этого было -3,00, это означало бы, что изменение объясняющей переменной на 1 пункт приводит к 3-кратному изменению зависимой переменной в противоположном направлении.
Как узнать, является ли регресс значительным?
В дополнение к получению бета-коэффициентов, регрессионный результат также покажет тесты статистической значимости на основе стандартной ошибки каждого коэффициента (например, значение p и доверительные интервалы). Часто аналитики используют p-значение 0,05 или меньше, чтобы указать значимость; если p-значение больше, то вы не можете исключить шанс или случайность результирующего бета-коэффициента. Другими тестами значимости в регрессионной модели могут быть t-тесты для каждой переменной, а также F-статистика или хи-квадрат для совместной значимости всех переменных в модели вместе.
Как интерпретировать R-квадрат линейной регрессии?
R 2 (R-квадрат) — статистическая мера качества соответствия модели линейной регрессии (от 0,00 до 1,00), также известная как коэффициент детерминации. В целом, чем выше R 2 , тем лучше подходит модель. R-квадрат также можно интерпретировать как то, какая часть вариации зависимой переменной объясняется независимыми (пояснительными) переменными в модели. Таким образом, R-квадрат 0,50 предполагает, что половина всех изменений, наблюдаемых в зависимой переменной, может быть объяснена зависимой переменной (переменными).
Расчеты линейной регрессии и корреляции в Excel
В Excel можно выполнить простую линейную регрессию двумя способами: 1) с помощью встроенных функций Excel или 2) с помощью функции регрессии в пакете инструментов анализа (который необходимо установить). Сначала я проиллюстрирую встроенные функции, а затем ToolPak, который обычно проще.
Вот простой пример, не связанный с общественным здравоохранением, для иллюстрации анализа с помощью Excel.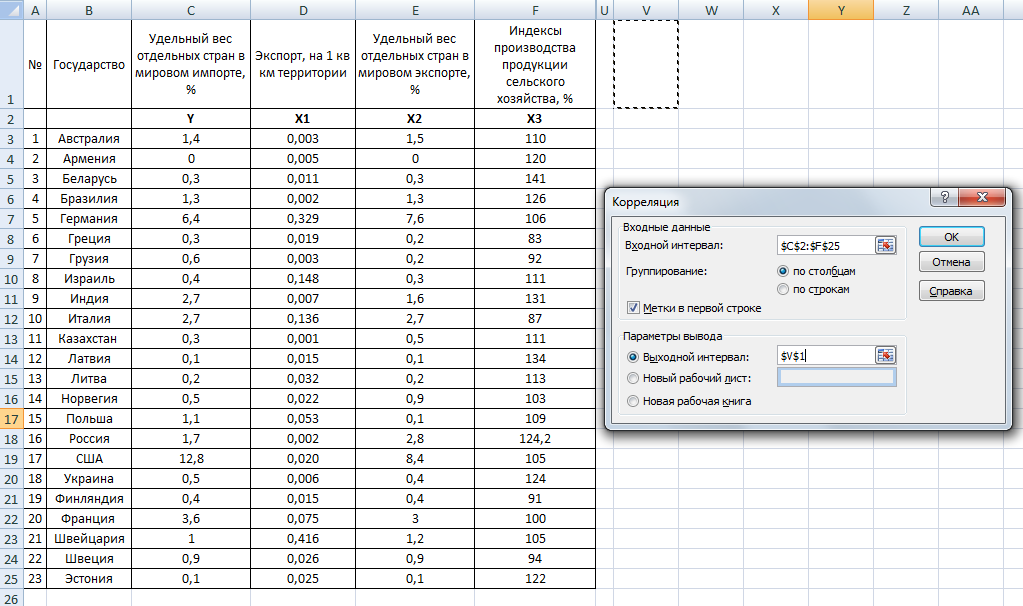
Человек начинает работать и составляет график своих сбережений за десятинедельный период. Независимая переменная (столбец «X»: интересующий «предиктор» или «воздействие») представляет собой время в неделях, а интересующий результат (столбец «Y», зависимая переменная) — это общие накопленные сбережения. Данные были записаны в два столбца рядом в Excel. На изображении ниже показан рабочий лист в Epi-Tools.XLSX под названием «Корреляция и линейная регрессия», в котором был проведен анализ этих данных.
Данные были введены в бирюзовые ячейки, и точечная диаграмма была построена, как описано в видео, которое вы видели ранее в модуле. Я щелкнул правой кнопкой мыши точку данных и выбрал «Добавить линию тренда», чтобы добавить линию, которая минимизирует расстояние от точек наблюдения до линии.
Линия тренда — это «линия наилучшего соответствия» для данных, она определяется наклоном и точкой пересечения с осью Y (линия пересекает ось Y, если ее продолжить влево).
92- Функции наклона и пересечения требуют, чтобы сначала был введен диапазон для переменной «Y» (результат), а затем переменная «X» (предиктор).
- Коэффициент вариации — это просто квадрат « р».
- Стьюдентная статистика вычисляется с использованием приведенного ниже уравнения. 92)}{(n-2}})}\;\;\;степени\;свободы\;свободы=n-2\)
- Значение p для корреляции и линейной регрессии вычисляется на основе t-статистики, степеней свободы (n-2). Для корреляции и простой линейной регрессии гипотеза всегда двусторонняя.
Создание уравнения линейной регрессии
Анализ в приведенной выше таблице предоставляет всю информацию, необходимую для обобщения этой взаимосвязи.
Линия регрессии определяется по математической модели, минимизирующей расстояние между точками наблюдения и прямой линией. Насколько точно отдельные точки наблюдения соответствуют линии регрессии, измеряется коэффициент корреляции («r») .
Крутизна линии – это наклон , мера среднего изменения переменной Y при каждом приращении переменной X. Полезная аналогия для наклона — подумать о шагах.
На изображении ниже каждый шаг имеет ширину (X), равную 1, и подъем (Y), равный 2, поэтому для каждого приращения по горизонтали (X) на 1 шаг происходит увеличение вертикального измерения (Y) на 2 единицы.
Если каждый год увеличения возраста связан с прибавкой в весе в среднем на 2 фунта, то наклон или коэффициент для этой зависимости равен 2. Прогнозируемое увеличение веса составляет 2 фунта в год.
Наклон 0 означает, что изменения независимой переменной по оси X не связаны с изменениями зависимой переменной по оси Y. Другими словами, ассоциации нет.
Наконец, Y-пересечение является значением Y, когда значение X равно 0; можно думать об этом как о начальном или базовом значении, но это не всегда актуально. В этом случае точка пересечения по оси Y составляет минус 463,43 доллара, но реальное значение, вероятно, равно 0. Иногда точка пересечения имеет смысл, но чаще нет и служит лишь якорем для основания линии регрессии.
Взаимосвязь между двумя измеряемыми переменными можно обобщить с помощью простого уравнения линейной регрессии , общая форма которого имеет вид:
\(Y=b_0+b_1(X)\)
Где b 0 – значение точки пересечения по оси Y, а b 1 – наклон или коэффициент.