1 градус на 1 метр- Конвертация градусы-проценты
Содержание
- Как перевести градусы в проценты?
- 1 градус на 1 метр
- Как рассчитать уклон в процентах
- Определение наклона касательной
- Отношение стоимости к уклону крыши
Чтобы преобразовать градусы в проценты, вам нужно знать немного больше о том, что вы измеряете. Даже плоские углы в геометрии и астрономии, крепость спиртных напитков и лояльность членов масонской ложи измеряются в градусах.
Например, если вам нужно преобразовать кусок пирога в проценты, 1 оборот или 360 градусов — это 100 процентов. В этом случае 1 процент равен 1/100 от 360 градусов или 3,6 градуса. Итак, чтобы перевести известное значение угла в проценты, нам нужно разделить его на 3,6.
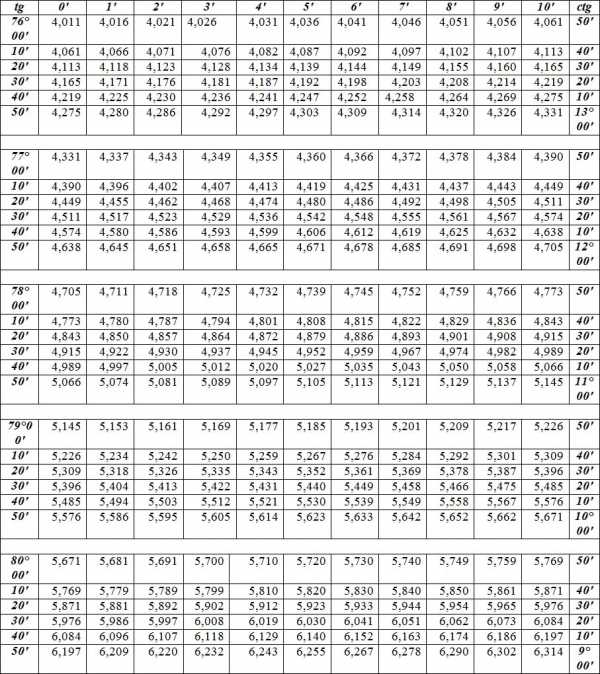
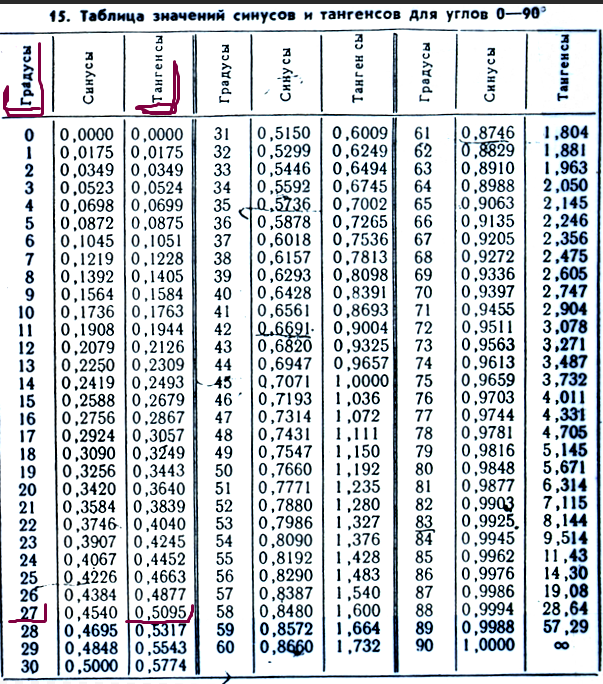
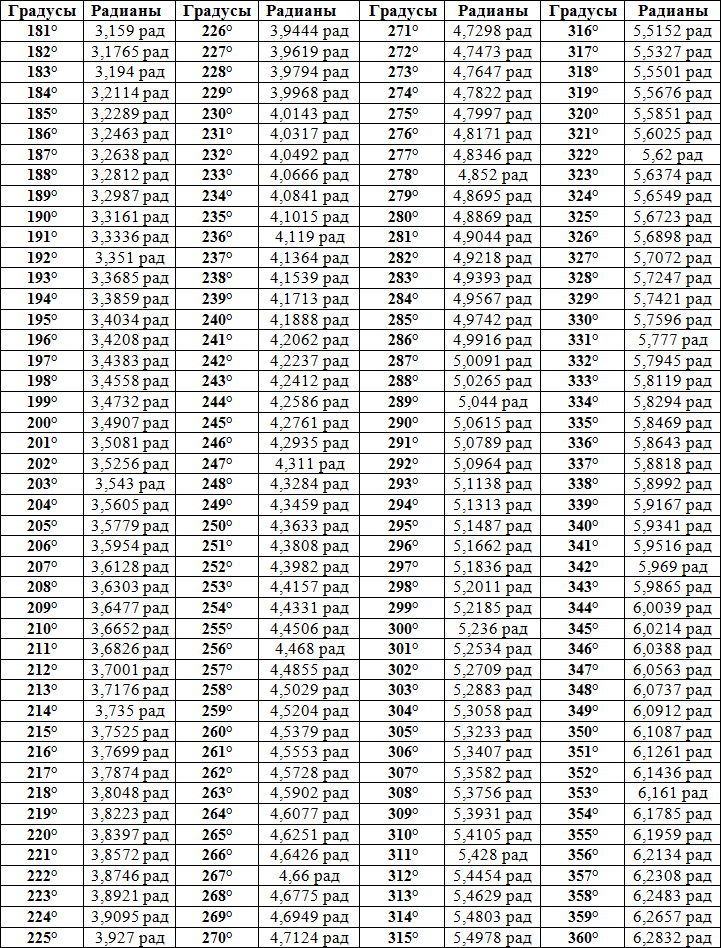
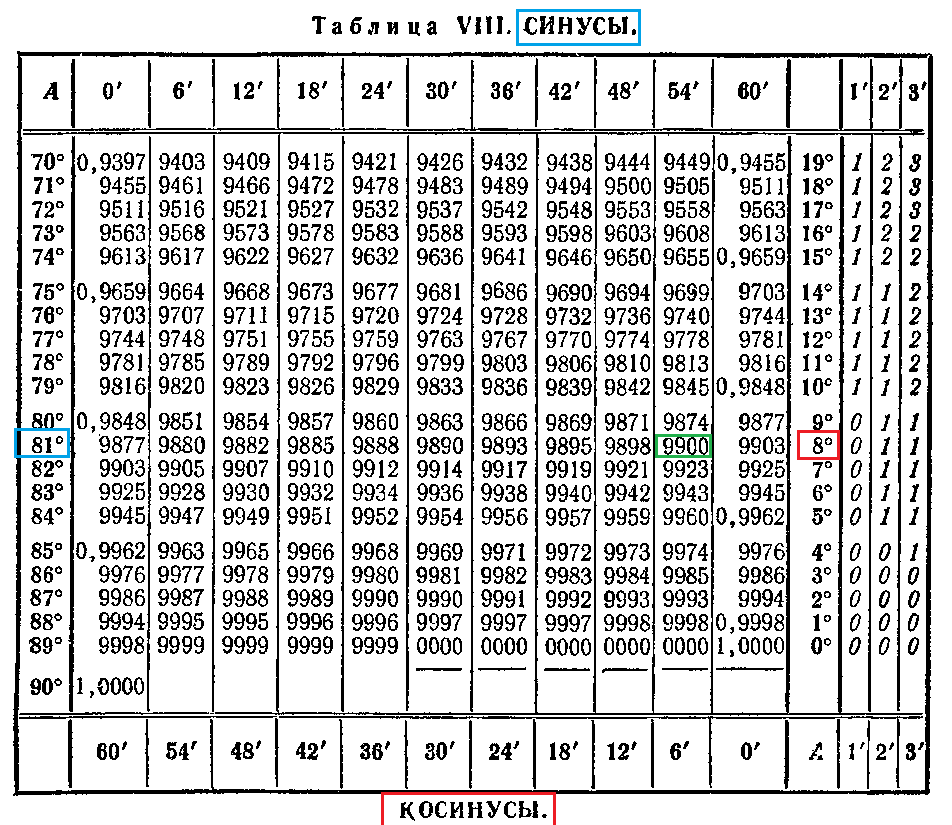
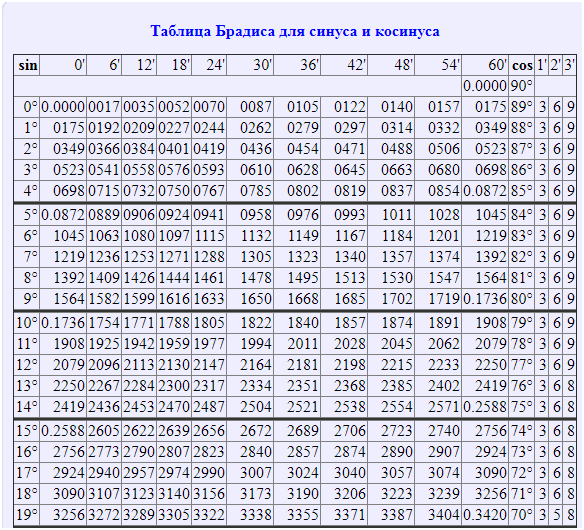
Однако преобразования в проценты, такие как процент уклона дороги для уличных знаков, следует рассматривать как 100% как 45 градусов. Уклон определяется как отношение высоты подъема к пройденному расстоянию от начальной точки измерения. С точки зрения геометрии в данном случае процент уклона соответствует значению тангенса угла в вершине треугольника, с которой началось измерение уклона. Чтобы получить правильное значение, воспользуйтесь обычным калькулятором, воспользуйтесь онлайн-калькулятором для вычисления тангенса известного угла или воспользуйтесь таблицей Брадиса. Windows также включает калькулятор, который запускается с помощью кнопки «Пуск» в главном меню. После его открытия нужно перейти в раздел «Все программы», затем в подраздел «Стандартные» и нажать на строку «Калькулятор».
С точки зрения геометрии в данном случае процент уклона соответствует значению тангенса угла в вершине треугольника, с которой началось измерение уклона. Чтобы получить правильное значение, воспользуйтесь обычным калькулятором, воспользуйтесь онлайн-калькулятором для вычисления тангенса известного угла или воспользуйтесь таблицей Брадиса. Windows также включает калькулятор, который запускается с помощью кнопки «Пуск» в главном меню. После его открытия нужно перейти в раздел «Все программы», затем в подраздел «Стандартные» и нажать на строку «Калькулятор».
Чтобы перевести крепость напитка в проценты, ничего считать не нужно. Эти величины равны друг другу и определяют долю (процентное содержание) этилового спирта. степени – устаревшие обозначения и требования ГОСТ,
Степень посвящения новых членов, принимаемых в масонскую ложу, нетрудно перевести в проценты. Всего существует 3 степени (степени) (Студент, Подмастерье и Мастер). Так, например, мы можем предположить, что ученичество началось с 67%. Это потому, что каждая из трех частот должна добавить третью (33,33%).
Это потому, что каждая из трех частот должна добавить третью (33,33%).
1 градус на 1 метр
Я искал 1 градус на метр. На нашем сайте вы можете получить ответы на интересующие вас вопросы по математике здесь. Подробные решения с пояснениями и пояснениями помогут вам справиться даже с самыми сложными задачами. Угол 5 градусов не является исключением. Я могу помочь вам подготовиться к домашнему заданию, тестам, олимпиаде и колледжу. Какой бы пример вы ни ввели, какой бы математический запрос ни ввели, решение уже есть. Например, «1 градус на метр».
Использование различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве зданий и даже спорте. Математика использовалась людьми с незапамятных времен, и с тех пор ее использование только увеличилось. Но и сейчас наука не стоит на месте и вы можете наслаждаться ее плодами. Например, есть онлайн-калькуляторы, которые могут решать такие задачи, как 1 градус на метр, углы в 5 градусов, градусы в процентах и градусы в процентах.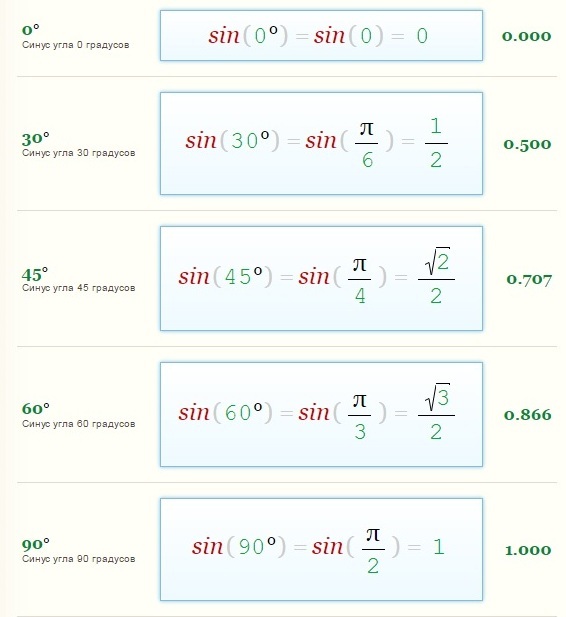
Как рассчитать уклон в процентах
Рулоны измеряются в градусах, процентах, ppm — тысячных долях целого числа. 1‰ = 1/10% = 1/1000, в зависимости от размера. Физический смысл уклона – это отношение перепада высот к наблюдаемой длине участка. Фактически это тангенс угла. 0,12 (тангенс) = 12% = 120 ‰ на 12 м 100-метровой дороги. Другими словами, чтобы рассчитать наклон в ppm, процентное значение необходимо умножить на 10. При проведении планировочных работ на земельном участке необходимо измерить уклон ската. Есть несколько способов сделать это.
- С помощью спиртового уровня снимите все необходимые измерения и сформируйте индикатор наклона с помощью простой математики. Как рассчитывается: Разделите разницу высот на расстояние между измеренными точками и умножьте результат на 100%.

- При проведении топографической разметки по плану земельных участков; Считайте разницу высот между требуемыми точками на чертеже и используйте масштабную линейку для измерения расстояния. Дальнейшие расчеты аналогичны предыдущему способу.
Кровельщики часто сталкиваются с необходимостью определения фактического уклона кровли, который можно рассчитать с помощью специального инструмента, называемого уклономером. Конструкция устройства проста. Рамка установлена на рейке с закрепленными внутри транспортиром и маятником и имеет груз и указатель.
Основание прибора размещают под мерной частью крыши и стрелкой указывает угол.
Определение наклона касательной
Из тригонометрии мы знаем, что тангенс — это дробь, нижняя — катет, примыкающий к углу, а верхняя — противоположный катет (разность высот). Необходимо провести измерения для определения касательного уклона крыши в процентах и градусах.
- Высота от потолка до конька крыши.

- Расстояние от края склона до проекции линии над стыком двух плоскостей.
После выполнения простых математических операций возьмите конкретное значение и с помощью таблицы Брадиса или инженерного калькулятора найдите угол, соответствующий нужному углу. Как рассчитать уклон в процентах. Как определено выше, если скаты одинакового размера, разделите высоту конька на половину ширины мансардного этажа. Или в проекции каждого края крыши, если стороны разного размера. Получается, что это тангенс угла, уже определенного в градусах.
Чтобы получить процент градиента, вам нужно выполнить действие: значение tg * 100. Результат – процент.
Отношение стоимости к уклону крыши
Каждый кровельный материал имеет минимально допустимый уклон. Другие факторы, влияющие на выбор угла ската крыши:
- Комплексная защита конструкций от внешних воздействий – техногенных и природных.
- Устойчивость к ветровым нагрузкам – крутые поверхности увеличивают парусность конструкций, ослабляя их.

- Преобладание конкретных решений Архитектора в определенных регионах.
- Осадки и загрязнение – наклонные крыши не накапливают нагрузки.
17.3 Trigonometry Octave предоставляет следующие тригонометрические функции, где углы указаны в радианах.
Octave предоставляет следующие тригонометрические функции, в которых углы указаны в радианах. Чтобы преобразовать градусы в радианы, умножьте число на pi/180 или используйте функцию deg2rad . Например, sin (30 * pi/180) возвращает синус 30 градусов. В качестве альтернативы Octave предоставляет ряд тригонометрических функций, которые работают непосредственно с аргументом, указанным в градусах. Эти функции названы в честь базовой тригонометрической функции с символом ‘dсуффикс.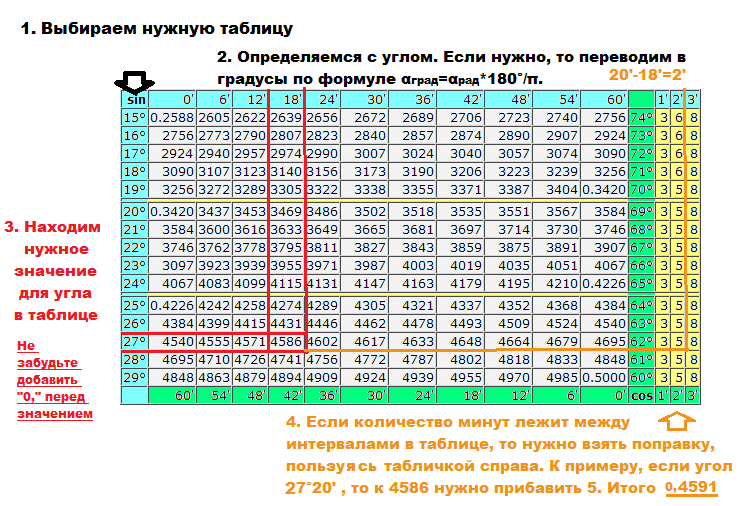 Например,
Например, sin ожидает угол в радианах, а sind — угол в градусах.
Octave использует тригонометрические функции библиотеки C. Ожидается, что эти функции определены стандартом ISO / IEC 9899. Этот стандарт доступен по адресу: http://www.open-std.org/jtc1/sc22/wg14/www/docs/n1124.pdf . Раздел F.9.1 посвящен тригонометрическим функциям. Поведение большинства функций относительно простое. Однако есть некоторые исключения из стандартного поведения. Многие исключения связаны с поведением -0. Самый сложный случай — atan2. Octave точно реализует поведение, указанное в Стандарте. Включение +- pi .
Следует отметить, что MATLAB использует разные определения, которые явно не различают -0.
- : rad = град2рад ( deg ) ¶
Преобразовывать градусы в радиан.
Входной deg должен быть скалярным, векторным или N-мерным массивом двойных или одинарных значений с плавающей запятой.
 deg может быть сложным, и в этом случае действительная и мнимая составляющие преобразуются отдельно.
deg может быть сложным, и в этом случае действительная и мнимая составляющие преобразуются отдельно.Выходное значение rad имеет тот же размер и форму, что и deg , с преобразованием градусов в радианы с использованием константы преобразования
pi/180.Example:
deg2rad ([0, 90, 180, 270, 360]) ⇒ 0.00000 1.57080 3.14159 4.71239 6.28319
See also:rad2deg.
- : deg = рад2град ( rad ) ¶
Преобразовать радиан в градусы.
Входной rad должен быть скалярным, векторным или N-мерным массивом двойных или одинарных значений с плавающей запятой. rad может быть сложным, и в этом случае действительная и мнимая составляющие преобразуются отдельно.
Выходные deg имеют тот же размер и форму, что и rad с радианами, преобразованными в градусы с использованием константы преобразования
180/pi.
Example:
rad2deg ([0, pi/2, pi, 3/2*pi, 2*pi]) ⇒ 0 90 180 270 360
See also:deg2rad.
- : грех ( x ) ¶
Вычислите синус для каждого элемента x в радианах.
См. Также: asin , sind , sinh .
- : потому что ( x ) ¶
Вычислите косинус для каждого элемента x в радианах.
См. Также: acos , cosd , cosh .
- : загар ( z ) ¶
Вычислите касательную для каждого элемента x в радианах.
Смотрите также: Атан , Tand , гиперболический тангенс .
- : сек ( x ) ¶
Вычислите секанс для каждого элемента x в радианах.
Смотрите также: ASEC , SECD , сечь .

- : csc(x ) ¶
Вычислите косеканс для каждого элемента x в радианах.
См. Также: acsc , cscd , csch .
- : детская кроватка ( x ) ¶
Вычислите котангенс для каждого элемента x в радианах.
См. Также: acot , cotd , coth .
- : асин ( x ) ¶
Вычислите обратный синус в радианах для каждого элемента x .
См. Также: sin , asind .
- : акос ( x ) ¶
Вычислите обратный косинус в радианах для каждого элемента x .
Также: cos , acosd .
- : атан ( x ) ¶
Вычислите арктангенс в радианах для каждого элемента x .

См. Также: tan , atand .
- : асек ( x ) ¶
Вычислите обратный секанс в радианах для каждого элемента x .
См. Также: sec , asecd .
- : acsc(x) ¶
Вычислите обратный косеканс в радианах для каждого элемента x .
См. Также: csc , acscd .
- : acot(x) ¶
Вычислите обратный котангенс в радианах для каждого элемента x .
См. Также: детская кроватка , acotd .
- : грех ( x ) ¶
Вычислите гиперболический синус для каждого элемента x .
См. Также: asinh , cosh , tanh .
- : кош ( x ) ¶
Вычислите гиперболический косинус для каждого элемента x .

См. Также: acosh , sinh , tanh .
- : танх ( x ) ¶
Вычислить гиперболический тангенс для каждого элемента x .
См. Также: atanh , sinh , cosh .
- : сечь ( x ) ¶
Вычислите гиперболический секанс каждого элемента x .
See also:asech.
- : csch(x) ¶
Вычислите гиперболический косеканс каждого элемента x .
See also:acsch.
- : coth(x) ¶
Вычислите гиперболический котангенс каждого элемента x .
See also:acoth.
- : asinh(x) ¶
Вычислите обратный гиперболический синус для каждого элемента x .

See also:sinh.
- : акош ( x ) ¶
Вычислите обратный гиперболический косинус для каждого элемента x .
See also:cosh.
- : атанх ( x ) ¶
Вычислите обратный гиперболический тангенс для каждого элемента x .
See also:tanh.
- : асеч ( x ) ¶
Вычислите обратный гиперболический секанс каждого элемента x .
See also:sech.
- : акш ( x ) ¶
Вычислите обратный гиперболический косеканс каждого элемента x .
See also:csch.
- : acoth(x) ¶
Вычислите обратный гиперболический котангенс каждого элемента x .

See also:coth.
- : atan2(y, x) ¶
Вычислите atan ( y / x ) для соответствующих элементов y и x .
y и x должны совпадать по размеру и ориентации. Знаки элементов y и x используются для определения квадрантов каждого результирующего значения.
Эта функция эквивалентна
arg (complex (x, y)).Смотрите также: загар , TAND , Таня , ATANH .
Октава обеспечивает следующие тригонометрические функции,где углы задаются в градусах.Эти функции производят истинные нули на соответствующих интервалах,а не небольшую ошибку округления,возникающую при использовании радианов.Например:
cosd (90)
⇒ 0
cos (pi/2)
⇒ 6.1230e-17- : синд ( x ) ¶
Вычислите синус для каждого элемента x в градусах.

Функция более точна, чем
sin, для больших значений x и для углов, кратных 180 градусам (x/180— целое число), гдеsindвозвращает 0, а не малое значение порядка eps.См. Также: asind , sin .
- : cosd(x) ¶
Вычислите косинус для каждого элемента x в градусах.
Функция более точна, чем
cos, для больших значений x и для углов, кратных 90 градусам (x = 90 + 180*n, где n — целое число), гдеcosdвозвращает 0, а не малое значение порядка eps.См. Также: acosd , cos .
- : т и ( x ) ¶
Вычислите касательную для каждого элемента x в градусах.
Возвращает ноль для элементов, где
x/180— целое число, иInfдля элементов, где(x-90)/180— целое число.
См. Также: атанд , загар .
- : секд ( x ) ¶
Вычислите секанс для каждого элемента x в градусах.
См. Также: asecd , sec .
- : cscd(x) ¶
Вычислите косеканс для каждого элемента x в градусах.
См. Также: acscd , csc .
- : cotd(x) ¶
Вычислите котангенс для каждого элемента x в градусах.
См. Также: acotd , детская кроватка .
- : asind(x) ¶
Вычислите обратный синус в градусах для каждого элемента x .
См. Также: sind , asin .
- : acosd(x) ¶
Вычислите обратный косинус в градусах для каждого элемента x .

См. Также: cosd , acos .
- : at и ( x ) ¶
Вычислите арктангенс в градусах для каждого элемента x .
Смотрите также: Tand , Atan .
- : atan2d(y, x) ¶
Вычислите atan ( y / x ) в градусах для соответствующих элементов из y и x .
См. Также: tand , atan2 .
- : asecd(x) ¶
Вычислите обратный секанс в градусах для каждого элемента x .
Также: secd , asec .
- : acscd(x) ¶
Вычислите обратный косеканс в градусах для каждого элемента x .
См. Также: cscd , acsc .
- : acotd(x) ¶
Вычислите обратный котангенс в градусах для каждого элемента x .

См. Также: cotd , acot .
Наконец,есть две тригонометрические функции,которые вычисляют специальные аргументы с повышенной точностью.
- : y =sinpi(x) ¶
Точно вычислить синус ( x * pi ) для каждого элемента x .
Обычная функция
sinиспользует числа с плавающей запятой IEEE и может давать результаты, очень близкие (в пределах нескольких eps) к правильному значению, но не являющиеся точными. Функцияsinpiявляется более точной и возвращает 0 точно для целых значений x и +1/-1 для полуцелых значений (например, …, -3/2, -1/2, 1/2, 3/2, … ).Example
сравнениеsinиsinpiдля целых значений xsin ([0, 1, 2, 3] * pi) ⇒ 0 1.2246e-16 -2.4493e-16 3.6739e-16 sinpi ([0, 1, 2, 3]) ⇒ 0 0 0 0См. также: коспи , грех .

- : y =cospi(x) ¶
Точно вычислить косинус ( x * pi) для каждого элемента x .
Обычная функция
cosиспользует числа с плавающей запятой IEEE и может давать результаты, очень близкие (в пределах нескольких eps) к правильному значению, но не являющиеся точными. Функцияcospiявляется более точной и возвращает 0 точно для полуцелых значений x (например, …, -3/2, -1/2, 1/2, 3/2, …) и +1/-1 для целочисленные значения.Example
сравнениеcosиcospiдля полуцелых значений xcos ([-3/2, -1/2, 1/2, 3/2] * pi) ⇒ -1.8370e-16 6.1232e-17 6.1232e-17 -1.8370e-16 cospi ([-3/2, -1/2, 1/2, 3/2]) ⇒ 0 0 0 0См. также: sinpi , cos .
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
TAN в Excel (формула, примеры)
Функция TAN в Excel (оглавление)
- TAN в Excel
- Как использовать функцию TAN в Excel?
Функция загара в Excel — это еще одна математическая тригонометрическая функция, используемая для расчета значения загара под любым углом. В математике Tan — это отношение перпендикуляра к основанию, и благодаря этому мы получаем значение касательной под любым углом. Если мы хотим сначала преобразовать какой-либо угол, нам нужно использовать функцию RADIANS или Pi()/4, чтобы получить фактическое значение Tan.
В математике Tan — это отношение перпендикуляра к основанию, и благодаря этому мы получаем значение касательной под любым углом. Если мы хотим сначала преобразовать какой-либо угол, нам нужно использовать функцию RADIANS или Pi()/4, чтобы получить фактическое значение Tan.
Фактическое значение TAN — ТАНГЕНТ. Это одна из тригонометрических функций, таких как COS, SIN и т. д. ТАНГЕНТ основан на прямоугольном треугольнике. С помощью этой функции намного проще найти касательную, если сравнить это с выполнением вручную. Единственное, что мы должны сначала найти РАДИАНЫ для данного угла, только тогда мы можем легко вычислить ТАНГЕНТ.
Все требуемые углы должны быть в радианах.
Есть два способа найти радианы для заданного угла:
- Используя функцию RADIANS внутри функции TAN, или сначала мы можем использовать функцию RADIANS для градусов, а затем найти TAN из радианов. Ниже приведены расчеты в Microsoft Excel в обоих направлениях:
ИЛИ
- Мы также можем преобразовать это в радианы с помощью функции PI, которая выглядит следующим образом: градусы * PI()/180.
 Ниже приведен расчет функции TAN в Excel: .
Ниже приведен расчет функции TAN в Excel: .
Функция ТАНГЕНТ используется и в нашей реальной жизни. ТАНГЕНТ используется в архитектуре, где для геометрических фигур требуется вычисление длины и высоты. Он также используется в аэронавтике, навигационных системах, машиностроении, кровле, многих тригонометрических приложениях, GPS и т. д. Пилот в основном использовал функцию ТАНГЕНТ для расчета расстояния от земли в целях посадки и безопасности.
- Функция ТАНГЕНТ возвращает тангенс угла, и он всегда будет числовым.
В математике формула будет выглядеть так: TAN 0 = противоположная сторона/прилегающая сторона
Таким образом, на приведенном выше рисунке мы можем сказать c = a/b
Формула TAN
Ниже приведена формула TAN:
Параметры или аргументы:
Число: это число или числовое значение, для которого необходимо вычислить тангенс угла.
Результат: Функция TAN всегда возвращает числовое значение после применения к определенной ячейке.
Тип:
- Функция рабочего листа
- Функция VBA
Следовательно, функцию TAN можно использовать двумя способами, то есть функцией рабочего листа, в которой формулу функции TAN необходимо ввести в определенную ячейку рабочего листа, чтобы найти тангенс, и мы также можем использовать функцию TAN в VBA , и мы должны написать формулу в редакторе Microsoft Visual Basic.
Как использовать функцию TAN в Excel?
Функция TAN очень проста в использовании. Давайте теперь посмотрим, как использовать функцию TAN в Excel с помощью нескольких примеров.
Вы можете скачать этот шаблон Excel для функции TAN здесь — Шаблон Excel для функции TAN
Пример №1
Для вычисления тангенса мы должны вычислить радианы, чтобы иметь правильные данные или выходные данные.
Шаг 1: Мы должны проверить необработанные данные, для которых мы должны вычислить тангенс, и проверить их; ниже фото:
Шаг 2: Затем нажмите «Формулы» на ленте Microsoft Excel, а затем мы должны нажать «Математика и триггер». Ниже приведено изображение для справки:
Ниже приведено изображение для справки:
Шаг 3: Теперь мы должны применить формулу радианов из доступного списка. Итак, просто найдите RADIANS и щелкните по нему, как показано на рисунке ниже:
Шаг 4: После нажатия мы имеем, как показано ниже на экране, затем введите адрес ячейки или просто выберите его из курсора, для которого RADIANS нужно рассчитать:
Таким образом, в этом случае адрес ячейки — B5, для которого необходимо вычислить РАДИАНЫ.
Шаг 5: После выбора адреса ячейки нам нужно просто нажать OK или Enter; результатом будут РАДИАНЫ данного угла.
Затем мы можем перетащить формулу во все необходимые ячейки, чтобы узнать РАДИАНЫ. Ниже приведен результат:
Шаг 6: Теперь мы должны вычислить ТАНГЕНТ, чтобы выполнить шаги 2 и 3, а затем найти TAN и щелкнуть по нему. Ниже приведено изображение для справки:
Шаг 7: Теперь нам нужно выбрать адрес ячейки, для которой необходимо вычислить ТАНГЕНТ, поэтому, как мы знаем, мы должны выбрать радианы данного угла, тогда, в этом случае, мы выберем адрес ячейки C5 в качестве аргумента или параметра. Ниже приведено изображение для справки:
Ниже приведено изображение для справки:
Шаг 8: Теперь мы можем нажать ОК, нажать Enter, чтобы получить результаты
, и мы также можем перетащить формулу TAN в другую нужную ячейку, как показано ниже:
Итак, выше мы видели, как вычислить ТАНГЕНТ с помощью функции TAN в Excel.
Пример #2
Поставив формулу
Мы также можем вычислить ТАНГЕНТ, используя формулу или введя формулу TAN в нужную ячейку. Ниже приведена формула:
=TAN(число)
Шаг 1: Во-первых, у нас должны быть готовые радианы для требуемого угла, который мы видели выше, то, как рассчитать на шагах 3-5, который имеет формула = РАДИАНЫ (угол).
Результат будет:
Шаг 2: Теперь мы можем ввести формулу ТАНГЕНСА в ячейку с адресом E4, которая равна =TAN(число). Итак, мы должны ввести =TAN, а затем клавишу табуляции. Ниже приведен скриншот для справки:
Шаг 3: Теперь мы должны выбрать адрес ячейки вычисляемых радиан, который в данном примере равен D4, вместо числа в качестве аргумента или параметра. Ниже приведено изображение для справки:
Ниже приведено изображение для справки:
Шаг 4: После ввода номера нам нужно просто закрыть скобку, чтобы завершить формулу, или нажать Enter; оба имеют тот же результат. Ниже приведено изображение:
Шаг 5: У нас есть требуемый результат расчета ТАНГЕНТ после выполнения вышеуказанных шагов. Ниже результат на картинке:
Функция TAN в VBA:
Как мы обсуждали выше, эта функция TAN также может использоваться в коде VBA, поэтому мы можем взять один пример, чтобы увидеть, как это работает и каковы будут ввод и процедура. Ниже приведен код VBA для расчета касательной:
DimLnumber As Double
LNmuber = Tan(5)
Итак, в приведенном выше примере LNumber 5 содержит значение -3,380515006.
Что нужно помнить
- Если угол задан в градусах, для которых мы должны рассчитать TAN, мы должны рассчитать для него РАДИАНЫ, используя формулу =РАДИАН(градус), или мы можем умножить угол на PI() /180.




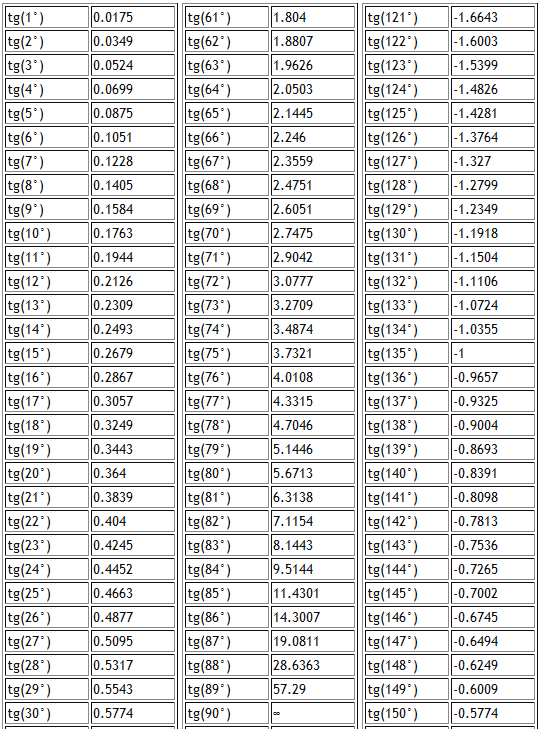 deg может быть сложным, и в этом случае действительная и мнимая составляющие преобразуются отдельно.
deg может быть сложным, и в этом случае действительная и мнимая составляющие преобразуются отдельно.