Как проверить функцию на периодичность: Периодические функции — урок. Алгебра, 10 класс.

Периодичность проверок оборудования ГМССБ

27.11.2019

Периодичность проверок оборудования ГМССБ

Ежедневные, еженедельные и ежемесячныеиспытания оборудования ГМССБ на борту

Разработка правил ГМССБ (Глобальной морской системы связи при бедствии и для обеспечения безопасности) для судоходной отрасли прошла большой путь. Система ГМССБ была создана с целью улучшения радиосвязи и процедур в случае бедствия и обеспечения безопасности на море.

Наибольшее преимущество оборудования ГМССБ заключается в том, что оно значительно снижает шансы исчезновения судов без следа и позволяет незамедлительно запускать поисково-спасательные операции и направлять их на конкретный участок морской катастрофы.

Прошли те времена, когда на судах требовалось иметь специальных радиоинженеров для управления радиооборудованием. С внедрением ГМССБ каждый офицер палубы с общим сертификатом оператора (GOC) и лицензией имеет право использовать оборудование ГМССБ и осуществлять радиосвязь, когда это необходимо.

Чтобы оборудование ГМССБ функционировало должным образом и эффективно в случае чрезвычайной ситуации, важно, чтобы моряки понимали его назначение и выполняли необходимое обслуживание на борту судна, чтобы поддерживать его в рабочем состоянии и наилучшим образом использовать оборудование ГМССБ.

Ежедневные, еженедельные и ежемесячные испытания всего оборудования ГМССБ должны выполняться каждым ответственным за него штурманом без каких-либо компромиссов. Мы не должны забывать, что это наш единственный лучший друг в бедственном положении на море.

Морские суда должны быть способны выполнять девять функциональных требований ГМССБ .

1. Оповещение о бедствии с судна на берег
2. Предупреждение о бедствии с берега на судно
3. Оповещение о бедствии с судна на судно
4. Координация SAR
5. Связь на борту во время происшествия
6. Передача и прием сигналов аварийной локации
7. Передача и получение MSI
8. Общесудовая радиосвязь
9. Связь на мостике

Это может быть обеспечено путем регулярного тестирования оборудования ГМССБ.

Оборудование и системы ГМССБ включают VHF DSC / RT, MF / HF DSC / RT, INMARSAT, SART, EPIRB, NAVTEX.

Ежедневные испытания оборудования ГМССБ

Надлежащее функционирование средств цифрового избирательного вызова (ЦИВ) должно проверяться, по крайней мере, один раз в день, без излучения сигналов, с использованием оборудования для внутренних испытаний оборудования. Ежедневный тест проверяет внутреннее соединение, передавая выходную мощность и дисплей. Процесс может отличаться от оборудования к оборудованию в зависимости от марки.

Ежедневные испытания также должны выполняться на оборудовании ПВ/ КВ, чтобы убедиться, что оно будет функционировать должным образом в случае бедствия.

Аккумуляторы, обеспечивающие резервный источник энергии, следует также проверять ежедневно. Главным образом напряжения аккумулятора ON-LOAD и OFF-LOAD проверяются вольтметром, подключенным к зарядному устройству.

OFF-LOAD: если оборудование не подключено, батарея должна показывать 24 В или чуть больше.

ON-LOAD: выключите питание переменного тока и запишите напряжение батареи. Нажмите PTT на MF / HF трансивере на частоте R / T без бедствия и холостого хода. Напряжение будет падать в зависимости от нагрузки. Если напряжение падает более чем на 10%, это указывает на то, что батарея слаба или заряжена не полностью. В этом случае аккумуляторы следует заряжать.

Также важно убедиться, что все принтеры находятся в рабочем состоянии и имеется достаточное количество бумаги.

Еженедельные испытания оборудования ГМССБ

Необходимо проверять правильную работу средств ЦИВ, по крайней мере, один раз в неделю с помощью тестового вызова на одной из шести частот бедствия и безопасности, когда они находятся в пределах дальности связи береговой станции, оборудованной оборудованием ЦИВ. Тестовый звонок на береговую станцию ​​можно отправить следующими способами:

ПВ/ КВ DSC:

1.  Нажмите клавишу [ DSC] на экране ожидания DSC, а затем нажмите [ENTER], чтобы открыть меню CALL TYPE.

2. Поверните ручку [ENTER], чтобы выбрать TEST CALL, а затем нажмите ручку [ENTER]. Снова нажмите ручку [ENTER], чтобы открыть меню COAST ID.

3. С помощью цифровых клавиш введите идентификатор береговой станции (семь цифр), куда вы хотите отправить вызов, в зависимости от области, в которой вы находитесь, а затем нажмите ручку [ENTER]. Идентификатор береговой станции можно найти в Адмиралтейском списке радиосигналов, том 1 — Морские радиостанции.

4. Теперь нажмите ручку [ENTER], чтобы открыть меню DSC FREQ. (Обратите внимание, что здесь ПРИОРИТЕТ автоматически выбирается как БЕЗОПАСНОСТЬ.)

5. Поверните ручку [ENTER], чтобы выбрать подходящую частоту, а затем нажмите ручку [ENTER].

6. Теперь нажмите клавишу [CALL], чтобы отправить тестовый вызов на соответствующую береговую станцию. После того, как тестовый вызов был успешно отправлен, подтверждение получено от береговой станции. При получении подтверждения будет подан звуковой сигнал.

Много раз часто случается так, что офицер не получает никакого подтверждения от береговой станции. В таких случаях мы часто принимаем как должное, что береговая станция не отправляет подтверждение. Однако в действительности это может быть не так.

Проблема может быть и с нашим оборудованием. Чтобы убедиться, что оборудование ПВ/КВ в порядке, лучше попытаться отправить тестовый вызов на других частотах и ​​на другие станции. Даже если тогда мы не получим никакого подтверждения, тестовый вызов может быть отправлен на проходящее судно, если это возможно. Вместо ввода идентификатора побережья введите MMSI проходящего мимо судна. Лучше позвонить на судно и подтвердить, получили ли они тестовый вызов. Так же можно попросить их отправить вам пробный звонок, чтобы убедиться, что оборудование для приема оборудования функционирует нормально.

Также рекомендуется, чтобы тестирование от станции к станции проводилось с использованием УКВ ЦИВ.

1. Нажмите клавишу вызова. Откроется экран создания сообщения, где можно выбрать тип вызова. Поверните ручку канала, чтобы выбрать TEST call.

2. Введите идентификатор станции, в данном случае это MMSI вашего судна, а затем нажмите клавишу CALL для его передачи.

Звуковой и визуальный сигнал тревоги генерируется, и тестовый вызов принимается на другой станции УКВ. Нажмите Отмена, чтобы завершить тестовый вызов.

Ежемесячные испытания оборудования ГМССБ

АРБ:

Радиомаяк, указывающий на аварийное положение, или EPIRB следует проверить, выполнив функцию самопроверки без использования спутниковой системы. Во время самотестирования аварийный сигнал не передается.

Во время самопроверки проверяются напряжение батареи, выходная мощность и частота. EPIRB также должен быть проверен на предмет физического повреждения. Срок годности батарейного блока и срок годности гидростата должны быть проверены.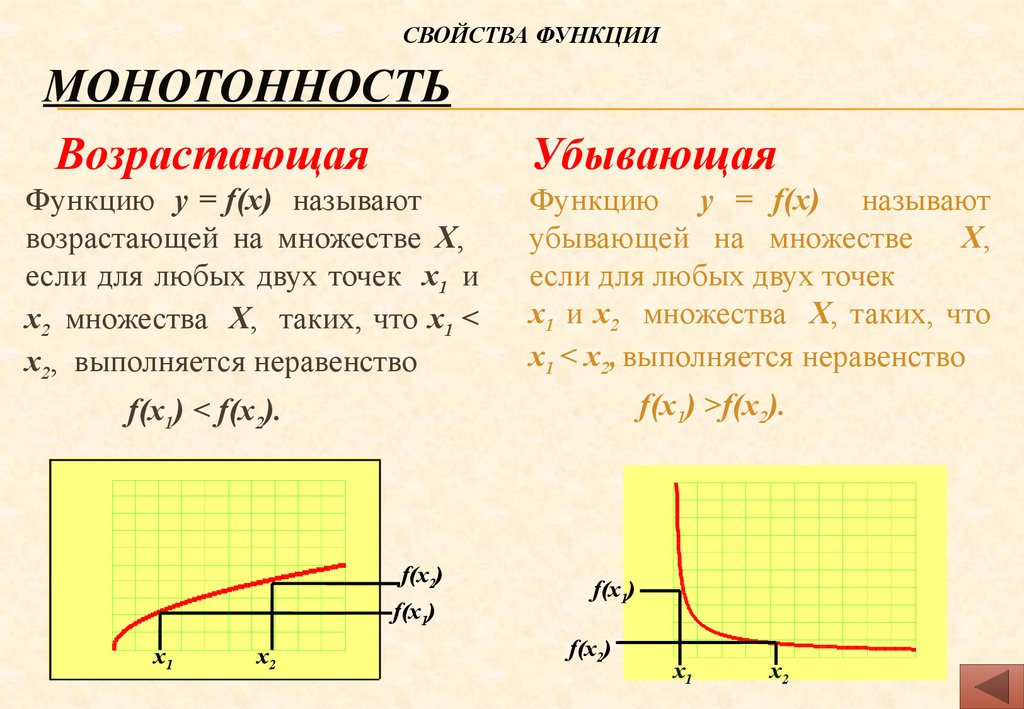

 Кроме того, убедитесь, что предохранительный зажим правильно установлен и на месте.

Чтобы выполнить самодиагностику EPIRB:

1.EPIRB следует сначала снять с кронштейна.

2. Подпружиненный выключатель в верхней части EPIRB поднимается в положение TEST.

Успешный тест будет состоять из серии миганий на светодиодном тестовом индикаторе, сопровождаемых непрерывным светом и вспышкой примерно через 15 секунд. Последний зеленый светодиод указывает на успешное тестирование.

3. После успешного завершения теста выключатель отпускается, и EPIRB помещается обратно в кронштейн.

РЛО:

Поисково-спасательный приемоответчик или SART также оснащен механизмом самопроверки для проверки работоспособности маяка. SART проверяется с помощью судового радара Х-диапазона. Желательно, чтобы испытание проводилось в открытом море, чтобы избежать помех на дисплее радара.

1. Снимите РЛО с монтажного кронштейна.

2. Тест РЛО должен проводиться одним человеком в поле зрения радиолокационного сканера. Это можно сделать с крыльев моста. Затем SART следует перевести в режим TEST, повернув его влево на позицию TESTPREVUE на короткое время.

Визуальные огни работают, и раздаются звуковые сигналы, указывающие на то, что РЛО сработал.

3.Одновременно другой человек должен наблюдать за радарным дисплеем для правильной картины. По крайней мере 11 концентрических кругов появляются на дисплее радара, если они сохраняются в масштабе 12 М. Расстояние между двумя кольцами составляет примерно 0,64 м. Миль.

4. SART также должен быть визуально проверен на наличие каких-либо признаков физического повреждения. Срок годности батареи также следует отметить. Предохранительный зажим должен быть на месте.

Портативные УКВ радиостанции ГМССБ

Каждая радиостанция для спасательных средств должна проверяться не реже одного раза в месяц, чтобы обеспечить ее надлежащую работу в случае аварийной ситуации.  Ее следует проверять на частоте, отличной от канала 16 (156,8 МГц). Срок годности батареи необходимо проверить и при необходимости изменить.

1. Нажмите кнопку питания, чтобы включить или выключить.

2. Чтобы выбрать другой канал, нажмите клавишу CH и с помощью клавиш со стрелками выберите нужный канал. Выбранный канал обозначается номером канала и частотой на экране.

3. Нажмите PTT (Push-to-Talk) для связи с другим радиотелефоном для проверки функций приема и передачи. Один человек может стоять возле приемника УКВ для получения тестового вызова с портативного радио.

Символ «TX» отображается при нажатии PTT и передаче. Индикатор «TX» указывает, что производится передача сигнала, антенна работает на передачу.

Когда радиостанция работает на прием сигнала, на дисплее отображается символ «RX».

НАВТЕКС:

Navtex является столь же важным оборудованием ГМССБ и является источником информации по безопасности на море.  Он также оснащен функцией тестирования, которая может проверять батарею, клавиатуру, ЖК-дисплей, ПЗУ и ОЗУ. Хорошей практикой является тестирование Navtex и обнаружение ошибки, если таковая имеется.

1. Нажмите клавишу MENU / ESC, чтобы открыть главное меню.

2. Теперь используйте навигационные стрелки, чтобы выбрать SERVICE, а затем нажмите ENT. Подменю SERVICE содержит опцию TEST. Используйте клавишу со стрелкой вниз, чтобы выбрать ТЕСТ и нажмите клавишу ENT. Выберите ДА и снова нажмите клавишу ENT. ТЕСТ начнется, и результаты будут отображены на экране через несколько секунд.

Если тест пройден успешно, результаты показывают OK, в противном случае он показывает значение NG.

Он также проверяет правильность функционирования каждого ключа.

Результаты теста могут быть распечатаны и сохранены в журнале ГМССБ.

ИНМАРСАТ:

INMARSAT также оснащен диагностическим тестом, который проверяет его на правильность работы. Примерно шаги для выполнения диагностического теста приведены ниже;

1.    На клавиатуре нажмите клавишу F7, чтобы открыть меню «ОПЦИИ».

2.    Используйте стрелку вниз, чтобы открыть меню ТЕСТ, а затем выберите ДИАГНОСТИЧЕСКИЙ ТЕСТ. Выберите ДА, чтобы начать тестирование.

По завершении теста результаты отображаются на экране, как показано ниже. Клавиша ESC используется для возврата в главное меню.

Тест PV или тест проверки производительности могут проводиться каждый месяц. Этот тест состоит из приема тестового сообщения от LES (Локальная земная станция), передачи сообщения в LES и теста оповещения о бедствии. PV TEST можно открыть из меню TEST в разделе OPTIONS, как упомянуто выше.

Статус показывает «ТЕСТИРОВАНИЕ» во время теста.

Статус изменится на IDLE после завершения теста PV.

Результаты теста можно увидеть в пункте «Результат теста PV» в меню «ТЕСТ».  Результаты теста могут быть распечатаны и зарегистрированы. BBER обозначает частоту появления ошибок на доске объявлений. Проход появляется без ошибок. «PASS» появляется для удовлетворительного завершения теста.

Батарея ГМССБ:

Соединения аккумулятора и отсек также должны быть проверены. Уровень электролита и удельный вес каждого элемента должны быть проверены и зарегистрированы. Сульфатирование может снизить удельный вес, тем самым уменьшая емкость батареи. Необслуживаемые батареи на борту не требуют таких проверок.

Рекомендуется каждый месяц визуально проверять все антенны на предмет надежности монтажа и видимых повреждений кабелей. Антенны расположены на «острове обезьян». Любые отложения грязи и соли должны быть удалены. Также важно проверить состояние антенн и изоляторов с помощью электрика. Перед выполнением любых работ с антенной убедитесь, что оборудование выключено и изолировано.

GMDSS позволяет судну, терпящему бедствие, отправлять оповещения с использованием различных систем радиосвязи.  Поэтому важно, чтобы все оборудование ГМССБ поддерживалось в состоянии готовности и в рабочем состоянии. Для этого необходимо проводить ежедневные, еженедельные и ежемесячные тесты. Только тогда мы сможем обеспечить безопасность корабля и его экипажа.

 

Y x 2 четная. Основные свойства функции: четность, нечетность, периодичность, ограниченность

Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у . Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x ) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y ), образуют область значений функции.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x , а по оси ординат откладываются значения переменной y . Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!

Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!

Основные свойства функций.

1) Область определения функции и область значений функции .

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y , которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции .

Значения х , при которых y=0 , называется нулями функции . Это абсциссы точек пересечения графика функции с осью Ох.

3) Промежутки знакопостоянства функции .

Промежутки знакопостоянства функции – такие промежутки значений x , на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.

4) Монотонность функции .

Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции .

Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х f(-x) = f(x) . График четной функции симметричен относительно оси ординат.

Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = — f(x ).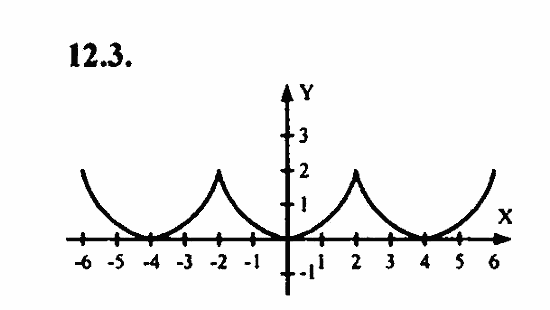 График нечетной функции симметричен относительно начала координат.

Четная функция
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.

Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x , принадлежащего области определения, выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).

Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.

6) Ограниченная и неограниченная функции .

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

7) Периодическость функции .

Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Функция f называется периодической, если существует такое число, что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T) . T — это период функции.

Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.

Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.

Функция называется четной (нечетной), если для любогои выполняется равенство

.

График четной функции симметричен относительно оси
.

График нечетной функции симметричен относительно начала координат.

Пример 6.2. Исследовать на четность или нечетность функции

1)
; 2)
; 3)
.

Решение .

1) Функция определена при
. Найдем
.

Т.е.
. Значит, данная функция является четной.

2) Функция определена при

Т.е.
. Таким образом, данная функция нечетная.

3) функция определена для , т.е. для

,
. Поэтому функция не является ни четной, ни нечетной. Назовем ее функцией общего вида.

3. Исследование функции на монотонность.

Функция
называется возрастающей (убывающей) на некотором интервале, если в этом интервале каждому большему значению аргумента соответствует большее (меньшее) значение функции.

Функции возрастающие (убывающие) на некотором интервале называются монотонными.

Если функция
дифференцируема на интервале
и имеет положительную (отрицательную) производную
, то функция
возрастает (убывает) на этом интервале.

Пример 6.3 . Найти интервалы монотонности функций

1)
; 3)
.

Решение .

1) Данная функция определена на всей числовой оси. Найдем производную .

Производная равна нулю, если
и
. Область определения – числовая ось, разбивается точками
,
на интервалы. Определим знак производной в каждом интервале.

В интервале
производная отрицательна, функция на этом интервале убывает.

В интервале
производная положительна, следовательно, функция на этом интервале возрастает.

2) Данная функция определена, если
или

.

Определяем знак квадратного трехчлена в каждом интервале.

Таким образом, область определения функции

Найдем производную
,
, если
, т.е.
, но
. Определим знак производной в интервалах
.

В интервале
производная отрицательна, следовательно, функция убывает на интервале
. В интервале
производная положительна, функция возрастает на интервале
.

4. Исследование функции на экстремум.

Точка
называется точкой максимума (минимума) функции
, если существует такая окрестность точки, что для всех
из этой окрестности выполняется неравенство

.

Точки максимума и минимума функции называются точками экстремума.

Если функция
в точкеимеет экстремум, то производная функции в этой точке равна нулю или не существует (необходимое условие существования экстремума).

Точки, в которых производная равна нулю или не существует называются критическими.

5. Достаточные условия существования экстремума.

Правило 1 . Если при переходе (слева направо) через критическую точку производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то минимум; если
не меняет знак, то экстремума нет.

Правило 2 . Пусть в точке
первая производная функции
равна нулю
, а вторая производная существует и отлична от нуля. Если
, то– точка максимума, если
, то– точка минимума функции.

Пример 6.4 . Исследовать на максимум и минимум функции:

1)
; 2)
; 3)
;

4)
.

Решение.

1) Функция определена и непрерывна на интервале
.

Найдем производную
и решим уравнение
, т.е.
.Отсюда
– критические точки.

Определим знак производной в интервалах ,
.

При переходе через точки
и
производная меняет знак с «–» на «+», поэтому по правилу 1
– точки минимума.

При переходе через точку
производная меняет знак с «+» на «–», поэтому
– точка максимума.

,
.

2) Функция определена и непрерывна в интервале
. Найдем производную
.

Решив уравнение
, найдем
и
– критические точки. Если знаменатель
, т.е.
, то производная не существует. Итак,
– третья критическая точка. Определим знак производной в интервалах.

Следовательно, функция имеет минимум в точке
, максимум в точках
и
.

3) Функция определена и непрерывна, если
, т.е. при
.

Найдем производную

.

Найдем критические точки:

Окрестности точек
не принадлежат области определения, поэтому они не являются т. экстремума. Итак, исследуем критические точки
и
.

4) Функция определена и непрерывна на интервале
. Используем правило 2. Найдем производную
.

Найдем критические точки:

Найдем вторую производную
и определим ее знак в точках

В точках
функция имеет минимум.

В точках
функция имеет максимум.

Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.

Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными. (-x))=- h(x). Следовательно, h(x) — нечетная.

Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.

Четные функции обладают рядом интересных свойств:

• в результате сложения подобных функций получают четную;
• в результате вычитания таких функций получают четную;
• четной, также четная;
• в результате умножения двух таких функций получают четную;
• в результате умножения нечетной и четной функций получают нечетную;
• в результате деления нечетной и четной функций получают нечетную;
• производная такой функции — нечетная;
• если возвести нечетную функцию в квадрат, получим четную.

Четность функции можно использовать при решении уравнений.

Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами. 2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.

Исследование функции.

1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.

Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.

2) Свойства функции: четность/нечетность, периодичность:

Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.

Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).

Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).

Ни чётная ни нечётная функция (функция общего вида) — функция, не обладающая симметрией. В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).

Нечётные функции

Нечётная степень где — произвольное целое число.

Чётные функции

Чётная степень где — произвольное целое число.

Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.

3) Нули (корни) функции — точки, где она обращается в ноль.

Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x ) = 0 (или убедиться в отсутствии корней).

Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.

4) Промежутки постоянства знаков, знаки в них.

Промежутки, где функция f(x) сохраняет знак.

Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.

ВЫШЕ оси абсцисс.

НИЖЕ оси .

5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Устранимые точки разрыва

Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:

,

то точка называется точкой устранимого разрыва функции (в комплексном анализе -устранимая особая точка).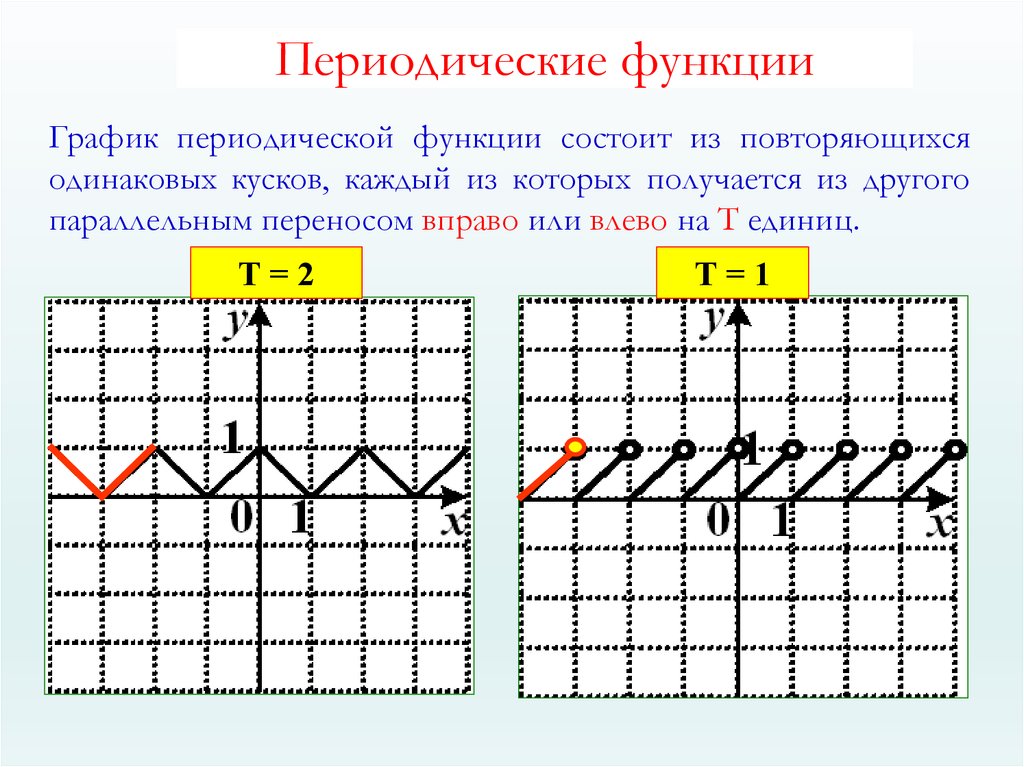

Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности , что и обосновывает название точки, как точки устранимого разрыва.

Точки разрыва первого и второго рода

Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :

если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода . Точки устранимого разрыва являются точками разрыва первого рода;

если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода .

Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.

Вертикальная

Вертикальная асимптота — прямая предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

Горизонтальная

Горизонтальная асимптота — прямая вида при условии существования предела

.

Наклонная

Наклонная асимптота — прямая вида при условии существования пределов

Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.

Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.

если в п. 2. ), то , и предел находится по формуле горизонтальной асимптоты, .

6) Нахождение промежутков монотонности. Найти интервалы монотонности функции f (x )(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f (x ). Для этого находят производную f (x ) и решают неравенство f (x )0. На промежутках, где это неравенство выполнено, функция f (x )возрастает. Там, где выполнено обратное неравенство f (x )0, функция f (x )убывает.

Нахождение локального экстремума. Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием — локальные минимумы. Вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке (продолжение)

1. Найти производную функции: f (x ). 2. Найти точки, в которых производная равна нулю: f (x )=0x 1, x 2 ,… 3. Определить принадлежность точек х 1 , х 2 , … отрезку [a ; b ]: пусть x 1a ;b , а x 2a ;b . 4. Найти значения функции в выбранных точках и на концах отрезка:f (x 1), f (x 2),…, f (x a ),f (x b ), 5. Выбор наибольшего и наименьшего значений функции из найденных. Замечание. Если на отрезке [a ; b ] имеются точки разрыва, то необходимо в них вычислить односторонние пределы, а затем их значения учесть в выборе наибольшего и наименьшего значений функции.

7) Нахождение интервалов выпуклости и вогнутости . Это делается с помощью исследования знака второй производной f (x ). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. Найдя f (x ) , мы решаем неравенство f (x )0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f (x )0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута). Определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).

Точка перегиба функции — это точка, в которой функция непрерывна и при переходе через которую функция меняет направление выпуклости.

Условия существования

Необходимое условие существования точки перегиба: если функция дважды дифференцируемая в некоторой выколотой окрестности точки , то или .

Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.

Определение 1.

Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).

Определение 2.

Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).

Доказать, что у = х 4 — четная функция.

Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.

Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.

Доказать, что у = х 3 ~ нечетная функция.

Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.

Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.

Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.

Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).

Итак, функция может быть четной, нечетной, а также ни той ни другой.

Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.

В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как }

Как найти период функции?

Периодическая функция — это функция, которая повторяется через равные промежутки времени. В следующем пошаговом руководстве вы узнаете, как найти период функции.

Временной интервал между двумя волнами называется периодом, а функция, которая повторяет свои значения через равные интервалы или периоды, называется периодической функцией. Другими словами, периодическая функция — это функция, которая повторяет свои значения через каждый конкретный период.

Пошаговое руководство по периодической функции

Функция \(y = f (x)\) — это периодическая функция, в которой существует положительное вещественное число \(P\) такое, что \(f (x + P ) = f (x)\, ибо все \(x\) принадлежат действительным числам. Наименьшее значение положительного действительного числа \(P\) называется фундаментальным периодом функции . Этот фундаментальный период функции также называется периодом функции , в котором функция повторяется.

\(\color{синий}{f(x+P)=f(x)}\)

Примечание:  синус – это периодическая функция с периодом \(2π\). \(sin(2π + x) = sinx\).

Ниже приведены диаграммы некоторых периодических функций. График каждой из следующих периодических функций имеет трансляционную симметрию.

Периоды некоторых важных периодических функций

Период функции помогает нам узнать интервал, после которого повторяется диапазон периодической функции. Область определения периодической функции \(f(x)\) включает действительные числовые значения \(x\), область значений периодической функции представляет собой ограниченный набор значений в интервале. Длина этого повторяющегося интервала или интервал, после которого диапазон функции повторяется, называется период периодической функции .

Периоды некоторых важных периодических функций следующие:

• Период \(sinx\) и \(cosx\) равен \(2π\).
• Период \(tanx\) и \(cotx\) равен \(π\).
• Период \(secx\) и \(cosecx\) равен \(2\).

Свойства периодических функций

Следующие функции полезны для более глубокого понимания концепции периодической функции:

• График периодической функции симметричен и повторяется вдоль горизонтальной оси.
• Область определения периодической функции включает все значения действительных чисел, а диапазон периодической функции определяется для фиксированного интервала.
• Период периодической функции, относительно которого период повторяется, равен константе во всем диапазоне функции.
• Если \(f (x)\) периодическая функция с периодом \(P\), \(\frac{1}{f(x)}\) также будет периодической функцией с тем же основным периодом \ (П\).
• Если \(f(x)\) периодическая функция с периодом \(P\), то \(f(ax + b)\) также является периодической функцией с периодом \(\frac { Р}{|а|}\).
• Если \(f(x)\) периодическая функция с периодом \(P\), то \(af(x) + b\) также является периодической функцией с периодом \(P\) .

Периодическая функция – Пример 1:

Найдите период периодической функции \(y=sin(4x + 5)\).

Решение:

Период \(sinx\) равен \(2π\), а период \(sin(4x + 5)\) равен:

\(\frac{2π}{4 }=\frac{π}{2}\)

Следовательно, период \(sin(4x + 5)\) равен \(\frac{π}{2}\).

Периодическая функция – Пример 2:

Найдите период периодической функции \(y=9 cos(6x + 4)\).

Период \(cosx\) равен \(2π\), а период \(9 cos(6x + 4)\) равен:

\(\frac{2π}{6}=\frac{ π}{3}\)

Следовательно, период \(9 cos(6x + 4)\) равен \(\frac{π}{3}\).

Упражнения для периодической функции

Найдите период функции.

1. \(\color{blue}{y= tan3x + sin\frac{5x}{2}}\)
2. \(\color{blue}{y=sec(\pi x-2)}\)
3. \(\color{blue}{y=cot(-(\frac{2\pi}{3}) x)}\)
4. \(\color{blue}{\:y=cos\left(-\left(\frac{2}{3}\right)x-\pi \right)}\)

1. \(\color{blue}{4\pi}\)
2. \(\color{blue}{2}\)
3. \(\color{blue}{\frac{3}{2}}\ )
4. \(\color{blue}{3\pi}\)

Effortless Math Team

4 месяца назад

Функции Период функции Периодическая функция

Другие статьи по математике

• О нас
• Свяжитесь с нами
• Оптовые заказы
• Политика возврата

Математика без усилий: мы помогаем учащимся полюбить математику — © 2022

Калькулятор периодической функции — Онлайн-поиск периода

Поиск инструмента

Поиск инструмента в dCode по ключевым словам:

Просмотр полного списка инструментов dCode

Период функции

Инструмент для вычисления периода функции: значение t, при котором функция повторяется: f(x+t) =f(x-t)=f(x), что имеет место для триго-функций (cos, sin и т. д.)

Результаты

Период функции — dCode

Тег(и) : Функции

Поделиться

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах решать каждый день!
Предложение ? обратная связь? Жук ? идея ? Запись в dCode !

Период вычисления функции

Функция (f(x)=)
Переменная

См. также: Четная или нечетная функция — решение уравнений

Ответы на вопросы (FAQ)

Каков период функции? (Определение)

Период $ t $ периодической функции $ f(x) $ — это наименьшее значение $ t $ такое, что $$ f(x+t) = f(x) $$

Графически его кривая повторяется на интервале каждого периода. Функция равна самой себе для каждого цикла длины $t$ (представляет собой шаблон/график, который повторяется при переносе).

Значение периода $t$ также называют периодичностью функции или фундаментальным периодом.

Как найти период функции?

Чтобы найти период $ t $ сигнала или функции $ f(x) $, покажите, что $$ f(x+t)=f(x) $$

Пример: Тригонометрическая функция $ \ sin(x + 2\pi) = \sin(x) $, поэтому $ \sin(x) $ периодична с периодом $ 2\pi $

Тригонометрические/синусоидальные функции обычно являются периодическими с периодом $ 2\pi $ , чтобы угадать период, попробуйте число, кратное пи, для значения $t$.

Если период равен 0, то функция непериодическая.

Как найти значение f(x) периодической функции?

Любая периодическая функция периода $t$ повторяется каждые $t$ значений. Чтобы предсказать значение цикла периодической функции , для значения $ x $ вычислите $ x_t = x \mod t $ (по модулю t) и найдите известное значение $ f(x_t) = f(x) $

Пример: Функция $ f(x) = \cos(x) $ имеет период $ 2\pi $, значение при $ x = 9 \pi $ такое же, как при $ x \equiv 9 \pi \mod 2 \pi \equiv \pi \mod 2 \pi $ и, следовательно, $ \cos(9\pi) = \cos(\pi) = -1 $

Как найти амплитуду периодической функции?

Амплитуда представляет собой абсолютное значение непериодической части функции.

Пример: $ a \sin(x) $ имеет для амплитуды $ | а | $

Как доказать периодичность функции?

Демонстрация существования периода $t$ у функции $f$ заключается в вычислении, верно ли равенство $f(x+t)=f(x)$.

Как доказать, что функция не периодична?

Если $f$ периодична, то существует ненулевое вещественное число, такое как $$ f(x+t)=f(x) $$

Демонстрация состоит в том, чтобы доказать, что это невозможно. Например, с доведением до абсурда или выполнением вычисления, которое приводит к противоречию.

Какие обычные периодические функции?

Наиболее распространенными периодическими функциями являются тригонометрические функции, основанные на функциях синуса и косинуса (с периодом 2 Пи).

Функция	Период
SINE $ \ SIN (x) $	$ 2 \ PI $
COSIN (x) $	$ \pi $

Исходный код

dCode сохраняет за собой право собственности на исходный код «Период функции». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Период функции», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Периода функций» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанных на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Периода функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильном телефоне, планшете, iPhone или в приложении для Android!
Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Период функции» или любого из ее результатов разрешено, пока вы цитируете dCode!
Цитировать как источник (библиографию):
Период функции на dCode.