Кто знает, как строить график уравнения? №7.17 по алгебре 7 класс, Мордкович – Рамблер/класс
Кто знает, как строить график уравнения? №7.17 по алгебре 7 класс, Мордкович – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
На координатной плоскости хОу постройте график уравнения
а) x + у — 4 = 0; в) -х — у + 6 = 0;
ответы
У меня такие получились графики
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
9 класс
11 класс
похожие вопросы 5
Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра
10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее…)
ГДЗМордкович А.Г.Алгебра8 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.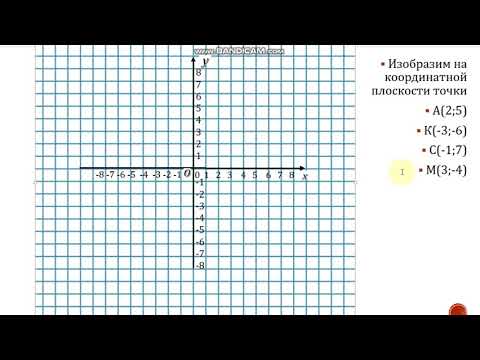
..)
ГДЗ11 классКолмогоров А.Н.Алгебра
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.
П.
Урок по алгебре 7 класс «Линейная функция и ее график»
Открытый урок по алгебре
(7 класс)
Тема: «Раскрываем секреты линейной функции и ее графика»
Цель урока: используя ранее изученный материал систематизировать, обобщить и закрепить навыки решения задач с помощью понятия линейной функции; развивать познавательный интерес к математике.
Планируемые образовательные результаты
Предметные:
— знать понятие линейной функции, условия пересечения и параллельности графиков линейных функций.-уметь записывать формулу линейной функции, строить график, характеризовать отличительные черты, задавать линейную функцию различными способами, распознавать линейную функцию по формуле.
Метапредметные:
Регулятивные: — контроль по образцу и внесение корректив;
– постановка и удерживание учебной задачи;
– умение адекватно оценивать правильность или ошибочность выполнения учебной задачи и собственные возможности её решения, сличать способ действия с эталоном;
Познавательные: – понимание математических рисунков, анализ, сравнение, использование знаково-символических средств;
— целеполагание;
— выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство;
Коммуникативные: – учебное сотрудничество и совместная деятельность с учителем и сверстниками;
– умение слушать;
– умение аргументировать свою позицию и
координировать её при выработке общего решения в совместной деятельности.
Личностные: формирование у учащихся готовности и способности к самообразованию на основе мотивации к обучению и познанию;
формирование уважительного и доброжелательного отношения к другому человеку, его мнению;
формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в процессе учебно-исследовательской деятельности.
Формы работы: фронтальный опрос, устная работа, работа с готовым чертежом, работа с презентацией, тестовая работа, исследовательская работа.
ХОД УРОКА
I. Мотивация учебной деятельности.
Здравствуйте, ребята. Тема нашего урока «Раскрываем
секреты линейной функции и ее графика». На уроке мы повторим основные
теоретические сведения, связанные с понятием линейная функция и ее график,
закрепим навыки построения графика линейной функции, научить определять по
формулам, задающих линейные функции взаимное расположение их графиков.
«Скажи мне – и я забуду,
Покажи мне – и я запомню,
Вовлеки меня – и я пойму»
II. Актуализация знаний.
Крупнейший физиолог Иван Петрович Павлов говорил: «Изучайте азы науки, прежде чем войти на ее вершины, никогда не беритесь за последующее, не усвоив предыдущее», поэтому начинаем урок с небольшой разминки.
1) Какая функция называется линейной?
(Линейной функцией называется функция, которую можно задать формулой вида , где х – независимая переменная,
2) Как называется коэффициент k при х в уравнении линейной функции?
(Коэффициент k при х называется угловым коэффициентом.)
3) Что является графиком линейной функции?
(Графиком линейной функции является
прямая линия.
)
4) Как построить график линейной функции?
(Для построения графика линейной функции достаточно найти координаты двух точек графика, отметить эти точки в координатной плоскости и провести через них прямую.)
5) Почему для построения графика линейной функции достаточно найти только две точки?
(Из начальных геометрических сведений мы знаем, что через две точки плоскости можно провести прямую и притом только одну.)
1. Чтение графика
На рисунке построены графики движения пешехода (отрезок ОВ) и велосипедиста (отрезок ОА). С помощью графиков ответьте на вопросы:
А) Какое время был в пути пешеход? Велосипедист?
(Пешеход был в пути 4ч, а велосипедист 2ч.)
Б) Какой путь проделал пешеход? Велосипедист?
(Пешеход прошел 20км, а велосипедист 30км.)
В) С какой скоростью двигался пешеход? Велосипедист?
(Пешеход двигался со скоростью 5 км/ч, велосипедист со скоростью 15 км/ч)
Г) Во сколько раз путь, который проехал за 2 ч велосипедист, больше пути, пройденного за то же время пешеходом?
(За 2 ч
велосипедист проехал 30 км, а пешеход прошел 10
км.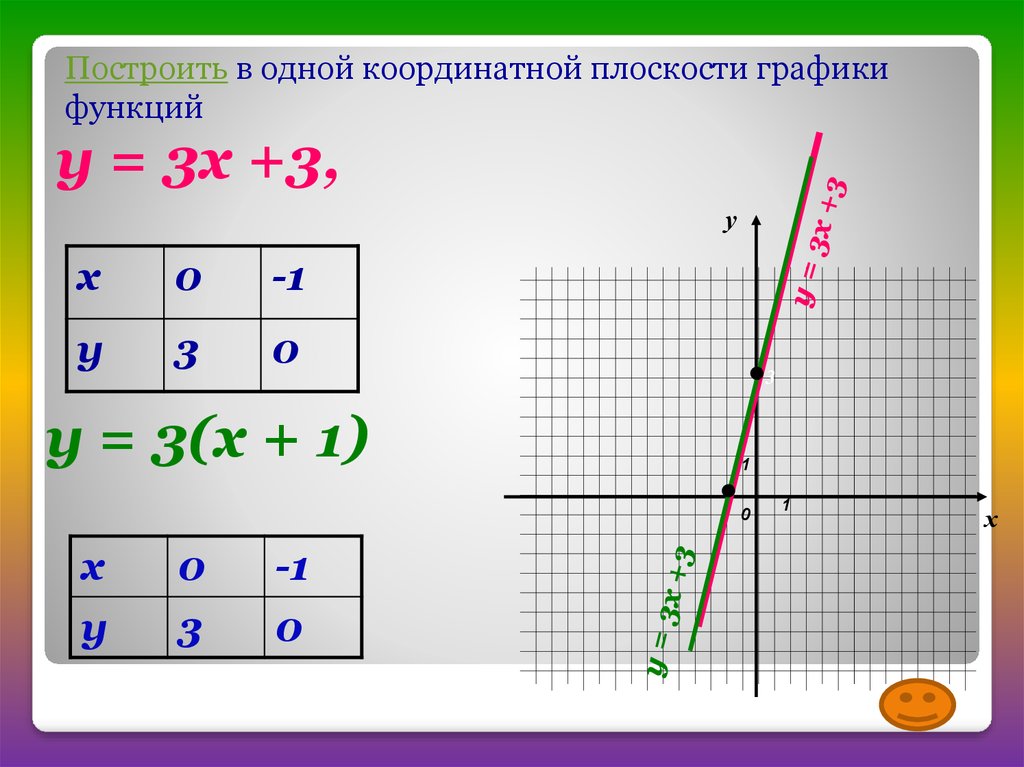
30:10=3. Путь, который проехал велосипедист в 3 раза больше пути,
пройденного пешеходом)
2. Какая из функций является линейной
а) у = -2, б) у = -3х-1, в) у = х2 + 4, г) у = 7-?
3. Какой из графиков является графическим изображением линейной функции?
III. Изучение нового материала
Известный математик Рене Декарт утверждал: «Для того чтобы усовершенствовать ум, надо больше размышлять, чем заучивать». Заученный материал мы повторили, а теперь покажите, как вы умеете размышлять.
– Что можно сказать про графики линейных функций?
(Графики линейных функций параллельны)
– Что можно сказать про коэффициенты при х в формулах? (Коэффициенты при х одинаковы)
Вывод: Графики
двух линейных функций параллельны, если коэффициенты при х одинаковы.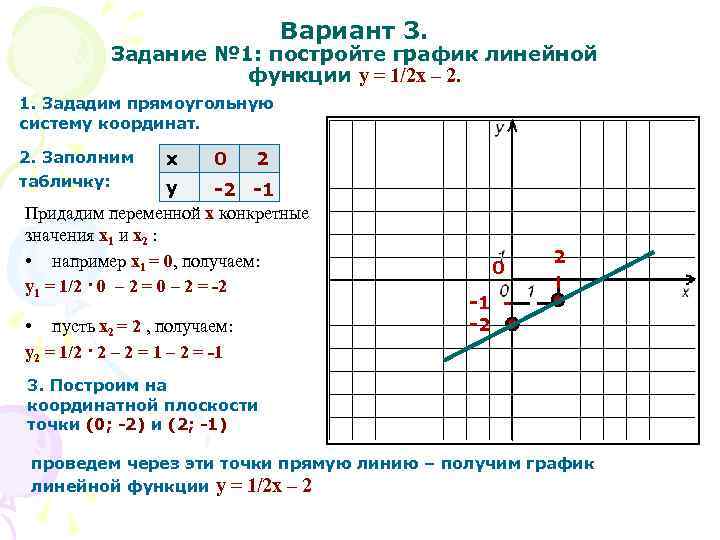
y1=к1+b1, y2=к2+b2
Если k1=k2, то графики линейных функций параллельны.
– Что можно сказать про графики линейных функций?
(Графики линейных функций пересекаются)
– Что можно сказать про коэффициенты при х в формулах?
(Коэффициенты при х различны)
Вывод: Графики двух линейных функций пересекаются, если коэффициенты при х различны.
Если k1 ≠k2, то графики линейных функций пересекаются.
-Что можно сказать про графики линейных функций?
(Графики линейных функций пересекаются)
-Что можно сказать про коэффициенты k и b в формулах?
(Коэффициенты при х различны, а коэффициенты b одинаковы)
Вывод: Если
коэффициенты при х различны, а значения b
одинаковы, то графики линейных функций пересекаются в одной точке лежащей на
оси у.
Если k1 ≠k2 и b1=b2, то графики линейных функций пересекаются в точке с координатами (0;b).
Задание 1: Выберите функции, графики которых пересекают график функции у=5х+19.
1) у=6х+19
2) у=21+5х
3) у=5х-8
4) у=19х+5
Задание 2: Выберите функции, графики которых параллельны графику функции у= -4х-2.
1) у=7х-2
2) у=3-4х
3) у=-4х+18
4) у=4х-5
IV. Первичное закрепление знаний
Задание 1. Дана функция у=3х-8. Найти значение функции
при х=0, 2, 4, 5, 7 , 8, 10.
Каждому значению функции соответствует буква.
У= 7 — Б
У= 4 — Й
У= -2 — Е
У= 22 — Ц
У= -8 — Л
У= 16 — И
У= 13 — Н
Готфрид Вильгельм фон Лейбниц – это
имя немецкого математика, который и ввел термин «функция».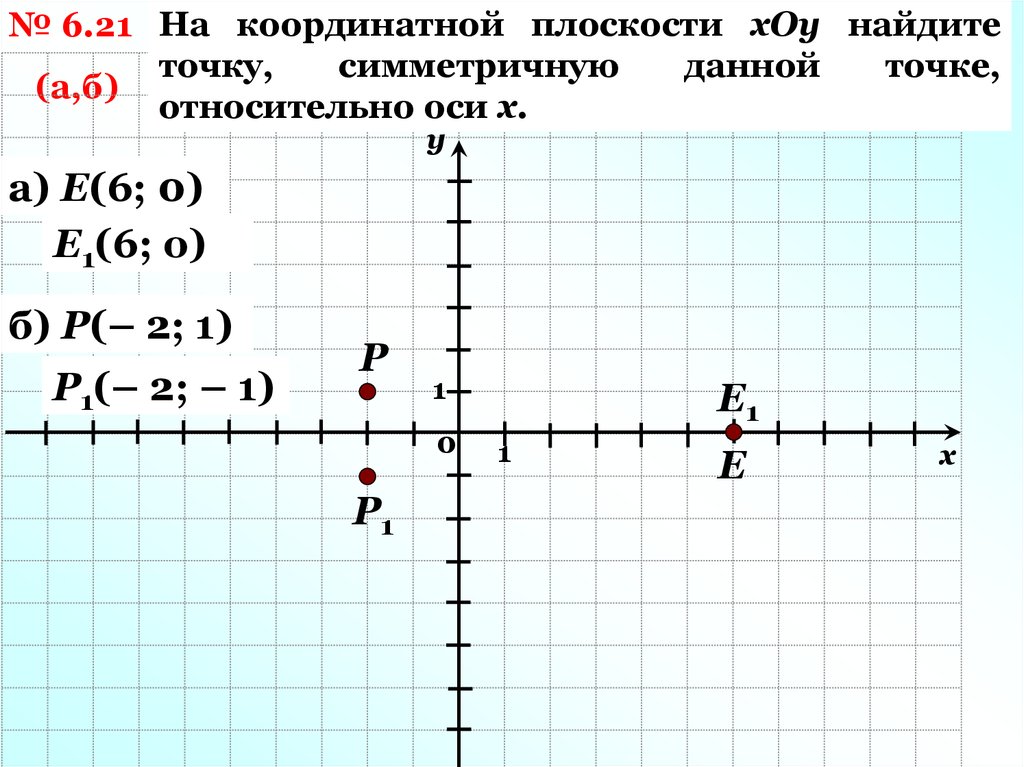
V. Исследовательская работа.
Задание 1. В одной координатной плоскости построить графики функций: у=-2х+4, у=-2х+3, у=-2х-2.
Ответить на вопросы:
1) Что представляют собой графики функций?
2) Что общего в формулах этих функций?
3) Каково значение коэффициента по знаку?
4) Опишите, каков угол наклона графиков функций к оси Ох.
Задание 2. В одной координатной плоскости построить графики функций: у=х+1, у=3х+1, у=0,5х+1.
Ответить на вопросы:
1) Что представляют собой графики функций?
2) В какой точке пересекаются графики функций?
3) Каково значение коэффициента по знаку?
4) Каков угол наклона графиков функций к оси Ох.
Вывод:
VI. Проверка усвоения новых знаний
Тест по теме «Линейная функция»
1.
Какая функция является линейной?
1) y = 2х2
2) y = 2/х
3) y = 2х +7
2.
Графиком линейной функции является?
1) Гипербола
2) Прямая
3) Парабола
3.
Угловым коэффициентом называется…
1) Коэффициент при «х»
2) Свободный член
3) Произведение коэффициента при «х» и свободного члена
4.
Графики линейных функций параллельны, если
1) Угловые коэффициенты различны
2) Угловые коэффициенты равны
3) Угловые коэффициенты пропорциональны
5.
Определите взаимное расположение графиков линейных функций y = 2х + 5 и y = -3х
+ 5.
1) Параллельны
2) Пересекаются
3) Совпадают
6. График линейной функции образует тупой угол с осью ОХ, если:
1) угловой коэффициент <0
2) угловой коэффициент >0
3) угловой коэффициент =0
Взаимопроверка тестов. Поменяйтесь с соседом тестами и выполните взаимопроверку.
VII.
Рефлексия
Итак, ребята. Сегодня мы повторили определение линейной функции, что является графиком линейной функции и как построить график этой функции.
— Какие секреты линейной функции вы узнали сегодня на уроке?
VIII. Домашнее задание.
1) п. 15, №337, 341, 342.
2) Подобрать и наглядно оформить материал из различных областей, по теме: “Где используется
и применяется линейная функция”.
Заключение.
«Прямая – есть кратчайшее расстояние между двумя точками» — сказал Рене Декарт. И следуя этому правилу, я призываю вас в своем развитии по восходящей линии, не страшась усталости, не обходя трудностей, идти по прямой от точки незнания к точке знания».
Спасибо за урок, ребята!
7.3: Построение точек на плоскости
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49382
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX0010
Самолет
Заказанный Пары
Теперь нас интересует изучение графиков линейных уравнений с двумя переменными.
Мы знаем, что решения уравнений с двумя переменными состоят из пары значений, по одному значению для каждой переменной. Мы назвали эти пары значений упорядоченными парами. Поскольку у нас есть пара значений для построения графика, у нас должна быть пара осей (числовых линий), на которых можно расположить значения.
Происхождение
Мы рисуем оси так, чтобы они были перпендикулярны друг другу и пересекались друг с другом в своих 0-х точках. Эта точка называется началом координат .
Прямоугольная система координат Система
Эти две линии образуют так называемую прямоугольную систему координат . Они также определяют самолет.
\(xy\)-плоскость
Плоскость является плоской поверхностью, и согласно геометрии, через любые две пересекающиеся линии (оси) можно пройти ровно одну плоскость (плоскую поверхность). Если мы имеем дело с линейным уравнением с двумя переменными \(x\) и \(y\), мы иногда говорим, что строим уравнение в прямоугольной системе координат, или что мы строим уравнение в \(xy \)-самолет.
Квадрант
Обратите внимание, что две пересекающиеся оси координат делят плоскость на четыре равные области. Поскольку регионов четыре, мы называем каждый из них квадрантом и нумеруем их против часовой стрелки римскими цифрами.
Вспомним, что когда мы впервые изучали числовую прямую, мы заметили следующее:
Для каждого действительного числа существует уникальная точка на числовой прямой, и каждой точке на числовой прямой мы можем связать уникальное действительное число .
У нас аналогичная ситуация с самолетом.
Для каждой упорядоченной пары \((a, b)\) существует единственная точка на плоскости, и каждой точке на плоскости можно поставить в соответствие уникальную упорядоченную пару \((a, b)\) вещественных числа.
Координаты точки
Координаты точки
Числа в упорядоченной паре, связанные с определенной точкой, называются координатами точки.
Первая цифра в упорядоченной паре выражает горизонтальное расстояние и направление точки (влево или вправо) от начала координат. Второе число выражает вертикальное расстояние и направление точки (вверх или вниз) от начала координат.
Координаты определяют расстояние и направление
положительное число означает направление вправо или вверх . отрицательное число означает направление на влево или вниз .
Точки на графике
Поскольку точки и упорядоченные пары очень тесно связаны, эти два термина иногда используются взаимозаменяемо. Следующие две фразы имеют одинаковое значение:
- Нарисуйте точку \((a, b)\).
- Постройте упорядоченную пару \((a, b)\).
Построение Точки
Обе фразы означают: Найдите на плоскости точку, связанную с упорядоченной парой \((a, b)\) и нарисуйте метку в этом месте.
Образец набора A
Пример \(\PageIndex{1}\)
Постройте упорядоченную пару \((2, 6)\).
Начнем с начала. Первое число в упорядоченной паре, 2, говорит нам, что мы перемещаемся на 2 единицы вправо (\(+2\) означает 2 единицы вправо). Второе число в упорядоченной паре, 6, говорит нам, что мы перемещаемся на 6 единиц вверх. (\(+6\) означает увеличение на 6 единиц).
Иногда полезно читать \((2,6)\) как «если \(x = 2\), то \(y = 6\).
Практический набор A
Практическая задача \( \PageIndex{1}\)
Постройте упорядоченные пары.
\((1, 3), (4, −5), (0, 1), (−4, 0)\).
- Ответить
(Обратите внимание, что пунктирные линии на графике служат только для иллюстрации и не должны использоваться при построении точек.)
Упражнения
Упражнение \(\PageIndex{1}\)
Нарисуйте следующие упорядоченные пары.
(Не рисуйте стрелки, как в практическом наборе A.)
\((8, 2), (10, −3), (−3, 10), (0, 5), (5, 0), (0 , 0), (−7, -\dfrac{3}{2})\).
- Ответить
Упражнение \(\PageIndex{2}\)
Как можно точнее укажите координаты точек, нанесенных на следующий график.
Упражнение \(\PageIndex{3}\)
Используя упорядоченную парную запись, каковы координаты начала координат?
- Ответить
Координаты места исходной точки равны \((0,0)\).
Упражнение \(\PageIndex{4}\)
Мы знаем, что решения линейных уравнений с двумя переменными можно представить в виде упорядоченных пар. Следовательно, решения можно представить в виде точек на плоскости. Рассмотрим линейное уравнение \(y=2x−1\). Найдите не менее десяти решений этого уравнения, выбирая значения \(x\) между \(−4\) и \(5\) и вычисляя соответствующие значения y.
Постройте эти решения в системе координат ниже. Заполните таблицу, чтобы помочь вам отслеживать заказанные пары.
| \(х\) | — | — | — | — | — | — | — | — | — | — | — | — |
| \(у\) | — | — | — | — | — | — | — | — | — | — | — | — |
Имея в виду, что существует бесконечно много упорядоченных парных решений \(y=2x−1\), порассуждайте о геометрической структуре графа всех решений.
Заполните следующую инструкцию:
Название типа геометрической структуры графика всех решений линейного уравнения
\(y=2x−1\) похоже на __________ .
Где эта фигура пересекает ось Y? Встречается ли это число в уравнении \(y=2x−1\)?
Поместите карандаш в любую точку на рисунке (возможно, вам придется соединить точки, чтобы четко видеть рисунок). Переместите карандаш ровно на одну единицу вправо (по горизонтали). Чтобы вернуться к рисунку, вы должны переместить карандаш вверх или вниз на определенное количество единиц. На сколько единиц нужно переместиться по вертикали, чтобы вернуться на фигуру, и видите ли вы это число в уравнении \(y=2x−1\)?
Упражнение \(\PageIndex{5}\)
Рассмотрим плоскость \(xy\).
Заполните таблицу, записав соответствующие неравенства.
| я | II | III | IV |
| \(х > 0\) | \(х < 0\) | \(х\) | \(х\) |
| \(у > 0\) | \(у\) | \(у\) | \(у\) |
В следующих задачах графики точек называются диаграммами рассеяния и часто используются статистиками для определения наличия связи между двумя рассматриваемыми переменными.
Первый компонент упорядоченной пары называется входной переменной , а второй компонент называется выходной переменной . Построить диаграммы разброса. Определите, существует ли взаимосвязь между двумя рассматриваемыми переменными, сделав следующие наблюдения: Связь может существовать, если
- при увеличении одной переменной увеличивается другая переменная
- при увеличении одной переменной другая уменьшается
- Ответить
я II III IV \(х > 0\) \(х < 0\) \(х < 0\) \(х > 0\) \(у > 0\) \(у > 0\) \(у <0\) \(у <0\)
Упражнение \(\PageIndex{6}\)
Психолог, изучавший воздействие плацебо на рабочих сборочной линии на конкретном промышленном объекте, отметил время, необходимое для сборки определенного предмета, прежде чем испытуемому дали плацебо.
, \(x\) и время, необходимое для сборки аналогичного предмета после того, как испытуемому дали плацебо, \(y\). Данные психолога
| \(х\) | \(у\) |
| 10 | 8 |
| 12 | 9 |
| 11 | 9 |
| 10 | 7 |
| 14 | 11 |
| 15 | 12 |
| 13 | 10 |
Упражнение \(\PageIndex{7}\)
Следующие данные были получены в ходе исследования инженером взаимосвязи между величиной давления, используемого для формирования части машины, \(x\) и количество выпущенных бракованных машин, \(y\).
| \(х\) | \(у\) |
| 50 | 0 |
| 60 | 1 |
| 65 | 2 |
| 70 | 3 |
| 80 | 4 |
| 70 | 5 |
| 90 | 5 |
| 100 | 5 |
- Ответить
Да, связь есть.
Упражнение \(\PageIndex{8}\)
Следующие данные представляют количество пропущенных рабочих дней в году \(x\) сотрудниками страховой компании и количество минут, на которые они опаздывают после обеда. , \(у\).
| \(х\) | \(у\) |
| 1 | 3 |
| 6 | 4 |
| 2 | 2 |
| 2 | 3 |
| 3 | 1 |
| 1 | 4 |
| 4 | 4 |
| 6 | 3 |
| 5 | 2 |
| 6 | 1 |
Упражнение \(\PageIndex{9}\)
Производитель стоматологического оборудования имеет следующие данные о стоимости единицы (в долларах), \(y\), конкретного изделия и количестве единиц, \(х\), изготовленных для каждого заказа.
| \(х\) | \(у\) |
| 1 | 85 |
| 3 | 92 |
| 5 | 99 |
| 3 | 91 |
| 4 | 100 |
| 1 | 87 |
| 6 | 105 |
| 8 | 111 |
3: Plotting Points in the Plan доступна в соответствии с лицензией CC BY, автором, ремиксом и/или куратором являются Денни Бурзински и Уэйд Эллис-младший (OpenStax CNX).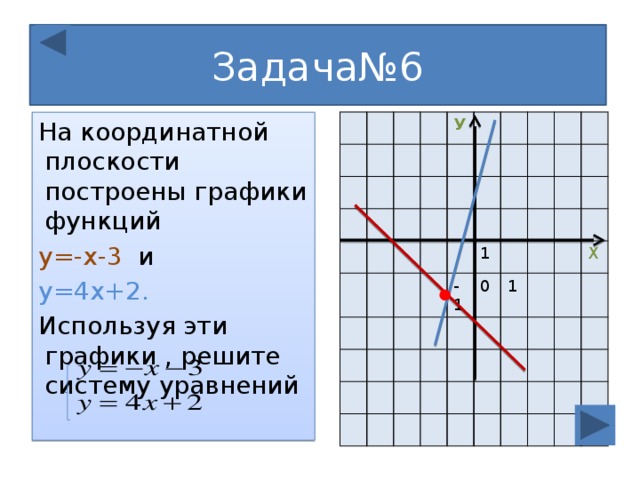
..
..