По какой формуле вычисляется высота параллелограмма? Геометрия / Справочник :: Бингоскул
К параллелограммам относят четырёхугольники с попарно параллельными сторонами. Частными случаями таких геометрических фигур являются квадраты, ромбы и прямоугольники. В публикации рассмотрим, что такое высота параллелограмма, как её провести и вычислить через стороны, диагонали и углы. Рассмотрим признаки и свойства фигуры.
Особенности геометрической фигуры
Рассматриваемый 4-угольник обладает рядом присущих только ему свойств. У него одинаковые противоположные стороны и углы. Сумма последних, примыкающих к одной стороне, равняется 180°. Место пересечения диагоналей делит их пополам, является центром симметрии параллелограмма и точкой пересечения средних линий. Также диагональ образует два одинаковых треугольника.
Определение высоты параллелограмма
Высота параллелограмма – это перпендикуляр – линия, опущенная из одной стороны на другую, противоположную или параллельную ей. Обозначится двумя буквами, например, DE, либо одной – h.
Обозначится двумя буквами, например, DE, либо одной – h.
Перпендикуляр проводится не из каждой точки геометрической фигуры, ведь иногда находится за её пределами. Тогда высоту (BE) опускают на продолжение стороны (CE).
Как провести высоту в параллелограмме
Для построения высоты одна сторона угольника ставится на основание, перпендикулярная ей пересекает противоположную в месте, где будет проводиться перпендикуляр. Точки, принадлежащие параллелограмму, соединяются.
В итоге получается высота FG.
Также она может проводиться с одной боковой стороны на вторую.
Все формулы высоты параллелограмма
Рассмотрим способы вычислить длину перпендикуляра четырёхугольника.
Как найти высоту параллелограмма, зная его стороны
Высота – отношение площади геометрической фигуры к длине стороны, из которой опущен перпендикуляр:
h = S / a,
- S = площадь фигуры;
- a – размер основания, на который опущен перпендикуляр.
 2 }.
2 }.Существует более сложная формула, позволяющая найти одну высоту параллелограмма через другую и стороны. Обратно пропорциональное отношение одной высоты ко второй равно соотношению длин оснований:
\frac { a } { b } = \frac { 1 } { h_a} : \frac { 1 } { h_b }.
Задача
Дан параллелограмм с высотой BE, проведённой из тупого угла 4-угольника. Она делит основание на равные отрезки. Острый угол между ней и стороной равен 30°, а диагональ, проведённая между вершинами тупых углов – 10 см. Вычислить h геометрической фигуры и градусную меру ∠ABD.
Начнём из рассмотрения получившихся треугольников: ABE, BED – в соответствии с первым признаком их равенства, эти 3-угольники равны между собой: имеют равные катеты AE = ED и углы BEA = BED = 90°. Отсюда следует, что AB = BD. Получим равнобедренный треугольник BDA с равными 30° углами при основании: BAD = BDA.
Расположенный накрест угол при параллельных отрезках DA с CB тоже равняется 30°.
Присмотримся к треугольнику ABE.
 Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.
Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.∠ABD = ∠ABE + ∠DBE = 60 = 60 = 120°.
∠CDB = ∠ABD = 120° ведь он внутренний накрест лежащий.
Для нахождения высоты параллелограмма подойдёт формула:
EB / DB = cos (EBD), градусная мера EBD = 60°.
EB / DB = cos (60) = ½.
DB из условий задачи равняется 10 см. Подставим в формулу.
EB / 10 = ½.
EB = 10 * ½ = 5 (см).
Ответ: ∠ABD, EB = 5 (см).
Замечательные линии и точки треугольников 7 класс онлайн-подготовка на Ростелеком Лицей
Площадь прямоугольного треугольника
Одной из важнейших характеристик геометрической фигуры на плоскости является ее площадь. Мы уже выводили формулу площади треугольника, используя формулу площади прямоугольника.
Рассмотрим прямоугольный треугольник со сторонами и , которые образуют прямой угол (см. рис. 1). Эти стороны в прямоугольном треугольнике называются катетами, а третья сторона – гипотенузой.

Рис. 1. Прямоугольный треугольник с катетами и
Теперь рассмотрим прямоугольник со сторонами и . Проведем в нем диагональ (см. рис. 2).
Рис. 2. Прямоугольник со сторонами и и проведенной диагональю
Несложно доказать, используя признак равенства треугольников (по двум сторонам и углу между ними), что получились два равных прямоугольных треугольника. У равных треугольников равные площади, получаем:
Откуда:
Итак, мы получили, что площадь любого прямоугольного треугольника равна полупроизведению длин его катетов.
Площадь произвольного треугольника
Воспользуемся этой формулой для того, чтобы получить формулу площади произвольного треугольника. Опустим перпендикуляр из вершины треугольника на сторону (см. рис. 3).
Рис. 3. Произвольный треугольник с опущенным на сторону перпендикуляром
Наш треугольник разбился на два прямоугольных треугольника и , и его площадь равна:
Используем распределительный закон справа налево и вынесем общий множитель за скобки:
Итак, мы получили, что площадь произвольного треугольника можно вычислить как полупроизведение длины перпендикуляра, опущенного из вершины на противоположную сторону треугольника, и длины этой стороны.

Но такая формулировка слишком громоздкая, а формула используется достаточно часто, поэтому для перпендикуляра придумали специальное название – высота треугольника .
Сторона, к которой проведена высота, называется основанием треугольника . Точка, в которую опускается перпендикуляр, называется основанием высоты . Тогда площадь произвольного треугольника – это полупроизведение высоты на основание:
Ортоцентр треугольника
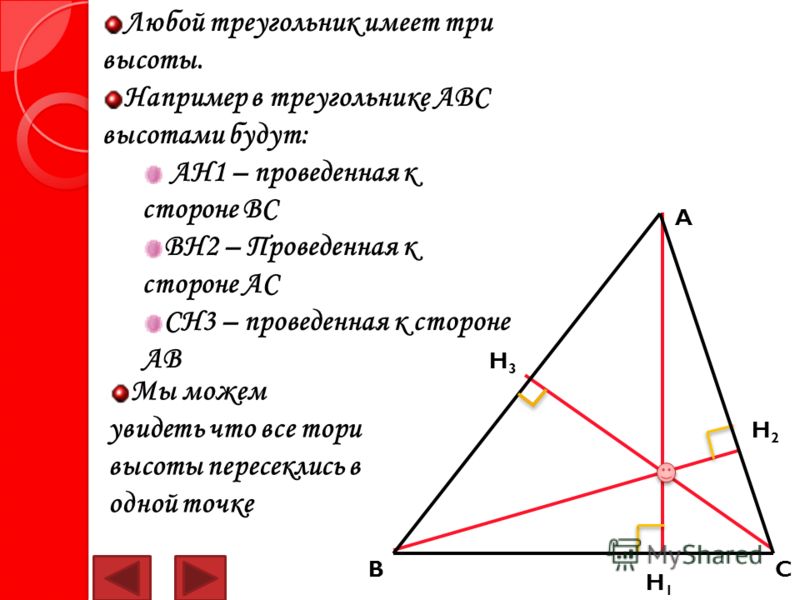
Поскольку вершин у треугольника три, то и высот можно провести три (каждая из сторон может выступать в качестве основания) (см. рис. 4).
Рис. 4. Три высоты, проведенные в треугольнике
Поскольку в доказательстве формулы для площади мы не накладывали никаких условий на выбор основания и высоты, то площадь треугольника не будет зависеть от того, какую пару «высота – основание» выбрать.
Почему такое название – высота? Представьте себе большую треугольную конструкцию, одна сторона которой лежит на земле.
 Какова ее высота? Именно та самая, что в определении. А если конструкцию повернуть на другую сторону? Соответственно – другая высота треугольника (см. рис. 5).
Какова ее высота? Именно та самая, что в определении. А если конструкцию повернуть на другую сторону? Соответственно – другая высота треугольника (см. рис. 5).Рис. 5. Высоты лежащей и перевернутой конструкций
Если вернуться к формуле для площади прямоугольного треугольника, которую мы получили в самом начале, то можно заметить, что она очень похожа на формулу площади произвольного треугольника. Это не случайность.
Рассмотрим прямоугольный треугольник (один угол прямой). Высота, проведенная из вершины прямого угла к гипотенузе, также лежит внутри треугольника (см. рис. 6).
Рис. 6. В прямоугольном треугольнике проведена высота к гипотенузе
Но как будут выглядеть высоты, опущенные из вершин и ? По определению: высота – это перпендикуляр, опущенный из вершины на противолежащую сторону. Но – это и есть перпендикуляр к , аналогично: – перпендикуляр к (см. рис. 7).
Рис. 7. В прямоугольном треугольнике две высоты равны катетам
Получаем, что в прямоугольном треугольнике две высоты совпадают с катетами.
 И формула площади прямоугольного треугольника – частный случай формулы площади произвольного треугольника.
И формула площади прямоугольного треугольника – частный случай формулы площади произвольного треугольника.В остроугольном треугольнике (все углы меньше прямого): все три высоты будут лежать внутри треугольника (см. рис. 8).
Рис. 8. В остроугольном треугольнике все три высоты лежат внутри треугольника
В тупоугольном треугольнике две высоты, проведенные из вершин острых углов, будут лежать вне треугольника (см. рис. 9).
Рис. 9. В тупоугольном треугольнике две высоты лежат вне треугольника
Обратите внимание, что во всех рассмотренных случаях высоты (или их продолжения) пересекались в одной точке. Это не случайность.
В треугольнике все высоты (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (от греч. orthos – «прямой»: высоты образуют прямые углы со сторонами, на которые они опущены). Этот факт мы пока не можем доказать, но вернемся к его доказательству позже.
Из сказанного выше можно сделать вывод, что в остроугольном треугольнике ортоцентр лежит внутри треугольника, в прямоугольном треугольнике – совпадает с вершиной прямого угла, а в тупоугольном треугольнике – лежит вне треугольника (см.
 рис. 10).
рис. 10).Рис. 10. Расположение ортоцентра в остроугольном, прямоугольном, тупоугольном треугольниках
Медиана треугольника
Итак, площадь треугольника можно найти как полупроизведение высоты на основание, где – высота треугольника, – основание:
А как разделить участок треугольной формы на два участка равной площади? Предположим, нам это удалось (см. рис. 11).
Рис. 11. Треугольник разделен на два участка равной площади
У треугольников и есть общая высота: (мы знаем, что из точки к прямой можно провести только один перпендикуляр) (см. рис. 12).
Рис. 12. – общая высота треугольников и
Получаем, что:
Мы разбиваем треугольник на два треугольника равной площади, поэтому:
Получаем, что точка должна быть серединой стороны .
Линия называется медианой (от лат. mediana – «средняя») треугольника – это линия, соединяющая вершину с серединой противоположной стороны треугольника.

Как мы только что доказали, медиана делит треугольник на два треугольника с равной площадью (мы уже знаем, что такие треугольники называются равновеликими).
Как и высот, медиан в треугольнике можно провести три (см. рис. 13). В отличие от высот, независимо от вида треугольника, медианы всегда лежат внутри треугольника.
Рис. 13. Три медианы треугольника
Медианы, как и высоты, пересекаются в одной точке (этот факт мы тоже докажем позже). Эта точка называется центром тяжести треугольника (или центроидом).
Если вырезать из бумаги треугольник и положить его на иголку так, чтобы ее острие было в точке пересечения медиан (см. рис. 14), то треугольник будет оставаться в равновесии.
Рис. 14. Треугольник находится в равновесии, если острие иголки расположить в центре тяжести
Если сдвинуть иголку в любую другую точку, то треугольник упадет. Можете провести этот эксперимент сами и убедиться в истинности данного утверждения.

Почему центр тяжести треугольника находится в точке пересечения медианПочему именно точка пересечения медиан обладает таким свойством? Мы рассматриваем однородный треугольник, который состоит из одного вещества или сплава. У всех его частей одинаковая плотность, поэтому масса любой части будет тем больше, чем больше ее объем (вспомним из курса физики: , где – масса, – объем).
Но в планиметрии у треугольника толщины нет, поэтому масса будет тем больше, чем больше площадь соответствующей части (на практике, например в вырезанном из бумаги треугольнике, толщина, хоть и очень маленькая, но есть; но поскольку эта толщина постоянна, то масса любой части треугольника все равно будет зависеть от площади этой части).
Мы уже говорили о том, что медиана делит треугольник на две площади равной части. Значит, логично предположить, что центр тяжести лежит где-то на медиане (иначе какая-то из частей треугольника перевешивала бы). Но медиан в треугольнике три, значит, центр тяжести должен лежать на каждой из них, т.
 е. в точке их пересечения (см. рис. 15).
е. в точке их пересечения (см. рис. 15).Рис. 15. Центр тяжести лежит в точке пересечения трех медиан треугольника
Конечно, это не строгое доказательство, а соображение. Но оно полезно для понимания того, почему точка пересечения медиан – это и есть центр тяжести треугольника.
Биссектриса треугольника
Мы поговорили о медиане – линии, которая делит сторону на равные части. Логично рассмотреть линию, которая делит на равные части угол треугольника (см. рис. 16).
Такая линия, которая делит угол на два равных угла, называется биссектрисой (от греч. bi – «двойное», section – «разрезание»).
Рис. 16. Биссектриса треугольника делит на равные углы и
По аналогии с уже рассмотренными линиями в треугольнике можно провести три биссектрисы, т. к. в треугольнике три угла. Как и медианы, все биссектрисы лежат внутри треугольника. И они также пересекаются в одной точке, которая лежит внутри треугольника и называется инцентром (см.
 рис. 17).
рис. 17).Рис. 17. Инцентр треугольника
Название «инцентр» связано с особенным свойством этой точки, о котором мы сейчас поговорим. Рассмотрим и его биссектрису . Опустим из точки перпендикуляры и на стороны угла (см. рис. 18).
Рис. 18. – биссектриса , ,
Треугольники и равны по второму признаку равенства треугольников: они прямоугольные , у них равны острые углы и общая гипотенуза . Значит, равны и их катеты, в частности . Т. е. любая точка на биссектрисе равноудалена от сторон угла (см. рис. 19).
Рис. 19. Любая точка на биссектрисе равноудалена от сторон угла
Несложно доказать, что любая точка не на биссектрисе не будет равноудалена от сторон угла.
Тогда можно дать эквивалентное определение биссектрисы – это геометрическое место точек (ГМТ), равноудаленных от сторон угла.
ДоказательствоКак доказать, что любая точка, которая не лежит на биссектрисе, не равноудалена от сторон угла? Воспользуемся методом от противного.

Пусть точка не лежит на биссектрисе , но при этом она равноудалена от сторон этого угла: длины перпендикуляров и на стороны равны (см. рис. 20).
Рис. 20. – биссектриса , , , ,
Соединим точку с точкой и рассмотрим треугольники и (см. рис. 21). В них: , общая, .
Рис. 21. Рассматриваемые треугольники и
Формально у нас нет такого признака равенства (по двум сторонам и углу не между ними). Но на следующем уроке мы докажем, что для равенства прямоугольных треугольников достаточно равенства любых двух сторон (в частности, гипотенузы и любого из катетов). Тогда мы получим, что треугольники и равны, но тогда равны , т. е. точка лежит на биссектрисе. Получили противоречие. Значит, исходное предположение неверно, и если точка не лежит на биссектрисе, то она не будет равноудалена от сторон угла.
Вписанная окружность треугольника
Предположим, что нам надо найти точку, равноудаленную от двух дорог (например, чтобы разместить там станцию отдыха или техобслуживания).
 Если эти две дороги параллельны, то задача решается легко. Все такие точки будут лежать на параллельной прямой, равноудаленной от двух данных (см. рис. 22).
Если эти две дороги параллельны, то задача решается легко. Все такие точки будут лежать на параллельной прямой, равноудаленной от двух данных (см. рис. 22).Рис. 22. Точки, равноудаленные от двух параллельных дорог, лежат на параллельной прямой, равноудаленной от двух данных
Но что делать, если прямые пересекаются? Рассмотрим один из углов, образованный двумя пересекающимися прямыми. Как мы только что доказали, все интересующие нас точки лежат на биссектрисе этого угла (см. рис. 23).
Рис. 23. Точки, равноудаленные от двух пересекающихся дорог, лежат на биссектрисе угла, образованного этими прямыми
Вернемся к треугольнику: биссектрисы всех трех его углов пересекаются в одной точке (см. рис. 24).
Рис. 24. – биссектрисы , – инцентр треугольника
Поскольку точка лежит на биссектрисе , то она равноудалена от сторон и . Но она также лежит на биссектрисе угла – равноудалена от и , и на биссектрисе – равноудалена от и . Т.
 e. точка равноудалена ото всех трех сторон треугольника (см. рис. 25):
e. точка равноудалена ото всех трех сторон треугольника (см. рис. 25):Рис. 25. Точка равноудалена от всех трех сторон треугольника
Если провести окружность с центром в точке и радиусом, который равен расстоянию от точки до сторон треугольника, то получится вписанная окружность (см. рис. 26):
Рис. 26. Вписанная окружность с центром в точке и радиусом
Окружность вписана в треугольник, все три его стороны не пересекают окружность, а как бы касаются ее в одной точке (они так и называются – касательными к окружности, но о них и об их свойствах подробнее мы поговорим позже).
Для нас важно запомнить, что окружность, обладающая таким свойством, у любого треугольника ровно одна и ее центр всегда лежит в точке пересечения биссектрис – инцентре.
Почему вписанная окружность касается сторон треугольникаПрямая и окружность на плоскости могут располагаться тремя способами: не иметь общих точек, иметь одну общую точку (касаться) и иметь две общие точки (пересекаться) (см.
 рис. 27).
рис. 27).Рис. 27. Взаимные расположения прямой и окружности
Стороны треугольники будут касаться вписанной окружности (см. рис. 28). Почему именно так?
Рис. 28. Стороны треугольники касаются вписанной окружности
Вспомним определение окружности: множество точек плоскости, расстояние от которых до данной точки одинаково. Пусть это расстояние (радиус окружности) равно (см. рис. 29).
Рис. 29. Окружность с радиусом
Тогда любая точка, которая лежит внутри окружности, удалена от центра на расстояние, меньшее , а любая точка вне окружности – на расстояние, большее (см. рис. 30). Верно и обратное утверждение: если расстояние от точки до центра окружности больше , она лежит вне окружности; меньше – внутри нее.
Рис. 30. Любая точка, которая лежит внутри окружности, удалена от центра на расстояние, меньшее , а любая точка вне окружности – на расстояние, большее .
Рассмотрим треугольник и вписанную окружность с центром в точке .
 Пусть – расстояние от точки до стороны , т. е. радиус вписанной окружности (см. рис. 31).
Пусть – расстояние от точки до стороны , т. е. радиус вписанной окружности (см. рис. 31).Рис. 31. Вписанная в треугольник окружность; – расстояние от точки до стороны :
Мы знаем, что длина перпендикуляра – кратчайшее расстояние от точки до прямой и что длина любой наклонной больше длины перпендикуляра. Тогда для любой точки стороны : , и (по свойству окружности, которое мы обсуждали выше) она будет лежать вне окружности (см. рис. 32).
Рис. 32. Для любой точки : точка лежит вне окружности радиуса
Таким образом, все точки стороны , кроме точки , будут лежать вне вписанной окружности. Т. е. у окружности и прямой ровно одна общая точка – точка . Поэтому сторона касается вписанной окружности. Аналогичное рассуждение можно провести для оставшихся двух сторон треугольника.
Серединный перпендикуляр и описанная окружность треугольника
Рассмотрим практическую задачу. Пусть у нас есть три поселка .
 И нужно разместить станцию скорой помощи так, чтобы она могла обслуживать все три поселка (см. рис. 33). Понятно, что станция должна быть расположена так, чтобы расстояние от нее до каждого из трех поселков было одинаковым.
И нужно разместить станцию скорой помощи так, чтобы она могла обслуживать все три поселка (см. рис. 33). Понятно, что станция должна быть расположена так, чтобы расстояние от нее до каждого из трех поселков было одинаковым.Рис. 33. Необходимо разместить станцию скорой помощи так, чтобы она могла обслуживать все три поселка
Сначала решим более простую задачу. Пусть поселков всего два – и (отрезок ). Где должна быть расположена станция в этом случае?
Рассмотрим прямую, которая проходит через середину отрезка и перпендикулярна ему. Эта линия называется серединным перпендикуляром (см. рис. 34).
Рис. 34. Серединный перпендикуляр к отрезку
Рассмотрим любую точку , которая принадлежит серединному перпендикуляру . Треугольники и равны по первому признаку равенства треугольников (два катета и угол между ними): , т. к. – середина , – общая, . Значит, (см. рис. 35).
Рис. 35. Равные треугольники и
Несложно доказать, что любая точка, например , которая не лежит на серединном перпендикуляре, не будет удовлетворять этому свойству, т.
 е. (см. рис. 36).
е. (см. рис. 36).Рис. 36. Точка , – серединный перпендикуляр:
ДоказательствоКак доказать, что любая точка, которая не лежит на серединном перпендикуляре, не равноудалена от концов отрезка? Снова воспользуемся методом от противного.
Пусть точка не лежит на серединном перпендикуляре к отрезку , но при этом она равноудалена от концов отрезка: (см. рис. 37).
Рис. 37. Точка – серединный перпендикуляр к ,
Соединим точку с серединой отрезка – точкой . Рассмотрим треугольники и (см. рис. 38).
Рис. 38. Рассматриваемые треугольники и
В них: (по нашему предположению), , т. к. – середина отрезка , – общая. По третьему признаку треугольника (три стороны) треугольники и равны.
Но тогда : они смежные (т.е. образуют развернутый угол и их сумма равна ). Значит, . Но тогда прямая перпендикулярна отрезку и проходит через его середину. Значит, – серединный перпендикуляр к отрезку .
Получаем противоречие (точка не должна лежать на серединном перпендикуляре).
 Значит, исходное предположение неверно, и если точка не лежит на серединном перпендикуляре, то она не будет равноудалена от концов отрезка.
Значит, исходное предположение неверно, и если точка не лежит на серединном перпендикуляре, то она не будет равноудалена от концов отрезка.Сформулируем эквивалентное определение серединного перпендикуляра – это геометрическое место точек (ГМТ), равноудаленных от концов отрезка.
Понятно, что станция скорой помощи должна располагаться на серединном перпендикуляре к отрезку (в идеале – в точке , середине отрезка, т. к. в этом случае расстояние от нее до точек и будет наименьшим).
Описанная окружность треугольника
Вернемся теперь к задаче про три поселка . Если интересующая нас точка , равноудаленная от всех трех вершин, существует, то она должна лежать на серединном перпендикуляре к , т. к. равноудалена от и . Построим – серединный перпендикуляр к стороне (если , то ).
Аналогично построим серединный перпендикуляр к стороне (если , то ) и серединный перпендикуляр к стороне (если , то ). Т. е. точка лежит на пересечении всех трех серединных перпендикуляров треугольника (см.
 рис. 39).
рис. 39).Рис. 39. Точка лежит на пересечении всех трех серединных перпендикуляров треугольника
Оказывается, в любом треугольнике серединные перпендикуляры (как и высоты, медианы, биссектрисы) пересекаются в одной точке (т. е. задача про три поселка и станцию скорой помощи всегда имеет решение). Обычно эту точку обозначают буквой (от англ. outcentr).
Это название неслучайно и также связано с особенностью этой точки. Раз она равноудалена от всех трех вершин треугольника, то можно провести окружность с центром в этой точке и радиусом, равным расстоянию от этой точки до вершин (см. рис. 40). Такая окружность называется описанной (она описывает треугольник). У нее только три общие точки с треугольником – это его вершины.
Рис. 40. Описанная окружность треугольника
Как и ортоцентр, точка может лежать как внутри треугольника (для остроугольных треугольников), так и на одной из сторон (прямоугольный треугольник) или вне треугольника (тупоугольный треугольник) (см.
 рис. 41).
рис. 41).Рис. 41. Возможные расположения центров описанных окружностей
Всегда ли можно провести вписанную и описанную окружностиМы уже говорили, что треугольник обладает рядом уникальных для многоугольника свойств – например, это наименьшая возможная замкнутая ломаная (из двух звеньев составить нельзя, из трех – можно).
Хотя мы и не доказали пока строго эти факты, но упомянули, что в любой треугольник можно вписать окружность, потому что три биссектрисы любого треугольника всегда пересекаются в одной точке (см. рис. 42).
Рис. 42. В любой треугольник всегда можно вписать окружность
И вокруг любого треугольника всегда можно описать окружность, потому что три серединных перпендикуляра любого треугольника всегда пересекаются в одной точке (см. рис. 43).
Рис. 43. Вокруг любого треугольника всегда можно описать окружность
Оказывается, это свойство также делает треугольник уникальным многоугольником. Действительно, даже в прямоугольник не всегда удастся вписать окружность (только если это не квадрат) (см.
 рис. 44). Аналогично вокруг ромба не всегда удастся описать окружность (опять же, если это не квадрат).
рис. 44). Аналогично вокруг ромба не всегда удастся описать окружность (опять же, если это не квадрат).Рис. 44. В прямоугольник не всегда удастся вписать окружность (только если это не квадрат)
Про другие многоугольники (пятиугольники, шестиугольники и т. д.) и говорить не приходится. Для того чтобы в них можно было вписать или описать окружность, они должны удовлетворять определенным требованиям.
Замечательные линии и точки треугольника
Ранее мы выделили четыре важные линии в треугольнике:
- высота – перпендикуляр, опущенный из вершины на противолежащую сторону;
- медиана – линия, соединяющая вершину треугольника с серединой противолежащей стороны;
- биссектриса – линия, которая делит угол пополам;
- серединный перпендикуляр – перпендикуляр к стороне, проведенный через ее середину.
Конечно, можно придумать и вывести свойства для многих линий в треугольнике (например, линия, которая делит угол в отношении к ).
 Но рассмотренные нами линии наиболее часто встречаются при решении различных практических задач (некоторые из них мы сегодня рассмотрели), поэтому им будет уделяться внимание на уроках планиметрии. Их даже называют замечательные линии треугольника. А точки, в которых эти линии пересекаются –
Но рассмотренные нами линии наиболее часто встречаются при решении различных практических задач (некоторые из них мы сегодня рассмотрели), поэтому им будет уделяться внимание на уроках планиметрии. Их даже называют замечательные линии треугольника. А точки, в которых эти линии пересекаются –
Часто ли три прямые пересекаются в одной точкеМы говорили, что если бросить на плоскость наугад три прямых, то получится треугольник (см. рис. 45) (все остальные случаи настолько же вероятны, насколько и выпадение монеты на ребро).
Рис. 45. Если бросить на плоскость наугад три прямых, то получится треугольник
Пересечение трех прямых в одной точке – это предельный случай (см. рис. 46). Как раз такие случаи часто и представляют интерес (вспомните, например, параллельные или перпендикулярные прямые).
Рис.
 46. Пересечение трех прямых в одной точке
46. Пересечение трех прямых в одной точкеМожет показаться странным, что это очень редкий случай, но мы рассмотрели сразу четыре вида линий в треугольнике, которые обладают таким свойством. Это не должно удивлять, поскольку мы рассматривали не произвольные линии, а особые, обладающие определенными уникальными свойствами. Именно потому, что они обладают целым набором таких свойств (в частности, пересечение в одной точке), мы их отдельно изучаем.
Будьте внимательнее при решении задач – даже если по рисунку видно, что три произвольные прямые пересекаются в одной точке, это еще не дает нам право утверждать, что так и будет. Нужно доказать это (для высот, медиан, биссектрис и серединных перпендикуляров мы это сделаем позже) с использованием уже известных теорем. То же самое касается трех точек, которые могут лежать на одной прямой.
Заключение
В дальнейшем мы еще не раз вернемся к различным свойствам этих линий и точек, поговорим о том, в каких треугольниках некоторые из них могут совпадать друг с другом, и т.
 д.
д.Список литературы
- Александров А. Д., Вернер А. Л., Рыжик В. И. Геометрия, 7 класс. Учебник. – М.: «Просвещение», 2017.
- Бутузов В. Ф., Кадомцев С. Б., Прасолов В. В. / Под ред. Садовничего В. А. Геометрия, 7 класс. Учебник. – М.: «Просвещение», 2017.
- Мерзляк А. Г., Полонский В. Б., Якир М. С. Геометрия, 7 класс. Учебник. – М.: «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «yaklass.ru» (Источник)
- Интернет-портал «school-assistant.ru» (Источник)
- Интернет-портал «helpiks.org» (Источник)
Домашнее задание
- В равнобедренном треугольнике с основанием провели биссектрису . Найти градусную меру , если .
- Медиана, проведенная к гипотенузе прямоугольного треугольника , делит в отношении и равна половине гипотенузы. Найти градусные меры .
- Высота прямоугольного треугольника делит гипотенузу на отрезки см и см.
 Найти площадь треугольника , если площадь треугольника равна .
Найти площадь треугольника , если площадь треугольника равна .
Перспектива и ракурс с Эми Винн
Классный трейлер
1Введение в класс
04:40 2Применение 3D-прямоугольников к архитектуре
20:34 3Демонстрация: 1-точечная перспектива
20:42 4Демонстрация: 2-точечная перспектива
16:18 5Углы прицеливания и размещения
13:10 6Измерение высоты и ширины
11:56Lesson Info
Измерение высоты и ширины
Мы говорили о высоте и ширине, и мы говорили об измерении.
 И я просто хочу, используя это в качестве мотива, я просто хочу рассмотреть некоторые из этих идей, потому что в дополнение к перспективе, которая очень важна, просто чисто перцептивное рисование объекта, и возможность соотносить и говорить о его положение и его относительное измерение по отношению к себе в пространстве очень важны. Поэтому я хочу убедиться, что вы понимаете эти идеи, и я хочу обсудить некоторые из идей, о которых я думаю, когда пытаюсь это установить. Итак, еще раз, мы просто будем использовать тот же мотив этого блока в двухточечной перспективе. Так что я просто быстро пройдусь и снова создам этот блок. И я хочу просто посмотреть на некоторые относительные высоты и ширины блока, что иногда может удивить, когда вы на самом деле смотрите на него и говорите: «Вау, я не могу поверить, что он такой маленький или такой большой». Так что все относительно. Я не сравниваю этот блок с чем-то другим. Я на самом деле…
И я просто хочу, используя это в качестве мотива, я просто хочу рассмотреть некоторые из этих идей, потому что в дополнение к перспективе, которая очень важна, просто чисто перцептивное рисование объекта, и возможность соотносить и говорить о его положение и его относительное измерение по отношению к себе в пространстве очень важны. Поэтому я хочу убедиться, что вы понимаете эти идеи, и я хочу обсудить некоторые из идей, о которых я думаю, когда пытаюсь это установить. Итак, еще раз, мы просто будем использовать тот же мотив этого блока в двухточечной перспективе. Так что я просто быстро пройдусь и снова создам этот блок. И я хочу просто посмотреть на некоторые относительные высоты и ширины блока, что иногда может удивить, когда вы на самом деле смотрите на него и говорите: «Вау, я не могу поверить, что он такой маленький или такой большой». Так что все относительно. Я не сравниваю этот блок с чем-то другим. Я на самом деле…ally сравнивает этот блок с самим собой с точки зрения измерения.
Итак, вот у нас есть блок, отлично. Как бы я решил, что эта грань между здесь и здесь имеет определенное измерение? Итак, давайте поговорим о расстоянии, мы сделали это немного. Таким образом, это действительно легко измеряемое расстояние. Он идет прямо на меня. Я могу видеть это в космосе и могу связать это с тем, что происходит наверху. Это то, что мы действительно должны преодолеть, это то, что мы говорим себе об измерении интеллектуально. Потому что с точки зрения есть ракурс. Ракурс в основном означает, что что-то, что составляет три дюйма, если я измерил это, это три дюйма в длину, когда я помещу это в пространство и посмотрю через него, оно уменьшится. Его длина визуально уменьшится. И если мы не сможем установить этот ракурс или это уменьшение, тогда он не будет хорошо сидеть в пространстве. Так бывает, например, если кто-то рисует… Итак, камера на этом карандаше. Если кто-то рисует вот так карандашом, значит, это то, что есть. Вероятно, я не знаю, около восьми дюймов в длину.
 Но если я вот так поверну его в пространстве, и кто-нибудь попытается его нарисовать, его длина уже не восемь дюймов. Это больше похоже на два дюйма в длину. И это действительно важная вещь, о которой нужно начать узнавать, это ракурс. Здесь это происходит более тонким способом, где этот блок не наклоняется и не рисуется под этим углом, посмотрите, смогу ли я сделать это в камере, он рисуется под этим углом. Итак, большой, маленький. Большой маленький. Но это все та же поверхность. Мозг хочет, чтобы это было так. Мозг продолжает говорить глазу, что это так. Но на самом деле, вы должны сделать его меньше, чтобы сделать его правдоподобным. Так что да. Так что измерение для меня — верный способ подкрепить это. Так что давайте пройдемся по этому еще раз. Если я измерю эту сторону, а я смогу сделать это визуально, просто возьму карандаш и прочту его. И тогда я могу взять это и сказать, сколько из них помещается по верхнему краю? Ну, с моей точки зрения, рисуя эту коробку, расстояние между здесь и здесь примерно такое же, как и расстояние оттуда до туда.
Но если я вот так поверну его в пространстве, и кто-нибудь попытается его нарисовать, его длина уже не восемь дюймов. Это больше похоже на два дюйма в длину. И это действительно важная вещь, о которой нужно начать узнавать, это ракурс. Здесь это происходит более тонким способом, где этот блок не наклоняется и не рисуется под этим углом, посмотрите, смогу ли я сделать это в камере, он рисуется под этим углом. Итак, большой, маленький. Большой маленький. Но это все та же поверхность. Мозг хочет, чтобы это было так. Мозг продолжает говорить глазу, что это так. Но на самом деле, вы должны сделать его меньше, чтобы сделать его правдоподобным. Так что да. Так что измерение для меня — верный способ подкрепить это. Так что давайте пройдемся по этому еще раз. Если я измерю эту сторону, а я смогу сделать это визуально, просто возьму карандаш и прочту его. И тогда я могу взять это и сказать, сколько из них помещается по верхнему краю? Ну, с моей точки зрения, рисуя эту коробку, расстояние между здесь и здесь примерно такое же, как и расстояние оттуда до туда. То есть, опять же, мой мозг не хочет, чтобы это было так, но это так. Итак, у меня это расстояние в ракурсе. У меня есть это расстояние, которое более прямолинейно. Итак, эти отношения, просто знание того, что они одинаковые, действительно помогает нам. Потому что, если бы мы сделали эту коробку больше, сделали бы это больше, снова возникло бы ощущение, что она переворачивается к нам. Это становится интересным, потому что с точки зрения измерения то, что происходит между здесь и здесь, из-за перспективы, расстояние между здесь и здесь на самом деле будет больше, чем расстояние между здесь и здесь. Из-за того, что эти две линии сужаются друг к другу, сходятся в пространстве, по мере того как мы идем по этой линейной прогрессии, если бы мы измеряли на переднем плане этой линейной прогрессии, здесь будет большее расстояние, чем здесь. Так что это еще одна вещь измерения, которую вы действительно хотите отслеживать, это то, что это станет уже, если вы будете следовать этой перспективе, и это поможет ему снова немного сжаться и стать более правдоподобным.
То есть, опять же, мой мозг не хочет, чтобы это было так, но это так. Итак, у меня это расстояние в ракурсе. У меня есть это расстояние, которое более прямолинейно. Итак, эти отношения, просто знание того, что они одинаковые, действительно помогает нам. Потому что, если бы мы сделали эту коробку больше, сделали бы это больше, снова возникло бы ощущение, что она переворачивается к нам. Это становится интересным, потому что с точки зрения измерения то, что происходит между здесь и здесь, из-за перспективы, расстояние между здесь и здесь на самом деле будет больше, чем расстояние между здесь и здесь. Из-за того, что эти две линии сужаются друг к другу, сходятся в пространстве, по мере того как мы идем по этой линейной прогрессии, если бы мы измеряли на переднем плане этой линейной прогрессии, здесь будет большее расстояние, чем здесь. Так что это еще одна вещь измерения, которую вы действительно хотите отслеживать, это то, что это станет уже, если вы будете следовать этой перспективе, и это поможет ему снова немного сжаться и стать более правдоподобным.
 Таким образом, измерение действительно ключевое. Углы размещения действительно важны. Мы хотим убедиться, что со всем, что мы теперь знаем об одноточечной и двухточечной перспективе, мы действительно хотим убедиться, что мы понимаем, что, в дополнение к этому концептуальному знанию, в дополнение ко всем измерениям, наше перцептивное рисование физические объекты перед нами, мы можем использовать все эти инструменты, чтобы помочь нам, объединить, чтобы помочь нам нарисовать их с большей точностью и, в конечном итоге, с большей выразительностью. Вещи, которые мы рассмотрели на этом занятии, включали одноточечную и двухточечную перспективу. Каковы различия, какие сценарии мы будем использовать для одного или другого? Мы говорили о размещении углов, установке углов, измерении форм. Мы также немного поговорили о композиции, негативном пространстве и ракурсе. Итак, все это вступает в игру, когда мы пытаемся нарисовать эти фигуры в пространстве. Что будет дальше? Итак, вы практикуетесь в рисовании блоков.
Таким образом, измерение действительно ключевое. Углы размещения действительно важны. Мы хотим убедиться, что со всем, что мы теперь знаем об одноточечной и двухточечной перспективе, мы действительно хотим убедиться, что мы понимаем, что, в дополнение к этому концептуальному знанию, в дополнение ко всем измерениям, наше перцептивное рисование физические объекты перед нами, мы можем использовать все эти инструменты, чтобы помочь нам, объединить, чтобы помочь нам нарисовать их с большей точностью и, в конечном итоге, с большей выразительностью. Вещи, которые мы рассмотрели на этом занятии, включали одноточечную и двухточечную перспективу. Каковы различия, какие сценарии мы будем использовать для одного или другого? Мы говорили о размещении углов, установке углов, измерении форм. Мы также немного поговорили о композиции, негативном пространстве и ракурсе. Итак, все это вступает в игру, когда мы пытаемся нарисовать эти фигуры в пространстве. Что будет дальше? Итак, вы практикуетесь в рисовании блоков.
 Потому что, когда свет попадает на объект, он начинает сильно усиливать его трехмерность. Итак, когда мы говорим об этом, вот скетч, где у нас есть куча блоков. На самом деле, вот эти блоки, которые были у меня на столе во время этого разговора. Работа с базовыми блоками и прямым источником света, чтобы можно было перемещаться туда-сюда. Это глазурь на торте, на мой взгляд. Вы можете заштриховывать, пока коровы не вернутся домой, то есть заштриховывать, но если ваши блоки не нарисованы правдоподобно или хорошо, это действительно не выдержит. Так что все, что мы только что сделали в этом разделе, очень важно в этом курсе, чтобы создать сильные, стабильные формы, к которым мы можем добавить этот красивый тональный рендеринг. А потом, со временем, это мой друг-художник, Эндрю Эдман, работу, которую он сделал несколько лет назад, довольно много лет назад. Со временем вы можете как бы развернуть его. И используйте эти идеи о перспективе, чтобы создать более творческую работу. Скорее драматическая работа.
Потому что, когда свет попадает на объект, он начинает сильно усиливать его трехмерность. Итак, когда мы говорим об этом, вот скетч, где у нас есть куча блоков. На самом деле, вот эти блоки, которые были у меня на столе во время этого разговора. Работа с базовыми блоками и прямым источником света, чтобы можно было перемещаться туда-сюда. Это глазурь на торте, на мой взгляд. Вы можете заштриховывать, пока коровы не вернутся домой, то есть заштриховывать, но если ваши блоки не нарисованы правдоподобно или хорошо, это действительно не выдержит. Так что все, что мы только что сделали в этом разделе, очень важно в этом курсе, чтобы создать сильные, стабильные формы, к которым мы можем добавить этот красивый тональный рендеринг. А потом, со временем, это мой друг-художник, Эндрю Эдман, работу, которую он сделал несколько лет назад, довольно много лет назад. Со временем вы можете как бы развернуть его. И используйте эти идеи о перспективе, чтобы создать более творческую работу. Скорее драматическая работа. Так что эта деталь рисунка, который он нарисовал, который мне нравится, имеет своего рода распад, но также и структуру. И есть много действительно классных марок. Но ясно, что он знает кое-что о перспективе здесь, не так ли? Это не формальный рисунок в перспективе, но ясно, что это какая-то структура, существующая в пространстве. Это своего рода двухточечная перспектива. Так что очень интересно посмотреть, что с этим сделают разные художники. Итак, в нашем следующем фильме, на нашем следующем уроке, в нашем классе, мы будем работать с такими формами, как блоки, а также с формами яиц, и как мы можем преобразовать их в тональную визуализацию таким образом. Как мы оборачиваем линии вокруг них. И потом, как это может перейти в, это старый рисунок из, я думаю, начала 1900-х, где кто-то рисовал айву, но посмотрите, как красиво у них получилось не только отрисовка фигур, но и тональность. Итак, я так рад, что вы смогли быть с нами сегодня на CreativeLive. Было здорово поговорить с вами об одной и двух точках зрения.
Так что эта деталь рисунка, который он нарисовал, который мне нравится, имеет своего рода распад, но также и структуру. И есть много действительно классных марок. Но ясно, что он знает кое-что о перспективе здесь, не так ли? Это не формальный рисунок в перспективе, но ясно, что это какая-то структура, существующая в пространстве. Это своего рода двухточечная перспектива. Так что очень интересно посмотреть, что с этим сделают разные художники. Итак, в нашем следующем фильме, на нашем следующем уроке, в нашем классе, мы будем работать с такими формами, как блоки, а также с формами яиц, и как мы можем преобразовать их в тональную визуализацию таким образом. Как мы оборачиваем линии вокруг них. И потом, как это может перейти в, это старый рисунок из, я думаю, начала 1900-х, где кто-то рисовал айву, но посмотрите, как красиво у них получилось не только отрисовка фигур, но и тональность. Итак, я так рад, что вы смогли быть с нами сегодня на CreativeLive. Было здорово поговорить с вами об одной и двух точках зрения. Большое вам спасибо за просмотр, и, пожалуйста, не забывайте, что практика, практика и практика в большом количестве рисунков — это действительно единственный способ сделать эти идеи плавными и изложить их на бумаге. И вы можете загрузить эти рисунки в нашу студенческую галерею. И есть возможность получить некоторую критику по ним, и это также отличный форум, где люди могут делиться своими рисунками. И это также очень мотивирует, чтобы сказать: «Знаешь что, я загружу это». И посмотрите, сможете ли вы получить какие-то отзывы об этом. Так что большое спасибо за просмотр и продолжайте рисовать.
Большое вам спасибо за просмотр, и, пожалуйста, не забывайте, что практика, практика и практика в большом количестве рисунков — это действительно единственный способ сделать эти идеи плавными и изложить их на бумаге. И вы можете загрузить эти рисунки в нашу студенческую галерею. И есть возможность получить некоторую критику по ним, и это также отличный форум, где люди могут делиться своими рисунками. И это также очень мотивирует, чтобы сказать: «Знаешь что, я загружу это». И посмотрите, сможете ли вы получить какие-то отзывы об этом. Так что большое спасибо за просмотр и продолжайте рисовать.В постоянном состоянии сонливости и растерянности — Как я рисую Перепады Высот!
Многие люди спрашивали меня о том, как я рисую разницу в росте между Призраком и Джейд, так что здесь я попытаюсь объяснить ход своих мыслей!
Итак, сначала мне нужно визуализировать разницу высот с помощью симулятора. Эти симуляторы можно найти в Интернете. Просто наберите «сравнение роста» , и вы найдете множество веб-сайтов, предоставляющих эти услуги.
 Мой любимый defo hikaku-sitatter.com/en или heightcomparison.com
Мой любимый defo hikaku-sitatter.com/en или heightcomparison.comВот скриншоты! (Слева — хикаку ситтер, справа — сравнение роста
Теперь важно помнить, что сравнение роста — это НЕ изменение размеров людей, а разница в длине частей тела. Изменение размеров людей приведет к голова слишком маленькая и не выглядит естественно
Теперь, когда у меня есть визуальный ориентир, пришло время поставить Контрольные точки !В основном контрольные точки — это заметки, которые я учитываю при их рисовании, относительно какие части тела соответствуют каким частям тела.
Вот некоторые контрольные точки, которые я отметил на GhostJade!
В заключение, причина преимущества Призрака в росте над Джейд заключается в том, что у него более длинный позвоночник и более длинные бедра! У них все та же высота колена. Кроме того, конечности Джейд короче.
Теперь, когда у нас есть контрольно-пропускные пункты, давайте посмотрим, как я нарисовал эту штуку «Ударь сначала спроси потом»!
Ницца.


 2 }.
2 }. Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.
Сумма углов равна 180°. Если один угол прямой, второй – 30°, значит третий – ABE – находится по формуле: ABE = 80 – 90 – 30 = 60°. Он такой, как DBE = 60°.

 Какова ее высота? Именно та самая, что в определении. А если конструкцию повернуть на другую сторону? Соответственно – другая высота треугольника (см. рис. 5).
Какова ее высота? Именно та самая, что в определении. А если конструкцию повернуть на другую сторону? Соответственно – другая высота треугольника (см. рис. 5). И формула площади прямоугольного треугольника – частный случай формулы площади произвольного треугольника.
И формула площади прямоугольного треугольника – частный случай формулы площади произвольного треугольника.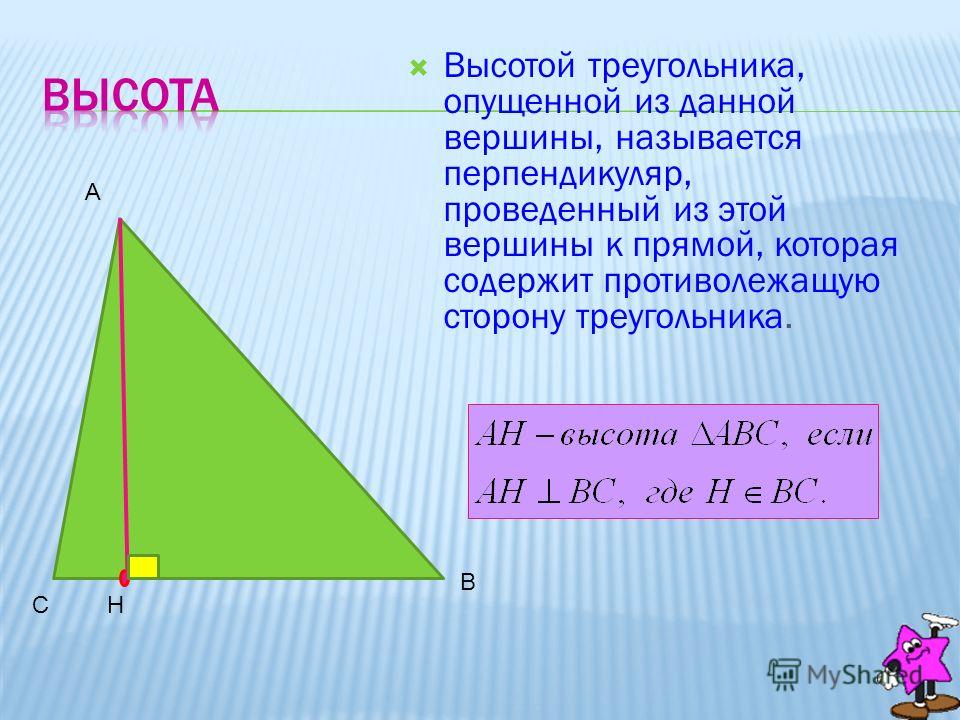 рис. 10).
рис. 10).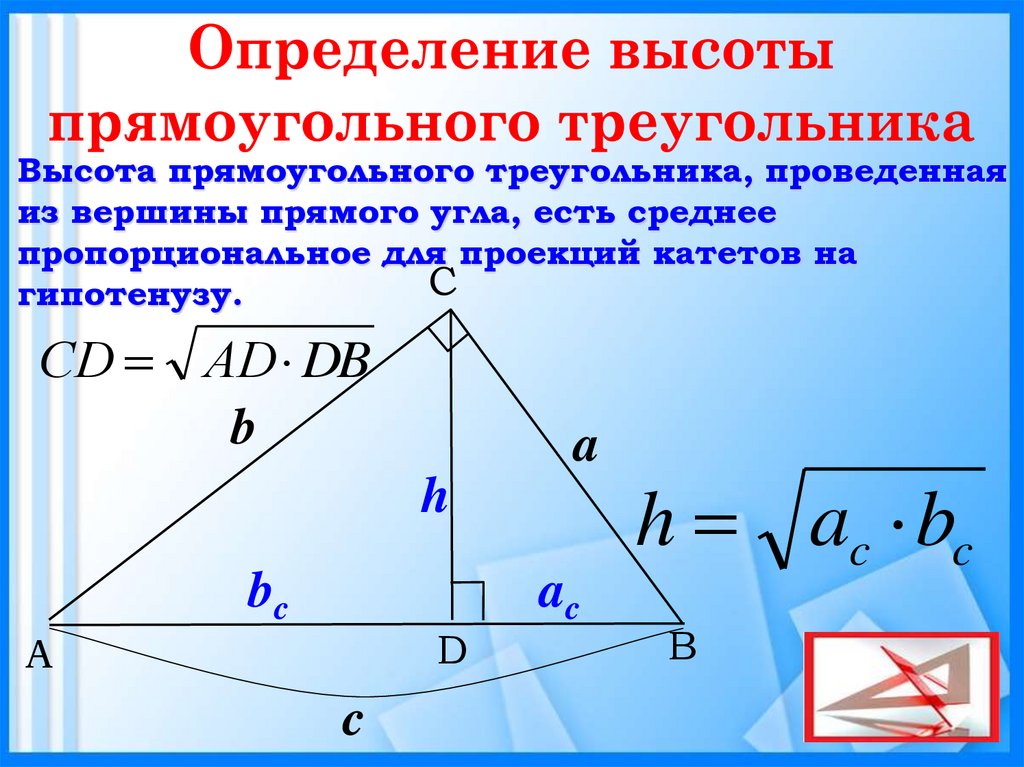

 е. в точке их пересечения (см. рис. 15).
е. в точке их пересечения (см. рис. 15). рис. 17).
рис. 17).
 Если эти две дороги параллельны, то задача решается легко. Все такие точки будут лежать на параллельной прямой, равноудаленной от двух данных (см. рис. 22).
Если эти две дороги параллельны, то задача решается легко. Все такие точки будут лежать на параллельной прямой, равноудаленной от двух данных (см. рис. 22).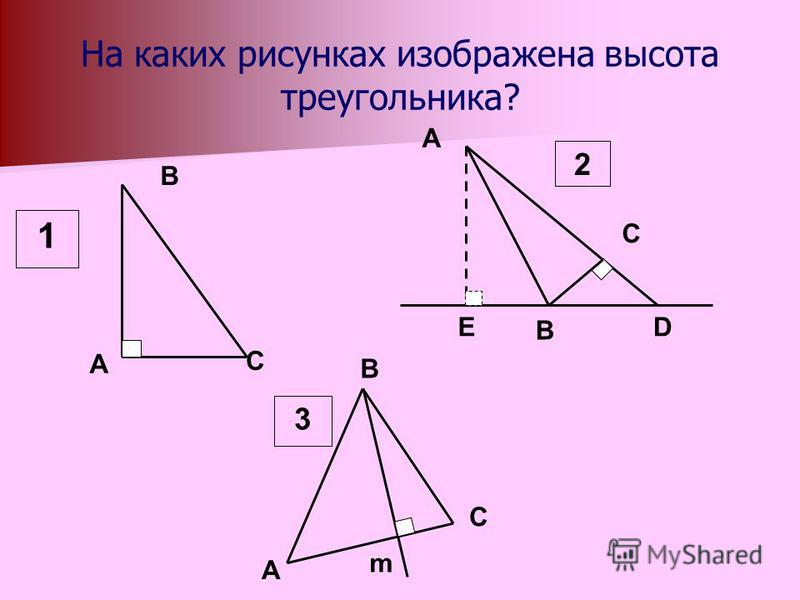 e. точка равноудалена ото всех трех сторон треугольника (см. рис. 25):
e. точка равноудалена ото всех трех сторон треугольника (см. рис. 25):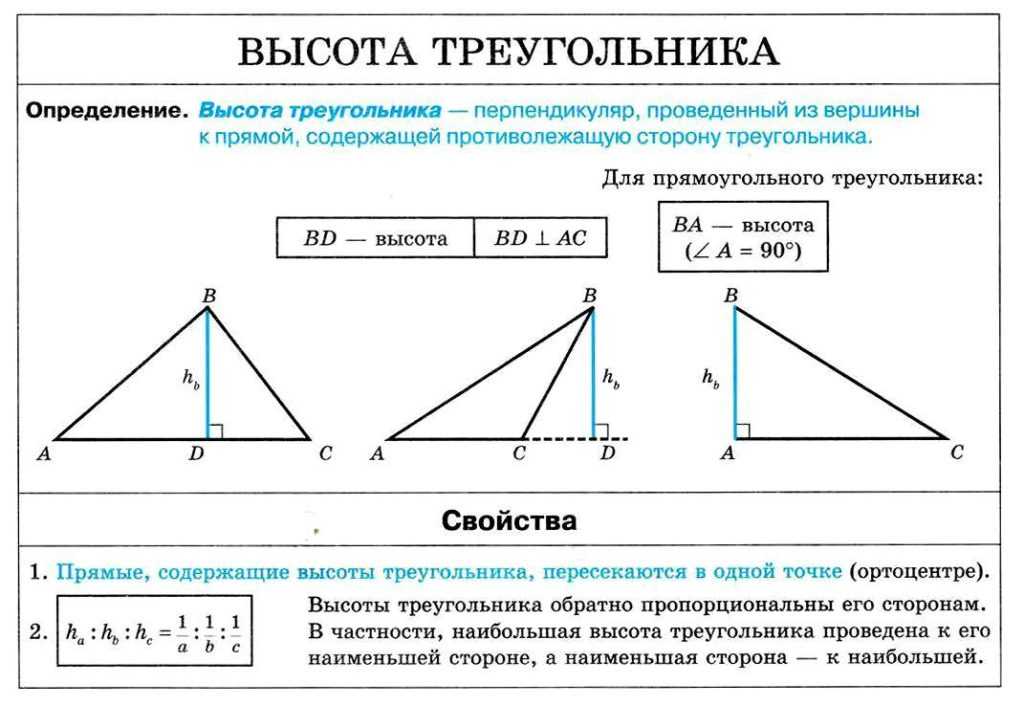 рис. 27).
рис. 27). Пусть – расстояние от точки до стороны , т. е. радиус вписанной окружности (см. рис. 31).
Пусть – расстояние от точки до стороны , т. е. радиус вписанной окружности (см. рис. 31).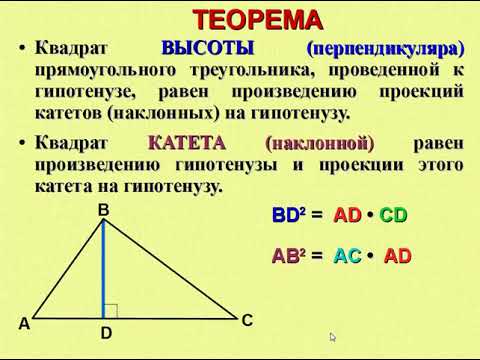 И нужно разместить станцию скорой помощи так, чтобы она могла обслуживать все три поселка (см. рис. 33). Понятно, что станция должна быть расположена так, чтобы расстояние от нее до каждого из трех поселков было одинаковым.
И нужно разместить станцию скорой помощи так, чтобы она могла обслуживать все три поселка (см. рис. 33). Понятно, что станция должна быть расположена так, чтобы расстояние от нее до каждого из трех поселков было одинаковым. е. (см. рис. 36).
е. (см. рис. 36). Значит, исходное предположение неверно, и если точка не лежит на серединном перпендикуляре, то она не будет равноудалена от концов отрезка.
Значит, исходное предположение неверно, и если точка не лежит на серединном перпендикуляре, то она не будет равноудалена от концов отрезка.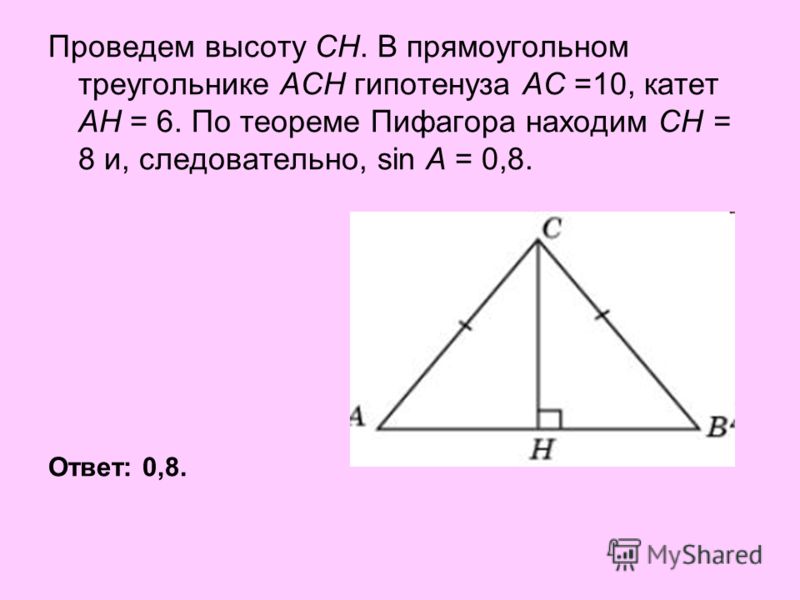 рис. 39).
рис. 39).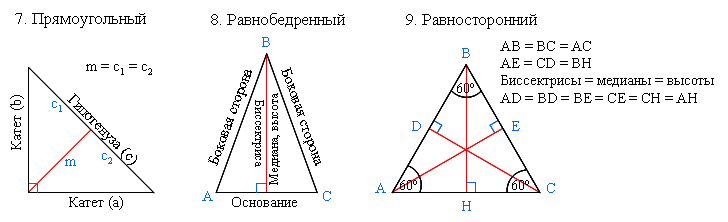 рис. 41).
рис. 41). рис. 44). Аналогично вокруг ромба не всегда удастся описать окружность (опять же, если это не квадрат).
рис. 44). Аналогично вокруг ромба не всегда удастся описать окружность (опять же, если это не квадрат). Но рассмотренные нами линии наиболее часто встречаются при решении различных практических задач (некоторые из них мы сегодня рассмотрели), поэтому им будет уделяться внимание на уроках планиметрии. Их даже называют замечательные линии треугольника. А точки, в которых эти линии пересекаются –
Но рассмотренные нами линии наиболее часто встречаются при решении различных практических задач (некоторые из них мы сегодня рассмотрели), поэтому им будет уделяться внимание на уроках планиметрии. Их даже называют замечательные линии треугольника. А точки, в которых эти линии пересекаются –  46. Пересечение трех прямых в одной точке
46. Пересечение трех прямых в одной точке д.
д. Найти площадь треугольника , если площадь треугольника равна .
Найти площадь треугольника , если площадь треугольника равна . И я просто хочу, используя это в качестве мотива, я просто хочу рассмотреть некоторые из этих идей, потому что в дополнение к перспективе, которая очень важна, просто чисто перцептивное рисование объекта, и возможность соотносить и говорить о его положение и его относительное измерение по отношению к себе в пространстве очень важны. Поэтому я хочу убедиться, что вы понимаете эти идеи, и я хочу обсудить некоторые из идей, о которых я думаю, когда пытаюсь это установить. Итак, еще раз, мы просто будем использовать тот же мотив этого блока в двухточечной перспективе. Так что я просто быстро пройдусь и снова создам этот блок. И я хочу просто посмотреть на некоторые относительные высоты и ширины блока, что иногда может удивить, когда вы на самом деле смотрите на него и говорите: «Вау, я не могу поверить, что он такой маленький или такой большой». Так что все относительно. Я не сравниваю этот блок с чем-то другим. Я на самом деле…
И я просто хочу, используя это в качестве мотива, я просто хочу рассмотреть некоторые из этих идей, потому что в дополнение к перспективе, которая очень важна, просто чисто перцептивное рисование объекта, и возможность соотносить и говорить о его положение и его относительное измерение по отношению к себе в пространстве очень важны. Поэтому я хочу убедиться, что вы понимаете эти идеи, и я хочу обсудить некоторые из идей, о которых я думаю, когда пытаюсь это установить. Итак, еще раз, мы просто будем использовать тот же мотив этого блока в двухточечной перспективе. Так что я просто быстро пройдусь и снова создам этот блок. И я хочу просто посмотреть на некоторые относительные высоты и ширины блока, что иногда может удивить, когда вы на самом деле смотрите на него и говорите: «Вау, я не могу поверить, что он такой маленький или такой большой». Так что все относительно. Я не сравниваю этот блок с чем-то другим. Я на самом деле…

 То есть, опять же, мой мозг не хочет, чтобы это было так, но это так. Итак, у меня это расстояние в ракурсе. У меня есть это расстояние, которое более прямолинейно. Итак, эти отношения, просто знание того, что они одинаковые, действительно помогает нам. Потому что, если бы мы сделали эту коробку больше, сделали бы это больше, снова возникло бы ощущение, что она переворачивается к нам. Это становится интересным, потому что с точки зрения измерения то, что происходит между здесь и здесь, из-за перспективы, расстояние между здесь и здесь на самом деле будет больше, чем расстояние между здесь и здесь. Из-за того, что эти две линии сужаются друг к другу, сходятся в пространстве, по мере того как мы идем по этой линейной прогрессии, если бы мы измеряли на переднем плане этой линейной прогрессии, здесь будет большее расстояние, чем здесь. Так что это еще одна вещь измерения, которую вы действительно хотите отслеживать, это то, что это станет уже, если вы будете следовать этой перспективе, и это поможет ему снова немного сжаться и стать более правдоподобным.
То есть, опять же, мой мозг не хочет, чтобы это было так, но это так. Итак, у меня это расстояние в ракурсе. У меня есть это расстояние, которое более прямолинейно. Итак, эти отношения, просто знание того, что они одинаковые, действительно помогает нам. Потому что, если бы мы сделали эту коробку больше, сделали бы это больше, снова возникло бы ощущение, что она переворачивается к нам. Это становится интересным, потому что с точки зрения измерения то, что происходит между здесь и здесь, из-за перспективы, расстояние между здесь и здесь на самом деле будет больше, чем расстояние между здесь и здесь. Из-за того, что эти две линии сужаются друг к другу, сходятся в пространстве, по мере того как мы идем по этой линейной прогрессии, если бы мы измеряли на переднем плане этой линейной прогрессии, здесь будет большее расстояние, чем здесь. Так что это еще одна вещь измерения, которую вы действительно хотите отслеживать, это то, что это станет уже, если вы будете следовать этой перспективе, и это поможет ему снова немного сжаться и стать более правдоподобным. Таким образом, измерение действительно ключевое. Углы размещения действительно важны. Мы хотим убедиться, что со всем, что мы теперь знаем об одноточечной и двухточечной перспективе, мы действительно хотим убедиться, что мы понимаем, что, в дополнение к этому концептуальному знанию, в дополнение ко всем измерениям, наше перцептивное рисование физические объекты перед нами, мы можем использовать все эти инструменты, чтобы помочь нам, объединить, чтобы помочь нам нарисовать их с большей точностью и, в конечном итоге, с большей выразительностью. Вещи, которые мы рассмотрели на этом занятии, включали одноточечную и двухточечную перспективу. Каковы различия, какие сценарии мы будем использовать для одного или другого? Мы говорили о размещении углов, установке углов, измерении форм. Мы также немного поговорили о композиции, негативном пространстве и ракурсе. Итак, все это вступает в игру, когда мы пытаемся нарисовать эти фигуры в пространстве. Что будет дальше? Итак, вы практикуетесь в рисовании блоков.
Таким образом, измерение действительно ключевое. Углы размещения действительно важны. Мы хотим убедиться, что со всем, что мы теперь знаем об одноточечной и двухточечной перспективе, мы действительно хотим убедиться, что мы понимаем, что, в дополнение к этому концептуальному знанию, в дополнение ко всем измерениям, наше перцептивное рисование физические объекты перед нами, мы можем использовать все эти инструменты, чтобы помочь нам, объединить, чтобы помочь нам нарисовать их с большей точностью и, в конечном итоге, с большей выразительностью. Вещи, которые мы рассмотрели на этом занятии, включали одноточечную и двухточечную перспективу. Каковы различия, какие сценарии мы будем использовать для одного или другого? Мы говорили о размещении углов, установке углов, измерении форм. Мы также немного поговорили о композиции, негативном пространстве и ракурсе. Итак, все это вступает в игру, когда мы пытаемся нарисовать эти фигуры в пространстве. Что будет дальше? Итак, вы практикуетесь в рисовании блоков.
 Потому что, когда свет попадает на объект, он начинает сильно усиливать его трехмерность. Итак, когда мы говорим об этом, вот скетч, где у нас есть куча блоков. На самом деле, вот эти блоки, которые были у меня на столе во время этого разговора. Работа с базовыми блоками и прямым источником света, чтобы можно было перемещаться туда-сюда. Это глазурь на торте, на мой взгляд. Вы можете заштриховывать, пока коровы не вернутся домой, то есть заштриховывать, но если ваши блоки не нарисованы правдоподобно или хорошо, это действительно не выдержит. Так что все, что мы только что сделали в этом разделе, очень важно в этом курсе, чтобы создать сильные, стабильные формы, к которым мы можем добавить этот красивый тональный рендеринг. А потом, со временем, это мой друг-художник, Эндрю Эдман, работу, которую он сделал несколько лет назад, довольно много лет назад. Со временем вы можете как бы развернуть его. И используйте эти идеи о перспективе, чтобы создать более творческую работу. Скорее драматическая работа.
Потому что, когда свет попадает на объект, он начинает сильно усиливать его трехмерность. Итак, когда мы говорим об этом, вот скетч, где у нас есть куча блоков. На самом деле, вот эти блоки, которые были у меня на столе во время этого разговора. Работа с базовыми блоками и прямым источником света, чтобы можно было перемещаться туда-сюда. Это глазурь на торте, на мой взгляд. Вы можете заштриховывать, пока коровы не вернутся домой, то есть заштриховывать, но если ваши блоки не нарисованы правдоподобно или хорошо, это действительно не выдержит. Так что все, что мы только что сделали в этом разделе, очень важно в этом курсе, чтобы создать сильные, стабильные формы, к которым мы можем добавить этот красивый тональный рендеринг. А потом, со временем, это мой друг-художник, Эндрю Эдман, работу, которую он сделал несколько лет назад, довольно много лет назад. Со временем вы можете как бы развернуть его. И используйте эти идеи о перспективе, чтобы создать более творческую работу. Скорее драматическая работа. Так что эта деталь рисунка, который он нарисовал, который мне нравится, имеет своего рода распад, но также и структуру. И есть много действительно классных марок. Но ясно, что он знает кое-что о перспективе здесь, не так ли? Это не формальный рисунок в перспективе, но ясно, что это какая-то структура, существующая в пространстве. Это своего рода двухточечная перспектива. Так что очень интересно посмотреть, что с этим сделают разные художники. Итак, в нашем следующем фильме, на нашем следующем уроке, в нашем классе, мы будем работать с такими формами, как блоки, а также с формами яиц, и как мы можем преобразовать их в тональную визуализацию таким образом. Как мы оборачиваем линии вокруг них. И потом, как это может перейти в, это старый рисунок из, я думаю, начала 1900-х, где кто-то рисовал айву, но посмотрите, как красиво у них получилось не только отрисовка фигур, но и тональность. Итак, я так рад, что вы смогли быть с нами сегодня на CreativeLive. Было здорово поговорить с вами об одной и двух точках зрения.
Так что эта деталь рисунка, который он нарисовал, который мне нравится, имеет своего рода распад, но также и структуру. И есть много действительно классных марок. Но ясно, что он знает кое-что о перспективе здесь, не так ли? Это не формальный рисунок в перспективе, но ясно, что это какая-то структура, существующая в пространстве. Это своего рода двухточечная перспектива. Так что очень интересно посмотреть, что с этим сделают разные художники. Итак, в нашем следующем фильме, на нашем следующем уроке, в нашем классе, мы будем работать с такими формами, как блоки, а также с формами яиц, и как мы можем преобразовать их в тональную визуализацию таким образом. Как мы оборачиваем линии вокруг них. И потом, как это может перейти в, это старый рисунок из, я думаю, начала 1900-х, где кто-то рисовал айву, но посмотрите, как красиво у них получилось не только отрисовка фигур, но и тональность. Итак, я так рад, что вы смогли быть с нами сегодня на CreativeLive. Было здорово поговорить с вами об одной и двух точках зрения. Большое вам спасибо за просмотр, и, пожалуйста, не забывайте, что практика, практика и практика в большом количестве рисунков — это действительно единственный способ сделать эти идеи плавными и изложить их на бумаге. И вы можете загрузить эти рисунки в нашу студенческую галерею. И есть возможность получить некоторую критику по ним, и это также отличный форум, где люди могут делиться своими рисунками. И это также очень мотивирует, чтобы сказать: «Знаешь что, я загружу это». И посмотрите, сможете ли вы получить какие-то отзывы об этом. Так что большое спасибо за просмотр и продолжайте рисовать.
Большое вам спасибо за просмотр, и, пожалуйста, не забывайте, что практика, практика и практика в большом количестве рисунков — это действительно единственный способ сделать эти идеи плавными и изложить их на бумаге. И вы можете загрузить эти рисунки в нашу студенческую галерею. И есть возможность получить некоторую критику по ним, и это также отличный форум, где люди могут делиться своими рисунками. И это также очень мотивирует, чтобы сказать: «Знаешь что, я загружу это». И посмотрите, сможете ли вы получить какие-то отзывы об этом. Так что большое спасибо за просмотр и продолжайте рисовать. Мой любимый defo hikaku-sitatter.com/en или heightcomparison.com
Мой любимый defo hikaku-sitatter.com/en или heightcomparison.com