Число 324
Свойства и характеристики одного числа
Все делители числа, сумма и произведение цифр, двоичный вид, разложение на простые множители…
Свойства пары чисел
Наименьшее общее кратное, наибольший общий делитель, сумма, разность и произведение чисел…
Сейчас изучают числа:
19 и 13 11011 6205 и 893438 15 и 25 972046 и 126586 25815 1 3157834937 25814 9 441 1001 и 20000 1001 24 и 7500 13 и 22 8179537263154 654187 53686 1911 74 7107235349760 59 60 9359672004566
Триста двадцать четыре
Описание числа 324
Рациональное целое
число 324
является составным числом. Сумма и произведение цифр числа: 9, 24.
У числа 324 15 делителей: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324.
И сумма этих делителей: 847.
Обратное число к 324 – это 0.0030864197530864196.
Сумма и произведение цифр числа: 9, 24.
У числа 324 15 делителей: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 81, 108, 162, 324.
И сумма этих делителей: 847.
Обратное число к 324 – это 0.0030864197530864196.
Другие системы счисления: двоичная система: 101000100, троичная система: 110000, восьмеричная система: 504, шестнадцатеричная система: 144. 324 байта представляет из себя число байт 324.
Число 324 азбукой Морзе: …— ..— ….-
Синус числа 324: -0.4041, косинус числа 324: -0.9147, тангенс числа 324: 0.4417.
Логарифм натуральный числа равен 5.7807.
Десятичный логарифм числа: 2.5105.
Если извлечь квадратный корень, получится 18, а если кубический — 6.8683
Возведение в квадрат: 1.
Перевод из числа секунд — 5 минут 24 секунды . Нумерологическое цифра числа 324 — 9.
- ← 323
- 325 →
Как правильно извлечь корень числа?
Благодаря прочтению этой статьи вы научитесь:
- Извлекать корни из разных чисел;
- Решать разнообразные задания по этой тематике;
- Применять удобные таблицы на практике.
А также пополните свой мозг новыми знаниями, что всегда хорошо и полезно! Приятным бонусом для вас будут задания для отработки материала с ответами, которые вы сможете найти в конце этой статьи. Что значит понятие: «Извлечение корня из числа»?
Определение
Извлечение корня из числа — это нахождение значения корня, т.е. действие, обратное возведению в степень.
Числа b и a равны, ведь при извлечении корня n-ной степени одного из чисел, мы, соответственно, находим и второе.
- n — натуральное число, являющиеся степенью корня.

- a — подкоренное значение.
Интересно
При помощи разложения функции в ряд можно показать, что сумма всех натуральных чисел равна:
1/12[18]
Когда следует извлекать корень? Если вы видите, что a можно представить в виде n-ной степени какого-либо числа b, то корень a можно извлечь.
Определение
Квадратный корень из числа — это неизвестное число, которое дает это же число при возведении его в квадрат.
Пример извлечения корня:
√25=5×5 — из этого становится ясно, что квадратный корень числа равен 5.
В обратной ситуации, когда нельзя представить корень n-ной степени из числа a, в виде n-ной степени числа b, корень не извлекается или находится лишь приближенное значение этого корня.
Пример:
√6≈√2,44949
Для этого используют различные виды решений, начиная с калькулятора, заканчивая формулами. Калькулятор хоть и посчитает все вместо нас, но не всегда мы можем его применить. Поэтому важно знать другие варианты нахождения приближенного значения корня.
Способы извлечения корня
Для того, чтобы найти значение корня, существуют такие способы извлечения корня, как:
- Применение различных таблиц.
- Разложение чисел или выражений на простые множители.
- Извлечение корней из дробных чисел.
- Извлечение отрицательного корня.
- Поразрядное нахождение значения корня.
Они основываются на свойствах корней. Далее рассмотрим таблицы, которые могут помочь в процессе извлечения корней.
Квадраты натуральных чисел
Основной является таблица квадратов натуральных чисел:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Она, пожалуй, самая распространенная среди школьников. Если в какой-то важный момент она вам необходима, но у вас отсутствует к ней доступ, можно воспользоваться несколькими хитростями:
Если в какой-то важный момент она вам необходима, но у вас отсутствует к ней доступ, можно воспользоваться несколькими хитростями:
- Чтобы быстро возвести в квадрат число, на конце которого 0, можно добавить к нему парочку нулей: 80×80=6400; 30×30=900. Т.е., первые цифры умножаем и дописываем два 0 к этому числу.
- Теперь возьмём какое-нибудь число так, чтобы вторая его цифра оканчивалась на 5. Так, например, число 75. Чтобы быстро возвести его в квадрат, прибавьте к первой цифре единицу, из чего получаются цифры 7 и 8.
- Умножаем их и приписываем в конец число 25 и получаем конечный результат в виде числа 5625.
Квадратные корни
Вторая таблица — это таблица квадратных корней:
| √x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 1,41421 | 1,73205 | 2 | 2,23607 | 2,44949 | 2,64575 | 2,82843 | 3 |
| 1 | 3,16228 | 3,31662 | 3,4641 | 3,60555 | 3,74166 | 3,87298 | 4 | 4,12311 | 4,24264 | 4,3589 |
| 2 | 4,47214 | 4,58258 | 4,69042 | 4,79583 | 4,89898 | 5 | 5,09902 | 5,19615 | 5,2915 | 5,38516 |
| 3 | 5,47723 | 5,56776 | 5,65685 | 5,74456 | 5,83095 | 5,91608 | 6 | 6,08276 | 6,16441 | 6,245 |
| 4 | 6,32456 | 6,40312 | 6,48074 | 6,55744 | 6,63325 | 6,7082 | 6,78233 | 6,85565 | 6,9282 | 7 |
| 5 | 7,07107 | 7,14143 | 7,2111 | 7,28011 | 7,34847 | 7,4162 | 7,48331 | 7,54983 | 7,61577 | 7,68115 |
| 6 | 7,74597 | 7,81025 | 7,87401 | 7,93725 | 8 | 8,06226 | 8,12404 | 8,18535 | 8,24621 | 8,30662 |
| 7 | 8,3666 | 8,42615 | 8,48528 | 8,544 | 8,60233 | 8,66025 | 8,7178 | 8,77496 | 8,83176 | 8,88819 |
| 8 | 8,94427 | 9 | 9,05539 | 9,11043 | 9,16515 | 9,21954 | 9,27362 | 9,32738 | 9,38083 | 9,43398 |
| 9 | 9,48683 | 9,53939 | 9,59166 | 9,64365 | 9,69536 | 9,74679 | 9,79796 | 9,84886 | 9,89949 | 9,94987 |
Числа в кубе
И, конечно же, третья — таблица кубов, при помощи которой осуществляется извлечение кубического корня.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |
| 2 | 8000 | 9261 | 10648 | 12167 | 13824 | 15625 | 17576 | 19683 | 21952 | 24389 |
| 3 | 27000 | 29791 | 32768 | 35937 | 39304 | 42875 | 46656 | 50653 | 54872 | 59319 |
| 4 | 64000 | 68921 | 74088 | 79507 | 85184 | 91125 | 97336 | 103823 | 110592 | 117649 |
| 5 | 125000 | 132651 | 140608 | 148877 | 157464 | 166375 | 175716 | 185193 | 195112 | 205379 |
| 6 | 216000 | 226981 | 238328 | 250047 | 262144 | 274625 | 287496 | 300763 | 314432 | 328509 |
| 7 | 343000 | 357911 | 373248 | 389017 | 405224 | 421875 | 438976 | 456533 | 474552 | 493039 |
| 8 | 512000 | 531441 | 551368 | 571787 | 592704 | 614125 | 636056 | 658503 | 681472 | 704969 |
| 9 | 729000 | 753571 | 778688 | 804357 | 830584 | 857375 | 884736 | 912673 | 941192 | 970299 |

Интересно
Название «Куб» приобрелось из-за того, что такая операция проводится для нахождения объема куба. Т.е., для этого нужно возвести длину ребра куба в третью степень.
Такие таблицы достаточно просты в использовании. Слева — десятки, а справа — единицы. С их помощью можно быстро и легко извлечь корень числа от 0 до 99. Это был один из методов извлечения корней, как мне кажется, самый простой после вычислительного средства — калькулятора, но, зачастую, мы не всегда можем им воспользоваться, как говорилось ранее. Так давайте же перейдем к другим интересным и сложным на первый взгляд вариантам решения.
Разложение подкоренного числа на простые множители
Двигаясь от наиболее удобного и быстрого способа к более сложному, давайте разберемся во втором из них — разложение подкоренного числа на простые множители.
Этот метод состоит в том, чтобы представить какое-либо число в виде степени с нужным нам показателем, из чего мы можем получить значение этого корня.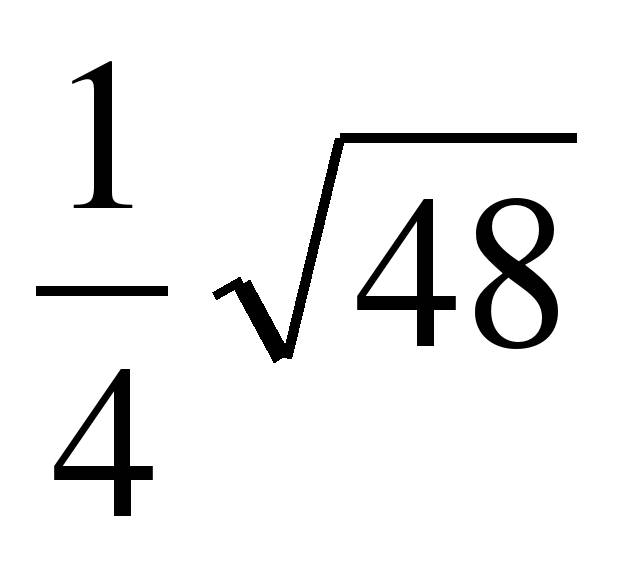
Пример 1:
Возьмём число 196. Для извлечения его квадратного корня, разложим это число на простые множители: √196=2×2×7×7=2²×7²
Теперь делаем следующие действия: 2×7=14.
Ответ: √196=14.
Объяснение:
Множители находятся так: 196 делим на 2, а полученное число 98 мы тоже делим на 2. Делим до тех пор, пока деление станет невозможным. Так, число 49 нельзя поделить пополам, поэтому мы действуем методом подбора. Находим такое число, которое делится. В данном случае — это 7. Два числа, что у нас получились (2 и 7), мы умножаем друг на друга, но уже без степени и получаем число 14, что есть извлечённый корень из числа 196.
Пример 2:
Для того, чтобы лучше понять, как раскладывать на множители, приведем ещё одно число и перейдем к действиям. Деление 441 на 2 невозможно, поэтому подбираем число. Оно делится на 3 два раза. Опять выходит число 49, которое мы делим 2 раза на 7. Из этого следует: √441=3×3×7×7=3²×7²
Из этого следует: √441=3×3×7×7=3²×7²
3×7=21. Значит, ответ: √441=21.
Объяснение:
3 мы умножили на 7, так как это два числа, имеющих 2 степень. Будь у одного из них 4 степень, например: 3⁴×7² — нужно было бы сделать так: 3×3×7. Проще сказать, что мы сокращаем степени ⁴ и ².
Интересно
Подкоренные числа, разложенные на простые множители, могут иметь лишь чётную степень.
Извлечение корней из дробных чисел
Перед тем, как начать вычисления, убедитесь, что дробное число представлено в виде обыкновенной дроби.
Перейдем к свойству корня из частного:
\[\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\]
Далее нужно воспользоваться правилом извлечения корня из дроби, которое гласит: корень из дроби равен от деления корня числителя на корень знаменателя.
Пример 1:
Давайте возьмем любую десятичную дробь и на её примере посмотрим, как нужно извлекать корень.
Так, например, найдем кубический корень из 373,248.
Первый ход — это представление десятичной дроби в виде обыкновенной:
³√373248/³√1000. После этого найдем кубический корень в числе и знаменателе:
³√373248=2×2×2×2×2×2×2×2×2×3×3×3×3×3×3=2⁹×3⁶=72³
Эти действия происходят как с квадратными корнями, но здесь уже мы считаем числа 2 и 3 не по двойке, а тройке, т.е. 2⁹=2×2×2, а 3⁶=3×3. Или же сокращаем ⁹ и ⁶.
Проверим таким образом: из 9 вычитаем тройки до тех пор, пока не придем к 0: 9-3-3-3 – это значит, что двоек у нас будет именно 3. Так и с 3⁶. Если от 6 отнять 3 два раза, то будет 0. Выходит, что троек у нас именно две.
А 1000=10³.
Получается, ³√373248/³√1000=72/10=7,2.
Извлечение отрицательного корня
Существуют вещественные числа, из которых невозможно извлечь корень, т.е. решения нет. А вот из комплексных чисел можно извлекать корень. Для начала узнаем, что это за числа.
Определение
Вещественные (действительные) числа— это рациональные и иррациональные числа, которые можно записать в форме конечной или бесконечной десятичной дроби.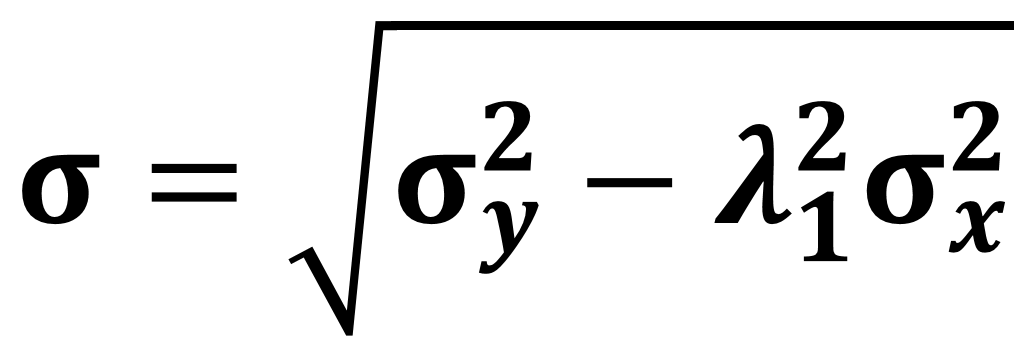
Комплексные числа — это выражение, в котором есть:
- вещественные числа a и b;
- i — мнимая единица.
Итак, чтобы извлечь корень из отрицательного числа, нужно помнить, что если знаменатель является нечётным, то число под знаком корня может оказаться отрицательным.
Далее, чтобы провести эту операцию с отрицательным числом, перейдем к следующим действиям:
- Извлекаем корень из противоположного ему положительного числа.
- Ставим перед полученным числом знак минус.
Пример 1:
1. Преобразуем выражение ⁵√-12 640/32 так, чтобы вместо отрицательного числа под корнем оказалось положительное:
⁵√-12 640/32 = -⁵√12 640/32
2. Избавимся от смешанного числа, заменив его обыкновенной дробью:
-⁵√12 640/32= -⁵√1024/32
3. С помощью правила извлечения корней из обыкновенной дроби, начнем извлекать:
-⁵√1024/32 = — ⁵√1024/⁵√32.
4. Теперь нужно вычислить корни в числителе и знаменателе:
— ⁵√1024/⁵√32 = — ⁵√4⁵/⁵√2⁵ = — 4/2 = -2.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Поразрядное нахождение значения корня
Мы разобрали несколько методов, которые вы можете выбрать на своё усмотрение. Однако, есть еще один, который может понадобиться в таких ситуациях, когда нужно знать полное значение корня, а число, находящееся под корнем нельзя представить в виде n-ной степени определенного числа.
Для таких случаев существует алгоритм поразрядного нахождения значения корня, который нужно использовать, чтобы получить нужное количество значений определяемого числа.
Пример 1:
Итак, чтобы в этом разобраться, найдем значение квадратного корня из 7:
1. Находим значение разряда единиц, перебирая значения 0, 1, 2, …, 9, в это же время вычисляя их во 2 степени до нужного значения, которое больше подкоренного числа 7. Значение ряда единиц равняется 2 (потому как 2² < 7, а 2³ > 7).
2. Следующий на очереди — разряд десятых. Здесь мы будем возводить в квадрат числа: 2.0, 2.1, 2.2, …, 2.9, сравнивая результат с нужным нам числом 7. Так как 2.6² < 7, а 2.7² > 7, то значение десятых равняется 6.
3. Значение сотых. По аналогии находим приближенное значение к 7.
2.64² = 6,9696 подходит нам, так как 2.65²=7.0225, а это больше 7. Действуя таким же образом, можно и дальше находить значение √7 ≈ 2.64.
Теперь, когда мы разобрались с извлечением корней, перейдем к практике. Специально для вас составлены задания с ответами, чтобы вы попробовали воспользоваться приобретенными знаниями. Решайте без таблиц и калькулятора.
Задания для отработки материала1 задание
а)√324
б)√900
в)√1369
2 задание
а)³√531,441
б)³√166,375
3 задание
а) ⁵√-14 2471/1024
б) ⁵√-5 1182/3125
4 задание
а)Найдите квадратный корень из 3.
б)Найдите квадратный корень из 5.
в)Найдите квадратный корень из 9.
Ответы с решением1 задание
а)√324
1)2×2×3×3×3×3=2²×3⁴=√324, а чтобы извлечь, мы умножаем:
2)2×3×3=18. Получается, √324=18.
б)√900
1)2×2×3×3×5×5=2²×3²×5²=√900.
Извлекаем:
2)2×3×5=30. Мы получили √900=30.
в)√1369
1)37×37=37²=√1369.
А здесь мы оставляем 37, так как это единственное число в квадрате. Конечным ответом будет: √1369=37.
2 задание
а)³√531441.
1)3×3×3×3×3×3×3×3×3×3×3×3=3¹²=³√531441.
Разложили на простые множители, а теперь найдем квадратный корень.
2)3¹² это 3×3×3×3, т.к. 3 у нас в 12 степени. Это можно проверить, отняв из 12 столько троек, чтобы вышел 0: 12-3-3-3-3. Так что, 3⁴=81; ³√531441=81.
3)1000=10³.
4)³√531441/³√1000=81/10=8,1.
б)³√166,375.
1) 5×5×5×11×11×11=5³×11³=³√166375.
2)5³×11³=55. Так как числа в кубе – они в степени 1.
3) 1000=10³.
4)³√166375/³√1000=55/10=5,5.
3 задание
а)
1) ⁵√-14 2471/1024 = -⁵√14 2471/1024.
2) -⁵√14 2471/1024= -⁵√16801/1024.
3) -⁵√16801/1024 = — ⁵√16801/⁵√1024.
4) ⁵√16801/⁵√1024 = — ⁵√6⁵/⁵√4⁵ = — 6/4 = — 1,5.
б)
1) ⁵√-5 1182/3125 = -⁵√5 1182/3125.
2) -⁵√5 1182/3125= -⁵√16807/3125.
3) -⁵√16807/3125 = — ⁵√16807/⁵√3125.
4) ⁵√16807/⁵√3125 = — ⁵√7⁵/⁵√5⁵ = — 7/5 = — 1,4.
4 задание
а)√3≈1,73.
б√5≈2,23.
в)√8≈2,82.
Чему равен квадратный корень из 324?
| Square root of 324.00 | 18 |
| Square root of 324.01 | 18.0003 |
| Square root of 324.02 | 18.0006 |
| Square root of 324.03 | 18.0008 |
| Square корень из 324,04 | 18,0011 |
| корень квадратный из 324,05 | 18,0014 |
| корень квадратный из 324,06 | 18. 0017 0017 |
| Square root of 324.07 | 18.0019 |
| Square root of 324.08 | 18.0022 |
| Square root of 324.09 | 18.0025 |
| Square root of 324.10 | 18.0028 |
| Квадратный корень из 324,11 | 18,0031 |
| Квадратный корень из 324,12 | 18,0033 |
Квадратный корень из 3,0 9 190636 | |
| Square root of 324.14 | 18.0039 |
| Square root of 324.15 | 18.0042 |
| Square root of 324.16 | 18.0044 |
| Square root of 324.17 | 18.0047 |
| Square root из 324,18 | 18,005 |
| квадратный корень 324,19 | 18,0053 |
| квадратный корень 324,20 | 18,0056 |
| Square root of 324.21 | 18.0058 |
Square root of 324. 22 22 | 18.0061 |
| Square root of 324.23 | 18.0064 |
| Square root of 324.24 | 18.0067 |
| Square root of 324.25 | 18.0069 |
| квадратный корень 324,26 | 18.0072 |
| квадратный корень 324,27 | 18.0075 |
| квадратный корень 324,28 9000 | 18.0078 |
| Square root of 324.29 | 18.0081 |
| Square root of 324.30 | 18.0083 |
| Square root of 324.31 | 18.0086 |
| Square root of 324.32 | 18.0089 |
| Квадратный корень из 324,33 | 18,0092 |
| Квадратный корень из 324,34 | 18,0094 |
| Квадратный корень из 324,065 100065 | 7 |
| Square root of 324.36 | 18.01 |
Square root of 324. 37 37 | 18.0103 |
| Square root of 324.38 | 18.0106 |
| Square root of 324.39 | 18.0108 |
| Square Корень 324,40 | 18.0111 |
| квадратный корень 324,41 | 18.0114 |
| квадратный корень 324,42 | 18,0117 |
| Square root of 324.43 | 18.0119 |
| Square root of 324.44 | 18.0122 |
| Square root of 324.45 | 18.0125 |
| Square root of 324.46 | 18.0128 |
| Square root of 324.47 | 18.0131 |
| квадратный корень 324,48 | 18.0133 |
| квадратный корень 324,49 | 18.0136 |
| квадратный корень 324,50 9000 9.0136 | |
| квадратный корень 324,50 9000 9.01360006 | 18.0139 |
| Square root of 324.51 | 18. 0142 0142 |
| Square root of 324.52 | 18.0144 |
| Square root of 324.53 | 18.0147 |
| Square root of 324.54 | 18.015 |
| Корень квадратный из 324,55 | 18,0153 |
| Корень квадратный из 324,56 | 18,0155 |
| Корень квадратный из 324,570006 | |
| Square root of 324.58 | 18.0161 |
| Square root of 324.59 | 18.0164 |
| Square root of 324.60 | 18.0167 |
| Square root of 324.61 | 18.0169 |
| Square root из 324,62 | 18,0172 |
| Квадратный корень из 324,63 | 18,0175 |
| Квадратный корень из 324,64 9 901 | 8 180005 |
| Square root of 324.65 | 18.018 |
| Square root of 324.66 | 18.0183 |
Square root of 324.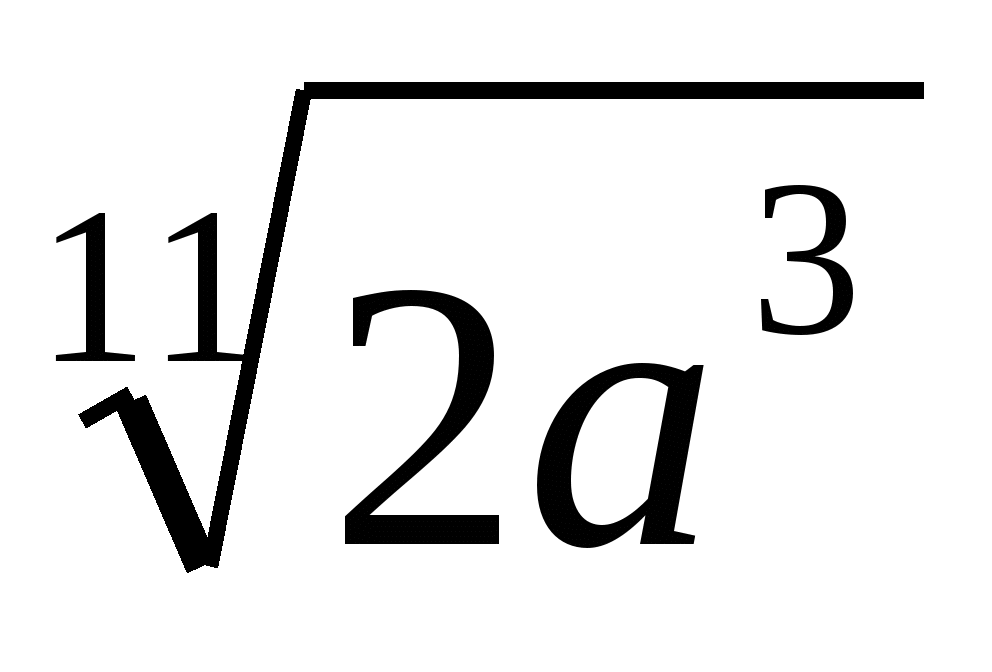 67 67 | 18.0186 |
| Square root of 324.68 | 18.0189 |
| Square root of 324.69 | 18.0192 |
| квадратный корень 324,70 | 18.0194 |
| квадратный корень 324,71 | 18.0197 |
| квадратный корень 324.72 9.0197 | |
| квадратный корень 324,72 9000 | |
| квадратный корень 324,72 92.0006 | 18.02 |
| Square root of 324.73 | 18.0203 | |
| Square root of 324.74 | 18.0205 | |
| Square root of 324.75 | 18.0208 | |
| Square root of 324.76 | 18.0211 | |
| квадратный корень 324,77 | 18.0214 | |
| квадратный корень 324,78 | 18.0217 | |
| квадратный корень 324,79 | 18.0219 | |
| Square root of 324.80 | 18. 0222 0222 | |
| Square root of 324.81 | 18.0225 | |
| Square root of 324.82 | 18.0228 | |
| Square root of 324.83 | 18.023 | |
| Квадратный корень из 324,84 | 18,0233 | |
| Квадратный корень из 324,85 | 18,0236 | |
| Квадратный корень из 324,86 205 80006 | ||
| Square root of 324.87 | 18.0242 | |
| Square root of 324.88 | 18.0244 | |
| Square root of 324.89 | 18.0247 | |
| Square root of 324.90 | 18.025 | |
| Square root из 324,91 | 18,0253 | |
| Квадратный корень из 324,92 | 18,0255 | |
| Квадратный корень из 324,93 9002 | 8 180005 | |
| Square root of 324.94 | 18.0261 | |
| Square root of 324.95 | 18.0264 | |
Square root of 324.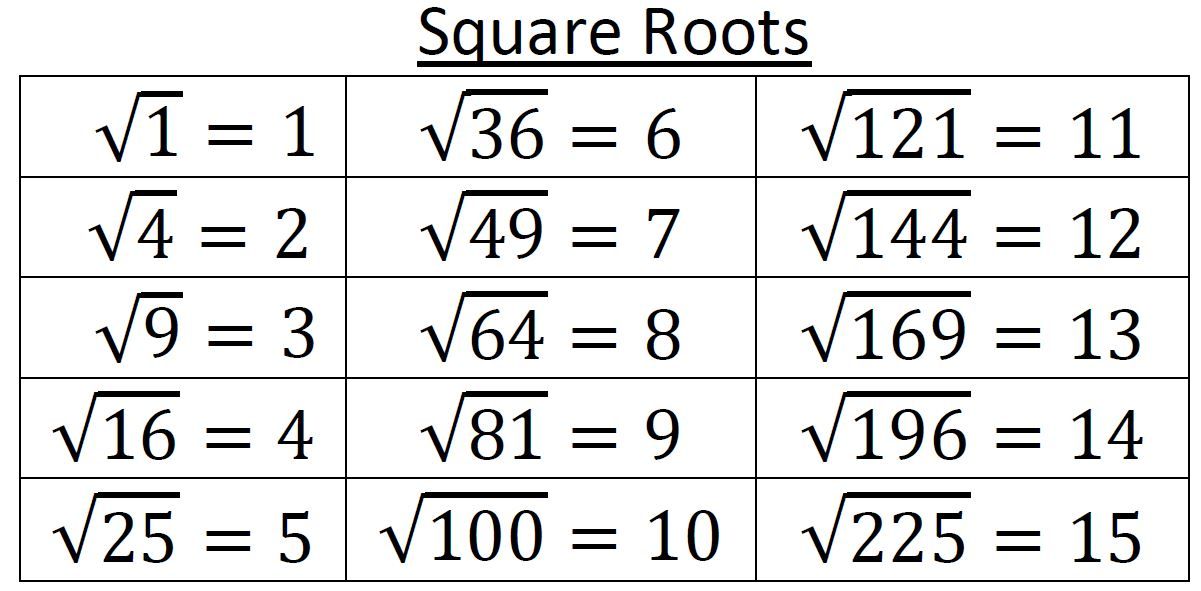 96 96 | 18.0266 | |
| Square root of 324.97 | 18.0269 | |
| Square root of 324.98 | 18.0272 | |
| квадратный корень 324,99 | 18.0275 | |
| квадратный корень 424 | 20.5913 | |
| квадратный корень 524 | 0006 | 22.891 |
| Square root of 624 | 24.98 | |
| Square root of 724 | 26.9072 | |
| Square root of 824 | 28.7054 | |
| Square root of 924 | 30.3974 | |
| квадратный корень 1 024 | 32 | |
| квадратный корень из 1124 | 33.5261 | |
| квадратный корень 1 0,224 | 34.9857 | |
| Square root of 1,324 | 36.3868 | |
| Square root of 1,424 | 37.7359 | |
| Square root of 1,524 | 39.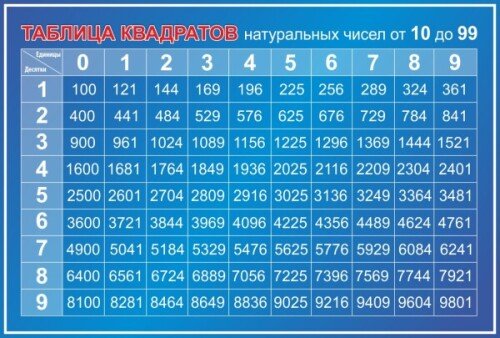 0384 0384 | |
| Square root of 1,624 | 40.2989 | |
| Square root of 1,724 | 41.5211 | |
| квадратный корень 1 824 | 42.7083 | |
| квадратный корень 1 924 | 43.8634 | |
| квадратный корень 2,024 99.8634 | ||
| квадратный корень 2,024 9.0006 | 44.9889 | |
| Square root of 2,124 | 46.0869 | |
| Square root of 2,224 | 47.1593 | |
| Square root of 2,324 | 48.2079 | |
| Square root of 2,424 | 49.2341 | |
| Корень квадратный из 2524 | 50,2394 | |
| Корень квадратный из 2624 | 51,225 | |
Корень квадратный из 2,724660006 | ||
| Square root of 2,824 | 53.1413 | |
| Square root of 2,924 | 54.074 | |
| Square root of 3,024 | 54. 9909 9909 | |
| Square root of 3,124 | 55.8928 | |
| Square root 3224 | 56,7803 | |
| квадратный корень 3 324 | 57,6541 | |
| Квадратный корень 3,424 | 58,515 | |
| 58,515 | ||
| 59.3633 | ||
| Square root of 3,624 | 60.1997 | |
| Square root of 3,724 | 61.0246 | |
| Square root of 3,824 | 61.8385 | |
| Square root of 3,924 | 62.6418 | |
| квадратный корень из 4 024 | 63.435 | |
| квадратный корень 4,124 | 64.2184 | |
| квадратный корень 4,224 99.0006 | 64.9923 | |
| Square root of 4,324 | 65.7571 | |
| Square root of 4,424 | 66.5132 | |
| Square root of 4,524 | 67. 2607 2607 | |
| Square root of 4,624 | 68 | |
| Квадратный корень из 4 724 | 68,7314 | |
| Квадратный корень из 4 824 | 69,455 | |
| Квадратный корень из 4,924 | 2 | |
| Square root of 5,024 | 70.8802 | |
| Square root of 5,124 | 71.5821 | |
| Square root of 5,224 | 72.2772 | |
| Square root of 5,324 | 72.9657 | |
| Квадратный корень из 5 424 | 73,6478 | |
| Квадратный корень из 5 524 | 74,3236 | |
Квадратный корень из 5,62450006 | ||
| Square root of 5,724 | 75.6571 | |
| Square root of 5,824 | 76.3151 | |
| Square root of 5,924 | 76.9675 | |
| Square root of 6,024 | 77. 6144 6144 | |
| Square root 6,124 | 78.256 | |
| квадратный корень из 6 224 | 78,8923 | |
| Квадратный корень 6 324 | 79,5236 | |
| 79,5236 | ||
| 80.1499 | ||
| Square root of 6,524 | 80.7713 | |
| Square root of 6,624 | 81.388 | |
| Square root of 6,724 | 82 | |
| Square root of 6,824 | 82.6075 | |
| квадратный корень из 6 924 | 83.2106 | |
| Квадратный корень 7,024 | 83.8093 | |
| Квадратный корень 7,124 99.8093 | ||
| Квадратный корень 7,124 99.0006 | 84.4038 | |
| Square root of 7,224 | 84.9941 | |
| Square root of 7,324 | 85.5804 | |
| Square root of 7,424 | 86.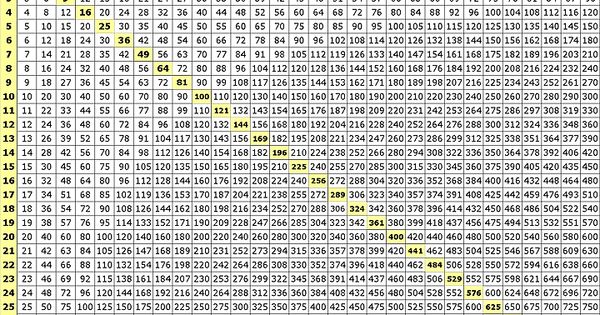 1626 1626 | |
| Square root of 7,524 | 86.741 | |
| Квадратный корень из 7 624 | 87,3155 | |
| Квадратный корень из 7 724 | 87,8863 | |
| Квадратный корень из 7,823 8 824 | 60006 | |
| Square root of 7,924 | 89.0169 | |
| Square root of 8,024 | 89.5768 | |
| Square root of 8,124 | 90.1332 | |
| Square root of 8,224 | 90.6863 | |
| Square root 8,324 | 91.236 | |
| квадратный корень из 8 424 | 91.7824 | |
| Квадратный корень 8 524 | 92.3255 | |
| 92.3255 | ||
| 92.8655 | ||
| Square root of 8,724 | 93.4024 | |
| Square root of 8,824 | 93.9361 | |
| Square root of 8,924 | 94. 4669 4669 | |
| Square root of 9,024 | 94.9947 | |
| квадратный корень 9,124 | 95.5196 | |
| квадратный корень 9,224 | 96.0417 | |
| квадратный корень | 96.0417 | |
| квадратный корень | ,324 | 96.5609 |
| Square root of 9,424 | 97.0773 | |
| Square root of 9,524 | 97.591 | |
| Square root of 9,624 | 98.102 | |
| Square root of 9,724 | 98.6103 | |
| квадратный корень 9 824 | 99.1161 | |
| квадратный корень 9 924 | 99,6193 | |
| квадратный корень 10,024 | 100,1199 | |
| Square root of 10,124 | 100.6181 | |
| Square root of 10,224 | 101.1138 | |
| Square root of 10,324 | 101.6071 | |
| Square root of 11,324 | 106.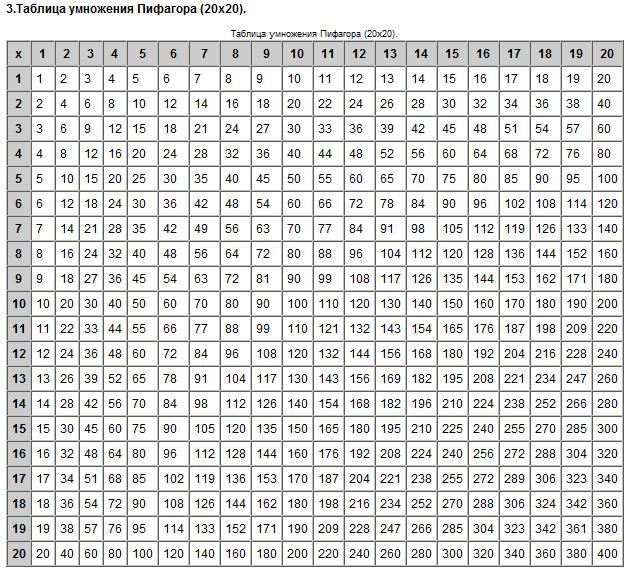 4143 4143 | |
| Square корень из 12 324 | 111,0135 | |
| корень квадратный из 13 324 | 115,4296 | |
| корень квадратный из 14,324 9 | 9 000506 60009||
| Square root of 15,324 | 123.7901 | |
| Square root of 16,324 | 127.7654 | |
| Square root of 17,324 | 131.6207 | |
| Square root of 18,324 | 135.3662 | |
| Square root of 19 324 | 139,0108 | |
| квадратный корень из 20 324 | 142.5623 | |
| квадратный корень 21 324 | 146,0274 | |
| Square root of 22,324 | 149.4122 | |
| Square root of 23,324 | 152.722 | |
| Square root of 24,324 | 155.9615 | |
| Square root of 25,324 | 159.1352 | |
| Square root of 26,324 | 162. 2467 2467 | |
| квадратный корень 27 324 | 165.2997 | |
| квадратный корень 28 324 | 168.2974 | |
| Square root of 29,324 | 171.2425 |
| Square root of 30,324 | 174.1379 | |||
| Square root of 31,324 | 176.9859 | |||
| Square root of 32,324 | 179.7888 | |||
| Square корень из 33 324 | 182,5486 | |||
| корень квадратный из 34 324 | 185,2674 | |||
| корень квадратный из 35,324 7 8 | ||||
| Square root of 36,324 | 190.5886 | |||
| Square root of 37,324 | 193.1942 | |||
| Square root of 38,324 | 195.7652 | |||
| Square root of 39,324 | 198.3028 | |||
| Square root из 40 324 | 200,8084 | |||
| Квадратный корень из 41 324 | 203,2831 | |||
| Квадратный корень из 42,324 9 0724 | 29 | |||
| Square root of 43,324 | 208.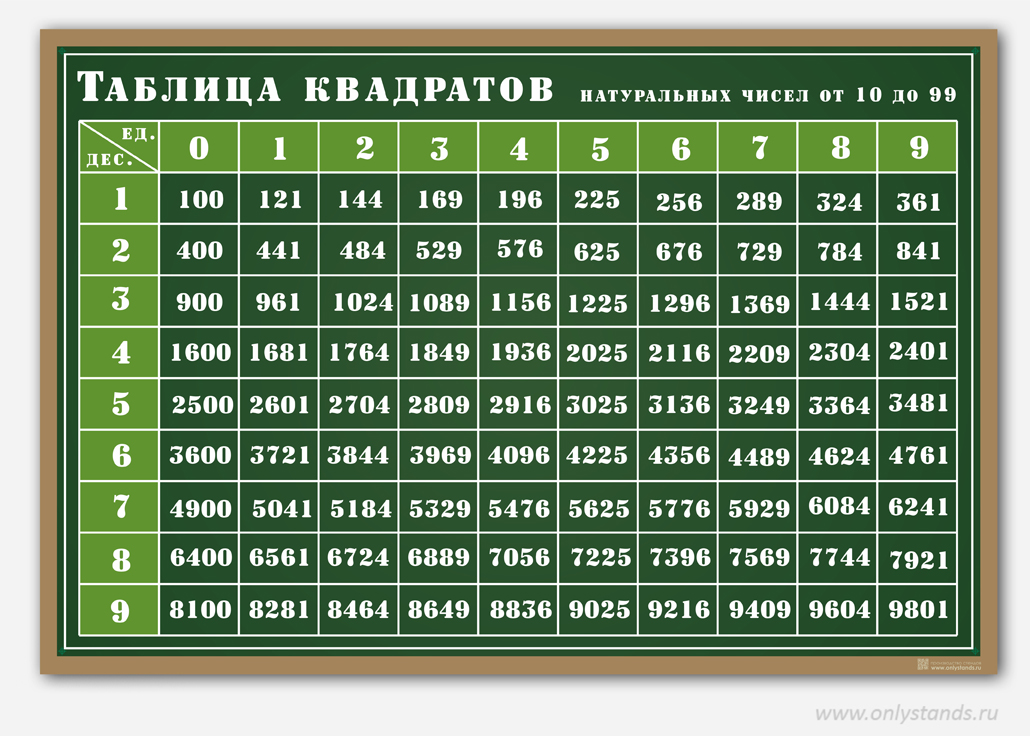 1442 1442 | |||
| Square root of 44,324 | 210.5327 | |||
| Square root of 45,324 | 212.8943 | |||
| Square root of 46,324 | 215.2301 | |||
| Square root of 47 324 | 217,5408 | |||
| Квадратный корень из 48 324 | 219,8272 | |||
| Квадратный корень 49,324 | 222.0901 | |||
| Square root of 50,324 | 224.3301 | |||
| Square root of 51,324 | 226.548 | |||
| Square root of 52,324 | 228.7444 | |||
| Square root of 53,324 | 230.9199 | |||
| Square root of 54,324 | 233.0751 | |||
| квадратный корень 55 324 | 235.2105 | |||
| квадратный корень 56 324 | 237,3268 | |||
| Square root of 57,324 | 239.4243 | |||
| Square root of 58,324 | 241. 5036 5036 | |||
| Square root of 59,324 | 243.5652 | |||
| Square root of 60,324 | 245.6094 | |||
| Square root of 61,324 | 247.6368 | |||
| Square root of 62,324 | 249.6478 | |||
| Square root of 63,324 | 251.6426 | |||
| Square root of 64,324 | 253.6218 | |||
| Square root of 65,324 | 255.5856 | |||
| Square root of 66,324 | 257.5345 | |||
| Square root of 67,324 | 259.4687 | |||
| Square root of 68,324 | 261.3886 | |||
| Квадратный корень из 69 324 | 263,2945 | |||
| Квадратный корень из 70 324 | 265,1867 | |||
| Квадратный корень из | 4267.0655 | |||
| Square root of 72,324 | 268.9312 | |||
| Square root of 73,324 | 270. 784 784 | |||
| Square root of 74,324 | 272.6243 | |||
| Square root of 75,324 | 274.4522 | |||
| Квадратный корень из 76 324 | 276,268 | |||
| Квадратный корень из 77 324 | 278,0719 | |||
| Квадратный корень из 78 324 90 | ||||
| 06 | 06 | 06 | 06 | 06.8643 |
| Square root of 79,324 | 281.6452 | |||
| Square root of 80,324 | 283.4149 | |||
| Square root of 81,324 | 285.1736 | |||
| Square root of 82,324 | 286.9216 | |||
| Квадратный корень из 83 324 | 288,659 | |||
| Квадратный корень из 84 324 | 290,386 | |||
| Квадратный корень из 85,324 | ||||
| Square root of 86,324 | 293.8095 | |||
| Square root of 87,324 | 295.5063 | |||
| Square root of 88,324 | 297. 1935 1935 | |||
| Square root of 89,324 | 298.8712 | |||
| Square root из 90 324 | 300,5395 | |||
| Квадратный корень из 91 324 | 302,1986 | |||
Квадратный корень из 92,324 3000439 | ||||
| Square root of 93,324 | 305.4898 | |||
| Square root of 94,324 | 307.1221 | |||
| Square root of 95,324 | 308.7459 | |||
| Square root of 96,324 | 310.3611 | |||
| Square root of 97 324 | 311.9679 | |||
| Квадратный корень 98 324 | 313.5666 | |||
| Квадратный корень 99,324 | 315.1571 | |||
| Квадратный корень из 100 324 | 316,7396 |
Квадратный корень из 324 | Как найти квадратный корень из 324
Реклама
Как найти квадратный корень из 324Квадрат 324 :
- этого числа.

Например:
- Предположим, нам нужно найти квадрат любого числа, скажем, X , затем мы умножим X само на себя, то есть X , и мы получим его квадрат как Y . Это можно записать как (X) 2 = X*X= Y
- Аналогичным образом находим квадрат числа 18 .
- Чтобы найти квадрат 18, умножаем 18 на само число, то есть на 18, и записываем его следующим образом: (324) 2 = 18*18= 324
- Теперь в обратном порядке, если нам нужно найти квадратный корень из Y . Квадратный корень из Y — это единственное значение, которое при умножении само на себя дает значение Y .
- Это означает, что √ Y = √(X*X) = X
Где √ — символ, названный радикалом.
Например:
- Квадратный корень из 18 можно записать как
√324 = √ (18*18) = 18
Где √ — это символ, который называется подкоренным знаком.
- Короче говоря, мы помним квадрат из 18 и квадратный корень из 324 как .
Примечание:
- Каждое положительное действительное число имеет два корня.
- Квадрат любого отрицательного числа всегда является положительным числом.
Например:
- 324 — положительный совершенный квадрат, который также имеет два корня +18 и -18. г.
- Но в основном берется положительное значение квадратного корня, которое называется главным квадратным корнем или неотрицательным квадратным корнем.
- Следовательно, √324 = √(-18)*(-18) = -18 и √324 = √(18)*(18) = 18
Аналогично,
- (-18)*(-18) = (-18) 2 = +324 и (+18)*(+18) = (+18) 2 = 324
Существует много методов нахождения квадратного корня из полных квадратов, из которых мы подробно рассмотрим следующий метод.
- Метод многократного вычитания
- Метод простой факторизации
- В методе многократного вычитания мы должны вычесть последовательные нечетные числа, начиная с 1, из совершенного квадратного числа, квадратный корень которого мы должны найти. г.
- эл. чтобы найти квадратный корень из 324, сначала мы вычитаем из него 1.
324 – 1 =323
- Тогда следующее нечетное число равно 3, поэтому мы должны вычесть его из 323
323–3 = 320.
- Таким образом, мы вычитаем последовательные нечетные числа из соответствующих значений, полученных после непрерывного вычитания, пока не получим окончательное значение 0, .
- И значение количества нечетных чисел, необходимых для получения 0, является искомым квадратным корнем.
Например:
- Квадратный корень из 324 находим методом многократного вычитания следующим образом:
324– 1 = 323
323– 3 = 320
320– 5 = 315
315– 7 = 308
308– 9 = 299
299– 11 = 288
288 – 13 = 275
275– 15 = 260
260 – 17 =243
1 293 – 002= 224224 — 21 = 203
203 — 23 = 180
180 — 25 = 155
155 — 27 = 128
128 — 29. = 99
= 99
99 — 31 = 68
68 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33 — 33. = 3535 – 35 = 0
- Таким образом, здесь использовано общее количество нечетных чисел 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29. ,31,33 и 35, которые равны 17 числам.
- Следовательно, квадратный корень из 324 методом многократного вычитания равен 18.
- В методе простой факторизации мы должны разделить идеальное квадратное число, квадратный корень которого мы должны найти, на простое число, начиная с 2, 3, 5… и так далее, пока мы не получим остаток как 1.
- Сначала мы должны разделить на простое число 2, если это число не делится на 2, тогда мы должны взять следующее простое число, то есть 3, и процесс будет продолжаться до тех пор, пока мы не получим остаток как 1.
- Наконец, мы должны составить пары простых чисел, взятых в форме умножения, а затем мы должны извлечь из них квадратный корень.



