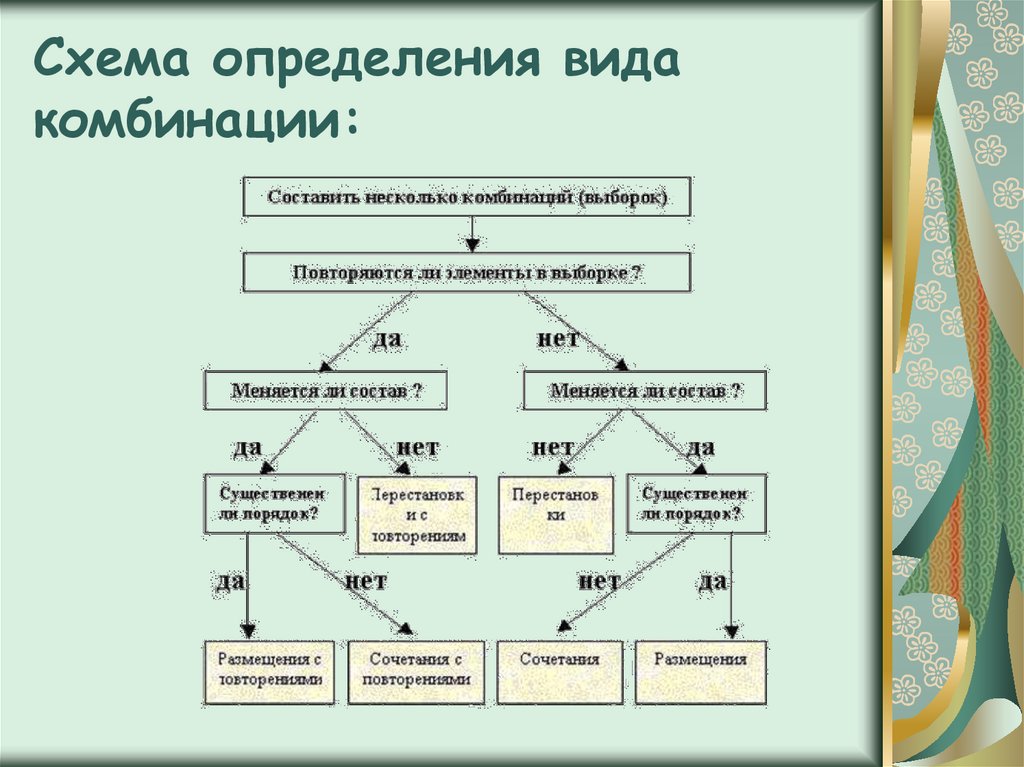
|
|||||||||||||
|
Характерная примета в задачах из области комбинаторики – вопрос в них обычно можно сформулировать так, чтобы он начинался со слов: «Сколькими способами…». Первые задачи такого типа встречались уже, например, в древней и средневековой Индии. «О друг, назови число различных ожерелий, которые можно получить из бриллиантов, сапфиров, изумрудов, кораллов и жемчугов» (Махавира, IX в.). Условие этой задачи, возможно, не очень понятно; судя по решению, здесь речь идет об ожерельях, которые бы отличались не по количеству или расположению камней одного и того же типа, а по наличию тех или иных камней – например, ожерелье из бриллиантов, из бриллиантов и кораллов, из бриллиантов, изумрудов и жемчугов и т.
«Повар готовит различные блюда с шестью вкусовыми оттенками: острым, горьким, вяжущим, кислым, соленым, сладким. Друг, скажи, каково число всех разновидностей» (Шридхара, IX–X вв.).
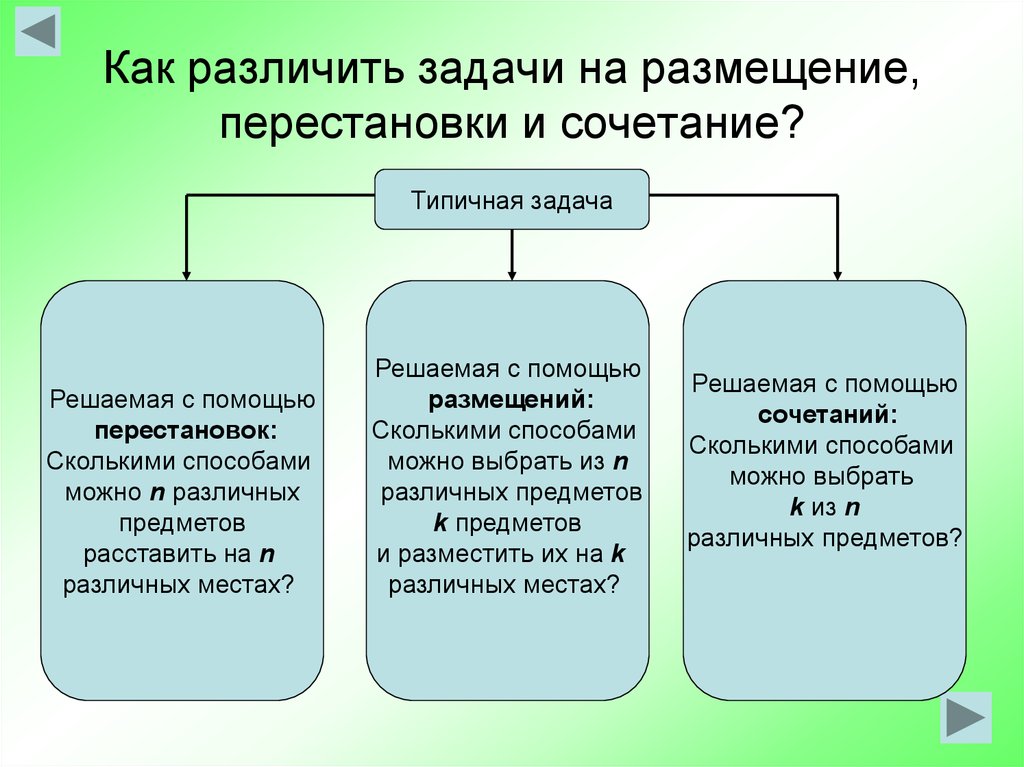
Классическими понятиями комбинаторики являются перестановки, размещения и сочетания. Перестановкой называется какой-либо способ упорядочения данного множества. Чтобы найти число всех перестановок множества из n предметов (это число обозначается Pn, от французского permutation – перестановка) – например, число способов, которыми можно расставить n томов на книжной полке, – обычно рассуждают таким образом. Первым можно поставить любой из n предметов, вторым – любой из (n – 1) оставшихся предметов, третьим любой из (n – 2) оставшихся предметов и т.
Упорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется размещением из n по m. С помощью рассуждений, аналогичных предыдущим, нетрудно найти, что число размещений из n по m (оно обозначается , от французского arrangement – размещение) равно произведению m множителей
Наконец, неупорядоченная совокупность m предметов, выбираемых из исходных n предметов, называется сочетанием из n по m. Число сочетаний обозначается , от французского combinaison – сочетание. Поскольку одному и тому же сочетанию соответствует Pm размещений (получаемых с помощью различных перестановок одного и того же набора m элементов), число сочетаний из n по m меньше числа размещений из n по m в Pm раз:
Впервые понятия перестановки, размещения и сочетания в их взаимосвязи появились в написанной на древенееврейском языке арифметике (1321 г. Например, термин permutation – перестановка – появился в учебнике «Теория и практика арифметика» (1656 г.) у работавшего в Лувене и Антверпене (ныне Бельгия) преподавателя математики Андре Таке, учебники которого получили большое распространение в XVII–XVIII вв. Понятие размещений и равенство вновь появились только у Я. Бернулли, давшего наиболее полное изложение комбинаторики во второй части «Искусства предположений», изданного в 1713 г. спустя четыре года после смерти автора и ставшего фундаментальной работой по теории вероятностей. А вот история сочетаний, как мы сейчас убедимся, более давняя: а именно, числа сочетаний – оказывается, ни что иное, как давно знакомые нам биномиальные коэффициенты, которые мы (вслед за Эйлером) обозначали Дело тут вот в чем: число
– это коэффициент при an – mbm в разложении выражения (a + b)n. Соответственно, на числа сочетаний переносятся все уже известные свойства биномиальных коэффициентов, в частности, свойство Это свойство можно доказать новым способом, исходя из комбинаторного смысла чисел . Сумма
– это совокупное число, которым можно выбрать последовательно из n имеющихся элементов: ноль элементов (это можно сделать только одним способом), один элемент (это, разумеется, можно сделать n способами), два элемента и т. Также по-новому, исходя из комбинаторного определения сочетаний, можно доказать и свойство
, гарантирующее, вместе с очевидными равенствами
, что числа сочетаний можно найти с помощью треугольника Паскаля.
Т. н. мультипликативное представление биномиальных коэффициентов
впервые (после Леви бен Гершона) установил парижский преподаватель математики П. Эригон (1634 г.), но широкую известность оно получило благодаря работе Паскаля «Трактат об арифметическом треугольнике», опубликованной в 1665 г. после смерти автора. Пожалуй, проще всего этот результат доказывается с помощью равенства
. Впрочем, мы сейчас обычно записываем «мультипликативное представление» несколько иначе, с помощью знака факториала. Факториалом натурального числа n называется произведение всех натуральных чисел от 1 до n. Факториалом 0 считается 1. Pn = n!, Что касается самого слова «комбинаторика», то оно восходит к «Рассуждению о комбинаторном искусстве» двадцатилетнего Лейбница (1666 г.), которое положило начало этому разделу математики как самостоятельной науке. «Рассуждение» Лейбница содержало ряд теорем о сочетаниях и перестановках, но, кроме того, автор провозглашал весьма широкую применимость новой науки к таким разнообразным предметам, как замки, органы, силлогизмы, смешение цветов, стихосложение, логика, геометрия, военное искусство, грамматика, юриспруденция, медицина и богословие. В дальнейшем Лейбниц продолжил вынашивать грандиозный замысел комбинаторики, полагая, что, как обычная математика занимается большим и малым, единым и многим, целым и частью, так комбинаторика должна заниматься одинаковым и различным, похожим и непохожим, абсолютным и относительным местоположением. |
Перестановки. Сочетания. Размещения — презентация онлайн
1. Учение без размышления бесполезно, но и размышление без учения опасно. Конфуций
Перестановки.Сочетания.
Размещения.
Проказница-Мартышка, Осел, Козел да косолапый
Мишка
Затеяли сыграть Квартет.
Достали нот, баса, альта, две скрипки
И сели на лужок под липки Пленять своим искусством свет.
Ударили в смычки, дерут, а толку нет.
«Стой, братцы, стой! — кричит Мартышка. — Погодите!
Как музыке идти? Ведь вы не так сидите.
И так, и этак пересаживались – опять музыка на лад не
идет.

Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
Решение:
1 * 2 * 3 * 4 = 24
«Проказница Мартышка, Осёл, Козёл
да косолапый Мишка задумали сыграт
квартет». Сколькими способами они
могут выбрать каждый для себя по
одному инструменту из 10 данных
различных инструментов?
7. Комбинаторика
Комбинаторикой называется раздел математики, вкотором исследуется, сколько различных комбинаций
(всевозможных объединений элементов), подчиненных
тем или иным условиям, можно составить из элементов,
принадлежащих данному множеству.
Слово «комбинаторика» происходит от латинского
слова combinare, которое означает «соединять, сочетать».
Термин «комбинаторика» был введён знаменитым
Готфридом Вильгельмом Лейбницем, — всемирно
известным немецким учёным.
ПОНЯТИЕ ФАКТОРИАЛА
n! = 1·2·3 … n, где n — натуральное число
Принято считать, что 0! = 1
Пример:
Решить уравнение:
Решение:
Ответ:
(n 2)!
20;
n!
n!( n 1)( n 2)
20; Решаем квадратное уравнение:
n!
n1 3; n2 6
( n 1)( n 2) 20;
n 3
8
9.
 Задания для повторенияВычислите:
Задания для повторенияВычислите:10. Ответы
1) 422) 3003
3)
11. Решаем самостоятельно
2 вариант1 вариант
• 1
• 1
• 2
• 2
• 3
• 3
12. Проверяем: «5» — верных ответов 4 «4» – верных ответов 3 «3» – верных ответов 2
Проверяем:1 вариант
1) 100
2) 8,25
3) 48,2
«5» — верных ответов 4
«4» – верных ответов 3
«3» – верных ответов 2
2 вариант
• 1) 2015
• 2) 40
• 3) 1,1
13. 1) установить различие между задачами 2) предположить, в какой задаче результат будет больше, и почему 3) предложить способ
решения• Задача 1.
Имеются три различных фрукта:
апельсин(A),банан (B), слива (C). Сколькими
способами можно два из них отдать Пете и Коле?
• Задача 2.
Имеются три различных фрукта:
апельсин(A),банан (B), слива (C). Сколькими
способами из них два для обеденного перекуса?
16. Различают три вида соединений: размещения, перестановки и сочетания.
 Сочетания
СочетанияВо 2 задаче идет речь о сочетании
Сочетаниями называют различные комбинации из объектов,
которые выбраны из множества различных объектов, и
которые отличаются друг от друга хотя бы одним объектом.
Иными словами, отдельно взятое сочетание – это уникальная
выборка из элементов, в которой не важен их порядок
(расположение). Общее же количество таких уникальных
сочетаний рассчитывается по формуле .
n = 3. m = 2 С32 = = 3
А теперь решим ту же задачу для случая m=8, n=3:
Решение задачи №2
17. Размещения
Размещениями называют различные комбинации из объектов,которые выбраны из множества различных объектов, и
которые отличаются друг от друга как составом объектов в
выборке, так и их порядком. Количество размещений
рассчитывается по формуле:
m!
Amn
(m n)!
Решение задачи №1
n = 3. m = 2 А32 = 6
А теперь решим ту же задачу для случая m=8, n=3:
A83
8!
1 2 3 4 5 6 7 8
6 7 8 336(способов)
(8 3)!
1 2 3 4 5
18.
 ПерестановкиПерестановками называют
ПерестановкиПерестановками называюткомбинации, состоящие из одних и тех
же различных объектов и отличающиеся
только порядком их расположения.
Количество всех возможных перестановок
выражается формулой
Решение задачи из басни :
n = 4.
P4 = 4! = 1*2*3*4=24
«Проказница Мартышка, Осёл, Козёл да
косолапый Мишка задумали сыграть
квартет». Сколькими способами они могут
выбрать каждый для себя по одному
инструменту из 10 данных различных
инструментов?
( Ответ:
)
21. Графический диктант
а) судья хоккейного матча и его помощник;
б) три ноты в аккорде;
в) «Шесть человек останутся убирать класс!»
г) две серии для просмотра из многосерийного фильма
д) составление букета
е) выбор солистов хора
ж) составление расписания уроков
з) составление меню блюд в столовой
и) очередь в кассе
к) распределение золотой и серебряной медали по итогам
олимпиады
Выбрать и решить задачи, где рассматривается комбинация
ПЕРЕСТАНОВКИ,СОЧЕТАНИЯ, РАЗМЕЩЕНИЯ
1.

2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Изменяя порядок слов: руки, мою, я, составьте всевозможные предложения.
Сколькими способами в игре «спортлото» можно выбрать 6 номеров из 49?
Сколькими способами можно выбрать 2 буквы из слова «конверт»?
Из коллектива работников в 25 человек нужно выбрать председателя, заместителя,
бухгалтера и казначея. Каким количеством способов это можно сделать?
Сколько существует способов выбора трёх ребят из 4-х желающих дежурить в столовой?
На собрании пожелали выступить 5 человек – Иванов, Петров, Сидоров, Белочкин и
Пеночкин. Сколькими способами можно составить список ораторов?
Сколько экзаменационных комиссий, состоящих из 3 человек, можно создать из 5
преподавателей?
Сколько различных трехзначных чисел, в каждом из которых все цифры различны, можно
составить из цифр 1, 2, 3, 4?
Сколько различных четырехзначных чисел, в каждом из которых все цифры различны,
можно составить из цифр 1, 2, 3, 4?
Сколькими способами можно составить расписание на день из 4 различных уроков, если
изучается 10 предметов?
Сколькими способами можно записать в виде произведения простых множителей число 30?
В хирургическом отделении работают 40 врачей.
 Сколькими способами из них можно
Сколькими способами из них можнообразовать бригаду в составе хирурга и ассистента?
24. ПЕРЕСТАНОВКИ
1Изменяя порядок слов: руки, мою, я, составьте
всевозможные предложения.
6 На собрании пожелали выступить 5 человек – Иванов,
Петров, Сидоров, Белочкин и Пеночкин. Сколькими
способами можно составить список ораторов.
9 Сколько различных четырехзначных чисел, в каждом из
которых все цифры различны, можно составить из цифр
1, 2, 3, 4?
11 Сколькими способами можно записать в виде
произведения простых множителей число 30?
25. СОЧЕТАНИЯ
2Сколькими способами в игре «спортлото»
можно выбрать 6 номеров из 49?
3 Сколькими способами можно выбрать 2 буквы
из слова «конверт»?
5 Сколько существует способов выбора трёх
ребят из 4-х желающих дежурить в столовой?
7 Сколько экзаменационных комиссий, состоящих
из 3 человек, можно создать из 5 преподавателей?
26. РАЗМЕЩЕНИЯ
4 Из коллектива работников в 25 человек нужно выбратьпредседателя, заместителя, бухгалтера и казначея.
 Каким
Какимколичеством способов это можно сделать?
8 Сколько различных трехзначных чисел, в каждом из
которых все цифры различны, можно составить из цифр 1,
2, 3, 4?
10 Сколькими способами можно составить расписание на
день из 4 различных уроков, если изучается 10 предметов?
12 В хирургическом отделении работают 40 врачей.
Сколькими способами из них можно образовать бригаду в
составе хирурга и ассистента?
27. Ответы
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12
Я мою руки. Руки мою я. Мою я руки. Я руки мою. Руки я мою.
Мою руки я. = 6
С499 = 1383816
С72 = 21
А254 = 303600
С43 = 4
Р5 = 120
С73 = 35
А43 = 24
Р4 = 24
А 104 = 30240
Р3 = 6
А402 = 1560
28. Проверь себя
1.Определите вид соединений:а) Соединения из n элементов, отличающиеся друг
от друга только порядком расположения в них
элементов, называются __________перестановки
б) Соединения из m элементов по n, отличающихся
друг от друга только составом элементов,
называются _______________сочетания
в) Соединения из m элементов по n, отличающихся
друг от друга составом элементом и порядком
их расположения, называются _________
размещения
29.
 2.Восстановите соответствие типов соединений и формул для их подсчёта1
2.Восстановите соответствие типов соединений и формул для их подсчёта1Amn
m!
(m n)!
2
Pn n!
3
m!
C
(m n)!n!
n
m
А сочетания
В размещения
С перестановки
30. Задача
Встретились несколько друзей и всеобменялись рукопожатиями. Всего было
сделано 15 рукопожатий. Сколько
встретилось друзей?
31. Исторические сведения
• Комбинаторика как наука стала развиваться в XIII в.параллельно с возникновением теории вероятностей.
• Первые научные исследования по этой теме
принадлежат итальянским ученым Дж. Кардано, Н.
Чарталье (1499-1557), Г. Галилею (1564-1642) и
французским ученым Б.Пискамо (1623-1662) и П.
Ферма.
• Комбинаторику,
как
самостоятельный
раздел
математики, первым стал рассматривать немецкий
ученый Г. Лейбниц в своей работе «Об искусстве
комбинаторики», опубликованной в 1666г. Он также
впервые ввел термин «Комбинаторика».
Пьер Ферма
1601-1665
Готфрид
Вильгельм
Лейбниц
1646-1716
Первые научные
исследования по
комбинаторике
принадлежат:
Леонард Эйлер
1707-1783
Блез Паскаль
1623-1662
33.
 Спасибо за внимание!!.
Спасибо за внимание!!.Перестановки, сочетания и размещения — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Учение без размышления бесполезно, но и размышление без учения опасно. Конфуций
Перестановки.Сочетания.
Размещения.
Проказница-Мартышка, Осел, Козел да косолапый
Мишка
Затеяли сыграть Квартет.
Достали нот, баса, альта, две скрипки
И сели на лужок под липки Пленять своим искусством свет.

Ударили в смычки, дерут, а толку нет.
«Стой, братцы, стой! — кричит Мартышка. — Погодите!
Как музыке идти? Ведь вы не так сидите.
И так, и этак пересаживались – опять музыка на лад не
идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
Решение:
1 * 2 * 3 * 4 = 24
5. Исторические сведения
• Комбинаторика как наука стала развиваться в XIII в.параллельно с возникновением теории вероятностей.
• Первые научные исследования по этой теме
принадлежат итальянским ученым Дж. Кардано, Н.
Чарталье (1499-1557), Г. Галилею (1564-1642) и
французским ученым Б.Пискамо (1623-1662) и П.
Ферма.
• Комбинаторику,
как
самостоятельный
раздел
математики, первым стал рассматривать немецкий
ученый Г. Лейбниц в своей работе «Об искусстве
комбинаторики», опубликованной в 1666г. Он также
впервые ввел термин «Комбинаторика».
Пьер Ферма
1601-1665
Готфрид
Вильгельм
Лейбниц
1646-1716
Первые научные
исследования по
комбинаторике
принадлежат:
Леонард Эйлер
1707-1783
Блез Паскаль
1623-1662
7.
 КомбинаторикаКомбинаторикой называется раздел математики, в
КомбинаторикаКомбинаторикой называется раздел математики, вкотором исследуется, сколько различных комбинаций
(всевозможных объединений элементов), подчиненных
тем или иным условиям, можно составить из элементов,
принадлежащих данному множеству.
Слово «комбинаторика» происходит от латинского
слова combinare, которое означает «соединять, сочетать».
Термин «комбинаторика» был введён знаменитым
Готфридом Вильгельмом Лейбницем, — всемирно
известным немецким учёным.
ПОНЯТИЕ ФАКТОРИАЛА
n! = 1·2·3 … n, где n — натуральное число
Принято считать, что 0! = 1
Пример:
Решить уравнение:
Решение:
Ответ:
(n 2)!
20;
n!
n!( n 1)( n 2)
20; Решаем квадратное уравнение:
n!
n1 3; n2 6
( n 1)( n 2) 20;
n 3
8
9. 1) установить различие между задачами 2) предположить, в какой задаче результат будет больше, и почему 3) предложить способ
решения• Задача 1.
Имеются три различных фрукта:
апельсин(A),банан (B), слива (C).
 Сколькими
Сколькимиспособами можно два из них отдать Пете и Коле?
• Задача 2.
Имеются три различных фрукта:
апельсин(A),банан (B), слива (C). Сколькими
способами можно два из них выбрать для
обеденного перекуса?
12. Различают три вида комбинаций: перестановки, размещения и сочетания.
Перестановками называют комбинации,состоящие из одних и тех же различных
объектов и отличающиеся только порядком их
расположения. Количество всех возможных
перестановок выражается формулой
Сочетания
Сочетаниями называют различные комбинации из объектов,
которые выбраны из множества различных объектов, и
которые отличаются друг от друга хотя бы одним объектом.
Иными словами, отдельно взятое сочетание – это уникальная
выборка из элементов, в которой не важен их порядок
(расположение). Общее же количество таких уникальных
сочетаний рассчитывается по формуле
n = 3. m = 2 С32 = 3
А теперь решим ту же задачу для случая m=3, n=8:
Решение задачи №2
14.
 РазмещенияРазмещениями называют различные комбинации из объектов,
РазмещенияРазмещениями называют различные комбинации из объектов,которые выбраны из множества различных объектов, и
которые отличаются друг от друга как составом объектов в
выборке, так и их порядком. Количество размещений
рассчитывается по формуле:
m!
Amn
(m n)!
Решение задачи №1
n = 2. m = 3 А32 = 6
А теперь решим ту же задачу для случая m=8, n=3:
A83
8!
1 2 3 4 5 6 7 8
6 7 8 336(способов)
(8 3)!
1 2 3 4 5
«Проказница Мартышка, Осёл, Козёл да
косолапый Мишка задумали сыграть
квартет». Сколькими способами они могут
выбрать каждый для себя по одному
инструменту из 10 данных различных
инструментов?
( Ответ:
)
17. Задания для повторения
Вычислите:18. Ответы
1) 422) 3003
1
3)
6
19. Практическое занятие
20. 1. Вычислите (каждое выражение – 1 балл).
1 вариант• 1
2 вариант
• 1
• 2
• 2
• 3
• 3
2. Решите задачи на подсчет перестановок, сочетаний,
размещений, подобрав соответствующую формулу
(Каждая задача – 2 балла).

1.
2.
3.
4.
5.
6.
Изменяя порядок слов: руки, мою, я, составьте всевозможные
предложения.
Сколькими способами в игре «спортлото» можно выбрать 6 номеров
из 49?
На собрании пожелали выступить 5 человек – Иванов, Петров,
Сидоров, Белочкин и Пеночкин. Сколькими способами можно
составить список ораторов?
Сколько экзаменационных комиссий, состоящих из 3 человек, можно
создать из 5 преподавателей?
Сколько различных трехзначных чисел, в каждом из которых все
цифры различны, можно составить из цифр 1, 2, 3, 4?
Сколькими способами можно составить расписание на день из 4
различных уроков, если изучается 10 предметов?
Критерии оценки:
«5» – 14-15 баллов
«4» – 10-до 14 баллов
«3» – 7- до 10 баллов
«2» – менее 7баллов
English Русский Правила
Подборка по базе: реферат Выбор места размещения предприятия.rtf, Петров Оптимизация размещения ЭС-конвертирован.  pdf, Особенности размещения интернет-рекламы.pptx, Курсовая Особенности организации службы приема и размещения.docx, Способы размещения государственного и муниципального контракта п, milanaarrt Курсовая работа Система классификации гостиниц и ины, Оптимизация размещения и порядка бурения многоствольных скважин , 17ЗСКД Кузнецова Планирование производственно технологической де, Регламент размещения КГТ.docx, Схема размещения (копия).pptx pdf, Особенности размещения интернет-рекламы.pptx, Курсовая Особенности организации службы приема и размещения.docx, Способы размещения государственного и муниципального контракта п, milanaarrt Курсовая работа Система классификации гостиниц и ины, Оптимизация размещения и порядка бурения многоствольных скважин , 17ЗСКД Кузнецова Планирование производственно технологической де, Регламент размещения КГТ.docx, Схема размещения (копия).pptxТема урока: Перестановки, размещения и сочетания. Цели урока: Образовательная: познакомить с понятием «комбинаторика»; познакомить с правилами комбинаторики; обеспечить в ходе урока усвоение понятия размещений, перестановок и сочетаний; сформировать умения решать комбинаторные задачи. Воспитательная: воспитание интереса к дисциплине, честности, аккуратности, эстетического отношения к оформлению математических решений; воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем.  Развивающая: развитие логического мышления посредством решения комбинаторных задач, сообразительности; развитие математической речи, внимания. Обучающийся должен: знать: определения трех важнейших понятий комбинаторики: размещения из n элементов по m; сочетания из n элементов по m; перестановки из n элементов; основные комбинаторные формулы уметь: отличать задачи на «перестановки», «сочетания», «размещения» друг от друга; применять основные комбинаторные формулы при решении простейших комбинаторных задач. Методы обучения: словесно-информационный (рассказ), словесно-репродуктивный(опрос), практически-репродуктивный( выполнение заданий), наглядно-иллюстративный .  Структура урока Организационный момент Мотивация учебной деятельности Сообщение темы и цели урока. Объяснение нового материала. Формирование умений и навыков в решении комбинаторных задач. Домашнее задание Подведение итогов Список литературы Ход урока Организационный момент Приветствие, определение отсутствующих, проверка готовности учащихся к уроку. Мотивация учебной деятельности Задача из басни С. Крылова «Квартет» Проказница Мартышка Осёл, Козёл, Да косолапый Мишка Затеяли играть квартет … Стой, братцы стой! – Кричит Мартышка, — погодите! Как музыке идти? Ведь вы не так сидите… И так, и этак пересаживались – опять музыка на лад не идет. Вот пуще прежнего пошли у них разборы И споры, Кому и как сидеть… — Как вы думаете сколько различных вариантов расположения музыкантов возможно? (учащиеся предлагают свои варианты) — В конце урока вы узнаете кто дал правильный ответ. 3. Сообщение темы и цели урока. Тема сегодняшнего урока «Основы комбинаторики. Размещения, перестановки, сочетания». Сегодня на уроке вам предстоит рассмотреть общие правила комбинаторики, ознакомится с основными понятиями комбинаторики (размещения, сочетания, перестановки), научиться решать простейшие комбинаторные задачи. 4.Объяснение нового материала. Одним из важнейших понятий современной математики является понятие множества. Говорят о множестве учащихся в группе, о множестве букв в алфавите, о множестве изделий в упаковке и т.д. Понятие множества относится к первоначальным, простейшим, понятиям и формально через другие более простые понятия не определяется. Множество будем записывать, располагая его элементы в фигурных скобка {a, b, c, … , e, f}. Во множестве порядок элементов роли не играет, так {a, b} = {b, a}. Множество, не содержащее ни одного элемента, называется пустым множествоми обозначается символом ø. Если каждый элемент множества А является элементом множества В, то говорят, что множество А является подмножеством множества В Множество {a, b} является подмножеством множества {a, b, c, … , e, f}. Задача: Перечислите возможные варианты подмножества множества {3, 4, 5, 7, 9}. При решении многих практических задач часто приходится имеющиеся предметы (элементы) соединять в разные наборы (комбинации). Например — парфюмерные наборы, конфеты, инструменты, спортивные команды. Задачи которые рассматривают такие соединения и находится число различных соединений, называют комбинаторными. Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству. В каждой из них требуется подсчитать число возможных вариантов осуществления некоторого действия, ответить на вопрос «сколькими способами». Комбинаторика возникла и развивалась одновременно с теорией вероятностей. И первоначально комбинаторные задачи касались в основном азартных игр. Комбинаторика – раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. Комбинаторика является важным разделом математики, который исследует закономерности расположения, упорядочения, выбора и распределения элементов с фиксированного множества. При большом числе возможных последствий испытания способы прямого перебора возможных вариантов малоэффективны. На помощь приходят комбинаторные методы, в основе которых лежат два следующих правила называемых соответственно правилами умножения и сложения. ПРАВИЛО СУММИРОВАНИЯ Если два взаимоисключающие действия могут быть выполнены в соответствии и способами, тогда какое-то одно из этих действий можно выполнить способами. Пример №1 Из города А в город В можно добраться 12 поездами, 3 самолетами, 23 автобусами. Решение. Проезд из А в В на поезде, самолете или автобусе являются событиями, которые не могут выполняться одновременно одним человеком (взаимоисключающими), поэтому общее количество маршрутов можно вычислить суммированием способов передвижения N=12+13+23=38 Пример № 2 В ящике имеется n разноцветных шариков. Произвольным образом вынимаем один шарик. Сколькими способами это можно сделать? Решение. Конечно, n способами. Теперь эти n шариков распределены по двум ящикам: В первом m шариков, во втором k. Произвольно из какого-нибудь ящика вынимаем один шарик. Сколькими разными способами это можно сделать? Решение. Из первого ящика шарик можно вытянуть m различными способами, из второго k различными способами, всего N = m + k способами. ПРАВИЛО ПРОИЗВЕДЕНИЯ Пусть две выполняемые одно за другим действия могут быть осуществлены в соответствии и способами. Пример № 3 В турнире принимают участие 8 хоккейных команд. Сколько существует способов распределить первое, второе и третье места? Решение. Первое место займет одна из 8 команд, второе — одна из 7, третье — одна из 6, так как каждая из них не может претендовать одновременно на два призовых места. Поэтому таких способов будет ровно N=8 7 6 =336 Пример № 4 Сколько можно записать двузначных чисел в десятичной системе счисления? Решение. Поскольку число двузначное, то число десятков (m) может принимать одно из девяти значений: 1,2,3,4,5,6,7,8,9. Число единиц (k) может принимать те же значения и может, кроме того быть равным нулю. Отсюда следует, что m = 9, а k= 10. Всего получим двузначных чисел N = m ·k = 9·10 =90. Пример № 5 В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола? Решение. Типы соединений Множества элементов называются соединениями. Различают три типа соединений: перестановки из n элементов; размещения из n элементов по m; сочетания из n элементов по m (m n). Перестановки. Число перестановок На практике часто возникают задачи, связанные с установлением порядка во множестве. Например, число мест равно количеству людей, на которых мы должны разместить их. Такая ситуация встречается часто – рассадить n человек на n мест, или приписать каждому человеку номер. Первый человек может выбрать любое из n мест, второй человек выбирает из (n — 1) оставшихся мест, третий человек может выбрать из уже (n — 2) мест, …, предпоследний человек выбирает из 2 мест, последний человек получает последнее место. В общем виде произведение всех целых чисел от 1 до n включительно обозначают n! = 1·2·3…(n – 2) · (n – 1) · n. Установленный в конечном множестве порядок называют перестановкой его элементов. Определение: Перестановкой из n элементов называется любое упорядоченное множество из n элементов. Иными словами, это такое множество, для которого указано, какой элемент находится на первом месте, какой – на втором, какой- на третьем, …, какой – на n-м месте. Перестановки можно образовывать из элементов любого конечного множества. Число перестановок из n элементов обозначают Рn. Возьмем одноэлементное множество {a}. Ясно, что один элемент можно упорядочить единственным образом, следовательно, Р1 = 1. Перестановки– это такие соединения по n элементам из данных элементов, которые отличаются одно от другого порядком элементов. Возьмем двух элементное множество {a, b}. В нем можно установить два порядка: {a, b} или {b, a}. Следовательно, число перестановок из двух элементов Р2 = 2. Три буквы во множестве {a, b, c} можно расположить, по порядку шестью способами: {a, b, c}{a, c, b}{b, a, c}{b, c, a}{c, b, a}{c, a, b}. Следовательно, общее число способов упорядочения трех элементов множества Р3 = 3 · Р2 = 3 · 2 · 1 = 6. Рn = n · (n — 1) · (n – 2) · … · 2 · 1 = n! Определение: Пусть n — натуральное число. Через n! (читается «эн факториал») обозначается число, равное произведению всех натуральных чисел 1 от до n: n! = 1 · 2 · 3 · . В случае, если n = 0, по определению полагается: 0! = 1. Пример № 6 Найдем значения следующих выражений: Пример № 7 Чему равно а)Р5 ; б) Р3. Решение. Рn = n! =n · (n — 1) · (n – 2) · … · 2 · 1 Р5=5! = 5 · 4 · 3 · 2 ·1 = 120 Р3=3! = 1 · 2 · 3 = 6 Пример № 8 Упростите а) 7! · 8 = 8! б) 12! · 13 ·14 = 14! в) κ! · (κ + 1) = (κ + 1)! Пример № 9 Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках? Решение. n =8 Р8=8! = 8·7·6·5 · 4 · 3 · 2 ·1 =40320 Размещения. Размещениями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения. Определение. Размещением из n элементов по m называется любое упорядоченное множество из m элементов, состоящее из элементов n элементного множества. Число размещений из m элементов по n обозначают (от французского «arrangement» — «размещение») и вычисляют по формуле: Пример № 9 Учащиеся 11-го класса изучают 9 учебных предметов. В расписании учебных занятий на один день можно поставить 4 различных предмета. Сколько существует различных способов составления расписания на один день? Решение. Имеем 9-элементное множество, элементы которого учебные предметы. При составлении расписания мы будем выбирать 4-элементное подмножество (урока) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре, то есть A94: Пример № 10 Сколькими способами из класса, где учатся 24 ученика, можно выбрать старосту и помощника старосты? Решение. Имеем 24-элементное множество, элементы которого ученики класса. При выборах старосты и помощника старосты мы будем выбирать 2-элементное подмножество (ученика) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре(m=24, n=2), то есть A242: Сочетания. Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом. Определение. Сочетанием без повторений из n элементов по m -называется любое m элементное подмножество n -элементного множества Число сочетаний из n элементов по m обозначают (от французского «combination» — «сочетание») и вычисляют по формуле: Пример № 11 Сколькими способами из класса, где учатся 24 ученика, можно выбрать два дежурных ? Решение. n =24, m=2 5.Формирование умений и навыков в решении комбинаторных задач. При решении комбинаторных задач и выборе типа соединений важно ответить на следующие вопросы: Учитывается ли порядок следования элементов в соединении? Все ли элементы входят в соединение?
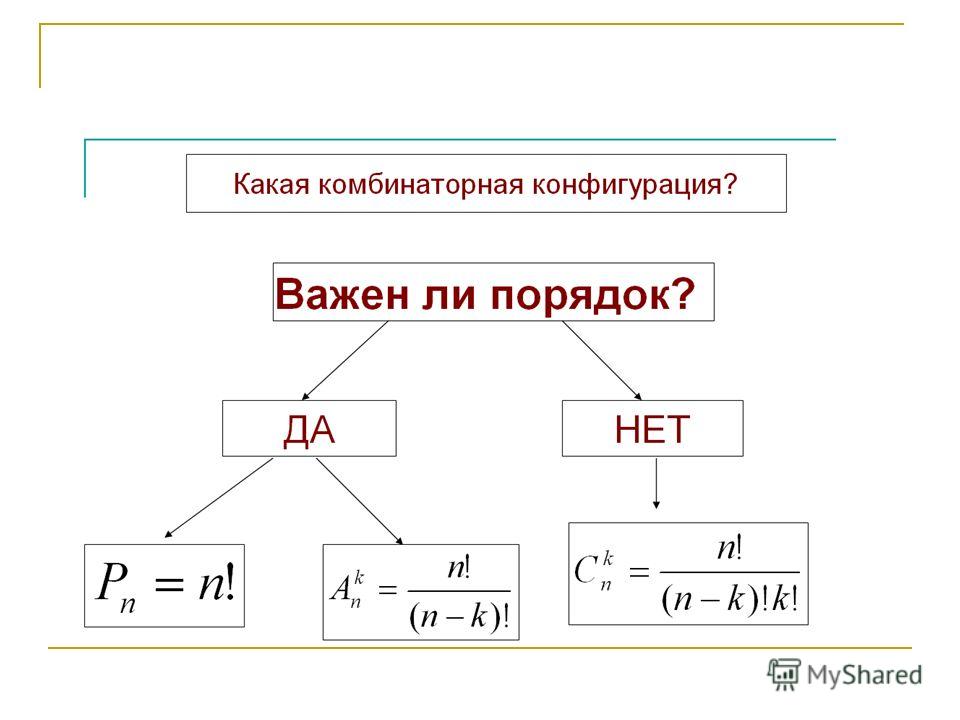
Определить к какому типу относится соединений относится задача. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков? Учитывается ли порядок следования элементов в соединении? ( да) Все ли элементы входят в соединение? (да) Вывод: перестановка В 9«Б» классе 12 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде? Учитывается ли порядок следования элементов в соединении? (нет) Все ли элементы входят в соединение? (на этот вопрос ответ не нужен) Вывод: сочетания 3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными? Учитывается ли порядок следования элементов в соединении? ( да) Все ли элементы входят в соединение? (нет) Вывод: размещение Решить задачи: У нас имеется 5 книг.  Известно, что у нас всего одна полка, и на ней вмещается лишь 3 книги. Сколькими способами можно расставить на полке 3 книги? Известно, что у нас всего одна полка, и на ней вмещается лишь 3 книги. Сколькими способами можно расставить на полке 3 книги?Решение. Учитывается ли порядок следования элементов в соединении? ( да) Все ли элементы входят в соединение? (нет) Вывод: размещение n =5, m=3 Сколькими способами можно расставить 3 тома на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 5 книг? Решение. Учитывается ли порядок следования элементов в соединении? (нет) Все ли элементы входят в соединение? (на этот вопрос ответ не нужен) Вывод: сочетания n =5, m=3 Сколькими способами могут занять I, II, III места 8 участниц финального забега на дистанции 100 м? Решение.  Учитывается ли порядок следования элементов в соединении? (да) Все ли элементы входят в соединение? (нет) Вывод: сочетания n =8, m=3 Вернемся к решению задачи о музыкальном квартете Проказница Мартышка Осёл, Козёл, Да косолапый Мишка Затеяли играть квартет … Стой, братцы стой! – Кричит Мартышка, — погодите! Как музыке идти? Ведь вы не так сидите… И так, и этак пересаживались – опять музыка на лад не идет. Вот пуще прежнего пошли у них разборы И споры, Кому и как сидеть… Сколько различных вариантов расположения музыкантов возможно? Решение. Учитывается ли порядок следования элементов в соединении? ( да) Все ли элементы входят в соединение? (да) Вывод: перестановка Рn = n! =n · (n — 1) · (n – 2) · … · 2 · 1 n =4 Р4 = 4! = 4 · 3 · 2 ·1=24 Задания для групп
Вторая группа
Третья группа
Четвертая группа
Ответы к заданиям Задания для первой группы:
Задания для второй группы:
Задания для третьей группы:
Задания для четвертой группы:
6. Домашнее задание Выучить конспект и формулы. С. 143 № 7,8,9 С. 145 №1,4 С. 145 №5 7. Подведение итогов урока Какие типы соединений вы знаете? В чем отличие перестановок и размещений? В чем отличие размещений и сочетаний? Список литературы Математика автор: Л.П.Стойлова | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определение, формула. Примеры решения задач из комбинаторики
- Размещения без повторений
- Размещения с повторениями
- Примеры
п.
 3=125. }\)
3=125. }\)Всего 125 паролей.
Результат можно получить непосредственно из правила произведения. Действительно, на первой позиции 5 вариантов символов, на второй – 5 вариантов, и на третьей – 5 вариантов. Итого, по правилу произведения: 5 · 5 · 5 = 53 = 125 паролей.
п.3. Примеры
Пример 1. Исследуйте различие между перестановкой без повторений и размещением без повторений 〈3,2〉-выборок для трёх разноцветных фишек. Изобразите полученные решения.
Рассматриваем фишки:
1) Для перестановок, 〈3,3〉-выборок, получаем:
| В каждом ряду – отдельная перестановка. Видно, как образуется факториал. Для каждой отдельной фишки – одна перестановка. Для каждой пары фишек – две перестановки: 2 · 1. Когда добавляем третью, получаем: 3 · 2 · 1 Итого: P3 = 3 · 2 · 1 = 6 перестановок. |
2) Для размещений без повторений, 〈3,2〉-выборок, получаем:
В каждом ряду – отдельное размещение. 3\cdot 9}{2}=8145 } $$ Ответ: 1) 604 800 2) 10 000 000; 3) 10 000; 4) 8145. 3\cdot 9}{2}=8145 } $$ Ответ: 1) 604 800 2) 10 000 000; 3) 10 000; 4) 8145.Рейтинг пользователейза неделю
Помогай другим Отвечай на вопросы и получай ценные призы каждую неделю См. подробности Основные понятия комбинаторики в теории вероятностейЭлементами называются объекты, из которых составлены соединения.Различают следующие три вида соединений: перестановки, размещения и сочетания. Перестановками из n элементов называют соединения, содержащие все n элементов и отличающиеся между собой лишь порядком элементов. Число перестановок из n элементов находится по формуле
Размещениями из n элементами по k в каждом (n > k) называются такие соединения, в каждое из которых входит k элементов, взятых из данных n элементов, и которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Сочетаниями из n элементов по k (n > k) называют соединения, в каждое из которых входит k элементов, взятых из данных n элементов и которые отличаются друг от друга, по крайней мере, одним элементом.
Производящей функцией вероятностей Pn(k) называют функцию, определяемую равенством:
Задача. Устройство состоит из двух независимо работающих элементов. Вероятность безотказной работы (за время t) первого элемента p1=0,8, а второго p2=0,9. Найти вероятности того, что за время t будут работать безотказно: а) 2 элемента, б) 1 элемент, в) ни один из элементов. Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.  Примеры потоков: поступление вызовов на АТС, поступление вызовов на пункт неотложной медицинской помощи, прибытие кораблей в порт, последовательность отказов элементов устройства. Примеры потоков: поступление вызовов на АТС, поступление вызовов на пункт неотложной медицинской помощи, прибытие кораблей в порт, последовательность отказов элементов устройства.
Простейшим называют поток, обладающий свойствами стационарности, отсутствием последействия и ординарности. Свойство стационарности характеризуется тем, что вероятность появления k событий за время длительностью t не зависит от начала отсчета промежутка времени, а зависит лишь от его длительности. Например, вероятности появления пяти событий на промежутках времени (1; 4), (6; 9), (8; 11) одинаковой длительности t = 3 ед. времени равны между собой. Свойство отсутствия последействия характеризуется тем; что вероятность появления k событий на любом промежутке времени не зависит от того, сколько событий появилось до начала рассматриваемого промежутка. Свойство ординарности характеризуется тем, что вероятность появления двух и более событий пренебрежимо мала, сравнительно с вероятностью появления одного события. 
Интенсивностью потока l называют среднее число событий, которые появляются в единицу времени. Доказано, что если известна постоянная интенсивность потока l , то вероятность появления k событий простейшего потока за время длительностью t определяется формулой . Задача. Среднее число заявок, поступающих на АТС в 1 мин равно двум. Найти вероятности того, что за 4 мин поступит а) три вызова, б) менее трёх вызовов, в) не менее трёх вызовов.
Перейти к онлайн решению своей задачи Задание:
Разница между перестановкой и комбинацией (с примером и сравнительной таблицей) В математике вы, возможно, неоднократно слышали понятия перестановки и комбинации, но представляли ли вы когда-нибудь, что это два разных понятия? Принципиальным отличием перестановки от комбинации является порядок предметов, в перестановке порядок предметов очень важен, т. В отличие от этого, в случае комбинации порядок вообще не имеет значения. Не только в математике, но и в практической жизни мы регулярно пользуемся этими двумя понятиями. Хотя мы никогда этого не замечаем. Итак, внимательно прочитайте статью, чтобы узнать, чем отличаются эти два понятия. Содержание: перестановка и комбинация
Сравнительная таблица
Определение перестановкиМы определяем перестановку как различные способы расположения некоторых или всех элементов множества в определенном порядке. Он подразумевает все возможные упорядочивания или перестановки данного набора в различимом порядке. Например, Все возможные перестановки, созданные с помощью букв x, y, z –
Общее количество возможных перестановок n вещей, взятых по r за раз, можно рассчитать как: Определение комбинацииКомбинация определяется как различные способы выбора группы путем взятия некоторых или всех элементы множества без следующего порядка. Например, Все возможные комбинации, выбранные с буквой m, n, o –
Общее количество возможных комбинаций из n вещей, взятых по r за один раз, может быть рассчитано как: Основные различия между перестановкой и комбинациейРазличия между перестановкой и комбинацией четко прочерчены на следующих основаниях:
Пример Предположим, имеется ситуация, когда необходимо узнать общее количество возможных выборок двух из трех объектов A, B, C. Если порядок значим, то вопрос связан с перестановкой, и возможные выборки будут такими: AB, BA, BC, CB, AC, CA. Где AB отличается от BA, BC отличается от CB, а AC отличается от CA. Если порядок не имеет значения, то вопрос связан с комбинацией, и возможные образцы будут AB, BC и CA. ЗаключениеИз приведенного выше обсуждения становится ясно, что перестановка и комбинация — это разные термины, которые используются в математике, статистике, исследованиях и в нашей повседневной жизни. В отношении этих двух концепций следует помнить, что для данного набора объектов перестановка всегда будет выше, чем ее комбинация. Знайте о разнице между перестановкой и комбинацией Перестановка и комбинация являются важными частями подсчета. Подсчет чисел с помощью чистой логики сам по себе является большой задачей.
Здесь мы увидим, как различать перестановку и комбинацию, в чем разница между комбинацией и перестановкой и разница между перестановкой и комбинацией на различных примерах.
Что такое перестановка?Перестановка — это процесс выбора, в котором порядок имеет значение. Перестановку можно просто определить как количество способов упорядочить несколько или все элементы в определенном порядке. Это все о термине Перестановка.
Пример. Перестановки букв в небольшом наборе {a, b, c}: набор или группа n. Обычно это записывается в \[nP_k\].
Формула: \[nP_{k} = \frac{n!}{(n — k)!} = \frac{n(n−1)(n−2)\ldots(n−n +1)}{(n-k)(n-k−1)(n-k−2)\ldots(n-k−n-k+1)} \]
Существует два типа перестановок:
При выборе r чего-либо (числа или любого элемента), имеющего n различных типов, перестановки будут следующими: \[n \times n \times \ldots\] (r times) (другими словами, нет возможностей для первого процесса выбора, ТОГДА нет возможностей для второго процесса выбора и т. , где n — количество элементов для выбора (т. е. набор или сток элементов), и мы выбираем r из них, повторение разрешено, и порядок имеет значение.
Без повторения наш выбор каждый раз уменьшается.
Давайте возьмем самый простой и широко используемый пример: Сколько различных четырехкарточных комбинаций можно составить из колоды карт?
В этой задаче порядок не имеет значения, так как не имеет значения, в каком порядке мы выбираем карты. Мы начинаем с четырех строк, чтобы представить нашу комбинацию из 4 карт.
Предполагая, что все 52 карты доступны для первого розыгрыша, поместите «52» в первый пробел. Когда вы выбираете карту, это означает, что одна карта уже выбрана, поэтому в следующем розыгрыше выбора будет на одну карту меньше. \[P\binom{n}{r} = nP_{r} = \frac{n!}{(n — k)!} \] По формуле получаем \[P\binom{ 52}{4} = 52P_{4} = \frac{52!}{48!} \] , где n — количество вещей, из которых можно выбирать (т. е. набор или сток элементов), и мы выбираем r из их, никаких повторений и порядок имеет значение.
Что такое комбинация? Комбинация — это способ выбора элементов из большой коллекции, при котором (несходные перестановки) порядок выбора не имеет значения. Мы можем сказать, что в меньших случаях мы сможем подсчитать количество комбинаций. Комбинация относится к комбинации n вещей, взятых k за раз без повторений. Комбинация — это выбор r вещей из набора n вещей без замены и порядок не имеет значения.
\[C\binom{n}{r} = nC_{r} =\frac{nP_r}{r!} = \frac{n!}{r!(n — k)!} \] Давайте возьмем пример и поймем это,
У нас есть три цифры (1,2,3), и мы хотим сделать трехзначное число, Таким образом, следующие числа, которые будут возможны, это 123, 132, 213, 231, 312, 321..
Комбинации дают нам простой способ вычислить, сколькими способами «1 2 3» можно расположить в определенном порядке, и мы это уже видели. Ответ:
3! = 3 \[\times\] 2 \[\times\] 1 = 6
Итак, мы перепечатываем формулу нашей Перестановки, чтобы сократить ее количество способов, которыми объекты могут располагаться по порядку (поскольку нас не интересует их закажи еще).
Разница между перестановкой и комбинацией с примерами Получить разницу между перестановкой и комбинацией не слишком легко и не слишком сложно. Перестановки
Комбинации
Как отличить перестановку от комбинацииПерестановки и комбинации относятся к различным способам выбора объектов из набора, как правило, без замены, для формирования подмножеств (или мы можем сказать количество подмножеств). за комплект). Этот выбор подмножеств называется перестановкой, когда порядок выбора является фактором, и комбинацией, когда порядок не является фактором. (Проще говоря, выбор подмножеств — это перестановка, а не дробный порядок выбора называется комбинацией).
Сходства между перестановкой и комбинацией С точки зрения математических понятий «перестановка» и «комбинация» связаны друг с другом. Комбинация — это подсчет выборок, которые мы делаем из n объектов. Принимая во внимание, что перестановка подсчитывает количество аранжировок из n объектов. Мы должны помнить, что Комбинации делают акцент не на порядке, расположении или размещении, а на выборе. Как учащиеся могут повторять перестановки и комбинации в Веданту?Vedantu — это надежная онлайн-платформа для обучения студентов, которую могут использовать все студенты абсолютно бесплатно. В нем есть соответствующий материал о перестановках и комбинациях для изучения, если кто-то узнает о разнице между перестановками и комбинациями. На этой странице описаны основы каждого из них, а затем описаны сходства и различия. Все расписано доходчиво и простым языком. Объяснено, как происходит подбор музыки, еды, одежды и других предметов быта. Где учащиеся узнают о разнице между перестановками и комбинациями в Интернете? Студенты могут найти то же самое на Vedantu. комбинаторика — Разница между перестановкой и комбинацией?спросил Изменено 6 лет, 10 месяцев назад Просмотрено 75 тысяч раз $\begingroup$ Перестановка: $$P(n,r) = \frac{n!}{(n-r)!}$$ Комбинация: $$C(n,r) = \frac{n!}{(n-r)!r!}$$ Очевидно, вы используете комбинацию, когда порядок не имеет значения .
$\endgroup$ 1 $\begingroup$ Если вы видите, как работают комбинации, значит, вы почти у цели. Скажем, я хочу выбрать 3 буквы из ABCDE. Есть $C(5,3)$ способы сделать это. Но если порядок имеет значение, то некоторые вещи, которые я считал одинаковыми, теперь изменились. Выбор $ABC$ теперь генерирует $ABC,ACB,BAC,BCA,CBA,CAB$ как различных вариантов, которых раньше не было. Сколько существует различных вариантов? Ну, это количество способов, которыми я могу переставить выбранные буквы $r$, то есть $r!$. Итак, если перестановки имеют значение: $$P(n,r)=r!\cdot C(n,r)=\frac{r!n!}{(n-r)!r!}=\frac{n!}{(n-r)! }$$ Перестановки — это количество различных упорядоченных вариантов выбора $r$ элементов из набора $n$. $\endgroup$ $\begingroup$ Я просто хочу продемонстрировать на рисунке разницу между перестановкой и комбинацией. Надеюсь, полезно для вас. $\endgroup$ $\begingroup$ 9{th}$ один. Перемножив все вместе, вы получите ряд возможностей: $$ n(n-1)\cdots (n-r+1)=\frac{n!}{(n-r)!} $$ $\endgroup$ $\begingroup$ Существует некоторая путаница между этими двумя терминами. Слово «перестановка» обычно относится к одному из трех вещей в зависимости от контекста. Это может означать порядок (расположение) множества, как в комбинаторике. Или это может относиться к расположению подмножества заданного размера, как и в комбинаторике. Или это может относиться к ОПЕРАЦИИ ПЕРЕМЕЩЕНИЯ в пространстве
такие операции, как в теории групп, что совсем другое дело. «Комбинация» относится только к составу (электорату) подмножества без понятия порядка. Термин «комбинации» относится к количеству подмножеств заданного размера, содержащих различные составляющие. Комбинаторные значения обоих этих терминов остаются действительными применительно к наборам с повторяющимися элементами. Перестановка (расстановка или перестановка) может применяться к набору или подмножеству, содержащему дубликаты. Но «комбинация» обычно предполагает отдельные элементы в подмножестве, хотя исходный набор может содержать дубликаты. Конечно, если это указано, комбинация также может содержать дубликаты. Наличие дубликатов влияет на комбинаторные формулы для всех из них. $\endgroup$ Твой ответЗарегистрируйтесь или войдите в системуЗарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Опубликовать как гостьЭлектронная почта Требуется, но не отображается Опубликовать как гостьЭлектронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie . Комбинаторика — Разница между формулами перестановки и комбинации для повторения и неКомбинации Формула $$\binom{n}{k} = \frac{n!}{k!(n — k)!}$$ — количество способов выбрать подмножество из $k$ объектов из набора $n$ объектов, то есть количество способов сделать неупорядоченный выбор $k$ объектов из набора $n$ объектов. Пример. Сколькими способами можно выбрать комитет из пяти человек из группы из двенадцати человек? Решение. Поскольку порядок, в котором выбираются члены комитета, не имеет значения, количество таких комитетов равно количеству подмножеств по пять человек, которые могут быть выбраны из группы из двенадцати человек, т.е. $$\binom{12}{5}$$ Примечание. Формула
$$\binom{n}{k}$$
также подсчитывает количество способов, которыми $k$ неразличимых объектов можно поместить в $n$ различных ящиков, если мы ограничены размещением одного объекта в каждом ящике. Перестановки Формула $$P(n, k) = \frac{n!}{(n — k)!}$$ представляет количество способов сформировать последовательность из $k$ различных объектов из набора из $n$ объектов, то есть сделать выборку $k$ объектов из набора из $n$ объектов, когда порядок имеет значение. Пример. Сколькими способами можно выбрать президента, секретаря и казначея французского клуба с двенадцатью членами, если каждый из них занимает не более одной должности? Раствор. Поскольку выбор Андреа в качестве президента, Брюса в качестве секретаря и Клары в качестве казначея отличается от выбора Андреа в качестве президента, Клары в качестве секретаря и Брюса в качестве казначея, порядок выбора имеет значение. Примечание. Формула $P(n, k)$ также подсчитывает количество инъективных (однозначных) функций $$f: \{1, 2, 3, \ldots, k\} \to \{1, 2, 3, \ldots, n\}$$ Примечание. Еще одна интерпретация состоит в том, что $P(n, k)$ – это число способов распределения $k$ различных объектов по $n$ различным ящикам, если в каждый ящик можно положить только один предмет, поскольку важно, какой предмет помещен в какая коробка. Комбинации с повторением Формула
$$\binom{k + n — 1}{n — 1} = \binom{k + n — 1}{k}$$
подсчитывает количество способов, которыми можно выбрать $k$ объектов из $n$ типов объектов, когда разрешено повторение. Пример. Сколькими способами можно выбрать двенадцать шоколадок из шести сортов шоколада? Раствор. Пусть $x_i$ — количество выбранных конфет типа $i$. затем $$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 12$$ которое представляет собой уравнение с целыми неотрицательными числами. Частное решение уравнения соответствует размещению пяти знаков сложения в ряд из двенадцати единиц. Например, $$1 1 1 + + 1 1 1 1 1 + 1 + 1 1 + 1$$ соответствует решению $x_1 = 3$, $x_2 = 0$, $x_3 = 5$, $x_4 = 1$, $x_5 = 2$, $x_6 = 1$. Число таких решений равно $$\бином{12 + 6 — 1}{6 — 1} = \бином{17}{5}$$ так как мы должны выбрать, какие пять из семнадцати позиций, необходимых для двенадцати единиц и пяти знаков сложения, будут заполнены знаками сложения. Примечание. Формула
$$\binom{n + k — 1}{k — 1}$$
также подсчитывает количество способов поместить $k$ неразличимых предметов в $n$ различных ящиков, если каждый ящик может содержать не менее $k$ предметов. Пример. Сколькими способами можно раздать двенадцать неразличимых карандашей шести детям? Раствор. Пусть $x_i$ — количество карандашей, подаренных $i$-му ребенку. затем $$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 12$$ Поскольку мы не обязаны давать карандаш каждому ребенку, это уравнение с целыми неотрицательными числами. Выше мы показали, что это уравнение имеет $$\бином{12 + 6 — 1}{6 — 1} = \бином{17}{5}$$ решения. Примечание. Количество способов разместить $k$ неразличимых предметов в $n$ различных ящиках, если в каждый ящик помещен хотя бы один предмет, равно $$\binom{n — 1}{k — 1}$$ Пример. Сколькими способами можно раздать двенадцать неразличимых карандашей пятерым детям, если каждый ребенок получит хотя бы один карандаш? Раствор. Пусть $x_i$ — количество карандашей, подаренных $i$-му ребенку. затем
$$x_1 + x_2 + x_3 + x_4 + x_5 + x_6 = 12$$
Это уравнение с целыми положительными числами, поскольку каждый ребенок получает хотя бы один карандаш. GRE Math: в чем разница между комбинацией и перестановкой?Крис Леле, , 10 августа 2016 г. , ОБНОВЛЕНО 20 апреля 2019 г., анализ данных GRE, GRE Math Знаете ли вы разницу между перестановкой и комбинацией? Нет? Ты не одинок. Когда дело доходит до анализа данных GRE, комбинации и перестановки становятся бичом многих студентов. Комбинации и перестановкиОдин из способов думать об этом состоит в том, чтобы думать о перестановках как о количестве аранжировок или порядков внутри фиксированной группы. Например, если у меня есть пять учеников, и я хочу выяснить, сколькими способами они могут сесть на пять стульев, я воспользуюсь формулой перестановок. Во-первых, номер в группе фиксированный. Во-вторых, я ищу, сколькими способами я могу «рассадить» учеников на пять стульев. Комбинации , с другой стороны, полезны при выяснении того, сколько групп я могу сформировать из большего числа людей. Чтобы убедиться, что вы понимаете это важное различие, вот три разных сценария. Ваша задача состоит не в том, чтобы решить вопрос, а в том, чтобы определить, используете ли вы комбинации или формулу перестановок для их решения. Комбинация против перестановки: решать вам1. У Джоан дома есть пять панно, которые она хочет раскрасить. У нее есть пять разноцветных красок, и она собирается раскрасить каждую панель в свой цвет. Сколькими способами она может раскрасить пять панелей? 2. Сколько уникальных комбинаций слова МАГУШ можно составить, перепутав буквы? 3. Семь астронавтов пытаются попасть в команду из трех человек для космического полета. Сколько разных летных групп можно сформировать?
Разница между комбинацией и перестановкой: ответы1. Перестановки Она хочет расставить цвета. 2. Перестановки Хорошо, это был небольшой трюк, так как я использовал слово «комбинации». Но это слово я использовал в разговорной речи, а не математически. В этом случае количество букв фиксировано. Мы просто их переставляем. 3. Комбинации Мы выбираем группу из большей группы. Один из способов представить это так: когда вы используете слово «выбирать» в контексте выбора из группы, вы имеете дело с комбинациями. И «выбрать», и «комбинации» начинаются с буквы «С». Из этого правила есть исключение, о котором я расскажу в следующем разделе. Разница между перестановкой и комбинацией: сутьБольшая идея: если вы формируете группу из большей группы и размещение внутри меньшей группы важно, то вы хотите использовать перестановки. Представьте, что группа из 12 спринтеров борется за золотую медаль. Помните, что порядок перестановок является ключевым. Несмотря на то, что первые три места для спринтеров образуют подгруппу, большое значение имеет порядок внутри этой подгруппы, и это разница между золотой, серебряной и бронзовой медалью. Простой способ решить этот вопрос математически — представить, что черточки внизу — это подиум, на котором будет стоять каждый спринтер (хотя черточки находятся на одном уровне): ____ ____ ____ Чтобы узнать количество различных расстановок, спросите себя, сколько спортсменов может стоять на пьедестале почета? Всего у нас 12 спортсменов. А как насчет подиума с серебряной медалью? Теперь у нас на одного спортсмена меньше, так как один уже на пьедестале почета. Таким образом, у нас всего 11 очков за серебряную медаль. Наконец, это оставляет нам 10 спортсменов для бронзовой медали. Математика выглядит так: 12 х 11 х 10 = 1320 Вы могли заметить, что это основной принцип счета. Идея в том, что когда мы ищем общее количество результатов, мы перемножаем числа — или, в данном случае, числа, которые стоят над каждым тире — вместе. Например, если у меня есть шесть пар шорт и четыре пары футболок, и мне интересно, сколько различных комбинаций шорт и футболок я могу надеть, я хочу умножить каждую, а не умножить их: ___4_______ х _____6______ = 24 Я не хочу добавлять их, что дало бы мне 10, неправильный ответ, в данном случае. Причина, по которой я упоминаю фундаментальный принцип подсчета, заключается в том, что некоторые вопросы на самом деле будут сочетать комбинации с фундаментальным принципом подсчета (хотя вы, вероятно, будете чаще использовать фундаментальный принцип подсчета с вопросами о перестановках). Чтобы дать вам представление о том, как комбинации могут проявляться вместе с фундаментальным принципом подсчета, попробуйте ответить на следующий вопрос: В классе миссис Пирсон 4 мальчика и 5 девочек. Первым шагом в решении этой проблемы является определение того, имеем ли мы дело с комбинациями или перестановками. Поскольку я «выбираю» из большей группы, в данном случае из двух отдельных групп, я хочу использовать комбинации. Помните: после того, как мы выбрали 2 мальчиков или 3 девочек, позиция в комитете не имеет значения. То есть либо вы в комитете, либо вне комитета (золотых медалистов здесь нет!) Следующее, на что следует обратить внимание в этой задаче, это то, что из первоначальных 9 учеников, 2 уволенных, один мальчик и одна девочка. Итак, у нас осталось 3 мальчика и 4 девочки. Мы хотим выбрать по два. Поэтому мы должны установить одну комбинацию для мальчиков и одну для девочек. Для мальчиков у нас 3C2, а для девочек 4C2. Это дает нам: 3C2 = 3 и 4C2 = 6 Мой совет — попробовать еще 5 или 6 задач на комбинации/перестановки, чтобы вы могли освоиться. Немного попрактиковавшись, вы сможете справиться с большинством проблем, которые ставит перед вами GRE. Даже если вы пропустили какой-то вопрос — вероятно, потому, что он очень сложный — основ в этом посте должно быть достаточно, чтобы помочь вам понять объяснение этого вопроса, чтобы вы могли правильно задать аналогичный вопрос в будущем.
Примечание редактора. Этот пост был первоначально опубликован в мае 2011 г. и был обновлен для обеспечения свежести, точности и полноты. Автор
← Предыдущий Следующий → Разница между перестановками и комбинациями Вероятность связана со шансом или возможностью того, что событие может произойти или не произойти, если существует «n» возможностей. СобытиеСобытие означает результат эксперимента. Например, когда мы бросаем кубик (бросание кубика — это эксперимент), на верхней грани игрального кубика может выпасть любое число из 1, 2, 3, 4, 5 и 6. Появление любого из этих цифры на кубике — это событие. Как указано выше, вероятность находится в пределах от 0 до 1. Событие, которое обязательно произойдет, имеет вероятность 1 (100%), а событие, которое вообще не может произойти, называется невозможным событием, и его вероятность равна 0,9.0005 Пространство выборкиПространство выборки — это набор всех возможных результатов эксперимента. В приведенном выше примере с бросанием игральной кости набор всех возможных исходов (1, 2, 3, 4, 5, 6) представляет собой выборочное пространство. Другой пример — подбрасывание двух монет или подбрасывание одной монеты два раза. Формула вероятности Самая основная формула для расчета вероятности:
Например, при подбрасывании двух монет мы видим, что общее количество исходов равно 4, из которых орёл выпадает 2 раза (HT, TH). Таким образом, вероятность выпадения одной решки равна P(выпадение одной решки) = 2/4 = 1/2. Перестановки Перестановка – это понятие, означающее расположение заданного набора элементов в определенном порядке. Здесь важна последовательность расположения. Простой способ понять перестановку: если у нас есть какие-то объекты и мы хотим их упорядочить (неважно, какой объект вы выберете первым или последним), то сколькими способами вы можете их упорядочить. Если взять три английских алфавита – p, q и r и мы хотим расположить их, то их можно расположить так (p, q, r), (p, r, q), (q, p, r ), (q, r, p), (r, p, q) и (r, q, p). Возможны только эти шесть вариантов. Теперь расположение слов здесь называется Перестановкой, т.е. возможны только эти шесть перестановок. Формула для нахождения количества перестановок Если даны «n» элементов, из которых мы хотим упорядочить «r» элементов, то количество возможных перестановок или перестановок определяется как,
Посмотрите на несколько примеров в конце этой статьи. Комбинация Комбинация – это понятие, связанное с выбором некоторых элементов из заданного набора элементов. Здесь порядок, в котором выбираются элементы, не важен. Теперь мы рассмотрим концепцию комбинирования дальше. Понятие комбинирования подразумевает выделение некоторых объектов из данных объектов. Например, выбор 11 игроков из большого количества игроков для команды по крикету подпадает под комбинацию (вот и все, только выбор), но какой игрок будет бить первым, кто вторым и так далее, такое расположение игроков попадает под перестановку. Формула для нахождения количества комбинаций Если у нас есть «n» элементов, из которых мы хотим выбрать «r» элементов, то количество возможных комбинаций определяется как n г С = п! / г!(п – г)! В чем разница между комбинациями и перестановками?Определения перестановки и комбинации приведены выше и подробно описаны. Теперь давайте посмотрим на разницу между ними:
Примеры задачВопрос 1: Сколькими способами можно расположить буквы слова СТАТЬЯ, беря по 4 буквы за раз, без повторений, чтобы образовать слова со смыслом или без? Решение:
Вопрос 2: Сколько шестизначных пин-кодов можно составить из цифр от 0 до 9, если каждый пин-код начинается с 48 и ни одна цифра не повторяется? Решение:
Вопрос 3: Из 10 студентов выбрать 4 для поездки. Сколькими способами можно сделать выбор? Решение:
Вопрос 4: В мешке находятся 3 красных, 5 черных , и 4 синих шара. Сколькими способами можно вынуть три шара так, чтобы вынуть все цвета? Решение:
|



 2. Размещения (варианты размещения четырех предметов по трем ячейкам)
2. Размещения (варианты размещения четырех предметов по трем ячейкам) ) жившего в Провансе (Юго-Восточная Франция) Льва Герсонида, или Леви бен Гершона, однако его труд не был известен большинству последующих европейских математиков. В основном элементы комбинаторики были открыты и упорядочены математиками XVII и начала XVIII вв.
) жившего в Провансе (Юго-Восточная Франция) Льва Герсонида, или Леви бен Гершона, однако его труд не был известен большинству последующих европейских математиков. В основном элементы комбинаторики были открыты и упорядочены математиками XVII и начала XVIII вв.

 Попробуйте!
Попробуйте!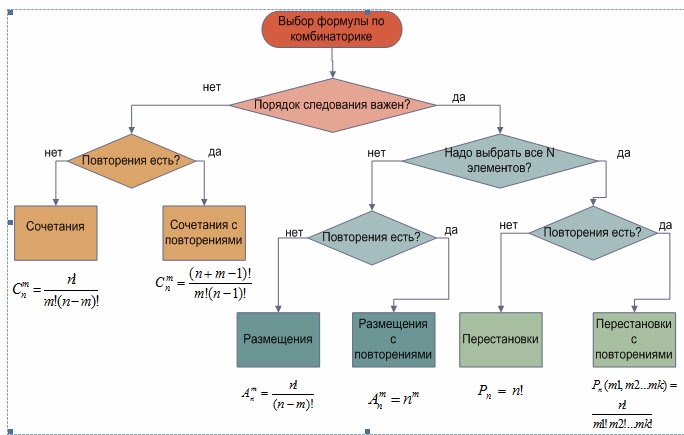


 Оно воспринимается конкретно, посредством знакомства с различными примерами множества. Множество характеризуется объединением некоторых однородных объектов в одно целое. Объекты, образующие множество, называются элементами множества.
Оно воспринимается конкретно, посредством знакомства с различными примерами множества. Множество характеризуется объединением некоторых однородных объектов в одно целое. Объекты, образующие множество, называются элементами множества.
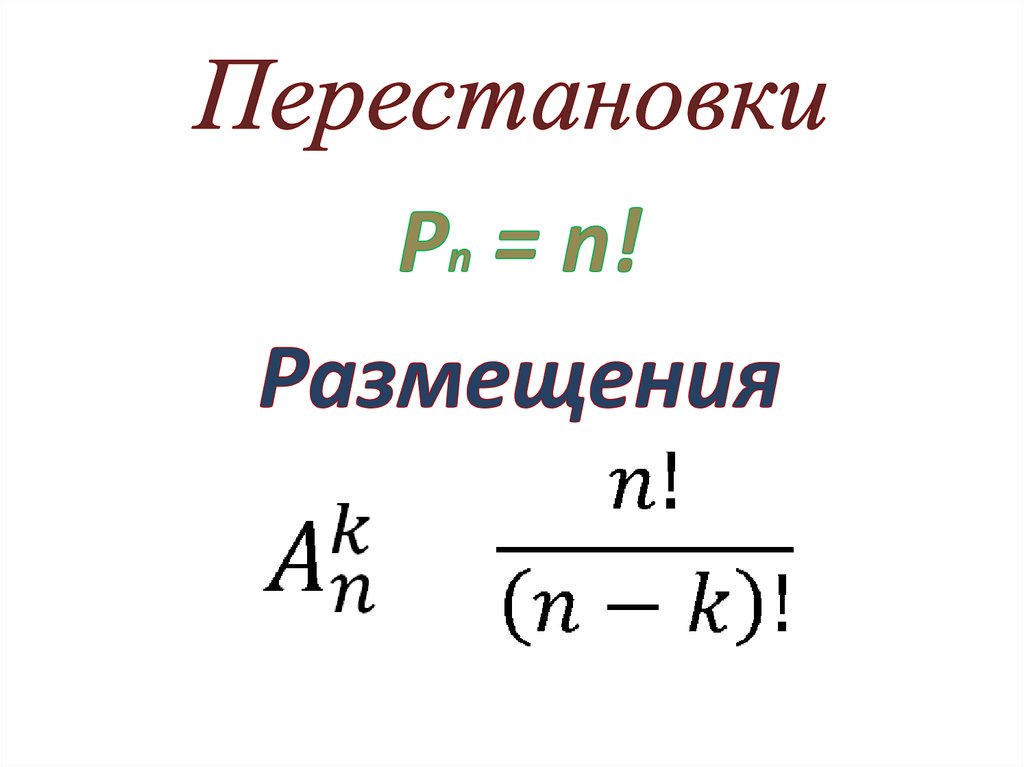 Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Термин «комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем, — всемирно известным немецким учёным.
Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Термин «комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем, — всемирно известным немецким учёным. Сколькими способами можно добраться из города А в город В?
Сколькими способами можно добраться из города А в город В? Тогда обе они могут быть выполнены способами.
Тогда обе они могут быть выполнены способами. По правилу умножения двух девушек можно выбрать 14 ·13 = 182 способами, а двух юношей 6·5 = 30 способами. Следует выбрать двух студентов одного пола: двух студентов или студенток. Согласно правилу сложения таких способов выбора будет N =182 + 30 = 212.
По правилу умножения двух девушек можно выбрать 14 ·13 = 182 способами, а двух юношей 6·5 = 30 способами. Следует выбрать двух студентов одного пола: двух студентов или студенток. Согласно правилу сложения таких способов выбора будет N =182 + 30 = 212. Мы получаем произведение всех целых чисел от n до 1.
Мы получаем произведение всех целых чисел от n до 1.
 .. · n.
.. · n.



 Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?
Сколькими способами теннисисты могут завоевать золото, серебро и бронзу? Сколькими способами это можно сделать
Сколькими способами это можно сделать Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?
Сколькими способами теннисисты могут завоевать золото, серебро и бронзу? Сколькими способами это можно сделать
Сколькими способами это можно сделать е.
е.
 На каждой из пяти одинаковых карточек напечатана одна из следующих букв: а, м, р, т, ю. Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной и расположенных “в одну линию” карточках можно будет прочесть слово “юрта”.
На каждой из пяти одинаковых карточек напечатана одна из следующих букв: а, м, р, т, ю. Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной и расположенных “в одну линию” карточках можно будет прочесть слово “юрта”.
 8*0.9=0.72
8*0.9=0.72
 Следовательно,
Следовательно,  Например, если n=2, то
Например, если n=2, то

 01 = 0.99
01 = 0.99
 Найти вероятность того, что: а) только один снаряд попадёт в цель; б) только два снаряда попадут в цель; в) все три снаряда попадут в цель.
Найти вероятность того, что: а) только один снаряд попадёт в цель; б) только два снаряда попадут в цель; в) все три снаряда попадут в цель.
 9. Из аэровокзала отправились 2 автобуса-экспресса к трапам самолётов. Вероятность своевременного прибытия каждого автобуса в аэропорт равна 0,95. Найти вероятность того, что: а) оба автобуса придут вовремя; б) оба автобуса опоздают; в) только один автобус прибудет вовремя; г) хотя бы один автобус прибудет вовремя.
9. Из аэровокзала отправились 2 автобуса-экспресса к трапам самолётов. Вероятность своевременного прибытия каждого автобуса в аэропорт равна 0,95. Найти вероятность того, что: а) оба автобуса придут вовремя; б) оба автобуса опоздают; в) только один автобус прибудет вовремя; г) хотя бы один автобус прибудет вовремя.
 Предполагается, что поток вызовов – простейший.
Предполагается, что поток вызовов – простейший.
 Найти вероятность того, что в 100 испытаниях событие появится не менее 20 и не более 30 раз.
Найти вероятность того, что в 100 испытаниях событие появится не менее 20 и не более 30 раз.
 е. расположение должно быть в оговоренном порядке количества предметов, взятых только по частям или все сразу.
е. расположение должно быть в оговоренном порядке количества предметов, взятых только по частям или все сразу.

 Комбинация подразумевает несколько способов выбора элементов из большого пула объектов, порядок которых не имеет значения.
Комбинация подразумевает несколько способов выбора элементов из большого пула объектов, порядок которых не имеет значения. В этом вопросе, прежде всего, необходимо понять, вопрос связан с перестановкой или комбинацией, и единственный способ узнать это — проверить, важен ли порядок или нет.
В этом вопросе, прежде всего, необходимо понять, вопрос связан с перестановкой или комбинацией, и единственный способ узнать это — проверить, важен ли порядок или нет.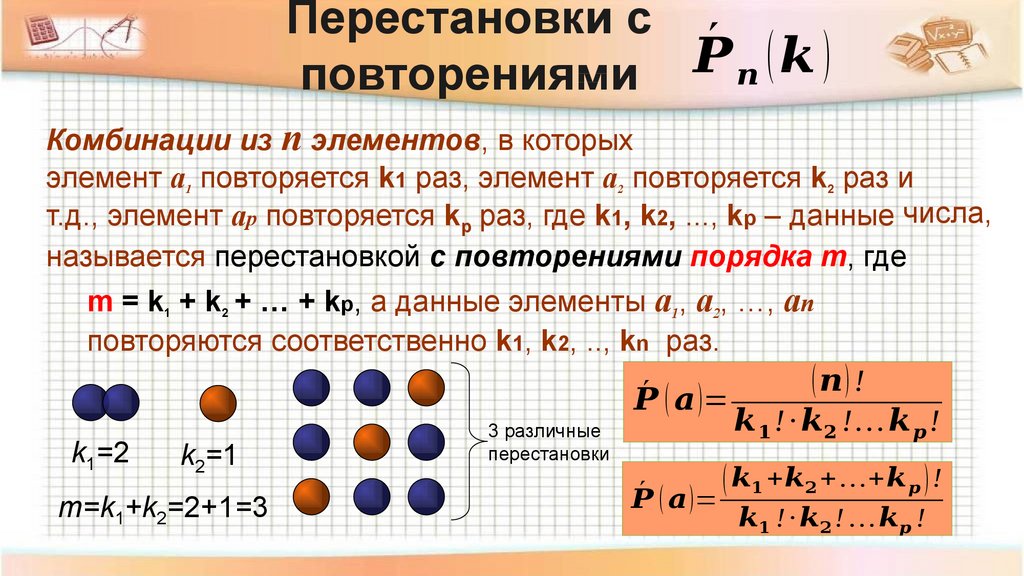 Без подсчета мы не можем решить вероятностные задачи. Вот почему мы изучаем перестановки и комбинации непосредственно перед вероятностью.
Без подсчета мы не можем решить вероятностные задачи. Вот почему мы изучаем перестановки и комбинации непосредственно перед вероятностью. д., и каждый раз умножается.) 9{r}\]
д., и каждый раз умножается.) 9{r}\] Таким образом, во втором бланке будет доступен 51 вариант. Кроме того, в следующем розыгрыше в колоде будет на две карты меньше, так что теперь есть 50 вариантов и так далее. Формула написана:
Таким образом, во втором бланке будет доступен 51 вариант. Кроме того, в следующем розыгрыше в колоде будет на две карты меньше, так что теперь есть 50 вариантов и так далее. Формула написана:
 Мы рассмотрим несколько примеров, чтобы понять разницу между ними.
Мы рассмотрим несколько примеров, чтобы понять разницу между ними.

 Эта страница очень информативна с точки зрения объяснения перестановок и комбинаций. Эта глава имеет решающее значение в математике, и если учащиеся усвоят основы этой темы, они будут хорошо подготовлены к таким темам, как вероятность и статистика позже. Студентам просто нужно войти на портал Vedantu, чтобы получить к ним доступ.
Эта страница очень информативна с точки зрения объяснения перестановок и комбинаций. Эта глава имеет решающее значение в математике, и если учащиеся усвоят основы этой темы, они будут хорошо подготовлены к таким темам, как вероятность и статистика позже. Студентам просто нужно войти на портал Vedantu, чтобы получить к ним доступ. Большой. Я вижу, как комбинация даст вам все возможные комбинации. Однако я не вижу , что именно тогда делает перестановка .
Большой. Я вижу, как комбинация даст вам все возможные комбинации. Однако я не вижу , что именно тогда делает перестановка .

 В этом случае мы выбираем подмножество из $k$ ящиков, которые будут заполнены объектом. 9k$ подсчитывает количество способов разместить $k$ различных объектов в $n$ различных ящиках, если каждый ящик может содержать не менее $k$ объектов, поскольку у нас есть выбор из $n$ ящиков для каждого из $k$ объектов.
В этом случае мы выбираем подмножество из $k$ ящиков, которые будут заполнены объектом. 9k$ подсчитывает количество способов разместить $k$ различных объектов в $n$ различных ящиках, если каждый ящик может содержать не менее $k$ объектов, поскольку у нас есть выбор из $n$ ящиков для каждого из $k$ объектов. Следовательно, президента можно выбрать двенадцатью способами, секретаря — одиннадцатью способами, а казначея — десятью способами. Таким образом, офисы могут быть заполнены
$$12 \cdot 11 \cdot 10 = \frac{12 \cdot 11 \cdot 10 \cdot 9!}{9!} = \frac{12!}{9!} = \frac{12!}{(12 — 3)!} = P(12, 3)$$
способы.
Следовательно, президента можно выбрать двенадцатью способами, секретаря — одиннадцатью способами, а казначея — десятью способами. Таким образом, офисы могут быть заполнены
$$12 \cdot 11 \cdot 10 = \frac{12 \cdot 11 \cdot 10 \cdot 9!}{9!} = \frac{12!}{9!} = \frac{12!}{(12 — 3)!} = P(12, 3)$$
способы.

 Частное решение уравнения соответствует размещению пяти знаков сложения в одиннадцати промежутках между последовательными в ряду из двенадцати единиц.
$$1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1$$
Например,
$$1 1 + 1 1 1 + 1 + 1 1 1 + 1 + 1$$
соответствует решению $x_1 = 2$, $x_2 = 3$, $x_3 = 1$, $x_4 = 3$, $x_5 = 1$, $x_6 = 1$. Количество таких решений — это количество способов, которыми мы можем разместить знак сложения в пяти из одиннадцати пробелов между последовательными знаками в ряду из двенадцати единиц, т. е.
$$\binom{12 — 1} {6 — 1} = \binom{11} {5}$$
Частное решение уравнения соответствует размещению пяти знаков сложения в одиннадцати промежутках между последовательными в ряду из двенадцати единиц.
$$1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1 \квадрат 1$$
Например,
$$1 1 + 1 1 1 + 1 + 1 1 1 + 1 + 1$$
соответствует решению $x_1 = 2$, $x_2 = 3$, $x_3 = 1$, $x_4 = 3$, $x_5 = 1$, $x_6 = 1$. Количество таких решений — это количество способов, которыми мы можем разместить знак сложения в пяти из одиннадцати пробелов между последовательными знаками в ряду из двенадцати единиц, т. е.
$$\binom{12 — 1} {6 — 1} = \binom{11} {5}$$ Тем не менее, за прошедшие годы я заметил, что проблема не столько в том, что они оба, сколько в том, какой из них использовать для конкретной проблемы: вопрос о комбинации или перестановке. Другими словами, учащимся нетрудно определить, является ли вопрос проблемой комбинаций/перестановок. Трудность заключается в том, чтобы точно знать, что это — комбинации или перестановки?
Тем не менее, за прошедшие годы я заметил, что проблема не столько в том, что они оба, сколько в том, какой из них использовать для конкретной проблемы: вопрос о комбинации или перестановке. Другими словами, учащимся нетрудно определить, является ли вопрос проблемой комбинаций/перестановок. Трудность заключается в том, чтобы точно знать, что это — комбинации или перестановки? Например, если я тренер по баскетболу и хочу узнать, сколько различных команд я могу сформировать на основе группы людей, я хочу использовать комбинации.
Например, если я тренер по баскетболу и хочу узнать, сколько различных команд я могу сформировать на основе группы людей, я хочу использовать комбинации. Количество панелей фиксировано. Если бы она выбирала пять панелей из 8, скажем, тогда нам нужно было бы использовать комбинации.
Количество панелей фиксировано. Если бы она выбирала пять панелей из 8, скажем, тогда нам нужно было бы использовать комбинации.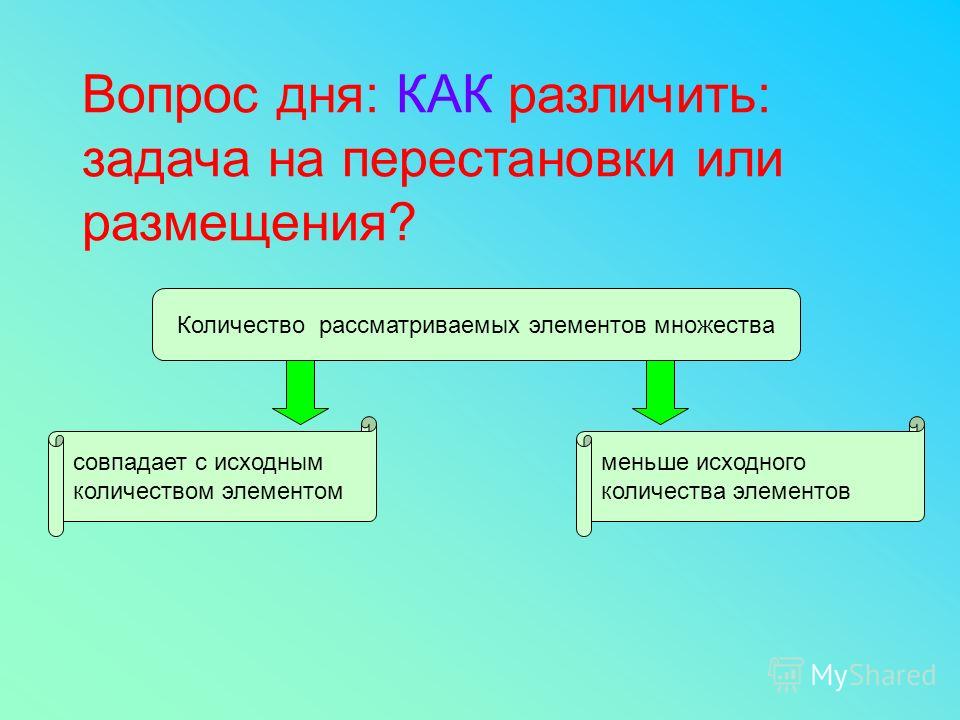 Во время церемонии награждения будут вручены золотая, серебряная и бронзовая медали. Сколькими способами можно раздать эти три медали?
Во время церемонии награждения будут вручены золотая, серебряная и бронзовая медали. Сколькими способами можно раздать эти три медали?
 Она должна выбрать 2 мальчиков и 2 девочек для работы в своей аттестационной комиссии. Если одна девочка и один мальчик уйдут до того, как она сможет сделать выбор, то сколько уникальных комитетов может получиться в результате приведенной выше информации?
Она должна выбрать 2 мальчиков и 2 девочек для работы в своей аттестационной комиссии. Если одна девочка и один мальчик уйдут до того, как она сможет сделать выбор, то сколько уникальных комитетов может получиться в результате приведенной выше информации? 

 Проще говоря, вероятность говорит нам о проценте наступления события. Вероятность может быть выражена числом от 0 до 1 или в процентах.
Проще говоря, вероятность говорит нам о проценте наступления события. Вероятность может быть выражена числом от 0 до 1 или в процентах.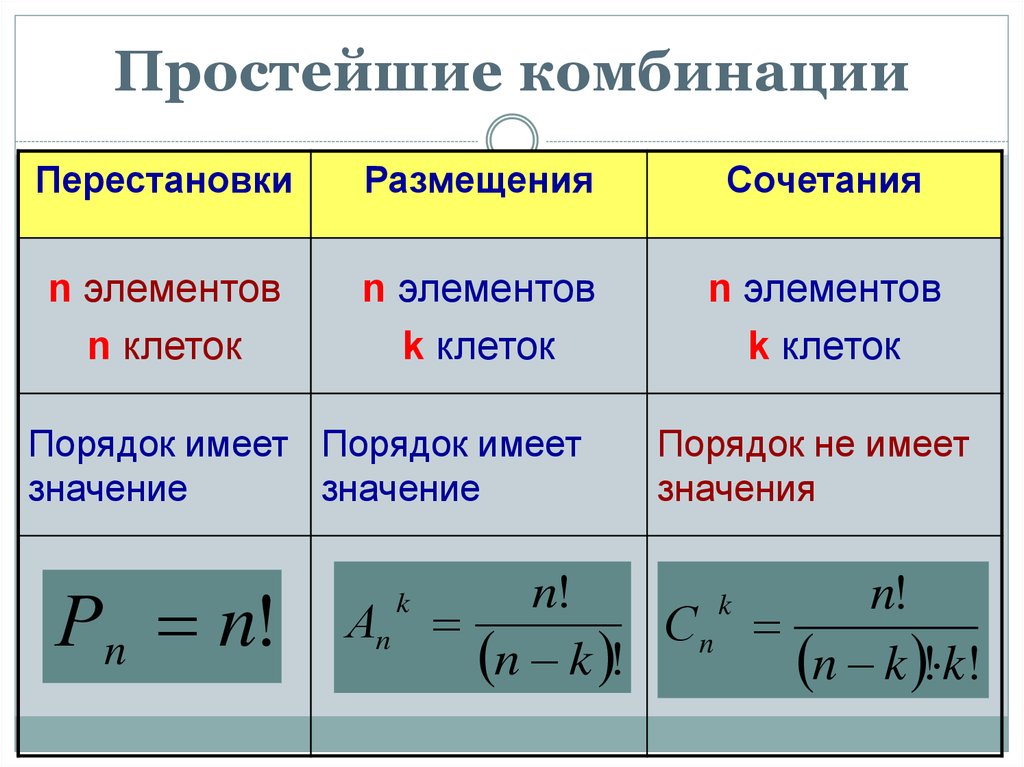 Здесь выборочное пространство равно (HH, HT, TH, TT). Необходимо четко понимать, что сумма вероятностей всех отдельных событий в пространстве выборки всегда равна 1.
Здесь выборочное пространство равно (HH, HT, TH, TT). Необходимо четко понимать, что сумма вероятностей всех отдельных событий в пространстве выборки всегда равна 1. Возьмем пример,
Возьмем пример, Комбинация не связана с расположением выбранных объектов.
Комбинация не связана с расположением выбранных объектов.