Равносильные формулы алгебры высказываний / Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] / 3dstroyproekt.ru
Две формулы алгебры высказываний $A$ и $B$ называются равносильными или эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний.
Равносильность формул будем обозначать знаком $\equiv$, а запись $A\equiv B$ означает, что формулы $A$ и $B$ равносильны.
Например, равносильны формулы:
$\overline { \overline { X } } \equiv X$,
$X\vee X\equiv X$,
Тождественно истинная формула
Формула $A$ называется тождественно истинной { или тавтологией } , если она принимает значение 1 при всех значениях входящих в нее переменных.
Например, тожественно истинны формулы $X\vee \overline { X } $, $X\rightarrow (Y\rightarrow X)$
Тождественно ложная формула
Формула $A$ называется тождественно ложной { или противоречием } , если она принимает значение 0 при всех значениях входящих в нее высказываний.
Например, тождественно ложна формула $X\wedge \overline { X } $
Выполнимая формула
Формула $A$ называется выполнимой, если она принимает значение 1 при всех значениях входящих в нее высказываний.
Например, выполнима формула $X\vee \overline { X } $
Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно.
Группы равносильностей
Между понятиями равносильности и операцией $\leftrightarrow$ существует следующая связь: если формулы $A$ и $B$ равносильны, то формула $A\leftrightarrow B$ — тавтология, и обратно, если формула $A\leftrightarrow B$ — тавтология, то формулы $A$ и $B$ равносильны.
Важнейшие равносильности алгебры высказываний можно разбить на следующие группы.
Равносильности алгебры Буля
Закон двойного отрицания: $\overline { \overline { X } } \equiv X$
Коммутативность: $X\wedge Y\equiv Y\wedge X$; $X\vee Y\equiv Y\vee X$
Ассоциативность: $X\wedge (Y\wedge Z)\equiv (X\wedge Y)\wedge Z$; $X\vee (Y\vee Z)\equiv (X\vee Y)\vee Z$
Дистрибутивность $\wedge$ относительно $\vee$: $X\wedge (Y\vee Z)\equiv (X\wedge Y)\vee (X\wedge Z)$; $(X\vee Y)\wedge Z\equiv (X\wedge Z)\vee (Y\wedge Z)$
Дистрибутивность $\vee $ относительно $\wedge $: $X\vee (Y\wedge Z)\equiv (X\vee Y)\wedge (X\vee Z)$; $(X\wedge Y)\vee Z\equiv (X\vee Z)\wedge (Y\vee Z)$
Законы де Моргана: $\overline { X\wedge Y } \equiv \overline { X } \vee \overline { Y } $; $\overline { X\vee Y } \equiv \overline { X } \wedge \overline { Y } $
Законы поглощения: $X\wedge (Y\vee X)\equiv X$; $X\vee (Y\wedge X)\equiv X$
Законы идемпотентности: $X\wedge X\equiv X$; $X\vee X\equiv X$
Свойства констант: $X\wedge 1\equiv X$; $X\vee 1\equiv 1$; $X\wedge 0\equiv 0$; $X\vee 0\equiv X$
Закон противоречия: $X\wedge \overline { X } \equiv 0$
Закон исключения третьего: $X\vee \overline { X } \equiv 1$
Равносильности, выражающие одни логические операции через другие
$X\leftrightarrow Y\equiv (X\rightarrow Y)\wedge (Y\rightarrow X)$
$X\leftrightarrow Y\equiv (\overline { X } \vee Y)\wedge (\overline { Y } \vee X)$
$X\leftrightarrow Y\equiv (X\wedge Y)\wedge (\overline { Y } \wedge \overline { X } )$
$X\rightarrow Y\equiv \overline { X } \vee Y$
$X\wedge Y\equiv \overline { \overline { X } \vee \overline { Y } } $
$X\vee Y\equiv \overline { \overline { X } \wedge \overline { Y } } $
$X | Y\equiv \overline { X\cdot Y } $
$X \downarrow Y\equiv \overline { X\vee Y } $
$X \rightarrow Y\equiv \overline { X } \vee Y$
$X \bigoplus Y\equiv (X \cdot \bar { Y } )\vee (\bar { X } \cdot Y)$
$X \sim Y\equiv \overline { X \bigoplus Y } \equiv (XY)\vee (\bar { X } \bar { Y } )$
Далее:
Вычисление двойного интеграла
Вычисление криволинейного интеграла второго рода. Примеры.
Примеры.
Вычисление двойного интеграла. Двукратный интеграл
Теорема об аналоге СДНФ в Pk
Вычисление криволинейного интеграла первого рода. Плоский случай
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Класс M. Теорема о замкнутости класса M
Механические приложения криволинейного интеграла 1-го рода
Логические операции над высказываниями
Примеры применения цилиндрических и сферических координат
Равносильные формулы алгебры высказываний
Несобственные интегралы от неограниченной функции
Полином Жегалкина. Пример.
Линейный интеграл и циркуляция векторного поля
Определение криволинейного интеграла второго рода
Огравление $\Rightarrow $
04 сентября 2016, 13:38 проектирование км, кмд, кж Алгебра логики [Г. И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] 0 21960 0
И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] 0 21960 0
1. Основные равносильности.
законы идемпотентности.
— закон противоречия
— закон исключенного третьего
— закон снятия двойного отрицания
законы поглощения
2. Равносильности, выражающие одни логические операции через другие.
1. 4..
2. . 5..
3. . 6..
Здесь 3, 4, 5, 6 – законы Моргана.
Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4, соответственно, если от обеих частей последних взять отрицания и воспользоваться законом снятия двойного отрицания.
Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем одну из них : первую .
Так как при одинаковых
логических значениях x
и y
истинными являются формулы
,
то истинной будет и конъюнкция.
Следовательно, в этом случае обе части
равносильности имеют одинаковые истинные
значения.
Пусть теперь x и y имеют различные логические значения. Тогда будут ложными эквивалентность и одна из двух импликацийили. Но при этом будет ложной и конъюнкция.
Таким образом, и в этом случае обе части равносильности имеют одинаковые логические значения.
Аналогично доказываются равносильности 2 и 4.
Из равносительностей этой группы следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
Дальнейшее исключение логических операций невозможно. Так, если мы будем использовать только конъюнкцию, то уже такая формула как отрицание не может быть выражена с помощью операции конъюнкции.
Однако существуют
операции, с помощью которых может быть
выражена любая из пяти логических
операций, которыми мы пользуемся. Такой
операцией является, например, операция
“Штрих Шеффера”.
x | y | xy |
1 | 1 | 0 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 1 |
3. Равносильности, выражающие основные законы алгебры логики.
2. — коммутативность дизъюнкции.
3. — ассоциативность конъюнкции.
— ассоциативность конъюнкции.
4. — ассоциативность дизъюнкции.
5. — дистрибутивность конъюнкции относительно
дизъюнкции.
6. — дистрибутивность дизъюнкции относительно
конъюнкции.
4. Дополнительные законы.
1. Закон склеивания (расщепления).
, ;
, .
2. Законы поглощения.
; .
3. Закон Блейка- Порецкого.
.
4. Закон свертки логического выражения (СЛВ).
.
5. Закон двойственности.
Определение.
Формулы А и А*называются двойственными, если формула А*получается из формулы А путем замены в ней каждой операции на двойственную.
Имеет место следующий
закон двойственности: если формулы А и
В равносильны, то равносильны и им
двойственные формулы, т.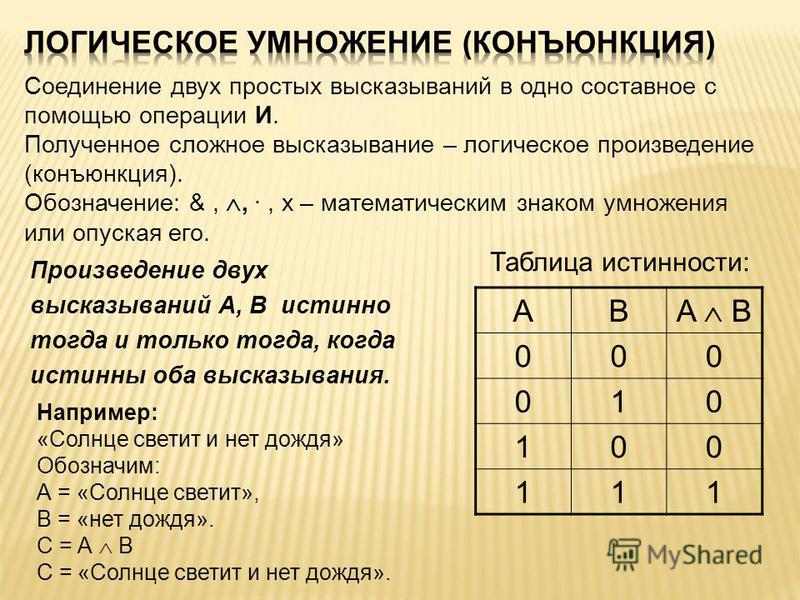 е. А*В*.
е. А*В*.
Равносильные преобразования формул.
Используя равносильности, приведенные в §4, можно часть формулы или всю формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными. (Аналог тождественным преобразованиям в арифметике, алгебре и тригонометрии).
Равносильные преобразования используются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
Формула А считается проще равносильной ей формулы В, если она содержит меньше букв, меньше логических операций. При этом обычно операции эквивалентность и импликация заменяются операциями дизъюнкция и конъюнкция, а отрицание относят к элементарным высказываниям.
Для удобства
использования и ссылок при проведении
равносильных преобразований перечень
наиболее часто употребляемых
равносильностей (законов логических
операций над высказываниями) можно
свести в единую таблицу (см. следующий
лист), в которой рассмотренные выше
равносильности даны в сквозной нумерации.
следующий
лист), в которой рассмотренные выше
равносильности даны в сквозной нумерации.
При проведении равносильных преобразований каждый шаг основывается на использовании того или иного закона. Номер соответствующей формулы (из общей таблицы) мы будем указывать над знаком равносильности, предшествующим очередному шагу.
Рассмотрим ряд примеров равносильных преобразований.
Пример 1. Доказать равносильность .
6-10.
Нормальные формы функций.
При решении ряда задач, связанных с использованием формул алгебры высказываний, важную роль играют формулы, построенные особым образом из высказывательных переменных с помощью только операций дизъюнкции, конъюнкции и отрицания и называемые ДИЗЪЮНКТИВНЫМИ и КОНЪЮНКТИВНЫМИ НОРМАЛЬНЫМИ ФОРМАМИ (ДНФ и КНФ).
8.1 Элементарные дизъюнкции и конъюнкции.
Пусть задана система высказывательных переменных
(x1,x2,…,xn). (1)
(1)
Элементарной дизъюнкцией высказывательных переменных из системы (1) называется дизъюнкция некоторых высказывательных переменных этой системы или их отрицаний.
ЭЛЕМЕНТАРНОЙ КОНЪЮНКЦИЕЙ называется конъюнкция некоторых высказывательных переменных этой системы или их отрицаний.
Если в элементарную дизъюнкцию (конъюнкцию) входит каждое высказывательное переменное из системы (1) (с отрицанием или без него) и притом только один раз, то она называется ПОЛНОЙ ЭЛЕМЕНТАРНОЙ ДИЗЪЮНКЦИЕЙ (КОНЪЮНКЦИЕЙ).
Из “n”
высказывательных переменных можно
образовать 2n всевозможных неэквивалентных полных
элементарных дизъюнкций и столько же
полных элементарных конъюнкций. Каждая
полная элементарная дизъюнкция
только для одного варианта значений
высказывательных переменных системы
(1) принимает значение, равное нулю, а
именно – когда каждое высказывательное
переменное xi,
не находящееся в
под знаком отрицания, равно нулю, а
каждое отрицательное – единице.
Систему значений высказывательных переменных, для которой данная полная элементарная дизъюнкция принимает значение, равное нулю, назовем нулем этой полной элементарной дизъюнкции.
Так, нулями элементарных дизъюнкций (2) являются: (0,0,0), (0,0,1), (0,1,0), (1,0,0), (0,1,1), (1,0,1), (1,1,0), (1,1,1).
Если обратиться к полным элементарным конъюнкциям, то можно обнаружить, что каждая из них только один раз принимает значение, равное единице – когда неотрицаемое переменное равно единице, а отрицаемое – нулю. Такую систему значений высказывательных переменных назовем ЕДИНИЦЕЙ соответствующей ПОЛНОЙ ЭЛЕМЕНТАРНОЙ КОНЪЮНКЦИИ.
3. Равносильные формулы алгебры логики
Формула Хназываетсятождественно истинной
(или тавтологией),если она превращается
в истинное высказывание, то есть принимает
значение 1, при всех наборах значений
входящих в нее переменных. Тавтологии
представляют собой схемы построения
истинных высказываний, независимо от
содержания и истинности составляющих
элементарных высказываний.
Формула Хназываетсятождественно ложной
Две формулы алгебры логики XиYназываютсяравносильными, если при любых значениях входящих в них высказывательных переменных логические значения высказываний, получающихся из формулXиY, совпадают. Для указания равносильности формул используют обозначение.
Существует тесная связь между понятием равносильности формул и понятием тавтологии.
Признак равносильности формул.Две формулыXиYалгебры высказываний равносильны тогда и только тогда, когда формулаявляется тавтологией, и обратно, если формула– тавтология, то формулыXиYравносильны.
Отношение равносильности между формулами алгебры высказываний:
а) рефлексивно: ;
б) симметрично: если , то ;
в) транзитивно:
если
и,
то.
3.2 Примеры равносильных формул.Равносильности формул алгебры логики часто называютзаконами логики.
Вот наиболее важные из них:
–закон тождества.
–закон противоречия.
–закон исключенного третьего.
–закон двойного отрицания.
.
.
.
.
; – законы идемпотентности.
; – законы поглощения.
; – законы склеивания.
законы коммутативности (переместительности):
–коммутативность конъюнкции;
–коммутативность дизъюнкции.
законы ассоциативности (сочетательности):
–ассоциативность конъюнкции;
–ассоциативность
дизъюнкции.
законы дистрибутивности (распределительности):
–дистрибутивность конъюнкции относительно дизъюнкции;
–дистрибутивность дизъюнкции относительно конъюнкции.
; – законы де Моргана.
Доказать эти равносильности можно, например, с помощью таблиц истинности.
Пример.
Докажем равносильность – закон де Моргана. При любых комбинациях значений, от которых зависят формулыXиY, эти формулы принимают некоторые логические значения. Всего будет четыре способа распределения логических значенийXиY. Надо показать, что в каждом из этих случаев значения левой и правой части равносильностисовпадают.
X | Y | ||||||
0 | 0 | 1 | 1 | 0 | 1 | 1 | |
0 | 1 | 1 | 0 | 0 | 1 | 1 | |
1 | 0 | 0 | 1 | 0 | 1 | 1 | |
1 | 1 | 0 | 0 | 1 | 0 | 0 |
Логические
значения в последних двух столбцах
совпадают, следовательно, закон де
Моргана справедлив.
Имеют место равносильности, выражающие одни логические операции через другие.
Импликация выражается через:
–дизъюнкцию и отрицание;
–конъюнкцию и отрицание.
Эквиваленциявыражается через:
–конъюнкцию и импликацию;
–конъюнкцию, дизъюнкцию и отрицание;
–конъюнкцию и отрицание.
Из этих равносильностей следует вывод, что любую формулу алгебры логики можно заменить равносильной ей формулой, которая будет содержать только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. Дальнейшее исключение логических операций невозможно.
Существует
логическая операция, через которую
можно выразить любую из пяти логических
операций, которыми мы пользуемся:
отрицание, конъюнкция, дизъюнкция,
импликация, эквиваленция. Эта операция
называется «штрих
Шеффера»,
обозначается символом
и определяется таблицей истинности
Эта операция
называется «штрих
Шеффера»,
обозначается символом
и определяется таблицей истинности
X | Y | |
1 | 1 | 0 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 1 |
Согласно таблице, имеем: ;.
Тема 2 Формулы алгебры логики
2.1 Равносильные формулы алгебры логики
2.2 Законы алгебры логики
Как и в элементарной математике из «элементарных» булевых функций с помощью логических операций можно строить формулы. В настоящем разделе изучаются формулы алгебры логики.
В настоящем разделе изучаются формулы алгебры логики.
2.1 Равносильные формулы алгебры логики. Приведем определение формулы алгебры логики.
1) каждая «элементарная» булева функция – формула;
2) если некоторое выражение N есть формула, то тоже формула;
3) если некоторые выражения M и N есть формулы, то выражения , , , тоже формулы;
4) других формул, кроме построенных по п. п.1), 2), 3), нет.
Формулы алгебры логики мы будет обозначать большими N, M, … Например, следующие выражения являются формулами алгебры логики:
, .
С целью упрощения формул, условимся, что операция конъюнкции «сильнее» операции дизъюнкции, импликации и эквивалентности, т. е. если нет скобок, то вначале выполняется операция конъюнкции.
Формула алгебры логики определяет некоторую булеву функцию, значение которой совпадает со значениями данной формулы для всех наборов значений переменных.
Две формулы N и M называются Равносильными, если они определяют одну и ту же булеву функцию (запись N=M будет означать, что формулы N и M равносильны).
Пример 1. Формулы и равносильны, т. е. .
Действительно, построим таблицы истинности для данных формул.
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Из таблицы видно, что формулы и определяют одну и ту же булеву функцию и, следовательно, являются равносильными.
Очевидно, что отношение равносильности формул алгебры логики является:
1. рефлексивным, т. е. N=N для любой формулы N;
2. симметричным, т. е. если N=M, то M=N для любых формул N и M;
3. транзитивным, т. е. если N=M и M=J, то N=J для любых формул N, M,J.
Таким образом, отношение равносильности является отношением эквивалентности.
Если какую-нибудь формулу N1, являющуюся частью формулы N заменить формулой N2, равносильной N1, то полученная формула окажется равносильной N. Это свойство лежит в основе преобразования формул с целью их упрощения или приведения к определенной форме.
При преобразовании формул алгебры логики используются свойства логических операций, которые будут рассмотрены ниже.
2.2 Законы алгебры логики. Приведем перечень важнейших равносильностей (законов) алгебры логики. Эти равносильности выражают свойства логических операций.
1. — закон тождества;
2. — закон противоречия;
3. — закон исключительного третьего;
4. — закон двойного отрицания;
— закон двойного отрицания;
5. , — законы идемпотентности;
6. , — законы коммутативности;
7. , — законы дистрибутивности;
8. , — законы ассоциативности;
9. , — законы де Моргана;
10. ,
11. ,
12. , — законы поглощения;
13. , — законы склеивания.
Перечисленные законы алгебры логики доказываются с помощью таблицы истинности. В качестве примера докажем справедливость закона .
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Из таблицы видно, что формулы и определяют одну и ту же булеву функцию.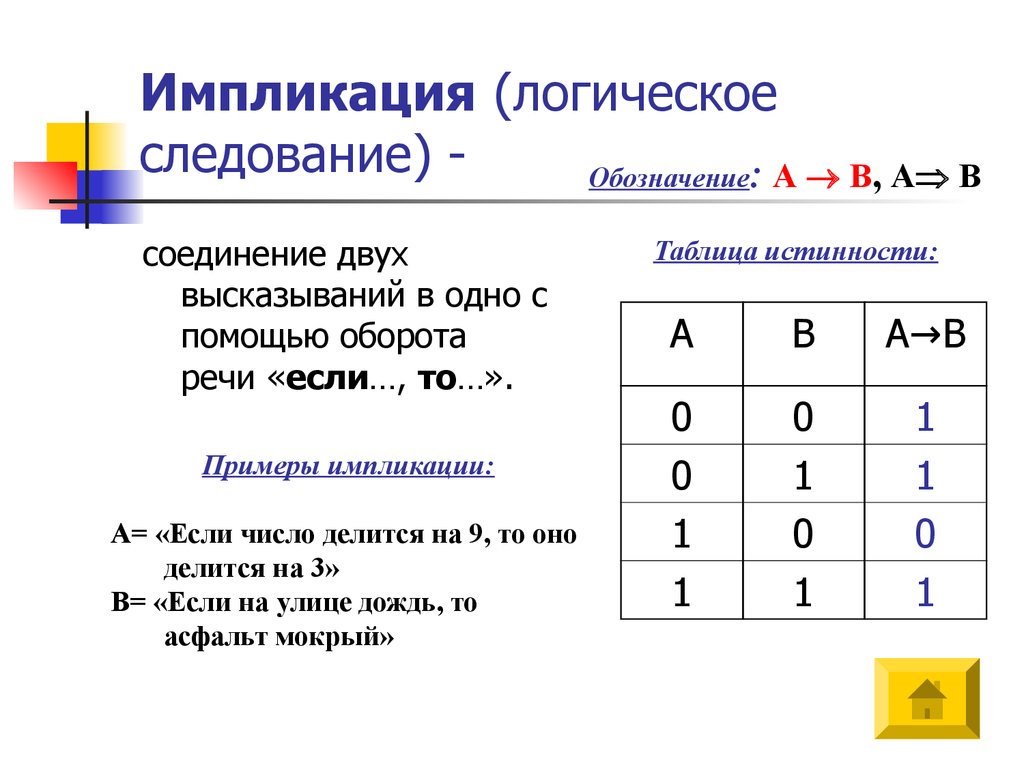 Следовательно, они равносильны.
Следовательно, они равносильны.
Логические операции – конъюнкция, дизъюнкция, импликация и эквивалентность, вообще говоря, не являются независимыми друг от друга. В самом деле,
,
,
Первые две равносильности легко доказываются с помощью таблиц истинности. Две последние равносильности докажем с помощью законов де Моргана и двойного отрицания:
; .
Итак, справедливы следующие утверждения:
1) импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание;
2) конъюнкцию можно выразить через дизъюнкцию и отрицание;
3) дизъюнкцию можно выразить через конъюнкцию и отрицание;
4) все операции посредством равносильных выражений можно заменить двумя: конъюнкцией и отрицанием или дизъюнкцией и отрицанием.
Естественно возникает следующий вопрос. Для чего вводить пять логических операций, когда можно обойтись двумя? Использование лишь двух операций существенным образом усложнило бы запись, что привело бы к громоздким формулам. Однако в некоторых приложениях математической логики удобно ограничиться двумя операциями. Аналогичная ситуация имеет место в арифметике. Всякое натуральное число можно записать с помощью цифр 0 и 1. Однако записи чисел и выкладки в двоичной системе громоздки. К этой системе прибегают лишь в некоторых случаях.
Однако в некоторых приложениях математической логики удобно ограничиться двумя операциями. Аналогичная ситуация имеет место в арифметике. Всякое натуральное число можно записать с помощью цифр 0 и 1. Однако записи чисел и выкладки в двоичной системе громоздки. К этой системе прибегают лишь в некоторых случаях.
Множество булевых функций, рассматриваемое вместе с операциями отрицания, конъюнкции и дизъюнкции, называют Булевой алгеброй. Законы 1-13 являются Основными законами булевой алгебры.
Обратим внимание на характер соответствий между равносильностями, объединенными в пару под номерами (5-13). В этих соответствиях проявляется так называемый закон двойственности.
Назовем формулу алгебры логики Двойственной к формуле , если =.
Будем говорить, что операция конъюнкции двойственна операции дизъюнкции и наоборот.
Как показано в пункте 2.2, всякая формула алгебры логики может быть приведена равносильными преобразованиями к формуле, содержащей только операции конъюнкции, дизъюнкции и отрицания. Поэтому, учитывая законы де Моргана и двойного отрицания, две формулы алгебры логики N и M, содержащие только операции конъюнкции, дизъюнкции и отрицания, будут двойственными, если одна получается из другой заменой каждой операции на двойственную и 1 заменяется на 0, а 0 на 1.
Поэтому, учитывая законы де Моргана и двойного отрицания, две формулы алгебры логики N и M, содержащие только операции конъюнкции, дизъюнкции и отрицания, будут двойственными, если одна получается из другой заменой каждой операции на двойственную и 1 заменяется на 0, а 0 на 1.
Например, формула двойственная к формуле , а формула двойственная к формуле .
Теперь сформулируем закон двойственности.
Теорема 2. Если формулы алгебры логики N и M равносильны, то и двойственные им формулы N* и M* равносильны.
Докажем данный закон. Пусть N(X1,X2,…,XN) = M(X1,X2,…,XN). Согласно определению двойственной формулы
и .
Так как N(X1,X2,…,XN) и M(X1,X2,…,XN) принимают одинаковые значения при любых значениях переменных X1,X2,…,XN, то
=.
Отсюда следует, что
.
Так как формулы и равносильны соответственно формулам и , то они равносильны между собой.
Принцип двойственности позволяет сократить усилие на вывод равносильностей.
Пример 2. Из равносильности вытекает равносильность . Из равносильности вытекает равносильность .
| < Предыдущая | Следующая > |
|---|
Классификация формул алгебры логики. Законы логики.
Классификация формул алгебры логики. Законы логики.
.
Определение. Две формулы алгебры логики A и B называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний (переменных).
Обозначение. A≡B.
Пример.
.
Определение. Формула A называется тождественно истинной (тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных (напр. , ).
, ).
Определение. Формула A называется тождественно ложной (противоречием), если она принимает значение 0 при всех значениях входящих в нее переменных (напр., ).
Утверждение. Отношение равносильности рефлексивно, симметрично, транзитивно.
Связь между понятиями равносильности и эквивалентности: если формулы A и B равносильны, то формула A↔B тавтология, и обратно, если формула A↔B тавтология, то формулы A и B равносильны.
Равносильности алгебры логики можно разбить на 3 группы:
1. Основные равносильности.
· – законы идемпотентности;
· ;
· ;
· ;
· ;
· – закон противоречия;
· – закон исключенного третьего;
· – закон снятия двойного отрицания;
· – законы поглощения.
2. Равносильности, выражающие одни логические операции через другие:
· ;
· ;
· ;
· ;
· ;
· .
Замечание. Из равносильностей группы 2 следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание, или дизъюнкцию и отрицание. Дальнейшее исключение операций невозможно. Например, если использовать только конъюнкцию, то уже такая простая формула, как не может быть выражена с помощью операции конъюнкции.
Существуют операции, с помощью которых может быть выражена любая из 5 логических операций:
1) Связка Шеффера – дизъюнкция отрицаний.
Обозначение. x|y≡ («x не совместно с y»).
Логические значения связки Шеффера описываются следующей таблицей истинности:
x | y | x|y |
1 | 1 | 0 |
1 | 0 | 1 |
0 | 1 | 1 |
0 | 0 | 1 |
Имеют место следующие равносильности: а) ; б) .
2) Стрелка Пирса – конъюнкция отрицаний.
Обозначение. x↓y≡ («ни x, ни y»).
x↓y≡ («ни x, ни y»).
Логические значения стрелки Пирса описываются следующей таблицей истинности:
x | y | x↓y |
1 | 1 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | 1 |
3. Равносильности, выражающие основные законы алгебры логики:
· – коммутативность конъюнкции;
· – коммутативность дизъюнкции;
· – ассоциативность конъюнкции;
· – ассоциативность дизъюнкции;
· – дистрибутивность конъюнкции относительно дизъюнкции;
· – дистрибутивность дизъюнкции относительно конъюнкции.
Замечание. Равносильности группы 3 показывают, что над формулами алгебры логики можно проводить те же преобразования, что и в алгебре чисел.
2
«Алгебра логики». Использование мобильных приложений на уроке информатики
Дисциплина: Информатика.
Цели урока:
Образовательные:
- закрепить знания учащихся по теме «Алгебра логики: основные законы алгебры логики»;
- дать учащимся представление о подходах к пониманию алгебры высказываний;
Воспитательные:
- воспитание самостоятельности, коммуникабельности, формирование понимания значения логики в современном информационном мире;
- сочетание индивидуальной и коллективной работы;
- ответственность за выполнение домашнего задания;
Развивающие:
- развитие познавательного интереса учащихся;
- памяти; внимания; развитие способности применять усвоенные теоретические знания в практической работе;
- развить логическое мышление;
- сформировать практические умения решать логические задачи.

Тип урока: Комбинированный урок.
Межпредметные связи: математика.
Оборудование урока: ПК, мультимедийное оборудование, презентация к уроку на тему «Алгебра логики: таблицы истинности и основные законы алгебры логики», раздаточный материал – карточки с заданиями, электронные таблицы Microsoft Excel, мобильное приложение «Сканер» и «Logic Calculator».
Ход урока
I. Теоретический этапДоброе утро, ребята! На прошлых уроках мы изучили тему «Алгебра логики», на которых познакомились с определениями логика и логическое высказывание и основными логическими операциями, которые задаются таблицами истинности. А также узнали, что в алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Давайте вспомним и повторим материал прошлых уроков? (Повторение пройдённого материала по предыдущей теме проводится в виде кроссворда, вопросы которого зашифрованы в QR-кодах и распечатаны на карточках (Приложение 1, Приложение 2, Приложение 3), для расшифровки, которых необходимо воспользоваться смартфоном с установленным приложением «Сканер QR-кодов». Кроссворд также выведен на экран (Слайд 2)).
Кроссворд также выведен на экран (Слайд 2)).
Интерактивная беседа сопровождается презентацией, содержащей теоретическое описание и иллюстративное отображение изучаемой темы, каждый элемент которых является обобщением или подтверждением некоторого этапа обсуждения, отдельных элементов выполнения решения, обучающихся под руководством преподавателя.
2. Постановка цели и задач урокаСкажите, пожалуйста, для чего нужна логика? Связана ли алгебра логики с появлением первого персонального компьютера? (Студенты должны ответить)
Поначалу алгебра логики не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.
Во-первых, для получения представления об устройстве компьютера необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Теперь мы можем сформулировать цель нашего урока: (Для понимания принципа работы таких элементов нужно изучить основные начальные понятия алгебры логики).
Теперь мы можем сформулировать цель нашего урока: (Для понимания принципа работы таких элементов нужно изучить основные начальные понятия алгебры логики).
Во-вторых, важной составляющей алгоритмов являются логические условия. Вычисление и построение, которых осуществляется в соответствии с законами алгебры логики.
В-третьих, человек с древних времен стремился познать законы правильного мышления, т. е. логические законы. Законы развития есть у природы, общества, любой сложной системы и, конечно же, у самого мышления. Существует даже мнение, что всякое движение нашей мысли, постигающей истину, добро и красоту, опирается на логические законы. Познание истины – одна из важнейших потребностей человека. Каждый человек и человечество в целом стремятся к истине, добру и красоте. Все люди нуждаются в истинном знании, получении новой информации о мире, в котором они живут. Для чего? Для того, чтобы жить, что в данном случае означает ориентироваться в быстро меняющейся обстановке, принимать правильные решения и на их основе совершать правильные действия.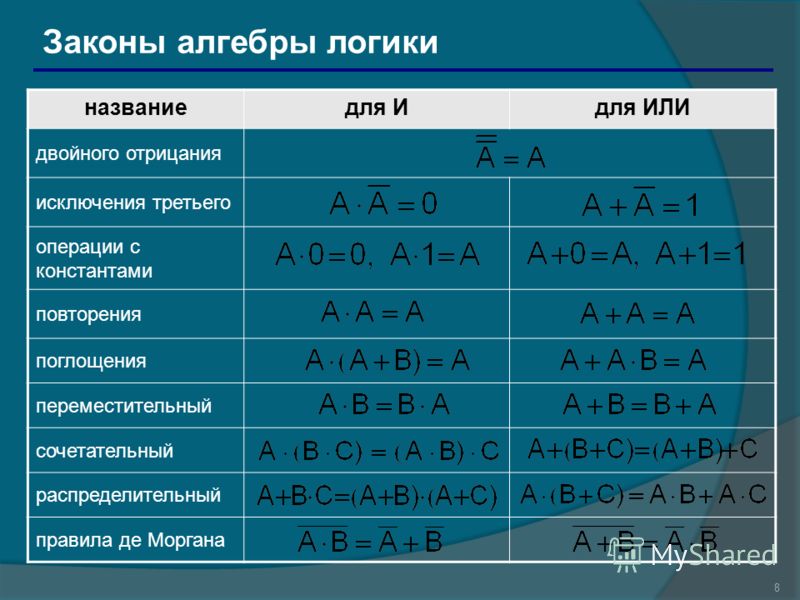
Таким образом, сегодня на уроке мы вспомним понятия основных логических операций и закрепим эти понятия на основе построения таблиц истинности по логическим выражениям с использованием компьютера и мобильного приложения.
3. Объяснение теоретического материалаВ кроссворде мы с вами встретили два имени знаменитых математиков и логиков, которые внесли большой вклад в развитие математической логики. Сейчас я расскажу о них подробнее.
(Слайд 4) Джордж Буль (англ. George Boole; 2 ноября 1815 – 8 декабря 1864) – английский математик и логик. Профессор математики Королевского колледжа Корка с 1849 года. Один из основателей математической логики.
Джордж Буль родился и вырос в семье небогатого ремесленника Джона Буля, увлечённого наукой. Отец, интересуясь математикой и логикой, дал первые уроки своему сыну, но тот не сумел рано обнаружить свои выдающиеся таланты в точных науках, и его первым увлечением стали классические авторы.
Лишь к семнадцати годам Буль дошёл до высшей математики, продвигаясь медленно из-за отсутствия действенной помощи.
С шестнадцати лет Буль начал работать помощником учителя в частной школе в Донкастере и, так или иначе, продолжал преподавание на разных должностях в течение всей жизни. Он был женат (с 1855 г.) на Мэри Эверест (з. Эверест-Буль), племяннице знаменитого географа Джорджа Эвереста, также занимавшейся наукой и преподаванием, а после смерти мужа много сил уделившей популяризации его вклада в логику.
Четыре их дочери снискали известность как учёные (геометр Алисия, химик Люси), или члены учёных семей (Мэри, жена математика и писателя Ч.Г.Хинтона, и Маргарет, мать математика Дж. И. Тейлора), а пятая – Этель Лилиан Войнич – прославилась как писатель.
Буль умер на пятидесятом году жизни от воспаления лёгких.
Огастес (Август) де Мо́рган (англ. Augustus de Morgan, 27 июня 1806 – 8 марта 1871) – шотландский математик и логик, профессор математики в Университетском колледже Лондона. Первый президент (1866) Лондонского математического общества.
Первый президент (1866) Лондонского математического общества.
Основные труды: по математической логике и теории рядов; к своим идеям в алгебре логики Огастес де Мо́рган пришёл независимо от Дж. Буля. В 1847 изложил элементы логики высказываний и логики классов, дал первую развитую систему алгебры отношений. С его именем связаны известные теоретико-множественные соотношения (законы де Моргана).
Законы де Мо́ргана (законы общей инверсии для логического сложения и для логического умножения) – логические правила, связывающие пары логических операций при помощи логического отрицания. И звучат так:
(Слайд 5-6) Общая инверсия двух логических слагаемых равносильна логическому умножению инвертированных переменных:
(A ˅ B) = A &B
Общая инверсия двух логических сомножителей равносильна логическому сложению инвертированных переменных:
(A & B) = A ˅B
Диаграммы Венна, описывающие законы де Моргана представлены на рисунках 1 и 2:
II.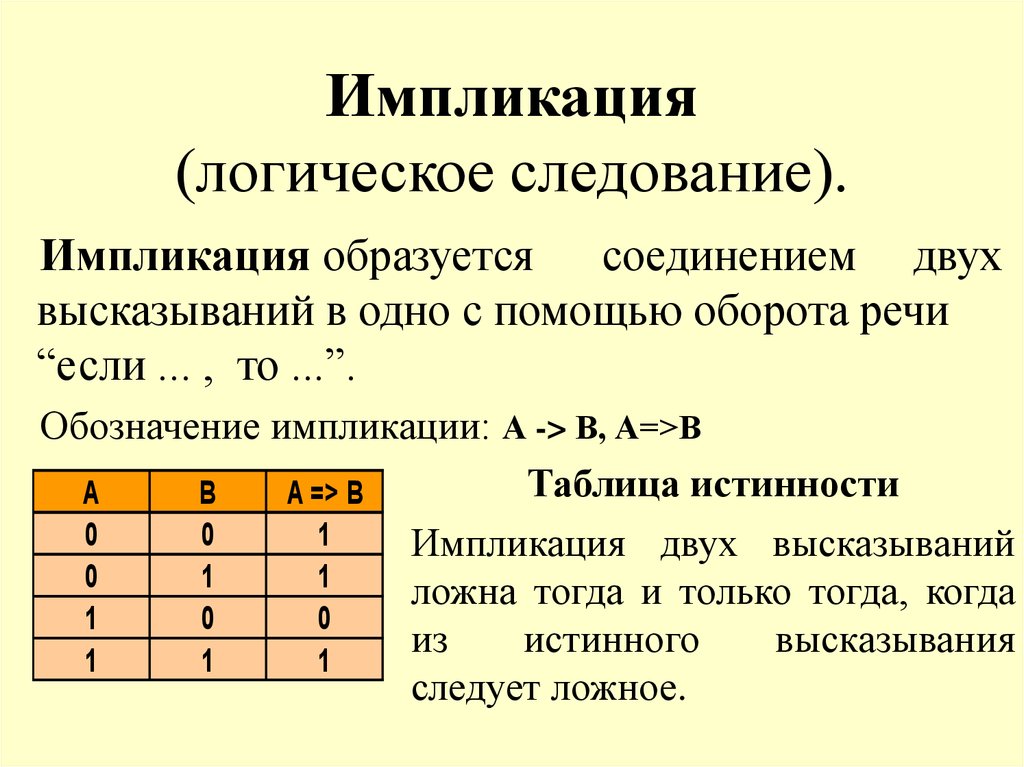 Практический этап Практическое задание №1
Практический этап Практическое задание №1В электронных таблицах доказать справедливость первого (A ˅ B) = A &B и второго (A & B) = A ˅ B законов де Моргана (Слайд 7), используя таблицы истинности (рис.3).
Рис.3
Далее студентам необходимо воспользоваться мобильным приложением Logic Calculator и доказать справедливость первого (A ˅ B) = A &B и второго (A & B) = A ˅ B законов де Моргана, используя приложение Logic Calculator.
1. (A ˅ B) = A &B
2. (A & B) = A ˅ B
Практическое задание №2
В мобильном приложении Logic Calculator построить таблицу истинности логического выражения: (A ˅ B) & (A ˅ B). Ответ записать в тетради.
В мобильном приложении Logic Calculator построить таблицу истинности логического выражения: A & (B ˅ B &C). Ответ записать в тетради.
III. Заключительный этап
- Сообщение о достижении целей урока.
- Оценка работы обучающихся, комментарии.
- Выдача домашнего задания. (Доказать с использованием приложения Logic Calculator равносильность выражений (A ˅ B ˅ C) & (A ˅ B ˅ C) и (B &A & C)
2.5: Логические эквивалентности — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 23239
- Harris Kwong
- Государственный университет Нью-Йорка во Фредонии через OpenSUNY
Тавтология и противоречие
Определение
Тавтология — это предложение, которое всегда истинно, независимо от значений истинности содержащихся в нем пропозициональных переменных.
Определение
Предложение, которое всегда ложно, называется противоречием .
Предложение, которое не является ни тавтологией, ни противоречием, называется случайностью . Термин случайность не так широко используется, как термины тавтология и противоречие.
Пример \(\PageIndex{1}\label{eg:logiceq-01}\)
Из следующей таблицы истинности \[\begin{array}{|c|c|c|c|} \hline p & \overline{p} & p \vee \overline{p} & p \wedge \overline{p} \\ \hline \text{T} & \text{F} & \text{T} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{F} \\ \hline \end{array}\] получаем, что \(p\vee\overline{p}\ ) — тавтология, а \(p\wedge\overline{p}\) — противоречие.
На словах \(p\vee\overline{p}\) говорит, что либо утверждение \(p\), либо утверждение \(\overline{p}\) истинно (то есть \( р\) неверно). Это утверждение всегда верно.
Составное утверждение \(p\wedge\overline{p}\) утверждает, что \(p\) истинно, и в то же время \(\overline{p}\) также истинно (что означает \( р\) неверно). Это явно невозможно. Следовательно, \(p\wedge \overline{p}\) должно быть ложным.
Это явно невозможно. Следовательно, \(p\wedge \overline{p}\) должно быть ложным.
Пример \(\PageIndex{2}\label{eg:logiceq-02}\)
Показать, что \((p \Rightarrow q) \Leftrightarrow (\overline{q} \Rightarrow \overline{p} )\) — тавтология.
- Ответить
Мы можем использовать таблицу истинности для проверки утверждения. \[\begin{array}{|*{7}{c|}} \hline p & q & p\Rightarrow q & \overline{q} & \overline{p} & \overline{q}\Rightarrow\overline {p} & (p \Rightarrow q) \Leftrightarrow (\overline{q} \Rightarrow \overline{p}) \\ \hline \text{T} & \text{T} & \text{T} & \text {T} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{F} & \text{T} & \text{ F} & \text{F} & \text{T} \\ \text{F} & \text{T} & \text{T} & \text{F} & \text{T} & \text{T } & \text{T} \\ \text{F} & \text{F} & \text{T} & \text{T} & \text{T} & \text{T} & \text{T} \\ \hline \end{array}\] Обратите внимание, как мы работаем над каждым компонентом составного оператора отдельно, прежде чем объединить их для получения окончательного ответа.

Пример \(\PageIndex{3}\label{eg:logiceq-03}\)
Показать, что аргумент
«Если \(p\) и \(q\), то \(r\). Следовательно, если не \(r\), то не \(p\) или не \(q\)».
действителен. Другими словами, покажите, что логика, использованная в аргументе, верна.
- Ответить
Символически аргумент выглядит так: \[[(p \wedge q) \Rightarrow r] \Rightarrow [\overline{r} \Rightarrow (\overline{p} \vee \overline{q})]. \label{eqn:tautology}\] Мы хотим показать, что это тавтология. Это легко проверить с помощью таблицы истинности. Мы также можем доказать, что это составное утверждение всегда истинно, показав, что оно никогда не может быть ложным.
Предположим, напротив, что ([уравнение: тавтология]) ложно для некоторых вариантов выбора \(p\), \(q\) и \(r\). Тогда \[(p \wedge q) \Rightarrow r \quad \mbox{должно быть true}, \qquad\mbox{and}\qquad \overline{r} \Rightarrow (\overline{p} \vee \overline{q }) \quad \mbox{должно быть ложным}.
 \] Чтобы второе следствие было ложным, нам нужно, чтобы \[\overline{r} \quad\mbox{было истинным}, \qquad\mbox{and}\qquad \overline{p} \vee \overline{q} \quad\mbox{to be false}.\] Они, в свою очередь, подразумевают, что \(r\) ложно, и оба \(\overline{p}\) и \ (\overline{q}\) ложны; следовательно, и \(p\), и \(q\) верны. Это сделало бы \((p \wedge q) \Rightarrow r\) ложным, что противоречит предположению, что это правда. Таким образом, ([eqn:tautology]) не может быть ложным, это должна быть тавтология.
\] Чтобы второе следствие было ложным, нам нужно, чтобы \[\overline{r} \quad\mbox{было истинным}, \qquad\mbox{and}\qquad \overline{p} \vee \overline{q} \quad\mbox{to be false}.\] Они, в свою очередь, подразумевают, что \(r\) ложно, и оба \(\overline{p}\) и \ (\overline{q}\) ложны; следовательно, и \(p\), и \(q\) верны. Это сделало бы \((p \wedge q) \Rightarrow r\) ложным, что противоречит предположению, что это правда. Таким образом, ([eqn:tautology]) не может быть ложным, это должна быть тавтология.
практическое упражнение \(\PageIndex{1}\label{he:logiceq-01}\)
Используйте таблицу истинности, чтобы показать, что \[[(p \wedge q) \Rightarrow r] \Rightarrow [\ overline{r} \Rightarrow (\overline{p} \vee \overline{q})]\] является тавтологией.
- Ответ
Нам нужно восемь комбинаций значений истинности в \(p\), \(q\) и \(r\). Мы перечисляем значения истинности в соответствии со следующим соглашением.
 В первом столбце для значений истинности \(p\) заполните верхнюю половину T, а нижнюю половину F. В следующем столбце для значений истинности \(q\) повторите тот же шаблон отдельно, с верхней половиной и нижней половиной. Таким образом, мы разделяем верхнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половину F. Аналогичным образом разделяем нижнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половина с F. Повторите тот же шаблон с третьим столбцом для значений истинности \(r\), и так далее, если у нас есть больше пропозициональных переменных.
В первом столбце для значений истинности \(p\) заполните верхнюю половину T, а нижнюю половину F. В следующем столбце для значений истинности \(q\) повторите тот же шаблон отдельно, с верхней половиной и нижней половиной. Таким образом, мы разделяем верхнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половину F. Аналогичным образом разделяем нижнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половина с F. Повторите тот же шаблон с третьим столбцом для значений истинности \(r\), и так далее, если у нас есть больше пропозициональных переменных.Заполните следующую таблицу: \[\begin{array}{|*{11}{c|}} \hline p & q & r & p\wedge q & (p\wedge q)\Rightarrow r & \overline{ r} & \overline{p} & \overline{q} & \overline{p}\vee\overline{q} & \overline{r} \Rightarrow (\overline{p}\vee\overline{q}) & [(p \клин q) \Rightarrow r] \Rightarrow [\overline{r}\Rightarrow(\overline{p} \vee \overline{q})] \\ \hline \text{T} & \text{T } & \text{T} &&&&&&&& \\ \text{T} & \text{T} & \text{F} &&&&&&&&& \\ \text{T} & \text{F} & \text{T} &&&&&&&& \\ \text{T} & \text{F} & \text{F} &&&&&&&& \\ \text{F} & \text{T} & \text{T} &&&&&&&& & \\ \text{F} & \text{T } & \text{F} &&&&&&&& \\ \text{F} & \text{F} & \text{T} &&&&&&&&& \\ \text{F} & \text{F} & \text{F} &&&&&&&& \\ \hline \end{array}\] Вопрос: Если в предложении четыре пропозициональных переменных, сколько строк в таблице истинности?
Биусловность и эквивалентность
Примечание
Две логические формулы \(p\) и \(q\) логически эквивалентны , обозначены \(p\equiv 90,\) 2.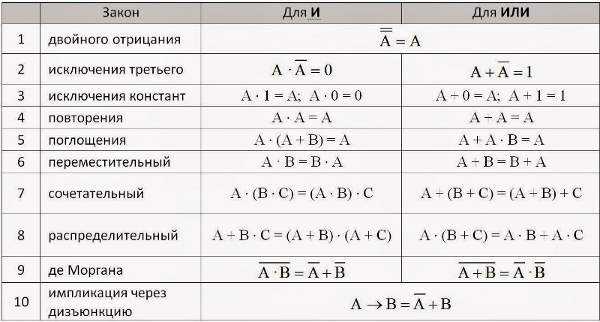 2) тогда и только тогда, когда \(p \Leftrightarrow q\) является тавтологией.
2) тогда и только тогда, когда \(p \Leftrightarrow q\) является тавтологией.
Мы , а не , говоря, что \(p\) равно \(q\). Поскольку \(p\) и \(q\) представляют два разных оператора, они не могут быть одинаковыми. Мы говорим о том, что они всегда дают одно и то же значение истинности, независимо от значений истинности лежащих в их основе пропозициональных переменных. Вот почему мы пишем \(p\equiv q\) вместо \(p=q\).
Пример \(\PageIndex{4}\label{eg:logiceq-04}\)
Мы узнали, что \[p\Leftrightarrow q \equiv (p\Rightarrow q) \wedge (q\Rightarrow p), \] именно поэтому мы называем \(p\Leftrightarrow q\) биусловным оператором.
Пример \(\PageIndex{5}\label{eg:logiceq-05}\)
Используйте таблицы истинности для проверки следующих эквивалентных утверждений.
- \(p \Rightarrow q \equiv \overline{p} \vee q\). [эквив1]
- \(p \клин (q \vee r) \equiv (p \клин q) \vee (p \клин r)\). [экв2]
- Ответить
Таблицы истинности для (а) и (б) изображены ниже.
 \[\begin{array}{|*{5}{c|}} \hline p & q & p\Rightarrow q & \overline{p} & \overline{p}\vee q \\ \hline \text{ T} & \text{T} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{F} & \text{F } & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{T} \\ \text{F} & \text{F } & \text{T} & \text{T} & \text{T} \\ \hline \end{массив}\] \[% \arraygap{1.25} \begin{массив}{|*{8}{ c|}} \hline p & q & r & q\vee r & p\клин (q\vee r) & p\клин q & q\клин r & (p\клин q)\vee(p\клин r ) \\ \hline \text{T} & \text{T} & \text{T} & \text{T} & \text{T}\phantom{(q\vee{})} & \text{T } & \text{T} & \text{T} \\ \text{T} & \text{T} & \text{F} & \text{T} & \text{T}\phantom{(q\ vee{})} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{T} & \text{T} & \ text{T}\phantom{(q\vee{})} & \text{F} & \text{T} & \text{T} \\ \text{T} & \text{F} & \text{ F} & \text{F} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{F}\phantom{(q\v ee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{F} & \text{T} & \ text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{ T} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{F} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text {F} \\ \hline \end{array}\] Пример ([equiv1]) является важным результатом.
\[\begin{array}{|*{5}{c|}} \hline p & q & p\Rightarrow q & \overline{p} & \overline{p}\vee q \\ \hline \text{ T} & \text{T} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{F} & \text{F } & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{T} \\ \text{F} & \text{F } & \text{T} & \text{T} & \text{T} \\ \hline \end{массив}\] \[% \arraygap{1.25} \begin{массив}{|*{8}{ c|}} \hline p & q & r & q\vee r & p\клин (q\vee r) & p\клин q & q\клин r & (p\клин q)\vee(p\клин r ) \\ \hline \text{T} & \text{T} & \text{T} & \text{T} & \text{T}\phantom{(q\vee{})} & \text{T } & \text{T} & \text{T} \\ \text{T} & \text{T} & \text{F} & \text{T} & \text{T}\phantom{(q\ vee{})} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{T} & \text{T} & \ text{T}\phantom{(q\vee{})} & \text{F} & \text{T} & \text{T} \\ \text{T} & \text{F} & \text{ F} & \text{F} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{F}\phantom{(q\v ee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{F} & \text{T} & \ text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{ T} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{F} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text {F} \\ \hline \end{array}\] Пример ([equiv1]) является важным результатом. Он говорит, что \(p \Rightarrow q\) истинно, когда происходит одно из следующих двух событий: (i) когда \(p\) ложно, (ii) в противном случае (когда \(p\) истинно) \(q \) должно быть правдой.
Он говорит, что \(p \Rightarrow q\) истинно, когда происходит одно из следующих двух событий: (i) когда \(p\) ложно, (ii) в противном случае (когда \(p\) истинно) \(q \) должно быть правдой.
Практическое упражнение \(\PageIndex{2}\label{he:logiceq-02}\)
Используйте таблицы истинности для установления этих логических эквивалентностей.
- \(p \Стрелка вправо q \equiv \overline{q} \Стрелка вправо \overline{p}\)
- \(p \vee p \equiv p\)
- \(p \клин q \equiv \overline{\overline{p} \vee \overline{q}}\)
- \(p \Стрелка влево q \equiv (p \Стрелка вправо q) \клин (q \Стрелка вправо p)\)
- Ответить
Мы накрыли стол для (а), а остальное предоставим вам.
\[\begin{array}[t]{|c|c|c|c|c|c|} \hline p & q & p\Стрелка вправо q & \overline{q} & \overline{p} & \ overline{q}\Rightarrow\overline{p} \\ \hline \text{T} & \text{T} &&&& \\ \text{T} & \text{F} &&&& \\ \text{F} & \ текст{T} &&&& \\ \text{F} & \text{F} &&&& \\ \hline \end{массив}\]
практическое упражнение \(\PageIndex{3}\label{he:logiceq-03}\)
Логическая связка исключающее ИЛИ, обозначаемая \(p\veebar q\), означает либо \(p\ ) или \(q\), но не оба вместе. Следовательно, \[p\veebar q \equiv (p\vee q) \wedge \overline{(p\wedge q)} \equiv (p\wedge\overline{q}) \vee (\overline{p}\wedge q).\] Постройте таблицу истинности для проверки этого утверждения
Следовательно, \[p\veebar q \equiv (p\vee q) \wedge \overline{(p\wedge q)} \equiv (p\wedge\overline{q}) \vee (\overline{p}\wedge q).\] Постройте таблицу истинности для проверки этого утверждения
Свойства
Свойства логической эквивалентности. Обозначим через \(T\) и \(F\) тавтологию и противоречие соответственно. Имеются следующие свойства для любых пропозициональных переменных \(p\), \(q\) и \(r\).
Коммутативные свойства : \(\begin{array}[t]{l} p \vee q \equiv q \vee p, \\ p \wedge q \equiv q \wedge p. \end{array} \)
Ассоциативные свойства : \(\begin{array}[t]{l} (p \vee q) \vee r \equiv p \vee (q \vee r), \\ (p \wedge q) \клин г \эквив п \клин (q \клин г).\end{массив}\)
Распределительные законы : \(\begin{array}[t]{l} p \vee (q \wee r) \equiv (p \vee q) \wedge (p \vee r), \\ p \клин (q \vee r) \equiv (p \клин q) \vee (p \клин r).
 \end{массив}\)
\end{массив}\)Законы идемпотента : \(\begin{array}[t]{l} p \vee p \equiv p, \\ p \wedge p \equiv p. \end{array}\)
Законы Де Моргана : \(\begin{array}[t]{l} \overline{p\vee q} \equiv \overline{p}\wedge\overline{q}, \\ \overline{ p\клин q} \equiv \overline{p}\vee \overline{q}.\end{массив}\)
Законы исключенного третьего , или обратные законы : \(\begin{array}[t]{l} p \vee \overline{p} \equiv T, \\ p \wedge \overline{p} \equiv F. \ конец{массив}\)
Законы тождества : \(\begin{array}[t]{l} p \vee F \equiv p, \\ p \wedge T \equiv p. \end{array}\)
Законы доминирования : \(\begin{array}[t]{l} p \vee T \equiv T, \\ p \wedge F \equiv F. \end{array}\)
Эквивалентность импликации и ее контрапозиции: \(p \Rightarrow q \equiv \overline{q} \Rightarrow \overline{p}\).

Запись импликации в виде дизъюнкции: \(p \Rightarrow q \equiv \overline{p} \vee q\).
Отрицание импликации: \(\overline{p \Rightarrow q} \equiv p \wedge \overline{q} \)
Убедитесь, что вы поняли и запомнили последние три эквивалентности, потому что мы будем часто использовать их в оставшейся части курса.
Запоминать названия всех этих свойств может быть непросто; однако все они должны иметь для вас смысл. Важное название — законы Де Моргана. Объясним их словами и сравним с аналогичными операциями над действительными числами:
Коммутативные свойства : Короче, говорят, что «порядок операции не имеет значения». Неважно, какое из двух логических утверждений стоит первым, результат конъюнкции и дизъюнкции всегда дает одно и то же истинностное значение. Сравните это со сложением действительных чисел: \(x+y=y+x\). Вычитание не является коммутативным, потому что не всегда верно, что \(x-y=y-x\).
 Это объясняет, почему мы должны убедиться, что операция коммутативна.
Это объясняет, почему мы должны убедиться, что операция коммутативна.Ассоциативные свойства : Грубо говоря, эти свойства также говорят о том, что «порядок выполнения не имеет значения». Однако между ними и коммутативными свойствами есть ключевое различие.
Коммутативные свойства применяются к операциям над двумя логическими операторами , но ассоциативные свойства включают три логических оператора . Поскольку \(\wedge\) и \(\vee\) равны двоичных операций, мы можем работать только с парой операторов одновременно. Учитывая три утверждения \(p\), \(q\) и \(r\), расположенные в указанном порядке, над какой парой утверждений мы должны работать в первую очередь? Ответ таков: это не имеет значения. Именно порядок группировки (отсюда термин ассоциативный) не имеет значения в ассоциативных свойствах.
Важным следствием свойства ассоциативности является то, что, поскольку не имеет значения, над какой парой утверждений мы должны выполнить операцию первой, мы можем убрать круглые скобки и записать, например, \[p\vee q\vee r\] не беспокоясь о какой-либо путанице.

Не все операции ассоциативны. Вычитание не ассоциативно. Имея три числа 5, 7 и 4 в таком порядке, как мы должны выполнить два вычитания? Какую интерпретацию мы должны использовать: \[(5-7)-4, \qquad\mbox{или}\qquad 5-(7-4)?\] Поскольку они приводят к разным результатам, мы должны быть осторожны, где разместить скобки.
Распределительные законы : Когда мы смешиваем два различных операций над тремя логическими операторами, один из них должен сначала работать с парой операторов, формируя «внутреннюю» операцию. Затем следует «внешняя» операция для завершения составного оператора. Распределительные законы говорят, что мы можем распределить «внешнюю» операцию по внутренней.
Законы идемпотента : Когда операция применяется к паре идентичных логических операторов, результатом является один и тот же логический оператор.
 2=x\), где \(x\) — действительное число. Это верно только тогда, когда \(x=0\) или \(x=1\). Но логические эквивалентности \(p\vee p\equiv p\) и \(p\wedge p\equiv p\) верны для всех \(p\).
2=x\), где \(x\) — действительное число. Это верно только тогда, когда \(x=0\) или \(x=1\). Но логические эквивалентности \(p\vee p\equiv p\) и \(p\wedge p\equiv p\) верны для всех \(p\).Законы Де Моргана : Когда мы отрицаем дизъюнктуру (соответственно конъюнкцию), мы должны отрицать два логических утверждения и менять операцию дизъюнкции на конъюнкцию (соответственно конъюнкцию дизъюнкции).
Законы исключенного третьего , или обратные законы : Любое утверждение либо истинно, либо ложно, поэтому \(p\vee\overline{p}\) всегда истинно. Точно так же утверждение не может быть одновременно истинным и ложным, поэтому \(p\wedge\overline{p}\) всегда ложно.
Законы тождества : Сравните их с уравнением \(x\cdot1=x\): значение \(x\) не меняется после умножения на 1. Мы называем число 1 мультипликативным тождеством.
 Для логических операций идентичность дизъюнкции — F, а идентичность конъюнкции — T.
Для логических операций идентичность дизъюнкции — F, а идентичность конъюнкции — T.Законы доминирования : Сравните их с уравнением \(x\cdot0=0\) для действительных чисел: результат всегда равен 0, независимо от значения \(x\). «Ноль» для дизъюнкции — это Т, а «ноль» для конъюнкции — это F.
Пример \(\PageIndex{6}\label{eg:logiceq-07}\)
Что такое отрицание \(2\leq x\leq 3\)? Дайте логическое объяснение, а также графическое объяснение.
- Ответить
Неравенство \(2\leq x\leq 3\) означает \[(x\geq 2) \клин (x\leq 3).\] Его отрицание, согласно законам Де Моргана, равно \[(x<2 ) \vee (x>3).\] Неравенство \(2\leq x\leq 3\) дает замкнутый интервал. Его отрицание дает два открытых интервала. Их графическое представление на прямой с действительными числами изображено ниже.
(130,60)(-20,-45) (-20,0)(1,0)130 (30,0)(30,0)2 (20,-25)(20,20)\(2 \) (50,-25)(20,20)\(3\) ( 0,-50)(90,20)\((x\geq 2)\клин(x\leq 3)\) (30, 0)(1,0)30
(130,60)(-20,-45) (-20,0)(1,0)130 (30,0)(30,0)2 (20,-25)(20,20)\(2 \) (50,-25)(20,20)\(3\) ( 0,-50)(90,20)\((x<2)\vee(x>3)\) (-20, 0 )(1,0)48 ( 62, 0)(1,0)48
Обратите внимание на две конечные точки 2 и 3.
 Они меняются от включения к исключению, когда мы принимаем отрицание.
Они меняются от включения к исключению, когда мы принимаем отрицание.
практическое упражнение \(\PageIndex{4}\label{he:logiceq-04}\)
Поскольку \(0\leq x\leq 1\) означает «\(x\geq 0\) и \(x\leq 1\)», его отрицание должно быть «\(x<0\) или \( х>1\)». Объясните, почему неуместно и даже неправильно писать «\(0>x>1\)».
практическое упражнение \(\PageIndex{5}\label{he:logiceq-05}\)
Развернуть \((p\vee q) \wedge (r\vee s)\).
Пример \(\PageIndex{7}\label{eg:logiceq-09}\)
Мы использовали таблицу истинности, чтобы убедиться, что \[[(p \wedge q) \Rightarrow r] \Rightarrow [ \overline{r} \Rightarrow (\overline{p} \vee \overline{q})]\] является тавтологией. Мы можем использовать свойства логической эквивалентности, чтобы показать, что это составное утверждение логически эквивалентно \(T\). Такому типу доказательства обычно труднее следовать, поэтому рекомендуется давать пояснения на каждом этапе. Вот полное доказательство: \[% \arraygap{1. 2} \begin{array}{lcl@{\quad}l} [(p \wedge q) \Rightarrow r] \Rightarrow [\overline{r} \Rightarrow ( \overline{p} \vee \overline{q})] &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [\overline{r} \Rightarrow (\overline{p} \vee \overline {q})] & \mbox{(импликация как дизъюнкция)} \\ &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [\overline{\overline{p} \vee \overline{q }} \Rightarrow r] & \mbox{(импликация как дизъюнкция)} \\ &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [(p \wedge q) \Rightarrow r] & \mbox {(Закон Де Моргана)} \\ &\equiv& T & \mbox{(обратный закон)} \end{массив}\] Это именно то, что мы назвали методом слева направо для доказательства тождества (в данном случае , логическая эквивалентность).
2} \begin{array}{lcl@{\quad}l} [(p \wedge q) \Rightarrow r] \Rightarrow [\overline{r} \Rightarrow ( \overline{p} \vee \overline{q})] &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [\overline{r} \Rightarrow (\overline{p} \vee \overline {q})] & \mbox{(импликация как дизъюнкция)} \\ &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [\overline{\overline{p} \vee \overline{q }} \Rightarrow r] & \mbox{(импликация как дизъюнкция)} \\ &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [(p \wedge q) \Rightarrow r] & \mbox {(Закон Де Моргана)} \\ &\equiv& T & \mbox{(обратный закон)} \end{массив}\] Это именно то, что мы назвали методом слева направо для доказательства тождества (в данном случае , логическая эквивалентность).
Пример \(\PageIndex{8}\label{eg:logiceq-10}\)
Напишите \(\overline{p \Rightarrow q}\) как союз.
- Ответ
Важно помнить, что \[\overline{p\Rightarrow q} \not\equiv q\Rightarrow p,\] и \[\overline{p\Rightarrow q} \not\equiv \overline{p}\Rightarrow \overline{q}\] либо.
 Вместо этого, поскольку \(p\Rightarrow q \equiv \overline{p}\vee q\), из закона Де Моргана следует, что \[\overline{p \Rightarrow q} \equiv \overline{\overline{p} \ vee q} \equiv p \wedge \overline{q}.\] В качестве альтернативы мы можем рассуждать следующим образом. Интерпретируйте \(\overline{p \Rightarrow q}\) как утверждение \(p \Rightarrow q\) ложно. Это требует, чтобы \(p\) было истинным, а \(q\) — ложным, что преобразуется в \(p \wedge \overline{q}\). Таким образом, \(\overline{p\Rightarrow q} \equiv p\wedge \overline{q}\).
Вместо этого, поскольку \(p\Rightarrow q \equiv \overline{p}\vee q\), из закона Де Моргана следует, что \[\overline{p \Rightarrow q} \equiv \overline{\overline{p} \ vee q} \equiv p \wedge \overline{q}.\] В качестве альтернативы мы можем рассуждать следующим образом. Интерпретируйте \(\overline{p \Rightarrow q}\) как утверждение \(p \Rightarrow q\) ложно. Это требует, чтобы \(p\) было истинным, а \(q\) — ложным, что преобразуется в \(p \wedge \overline{q}\). Таким образом, \(\overline{p\Rightarrow q} \equiv p\wedge \overline{q}\).
Резюме и обзор
- Два логических утверждения логически эквивалентны, если они всегда дают одно и то же значение истинности.
- Следовательно, \(p\equiv q\) равносильно утверждению, что \(p\Leftrightarrow q\) является тавтологией.
- Помимо дистрибутивного закона и закона Де Моргана, помните также и эти две эквивалентности; они очень полезны при работе с последствиями. \[p \Rightarrow q \equiv \overline{q} \Rightarrow \overline{p} \qquad\mbox{and}\qquad p \Rightarrow q \equiv \overline{p} \vee q.
 \]
\]
Упражнения \(\PageIndex{}\)
Упражнение \(\PageIndex{1}\label{ex:logiceq-01}\)
Используйте таблицу истинности для проверки закона Де Моргана \(\overline{p \vee q} \equiv \overline{p}\wedge\overline{q}\).
- Ответить
\(\begin{array}[t]{ {|c | c | c | c | c | c |}} \hline p & q & p\vee q & \overline{p\vee q} & \overline {p} & \overline{q} & \overline{p}\wedge\overline{q} \\ \hline T & T & T & F & F & F & F \\ T & F & T & F & F & T & F \\ F & T & T & F & T & F & F \\ F & F & F & T & T & T & T \\ \hline \end{array}\)
Упражнение \(\PageIndex{2}\label{ex:logiceq-02}\)
Используйте таблицы истинности для проверки двух ассоциативных свойств.
Упражнение \(\PageIndex{3}\label{ex:logiceq-03}\)
Постройте таблицу истинности для каждой приведенной ниже формулы. Какие из них являются тавтологиями?
- \((\overline{p} \vee q)\Стрелка вправо p\)
- \((p\Стрелка вправо q) \vee (p\Стрелка вправо \overline{q})\)
- \((p\Стрелка вправо q) \Стрелка вправо r\)
- Ответить
Только (b) является тавтологией, как указано в таблицах истинности ниже.

(a) \(\begin{array}[t]{|*{5}{c|}} \hline p & q & \overline{p} & \overline{p}\vee q & (\overline{ p}\vee q)\Rightarrow p \\ \hline T & T & F & T & \qquad\;T \\ T & F & F & F & \qquad\;T \\ F & T & T & T & \qquad\;F \\ F & F & T & T & \qquad\;F \\ \hline \end{массив}\)
(b) \(\begin{array}[t]{|*{6}{c|}} \hline p & q & p\Rightarrow q & \overline{q} & p\Rightarrow\overline{q} & (p\Rightarrow q)\vee(p\Rightarrow\overline{q}) \\ \hline T &T &T & F & F & F &T \\ T &F &F & T & T &T \\ F &T &T & F & T &T \\ F &F &T & T & T &T \\ \hline \end{массив}\)
(c) \(\begin{array}[t]{|*{5}{c|}} \hline p & q & r & p\Rightarrow q & (p\Rightarrow q)\Rightarrow r \\ \ hline T &T &T & T & \qquad\quad T \\ T & T & F & T & \qquad\quad F \\ T &F &T & F & \qquad\quad T \\ T &F &F & F & F & \qquad \quad T \\ F &T &T & T & \qquad\quad T \\ F &T &F & T & \qquad\quad F \\ F &F &T & T & \qquad\quad T \\ F &F &F & T & \qquad\quad F \\ \hline \end{массив}\)
Упражнение \(\PageIndex{4}\label{ex:logiceq-04}\)
Используйте таблицы истинности для проверки этих логических эквивалентностей.
- \((p\клин q)\стрелка влево p \equiv p\стрелка вправо q\)
- \((p\клин q)\Rightarrow r \equiv p\Rightarrow(\overline{q}\vee r)\)
- \((p\Rightarrow\overline{q}) \wedge (p\Rightarrow\overline{r}) \equiv \overline{p\wedge(q\vee r)}\)
Упражнение \(\PageIndex{5}\label{ex:logiceq-05}\)
Использовать только свойства логических эквивалентностей для проверки (b) и (c) в задаче 4.
- Ответ
Пробы показаны ниже без пояснений. Обязательно заполните их.
(b) \( \begin{array}[t]{lcl@{\quad(\hskip1.5in)}} (p\wedge q)\Rightarrow r &\equiv& \overline{p\wedge q}\vee r \\ &\equiv& (\overline{p}\vee\overline{q})\vee r \\ &\equiv& \overline{p}\vee(\overline{q}\vee r) \\ &\equiv& p\Rightarrow(\overline{q}\vee r) \end{массив}\)
(c) \( \begin{array}[t]{lcl@{\quad(\hskip1.5in)}} (p\Rightarrow\overline{q}) \wedge (p\Rightarrow\overline{r}) &\equiv& (\overline{p}\vee\overline{q}) \wedge (\overline{p}\vee\overline{r}) \\ &\equiv& \overline{p}\vee(\overline{q }\wedge\overline{r}) \\ &\equiv& \overline{p}\vee\overline{q\vee r} \\ &\equiv& \overline{p\wedge(q\vee r)} \end{ массив}\)
Упражнение \(\PageIndex{6}\label{ex:logiceq-06}\)
Определить, являются ли формулы \(u\) и \(v\) логически эквивалентными (можно использовать таблицы истинности или свойства логических эквивалентностей).
| \(u:\;(p\Rightarrow q)\клин (p\Rightarrow\overline{q})\) | \(v:\;\overline{p}\) |
| \(u:\;p\стрелка вправо q\) | \(v:\;q\стрелка вправо\) |
| \(u:\;p\Стрелка влево q\) | \(v:\;q\стрелка влево p\) |
| \(u:\;(p\Стрелка вправо q)\Стрелка вправо r\) | \(v:\;p\Стрелка вправо(q\Стрелка вправо r)\) |
Упражнение \(\PageIndex{7}\label{ex:logiceq-07}\)
Найдите обратное, обратное и противоположное этих следствий.
- Если треугольник \(ABC\) равнобедренный и содержит угол 45 градусов, то \(ABC\) прямоугольный.
- Если четырехугольник \(ABCD\) является квадратом, то он одновременно и прямоугольник, и ромб.

- Если четырехугольник \(ABCD\) имеет две стороны одинаковой длины, то это либо прямоугольник, либо ромб.
- Ответить
(а)
Конверс: Если треугольник \(ABC\) прямоугольный, то \(ABC\) равнобедренный и содержит угол 45 градусов. Обратное: Если треугольник \(ABC\) не равнобедренный или не содержит угла с углом 45 градусов, то \(ABC\) не является прямоугольным треугольником. Противоположный: Если треугольник \(ABC\) не прямоугольный, то \(ABC\) не равнобедренный или не содержит угол 45 градусов. (б)
Конверс: Если четырехугольник \(ABCD\) является и прямоугольником, и ромбом, , то \(ABCD\) — квадрат. 
Обратное: Если четырехугольник \(ABCD\) не является квадратом, то это не прямоугольник и не ромб. Противоположный: Если четырехугольник \(ABCD\) не прямоугольник и не ромб, , то \(ABCD\) не является квадратом. (с)
Конверс: Если четырехугольник \(ABCD\) является прямоугольником или ромбом, , то \(ABCD\) имеет две стороны одинаковой длины. Обратное: Если четырехугольник \(ABCD\) не имеет двух сторон одинаковой длины, , то это не прямоугольник и не ромб. 
Противоположный: 92>0 \Стрелка вправо x>0\). - Если \(PQRS\) — квадрат, то \(PQRS\) — параллелограмм.
- Если \(n>1\) простое, то \(n+1\) составное.
- Если \(x\) и \(y\) такие целые числа, что \(xy\geq1\), то либо \(x\geq1\), либо \(y\geq1\).
Упражнение \(\PageIndex{9}\label{ex:logiceq-09}\)
Определите, верны или нет следующие формулы:
- \(\overline{p\Leftrightarrow q} \equiv \overline {p} \Leftrightarrow \overline{q}\)
- \((p\Rightarrow q) \wedge (p\Rightarrow\overline{q}) \equiv \overline{p}\)
- \(p\Стрелка вправо q \equiv q\Стрелка вправо p\)
- Ответить
(а) неверно (б) верно (в) неверно
Упражнение \(\PageIndex{10}\label{ex:logiceq-10}\)
Определите, верны или нет следующие формулы:
- \((p\Rightarrow q)\Rightarrow r \equiv p \Стрелка вправо (q\Стрелка вправо r)\) 92\не>0\), затем \(х\не>0\).

- Ответить
Только (б).
Упражнение \(\PageIndex{12}\label{ex:logiceq-12}\)
Определите, являются ли следующие формулы тавтологией, противоречием или ни тем, ни другим:
- \((p\Rightarrow q) \wedge \ линия {p}\)
- \((p\Rightarrow\overline{q}) \клин (p\клин q)\)
- \((p\Стрелка вправо\над чертой{q}) \клин q\)
Упражнение \(\PageIndex{13}\label{ex:logiceq-13}\)
Упростите следующие формулы:
- \(p\wedge(p\wedge q)\)
- \(\overline{\overline{p}\vee q}\)
- \(\overline{p\Rightarrow\overline{q}}\)
- Ответить
(a) \(p\клин q\)
(b) \(p\клин \overline{q}\)
(c) \(p\клин q\)
Упражнение \(\PageIndex{14}\label{ex:logiceq-14}\)
Упростите следующие формулы:
- \((p\Rightarrow\overline{q}) \wedge (\overline{q}\Rightarrow p)\)
- \(\перечеркнутый {p\клин \перечеркнутый{q}}\)
- \(p\клин(\overline{p}\vee q)\)
Упражнение \(\PageIndex{15}\)
T означает тавтологию, а F означает противоречие.

Правда или ложь?
а. \(F\стрелка вправо\над чертой{q}\)
б. \(п\вее Т\)
с. \(F \клин p \)
d. \(\overline{T}\vee F\)
- Ответ
(а) верно (б) верно (в) неверно (г) неверно
Упражнение \(\PageIndex{16}\)
T означает тавтологию, а F означает противоречие.
Упростить до эквивалентного выражения, состоящего из одной буквы ( T , F , p или ~ p )
а. \(\overline{T} \vee F \equiv \)
b. \(T \клин p \эквив\)
c. \(F \клин\оверлайн{р} \эквив\)
d. \(F \vee \overline{p}\equiv\)
e. \((F \vee T) \vee F\equiv\)
f. \((F \vee T) \клин T\equiv\)
Эта страница под названием 2.5: Logical Equivalences распространяется в соответствии с лицензией CC BY-NC-SA, автором, ремиксом и/или куратором этой страницы является Харрис Квонг (OpenSUNY) .

- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Харрис Квонг
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- да
- Теги
Логические эквиваленты
Что означает совпадение двух логических утверждений? В этом разделе мы познакомимся с идеей логической эквивалентности и рассмотрим два метода, чтобы показать эквивалентность двух утверждений.

Подраздел
Определение 2.1.1. Тавтологии и противоречия.
Выражение, включающее логические переменные, истинное для всех значений, называется тавтологией .
Выражение с логическими переменными, которое является ложным для всех значений, называется противоречием .
Утверждения, не являющиеся тавтологиями или противоречиями, называются случайностями .
Большинство операторов являются непредвиденными. Именно тавтологии и противоречия являются особыми, которые мы будем выделять до конца семестра.
Определение 2.1.2. Логическая эквивалентность.
Мы говорим, что два предложения \(p\) и \(q\) логически эквивалентны , если \(p \leftrightarrow q\) является тавтологией. Мы обозначаем это через \(p \equiv q\text{.}\)
Первый способ показать, что два утверждения \(p \и q\) эквивалентны, состоит в том, чтобы построить таблицу истинности, чтобы найти значения истинности \(p \leftrightarrow q\text{.
 }\)
}\)Поскольку \(p \leftrightarrow q\) истинно, если \(p \и q\) имеют одинаковые значения истинности, в этом курсе мы будем часто строить таблицы истинности для двух утверждений, а затем отмечать, являются ли их столбцы истинными. одинаковые или разные.
Пример 2.1.3.
Докажите, что следующие утверждения эквивалентны, используя таблицу истинности.
\(\displaystyle (\neg p \to (q \wedge \neg q)) \equiv p\)
\(\displaystyle p \vee (p \wedge q) \equiv p \)
\(\displaystyle p \vee (q \wee r) \equiv (p \vee q) \wedge (p \vee r)\)
\(\displaystyle \neg(p \to q) \equiv p \wedge \neg q\)
\(\displaystyle p \to q \equiv \neg p \vee q\)
Мы используем \(p \to q \equiv \neg p \vee q\) достаточно часто, чтобы это имело название. Мы назовем это следствием
.Видео/Ответ.
Раствор.

Вот решение для \((\neg p \to (q \wedge \neg q)) \equiv p\text{:}\)
Таблица 2.1.4. Отображение \(( \neg p \to (q \wedge \neg q))\leftrightarrow p\) является тавтологиейT Т Ф Ф Т Т Т Ф Ф Ф Т Т Ф Т Т Ф Ф Т Ф Ф Т Ф Ф Т Следующая таблица представляет собой набор основных тавтологий, которые мы будем использовать до конца курса. В следующем за ними примере мы покажем, как мы можем использовать эти существующие тавтологии (которые мы будем называть законами), чтобы делать выводы о более сложных утверждениях.
Вам нужно их запомнить? Абсолютно!
Список 2.1.5. Фундаментальные логические эквивалентности. Пусть \(p, q\) и \(r\) — логические предложения.

- Коммутативные законы
\(p \lor q\equiv q\lor p\)
\(p \land q\equiv q \land p\)- Ассоциативные законы
\((p \lor q) \lor r \equiv p \lor (q \lor r)\)
\((p \land q) \land r\equiv p \land (q \land r)\ )- Распределительные законы
\(p \land (q \lor r) \equiv (p \land q ) \lor (p \land r)\)
\(p \lor (q \land r) \equiv (p \lor q ) \land (p \lor r)\)- Законы о личности
\(p \lor F\экв p\)
\(p \land T \equiv p\)- Законы отрицания
\(p\land \neg p\equiv F\)
\(p\lor \neg p\equiv T\)- Законы идемпотента
\(p \lor p \equiv p\)
\(p\land p \equiv p\)- Законы господства
\(p \land F \equiv F\)
\(p \lor T \equiv T\)- Законы о поглощении
\(p \land (p\lor q)\equiv p\)
\(p \lor (p \land q) \equiv p\)- Законы ДеМоргана
\(\neg (p \lor q) \equiv (\neg p) \land (\neg q)\)
\(\neg (p \land q) \equiv (\neg p) \lor (\ отрицательный q)\)- Закон двойного отрицания
\(\displaystyle \neg (\neg p)\equiv p\)
- Значение
\(\displaystyle p \to q \equiv \neg p \lor q\)
Вы заметите, что те законы, которые имеют две разные формы, выглядят очень похоже, только с разными операциями и заменой местами истинности и ложности.
 Это не только означает, что вам на самом деле нужно запомнить вдвое меньше, для этого есть четкая причина, которую мы рассмотрим, когда будем обсуждать булевы алгебры в Discrete 2!
Это не только означает, что вам на самом деле нужно запомнить вдвое меньше, для этого есть четкая причина, которую мы рассмотрим, когда будем обсуждать булевы алгебры в Discrete 2!Пример 2.1.6.
Используйте логические законы из списка 2.1.5, чтобы показать, что следующие эквивалентны.
\(\displaystyle p \wedge q \equiv \neg(p \to \neg q)\)
\(\displaystyle (p \to r) \vee (q \to r) \equiv (p \wedge q) \to r\)
\(\displaystyle q \to p \equiv \neg p \to \neg q\)
\(\displaystyle (\neg p \to (q \wedge \neg q)) \equiv p\)
Видео/Ответ.
Это ваш первый опыт работы с логическим доказательством! Это не будет последним. Большая часть этого класса посвящена тому, чтобы научиться понимать и аргументировать строго.
Упражнения Упражнения
1.
Определите, являются ли следующие два утверждения логически эквивалентными: \(\neg(p \to q)\) и \(p \wedge \neg q\text{.
 }\) Объясните, откуда вы знаете, что вы правы.
}\) Объясните, откуда вы знаете, что вы правы.Раствор.
Составьте для каждого таблицу истинности и сравните. Высказывания логически эквивалентны.
2.
Являются ли утверждения \(p \to (q\vee r)\) и \((p \to q) \vee (p \to r)\) логически эквивалентными?
Раствор.
Давайте начнем с левой стороны и будем двигаться вправо, чтобы выяснить это.
\begin{выравнивание*} p \to (q \lor r) \amp\equiv \neg p \lor (q \lor r) \amp \text{импликация} \\ \amp\equiv \neg p \lor q \lor r \amp \text{ассоциативный, убрать скобки}\\ \amp\equiv \neg p \lor \neg p \lor q \lor r \amp \text{idempotent}\\ \amp\equiv \neg p \lor q \lor \neg p \lor r \amp \text{communitive}\\ \amp\equiv (\neg p \lor q) \lor (\neg p \lor r) \amp \text{associative}\\ \amp\equiv (p \to q) \lor (p \to r) \amp \text{импликация} \end{выравнивание*}
, что мы и хотели показать.
3.
Используйте таблицу истинности, чтобы показать, что \((p \to q) \land (p \to r)\) и \(p \to (q \land r)\) логически эквивалентны.

Раствор.
Вот альтернативное решение, использующее предыдущие эквивалентности (не таблица истинности):
\begin{align*} (p \to q) \land (p \to r) & \equiv (\neg p \lor q) \land (\neg p \lor r) \\ &\equiv \neg p \lor (q \land r)\\ &\equiv p \to (q \land r) \end{выравнивание*}
4.
Упростите следующие операторы (чтобы отрицание появлялось только непосредственно перед переменными).
\(\neg(p \to \neg q)\text{.}\)
\((\neg p \vee \neg q) \to \neg (\neg q \wedge r)\text{.}\)
\(\neg((p \to \neg q) \vee \neg (r \wedge \neg r))\text{.}\)
Видео/Ответ.
\(p \клин q\text{.}\)
\((\neg p \vee \neg r) \to (q \vee \neg r)\) или, заменив импликацию сначала дизъюнктией: \((p \wedge q) \vee (q \vee \нег г)\текст{.}\)
\((p \клин q) \клин (r \клин \neg r)\text{.
 }\) Это обязательно ложно, поэтому также эквивалентно \(p \клин \neg p\text{. }\)
}\) Это обязательно ложно, поэтому также эквивалентно \(p \клин \neg p\text{. }\)Либо Сэм не мужчина, а Крис не женщина, либо Крис женщина.
5.
Используйте законы ДеМоргана и любые другие известные вам факты логической эквивалентности, чтобы упростить следующие утверждения. Покажи все свои шаги. В ваших окончательных утверждениях отрицания должны появляться только непосредственно рядом с переменными предложения или предикатами (\(p\text{,}\) \(q\text{,}\) и т. д.), а не двойными отрицаниями. Было бы неплохо использовать только союзы, дизъюнкции и отрицания.
\(\neg((\neg p \wedge q) \vee \neg(r \vee \neg s))\text{.}\)
\(\neg((\neg p \to \neg q) \wedge (\neg q \to k))\) (осторожнее с последствиями).
\(\displaystyle (p\land q) \to (p \lor q)\)
Раствор.
\begin{выравнивание*} \neg((\neg p \wedge q) \vee \neg(r \vee \neg s)) \amp\equiv \neg(\neg p \wedge q) \land \neg \neg(r \vee \neg с) \\ \amp\equiv \neg(\neg p \wedge q) \land (r \vee \neg s)\\ \amp\equiv (\neg\neg p \lor \neg q) \land (r \lor \neg s)\\ \amp\equiv (p \lor \neg q) \land (r \lor \neg s) \end{выравнивание*}
\begin{выравнивание*} \neg((\neg p \to \neg q) \wedge (\neg q \to k)) \amp \equiv \neg((\neg \neg p \lor \neg q) \wedge (\neg \neg д \лор к))\\ \amp\equiv \neg((p \lor \neg q) \wedge (q \lor k))\\ \amp \equiv \neg(p \lor \neg q) \lor \neg (q \lor k)\\ \amp \equiv (\neg p \land \neg \neg q) \lor (\neg q \land \neg k)\\ \amp \equiv (\neg p \land q) \lor (\neg q \land \neg k) \end{выравнивание*}
\begin{выравнивание*} (p\land q) \to (p \lor q) \amp\equiv \neg (p\land q) \lor (p \lor q) \\ \amp \equiv (\neg p \lor \neg q) \lor (p \lor q)\\ \amp \equiv \neg p \lor \neg q \lor p \lor q\\ \amp \equiv \neg p \lor p \lor \neg q \lor q\\ \amp \equiv (\neg p \lor p) \lor ( \neg q \lor q )\\ \амп\экв (Т) \лор (Т)\\ \ампер\экв Т \end{выравнивание*}
.
 .. это тавтология!
.. это тавтология!
Подраздел Форум Сообщения об этом разделе
таблиц истинности, тавтологии и логические эквивалентности
таблицы истинности, тавтологии и логические эквивалентностиМатематики обычно используют двузначное число . логика : Каждое утверждение либо Истинно , либо Ложь . Это называется Закон исключенного среднего .
Утверждение в сентенциальной логике строится из простых утверждений с использованием логические связки , , , и . Правда или ложь утверждения, построенного с помощью этих связок, зависит от истинности или ложность его составляющих.
Например, составной оператор строится с использованием логических связок , и . Правда или ложность зависит от истины или ложность P, Q и R.
Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен.
 Итак, мы начнем с рассмотрения
таблицы истинности для пяти логических связок.
Итак, мы начнем с рассмотрения
таблицы истинности для пяти логических связок.Вот таблица отрицания:
Эту таблицу легко понять. Если P равно true , его отрицание ложно . Если P равно false , то true .
должно быть true , когда оба P и Q true и false иначе:
является истинным , если либо P является истинным , либо Q является верно (или оба — помните, что мы используем «или» во включающем смысле). всего ложь , если оба P и Q ложно .
Вот таблица логических следствий:
Чтобы понять, почему эта таблица именно такая, рассмотрим следующее. пример:
«Если ты получишь пятерку, я дам тебе доллар».
Утверждение будет верным , если я сдержу свое обещание и ложь если нет.
Предположим, что верно , что вы получаете пятерку, а это 9.
 0037 правда что я даю вам доллар. Поскольку я сдержал свое обещание, верно . Это соответствует первой строке таблицы.
0037 правда что я даю вам доллар. Поскольку я сдержал свое обещание, верно . Это соответствует первой строке таблицы.Предположим, что верно , что вы получили пятерку, но ложно что я даю вам доллар. Поскольку я не сдержал своего обещания, подразумевается false . Это соответствует второму строку в таблице.
Что, если это ложь, что вы получили пятерку? Независимо от того, дам ли я вам долларов, я не нарушил своего обещания. Таким образом, вывод не может быть ложно, поэтому (поскольку это двузначная логика) оно должно быть истинным. Этот объясняет последние две строки таблицы.
означает, что P и Q равны эквивалент . Таким образом, двойная импликация верна , если P и Q оба истинны или если P и Q оба ложны ; в противном случае двойная импликация ложна.
Вы должны помнить — или уметь составлять — таблицы истинности для логических связок.
 Вы будете использовать эти таблицы для построения
таблицы для более сложных предложений. Легче продемонстрировать
что делать, чем описать это словами, так вы увидите порядок
выработано на примерах.
Вы будете использовать эти таблицы для построения
таблицы для более сложных предложений. Легче продемонстрировать
что делать, чем описать это словами, так вы увидите порядок
выработано на примерах.Примечание. (а) Когда вы строите правду таблице, вы должны рассмотреть все возможные назначения True (T) и False (F) для операторов компонентов. Например, предположим, составные операторы — это P, Q и R. Каждый из этих операторов может быть либо правда, либо ложь, так что есть возможности.
Когда вы перечисляете возможности, вы должны присвоить значения истинности к операторам компонентов систематическим образом, чтобы избежать дублирования или упущение. Самый простой подход — использовать лексикографический порядок . Таким образом, для составного оператора с три компонента P, Q и R, я бы перечислил возможности этого путь:
(б) Существуют различные способы составления таблиц истинности.
 Вы можете, для
например, запишите значения истинности «под» логическим
связки составного высказывания, постепенно дорастающие до
столбец для «основной» связки.
Вы можете, для
например, запишите значения истинности «под» логическим
связки составного высказывания, постепенно дорастающие до
столбец для «основной» связки.Я буду записывать вещи длинным путем, создавая столбцы для каждого «кусочек» составного высказывания и постепенно наращивая к составному утверждению. Любой стиль хорош, пока вы показываете достаточно работы, чтобы оправдать ваши результаты.
Пример. Построить таблицу истинности для формула .
Во-первых, я перечисляю все альтернативы для P и Q.
Затем в третьем столбце я перечисляю значения на основе значений P. Я использую таблицу истинности для отрицание: когда P истинно, ложно, а когда P ложно, правда.
В четвертом столбце я перечисляю значения для . Проверьте сами, что это только ложь («F»), если P истинно («T»), а Q ложно («Ф»).
В пятом столбце приведены значения моего составного выражения. Это «и» из (третий столбец) и (четвертый столбец).
 «И» верно только в том случае, если обе части
«и» верны; в противном случае оно ложно. Поэтому я смотрю на
третья и четвертая колонки; если оба верны («T»), я ставлю T
в пятой колонке, иначе ставлю F.
«И» верно только в том случае, если обе части
«и» верны; в противном случае оно ложно. Поэтому я смотрю на
третья и четвертая колонки; если оба верны («T»), я ставлю T
в пятой колонке, иначе ставлю F.тавтология есть формула, которая «всегда истинно» — то есть истинно для всякого присвоения истины значения его простых компонентов. Вы можете рассматривать тавтологию как правило логики .
Противоположностью тавтологии является число . противоречие , формула, которая «всегда ложна». В Другими словами, противоречие ложно для любого присвоения истины значения его простых компонентов.
Пример. Покажите, что это тавтология.
Я строю таблицу истинности и показываю, что формула всегда верна.
Последний столбец содержит только Т. Следовательно, формула представляет собой тавтология.
Пример. Построить таблицу истинности для .

Вы можете видеть, что построение таблиц истинности для утверждений с большим количеством связок или большого количества простых утверждений довольно утомительно и подвержен ошибкам. Хотя могут быть некоторые приложения этого (например, для цифровые схемы), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это наверняка было сделано).
Суть здесь в том, чтобы понять, как значение истинности сложного утверждение зависит от истинностных значений его простых утверждений и его логические связи. В большинстве работ математики обычно не операторы использования, которые очень сложны с логической точки зрения. Посмотреть.
Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинной стоимость не может быть определена.
б) Предположим, что это неверно. Рассказывать является ли Q истинным, ложным или его истинностное значение не может быть определено.

а) Поскольку истинно, то либо Р истинно, либо истинно. Поскольку P ложно, оно должно быть истинным. Следовательно, Q должно быть ложным.
(b) Утверждение «если-то» ложно, когда часть «если» истина, а часть «тогда» ложна. Поскольку ложно, верно. Утверждение «и» истинно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.
Пример. Предположим
» » правда.
» » неверно.
«У Кельвина Баттербола фиолетовые носки» — это правда.
Определить истинность утверждения
Для простоты пусть
П = «».
Q = «».
R = «У Кэлвина Баттербола фиолетовые носки».
Я хочу определить истинное значение . Поскольку мне были даны конкретные значения истинности для P, Q, и R, я составил таблицу истинности с одной строкой, используя данные значения для P, Q и R:
Следовательно, утверждение верно .

Пример. Определить истинное значение утверждение
Утверждение » » неверно. Вы не можете сказать действительно ли утверждение «Икабод Ксеркс ест шоколад кексы» истинны или ложны — но это не имеет значения. Если «если» часть утверждения «если-то» ложна, то утверждение «если-то» истинно. (Проверьте правду таблица для тех, кто не уверен в этом!) Так что данное утверждение должно быть истинным.
Два утверждения X и Y логически равны . эквивалент , если это тавтология. Другой способ сказать это: Для каждого присвоения значений истинности простым операторы , составляющие X и Y, операторы X и Y имеют одинаковые значения истинности.
С практической точки зрения вы можете заменить оператор в доказательство любым логически эквивалентным утверждением.
Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтологией — что есть ли «все Т в столбце».
 Однако проще настроить таблицу, содержащую X и Y, а затем
проверьте, совпадают ли столбцы для X и для Y.
Однако проще настроить таблицу, содержащую X и Y, а затем
проверьте, совпадают ли столбцы для X и для Y.Пример. Покажите, что и логически эквивалентны.
Поскольку столбцы для и идентичны, два оператора логически эквивалент. Эта тавтология называется Условное Разъединение . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.
Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.
Когда тавтология имеет форму бикондиционала, два утверждения которые составляют бикондиционал, логически эквивалентны. Следовательно, вы можно заменить одну сторону другой без изменения логического значение.
Вам часто придется отрицать математическое утверждение. К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символические заявления.

Пример. Запишите отрицание следующие операторы, упрощая так, чтобы только простые операторы отрицается.
(а)
(б)
(a) Я отрицаю данное утверждение, затем упрощаю, используя логические эквивалентности. Я дал имена логических эквивалентностей на правильно, чтобы вы могли видеть, какие из них я использовал.
(б)
Я показал это и есть логически эквивалентны в предыдущем примере.
В следующих примерах мы будем отрицать утверждения, написанные словами. Это более типично для того, что вам нужно делать в математике. идея состоит в том, чтобы преобразовать слово-выражение в символическое высказывание, затем используйте логические эквивалентности, как в предыдущем примере.
Пример. Используйте закон Де Моргана, чтобы написать отрицание следующего утверждения, упрощая так, что отрицаются только простые операторы:
«Кэлвина нет дома или Бонзо в кино».

Пусть С будет утверждением «Кальвин дома», а В будет заявление «Бонзо в движении». Данное утверждение является . Я должен отрицать утверждение, затем упростите:
Результат: «Кальвин дома, а Бонзо нет на кино».
Пример. Используйте закон Де Моргана, чтобы написать отрицание следующего утверждения, упрощая так, что отрицаются только простые операторы:
«Если Фиби покупает пиццу, то Кэлвин покупает попкорн».
Пусть P будет утверждением «Фиби покупает пиццу», а C будет заявление «Кэлвин покупает попкорн». Данное утверждение является . Чтобы упростить отрицание, я буду использовать тавтологию Условная дизъюнкция , которая гласит:
То есть я могу заменить на (или наоборот).
Вот вам и отрицание и упрощение:
Результат: «Фиби покупает пиццу, а Кэлвин не покупает». попкорн».
Далее мы применим нашу работу с таблицами истинности и отрицающими утверждениями к задачи на построение обратной, обратной и противопоставляется утверждению «если-то».

Пример. Замените следующий оператор на его противоположность:
«Если x и y рациональны, то рационально».
По контрапозитивной эквивалентности это утверждение совпадает с «Если не рационально, то это не так что и х, и у рациональны».
Этот ответ правильный в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей позитивное утверждение легче понять, чем отрицательное утверждение.
По определению, действительное число равно 9.0037 иррациональный если это не рационально. Поэтому я мог бы заменить часть «если» противопоставляется слову «иррационально».
Часть противопоставления «тогда» есть отрицание утверждение «и». Вы могли бы переформулировать это так: «Это не случае, когда и x рационально, и y рационально». (Слово «оба» гарантируют, что отрицание применяется ко всему утверждение «и», а не только «х рационально».
 )
)По закону Де Моргана это эквивалентно следующему: «x не является рациональным или y нерационально». В качестве альтернативы я мог бы сказать: «x есть иррационально или у иррационально».
Собрав все вместе, я мог бы выразить противоположное как: «Если иррационально, то либо х иррационально или у иррационально».
(Как обычно, я добавил слово «либо», чтобы было понятно, что часть «тогда» — это целое выражение «или».)
Пример. Покажите, что обратное и обратные условные логически эквивалентны.
Пусть условно. Обратное есть. Обратное.
Я мог бы показать, что обратное и обратное эквивалентны построение таблицы истинности для . Вместо этого я буду использовать некоторые известные тавтологии.
Начните с:
Помните, что я могу заменить утверждение логическим эквивалент. Например, на последнем шаге я заменил на Q, потому что два утверждения эквивалентны Двойное отрицание.

Пример. Предположим, что x — действительное число. Рассмотреть возможность заявление
«Если , то ».
Постройте обратное, обратное и контрапозитивное. Определите истинность или ложность четырех утверждений — исходное утверждение, обратное, обратное и контрапозитивное — используя свои знания по алгебре.
Обратное: «Если , то».
Обратное: «Если , то».
Противоположное: «Если , то».
Исходное утверждение неверно: , но . Поскольку исходное утверждение эквивалентно контрапозитив, то контрапозитив также должен быть ложным.
Обратное верно. Обратное логически эквивалентно обратное, значит верно и обратное.
\новая страница
\centerline{\bigssbold Список тавтологий}
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2019 Брюс Икенага
1.1 Логические операции
Математика обычно включает в себя объединение истинных (или гипотетически истинных) утверждения различными способами для получения (или доказательства) новых истинных утверждений.
 Начнем с разъяснения некоторых из этих фундаментальных идей.
Начнем с разъяснения некоторых из этих фундаментальных идей.Под предложением мы подразумеваем утверждение, имеющее определенное истинностное значение , истина (T) или ложь (F) — например,
«В 1492 году Колумб плыл по синему океану». (T)
«Наполеон выиграл битву при Ватерлоо». (Ф)
В более общем смысле под формулой мы подразумеваем утверждение, возможно, с некоторыми переменными, которое либо истинно, либо false всякий раз, когда мы присваиваем определенные значения каждой из переменных. Мы будем использовать заглавные буквы для обозначения формул. Если правда а формула зависит от значений, скажем, $x$, $y$ и $z$, мы будем использовать обозначение типа $P(x,y,z)$ для обозначения формулы. 92+y = 12$», то $P(2,8)$ и $P(3,3)$ верно, а $P(1,4)$ и $P(0,6)$ ложны. Если $Q(x,y,z)$ равно «$x+y
Является ли предложение истинным или ложным, обычно зависит от того, что мы говорят о том, что одно и то же предложение может быть истинным или ложным в зависимости от по контексту; например, формула $x|y$ означает, что `$x$ делит $у$’.
 То есть $x|y$, если существует некоторый $z$ такой, что $y=x\cdot z$. В настоящее время,
правда ли, что $3|2$? Это зависит: если мы говорим о целых числах,
ответ — нет; если мы говорим о рациональных числах, то ответ
да, потому что $2=3\cdot(2/3)$. (Конечно, если $x\not=0$ и $y$ любые рациональных чисел, затем $x|y$, так что это не очень
полезное понятие. При обычном использовании внешний вид формулы
«$x|y$» подразумевает , что $x$ и $y$ являются целыми числами.)
То есть $x|y$, если существует некоторый $z$ такой, что $y=x\cdot z$. В настоящее время,
правда ли, что $3|2$? Это зависит: если мы говорим о целых числах,
ответ — нет; если мы говорим о рациональных числах, то ответ
да, потому что $2=3\cdot(2/3)$. (Конечно, если $x\not=0$ и $y$ любые рациональных чисел, затем $x|y$, так что это не очень
полезное понятие. При обычном использовании внешний вид формулы
«$x|y$» подразумевает , что $x$ и $y$ являются целыми числами.)Вселенная дискурса для конкретной области математики представляет собой набор, который содержит все, что представляет интерес для этой темы. Когда мы изучение математических формул типа «$x$ делит $y$» на переменные предполагается, что они принимают значения в любом дискурсивном универсуме подходит для конкретного предмета. Вселенная дискурса обычно ясно из обсуждения, но иногда нам нужно будет идентифицируйте его явно для ясности. Вселенная дискурса обычно обозначается $U$.
Сложные предложения и формулы составляются из более простых, используя небольшое количество логических операций .
 Просто горстка
этих операций позволит нам сказать все, что мы должны сказать в
математика.
Просто горстка
этих операций позволит нам сказать все, что мы должны сказать в
математика.Если $P$ — это формула, то «не $P$» — это другая формула. формула, которую мы символически запишем как $\lnot P$. Конечно, $\lне P$ ложно, если $P$ истинно, и наоборот, например,
«6 не является простым числом» или «Неверно, что 6 премьер» или «$\lnot(\hbox{6 простое число})$» (T)
«Рональд Рейган не был президентом». (Ф)
Предположим, что $P$ и $Q$ — формулы. затем «$P$ и $Q$» — это формула, записанная символически как $P\land Q$, называемое соединением из $P$ и $Q$. Чтобы $P\land Q$ были истинными как $P$, так и $Q$ должно быть истинным, иначе оно ложно, например,
«5 долларов = 6 долларов и 7 долларов = 8 долларов». (F)
«Сиэтл находится в Вашингтоне, а Бойсе — в Айдахо». (T)
«Толстой был русским, а Диккенс был Французский.» (Ф)
Если $P$ и $Q$ являются формулами, то формула «$P$ или $Q$» записывается символически как $P\lor Q$, называемая дизъюнкция $P$ и $Q$.
 это
важно отметить, что это включительно или, то есть, «либо
или оба». Таким образом, если $P$, $Q$ или оба $P$ и $Q$ истинны,
то же самое и с $P\lor Q$. Единственный случай, когда $P\lor Q$ может быть ложным, состоит в том, что оба $P$
и $Q$ ложны, например,
это
важно отметить, что это включительно или, то есть, «либо
или оба». Таким образом, если $P$, $Q$ или оба $P$ и $Q$ истинны,
то же самое и с $P\lor Q$. Единственный случай, когда $P\lor Q$ может быть ложным, состоит в том, что оба $P$
и $Q$ ложны, например,«Вашингтон в Канаде или Лондон в Англии». (T)
«$5
«Ленин был испанцем или Ганди был итальянцем». (Ф)
Если $P$ и $Q$ — формулы, то «если $P$, то $Q$» или «$P$ означает, что $Q$» написано $P\подразумевает Q$, используя условный символ , $\подразумевает$. Не очевидно (по крайней мере, для большинства людей), под чем обстоятельства $P\имеет Q$ должно быть правдой. Отчасти это потому, что «if… then» используется в обычном английском языке более чем одним способом, однако нам нужно исправить правило, которое позволит нам точно знать, когда $P\ подразумевает Q$ верно. Конечно, если $P$ истинно, а $Q$ ложно, $P$ не может подразумевают $Q$, поэтому $P\implis Q$ в этом случае ложно.
 Чтобы помочь нам с
в других случаях рассмотрим следующее утверждение:
Чтобы помочь нам с
в других случаях рассмотрим следующее утверждение:«Если $x$ меньше 2, то $x$ меньше 4».
Это утверждение должно быть верным независимо от значения $x$. (при условии, что вселенная дискурса является чем-то знакомым, например целые числа). Если $x$ равно 1, оно оценивается как $\rm T\имплицитно T$, если $x$ равно 3, оно становится $\rm F\implis T$, а если $x$ равно 5, становится $\rm F\ подразумевает F$. Таким образом, оказывается, что $P\implis Q$ истинно, если только $P$ истинно, а $Q$ ложно. Это правило, которое мы принимаем.
Наконец, бикондиционал , написанный $\Leftrightarrow$, соответствует фраза «если и только если» или «если» коротко. Таким образом, $P \Leftrightarrow Q$ истинно, когда и $P$, и $Q$ имеют одинаковое истинностное значение, иначе оно ложно.
Пример 1.1.2 Предположим, что $P(x,y)$ равно «$x+y=2$» и $Q(x,y)$ равно «$xy>1$». Тогда, когда $x=1$ и $y=1$, $\lnot P(x,y)$, $P(x,y)\land Q(x,y)$, $P(x,y)\lor Q(x,y)$, $P(x,y)\имеет Q(x,y)$ и $P(x,y)\Leftrightarrow Q(x,y)$ имеют значения истинности F, F, T, F, F соответственно, а когда $x=2$ и $y=3$ имеют истинностные значения Т, Ф, Т, Т, Ф соответственно.
 $\квадрат$
$\квадрат$Используя операции $\lnot$, $\land$, $\lor$, $\implies$, $\Leftrightarrow$, мы можем построить составных выражений, таких как $$ (P\land (\lnot Q))\ подразумевает ((\lnot R)\lor ((\lnot P)\land Q)). $$ Как показывает этот пример, иногда необходимо включать много круглых скобок, чтобы группировать термины в формуле ясно. Как и в алгебре, где умножение имеет приоритет перед сложением, мы можем убрать некоторые скобки согласование определенного порядка, в котором логически операции выполняются. Мы будет применять операции в этом порядке, начиная с от первого к последнему: $\lnot$, $\land$, $\lor$, $\implies$ и $\Leftrightarrow$. Так $$A\подразумевает B\или C\land\lnot D $$ сокращение от $$A\подразумевает (B\или (C\land (\lnot D))). $$ Как и в алгебре, часто разумно включать несколько дополнительных скобок, чтобы убедиться, что предполагаемый смысл понятен. Большая часть информации, которую мы обсудили, может быть резюмирована в таблицы истинности .
 Например, таблица истинности для
$\lnot P$:
Например, таблица истинности для
$\lnot P$:$P$ $\lnot P$ Т Ж Ф Т В этой таблице две строки, потому что есть только две возможности для истинное значение $P$. Другие логические операции используют две переменные, поэтому им требуется 4 строки в их таблицах истинности.
$P$ $Q$ $P\land Q$ $P \lor Q$ $P\Rightarrow Q$ $P\Leftrightarrow Q$ Т Т Т Т Т Т Ж Т Ж Т Т Ж Т Ж Ж Т Ж Ж Ф Ф Ф Ф 9п$ строки в таблице, потому что есть много разных способов назначить T и F для $n$ простых формул в составном выражении.  Таблица истинности для $(P\land Q)\lor \lnot R$ такова:
Таблица истинности для $(P\land Q)\lor \lnot R$ такова:$P$ $Q$ $R$ $P \land Q$ $\lnot R$ $(P \land Q)\lor\lnot R$ Т Т Т Т Ф Т Ж Т Т Ж Ж Ж Т Ж Т Ж Ж Ж Ж Ж Т Ж Ж Ж Т Т Ж Т Т Т Ж Т Ж Ж Т Т Т Ф Ф Ф Т Т Ж Ж Ж Ж Т Т Обратите внимание, как включение промежуточных шагов облегчает работу с таблицей.
 посчитай и прочитай.
посчитай и прочитай.Тавтология — это логическое выражение, которое всегда оценивается как T, то есть последний столбец его таблицы истинности состоит только из Т. Иногда говорят, что тавтология равна 9.1693 действительный ; хотя «действительный» используется в других контекстах как ну, это не должно вызывать путаницы. Например, $(P\land Q)\lor P\Leftrightarrow P$ является тавтологией, поскольку ее таблица истинности такова:
$P$ $Q$ $P\land Q$ $(P\land Q)\lor P$ $(P\land Q)\lor P\Leftrightarrow P$ Т Т Т Т Т Ж Т Ф Ф Т Т Ж Ж Т Т Ж Ж Ж Ж Т Мы перечисляем несколько важных тавтологий в следующей теореме.

Теорема 1.1.3. Справедливы следующие утверждения.
а) $P\стрелка влево \lnot\lnot P$
б) $P\lor Q\Leftrightarrow Q\lor P$
c) $P\land Q\Стрелка влево Q\land P$
d) $(P\land Q)\land R\Стрелка влево P\land(Q\land R)$
e) $(P\lor Q)\lor R\Стрелка влево P\lor(Q\lor R)$
f) $P\land (Q\lor R)\Leftrightarrow (P\land Q)\lor (P\land R)$
g) $P\lor (Q\land R)\Стрелка влево (P\lor Q)\land (P\lor R)$
h) $(P\подразумевает Q)\Стрелка влево (\lnot P\lor Q)$
i) $P\имеет (P\или Q)$
j) $P\land Q\имплицит Q$
k) $(P\стрелка влево Q)\стрелка влево ((P\подразумевает Q)\land (Q\подразумевает P))$
l) $(P\подразумевается Q)\стрелка влево (\lnot Q\подразумевается \lnot P)$
Доказательство. Доказательства оставлены в качестве упражнений. $\qed$
Заметим, что (b) и (c) — коммутативные законы, (d) и (e) — ассоциативные законы и (е) и (ж) говорят, что $\land$ и $\lor$ распределяются друг над другом.
 Это говорит о том, что существует
форма алгебры для логических выражений, аналогичная алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений.
особенно в информатике.
Это говорит о том, что существует
форма алгебры для логических выражений, аналогичная алгебре
для числовых выражений. Этот предмет называется Булева алгебра и имеет множество применений.
особенно в информатике.Если две формулы всегда принимают одно и то же истинностное значение независимо от того, элементы из вселенной дискурса, которые мы заменяем различными переменных, то мы говорим, что они эквивалентны . Стоимость эквивалента формулы в том, что они говорят одно и то же. Это всегда правильный шаг в доказательстве заменить некоторую формулу эквивалентной. Кроме того, многие тавтологии содержат важные идеи для построения доказательств. За например, (k) говорит, что если вы хотите показать, что $P\Leftrightarrow Q$, это можно (и часто целесообразно) разбить доказательство на два части, одна из которых доказывает импликацию $P\implis Q$, а вторая доказывая обратное , $Q\имеет P$.
При чтении теоремы 1.1.3 у вас может возникнуть заметил, что $\land$ и $\lor$ обладают многими схожими свойствами.
 Они называются «двойственными» понятиями — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для своего двойственного без дополнительной работы.
Они называются «двойственными» понятиями — для любого свойства
один, есть почти идентичное свойство, которому удовлетворяет другой,
экземпляры двух операций поменялись местами. Это часто
означает, что когда мы доказываем результат, включающий одно понятие, мы получаем
соответствующий результат для своего двойственного без дополнительной работы.Джордж Буль. Буль (1815–1864) имел только обычное школьное образование, хотя и выучил Греческий и латынь самостоятельно. Он начал свою карьеру в качестве элементарного школьным учителем, но решил, что ему нужно больше узнать о математики, поэтому он начал изучать математику, а также языки, необходимые ему для чтения современной литературы на математика. В 1847 году он опубликовал короткую книгу «Математический анализ». Анализ логики , который, можно справедливо сказать, лег в основу исследования. математической логики. Ключевой вклад работы заключался в переопределить «математику» так, чтобы она означала не просто «изучение чисел и величина», но изучение символов и манипулирование ими в соответствии с к определенным правилам.
 Важность этого уровня абстракции для
будущее математики трудно переоценить. Вероятно, на
Благодаря этой работе он перешел на должность в Куинс-колледж в Корке.
Важность этого уровня абстракции для
будущее математики трудно переоценить. Вероятно, на
Благодаря этой работе он перешел на должность в Куинс-колледж в Корке.В «Исследовании законов мысли» , опубликованном в 1854 г., Буль установил настоящую формальную логику, развивая то, что сегодня называется Булева алгебра или иногда алгебра множеств . Он использовал символы для сложение и умножение как операторы, но в совершенно абстрактном смысл. Сегодня эти символы все еще иногда используются в булевых выражениях. алгебре, хотя символы `$\land$’ и `$\lor$’, и `$\cap$’ и `$\cup$’ также используются. Буль применил алгебраическую манипуляцию к процесс рассуждения. Вот простой пример типа манипуляцию, которую он проделал: уравнение $xy=x$ (которое сегодня можно было бы записать $x\land y = x$ или $x\cap y = x$) означает, что «все вещи, удовлетворяющие $x$ удовлетворяет $y$’, или, говоря нашим языком, $x\имеет y$. Если также $yz=y$ (что есть $y\implis z$), то подстановка $y=yz$ в $xy=x$ дает $x(yz)=x$ или $(xy)z=x$.
 Заменив $xy$ на $x$, получим $xz=x$, или
$x\подразумевает z$. Этот простой пример логического рассуждения используется более
и далее по математике.
92+bD+c=0$, обработка
$D$ как номер , предоставляет информацию о решениях для
дифференциальное уравнение.
Заменив $xy$ на $x$, получим $xz=x$, или
$x\подразумевает z$. Этот простой пример логического рассуждения используется более
и далее по математике.
92+bD+c=0$, обработка
$D$ как номер , предоставляет информацию о решениях для
дифференциальное уравнение.Информация здесь взята из A History of Mathematics, by Карл Б. Бойер, Нью-Йорк: John Wiley and Sons, 1968. Подробнее информацию см. Лекции о десяти британских математиках , автор Александр Макфарлейн, Нью-Йорк: John Wiley & Sons, 1916.
Пример 1.1.1 Постройте таблицы истинности для следующих логических выражений:
а) $(P\land Q)\или \lnot P$
б) $P\имеет (Q\land P)$
c) $(P\land Q)\Стрелка влево (P\lor \lnot R)$
d) $\lnot P\подразумевает \lnot(Q\lor R)$
Пример 1.1.2 Проверьте тавтологии в теореме 1.1.3.
Пример 1.1.3 Предположим, что $P(x,y)$ — это формула «$x+y=4$», а $Q(x,y)$ — это формула «$x
$P(x,y)\land Q(x,y)$, $\lnot P(x,y)\lor Q(x,y)$,
$P(x,y)\подразумевает \lnot Q(x,y)$, $\lnot(P(x,y)\Leftrightarrow Q(x,y))$,
, используя значения:
а) $x=1, y=3$ c) $x=1, y=2$ б) $x=3, y=1$ d) 95 $x=2, y=1$ Пример 1.
 1.4
1.4 \((\neg (p \land q))\leftrightarrow ( \neg p \lor \neg q)\text{.}\)
\(\displaystyle p \lor \neg p\)
\(\displaystyle (p \land q)\to p\)
\(\displaystyle q\to (p\lor q)\)
\(\displaystyle (p \lor q)\leftrightarrow (q \lor p)\)
\((p \land q)\lor (\neg p \land q)\iff q\text{.}\)
\(\displaystyle p \to q \iff\neg q \rightarrow \neg p\)
\(p \lor q \iff q \lor p\text{.
 }\)
}\)\(\displaystyle (p \land r) \lor q\)
\(\displaystyle p\lor (r\lor q)\)
\(\displaystyle r \land p\)
\(\displaystyle \neg r \lor p\)
\(\displaystyle (p\lor q)\land (r\lor q)\)
\(\displaystyle г\п\)
\(\displaystyle r \lor \neg p\)
\(\displaystyle p\to r\)
Построить таблицу истинности для \(x= (p \land \neg q) \lor (r \land p)\text{.}\)
Приведите пример, отличный от самого \(x\), предложения, порожденного \(p\text{,}\) \(q\text{,}\) и \(r\), которое эквивалентно \( х\текст{.}\)
Приведите пример предложения, отличного от \(x\), из которого следует \(x\text{.}\)
Приведите пример предложения, отличного от \(x\), которое следует из \(x\text{.}\)
Докажите, что \(p | q\) эквивалентно \(\neg (p \land q)\text{.}\)
Докажите, что \(\neg p \Leftrightarrow p | p\text{.}\)
Построить \(\land\), используя только обводку Шеффера.
Построить \(\lor\), используя только обводку Шеффера.
а) Найти таблицы истинности для $$ P\land (\lnot Q)\land R, \quad\quad (\lnot P)\land Q\land (\lnot R) $$
b) Используйте их, чтобы найти таблицу истинности для $$ (P\land (\lnot Q)\land R)\lor ((\lnot P)\land Q\land (\lnot R)) $$
c) Используйте метод, предложенный частями (a) и (b) найти формулу со следующей таблицей истинности.
$P$ $Q$ $R$ ??? Т Т Т Т Ж Т Т Ж Т Ж Т Ж Ж Ж Т 9n$ T и F — это последний столбец таблицы истинности для некоторой формулы из $n$ букв.Пример 1.1.5 Если $P_1, P_2,\ldots, P_n$ — это список из $n$ формул, максимальное количество составных формул, использующих этот список, может быть построено, никакие два из которых не эквивалентны?
Эквивалентность и значение ADS
Рассмотрим два предложения, порожденные \(p\) и \(q\text{:}\) \(\neg (p \land q)\) и \(\neg p \lor \neg q\text{.
 } \) На первый взгляд, это разные предложения. По форме они разные, но смысл у них один. Один из способов увидеть это — заменить \(p\) и \(q\text{;}\) фактическими предложениями, такими как \(p\text{:}\) Я был в Торонто; и \(q\text{:}\) я был в Чикаго.
} \) На первый взгляд, это разные предложения. По форме они разные, но смысл у них один. Один из способов увидеть это — заменить \(p\) и \(q\text{;}\) фактическими предложениями, такими как \(p\text{:}\) Я был в Торонто; и \(q\text{:}\) я был в Чикаго.Затем \(\neg (p \land q)\) переводится как «Я не был ни в Торонто, ни в Чикаго», а \(\neg p \lor \neg q\) — как «Я не был в Торонто или я не был в Чикаго». Определите истинностные значения этих предложений. Естественно, для одних они будут истинными, а для других ложными. Важно то, что независимо от того, какие значения истинности они имеют, \(\neg (p \land q)\) и \(\neg p \lor \neg q\) будут иметь одно и то же значение истинности. Самый простой способ убедиться в этом — изучить таблицы истинности этих утверждений.
Таблица 3.3.1. Таблицы истинности для \(\neg (p \land q)\) и \(\neg p \lor \neg q\)\(p\) \(к\) \(\neg (p\land q)\) \(\отр р\лор \отр д \) 0 0 1 1 0 1 1 1 1 0 1 1 1 1 0 0 Во всех четырех случаях \(\neg (p \land q)\) и \(\neg p \lor \neg q\) имеют одинаковое значение истинности.
 Кроме того, когда к ним применяется оператор биусловия, результатом во всех случаях является значение true. Такое предложение называется тавтологией.
Кроме того, когда к ним применяется оператор биусловия, результатом во всех случаях является значение true. Такое предложение называется тавтологией.Подраздел 3.3.1 Тавтологии и противоречия
Определение 3.3.2. Тавтология.
Выражение с логическими переменными, верное во всех случаях, является тавтологией. Число 1 используется для обозначения тавтологии.
Пример 3.3.3. Некоторые тавтологии.
Все нижеследующее является тавтологией, потому что их таблицы истинности состоят из столбца единиц.
Определение 3.3.4. Противоречие.
Выражение с логическими переменными, ложное во всех случаях, называется противоречием.
 Число 0 используется для обозначения противоречия.
Число 0 используется для обозначения противоречия.Пример 3.3.5. Некоторые противоречия.
\(p \land \neg p\) и \((p\lor q)\land (\neg p) \land (\neg q)\) являются противоречиями.
Подраздел 3.3.2 Эквивалентность
Определение 3.3.6. Эквивалентность.
Пусть \(S\) будет набором предложений, и пусть \(r\) и \(s\) будут предложениями, порожденными \(S\text{.}\) \(r\) и \(s\) эквивалентны тогда и только тогда, когда \(r\leftrightarrow s\) является тавтологией. Эквивалентность \(r\) и \(s\) обозначается \(r \iff s\text{.}\)
Эквивалентность для логики, как равенство для алгебры. Точно так же, как существует множество способов записи алгебраического выражения, одно и то же логическое значение может быть выражено многими различными способами.
Пример 3.3.7. Некоторые эквиваленты.
Ниже приведены все эквиваленты:
Все тавтологии эквивалентны друг другу.
Пример 3.3.8. Эквивалентность \(1\).
\(p\lor \neg p\iff 1\text{.}\)
Все противоречия эквивалентны друг другу.
Пример 3.3.9. Эквивалентность \(0\).
\(p\land \neg p\iff 0\text{.}\)
Подраздел 3.3.3 Значение
Рассмотрим два предложения:
Таблица 3.3.10.\(x\text{:}\) Деньги за дверью А; и \(y\text{:}\) Деньги находятся за дверью A или дверью B. Представьте, что вам сказали, что за одной из двух дверей, отмеченных A и B, находится крупная сумма денег, и что одно из двух утверждений \(x\) и \(y\) истинно, а другое ложно. Какую дверь вы бы выбрали? Все, что вам нужно понять, это то, что если \(x\) истинно, то \(y\) также будет истинно. Поскольку мы знаем, что это не может быть так, \(y\) должно быть истинным предложением, а деньги находятся за дверью B.
Это пример ситуации, в которой истинность одного предложения приводит к истинности другого.
 Конечно, \(y\) может быть истинным, когда \(x\) ложным; но \(х\) не может быть истинным, когда \(у\) ложным. В этом случае мы говорим, что \(x\) подразумевает \(y\text{.}\)
Конечно, \(y\) может быть истинным, когда \(x\) ложным; но \(х\) не может быть истинным, когда \(у\) ложным. В этом случае мы говорим, что \(x\) подразумевает \(y\text{.}\)Рассмотрим таблицу истинности \(p \to q\text{,}\) Таблица 3.1.7. Если из \(p\) следует \(q\text{,}\), то третий случай можно исключить, поскольку именно он делает условное суждение ложным.
Определение 3.3.11. Значение.
Пусть \(S\) будет набором предложений, и пусть \(r\) и \(s\) будут предложениями, порожденными \(S\text{.}\). Мы говорим, что \(r\) влечет \( s\), если \(r \to s\) — тавтология. Мы пишем \(r \Rightarrow s\), чтобы указать на это следствие.
Пример 3.3.12. Разделительное дополнение.
Часто используемая импликация, называемая «дизъюнктивным сложением», имеет вид \(p \Rightarrow (p \lor q)\text{,}\), что подтверждается таблицей истинности Таблица 3.3.13.
Таблица 3.3.13. Таблица истинности, чтобы убедиться, что \(p \Rightarrow (p \lor q)\)\(р\) \(к\) \(р\лор д\) \(п\к п\лор д\) 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 1 Если мы позволим \(p\) представлять «Деньги за дверью A», а \(q\) представлять «Деньги за дверью B», \(p \Rightarrow (p \lor q)\) является формализованной версией рассуждений, использованных в примере 3.
 3.12. Обычное название этой импликации — дизъюнктивное сложение. В следующем разделе мы рассмотрим некоторые из наиболее часто используемых импликаций и эквивалентностей.
3.12. Обычное название этой импликации — дизъюнктивное сложение. В следующем разделе мы рассмотрим некоторые из наиболее часто используемых импликаций и эквивалентностей.Когда мы определяли, что мы подразумеваем под предложением, порожденным набором, мы не включали условные и биусловные операторы. Это произошло из-за двух эквивалентностей \(p \to q \Leftrightarrow \neg p \lor q\) и \(p \leftrightarrow q \Leftrightarrow (p \land q) \lor (\neg p \land \neg q) \text{.}\) Таким образом, любое предложение, включающее условные или биусловные операторы, может быть записано эквивалентным образом с использованием только конъюнкции, дизъюнкции и отрицания. Мы могли бы даже обойтись без дизъюнкции, поскольку \(p \lor q\) эквивалентно предложению, в котором используются только конъюнкция и отрицание.
Подраздел 3.3.4 Универсальная операция
Мы завершаем этот раздел последней логической операцией, обводкой Шеффера, которая обладает тем интересным свойством, что из нее могут быть созданы все остальные логические операции.
. Вы можете изучить эту операцию в упражнении 3.3.5.8
Вы можете изучить эту операцию в упражнении 3.3.5.8Определение 3.3.14. Инсульт Шеффера.
Удар Шеффера — это логический оператор, определяемый следующей таблицей истинности:
Таблица 3.3.15. Таблица истинности для инсульта Шеффера\(р\) \(к\) \(п \середина кв\) 0 0 1 0 1 1 1 0 1 1 1 0 Упражнения 3.3.5 Упражнения
1.
Даны следующие предложения, порожденные \(p\text{,}\) \(q\text{,}\) и \(r\text{,}\), которые эквивалентны друг другу?
Ответ.

\(a\Стрелка влево e, d\Стрелка влево f, g\Стрелка влево h\)
2.
3.
Является ли импликация эквивалентной своей обратной? Проверьте свой ответ с помощью таблицы истинности.
Раствор.
Нет. В символической форме вопрос звучит так: Is \((p\to q)\Leftrightarrow (q\to p)\text{?}\) \(\begin{array}{ccccc} p & q & p\to q & q\to p & (p\to q)\leftrightarrow (q\to p) \\ \hline 0 и 0 и 1 и 1 и 1\\ 0 и 1 и 1 и 0 и 0\\ 1 и 0 и 0 и 1 и 0 \\ 1 и 1 и 1 и 1 и 1 \\ \конец{массив}\)
Эта таблица показывает, что импликация не всегда эквивалентна своей обратной.
 4\) возможных предложений.
4\) возможных предложений.6.
Найдите предложение, эквивалентное \(p \lor q\) и использующее только союз и отрицание.
7.
Объясните, почему противоречие влечет за собой любое суждение, а любое суждение влечет за собой тавтологию.
Ответ.
\(0\to p\) и \(p\to 1\) являются тавтологиями.
8.
Значение хода Шеффера состоит в том, что это «универсальная» операция, из которой можно построить все остальные логические операции.
9.
Эквивалентны ли обратное и обратное условного суждения? Проверьте свой ответ с помощью таблицы истинности.
Раствор.

Да. В символической форме вопрос заключается в том, является ли условное суждение \(p \to q\text{,}\) \((q\to p)\Leftrightarrow (\neg p\to \neg q)\text {?}\)
\(\begin{массив}{ccccc} p & q & q\to p & \neg p\to \neg q & (q \to p)\leftrightarrow (\neg p\to \neg q) \\ \hline 0 и 0 и 1 и 1 и 1\\ 0 и 1 и 0 и 0 и 1\\ 1 и 0 и 1 и 1 и 1 \\ 1 и 1 и 1 и 1 и 1 \\ \end{array}\)
Эта таблица показывает, что обратное всегда эквивалентно обратному.
Раздел 1.1
Раздел 1.1Логические формы и эквиваленты Логическая форма и логическая Эквивалентность | Определения | Сложный Заявления | Таблицы истинности
Логическая эквивалентность | Законы Де Моргана | Таблица логических эквивалентов Логический Форма и логическая эквивалентность
Содержание инструкции не совпадает с логической формой.
 Например,
рассмотрим 2 следующих утверждения:
Например,
рассмотрим 2 следующих утверждения:Если Салли проснется поздно или опоздает на автобус, она опоздает на работу. Поэтому, если Салли приходит на работу вовремя, она не проснулся поздно и не опоздал на автобус.
Если x действительное число такое, что x < -2 или x > 2, то x 2 > 4. Следовательно, если x 2 < 4, то х > -2 и х < 2.
Логический анализ не помогает определить ценность аргумента. Вместо это помогает проанализировать форму аргумента, чтобы определить, верна ли вывод следует из истинности предыдущих утверждений. В то время как содержание двух приведенных выше утверждений различно, их логическая форма похожий.
Пусть p обозначает утверждения «Салли просыпается поздно». и «x — действительное число, такое что x < -2».
Пусть q будет обозначать утверждения «Салли опаздывает на автобус». и «x — действительное число, такое что x > -2».
Пусть r обозначают утверждения «Салли опаздывает на работу». и «х 2 > 4».
Тогда общая форма для обоих приведенных выше аргументов:Практические упражнения
ОПРЕДЕЛЕНИЕАргумент: последовательность утверждений, направленных на демонстрацию истины высказывания или утверждения. Выписка: предложение, которое либо истинно, либо ложно, но не оба. Его еще называют предложением. Отрицание: если p — это операторная переменная, отрицание p — это «не p «, обозначаемое ~ p .  Если р верно, то ~ p ложно.
Если р верно, то ~ p ложно.Соединение: , если p и q являются переменными оператора, соединение p и q равно « p и q «, обозначен pq . Конъюнкция истинна только тогда, когда истинны обе переменные. Если 1 или обе переменные ложные, pq является ложным. Отключение: , если p и q являются переменными оператора, дизъюнкция p и q есть « p или q «, обозначен pq . Дизъюнкция истинна, если истинны одна или обе переменные. pq ложно, только если обе переменные ложны. Тавтология: Форма заявления, которая всегда верна.  Правда делает
не полагаться на значения отдельных утверждений, заменяемых
переменные оператора, а на логическую структуру самого оператора.
(т. е. вы получите пятерку в этом классе или нет).
Правда делает
не полагаться на значения отдельных утверждений, заменяемых
переменные оператора, а на логическую структуру самого оператора.
(т. е. вы получите пятерку в этом классе или нет).Противоречие: Форма заявления, которая всегда ложна. Как тавтология, ложность заключается не в отдельных переменных высказываниях, а в логическая структура самого высказывания. (т. е. я всегда лгу).
Составные операторыиспользовать символы (логический И), (логическое ИЛИ), и ~ (НЕ) для построения сложных логических утверждений из более простых.
Пусть p = «Жарко» и пусть q = «Солнечно» Тогда утверждение «Не жарко, но солнечно». можно написать символически как:
~ р д Практические упражнения
Однако утверждения должны иметь четко определенные значения истинности — они должны быть либо истинными, либо ложными. Истинность утверждения может быть выражена
на Таблица правды . А
таблица истинности для данного утверждения отображает результирующие значения истинности для различных
комбинации значений истинности для переменных. Истина о соединении
утверждение может быть логически выведено с использованием известных значений истинности для различных
части высказывания.
Истинность утверждения может быть выражена
на Таблица правды . А
таблица истинности для данного утверждения отображает результирующие значения истинности для различных
комбинации значений истинности для переменных. Истина о соединении
утверждение может быть логически выведено с использованием известных значений истинности для различных
части высказывания.Таблица истинности для ~п Таблица истинности для pq Таблица истинности для pq р ~р р q шт. 
р q шт. Т Ф Т Т Т Т Т Т Ф Т Т Ф Ф Т Ф Т Ф Т Ф Ф Т Т Ф Ф Ф Факс Ф Ф Практические упражнения Логическая эквивалентность:
Две инструкции логически эквивалентны тогда и только тогда, когда их результирующие формы логически эквивалентны, когда идентичны переменные операторов используются для представления операторов компонентов.

Две формы операторов логически эквивалентны тогда и только тогда, когда их результирующие таблицы истинности идентичны для каждого варианта переменных утверждения.
р q pq qp Т Т Т Т Т Ф Ф Ф Ф Т Ф Ф Ф Ф Ф Ф шт.
 и qp имеют одинаковые значения истинности, поэтому они равны логически эквивалентен.
и qp имеют одинаковые значения истинности, поэтому они равны логически эквивалентен. Другие логически эквивалентные операторы включают:
(стр. д) ~(р q) р xor д эксклюзивный или р ~(~п) Двойное отрицание Чтобы проверить логическую эквивалентность двух операторов, создайте таблицу истинности, которая включает каждую переменную для оценки, а затем проверить чтобы увидеть, эквивалентны ли результирующие значения истинности двух утверждений.
Законы Де Моргана
Отрицание союза (логическое И) двух операторов логически эквивалентна дизъюнкции (логическому ИЛИ) каждого оператора отрицание.
 Это звучит как полный рот, но это означает, что «не
(A и B) « логически эквивалентно » не
А или не В» .
Это звучит как полный рот, но это означает, что «не
(A и B) « логически эквивалентно » не
А или не В» . Аналогично, отрицание дизъюнкции двух утверждений логически эквивалентна конъюнкции отрицания каждого утверждения. Помещать просто, «не (А или Б)» логически эквивалентно «не А и не Б» . Символически это можно записать как
.~(pq) ~ р ~q . . . а также . . . ~(пк) ~ р ~q Эти два оператора логически эквивалентны (нажмите здесь для определения), и это можно проверить с помощью таблицы истинности.
Таблица логических Эквиваленты:
Следующая таблица может помочь сократить составные операторы до более простые формы.
 Учитывая переменные оператора p, q, и r ,
тавтология t и противоречие c, следующие
правил логики:
Учитывая переменные оператора p, q, и r ,
тавтология t и противоречие c, следующие
правил логики:Коммутативный р qq стр р д д стр Ассоциативный (стр. р) рп (q р) (стр. р) рп (q р) Распределительный р (q г) (р р) (р р) р (q г) (р р) (р г) Личность р тп р кп Отрицание р ~ пт ~шт. 
Двойное отрицание ~(~р)р Идемпотент р стр стр стр Законы Де Моргана ~(pq)~p ~q ~(pq)~p ~q Универсальный переплет р тт р копия Поглощение р (р д)р р (р к)р Отрицания t и c ~тк ~ карат Логические эквивалентности можно использовать для упрощения форм выписок, для подтверждения или опровергнуть эквивалентность, чтобы создать эффективный и логически правильный компьютер программ или для помощи в разработке цифровых логических схем.



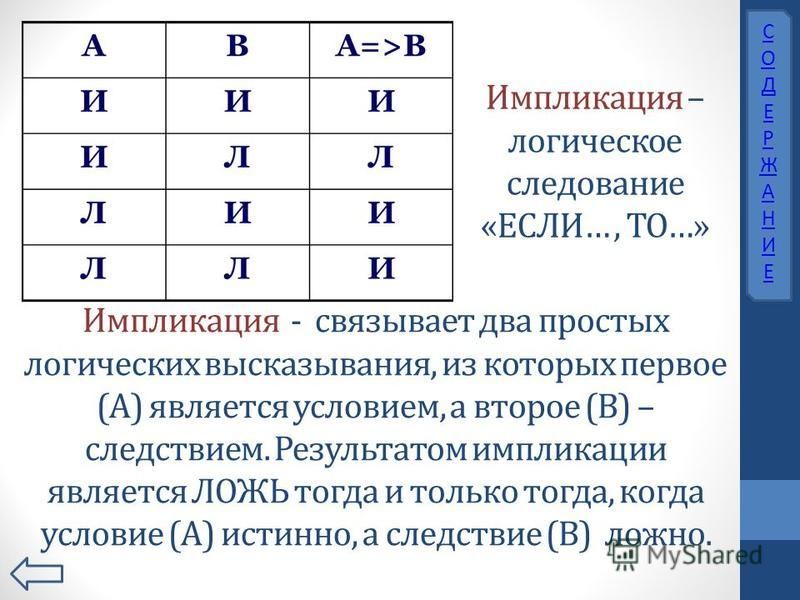
 \] Чтобы второе следствие было ложным, нам нужно, чтобы \[\overline{r} \quad\mbox{было истинным}, \qquad\mbox{and}\qquad \overline{p} \vee \overline{q} \quad\mbox{to be false}.\] Они, в свою очередь, подразумевают, что \(r\) ложно, и оба \(\overline{p}\) и \ (\overline{q}\) ложны; следовательно, и \(p\), и \(q\) верны. Это сделало бы \((p \wedge q) \Rightarrow r\) ложным, что противоречит предположению, что это правда. Таким образом, ([eqn:tautology]) не может быть ложным, это должна быть тавтология.
\] Чтобы второе следствие было ложным, нам нужно, чтобы \[\overline{r} \quad\mbox{было истинным}, \qquad\mbox{and}\qquad \overline{p} \vee \overline{q} \quad\mbox{to be false}.\] Они, в свою очередь, подразумевают, что \(r\) ложно, и оба \(\overline{p}\) и \ (\overline{q}\) ложны; следовательно, и \(p\), и \(q\) верны. Это сделало бы \((p \wedge q) \Rightarrow r\) ложным, что противоречит предположению, что это правда. Таким образом, ([eqn:tautology]) не может быть ложным, это должна быть тавтология. В первом столбце для значений истинности \(p\) заполните верхнюю половину T, а нижнюю половину F. В следующем столбце для значений истинности \(q\) повторите тот же шаблон отдельно, с верхней половиной и нижней половиной. Таким образом, мы разделяем верхнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половину F. Аналогичным образом разделяем нижнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половина с F. Повторите тот же шаблон с третьим столбцом для значений истинности \(r\), и так далее, если у нас есть больше пропозициональных переменных.
В первом столбце для значений истинности \(p\) заполните верхнюю половину T, а нижнюю половину F. В следующем столбце для значений истинности \(q\) повторите тот же шаблон отдельно, с верхней половиной и нижней половиной. Таким образом, мы разделяем верхнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половину F. Аналогичным образом разделяем нижнюю половину второго столбца на две половины, заполняем верхнюю половину T, а нижнюю половина с F. Повторите тот же шаблон с третьим столбцом для значений истинности \(r\), и так далее, если у нас есть больше пропозициональных переменных.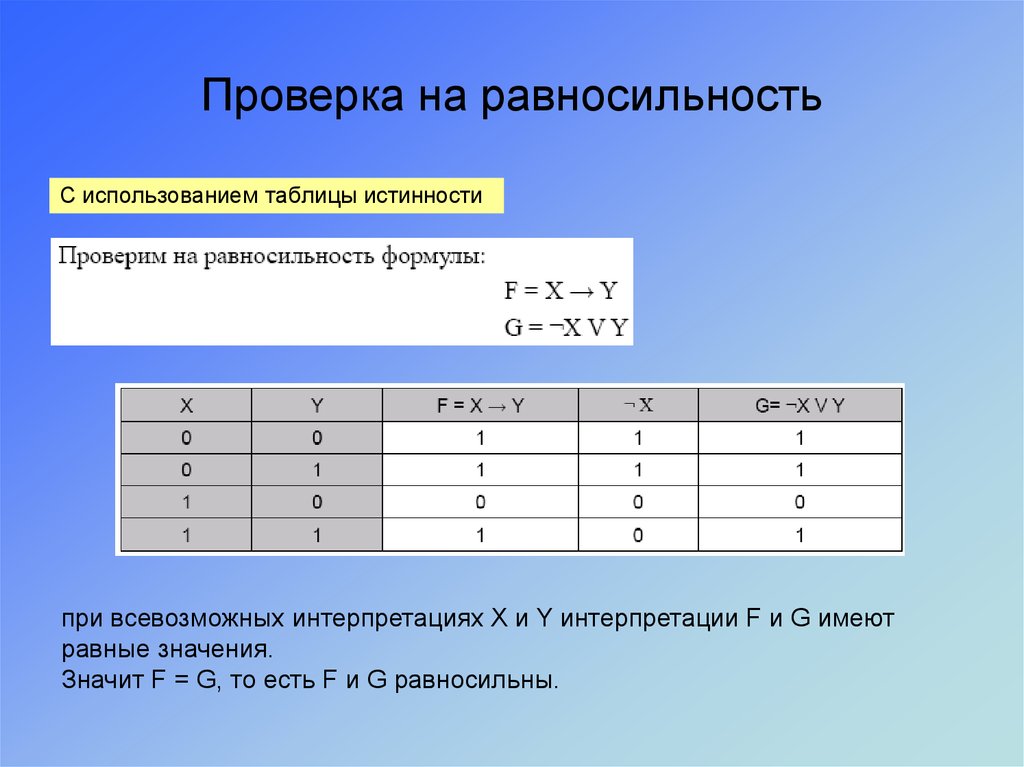 \[\begin{array}{|*{5}{c|}} \hline p & q & p\Rightarrow q & \overline{p} & \overline{p}\vee q \\ \hline \text{ T} & \text{T} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{F} & \text{F } & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{T} \\ \text{F} & \text{F } & \text{T} & \text{T} & \text{T} \\ \hline \end{массив}\] \[% \arraygap{1.25} \begin{массив}{|*{8}{ c|}} \hline p & q & r & q\vee r & p\клин (q\vee r) & p\клин q & q\клин r & (p\клин q)\vee(p\клин r ) \\ \hline \text{T} & \text{T} & \text{T} & \text{T} & \text{T}\phantom{(q\vee{})} & \text{T } & \text{T} & \text{T} \\ \text{T} & \text{T} & \text{F} & \text{T} & \text{T}\phantom{(q\ vee{})} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{T} & \text{T} & \ text{T}\phantom{(q\vee{})} & \text{F} & \text{T} & \text{T} \\ \text{T} & \text{F} & \text{ F} & \text{F} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{F}\phantom{(q\v ee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{F} & \text{T} & \ text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{ T} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{F} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text {F} \\ \hline \end{array}\] Пример ([equiv1]) является важным результатом.
\[\begin{array}{|*{5}{c|}} \hline p & q & p\Rightarrow q & \overline{p} & \overline{p}\vee q \\ \hline \text{ T} & \text{T} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{F} & \text{F } & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{T} \\ \text{F} & \text{F } & \text{T} & \text{T} & \text{T} \\ \hline \end{массив}\] \[% \arraygap{1.25} \begin{массив}{|*{8}{ c|}} \hline p & q & r & q\vee r & p\клин (q\vee r) & p\клин q & q\клин r & (p\клин q)\vee(p\клин r ) \\ \hline \text{T} & \text{T} & \text{T} & \text{T} & \text{T}\phantom{(q\vee{})} & \text{T } & \text{T} & \text{T} \\ \text{T} & \text{T} & \text{F} & \text{T} & \text{T}\phantom{(q\ vee{})} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{T} & \text{T} & \ text{T}\phantom{(q\vee{})} & \text{F} & \text{T} & \text{T} \\ \text{T} & \text{F} & \text{ F} & \text{F} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{F}\phantom{(q\v ee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{F} & \text{T} & \ text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{ T} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{F} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text {F} \\ \hline \end{array}\] Пример ([equiv1]) является важным результатом.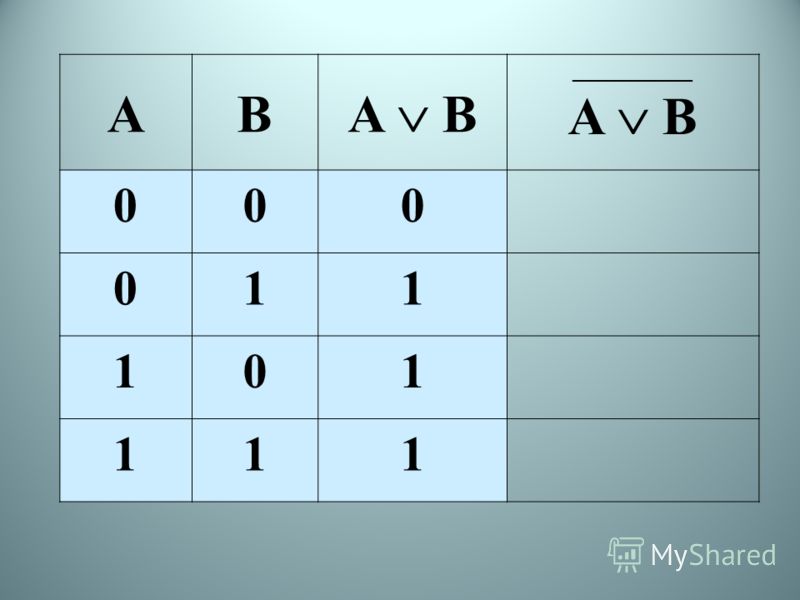 Он говорит, что \(p \Rightarrow q\) истинно, когда происходит одно из следующих двух событий: (i) когда \(p\) ложно, (ii) в противном случае (когда \(p\) истинно) \(q \) должно быть правдой.
Он говорит, что \(p \Rightarrow q\) истинно, когда происходит одно из следующих двух событий: (i) когда \(p\) ложно, (ii) в противном случае (когда \(p\) истинно) \(q \) должно быть правдой.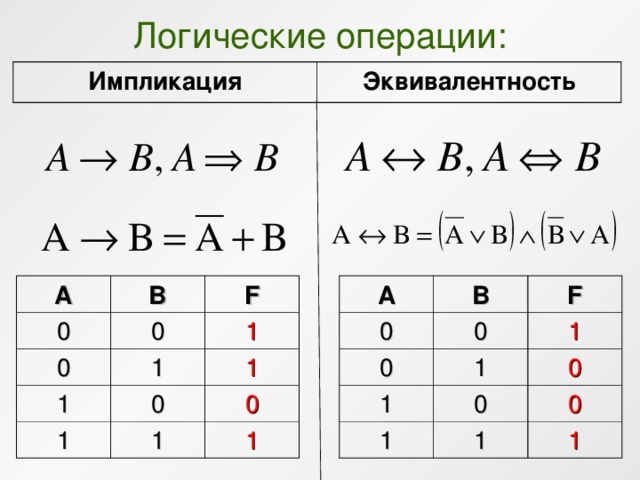 \end{массив}\)
\end{массив}\)
 Это объясняет, почему мы должны убедиться, что операция коммутативна.
Это объясняет, почему мы должны убедиться, что операция коммутативна.
 2=x\), где \(x\) — действительное число. Это верно только тогда, когда \(x=0\) или \(x=1\). Но логические эквивалентности \(p\vee p\equiv p\) и \(p\wedge p\equiv p\) верны для всех \(p\).
2=x\), где \(x\) — действительное число. Это верно только тогда, когда \(x=0\) или \(x=1\). Но логические эквивалентности \(p\vee p\equiv p\) и \(p\wedge p\equiv p\) верны для всех \(p\). Для логических операций идентичность дизъюнкции — F, а идентичность конъюнкции — T.
Для логических операций идентичность дизъюнкции — F, а идентичность конъюнкции — T. Они меняются от включения к исключению, когда мы принимаем отрицание.
Они меняются от включения к исключению, когда мы принимаем отрицание.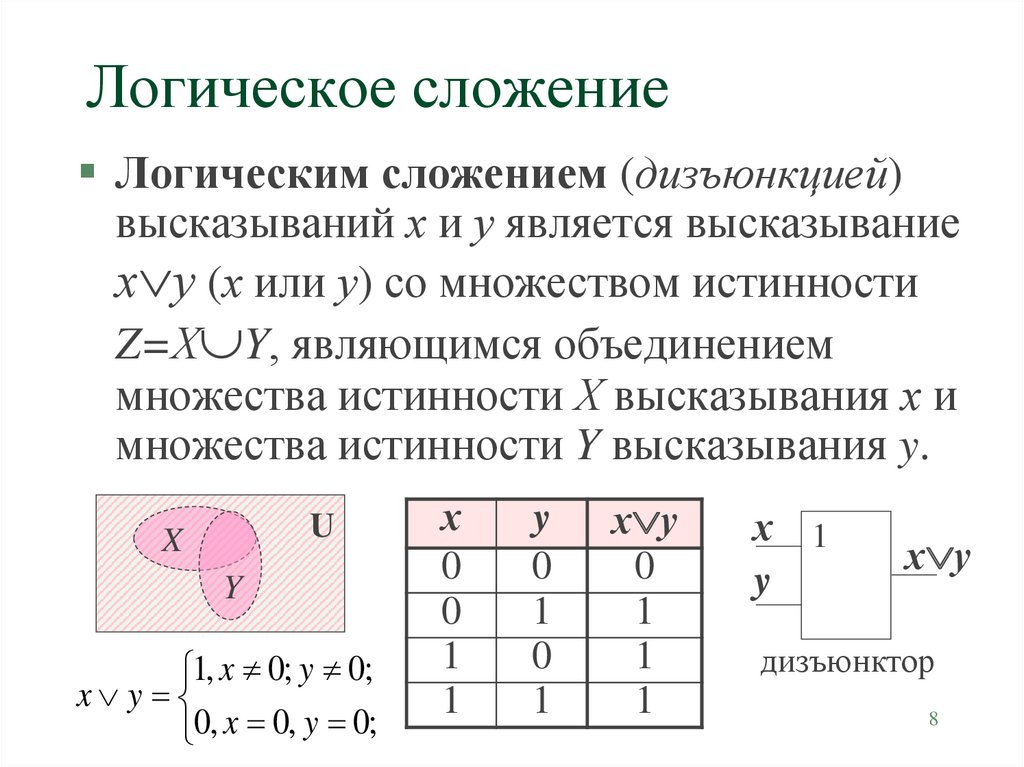 Вместо этого, поскольку \(p\Rightarrow q \equiv \overline{p}\vee q\), из закона Де Моргана следует, что \[\overline{p \Rightarrow q} \equiv \overline{\overline{p} \ vee q} \equiv p \wedge \overline{q}.\] В качестве альтернативы мы можем рассуждать следующим образом. Интерпретируйте \(\overline{p \Rightarrow q}\) как утверждение \(p \Rightarrow q\) ложно. Это требует, чтобы \(p\) было истинным, а \(q\) — ложным, что преобразуется в \(p \wedge \overline{q}\). Таким образом, \(\overline{p\Rightarrow q} \equiv p\wedge \overline{q}\).
Вместо этого, поскольку \(p\Rightarrow q \equiv \overline{p}\vee q\), из закона Де Моргана следует, что \[\overline{p \Rightarrow q} \equiv \overline{\overline{p} \ vee q} \equiv p \wedge \overline{q}.\] В качестве альтернативы мы можем рассуждать следующим образом. Интерпретируйте \(\overline{p \Rightarrow q}\) как утверждение \(p \Rightarrow q\) ложно. Это требует, чтобы \(p\) было истинным, а \(q\) — ложным, что преобразуется в \(p \wedge \overline{q}\). Таким образом, \(\overline{p\Rightarrow q} \equiv p\wedge \overline{q}\). \]
\]

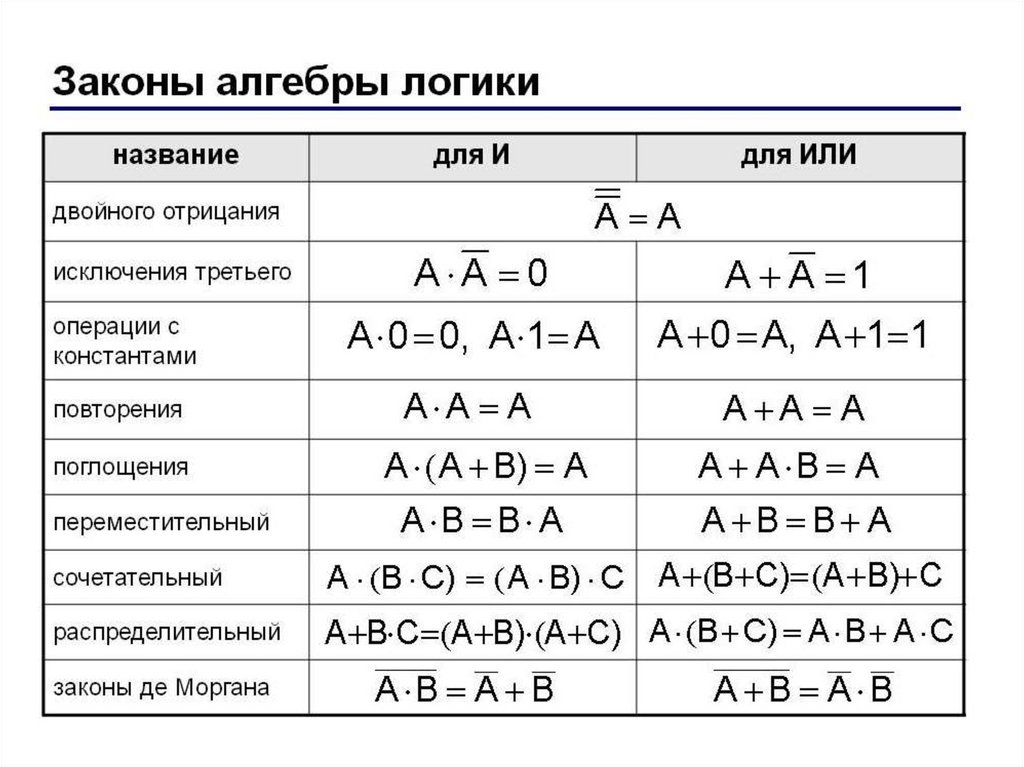
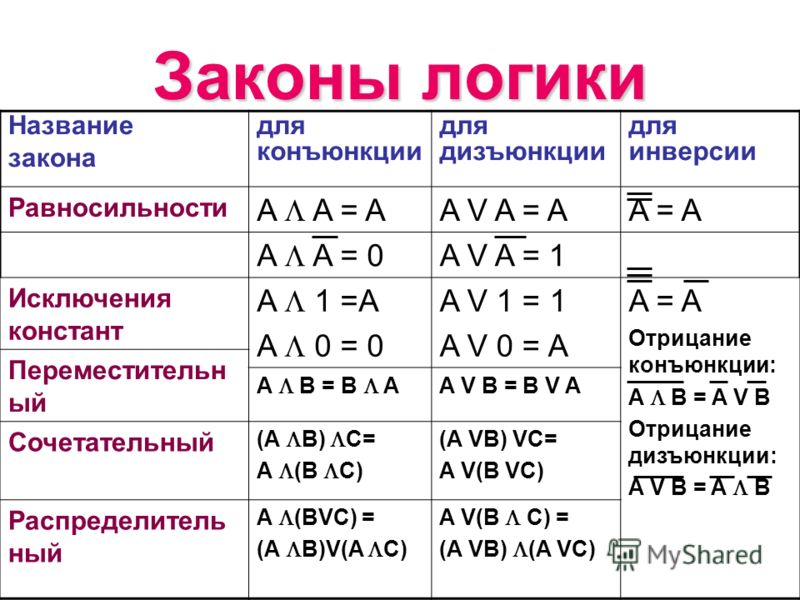



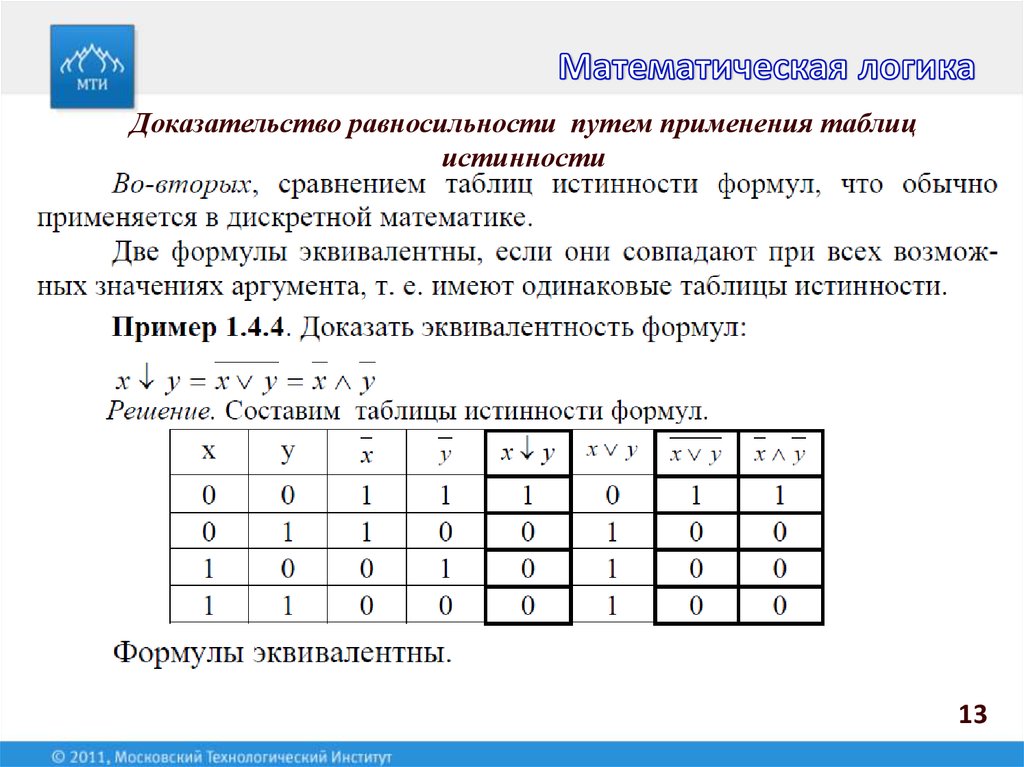
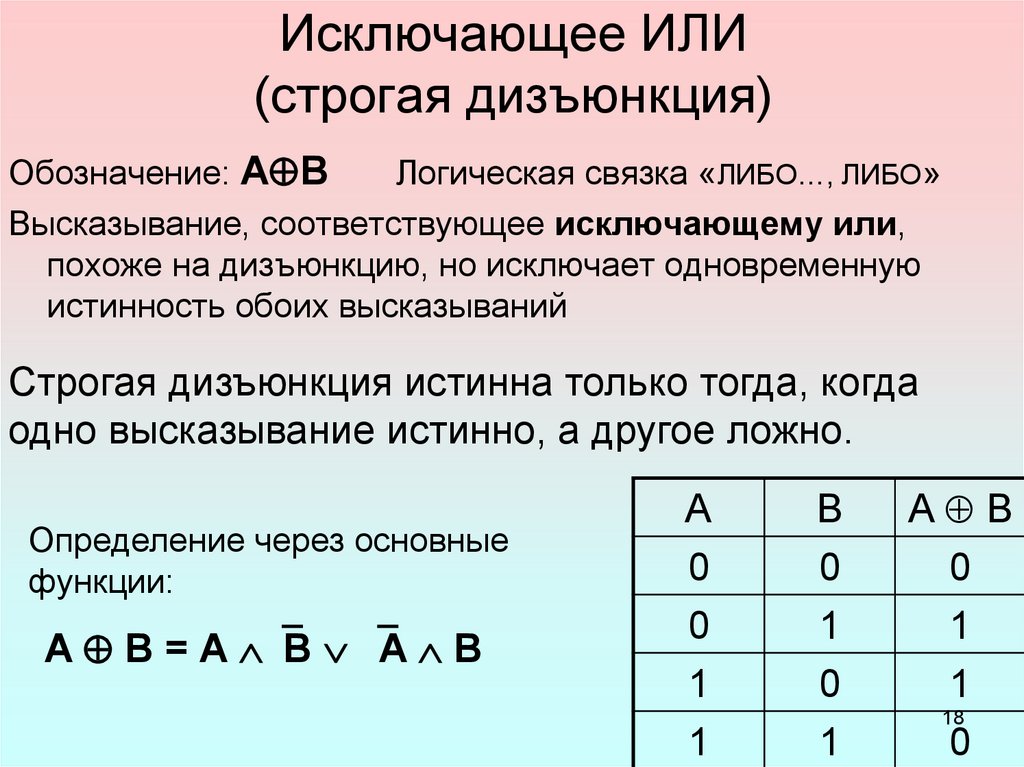 }\)
}\)

 Это не только означает, что вам на самом деле нужно запомнить вдвое меньше, для этого есть четкая причина, которую мы рассмотрим, когда будем обсуждать булевы алгебры в Discrete 2!
Это не только означает, что вам на самом деле нужно запомнить вдвое меньше, для этого есть четкая причина, которую мы рассмотрим, когда будем обсуждать булевы алгебры в Discrete 2!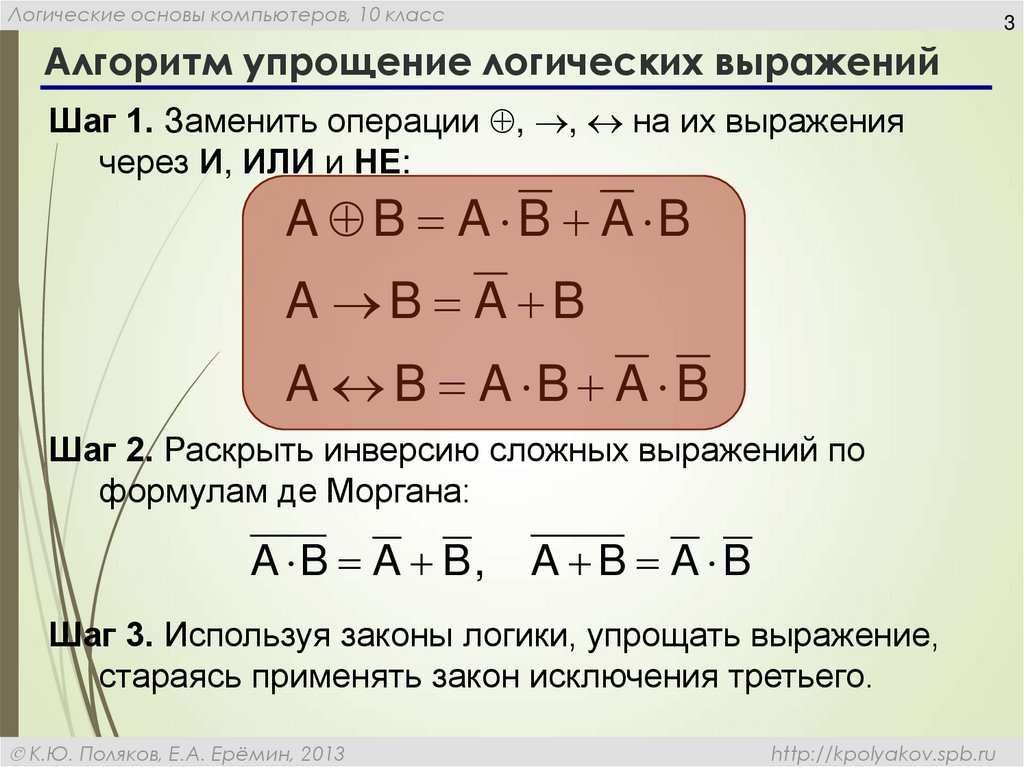 }\) Объясните, откуда вы знаете, что вы правы.
}\) Объясните, откуда вы знаете, что вы правы.
 }\) Это обязательно ложно, поэтому также эквивалентно \(p \клин \neg p\text{. }\)
}\) Это обязательно ложно, поэтому также эквивалентно \(p \клин \neg p\text{. }\) .. это тавтология!
.. это тавтология! Итак, мы начнем с рассмотрения
таблицы истинности для пяти логических связок.
Итак, мы начнем с рассмотрения
таблицы истинности для пяти логических связок.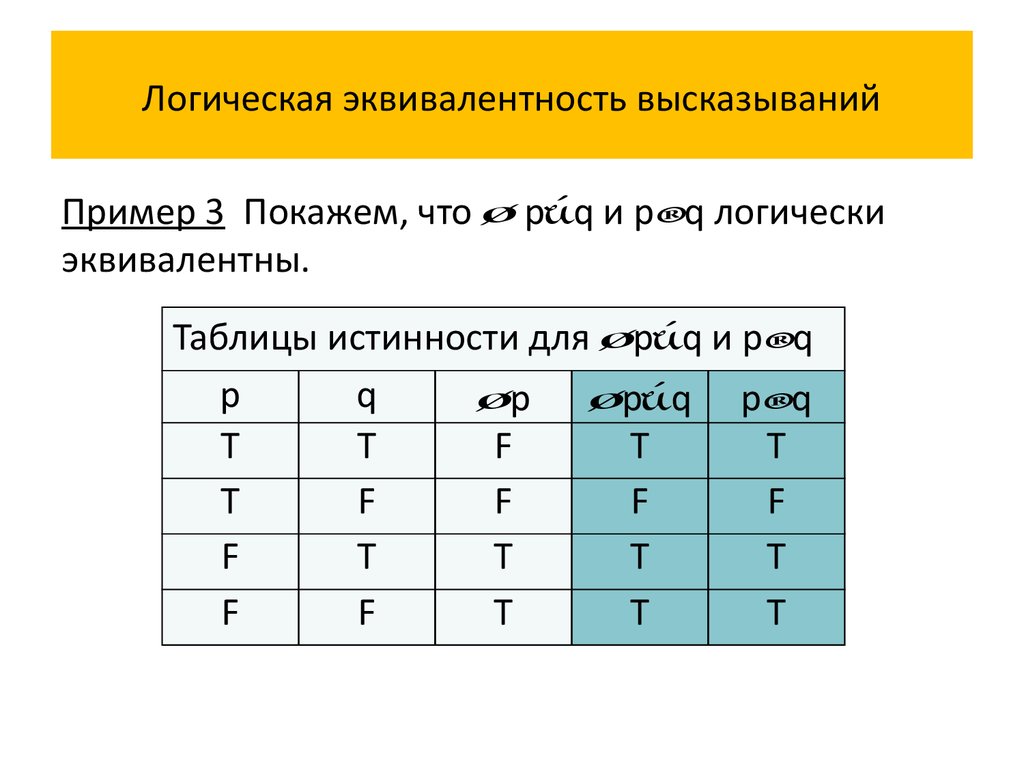 0037 правда что я даю вам доллар. Поскольку я сдержал свое обещание, верно . Это соответствует первой строке таблицы.
0037 правда что я даю вам доллар. Поскольку я сдержал свое обещание, верно . Это соответствует первой строке таблицы. Вы будете использовать эти таблицы для построения
таблицы для более сложных предложений. Легче продемонстрировать
что делать, чем описать это словами, так вы увидите порядок
выработано на примерах.
Вы будете использовать эти таблицы для построения
таблицы для более сложных предложений. Легче продемонстрировать
что делать, чем описать это словами, так вы увидите порядок
выработано на примерах. Вы можете, для
например, запишите значения истинности «под» логическим
связки составного высказывания, постепенно дорастающие до
столбец для «основной» связки.
Вы можете, для
например, запишите значения истинности «под» логическим
связки составного высказывания, постепенно дорастающие до
столбец для «основной» связки. «И» верно только в том случае, если обе части
«и» верны; в противном случае оно ложно. Поэтому я смотрю на
третья и четвертая колонки; если оба верны («T»), я ставлю T
в пятой колонке, иначе ставлю F.
«И» верно только в том случае, если обе части
«и» верны; в противном случае оно ложно. Поэтому я смотрю на
третья и четвертая колонки; если оба верны («T»), я ставлю T
в пятой колонке, иначе ставлю F.
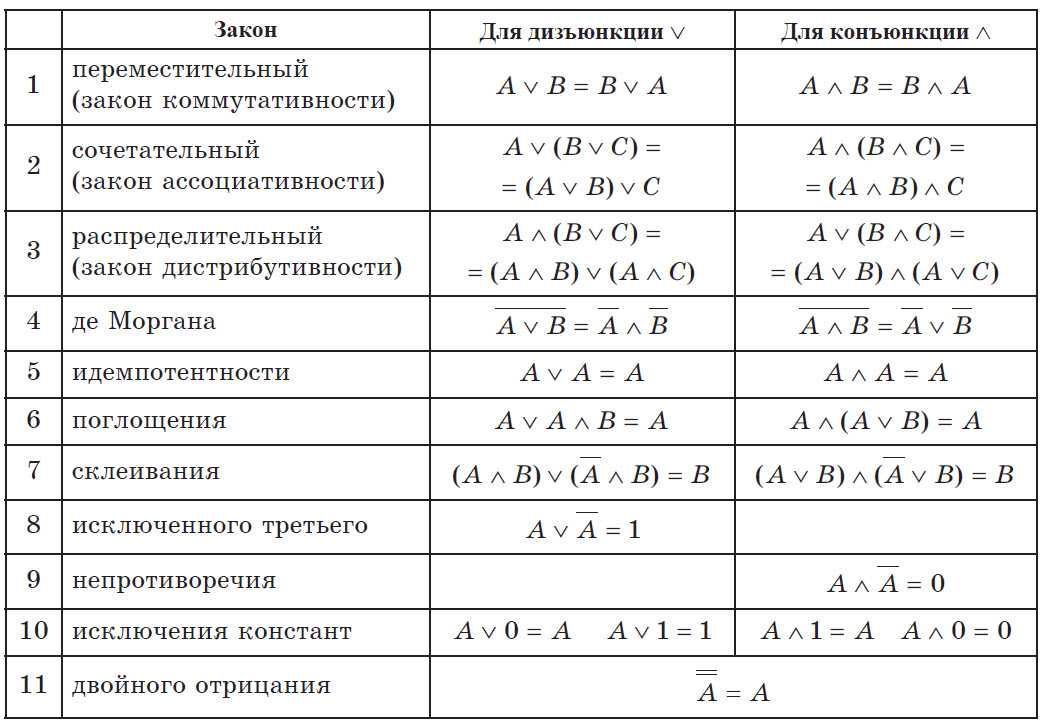

 Однако проще настроить таблицу, содержащую X и Y, а затем
проверьте, совпадают ли столбцы для X и для Y.
Однако проще настроить таблицу, содержащую X и Y, а затем
проверьте, совпадают ли столбцы для X и для Y.


 )
)