Как решается система уравнения: Решение систем уравнений — метод как решить систему линейных уравнений

Как решается система уравнений? Методы решения систем уравнения.

Home » 7 класс » Как решается система уравнений? Методы решения систем уравнения.

Posted on 22.05.201302.07.2021Author admin 43

Методы решения систем уравнения.

Разберем два вида решения систем уравнения:

1. Решение системы методом подстановки.
2. Решение системы методом почленного сложения (вычитания) уравнений системы.

Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения выражаем одну переменную.
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.

Чтобы решить систему методом почленного сложения (вычитания) нужно:
1.Выбрать переменную у которой будем делать одинаковые коэффициенты.

2.Складываем или вычитаем уравнения, в итоге получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение. Находим решение системы.

Решением системы являются точки пересечения графиков функции.

Рассмотрим подробно на примерах решение систем.

Пример №1:

Решим методом подстановки

Решение системы уравнений методом подстановки

2x+5y=1 (1 уравнение)
x-10y=3 (2 уравнение)

1. Выражаем
Видно что во втором уравнении имеется переменная x с коэффициентом 1,отсюда получается что легче всего выразить переменную x из второго уравнения.
x=3+10y

2.После того как выразили подставляем в первое уравнение 3+10y вместо переменной x.
2(3+10y)+5y=1

3.Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (раскрываем скобки )
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=-0,2

Решением системы уравнения является точки пересечений графиков, следовательно нам нужно найти x и у, потому что точка пересечения состоит их x и y. Найдем x, в первом пункте где мы выражали туда подставляем y.
x=3+10y
x=3+10*(-0,2)=1

Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2)

Пример №2:

Решим методом почленного сложения (вычитания).

Решение системы уравнений методом сложения

3x-2y=1 (1 уравнение)
2x-3y=-10 (2 уравнение)

1.Выбираем переменную, допустим, выбираем x. В первом уравнении у переменной x коэффициент 3, во втором 2. Нужно сделать коэффициенты одинаковыми, для этого мы имеем право домножить уравнения или поделить на любое число. Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.

3x-2y=1 |*2
6x-4y=2

2x-3y=-10 |*3
6x-9y=-30

2.Из первого уравнения вычтем второе, чтобы избавиться от переменной x.Решаем линейное уравнение.
__6x-4y=2
6x-9y=-30
-4y+9y=2+30

5y=32 | :5
y=6,4

3.Находим x. Подставляем в любое из уравнений найденный y, допустим в первое уравнение.

3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6

Точкой пересечения будет x=4,6; y=6,4
Ответ: (4,6; 6,4)

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

Category: 7 класс, Уроки Tag: Система уравнений 43 комментария

Элементарная алгебра

Элементарная алгебра

С.Т. Завало. Элементарная алгебра. Изд-во «Просвещение», М., 1964 г. В основу этой книги положен курс лекций по элементарной алгебре, читавшийся мною на протяжении ряда лет в Черкасском государственном педагогическом институте. Первая глава книги — вступительная. В ней сжато изложены сведения о некоторых математических понятиях, с которыми читателю придется встретиться в последующих главах. В главах II—X изложен учебный материал по элементарной алгебре, предусмотренный программой специального курса элементарной математики для студентов-математиков педагогических институтов. Книга рассчитана на студентов-математиков педагогических институтов. Она может быть также пособием для учителей математики средней школы. Оглавление Глава I. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ § 2. Понятия кольца и поля § 3. Упорядоченные поля § 4. Понятие функции и аналитического выражения § 5. Элементарные функции и их классификация § 6. Метод математической индукции Глава II. ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНЕНИЯХ § 1. Понятие уравнения. Решения уравнения § 2. Классификация уравнений, изучаемых в элементарной математике § 3. Равносильность уравнений § 4. Преобразование уравнений при их решении Глава III. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ОДНИМ НЕИЗВЕСТНЫМ § 1. Алгебраические уравнения n-й степени с одним неизвестным § 2. Корни квадратного трехчлена § 3. Исследование квадратного трехчлена над полем действительных чисел § 4. Двучленные уравнения § 5. Трехчленные уравнения, приводящиеся к квадратным § 6. Симметрические уравнения § 7. Алгебраическое уравнение n-й степени с рациональными коэффициентами § 8. Частные приемы решения уравнений высших степеней § 9. Дробно-рациональные уравнения Глава IV. ТЕОРИЯ СОЕДИНЕНИЙ § 2. Перестановки § 3. Сочетания § 4. Размещения § 5. Перестановки с повторениями § 6. Сочетания с повторениями § 7. Размещения с повторениями Глава V. БИНОМ НЬЮТОНА И ПОЛИНОМИАЛЬНАЯ ТЕОРЕМА § 1. Бином Ньютона § 2. Биномиальные коэффициенты и их основные свойства § 3. Треугольник Паскаля § 4. Полиномиальная теорема § 5. Вычисление сумм степеней первых n чисел натурального ряда Глава VI. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Многочлен от нескольких переменных и его каноническая форма § 2. Однородный многочлен от n переменных и число его членов § 3. Число членов в каноническом представлении многочлена от n переменных § 4. Тождественность двух многочленов § 5. Тождественные преобразования многочленов. Тождество Лагранжа § 6. Применение метода неопределенных коэффициентов при выполнении алгебраических действий над многочленами Глава VII. СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ § 1. Понятие системы уравнений § 2. Равносильность систем уравнений § 3. Уравнения и системы уравнений, являющиеся следствием данной системы уравнений § 4. Основные элементарные методы решения систем уравнений § 5. Решение нелинейных систем алгебраических уравнений элементарными методами 1. Решение системы двух уравнений с двумя неизвестными, из которых одно—второй степени, а другое — первой. 2. Решение системы двух уравнений второй степени с двумя неизвестными, которые не имеют членов первой степени. 3. Решение системы двух уравнений второй степени с двумя неизвестными в общем виде. 4. Решение системы двух однородных уравнений с двумя неизвестными. 5. Решение системы двух уравнений с двумя неизвестными, одно из которых однородное, а второе не однородное. 7. Решение нелинейной системы алгебраических уравнений, в состав которой входят линейные уравнения. 8. Решение нелинейной системы алгебраических уравнений, левая часть одного из которых представляется в виде произведения. § 6. Графическое решение нелинейных систем алгебраических уравнений с двумя неизвестными Глава VIII. НЕРАВЕНСТВА § 1. Основные свойства неравенств § 2. Тождественные неравенства § 3. Применение неравенств для определения наибольших и наименьших значений § 4. Решение неравенств § 5. Решение алгебраических неравенств с одним неизвестным первой и второй степени § 6. Решение систем алгебраических неравенств первой степени с двумя неизвестными § 7. Применение неравенств для задания числовых и точечных множеств Глава IX. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1. Корни с натуральными показателями в поле действительных чисел § 2. Тождественные преобразования иррациональных выражений в поле действительных чисел § 3. Решение иррациональных уравнений и систем, в состав которых входят иррациональные уравнения, в поле действительных чисел Глава X. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ В ПОЛЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 1. Теоретические основы решения показательных и логарифмических уравнений § 2. Решение показательных уравнений с одним неизвестным § 3. Решение логарифмических уравнений с одним неизвестным § 4. Решение трансцендентных уравнений, приводящихся к показательным и логарифмическим уравнениям § 5. Решение некоторых трансцендентных систем уравнений § 6. Графические способы решения трансцендентных уравнений и систем ЛИТЕРАТУРА

систем уравнений с тремя переменными | безграничная алгебра |

Системы уравнений

Решение систем уравнений с тремя переменными

Система уравнений с тремя переменными состоит из двух или более уравнений, каждое из которых содержит от одной до трех переменных.

Цели обучения

Решите систему уравнений с тремя переменными графически, используя замену или исключение

Ключевые выводы

Ключевые моменты

• В системе уравнений с тремя переменными можно иметь одно или несколько уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x , у и z . Введение переменной z  означает, что отображаемые на графике функции теперь представляют собой плоскости, а не линии.
• Метод подстановки включает в себя нахождение одной из переменных в одном из уравнений и подстановку ее в остальные уравнения для сокращения системы. Повторяйте, пока не останется одно уравнение, а затем, используя это уравнение, вернитесь назад, чтобы решить предыдущие уравнения.
• Графический метод включает построение системы в виде графика и нахождение единственной точки пересечения плоскостей.
• Метод исключения включает добавление или вычитание кратных значений одного уравнения из других уравнений, исключение переменных из каждого уравнения до тех пор, пока в каждом уравнении не останется одна переменная.

Ключевые термины

• система уравнений с тремя переменными : Набор из одного или нескольких уравнений, каждое из которых может содержать одну или более из трех переменных, обычно x, y и z.
• система уравнений : Набор уравнений с несколькими переменными, которые можно решить, используя определенный набор значений.

Системы уравнений с тремя переменными

В математике одновременные уравнения представляют собой набор уравнений, содержащих несколько переменных. Этот набор часто называют системой уравнений

. Решением системы уравнений является конкретная спецификация значений всех переменных, которая одновременно удовлетворяет всем уравнениям. Графически решение находится там, где функции пересекаются.

В системе уравнений с тремя переменными может быть одно или несколько уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x , y и z . Введение переменной z  означает, что отображаемые на графике функции теперь представляют собой плоскости, а не линии.

Простой пример

Это набор линейных уравнений, также известный как линейная система уравнений, с тремя переменными:

{3x+2y-z=6-2x+2y+z=3x+y+z=4\left\{\begin{matrix} 3x+2y-z=6\\ -2x+2y+z=3\ \ x+y+z=4\\ \end{matrix}\right.⎩

⎨

⎧​3x+2y−z=6−2x+2y+z=3x+y+z=4​

Решение этой системы уравнений:

{x=1y=2z=1\left\{\begin{matrix} x=1\\ y=2\\ z=1\\ \end{matrix}\right .⎩

⎨

⎧​x=1y=2z=1​

Подставьте эти значения к каждому из уравнений, чтобы убедиться, что решение удовлетворяет всем трем уравнениям.

Решение систем уравнений с тремя переменными

Графический метод

Графический метод решения системы уравнений с тремя переменными заключается в построении плоскостей, которые образуются при построении графика каждого уравнения системы, и последующем нахождении точки пересечения всех трех плоскостей. Единственная точка, в которой пересекаются все три плоскости, является единственным решением системы.

Система линейных уравнений: На этом изображении показана система из трех уравнений с тремя переменными. Точка пересечения (белая точка) является единственным решением этой системы.

Метод замены

Метод подстановки для решения системы уравнений с тремя переменными включает в себя определение уравнения, которое можно легко записать с одной переменной в качестве предмета (путем решения уравнения для этой переменной). Затем подставьте это выражение там, где эта переменная появляется в двух других уравнениях, тем самым получив меньшую систему с меньшим количеством переменных. После того, как эта меньшая система будет решена, будь то дальнейшее применение метода подстановки или других методов, подставьте решения, найденные для переменных, обратно в первое выражение в правой части.

Например, рассмотрим следующую систему уравнений:

{3x+2y−z=6−2x+2y+z=3x+y+z=4\left\{\begin{matrix} 3x+2y-z= 6\\ -2x+2y+z=3\\ x+y+z=4\\ \end{matrix}\right.⎩

⎨

⎧​3x+2y−z=6−2x+2y+ z=3x+y+z=4​

Поскольку коэффициент при z уже равен 1 в первом уравнении, найдите z , чтобы получить:

z=3x+2y−6z=3x+2y-6z =3x+2y−6

Подставим это выражение вместо z в два других уравнения:

{−2x+2y+(3x+2y−6)=3x+y+(3x+2y−6)=4\left \{\begin{matrix} -2x+2y+(3x+2y-6)=3\\ x+y+(3x+2y-6)=4\\ \end{matrix}\right.{−2x+2y+( 3x+2y−6)=3x+y+(3x+2y−6)=4​

Эта новая система упрощается до:

{x+4y=94x+3y=10\left\{\begin{matrix} x+4y=9\\ 4x+3y=10\\ \end{matrix}\right . {x+4y=94x+3y=10​

Теперь, решая x в первом уравнении, получаем:

x=9−4yx=9-4yx=9−4y

.

Подставьте это выражение для x в последнее уравнение системы и решите для y :

4(9−4y)+3y=1036−16y+3y=1013y=26y=2\displaystyle \begin{выравнивание} 4(9-4г)+3г &=10 \\36-16л+3г&=10 \\13г&=26 \\у&=2 \end{выравнивание}4(9−4y)+3y36−16y+3y13yy​=10=10=26=2​

Теперь, когда у вас есть значение y , повторите уравнение. Подставьте

y=2y=2y=2

 в уравнение

x=9−4yx=9-4yx=9−4y

, чтобы получить

x=1x=1x=1

.

Снова подставьте

(1,2)(1,2)(1,2)

в первое уравнение с подстановкой и найдите z :

z=3x+2y−6z=(3 ⋅1)+(2⋅2)−6z=1\begin {выравнивание}z&=3x+2y-6 \\z&=(3 \cdot 1)+(2 \cdot 2) -6 \\г&=1 \end{align}zzz​=3x+2y−6=(3⋅1)+(2⋅2)−6=1​

Следовательно, решение системы уравнений

(1,2,1)(1,2,1)(1,2,1)

.

Метод исключения

Исключение с помощью разумного умножения — еще один широко используемый метод решения одновременных линейных уравнений. Он использует общие принципы, согласно которым каждая часть уравнения по-прежнему равна другой, когда обе части умножаются (или делятся) на одну и ту же величину или когда одна и та же величина добавляется (или вычитается) из обеих частей.

По мере того, как уравнения упрощаются за счет исключения некоторых переменных, переменная в конечном итоге появляется в полностью решаемой форме, и это значение затем можно «обратно подставить» в ранее полученные уравнения, подставив это значение вместо переменной. Как правило, каждая «обратная замена» может позволить решить другую переменную в системе.

Рассмотрим следующую систему:

{x+y+z=2x−y+3z=42x+2y+z=3\left\{\begin{matrix} x+y+z=2\\ x -y+3z=4\\ 2x+2y+z=3\\ \end{matrix}\right.⎩

⎨

⎧​x+y+z=2x−y+3z=42x+2y+z=3​

Используя метод исключения, начните с вычитания первого уравнения из второго и упрощения:

x− y+3z−(x+y+z)=4−2−2y+2z=2\displaystyle \begin{выравнивание} x-y+3z-(x+y+z)&=4-2 \\-2y+2z&=2 \end{align}x−y+3z−(x+y+z)−2y+2z​=4−2=2​

Теперь у нас есть следующая система уравнений:

{x+y+z =2−2y+2z=22x+2y+z=3\left\{\begin{matrix} x+y+z=2\\ -2y+2z=2\\ 2x+2y+z=3\\ \ конец{матрица}\справа. ⎩

⎨

⎧​x+y+z=2−2y+2z=22x+2y+z=3​

Теперь вычтите два раза первое уравнение из третьего уравнения, чтобы получить

2x+2y+z−2 (x+y+z)=3−2(2)2x+2y+z−2x−2y−2z=−1z=1\begin {align}2x+2y+z-2(x+y+z)& =3-2(2) \\2x+2y+z-2x-2y-2z&=-1 \\г&=1 \end {align}2x+2y+z−2(x+y+z)2x+2y+z−2x−2y−2zz​=3−2(2)=−1=1​

Выполнение этого показывает новая система:

{x+y+z=2−2y+2z=2z=1\left\{\begin{matrix} x+y+z=2\\ -2y+2z=2\\ z= 1\\ \end{matrix}\right.⎩

⎨

⎧​x+y+z=2−2y+2z=2z=1​

Затем вычтите дважды третье уравнение из второго уравнения и упростите:

−2y+2z−2z=2−2y=0 \begin {выравнивание} -2y+2z-2z&=2-2 \\у&=0 \end {align}−2y+2z−2zy​=2−2=0​

Это показывает новую систему:

{x+y+z=2y=0z=1\left\{\begin{ матрица} x+y+z=2\\ y=0\\ z=1\\ \end{matrix}\right. ⎩

⎨

⎧​x+y+z=2y=0z=1​

Наконец, вычтите третье и второе уравнение из первого уравнения, чтобы получить

x+y+z-y-z=2-0-1x=1\begin {выравнивание} x+y+z-y-z&=2-0-1 \\х&=1 \end {align}x+y+z−y−zx​=2−0−1=1​​

Таким образом, окончательная решенная система будет следующей:

{x=1y=0z=1\left\ {\begin{matrix} x=1\\ y=0\\ z=1\\ \end{matrix}\right.⎩

⎨

⎧​x=1y=0z=1​

Несогласованный и зависимый Системы с тремя переменными

Системы уравнений с тремя переменными бывают независимыми, зависимыми или несовместными; каждый случай может быть установлен алгебраически и представлен графически.

Цели обучения

Объясните графически, что означает, что системы уравнений с тремя переменными являются несовместимыми или зависимыми, а также как алгебраически распознать, когда это так. решения. Графически бесконечное количество решений находится на линии или плоскости, которая служит пересечением трех плоскостей в пространстве.

Решение зависимой системы методом исключения приводит к выражению, которое всегда истинно, например

0=00 = 00=0

.

Несовместимые системы не имеют решения. Графически система без решения изображается тремя плоскостями, не имеющими общих точек.

Решение несовместной системы методом исключения приводит к утверждению, которое является противоречием, например,

3=03 = 03=0

.

Ключевые термины

• Независимая система : Система уравнений с единственным решением. Для систем уравнений с тремя переменными это решение представляет собой упорядоченную тройку

  (x,y,z)(x, y, z)(x,y,z)

  , который представляет единственную точку пересечения трех плоскостей.
• Зависимая система : Система уравнений с бесконечным числом решений. Для систем уравнений с тремя переменными существует бесконечное число решений на прямой или плоскости, являющейся пересечением трех плоскостей в пространстве.
• Несовместимая система : Система уравнений без решения. Система уравнений с тремя переменными, не имеющая решений, представлена ​​тремя плоскостями, не имеющими общих точек.

Идентификация зависимых и несовместимых систем

Напомним, что решение линейной системы — это такое присвоение чисел переменным, при котором одновременно выполняются все уравнения. Решение системы уравнений с тремя переменными представляет собой упорядоченную тройку

(x,y,z)(x, y, z)(x,y,z)

и описывает точку пересечения трех плоскостей в пространстве .

Возможны три варианта решения системы трех уравнений с тремя переменными:

• Независимые системы имеют единственное решение. Решение системы методом исключения приводит к одной упорядоченной тройке

  (x,y,z)(x, y, z)(x,y,z)

  . Графически упорядоченная тройка определяет точку, являющуюся пересечением трех плоскостей в пространстве.
• Зависимые системы имеют бесконечное количество решений. Графически решения попадают на линию или плоскость, являющуюся пересечением трех плоскостей в пространстве.
• Непоследовательный 9Системы 0021 не имеют решений. Графически система без решения изображается тремя плоскостями, не имеющими общих точек.

Зависимые системы уравнений с тремя переменными

Из работы с системами уравнений с двумя переменными мы знаем, что зависимая система уравнений имеет бесконечное число решений. То же верно и для зависимых систем уравнений с тремя переменными. Бесконечное количество решений может быть результатом нескольких ситуаций. Три плоскости могут быть одинаковыми, так что решение одного уравнения будет решением двух других уравнений. Все три уравнения могут быть разными, но они пересекаются на прямой, которая имеет бесконечные решения (графическое представление см. ниже). Или два уравнения могут быть одинаковыми и пересекать третье по прямой (см. пример задачи для графического представления).

Зависимые системы: Пример трех различных уравнений, пересекающихся на прямой.

Например, рассмотрим эту систему уравнений:

\left\\begin{matrix} \begin {выравнивание} 2x + y — 3z &= 0 \\ 4х + 2у — 6з &= 0 \\ х — у + г &= 0 \конец {выровнять} \end{матрица} \right.

Сначала умножьте первое уравнение на

−2-2−2

и добавьте его ко второму уравнению:

−2(2x+y−3z)+(4x+2y−6z)=0+0 (−4x+4x)+(−2y+2y)+(6z−6z)=00=0\begin {align} -2(2x + y — 3z) + (4x + 2y — 6z) &= 0 + 0 \\ (-4x + 4x) + (-2y + 2y) + (6z — 6z) &= 0 \\ 0 &= 0 \end {align}−2(2x+y−3z)+(4x+2y−6z)(−4x+4x)+(−2y+2y)+(6z−6z)0​=0+0=0= 0

Нам не нужно продолжать. В результате мы получаем тождество

0=00 = 00=0

, которое говорит нам, что эта система имеет бесконечное число решений. Есть и другие способы начать решать эту систему, например, умножить третье уравнение на

−2-2−2

и добавить его к первому уравнению. Затем мы проделаем те же шаги, что и выше, и получим тот же результат:

0=00 = 00=0

.

Если бы мы построили график каждого из трех уравнений, у нас были бы три плоскости, изображенные ниже. Обратите внимание, что две плоскости одинаковы и пересекают третью плоскость по прямой. Набор решений бесконечен, так как все точки вдоль линии пересечения будут удовлетворять всем трем уравнениям.

Зависимая система : Два уравнения представляют одну и ту же плоскость, и они пересекают третью плоскость по прямой.

Несовместные системы уравнений с тремя переменными

Так же, как и с системами уравнений с двумя переменными, мы можем столкнуться с несовместной системой уравнений с тремя переменными, а это означает, что она не имеет решения, удовлетворяющего всем трем уравнениям. Уравнения могут представлять три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые пересекают две другие, но не в одном и том же месте. Процесс исключения приведет к ложному утверждению, например,

3=73 = 73=7

или какое-то другое противоречие.

Несогласованные системы : Все три рисунка представляют системы три на три без решения. а) Три плоскости пересекаются друг с другом по трем различным параллельным прямым, не пересекающимся в одной точке. (b) Две плоскости параллельны и пересекаются с третьей плоскостью, но не друг с другом. в) Все три плоскости параллельны, поэтому точек пересечения нет.

Например, рассмотрим систему уравнений

\слева\\начать{матрицу} \begin {выравнивание} x — 3y + z &= 4\\ -х + 2у — 5з &= 3 \\ 5x — 13y + 13z &= 8 \конец {выровнять} \end{матрица} \right.

Используя метод исключения для решения системы уравнений с тремя переменными, обратите внимание, что мы можем сложить первое и второе уравнения, чтобы сократить

xxx

:

(x−3y+z)+(−x+2y− 5z)=4+3(x−x)+(−3y+2y)+(z−5z)=7−y−4z=7\begin {align}(x — 3y + z) + (-x + 2y — 5з)&=4+3\ (х — х) + (-3у + 2у) + (з-5з) &= 7 \\ -y — 4z &= 7 \end {выравнивание}(x−3y+z)+(−x+2y−5z)(x−x)+(−3y+2y)+(z−5z)−y−4z​=4+3=7 =7​

Затем умножьте первое уравнение на

−5-5−5

и добавьте к третьему уравнению:

−5(x−3y+z)+(5x−13y+13z)=−5 (4)+8(-5x+5x)+(15y-13y)+(-5z+13z)=-20+82y+8z=-12\begin {align} -5(x — 3y + z) + ( 5х — 13у + 13з) &= -5(4) + 8 \\ (-5x + 5x) + (15y — 13y) + (-5z + 13z) &= -20 + 8\ 2г + 8г &= -12 \end {align}−5(x−3y+z)+(5x−13y+13z)(−5x+5x)+(15y−13y)+(−5z+13z)2y+8z​=−5(4 )+8=−20+8=−12​​

Теперь обратите внимание, что у нас есть система уравнений с двумя переменными:

\слева\\начать{матрицу} \begin {выравнивание} -y — 4z &= 7 \\ 2г + 8г &= -12 \конец {выровнять} \end {матрица} \right.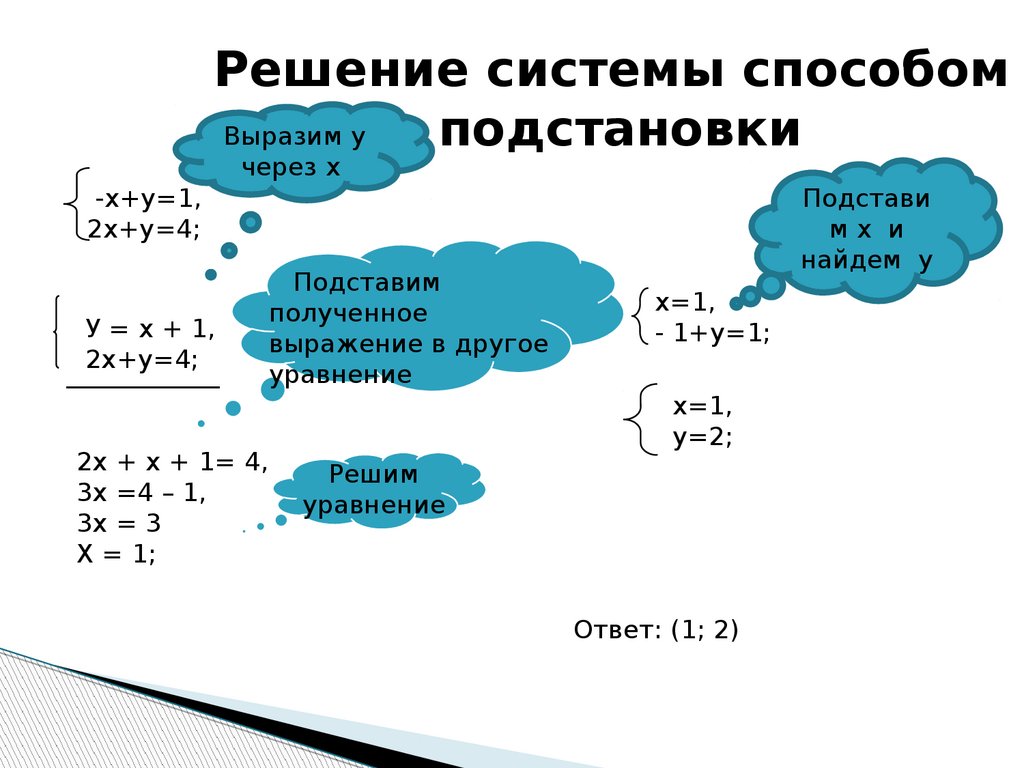

Мы можем решить это, умножив верхнее уравнение на 2 и добавив его к нижнему уравнению:

2(−y−4z)+(2y+8z)=2(7)−12(−2y+2y) +(−8z+8z)=14−120=2\begin {align} 2(-y-4z) + (2y + 8z) &= 2(7) -12 \\ (-2у + 2у) + (-8з + 8з) &= 14 — 12\ 0 &= 2 \end {align}2(-y-4z)+(2y+8z)(-2y+2y)+(-8z+8z)0​=2(7)−12=14−12=2​

Окончательное уравнение

0=20 = 20=2

противоречие, поэтому делаем вывод, что система уравнений несовместна, а значит, не имеет решения.

Лицензии и авторство

Контент под лицензией CC, совместно используемый ранее

• Курирование и пересмотр. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права

Лицензионный контент CC, конкретное указание авторства

• Линейная алгебра/Решение линейных систем. Предоставлено : Wikibooks. Лицензия : CC BY-SA: Attribution-ShareAlike
• Система уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
• Разделение секретов-3-точка. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/File:Secretsharing-3-point.png. Лицензия : Общественное достояние: неизвестно Авторские права
• Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Предварительный расчет. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution
• Обмен секретами — 3 точки. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторские права
• OpenStax Precalculus. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution
• Precalculus. Предоставлено : OpenStax. Лицензия : CC BY: Attribution
• Precalculus. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Атрибуция

Предыдущая

Следующая

Системы линейных уравнений

Цели

1. Понять определение Rn и что означает использование Rn для обозначения точек на геометрическом объекте.
2. Картинки: решений систем линейных уравнений, наборы параметризованных решений.
3. Словарный запас: согласованный , несовместимый , набор решений .

В первой половине этого учебника мы будем в основном заниматься пониманием решений систем линейных уравнений.

Определение

Уравнение с неизвестными x,y,z,… называется линейным , если обе части уравнения представляют собой сумму (постоянных) кратных x,y,z,… плюс необязательная константа.

Например,

3x+4y=2z-x-z=100

— это линейные уравнения, а

3x+yz=3sin(x)−cos(y)=2

нет.

Обычно мы переносим неизвестные в левую часть уравнения, а константы — в правую.

Система линейных уравнений представляет собой набор нескольких линейных уравнений, таких как

Ax+2y+3z=62x−3y+2z=143x+y−z=−2.(1.1.1)

Определение (наборы решений)

• Решение системы уравнений представляет собой список чисел x, y, z,…, которые делают все уравнения истинными одновременно.
• Набор решений системы уравнений представляет собой совокупность всех решений.
• Решить систему означает найти все решения с формулами, включающими некоторое количество параметров.

Система линейных уравнений может не иметь решения. Например, не существует чисел x и y, для которых одновременно верны следующие два уравнения:

Сх+2у=3х+2у=-3.

В этом случае набор решений пуст . Поскольку это довольно важное свойство системы уравнений, оно имеет собственное название.

Определение

Система уравнений называется несовместимой , если она не имеет решений. Он называется последовательным, иначе .

Решением системы уравнений с n переменными является список из n чисел. Например, (x,y,z)=(1,−2,3) является решением (1.1.1). Поскольку в этом тексте мы будем изучать решения систем уравнений, самое время закрепить наши представления о списках чисел.

Мы используем R для обозначения множества всех действительных чисел, т. е. числовой прямой. Он содержит такие числа, как 0,32,−π,104,…

.

Определение

Пусть n — целое положительное число. Определяем

Rn=все упорядоченные n-наборы вещественных чисел(x1,x2,x3,…,xn).

Набор из n действительных чисел называется точкой Rn.

Другими словами, Rn — это просто набор всех (упорядоченных) списков n действительных чисел. Через мгновение мы нарисуем Rn, но имейте в виду, что это определение . Например, (0,32,−π) и (1,−2,3) являются точками R3.

Пример (числовая строка)

Когда n=1, мы просто возвращаем R: R1=R. Геометрически это числовая линия.

−3−2−10123

Пример (евклидова плоскость)

Когда n=2, мы можем думать о R2 как о плоскости xy. Мы можем это сделать, потому что каждая точка на плоскости может быть представлена ​​упорядоченной парой действительных чисел, а именно ее координатами x и y.

(1,2)(0,−3)

Пример (3-пробел)

Когда n=3, мы можем думать о R3 как о пространстве , в котором мы (кажется) живем. Мы можем сделать это, потому что каждая точка в пространстве может быть представлена ​​упорядоченной тройкой действительных чисел, а именно ее x-, y- и z-координаты.

(1,−1,3)(−2,2,2)

Интерактивный: Точки в 3-пространстве

Так что же такое R4? или Р5? или Рн? Их труднее визуализировать, поэтому вам придется вернуться к определению: Rn — это множество всех упорядоченных n-кортежей действительных чисел (x1,x2,x3,…,xn).

Они по-прежнему являются «геометрическими» пространствами в том смысле, что наша интуиция относительно R2 и R3 часто распространяется на Rn.

Мы дадим определения и сформулируем теоремы, которые применимы к любому Rn, но мы будем рисовать только для R2 и R3.

Сила использования этих пространств заключается в возможности обозначать различные интересующие объекты, такие как геометрические объекты и решения систем уравнений, точками Rn.

Пример (цветовое пространство)

Пример (поток трафика)

Пример (QR-коды)

В приведенных выше примерах было полезно с психологической точки зрения заменить список из четырех чисел (представляющих транспортный поток) или 841 числа (представляющих QR-код) одним фрагментом данных: точкой в ​​некотором Rn. Это мощная концепция; начиная с раздела 2.2, мы почти исключительно будем записывать решения систем линейных уравнений таким образом.

Перед обсуждением того, как решить приведенную ниже систему линейных уравнений, полезно посмотреть на некоторые изображения того, как эти наборы решений выглядят геометрически.

Одно уравнение с двумя переменными

Рассмотрим линейное уравнение x+y=1. Мы можем переписать это как y=1−x, что определяет линию на плоскости: наклон равен −1, а точка пересечения с осью x равна 1.

Определение (линии)

Для наших целей линия — это луч, который является прямым и бесконечный в обоих направлениях.

Одно уравнение с тремя переменными

Рассмотрим линейное уравнение x+y+z=1. Это неявное уравнение для плоскости в пространстве.

Определение (плоскости)

Плоскость представляет собой плоский лист, бесконечный во всех направлениях.

Два уравнения с двумя переменными

Теперь рассмотрим систему двух линейных уравнений

Сх-3у=-32х+у=8.

Каждое уравнение индивидуально определяет линию на плоскости, показанную ниже.

Решением системы обоих уравнений является пара чисел (x,y), которая делает оба уравнения истинными одновременно. Другими словами, это как точка, лежащая одновременно на обеих прямых. На картинке выше видно, что есть только одна точка пересечения прямых: следовательно, эта система имеет ровно одно решение. (Это решение (3,2), как может убедиться читатель.)

Обычно две линии на плоскости пересекаются в одной точке, но, конечно, это не всегда так. Рассмотрим теперь систему уравнений

Сх-3у=-3х-3у=3.

Они определяют параллельных линий на плоскости.

Тот факт, что линии не пересекаются, означает, что система уравнений не имеет решения. Конечно, это легко увидеть алгебраически: если x−3y=−3, то не может быть и так, что x−3y=3.

Есть еще одна возможность. Рассмотрим систему уравнений

Сх-3у=-32х-6у=-6.

Второе уравнение кратно первому, поэтому эти уравнения определяют та же строка в плоскости.

В этом случае существует бесконечно много решений системы уравнений.

Два уравнения с тремя переменными

Рассмотрим систему двух линейных уравнений

Вх+у+г=1х-г=0.

Каждое уравнение индивидуально определяет плоскость в пространстве. Решениями системы обоих уравнений являются точки, лежащие на обеих плоскостях. На картинке ниже мы видим, что плоскости пересекаются по прямой. В частности, эта система имеет бесконечно много решений.

Рисунок 21. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по красной линии, которая является набором решений системы обоих уравнений.

Согласно этому определению, решение системы уравнений означает запись всех решений в терминах некоторого числа параметров. Мы дадим систематический способ сделать это в разделе 1. 3; пока мы даем параметрические описания в примерах предыдущего пункта.

строк

Рассмотрим линейное уравнение x+y=1 из этого примера. В этом контексте мы называем x+y=1 числом 9.0020 неявное уравнение линии. Мы можем записать ту же строку в параметрической форме следующим образом:

(x,y)=(t,1−t)для любого t∈R.

Это означает, что каждая точка на прямой имеет вид (t,1−t) для некоторого действительного числа t. В этом случае мы называем t параметром , так как он параметризует точек на линии.

t=0t=1t=−1

Теперь рассмотрим систему двух линейных уравнений

Вх+у+г=1х-г=0

этого примера. В совокупности они образуют неявные уравнения для линии в R3. (Для определения линии в пространстве необходимы как минимум два уравнения.) Эта линия также имеет параметрическую форму с одним параметром t:

(х, у, г) = (т, 1-2т, т).

Рисунок 24. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по желтой линии, которая параметризуется выражением (x,y,z)=(t,1−2t,t). Переместите ползунок, чтобы изменить параметризованную точку.

Обратите внимание, что в каждом случае параметр t позволяет нам использовать R до метка точек на линии. Однако ни одна из прямых не совпадает с числовой прямой R: действительно, каждая точка первой строки имеет две координаты, например точка (0,1), а каждая точка второй строки имеет три координаты, например (0,1 ,0).

Самолеты

Рассмотрим линейное уравнение x+y+z=1 из этого примера. Это неявное уравнение плоскости в пространстве. Эта плоскость имеет уравнение в параметрической форме : мы можем записать каждую точку на плоскости как

(x,y,z)=(1−t−w,t,w)для любого t,w∈R.

В этом случае нам нужны два параметра t и w для описания всех точек на плоскости.

Рисунок 26. Плоскость в R3 определяется уравнением x+y+z=1. Эта плоскость параметризуется двумя числами t,w; переместите ползунки, чтобы изменить параметризованную точку.

Обратите внимание, что параметры t,w позволяют нам использовать R2 для меток точек на плоскости.