Периметр трапеции прямоугольной: Периметр прямоугольной трапеции, описанной… — Задание 6 ЕГЭ по математике (Планиметрия)

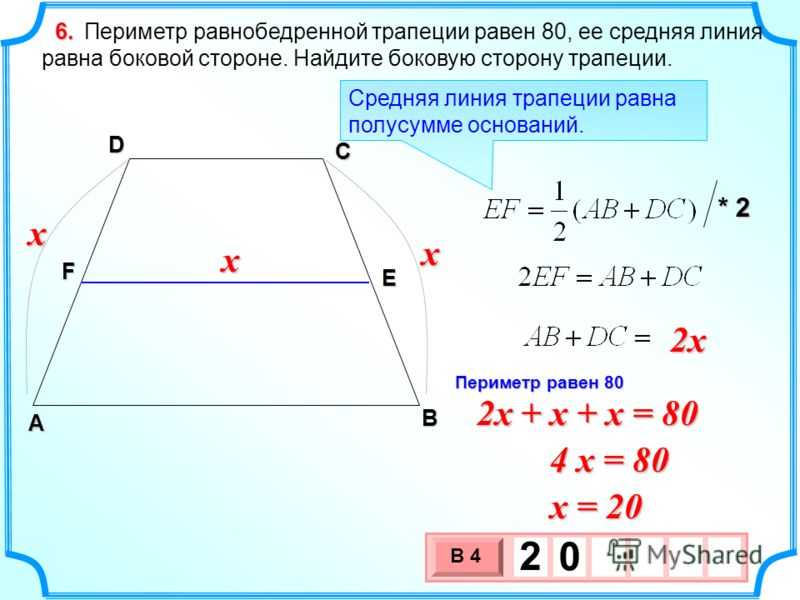
как найти, формула, через среднюю линию

Содержание:

• Основные свойства трапеции
• Способы нахождений периметра
  • По всем сторонам
  • По сторонам равнобедренной трапеции
  • Через среднюю линию
• Примеры решения задач

Содержание

• Основные свойства трапеции
• Способы нахождений периметра
  • По всем сторонам
  • По сторонам равнобедренной трапеции
  • Через среднюю линию
• Примеры решения задач

Определения

​Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.

Периметр трапеции — это сумма длин всех его сторон.

Основные свойства трапеции

• средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;

 

• биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;

 

• треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;

 

• треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;

 

• если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;

 

• точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;

 

• середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;

 

Свойства равнобедренной трапеции

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
• диагонали равны;
• равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
• если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.

Способы нахождений периметра

Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.

По всем сторонам

 

Формула для нахождения периметра выглядит так:

P=a+b+c+d

где a, b, c, d — стороны трапеции.

По сторонам равнобедренной трапеции

 

Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:

\(P=2\times a+b+c\)

или

\(P=2\times c+a+b\)

Через среднюю линию

 

Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:

\(P=2\times l+AB+CD\)

где l — средняя линия фигуры.

Примеры решения задач

Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.

Задача 1

Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.

Решение:

Нам пригодится самая первая формула для расчета:

P=a+b+c+d.

Подставляем значения и получаем:

P=4+7+5+10=26\;см.

Ответ: 26 см.

Задача 2

Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.

Решение:

Так как трапеция равнобедренная, удобнее всего будет использовать формулу:

\(P=2\times a+b+c\)

Таким образом, получается:

\(P=2\times 7+5+8=27\) см.

Ответ: 27 см.

Задача 3

Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.

Решение:

Считать будем по формуле

\(P=2\times l+a+c\)

\(P=2\times 6+5+9=26\) см.

Ответ: 26 см.

Насколько полезной была для вас статья?

Рейтинг: 3.82 (Голосов: 11)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Периметр трапеции в задачах ЕГЭ: что такое периметр трапеции

Главная » Геометрия » Периметр трапеции

Геометрия

Автор Ольга Викторовна Опубликовано 03.04.2020

Периметр трапеции часто нужно определить в задачах по геометрии. Периметр трапеции определяется также как и периметр любой другой фигуры на плоскости:

Периметр плоской фигуры – есть сумма всех сторон фигуры.

Периметр трапеции

Периметр трапеции – есть сумма всех сторон трапеции.

Чему равен периметр равнобедренной трапеции – то же самое – сумме всех ее сторон.

Содержание

В задачах ЕГЭ вы найдете периметр трапеции. Например,

Задача 1

Около окружности описана трапеция, периметр которой равен 60. Найдите длину ее средней линии.

Решение:

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противолежащих сторон равны:

 

АD+CD=DC+AB=P_ABCD /2,

Где P_ABCD  – периметр трапеции. В самом деле P_ABCD =AD+CB+DC+AB=2(DC+AB), а значит, DC+AB=P_ABCD /2

Средняя линия трапеции – это полусумма ее оснований, то есть MN=(DC+AB)/2=(P_ABCD /2)/2=P_ABCD /4 = 60/4=15 .

Ответ: 15.

Задача 2

Около окружности описана трапеция, периметр которой равен 44. Найдите длину ее средней линии.

Решение. Рассуждаем аналогично и получаем MN=(DC+AB)/2=(P_ABCD /2)/2=P_ABCD /4 = 44/4=11.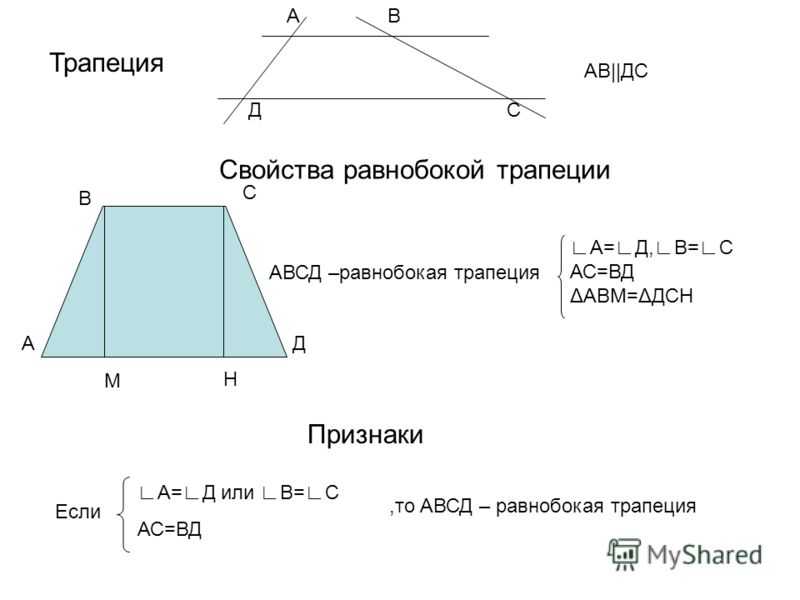

Ответ: 11.

То есть мы сами с вами вывели лайфхак для решения этой задачи:

Лайфхак 1

Если в трапецию вписана окружность, и дан периметр трапеции, то для того чтобы найти среднюю линию трапеции, нужно периметр разделить на 4.

И обратный лайфхак:

Лайфхак 2

Если в трапецию можно вписать окружность, и дана средняя линия трапеции (l), то формула периметра трапеции P:

P=4l

Применим наш лайфхак 1 к решению следующей задачи?

Задача 3

Около окружности описана трапеция, периметр которой равен 30. Найдите длину ее средней линии.

Вычисление

Делим периметр на 4 и получаем среднюю линию трапеции: 30/4=7,5.

Ответ: 7,5.

Задача 4

Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 37, найдите радиус окружности.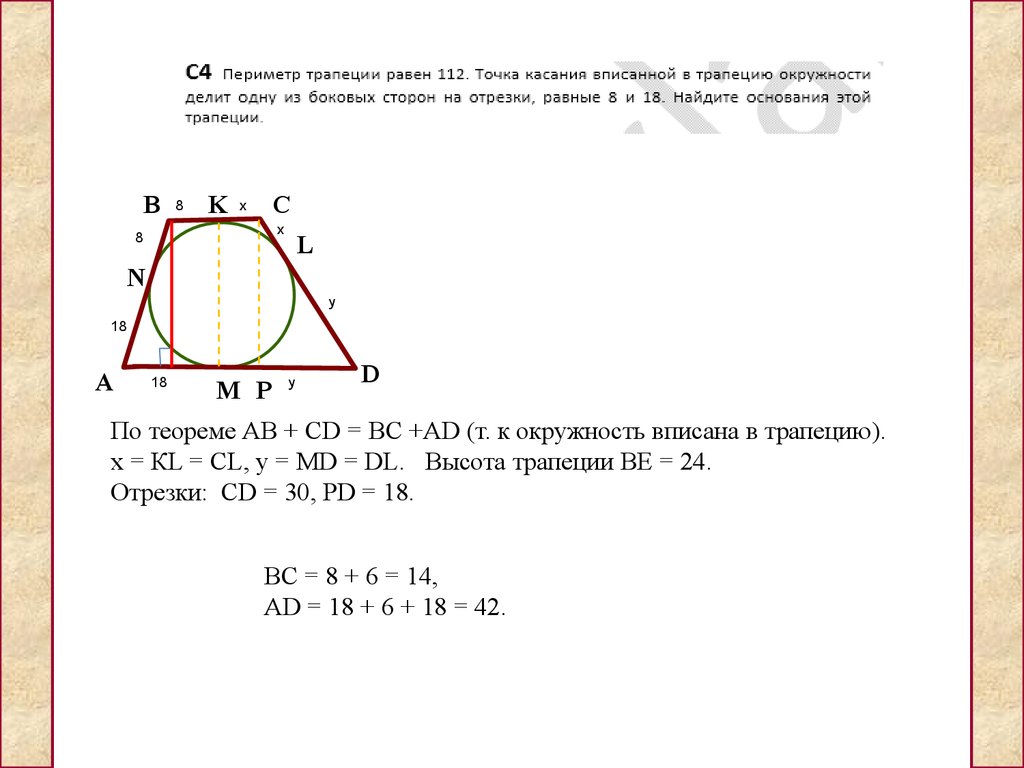

Решение. Периметр трапеции равен:  АD+DC+CB+AB=P_ABCD       (1)

В трапецию можно вписать окружность, если суммы длин противоположных сторон равны. То есть, имеем: AD+CB=DC+AB   (2)

С учетом (2) равенство (1) можно записать в виде:  2(АD+CB)=P_ABCD       (3)

Теперь давайте посмотрим на вот такой рисунок:

Видно, что сторона AD=2R, где R – радиус окружности.

Тогда, AD+CB=2R+37, тогда равенство (3): 2(2R+37)=100.

Решаем уравнение, относительно R:

4R+74=100

4R=100-74

4R=26

R=26/4

R= 6,5

Ответ: 6,5

Задача 5

Из сборника ЕГЭ по математике профильный уровень 2020 год вариант 19 задание 6.
Около окружности описана трапеция, периметр которой равен 28. Найдите длину ее средней линии.
Решение: пользуясь лайфхаком, который мы вывели выше, вычисляем длину средней линии трепеции: делим периметр трапеции на 4.
Получаем 28:4=7
Ответ: 7.

 

( 4 оценки, среднее 5 из 5 )

Поделиться с друзьями

Периметр трапеции — определение, формула и примеры

Периметр трапеции представляет собой сумму длин каждой стороны трапеции. Трапеция — это четырехугольник, у которого две стороны параллельны друг другу, а две непараллельные стороны называются соответственно основаниями и катетами. Давайте узнаем, как рассчитать периметр трапеции в этой статье.

1.	Что такое периметр трапеции?
2.	Формула периметра трапеции
3.	Как найти периметр трапеции?
4.	Часто задаваемые вопросы по периметру трапеции

Что такое периметр трапеции?

Периметр трапеции определяется как общая длина границы трапеции.

Трапеция — это двумерная фигура (2D-форма) и неправильный многоугольник. Таким образом, периметр трапеции вычисляется путем сложения длин всех ее сторон. Периметр трапеции выражается в линейных единицах, таких как «дюймы», «футы», «метры» или «сантиметры» и т. д.

Формула периметра трапеции

Формула периметра трапеции простая, в которой добавляются длины всех 4-х сторон. Обратите внимание на приведенную ниже трапецию ABCD, в которой стороны AB и CD (основания) параллельны друг другу, а стороны AD и BC (ножки) непараллельны.

Периметр трапеции ABCD можно рассчитать по формуле Периметр (P) = AB + BC + CD + DA. Его также можно записать в виде суммы длин параллельных сторон и суммы длин непараллельных сторон, где AB и CD — параллельные стороны, а AD и BC — непараллельные стороны.

Как найти периметр трапеции?

Периметр трапеции можно найти, выполнив следующие шаги:

• Шаг 1: Напишите размеры всех сторон трапеции.
• Шаг 2: Добавьте длину всех сторон.
• Шаг 3: Как только значение периметра получено, запишите единицу измерения с полученным таким образом значением.

Пример: Найдите периметр трапеции, параллельные стороны которой равны 5 единицам и 7 единицам, а непараллельные стороны равны 3 единицам и 4 единицам.
Решение: Даны длины параллельных сторон 5 единиц и 7 единиц, а длины непараллельных сторон 3 единицы и 4 единицы.
Таким образом, периметр трапеции равен P = сумме длин всех сторон

⇒ P = (5 + 7 + 3 + 4)

Следовательно, P = 19 единиц.

∴ Периметр трапеции 19 единиц.

Периметр трапеции с отсутствующей стороной

Периметр трапеции можно вычислить, даже если отсутствует сторона. В таких случаях мы используем заданные стороны трапеции и применяем теорему Пифагора и другие свойства, чтобы найти недостающую сторону, а затем можно вычислить периметр. Давайте разберемся в этом с помощью примера.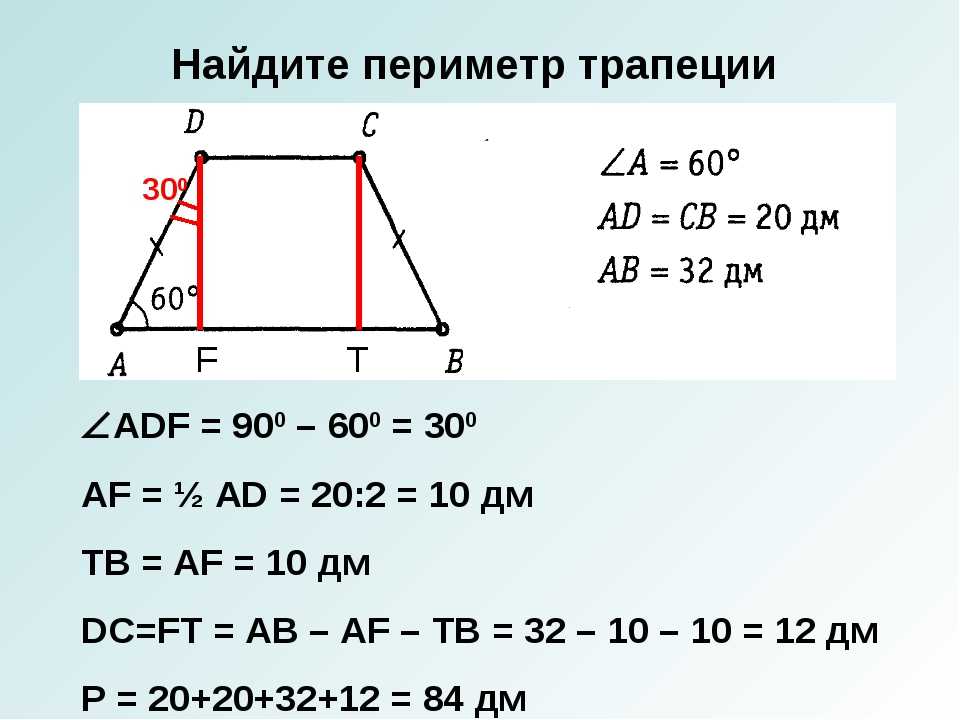

Пример: Найдите периметр трапеции ABCD, если ее размеры заданы следующим образом: AB = 120 м, DE = 50 м, EF = 120 м, FC = 80 м, BF = 90 м.

Решение: Используя заданные размеры, мы можем найти недостающие стороны AD и BC.

• Шаг 1: Если взять треугольник BFC, то дано, что BF = 90 м и FC = 80 м. Мы видим, что треугольник BFC прямоугольный. Итак, мы можем вычислить значение BC, используя теорему Пифагора.
• Шаг 2: Согласно теореме Пифагора, BC ² = BF ² + FC ² . Это означает, что БК ² = 90 ² + 80 ² . Следовательно, БК ² = 8100 + 6400 ⇒ БК = √14500 = 120,41 м
• Шаг 3: Поскольку BF = 90 м, AE также будет равно 90 м, поскольку AB параллельна DC. Теперь мы можем вычислить недостающую сторону AD трапеции.
• Шаг 4: Если взять прямоугольный треугольник ADE, мы знаем, что AE = 90 м, ДЭ = 50 м. Итак, после применения теоремы Пифагора мы получаем AD ² = AE ² + DE ² . Это означает, что ² = 90 ² + 50 ² . Следовательно, 90 102 2  = 8 100 + 2 500 ⇒ н.э. = √10 600 = 102,9 м.
• Шаг 5: Теперь, когда мы знаем все стороны трапеции, мы можем найти ее периметр, сложив все 4 стороны. Это означает, что периметр трапеции ABCD = AB + BC + CD + DE ⇒ 120 + 120,41 + 250 + 102,9 = 59.3,31 м. Следовательно, периметр трапеции равен 593,31 м.

☛ Статьи по теме

• Формула трапеции
• Калькулятор периметра трапеции
• Формулы периметра
• Периметр многоугольника
• Периметр прямоугольника
• Периметр квадрата
• Периметр треугольника
• Разница между площадью и периметром
• Площадь трапеции

 

Примеры по периметру трапеции

1. Пример 1: Найдите периметр трапеции со сторонами 10 м, 6 м, 8 м и 9 м.

   Решение: Размеры трапеции 10 метров, 6 метров, 8 метров и 9 метров. Таким образом, периметр трапеции можно рассчитать по формуле:

   Периметр трапеции = (10 + 6 + 8 + 9) метров. Таким образом, периметр трапеции = 33 метра

   ∴ Периметр трапеции 33 метра.

2. Пример 2: Каков периметр трапеции, у которой сумма длин непараллельных сторон равна 12 единицам, а сумма параллельных сторон равна 8 единицам?

   Решение: Учитывая, что сумма длин непараллельных сторон = 12 единиц, сумма параллельных сторон = 8 единиц.

   Периметр трапеции = сумма длин параллельных сторон + сумма длин непараллельных сторон ⇒ P = 12 единиц + 8 единиц.

   Таким образом, периметр (P) = 20 единиц

   Следовательно, периметр трапеции равен 20 единицам.

3. Пример 3: Верно или неверно:

   а.) Периметр трапеции вычисляется путем сложения длин всех ее сторон.

   б.) Трапеция – это четырехугольник, у которого две стороны параллельны друг другу и две непараллельны.

   Решение:

   а.) Верно, периметр трапеции вычисляется путем сложения длин всех ее сторон.

   б.) Верно, трапеция – это четырехугольник, у которого две стороны параллельны друг другу и две непараллельны.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.

Запись на бесплатный пробный урок

Практические вопросы по периметру трапеции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по периметру трапеции

Что такое периметр трапеции?

Общая длина границы трапеции называется периметром трапеции. Периметр трапеции зависит от длины всех ее сторон и выражается в линейных единицах.

Какая формула для периметра трапеции?

Формула периметра трапеции представляет собой сумму длин всех сторон трапеции. Для любой трапеции ABCD периметр трапеции ABCD выражается как P = AB + BC + CD + AD, где AB, CD — параллельные стороны (основания), а AD, BC — непараллельные стороны (катеты). Таким образом, периметр трапеции также можно записать как P = (сумма длин параллельных сторон) + (сумма длин непараллельных сторон).

Как найти периметр трапеции?

Периметр трапеции можно найти, выполнив следующие шаги:

• Шаг 1: Найдите длины всех 4 сторон трапеции.
• Шаг 2: Сложите длины всех сторон трапеции, чтобы получить значение периметра трапеции.
• Шаг 3: Как только значение периметра трапеции получено, мы указываем единицу, которая должна быть помещена вместе с ней.

Как найти длину недостающей стороны, если известен периметр трапеции?

Мы можем найти недостающую длину стороны трапеции, если известен периметр.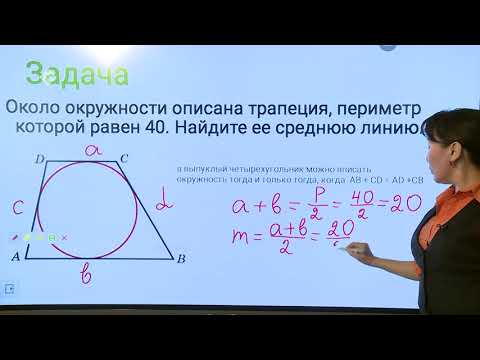 Давайте разберемся в этом на примере.

Пример: Если периметр трапеции равен 24 единицам, а остальные стороны равны: 5 единиц, 7 единиц, 4 единицы, найдем недостающую сторону.

• Шаг 1: Запишите данные размеры трапеции. Периметр = 24 единицы, Сторона 1 = 5 единиц, Сторона 2 = 7 единиц, Сторона 3 = 4 единицы.
• Шаг 2: Предположим, что недостающая длина стороны трапеции равна x единицам.
• Шаг 3: Сложите длины всех сторон трапеции и приравняйте полученное значение к периметру трапеции. Здесь это будет записано как 24 = 5 + 7 + 4 + x
.
• Шаг 4: Как только уравнение будет сформировано, решите «x», чтобы получить значение длины недостающей стороны трапеции. После решения для значения «x» мы получаем, x = 24 — 16 = 8 единиц. Следовательно, длина недостающей стороны равна 8 единицам.

Что произойдет с периметром трапеции, если все стороны трапеции удвоить?

Если длины всех сторон трапеции удвоить, то периметр также удвоится как P = (сумма длин параллельных сторон) + (сумма длин непараллельных сторон), а значение каждой стороны будет удвоится, тем самым удвоив значение периметра.

Как найти периметр равнобедренной трапеции?

Периметр равнобедренной трапеции можно вычислить так же, как мы находим периметр обычной трапеции. Однако у равнобедренной трапеции катеты одинаковой длины, поэтому найти периметр становится проще. В этом случае периметр можно рассчитать по формуле Периметр трапеции = a + b + 2c; где «а» и «b» — параллельные стороны, а с — катет трапеции. Поскольку две ноги равны по длине, мы представляем их как c + c = 2c в формуле.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист периметра

Периметр трапеции. Различные способы нахождения периметра

Периметр трапеции, где a, b, c, d — длины сторон, можно найти по формуле р = а + b + с + d. Как и любые другие двумерные фигуры, периметр — это просто сумма длин сторон.

Пример №1: Найдите периметр трапеции ниже

Периметр = 5 + 6 + 7 + 10 = 11 + 17 = 28

А теперь давайте немного поинтереснее. Как насчет рисунка ниже?

Пример #2: Можете ли вы найти периметр этой прямоугольной трапеции, где ABC — прямоугольный треугольник?

Этот пример немного сложен! Хотя даны 4 стороны, по одной из них нельзя найти периметр трапеции. Можете ли вы сказать, какой? Да, вы правильно угадали! Сторона, которую вы не можете использовать, – это AC = 10.

Можно использовать стороны AB, AD, BC и CD. Однако у нас есть другая проблема. БК отсутствует. Нам нужно найти БК.

BC — одна из сторон прямоугольного треугольника ABC. Следовательно, мы можем использовать теорему Пифагора, чтобы найти BC.

АС ² = АВ ² + ВС ²

10 ² = 8 ² + ВС ^{2 900 + БК 2}

100 — 64 = БК ²

36 = BC ²

Так как 6 ² = 36, BC = 6

Периметр = AB + BC + CD + AD = 8 + 6 + 10 + 12 = 136 + 920005

Нахождение периметра трапеции по заданным высоте, длине верхнего основания и длинам непараллельных сторон.

Пример №3: Найдите периметр следующей трапеции, длина основания которой неизвестна.

Создайте прямоугольник, проведя линию от другой вершины сверху.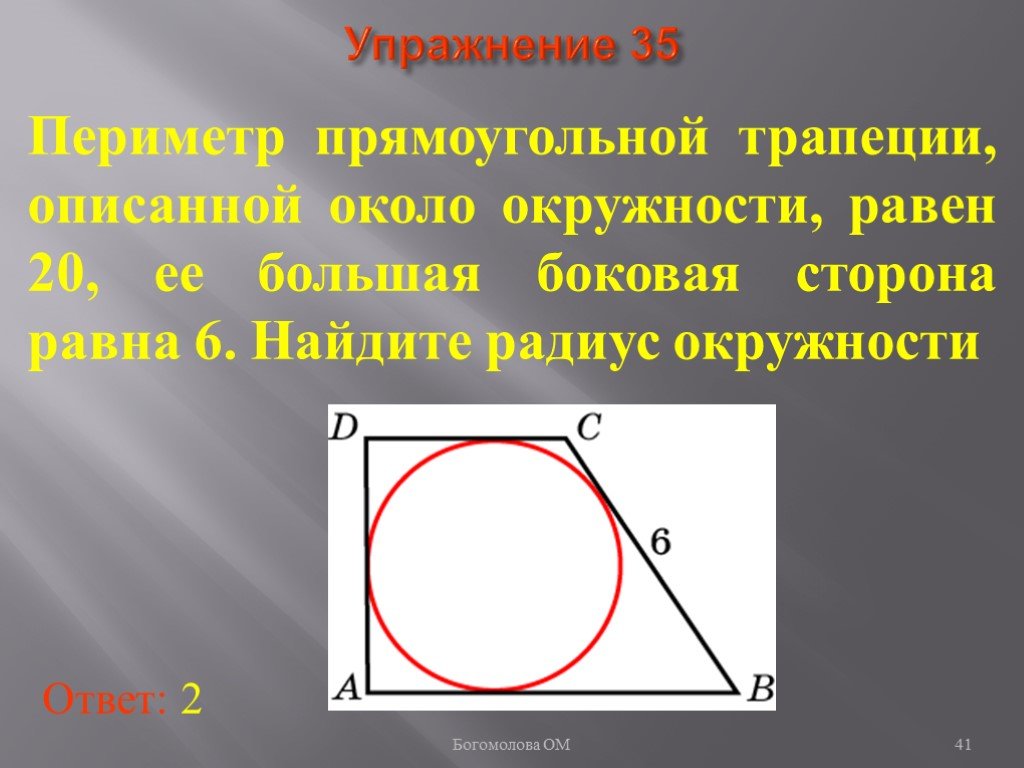

Теперь, когда мы найдем длину x и длину y, мы можем найти периметр.

Чтобы найти длину y, нам просто нужно использовать теорему Пифагора.

y ² + 8 ² = 10 ²

y ²  + 64 = 100

y 9 0 — 6 4 1 0 — 0 = 9 ^{2 9010 69}

y ²   = 36

С 6 ² = 36, y = 6

Таким же образом найдите x.

x ²  + 8 ²  = 9 ²

x ²  + 64 = 81

x ^{3 9018 9}

x ²   = 17

x  = √ 17 = 4,12

Периметр = 6 + 7 + 4,12 + 9 + 7 + 10 = 43,12

Нахождение периметра трапеции, когда известны высота, длина верхнего основания и углы нижнего основания.

Пример №4:  Найдите периметр следующей трапеции, у которой длина нижнего основания и длины непараллельных сторон неизвестны.

На этот раз нам может понадобиться тригонометрия, чтобы найти периметр этой трапеции.

Чтобы найти a, b, x и y, мы можем использовать тригонометрические отношения.

sin(60 градусов) = 15/ a или a = 15/sin(60 градусов) = 15/0,866 = 17,3

tan(60 градусов) = 15/ y или6 y /tan(60 градусов) = 15/1,732 = 8,66

sin(70 градусов) = 15/ b или b   = 15/sin(70 градусов) = 15/0,94 = 15,95

tan(70 градусов) = 15/ x или x = 15/tan(70 градусов) = 15/2,74 = 5,47

Периметр = 17,3 + 12 + 15,95 + 5,47 + 12 + 8,66 = 71,38

Нахождение периметра равнобедренной трапеции через х

Найдите периметр равнобедренной трапеции, если длина верхнего основания равна длине катета. Кроме того, мера одного противоположного угла в два раза больше другого противоположного угла.

Пусть x = длина верхнего основания = длина ноги.

Взгляните на рисунок ниже, чтобы немного лучше понять проблему.

Вот что мы знаем:

AB = x

AD = x

BC = x

Нам нужно найти DC

Поскольку трапеция равнобедренная, мы также знаем, что ∠D = ∠C

Кроме того, ∠A +∠D = 180 градусов, так как сумма внутренних углов на той же сторона секущей (AD в данном случае — секущей) равна 180 градусам.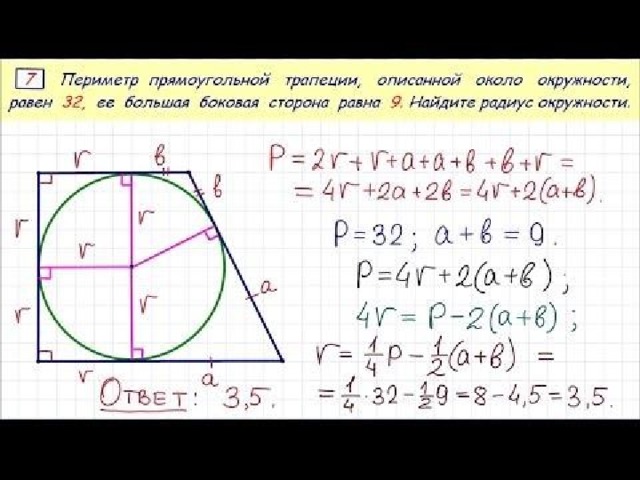

∠A противоположна ∠C. Поскольку ∠A больше, чем ∠C, то это тот, который в два раза больше.

∠A = 2∠C

∠A = 2∠D (поскольку ∠D = ∠C)

Замените 2∠D на ∠A в ∠A +∠D = 180

2∠D +∠D = 180

3∠D = 180

∠D = 180/3 = 60

Изобразите высоту трапеции, показанной красным, и затем найдите косинус угла D.

(∠D) = y/x  

cos(60 градусов) = y/x  

0,5 = y/x

Умножьте обе части на x.

0,5x = y

y = DE = FC = 0,5x

Периметр равнобедренной трапеции = AB + BC + CF + FE + ED + DA

Периметр равнобедренной трапеции = xx + x + 0,5 х + 0,5х + х = 5х

1. Треугольник 30-60-90

   3 апреля, 23 17:08

   Что такое треугольник 30-60-90? Определение, доказательство, площадь и простые примеры из реальной жизни.

   Подробнее

2. Расчет условной вероятности с помощью таблицы непредвиденных обстоятельств

   29, 23 марта 10:19

   Научитесь рассчитывать условную вероятность с помощью таблицы непредвиденных обстоятельств.

   No related posts.