Метод Крамера – теорема, примеры решений
Габриель Крамер – математик, создатель одноименного метода решения систем линейных уравнений
Габриель Крамер – известный математик, который родился 31 июля 1704 года. Ещё в детстве Габриель поражал своими интеллектуальными способностями, особенно в области математики. Когда Крамеру было 20 лет, он устроился в Женевский университет штатным преподавателем.
Во время путешествия по Европе Габриель познакомился с математиком Иоганном Бернулли, который и стал его наставником. Только благодаря Иоганну, Крамер написал много статей по геометрии, истории математики и философии. А в свободное от работы время изучал математику всё больше и больше.
Наконец-то наступил тот день, когда Крамер нашёл способ, при помощи которого можно было бы легко решать не только лёгкие, но и сложные системы линейных уравнений.
В 1740 году у Крамера были опубликованы несколько работ, где доступно изложено решение квадратных матриц и описан алгоритм, как находить обратную матрицу. Далее математик описывал нахождения линейных уравнений разной сложности, где можно применить его формулы. Поэтому тему так и назвали: «Решение систем линейных уравнений методом Крамера».
Далее математик описывал нахождения линейных уравнений разной сложности, где можно применить его формулы. Поэтому тему так и назвали: «Решение систем линейных уравнений методом Крамера».
Учёный умер в возрасте 48 лет (в 1752 году). У него было ещё много планов, но, к сожалению, он так и не успел их осуществить.
О чем статья
Вывод формулы Крамера
Пусть дана система линейных уравнений такого вида:
где , , – неизвестные переменные, – это числовые коэффициенты, в – свободные члены.
Решением СЛАУ (систем линейных алгебраических уравнение) называются такие неизвестные значения при которых все уравнения данной системы преобразовываются в тождества.
Если записать систему в матричном виде, тогда получается , где
В данной главной матрице находятся элементы, коэффициенты которых при неизвестных переменных,
Это матрица-столбец свободных членов, но есть ещё матрица-столбец неизвестных переменных:
После того, когда найдутся неизвестные переменные, матрица и будет решением системы уравнений, а наше равенство преобразовывается в тождество. . Если умножить , тогда . Получается: .
. Если умножить , тогда . Получается: .
Если матрица – невырожденная, то есть, её определитель не равняется нулю, тогда у СЛАУ есть только одно единственное решение, которое находится при помощи метода Крамера.
Как правило, для решения систем линейных уравнений методом Крамера, нужно обращать внимания на два свойства, на которых и основан данный метод:
1. Определитель квадратной матрицы равняется сумме произведений элементов любой из строк (столбца) на их алгебраические дополнения:
, здесь – 1, 2, …, n; – 1, 2, 3, …, n.
2. Сумма произведений элементов данной матрицы любой строки или любого столбца на алгебраические дополнения определённых элементов второй строки (столбца) равняется нулю:
,
,
где – 1, 2, …, n; – 1, 2, 3, …, n. .
Итак, теперь можно найти первое неизвестное . Для этого необходимо умножить обе части первого уравнения системы на , части со второго уравнения на , обе части третьего уравнения на и т. д. То есть, каждое уравнение одной системы нужно умножать на определённые алгебраические дополнения первого столбца матрицы :
Теперь прибавим все левые части уравнения, сгруппируем слагаемые, учитывая неизвестные переменные и приравняем эту же сумму к сумме правых частей системы уравнения:
.
Можно обратиться к вышеописанным свойствам определителей и тогда получим:
И предыдущее равенство уже выглядит так:
Откуда и получается .
Аналогично находим . Для этого надо умножить обе части уравнений на алгебраические дополнения, которые находятся во втором столбце матрицы .
Теперь нужно сложить все уравнения системы и сгруппировать слагаемые при неизвестных переменных. Для этого вспомним свойства определителя:
Откуда получается .
Аналогично находятся все остальные неизвестные переменные.
Если обозначить:
тогда получаются формулы, благодаря которым находятся неизвестные переменные методом Крамера:
, , .
Замечание.
Тривиальное решение при может быть только в том случае, если система уравнений является однородной . И действительно, если все свободные члены нулевые, тогда и определители равняются нулю, так как в них содержится столбец с нулевыми элементами. Конечно же, тогда формулы , , дадут
Конечно же, тогда формулы , , дадут
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Метод Крамера – теоремы
Прежде чем решать уравнение , необходимо знать:
- теорему аннулирования;
- теорему замещения.
Теорема замещения
Теорема
Сумма произведений алгебраических дополнений любого столбца (строки) на произвольные числа равняется новому определителю, в котором этими числами заменены соответствующие элементы изначального определителя, что отвечают данным алгебраическим дополнениям.
Например,
=
где – алгебраические дополнения элементов первого столбца изначального определителя:
Теорема аннулирования
Теорема
Сумма произведений элементов одной строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равняется нулю.
Например:
Алгоритм решения уравнений методом Крамера
Метод Крамера – простой способ решения систем линейных алгебраических уравнений. Такой вариант применяется исключительно к СЛАУ, у которых совпадает количество уравнений с количеством неизвестных, а определитель отличен от нуля.
Итак, когда выучили все этапы, можно переходить к самому алгоритму решения уравнений методом Крамера. Запишем его последовательно:
Шаг 1. Вычисляем главный определитель матрицы
и необходимо убедиться, что определитель отличен от нуля (не равен нулю).
Шаг 2. Находим определители
Это и есть определители матриц, которые получались из матрицы при замене столбцов на свободные члены.
Шаг 3. Вычисляем неизвестные переменные
Теперь вспоминаем формулы Крамера, по которым вычисляем корни (неизвестные переменные):
, , .
Шаг 4. Выполняем проверку
Выполняем проверку решения при помощи подстановки в исходную СЛАУ. Абсолютно все уравнения в системе должны быть превращены в тождества. Также можно высчитать произведение матриц . Если в итоге получилась матрица, которая равняется , тогда система решена правильно. Если же не равняется , скорей всего в одном из уравнений есть ошибка.
Абсолютно все уравнения в системе должны быть превращены в тождества. Также можно высчитать произведение матриц . Если в итоге получилась матрица, которая равняется , тогда система решена правильно. Если же не равняется , скорей всего в одном из уравнений есть ошибка.
Давайте для начала рассмотрим систему двух линейных уравнений, так как она более простая и поможет понять, как правильно использовать правило Крамера. Если вы поймёте простые и короткие уравнения, тогда сможете решить более сложные системы трёх уравнений с тремя неизвестными.
Кроме всего прочего, есть системы уравнений с двумя переменными, которые решаются исключительно благодаря правилу Крамеру.
Итак, дана система двух линейных уравнений:
Для начала вычисляем главный определитель (определитель системы):
Значит, если , тогда у системы или много решений, или система не имеет решений. В этом случае пользоваться правилом Крамера нет смысла, так как решения не получится и нужно вспоминать метод Гаусса, при помощи которого данный пример решается быстро и легко.
В случае, если , тогда у система есть всего одно решение, но для этого необходимо вычислить ещё два определителя и найти корни системы.
и
Часто на практике определители могут обозначаться не только , но и латинской буквой , что тоже будет правильно.
Корни уравнения найти просто, так как главное, знать формулы:
,
Так как мы смогли решить систему двух линейных уравнений, теперь без проблем решим и систему трёх линейных уравнений, а для этого рассмотрим систему:
(1)
Здесь алгебраические дополнения элементов – первый столбец . Во время решения не забывайте о дополнительных элементах. Итак, в системе линейных уравнений нужно найти три неизвестных – при известных других элементах.
Создадим определитель системы из коэффициентов при неизвестных:
Умножим почленно каждое уравнение соответственно на , , – алгебраические дополнения элементов первого столбца (коэффициентов при ) и прибавим все три уравнения. Получаем:
Согласно теореме про раскладывание, коэффициент при равняется . Коэффициенты при и будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается
Коэффициенты при и будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается
После этого можно записать равенство:
(2)
Для нахождения и перемножим каждое из уравнений изначальной системы в первом случае соответственно на , во втором – на и прибавим. Впоследствии преобразований получаем:
где
,
Если , тогда в результате получаем формулы Крамера:
= , = , =
Порядок решения однородной системы уравнений
Отдельный случай – это однородные системы:
(3)
Среди решений однородной системы могут быть, как нулевые решения , так и решения отличны от нуля.
Теорема
Если определитель однородной системы (3) отличен от нуля , тогда у такой системы может быть только одно решение.
Действительно, вспомогательные определители , как такие у которых есть нулевой столбец и поэтому, за формулами Крамера
Теорема
Если у однородной системы есть отличное от нуля решение, тогда её определитель равняется нулю
Действительно, пусть одно из неизвестных , например, , отличное от нуля. Согласно с однородностью Равенство (2) запишется: . Откуда выплывает, что
Согласно с однородностью Равенство (2) запишется: . Откуда выплывает, что
Примеры решения методом Крамера
Рассмотрим на примере решение методом Крамера и вы увидите, что сложного ничего нет, но будьте предельно внимательно, так как частые ошибки в знаках приводят к неверному ответу.
Пример 1
Задача
Решить систему линейных уравнений методом Крамера:
Решение
Первое, что надо сделать – вычислить определитель матрицы:
Как видим, , поэтому по теореме Крамера система имеет единственное решение (система совместна). Далее нужно вычислять вспомогательные определители. Для этого заменяем первый столбец из определителя на столбец свободных коэффициентов. Получается:
Аналогично находим остальные определители:
И проверяем:
,
.
Ответ
, .
Пример 2
Задача
Решить систему уравнений методом Крамера:
Решение
Находим определители:
Ответ
= = = = = =
Проверка
* = * = =
* = * = =
* = * = =
Уравнение имеет единственное решение.
Ответ
= = =
Пример 3
Задача
Решить систему методом Крамера
Решение
Как вы понимаете, сначала находим главный определитель:
Как мы видим, главный определитель не равняется нулю и поэтому система имеет единственное решение. Теперь можно вычислить остальные определители:
При помощи формул Крамера находим корни уравнения:
, , .
Чтобы убедиться в правильности решения, необходимо сделать проверку:
Как видим, подставив в уравнение решённые корни, у нас ответ получился тот же, что и в начале задачи, что говорит о правильном решении уравнений.
Ответ
Система уравнений имеет единственное решение: , , .
Есть примеры, когда уравнение решений не имеет. Это может быть в том случае, когда определитель системы равен нулю, а определители при неизвестных неравны нулю. В таком случае говорят, что система несовместна, то есть не имеет решений. Посмотрим на следующем примере, как такое может быть.
В таком случае говорят, что система несовместна, то есть не имеет решений. Посмотрим на следующем примере, как такое может быть.
Пример 4
Задача
Решить систему линейных уравнений методом Крамера:
Решение
Как и в предыдущих примерах находим главный определитель системы:
В этой системе определитель равняется нулю, соответственно, система несовместна и определенна или же несовместна и не имеет решений. Чтобы уточнить, надо найти определители при неизвестных так, как мы делали ранее:
Мы нашли определители при неизвестных и увидели, что все они не равны нулю. Поэтому система несовместна и не имеет решений.
Ответ
Система не имеет решений.
Часто в задачах на системы линейных уравнений встречаются такие уравнения, где есть не одинаковые буквы, то есть, кроме букв, которые обозначают переменные, есть ещё и другие буквы и они обозначают некоторое действительное число. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. Давайте и рассмотрим такой пример.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных – буквы. Давайте и рассмотрим такой пример.
Пример 5
Задача
Решить систему линейных уравнений методом Крамера:
Решение
В этом примере – некоторое вещественное число. Находим главный определитель:
Находим определители при неизвестных:
Используя формулы Крамера, находим:
, .
Ответ
,
.
И наконец, мы перешли к самой сложной системе уравнений с четырьмя неизвестными. Принцип решения такой же, как и в предыдущих примерах, но в связи с большой системой можно запутаться. Поэтому рассмотрим такое уравнение на примере.
Поэтому рассмотрим такое уравнение на примере.
Пример 6
Задача
Найти систему линейных уравнений методом Крамера:
Здесь действуют система определителей матрицы высших порядков, поэтому вычисления и формулы рассмотрены в этой теме, а мы сейчас просто посчитаем систему уравнений с четырьмя неизвестными.
Решение
В изначальном определители из элементов второй строки мы отнимали элементы четвёртой строки, а из элементов третьей строки отнимались элементы четвёртой строки, которые умножались на 2. Также отнимали из элементов четвёртой строки элементы первой строки, умноженной на два. Преобразования первоначальных определителей при трёх первых неизвестных произведены по такой же схеме. Теперь можно находить определители при неизвестных:
Для преобразований определителя при четвёртом неизвестном из элементов первой строки мы вычитали элементы четвёртой строки.
Теперь по формулам Крамера нужно найти:
,
,
,
.
Ответ
Итак, мы нашли корни системы линейного уравнения:
,
,
,
.
Подведём итоги
При помощи метода Крамера можно решать системы линейных алгебраических уравнений в том случае, если определитель не равен нулю. Такой метод позволяет находить определители матриц такого порядка, как на благодаря формулам Крамера, когда нужно найти неизвестные переменные. Если все свободные члены нулевые, тогда их определители равны нулю, так как в них содержится столбец с нулевыми элементами. И конечно же, если определители равняются нулю, лучше решать систему методом Гаусса, а не Крамера, только тогда ответ будет верный.
Рекомендуем почитать для общего развития
Анкилов А. В. Высшая математика, ч. 1: учеб. Пособие/П. А. Вельмисов, Ю. А. Решетников – Ульяновск – 2011 – 252 с.
В. Высшая математика, ч. 1: учеб. Пособие/П. А. Вельмисов, Ю. А. Решетников – Ульяновск – 2011 – 252 с.
Письменный Д. – Конспект лекций по высшей математике: учеб. для вузов/Письменный Д. – М. 2006 – 602 с.
Решение методом Крамера в Excel
Метод Крамера в Excel 2003 (XLS)
Метод Крамера в Excel от 2007 (XLSX)
Методическая разработка урока по математики на тему «Решение системы линейных уравнений методом Крамера» — Информио
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данная методическая разработка предназначена для проведения учебного занятия по дисциплине «Математика» на тему «Решение систем линейных уравнений методом Крамера» для студентов первого курса по программе учебной дисциплины, разработанной на основе Федерального государственного образовательного стандарта для специальностей среднего профессионального образования.
В результате изучения темы студент должен:
знать:
- решение систем линейных уравнений методом Крамера;
- применение знаний при решении систем линейных уравнений.

уметь:
- решать системы двух линейных уравнений с двумя неизвестными методом Крамера
- решать системы трех линейных уравнений с тремя неизвестными методом Крамера
При разработке данного урока в зависимости от специфики подготовки студентов можно внести дополнения и изменения в содержание, последовательность изучения материала урока и распределение времени.
Наблюдается связь истории с математикой, при изучении материала использована задача прикладного характера для будущей практической деятельности, что прививает интерес к предмету. Данная методическая разработка содержит: учебно-методическую карту, ход, где сформулированы цели занятия и последовательность проведения урока, указан список литературы.
При проведении занятия, использованы учебные пособия, технические и наглядные средства обучения
УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА
Дисциплина: Математика
Тема занятия: Решение систем линейных уравнений методом Крамера
Вид занятия (тип урока): Комбинированный
Цели урока:
Дидактическая:
- повторить пройденный материал;
- углубить знания студентов по теме «Решение систем линейных уравнений»;
3) изучить решение систем линейных уравнений c помощью метода Крамера;
4) научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.
Развивающая:
способствовать развитию:
- логического мышления;
- памяти;
- умению сравнивать, обобщать, анализировать;
- интереса к избранной специальности.
Воспитательная:
стремиться воспитывать:
- чувства ответственности, исполнительности, аккуратности;
- чувство гордости за избранную профессию;
- положительное отношение к знаниям, учениям;
- интерес к математике
Межпредметные связи:
Обеспечивающие: история, русский язык, информатика
Обеспечиваемые: специальные предметы
Обеспечение занятия:
- Наглядные пособия: Приложение (Презентация к уроку), меловые иллюстрации
- Раздаточный материал: карточки.
- Технические средства обучения: калькуляторы, компьютеры, интерактивная доска
ПЛАН УРОКА
1. Организационный момент
Здравствуйте, студенты. Тема урока: «Решение систем линейных уравнений методом Крамера». Ученый-математик Колмогоров А.Н. говорил: «Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления», поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности .
Ученый-математик Колмогоров А.Н. говорил: «Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления», поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности .
2. Постановка целей занятия
Цели урока: повторить пройденный материал; углубить знания по теме «Решение систем линейных уравнений»; изучить решение систем линейных уравнений с помощью метода Крамера; научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.
3. Проверка домашнего задания
4. Проверка знаний
Экспресс — опрос
- Какое уравнение называется линейным?
- Напишите систему m линейных уравнений с n переменными.
- Назовите коэффициенты при переменных.
- Какие числа называются свободными членами?
- Что является решением системы?
- Какие методы решения систем линейных уравнений знаете?
Ответы: Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
5. Изучение нового материала
В школьном курсе рассматриваются способ подстановки и способ сложения. В курсе высшей математике решают методом Крамера, методом Гаусса и с помощью обратной матрицы. Рассмотрим решение систем линейных уравнений методом Крамера
5.1 Знакомство с биографией Крамера
При изучении новой темы «Решение систем линейных уравнений методом Крамера» важное место занимает связь истории с математикой, что прививает интерес к предмету. Познакомимся с биографией Габриэля Крамера.
Сведения из истории
Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.
Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача.
Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.
В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Учёный много путешествовал по Европе, перенимая опыт у знаменитых математиков своего времени – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне и других. Со многими из них он продолжал переписываться всю жизнь.
В 1729 году Крамер возобновляет преподавательскую работу в Женевском университете. В это время он участвует в конкурсе Парижской Академии и занимает второе место. Талантливый учёный написал множество статей на самые разные темы: геометрия, история, математика, философия. В 1730 году он опубликовал труд по небесной механике.
В 1740-е гг. Иоганн Бернулли поручает Крамеру подготовить к печати сборник своих работ. В 1742 году Крамер публикует сборник в 4-х томах. В 1744 году он выпускает посмертный сборник работ Якоба Бернулли (брата Иоганна Бернулли), а также двухтомник переписки Лейбница с Иоганном Бернулли. Эти работы вызвали большой интерес со стороны учёных всего мира.
Габриэль Крамер скончался 4 января 1752 года во Франции
5.2 Решение системы линейных уравнений методом Крамера
Теорема Крамера.
Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка .
Заменяя столбец с коэффициентами соответствующей переменной свободными членами:
6. Закрепление.
6.1 Решение системы двух линейных уравнений с двумя неизвестными методом Крамера
2) Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн усл. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго – на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?
В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?
Решение. Пусть x и y – прибыли первого и второго отделений в минувшем году.
Тогда условие задачи можно записать в виде системы:
Решив систему, получим x = 4, y = 8.
Ответ: а) прибыль в минувшем году первого отделения — 4 млн усл. ед., второго — 8 усл.ед.:
б) прибыль в этом году первого отделения 1,7. 4 = 6,8 млн усл. ед.,
второго 1,4. 8 = 11,2 млн усл. ед.
При решении системы уравнений могут встретиться три случая:
1) система линейных уравнений имеет единственное решение
(система совместна и определённа)
Условия:
2) система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
Условия:
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
3) система линейных уравнений решений не имеет
(система несовместна)
Условия:
Система называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой
Совместная система уравнений, имеющая только одно решение, называется определённой
6.2 Решение системы трех линейных уравнений с тремя двумя неизвестными методом Крамера
Ответ: (1; 0; -1) .
Решение. Находим определители системы:
Ответ: (1; 0; -1) .
7. Домашнее задание (слайд № 23)
Решите системы:
8. Подведение итогов
Подведем итоги урока. По результатам работы на уроке выставляются оценки, с последующей демонстрацией успеваемости в виде диаграммы на интерактивной доске.
Урок окончен. Спасибо за внимание. До свидания.
Литература:
Основная
- Григорьев В.П.Дубинский Ю.А Элементы высшей математики. Москва, 2014
- Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика. Москва, 2008
Дополнительная
- Богомолов Н.В. Практические занятия по математики. Москва, 2013
Интернет-ресурсы: www.
ХОД УРОКА
№п/п | Элементы урока, содержание и последовательность изучаемых вопросов | Формы и методы обучения, контроля | Наглядные пособия, ТСО, дидактический материал | Преподаватель | Студенты | Время 45 мин. |
1. | Организационный момент. Взаимное приветствие. | Проверка отсутствующих, рабочих мест | Интерактивная доска слайд №1 | Приветствует, отмечает в журнале отсутствующих. | Приветствуют | 1 мин |
2. | Постановка целей занятия. | Организация внимания | Интерактивная доска | Ставит цели урока | Слушают | 1 мин |
3. | Проверка домашнего задания | Групповая работа | Интерактивная доска | Контролирует | Дежурный проверяет | 5 мин |
4. | Проверка знаний | Экспресс-опрос | Слайды № 2,3,4 | Задает вопрос, поправляет ответ | Думают, отвечают | 5 мин |
5. | Изучение нового материала | Организация внимания | Интерактивная доска | Объясняет | Слушают, рассуждают, отвечают на вопросы. |
|
5.1 | Знакомство с биографией Крамера | Рассказ материала | Слайды № 5-10 | Рассказывает | Смотрят | 5 мин |
5.2 | Решение системы линейных уравнений методом Крамера | Изучение темы | Слайды № 11-15 | Объясняет | Смотрят, слушают | 10 мин |
6. | Закрепление | Самостоятельная работа | Интерактивная доска | Выдает задания | Думают, решают |
|
6.1 | Решение системы двух линейных уравнений с двумя неизвестными методом Крамера | Групповая работа | Слайды № 16-19 | Выдает задания, проверяет | Решают | 5 мин |
6.2 | Решение системы трех линейных уравнений с тремя неизвестными методом Крамера | Самостоятельная работа | Слайды № 20-22 | Контролирует, проверяет | Думают, решают | 10 мин |
7. | Домашнее задание |
| Слайды № 23 | Выдает задания | Пишут | 1 мин |
8. | ||||||
| 6 | Risolvere per ? | cos(x)=1/2 | ||||
| 7 | Risolvere per x | sin(x)=-1/2 | ||||
| 8 | Преобразовать из градусов в радианы | 225 | ||||
| 9 | Risolvere per ? | cos(x)=( квадратный корень из 2)/2 | ||||
| 10 | Risolvere per x | cos(x)=( квадратный корень из 3)/2 | ||||
| 11 | Risolvere per x | sin(x)=( квадратный корень из 3)/2 | ||||
| 12 | График | g(x)=3/4* корень пятой степени из x | ||||
| 13 | Найти центр и радиус | x^2+y^2=9 | ||||
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) 2+n-72)=1/(n+9) |
Урок математики по теме «Решение системы линейных уравнений методом Крамера»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данная методическая разработка предназначена для проведения урока по дисциплине “Математика” на тему “Решение систем линейных уравнений методом Крамера” для студентов первого курса по программе учебной дисциплины, разработанной на основе Федерального государственного образовательного стандарта для специальностей среднего профессионального образования.
В результате изучения темы студент должен:
знать:
— решение систем линейных уравнений методом Крамера;
— применение знаний при решении систем линейных уравнений.
уметь:
— решать системы двух линейных уравнений с двумя неизвестными методом Крамера
— решать системы трех линейных уравнений с тремя неизвестными методом Крамера
При разработке данного урока в зависимости от
специфики подготовки студентов можно внести
дополнения и изменения в содержание,
последовательность изучения материала урока и
распределение времени.
Наблюдается связь истории с математикой, при изучении материала использована задача прикладного характера для будущей практической деятельности, что прививает интерес к предмету. Данная методическая разработка содержит: учебно-методическую карту, ход, где сформулированы цели занятия и последовательность проведения урока, указан список литературы.
При проведении занятия, использованы учебные пособия, технические и наглядные средства обучения
УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА
Дисциплина: Математика
Тема занятия: Решение систем линейных уравнений методом Крамера
Вид занятия (тип урока): Комбинированный
Цели урока:
Дидактическая:
- повторить пройденный материал;
- углубить знания студентов по теме “Решение систем линейных уравнений”;
- изучить решение систем линейных уравнений c помощью метода Крамера;
- научиться решать системы двух линейных
уравнений с двумя неизвестными и трех линейных
уравнений с тремя неизвестными, используя метод
Крамера.

Развивающая:
- способствовать развитию:
- логического мышления;
- памяти;
- умению сравнивать, обобщать, анализировать;
- интереса к избранной специальности.
Воспитательная:
- стремиться воспитывать:
- чувства ответственности, исполнительности, аккуратности;
- чувство гордости за избранную профессию;
- положительное отношение к знаниям, учениям;
- интерес к математике
Межпредметные связи:
- Обеспечивающие: история, русский язык, информатика
- Обеспечиваемые: специальные предметы
- Обеспечение занятия:
Наглядные пособия: Презентации к уроку
Раздаточный материал: карточки.
Технические средства обучения: калькуляторы, компьютеры, интерактивная доска
ПЛАН УРОКА
1. Организационный момент (слайд №1)
Организационный момент (слайд №1)
Здравствуйте, студенты. Тема урока: “Решение систем линейных уравнений методом Крамера”. Ученый-математик Колмогоров А.Н. говорил: “Без знаний математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления”, поэтому математика связана с будущей специальностью. В результате изучения темы научимся решать задачи прикладного характера для профессиональной деятельности.
2. Постановка целей занятия
Цели урока: повторить пройденный материал; углубить знания по теме “Решение систем линейных уравнений”; изучить решение систем линейных уравнений с помощью метода Крамера; научиться решать системы двух линейных уравнений с двумя неизвестными и трех линейных уравнений с тремя неизвестными, используя метод Крамера.
3. Проверка домашнего задания
4. Проверка знаний (слайды № 2,3,4).
Экспресс-опрос
- Какое уравнение называется линейным?
- Напишите систему m линейных уравнений с n переменными.
- Назовите коэффициенты при переменных.
- Какие числа называются свободными членами?
- Что является решением системы?
- Какие методы решения систем линейных уравнений знаете?
Ответы: Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
В системе m линейных уравнений с n переменными:
.
Числа называются коэффициентами при переменных, а – свободными членами.
Совокупность чисел называется решением системы линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.
5. Изучение нового материала
В школьном курсе рассматриваются способ
подстановки и способ сложения. В курсе высшей
математике решают методом Крамера, методом
Гаусса и с помощью обратной матрицы. Рассмотрим
решение систем линейных уравнений методом
Крамера
В курсе высшей
математике решают методом Крамера, методом
Гаусса и с помощью обратной матрицы. Рассмотрим
решение систем линейных уравнений методом
Крамера
5.1 Знакомство с биографией Крамера
При изучении новой темы “Решение систем линейных уравнений методом Крамера” важное место занимает связь истории с математикой, что прививает интерес к предмету. Познакомимся с биографией Габриэля Крамера.
| Сведения из истории (слайды № 5-10) Крамер
является одним из создателей линейной алгебры.
Одной из самых известных его работ является
“Введение в анализ алгебраических кривых”,
опубликованный на французском языке в 1750 году. В
ней Крамер строит систему линейных уравнений и
решает её с помощью алгоритма, названного позже
его именем – метод Крамера. Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария) в семье врача. |
Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.
В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Учёный много путешествовал по Европе, перенимая опыт у знаменитых математиков своего времени – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне и других. Со многими из них он продолжал переписываться всю жизнь.
В 1729 году Крамер возобновляет
преподавательскую работу в Женевском
университете. В это время он участвует в конкурсе
Парижской Академии и занимает второе место.
Талантливый учёный написал множество статей на
самые разные темы: геометрия, история,
математика, философия. В 1730 году он опубликовал
труд по небесной механике.
В 1730 году он опубликовал
труд по небесной механике.
В 1740-е гг. Иоганн Бернулли поручает Крамеру подготовить к печати сборник своих работ. В 1742 году Крамер публикует сборник в 4-х томах. В 1744 году он выпускает посмертный сборник работ Якоба Бернулли (брата Иоганна Бернулли), а также двухтомник переписки Лейбница с Иоганном Бернулли. Эти работы вызвали большой интерес со стороны учёных всего мира.
Габриэль Крамер скончался 4 января 1752 года во Франции
5.2 Решение системы линейных уравнений методом Крамера(слайды № 11-15)
Теорема Крамера.
Если определитель системы отличен от нуля, то
система линейных уравнений имеет одно
единственное решение, причём неизвестное равно
отношению определителей. В знаменателе –
определитель системы, а в числителе –
определитель, полученный из определителя
системы путём замены коэффициентов при этом
неизвестном свободными членами. Эта теорема
имеет место для системы линейных уравнений
любого порядка.
Эта теорема
имеет место для системы линейных уравнений
любого порядка.
Дана система
Формулы Крамера ………….
Заменяя столбец с коэффициентами соответствующей переменной свободными членами:
6. Закрепление.
6.1 Решение системы двух линейных уравнений с двумя неизвестными методом Крамера (слайды № 16-19)
1)
Ответ: (1;-1)
2) Фирма состоит из двух отделений, суммарная величина прибыли которых в минувшем году составила 12 млн усл. ед. На этот год запланировано увеличение прибыли первого отделения на 70%, второго – на 40%. В результате суммарная прибыль должна вырасти в 1,5 раза. Какова величина прибыли каждого из отделений: a) в минувшем году; б) в этом году?
Решение. Пусть x и y – прибыли первого и второго отделений в минувшем году.
Тогда условие задачи можно записать в виде системы:
Решив систему, получим x = 4, y = 8.
Ответ: а) прибыль в минувшем году первого отделения — 4 млн усл. ед., второго — 8 усл.ед.: б) прибыль в этом году первого отделения 1,7. 4 = 6,8 млн усл. ед., второго 1,4. 8 = 11,2 млн усл. ед.
При решении системы уравнений могут встретиться три случая:
1) система линейных уравнений имеет единственное решение
(система совместна и определённа)
Условия:
.
2) система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
Условия:
,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
3) система линейных уравнений решений не имеет
(система несовместна)
Условия:
Система называется несовместной, если у неё
нет ни одного решения, и совместной, если она
имеет хотя бы одно решение. Совместная система
уравнений, имеющая только одно решение,
называется определённой, а более одного – неопределённой.
6.2 Решение системы трех линейных уравнений с тремя двумя неизвестными методом Крамера (слайды № 20-22)
Ответ: (1; 0; -1) .
Решение. Находим определители системы:
Ответ: (1; 0; -1) .
7. Домашнее задание (слайд № 23)
Решите системы:
1)
2)
8. Подведение итогов
Подведем итоги урока. По результатам работы на уроке выставляются оценки, с последующей демонстрацией успеваемости в виде диаграммы на интерактивной доске.
Урок окончен. Спасибо за внимание. До свидания.
Литература:
Основная
- Григорьев В.П.Дубинский Ю.А Элементы высшей математики. Москва, 2011
- Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика. Москва, 2008
Дополнительная
- Богомолов Н.В. Практические занятия по
математики.
 Москва, 2013
Москва, 2013
Интернет-ресурсы: www.en.edu.ru
ХОД УРОКА
| № | Элементы урока, содержание и последовательность изучаемых вопросов | Формы и методы обучения, контроля | Наглядные пособия, ТСО, дидактический материал |
Преподаватель | Студенты | Время 45 мин. |
| 1 | Организационный момент. Взаимное привет-ствие. | Проверка отсутствующих, рабочих мест | Интерактивная доска слайд №1 |
Приветствует, отмечает в журнале
отсутствующих. |
Приветствуют | 1 мин |
| 2 | Постановка целей занятия. | Организация внимания | Интерактивная доска | Ставит цели урока | Слушают | 1 мин |
| 3 | Проверка домашнего задания | Групповая работа | Интерактивная доска | Контролирует | Дежурный проверяет | 5 мин |
| 4 | Проверка знаний | Экспресс-опрос | Слайды № 2,3,4 | Задает вопрос, поправляет ответ | Думают, отвечают | 5 мин |
| 5 | Изучение нового материала | Организация внимания | Интерактивная доска | Объясняет | Слушают, рассуждают, отвечают
на вопросы. |
|
| 5.1 | Знакомство с биографией Крамера | Рассказ материала | Слайды № 5-10 |
Рассказывает | Смотрят | 5 мин |
| 5.2 | Решение системы линейных уравнений методом Крамера | Изучение темы | Слайды № 11-15 |
Объясняет | Смотрят, слушают | 10 мин |
| 6 | Закрепление | Самостоятельная работа | Интерактивная доска | Выдает задания | Думают, решают | |
6. 1 1 |
Решение системы двух линейных уравнений с двумя неизвестными методом Крамера | Групповая работа | Слайды № 16-19 |
Выдает задания, проверяет | Решают | 5 мин |
| 6.2 | Решение системы трех линейных
уравнений с тремя неизвестными методом Крамера |
Самостоятельная работа | Слайды № 20-22 |
Контролирует, проверяет | Думают, решают | 10 мин |
| 7 | Домашнее задание | Слайды № 23 | Выдает задания | Пишут | 1 мин | |
| 8 | Подведение итогов. |
Анализ работы | Интерактивная доска | Подводит итоги, обобщает | Получают оценки | 2 мин |
Метод Крамера для решения системы двух линейных уравнений: алгоритм следования, примеры.
Квадратная матрица 2-го порядка и её определитель
Квадратной матрицей 2-го порядка A называется таблица из 4-х чисел вида: $$ A = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} $$
В квадратной матрице 2-го порядка две строки и два столбца.
Например: $ |A| = \begin{vmatrix} 1 & -4 \\ 2,5 & 3 \\ \end{vmatrix} $
Например: $\begin{vmatrix} 1 & -4 \\ 2,5 & 3 \\ \end{vmatrix} = 1\cdot3-2,5\cdot(-4) = 3+10 = 13$
Метод Крамера для решения системы 2-х линейных уравнений
Дана система 2-х линейных уравнений:
$$ {\left\{ \begin{array}{c} a_1 x+b_1 y=c_1 \\ a_2 x+b_2 y=c_2 \end{array} \right. } $$
} $$
Определим главный определитель системы:
$$ \Delta = \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \end{vmatrix} = a_1 b_2-a_2 b_1 $$
и вспомогательные определители:
$$ \Delta_x = \begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \\ \end{vmatrix} = c_1 b_2-c_2 b_1, \Delta_y = \begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \\ \end{vmatrix} = a_1 c_2-a_2 c_1 $$
Тогда решение системы:
$$ {\left\{ \begin{array}{c} x = \frac{\Delta_x}{\Delta} \\ y = \frac{\Delta_y}{\Delta} \end{array} \right.} $$
Соотношение коэффициентов уравнений, значений определителей, расположения прямых и количества решений:
$ \frac{a_1}{a_2} \neq \frac{b_1}{b_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $
$ \Delta \neq 0 $
$ \Delta = 0, \Delta _x \neq 0, \Delta_y \neq 0 $
$ \Delta = \Delta_x = \Delta_y = 0$
Прямые пересекаются
Прямые параллельны
Прямые совпадают
Одно решение
Нет решений
Бесконечное множество решений
Метод Крамера для N=3 (три уравнения, три переменных) рассмотрен в §49 данного справочника.
Алгоритм исследования системы 2-х линейных уравнений по методу Крамера
Примеры
Пример 1. Решите систему уравнений методом Крамера:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 \\ 2x-3y = 4 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 5 & -4 \\ 2 & -3 \\ \end{vmatrix} = 5\cdot(-3)-2\cdot(-4) = -15+8 =-7 $$
$$ \Delta_x = \begin{vmatrix} 3 & -4 \\ 4 & -3 \\ \end{vmatrix} = 3\cdot(-3)-4\cdot(-4) = -9+16 = 7 $$
$$ \Delta_y = \begin{vmatrix} 5 & 3 \\ 2 & 4 \\ \end{vmatrix} = 5\cdot4-2\cdot3 = 20-6 = 14 $$
$$ x = \frac{\Delta_x}{\Delta} = \frac{7}{-7} = -1, y = \frac{\Delta_y}{\Delta} = \frac{14}{-7} = -2 $$
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 \\ 3x-4y = 0 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 4 & -3 \\ 3 & -4 \\ \end{vmatrix} = 4\cdot(-4)-3\cdot(-3) = -16+9 = -7 $$
$$ \Delta_x = \begin{vmatrix} 7 & -3 \\ 0 & -4 \\ \end{vmatrix} = 7\cdot(-4)-0\cdot(-3) = -28 $$
$$ \Delta_y = \begin{vmatrix} 4 & 7 \\ 3 & 0 \\ \end{vmatrix} = 4\cdot0-3\cdot7 = -21 $$
$$ x = \frac{\Delta_x}{\Delta} = \frac{-28}{-7} = 4, y = \frac{\Delta_y}{\Delta} = \frac{-21}{-7} = 3 $$
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 \\ 2a+3b = -1 \end{array} \right. } $
} $
$$ \Delta = \begin{vmatrix} 5 & -4 \\ 2 & 3 \\ \end{vmatrix} = 5\cdot3-2\cdot(-4) = 15+8 = 23 $$
$$ \Delta_a = \begin{vmatrix} 9 & -4 \\ -1 & -3 \\ \end{vmatrix} = 9\cdot3-(-1)\cdot(-4) = 27-4 = 23 $$
$$ \Delta_b = \begin{vmatrix} 5 & 9 \\ 2 & -1 \\ \end{vmatrix} = 5\cdot(-1)-2\cdot9 = -5-18 = -23 $$
$$ a = \frac{\Delta_a}{\Delta} = \frac{23}{23} = 1, b = \frac{\Delta_b}{\Delta} = \frac{-23}{23} = -1 $$
Ответ: (1;-1)
$ r) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 7 & 4 \\ 3 & 2 \\ \end{vmatrix} = 7\cdot2-3\cdot4 = 14-12 = 2 $$
$$ \Delta_a = \begin{vmatrix} 5 & 4 \\ 1 & 2 \\ \end{vmatrix} = 5\cdot2-1\cdot4 = 10-4 = 6 $$
$$ \Delta_b = \begin{vmatrix} 7 & 5 \\ 3 & 1 \\ \end{vmatrix} = 7\cdot1-3\cdot5 = 7-15 = -8 $$
$$ a = \frac{\Delta_a}{\Delta} = \frac{6}{2} = 3, b = \frac{\Delta_b}{\Delta} = \frac{-8}{2} = -4 $$
Ответ: (3;-4)
Пример 2*. 2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $
2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $
Ответ: 1) $a \neq \pm5$; 2) a = 5; 3) a = -5
Решение систем уравнений методом крамера эксель
Содержание
- 1 Варианты решений
- 1.1 Способ 1: матричный метод
- 1.2 Способ 2: подбор параметров
- 1.3 Способ 3: метод Крамера
- 1.4 Способ 4: метод Гаусса
- 2 Краткое описание метода Крамера
- 3 Решение уравнений методом Крамера в Excel
Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
Решим систему из 3-х уравнений.
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Определитель основной матрицы вычислим с помощью формулы =МОПРЕД(A11:C13)
Определитель =12, это означает, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера.
В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера.
Теперь последовательно будем заменять столбцы матрицы А на столбец свободных членов и вычислять соответствующие определители полученных матриц. Отношение определителей позволяет вычислить переменные х.
В файле примера также приведено решение системы 4-х уравнений и прямая проверка решения.
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
 Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
- Принимаем значение x за равное . Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число , принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за . После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
 Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Одним из способов решения системы линейных уравнений является применение метода Крамера.
Давайте разберем принципы использования метода Крамера в Excel.
Краткое описание метода Крамера
Предположим у нас есть система из n линейных уравнений с n неизвестными.
Тогда, при определителе матрицы системы D, отличном от нуля, решение записывается в следующем виде:
Решение уравнений методом Крамера в Excel
Разберем систему из 3 линейных уравнений с 3 неизвестными и запишем систему линейных уравнений в матричном виде Ax = B.
Введем матрицы A (диапазон ячеек B3:D5) и B (диапазон ячеек G3:G5), для наглядности области ввода выделены зеленым цветом.
В ячейке B7, с помощью функции МОПРЕД, запишем расчет определителя матрицы A:
В случае если определитель системы не равен нулю, то система имеет единственное решение и систему можно решить методом Крамера.
Для поиска решения вычислим 3 дополнительных определителя матриц (диапазоны ячеек B9:D11, B13:D15 и B17:D19), в каждом из которых вместо одного из столбцов подставляется матрица B.
Например, вместо первого столбца (коэффициенты при переменной x1), ставим столбец матрицы B (свободные коэффициенты):
В ячейках F10, F14 и F18 рассчитываем определители матриц и записываем в ячейки I10, I14 и I18 (выделены голубым цветом) решение системы, по формуле Крамера получаем как отношение определителя дополнительных матриц к определителю матрицы системы (формулы =F10/B7, =F14/B7 и =F18/B7).
Решение СЛАУ методом Крамера для матриц большего размера (4×4, 5×5 и т.д.) аналогично рассмотренному выше.
Подробно ознакомиться с шаблоном решения для матриц 3×3 и 4×4 — скачать пример.
Видео с вопросами: Использование правила Крамера для решения системы уравнений, определяемой с помощью определителей матрицы два на два
Стенограмма видео
Решите, используя правило Крамера, одновременных уравнений определитель матрицы отрицательный, 𝑧, отрицательный четыре, 𝑦 равно 23; определитель матрицы два, 𝑦, минус пять, 𝑥 равно 13; а определитель матрицы три, 𝑥, пять, 𝑧 равен 51.
Нас попросили использовать формулу Крамера
правило, чтобы решить эту проблему. Это немного отличается от того, как
мы часто сталкиваемся с вопросами, связанными с использованием правила Крамера, потому что наша система
линейные уравнения были даны нам в терминах определителей. Но для начала вспомним
Правило Крамера. Правило Крамера говорит нам, что если
определитель матрицы коэффициентов в системе линейных уравнений отличен от нуля,
тогда существует единственное решение системы, заданной формулой 𝑥 равно Δ sub 𝑥 над Δ, 𝑦
равно Δ sub 𝑦 над Δ, а 𝑧 равно Δ sub 𝑧 над Δ.
Но для начала вспомним
Правило Крамера. Правило Крамера говорит нам, что если
определитель матрицы коэффициентов в системе линейных уравнений отличен от нуля,
тогда существует единственное решение системы, заданной формулой 𝑥 равно Δ sub 𝑥 над Δ, 𝑦
равно Δ sub 𝑦 над Δ, а 𝑧 равно Δ sub 𝑧 над Δ.
Но чтобы использовать правило Крамера, нам сначала нужно, чтобы наша система линейных уравнений была в виде матрицы уравнение. Поэтому нам придется использовать определители, которые нам дали, чтобы поместить эти одновременные уравнения в матрицу уравнение. Начнем этот вопрос с оценивая определители этих матриц два на два, которые мы получили в вопрос.
Напомним, что мы находим определитель
матрицы два на два 𝑎, 𝑏, 𝑐, 𝑑 путем вычисления 𝑎𝑑 минус 𝑏𝑐. Итак, давайте сначала посмотрим на это
матрица минус один, 𝑧, минус четыре, 𝑦. Определитель этой матрицы равен
будет отрицательным, умноженным на 𝑦. Это дает нам отрицательное 𝑦. А затем мы вычитаем 𝑧 умноженное
на минус четыре. Это дает нам минус четыре 𝑧. И поскольку мы вычитаем
отрицательный, мы можем записать это как плюс. Итак, определитель этой матрицы
отрицательно 𝑦 плюс четыре 𝑧. И как нам дано в вопросе,
это равно 23,
Определитель этой матрицы равен
будет отрицательным, умноженным на 𝑦. Это дает нам отрицательное 𝑦. А затем мы вычитаем 𝑧 умноженное
на минус четыре. Это дает нам минус четыре 𝑧. И поскольку мы вычитаем
отрицательный, мы можем записать это как плюс. Итак, определитель этой матрицы
отрицательно 𝑦 плюс четыре 𝑧. И как нам дано в вопросе,
это равно 23,
Мы можем сделать то же самое для второго матрица. Найдем определитель матрица два, 𝑦, минус пять, 𝑥. Сначала делаем два умножаем на 𝑥, что дает нам два 𝑥. И мы вычитаем 𝑦, умноженное на минус пять, то есть минус пять 𝑦. И снова, потому что мы вычитая минус, мы можем записать это как плюс. И как нам дано в вопросе, это равно 13,
Итак, теперь давайте сделаем третий и
конечная матрица. Умножаем три на 𝑧, чтобы получить
нас трое 𝑧. Мы вычитаем 𝑥, умноженное на
пять, то есть пять 𝑥. А мы знаем, что это равно
51.
Мы вычитаем 𝑥, умноженное на
пять, то есть пять 𝑥. А мы знаем, что это равно
51.
Итак, нам удалось взять нам даны три определителя и находим три линейных уравнения. Но для того, чтобы применить Крамера правило, нам нужно переписать систему в виде матричного уравнения. Но для этого перепишем наши уравнения так, что 𝑥-коэффициенты, 𝑦-коэффициенты и 𝑧-коэффициенты и константы совпадают. Однако мы должны быть осторожны, чтобы включить нулевые коэффициенты в нашу матрицу коэффициентов. Чтобы помочь нам сделать это, когда мы перепишем нашу систему уравнений, включим нулевые коэффициенты перед записью это как матричное уравнение.
Наше первое уравнение отрицательное 𝑦
добавить четыре 𝑧 равно 23. Но наши переменные 𝑥, 𝑦 и
𝑧 для этой системы. Таким образом, мы можем переписать это как ноль 𝑥
минус 𝑦 плюс четыре 𝑧 равно 23. Таким образом, мы можем сделать то же самое для нашего
второе уравнение. Второе уравнение не включает
любые коэффициенты для 𝑧. Поэтому мы перепишем это как два 𝑥 плюс
пять 𝑦 плюс ноль 𝑧 равно 13. Тогда мы можем сделать последнее
уравнение. Мы пишем это как минус пять 𝑥
плюс ноль 𝑦 плюс три 𝑧 равно 51. Мы включаем ноль 𝑦, потому что
уравнение изначально не имело 𝑦-коэффициентов. Кроме того, мы переставляем это так, чтобы 𝑥
сначала идут, потом 𝑦, потом 𝑧. Написание таким образом делает его
гораздо проще поместить эту систему в матричное уравнение.
Таким образом, мы можем сделать то же самое для нашего
второе уравнение. Второе уравнение не включает
любые коэффициенты для 𝑧. Поэтому мы перепишем это как два 𝑥 плюс
пять 𝑦 плюс ноль 𝑧 равно 13. Тогда мы можем сделать последнее
уравнение. Мы пишем это как минус пять 𝑥
плюс ноль 𝑦 плюс три 𝑧 равно 51. Мы включаем ноль 𝑦, потому что
уравнение изначально не имело 𝑦-коэффициентов. Кроме того, мы переставляем это так, чтобы 𝑥
сначала идут, потом 𝑦, потом 𝑧. Написание таким образом делает его
гораздо проще поместить эту систему в матричное уравнение.
Я собираюсь освободить место, так что
что у нас есть только наши уравнения, которые выделены оранжевым цветом. Итак, вот наши три уравнения,
и мы собираемся поместить это в матричное уравнение. Матричное уравнение имеет три
частей: матрица коэффициентов, которая представляет собой матрицу, состоящую из коэффициентов
наши переменные 𝑥, 𝑦 и 𝑧; переменная матрица, которая состоит из переменных
для нашей системы; и постоянная матрица, матрица, состоящая из констант.
Итак, давайте сначала заполним элементы для матрицы коэффициентов, то есть коэффициенты для наших переменных. Помните об осторожности с отрицательный 𝑦 в первом уравнении, потому что коэффициент отрицательный. Теперь вы понимаете, почему мы переписали уравнения таким образом, чтобы включить нулевые коэффициенты. Переменная матрица состоит из переменные в нашей системе. Это 𝑥, 𝑦 и 𝑧. И, наконец, постоянная матрица состоит из констант нашей системы уравнений. Это 23, 13 и 51.
Теперь мы можем начать думать о
применяя правило Крамера. Для этого нам понадобится Δ
суб 𝑥, Δ суб 𝑦, Δ суб 𝑧 и Δ. В этот момент мы помним, что Δ
sub 𝑥, Δ sub 𝑦 и Δ sub 𝑧 — определители матриц, которые формируются
в результате замены элементов матрицы констант на элементы
столбцов 𝑥-, 𝑦- и 𝑧-коэффициентов. Итак, давайте продолжим и найдем
значения для Δ sub 𝑥, Δ sub 𝑦 и Δ sub 𝑧.
Δ sub 𝑥 является определителем матрица, которую мы получаем, когда мы берем матрицу коэффициентов и подставляем элементы из постоянная матрица с элементами из столбца 𝑥-коэффициентов, что есть определитель матрицы 23, отрицательная единица, четыре, 13, пять, ноль, 51, ноль, три. В этот момент мы можем вспомнить, как мы найти определитель матрицы три на три. Мы используем эту формулу, которая включает нахождение определителей матриц два на два, известных как кофакторы матрица три на три. Итак, давайте воспользуемся этим, чтобы найти Δ 𝑥.
Обратите внимание, что у нас минус минус
здесь, так что мы можем написать это как плюс. Теперь мы можем решить это с помощью
вычисление определителей каждой из этих матриц кофакторов. Определитель первого
Матрица кофакторов находится путем умножения пяти на три минус ноль, умноженного на
нуль. Это дает нам 15. Тогда мы можем найти определитель
матрицы второго кофактора. Мы делаем это, делая 13 умножить
на три минус ноль, умноженное на 51. Это дает нам 39. Наконец, находим определитель
последняя кофакторная матрица. И мы делаем это, делая 13
умножить на ноль минус пять умножить на 51. Получится отрицательное число 255.
Это дает нам 15. Тогда мы можем найти определитель
матрицы второго кофактора. Мы делаем это, делая 13 умножить
на три минус ноль, умноженное на 51. Это дает нам 39. Наконец, находим определитель
последняя кофакторная матрица. И мы делаем это, делая 13
умножить на ноль минус пять умножить на 51. Получится отрицательное число 255.
Итак, теперь я подставлю эти значения. Так что нам просто нужно вычислить 23 умножить на 15 добавить один умножить на 39 добавить четыре умножить на минус 255. И мы можем вычислить это как отрицательный 636. Итак, мы обнаружили, что Δ sub 𝑥 отрицательное 636.
Теперь мы можем вычислить Δ sub 𝑦, используя
точно такой же метод. Сначала я освобожу немного места. Δ sub 𝑦 — это матрица, которую мы получаем, когда
заменяем элементы постоянной матрицы коэффициентами при 𝑦 из
матрица коэффициентов. И мы будем использовать тот же метод, что и
просто использовал, чтобы найти определитель для этой матрицы. Отсюда снова вычисляем
определитель этих кофакторов. будет 39, шесть и
167. Итак, мы вычисляем ноль
умножить на 39 минус 23 умножить на шесть добавить четыре умножить на 167. Это дает нам 530. Итак, Δ sub 𝑦 равно 530.
И мы будем использовать тот же метод, что и
просто использовал, чтобы найти определитель для этой матрицы. Отсюда снова вычисляем
определитель этих кофакторов. будет 39, шесть и
167. Итак, мы вычисляем ноль
умножить на 39 минус 23 умножить на шесть добавить четыре умножить на 167. Это дает нам 530. Итак, Δ sub 𝑦 равно 530.
И таким же образом мы теперь
рассчитать Δ к югу от 𝑧. Мы находим ∆ sub 𝑧, находя
определитель матрицы, который мы получим, если подставим элементы
постоянная матрица с коэффициентами 𝑧 из матрицы коэффициентов. Затем мы можем использовать тот же метод для
найти определитель. Затем вычисляем определители
кофакторов, то есть 255, 167 и 25. Итак, теперь мы можем вычислить ноль
умножить на 255, добавить единицу, умножить на 167, добавить 23, умножить на 25. И мы находим, что это дает нам 742. Таким образом, Δ sub 𝑧 равно 742.
Итак, последнее, что нам нужно найти это Δ. Δ – определитель матрица коэффициентов. Итак, еще раз, мы собираемся используйте тот же метод, чтобы найти определитель этой матрицы три на три. Опять же, нам нужно найти определитель каждой из этих матриц кофакторов. Мы находим, что первый равен 15. Второй равен шести. А третий — 25. Итак, мы вычисляем ноль умножить на 15 добавить один умножить на шесть добавить четыре умножить на 25. И это дает нам 106. Итак, Δ равно 106.
Теперь у нас есть все компоненты
что нам нужно использовать правило Крамера. У нас есть Δ суб 𝑥, Δ суб 𝑦, Δ суб
𝑧 и Δ. Итак, теперь мы можем заменить эти
значений в уникальное решение из правила Крамера, чтобы найти наши значения для 𝑥, 𝑦,
и 𝑧. Начиная с 𝑥 равно Δ sub 𝑥
над Δ, и поскольку мы обнаружили, что Δ sub 𝑥 отрицательное 636, а Δ равно 106, поэтому 𝑥
равно отрицательному 636 больше 106. Поскольку 106 входит в 636 шесть раз,
это всего лишь минус шесть. Правило Крамера также говорит нам, что 𝑦
равно ∆ sub 𝑦 над ∆. Это 530 на 106. А так как 530 разделить на 106 будет пять,
у нас есть, что 𝑦 равно пяти. И, наконец, мы находим 𝑧, выполняя Δ
суб 𝑧 над Δ. Это дает нам 742 на 106. И 742, деленное на 106, равно
Семь.
Поскольку 106 входит в 636 шесть раз,
это всего лишь минус шесть. Правило Крамера также говорит нам, что 𝑦
равно ∆ sub 𝑦 над ∆. Это 530 на 106. А так как 530 разделить на 106 будет пять,
у нас есть, что 𝑦 равно пяти. И, наконец, мы находим 𝑧, выполняя Δ
суб 𝑧 над Δ. Это дает нам 742 на 106. И 742, деленное на 106, равно
Семь.
Итак, наш окончательный ответ: 𝑥 равно минус шесть, 𝑦 равно пяти, а 𝑧 равно семи.
17Предварительное исчисление — правило Крамера
Мы можем использовать матрицы и определители для решения систем линейных уравнений, используя технику, называемую правилом Крамера. Мы покажем, как это сделать с двумя уравнениями и двумя неизвестными. Однако эту концепцию можно распространить и на системы более высокого порядка.
Дана система линейных уравнений вида
\(
\begin{массив}{ccccc}
топор & + & по & = & z_0 \\
cx & + & dy & = & z_1
\конец{массив}
\)
, где \( a, b, c, d, z_0, z_1 \) все вещественные константы, а переменные \( x\) и \(y \).
Нам нужно найти, какие значения \(x\) и \(y\) решают это уравнение. Возможны три случая.
1. \(x\) и \(y\) действительны, единственны и не равны.
2. \(x\) и \(y\) действительны и равны.
3. \(x\) и \(y\) комплексны.
Чтобы определить, какой случай имеет место, нужно посмотреть на определитель матрицы коэффициентов, т. е.
\(
\begin{vmatrix}
а и б \\
CD
\end{vmatrix}
\)
Если этот определитель равен нулю, то мы не можем использовать эту технику, и выполняется либо случай 2, либо случай 3. Если этот случай отличен от нуля, то имеет место случай 1, и мы можем решить эту проблему. Назовем матрицу коэффициентов \(A\) и так
\(
\абс{А} =
\begin{vmatrix}
а и б \\
CD
\end{vmatrix}
\)
Пока определитель матрицы коэффициентов НЕ равен нулю, мы можем решить эту систему уравнений, и значения будут равны
\(\displaystyle{
х = \ гидроразрыв {
\begin{vmatrix}
z_0 & б \\
z_1 и д
\end{vmatrix}
}{\абс{А}}
}\)
а также
\(\displaystyle{
у = \ гидроразрыв {
\begin{vmatrix}
а & z_0 \\
с и z_1
\end{vmatrix}
}{\абс{А}}
}\)
Обратите внимание, что в каждом случае выше мы заменили столбец матрицы \(A\), соответствующий вычисляемой нами переменной, константами \(z\).
Лучший способ изучить правило Крамера — понаблюдать за тем, как кто-то решает конкретные задачи, а затем много работать самостоятельно. Для начала вот видео, показывающее, в целом, как пользоваться правилом Крамера, затем он делает конкретный пример. После этого видео вы сможете решать задачи самостоятельно.
Хотя большинство приведенных ниже решений не показывают работу, важно проверять свою работу при использовании правила Крамера. Как вы видели из видео и увидите в решениях, очень и очень легко совершать ошибки, которые распространяются и дают вам все неправильные ответы. Поэтому важно снова подставить свои ответы ко всем уравнениям, чтобы убедиться, что у вас есть правильные ответы. Ваша работа может считаться незавершенной, если вы не проверите свои ответы (в зависимости от того, что ожидает ваш преподаватель). Так что просто привыкайте всегда проверять свои ответы. Это может быть разница между целой буквенной оценкой и занимает всего несколько секунд.
Практика. Системы 2×2
Системы 2×2
Если не указано иное, решите эти линейные системы с помощью правила Крамера.
\( 3x+4y=-14; \) \( -2x-3y=11 \)
Постановка задачи |
|---|
Решите \( 3x+4y=-14; \) \(-2x-3y=11 \) с помощью правила Крамера.
Окончательный ответ |
|---|
\(x=2, y=-5\)
Постановка задачи
Решить \( 3x+4y=-14; \) \(-2x-3y=-11x-3y= \) по правилу Крамера.
Решение
Криста Кинг Математика — 1884 видео решениевидео Криста Кинг Математика |
|---|
Окончательный ответ
, 0-52040005 Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( 5x+7y=-1; \) \( 6x+8y=1 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 5x+7y=-1; \) \( 6x+8y=1 \)
Окончательный ответ |
|---|
\(x=15/2, y=11/2\)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 5x+7y=-1; \) \( 6x+8y=1 \)
Решение
Thinkwell — 1885 видео решениевидео Thinkwell 5 |
|---|
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( 4x-2y=10; \) \( 3x-5y=11 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 4x-2y=10; \) \( 3x-5y=11 \)
Окончательный ответ |
|---|
\( x=2, y=-1 \)
Постановка задачи
4 Решите эту линейную систему, используя правило Крамера.
\( 4x-2y=10; \) \( 3x-5y=11 \)
Solution
mattemath — 1894 видео решениевидео от mattemath 900 092 |
|---|
Окончательный ответ
\( x=2, y=-1 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\(x-y=-3; \) \(x+4y=17 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( x-y=-3; \) \( x+4y=17 \)
Окончательный ответ |
|---|
\( x=1, y=4 \)
Постановка задачи
Решить это линейная система с использованием правила Крамера.
\( x-y=-3; \) \( x+4y=17 \)
Решение
MIP4U — 1895 видео решениевидео от MIP4U |
|---|
Окончательный ответ
\( x=1, y=4 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( 2x-3y=16;\) \(x+2y=1 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 2x-3y=16;\) \( x+2y=1 \)
Окончательный ответ |
|---|
\( x=5, y=-2 \)
Постановка задачи
5
5 Решите эту линейную систему, используя правило Крамера.
\( 2x-3y=16;\) \( x+2y=1 \)
Решение
MIP4U — 1897 видео решениевидео от MIP4U |
|---|
Окончательный ответ
\( x=5, y=-2 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( 2х + 5у = 26 \)
\( 5х — 4у = -1 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 2x + 5y = 26 \)
\( 5x — 4y = -1 \)
Окончательный ответ |
|---|
\( (3, 4) \)
Решите эту задачу0 Задача линейная система с использованием правила Крамера.
\( 2x + 5y = 26 \)
\( 5x — 4y = -1 \)
Решение
2855 видео решение
Окончательный ответ
\( (3, 4) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг. |
|---|
\( 3x — 2y = -4 \)
\( 4x — y = 3 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 3x — 2y = -4 \)
\( 4x — y = 3 \)
Окончательный ответ |
|---|
\( (2, 5) \)
5 Постановка задачи 0 линейная система с использованием правила Крамера.
\( 3x — 2y = -4 \)
\( 4x — y = 3 \)
Решение
2856 видео решение
Окончательный ответ
\( (2, 5) \)
- Постановка задачи
\( 2x + 3y = 13 \)
\( 3x — 5y = -9 \)
Окончательный ответ |
|---|
\( (2, 3) \)
4 Постановка задачи
4 линейная система с использованием правила Крамера.

\( 2x + 3y = 13 \)
\( 3x — 5y = -9 \)
Решение
2857 видео решение
Окончательный ответ
\( (2, 3) \)
4
8 Лог чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
- Постановка задачи
- Сеть TTU CAE
- Доступ к файлам вне кампуса г.
- Безопасный доступ к своим исследованиям или академическим файлам из дома или из любой точки мира.
- Отправка ссылки на личный файл по электронной почте
- Отправьте ссылку на файл в личном веб-пространстве по электронной почте, чтобы избежать превышения квоты электронной почты получателей и других технических проблем.
 г.
г. - Помощь и поддержка пользователей
- г. Лабораторный файловый сервер CAE
- Введение и документация по файловому серверу CAE Lab.
- Файловый сервер CAE Lab г.
- В следующем наборе документов подробно описываются возможности, предлагаемые на файловом сервере CAE Lab, и доступ к сохраненным файлам в кампусе и за его пределами.
- Подключение к файловому серверу CAE Lab (для пользователей Windows в кампусе) г.
- Следующие инструкции должны помочь вам подключиться к центральному файловому серверу CAE Lab из других мест в кампусе, при условии, что Windows 7 установлена на …
- Подключение к файловому серверу CAE Lab (пользователи Mac OS X в кампусе) г.
- Следующие инструкции должны помочь вам подключиться к центральному файловому серверу CAE Lab из других мест в кампусе, при условии, что Mac OS X установлена на …
- Подключение к файловому серверу CAE Lab (пользователи Windows за пределами кампуса) г.
- Следующие инструкции должны помочь вам подключиться к центральному файловому серверу CAE Lab из мест за пределами кампуса, при условии наличия последней версии …
- Подключение к файловому серверу CAE Lab (для пользователей Mac OS X за пределами кампуса) г.
- Следующие инструкции должны помочь вам подключиться к центральному файловому серверу CAE Lab из мест за пределами кампуса, при условии, что Mac OS X установлена на …
- Подключение к файловому серверу CAE Lab (для пользователей Unix в кампусе)
93-8
9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92 - Оцените 2 × 2 определителей.

- Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
- Вычислите 3 × 3 определителей.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
- Знать свойства определителей.
- [латекс] \,\,D:[/latex]определитель матрицы коэффициентов
- [латекс]{D}_{x}:[/latex]определитель числителя в решении [latex]x[/latex]
[латекс]x=\frac{{D}_{x}}{D}[/латекс]
- [латекс]{D}_{у}:[/латекс]определитель числителя в решении [латекс]\,у[/латекс]
[латекс]y=\frac{{D}_{y}}{D}[/латекс]
- Дополнить [latex]\,A\,[/latex] первыми двумя столбцами.
[латекс]\mathrm{det}\left(A\right)=|\begin{array}{ccc}{a}_{1}& {b}_{1}& {c}_{1}\ \ {a}_{2}& {b}_{2}& {c}_{2}\\ {a}_{3}& {b}_{3}& {c}_{3}\ конец {массив}\,\,\,|\,\,\,\begin{массив}{c}{a}_{1}\\ {a}_{2}\\ {a}_{3} \end{массив}\,\,\,\,\begin{массив}{c}{b}_{1}\\ {b}_{2}\\ {b}_{3}\end{массив }|[/латекс]
- От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали.
 Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали. - Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали. Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
- Умножить уравнение (1) на [латекс]\,-2.[/латекс]
- Добавить результат в уравнение[латекс]\,\влево(2\вправо).[/латекс]
- Умножьте уравнение (1) на [латекс]\,-2\,[/латекс] и добавьте результат к уравнению (3):
[латекс]\frac{\begin{array}{r}\hfill -2x+4y-6x=0\\ \hfill 2x-4y+6z=0\end{array}}{\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,0=0}[/латекс]
- Получение ответа [latex]\,0=0,\,[/latex] — утверждения, которое всегда истинно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой. См. (Рисунок).
Рисунок 2.[/hidden-answer]
- Если матрица имеет верхнетреугольную форму, определитель равен произведению элементов по главной диагонали.

- При перестановке двух строк определитель меняет знак. 9{-1}\,[/latex]является обратной величиной определителя матрицы[latex]\,A.[/latex]
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
- Умножьте уравнение (3) на –2 и добавьте результат к уравнению (1).
[латекс]\frac{\begin{array}{l}-2x-4y-4x=-8\hfill \\ \text{ }2x+4y+4z=2\,\,\,\,\,\ hfill \end{array}}{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,0=-6}[/латекс]
- Решение системы двух уравнений с помощью правила Крамера
- Решение системы трех уравнений с использованием правила Крамера
- Определитель для [латекс]\,\слева[\начало{массив}{cc}a& b\\ c& d\конец{массива}\справа]\,[/латекс][латекс]\ ,ad-bc.\,[/latex] См.
 (рисунок).
(рисунок). - Правило Крамера заменяет столбец переменной столбцом константы. Решения: [латекс]\,x=\frac{{D}_{x}}{D},y=\frac{{D}_{y}}{D}.\,[/latex] См. (рис. ).
- Чтобы найти определитель матрицы 3×3, увеличьте первые два столбца. Сложите три диагональных элемента (слева вверху справа внизу) и вычтите три элемента по диагонали (слева внизу справа вверху). См. (Рисунок).
- Чтобы решить систему из трех уравнений с тремя переменными с помощью правила Крамера, замените столбец переменных столбцом констант для каждого требуемого решения: [латекс]\,x=\frac{{D}_{x}}{D}, y=\frac{{D}_{y}}{D},z=\frac{{D}_{z}}{D}.\,[/latex] См. (рисунок).
- Правило Крамера также полезно для нахождения решения системы уравнений без решения или с бесконечным числом решений. См. (Рисунок) и (Рисунок).
- Некоторые свойства определителей полезны при решении задач. Например:
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.

- При перестановке двух строк определитель меняет знак.
- Если две строки или два столбца идентичны, определитель равен нулю. 9{-1}\,[/latex]является обратной величиной определителя матрицы[latex]\,A.[/latex]
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент. См. (Рисунок) и (Рисунок).
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
- Правило Крамера
- метод решения систем уравнений, имеющих такое же количество уравнений, что и переменных, с использованием определителей
- определитель
- число, рассчитанное с использованием элементов квадратной матрицы, определяющее такую информацию, как наличие решения системы уравнений
\( 2х — 7у = 1 \)
\( 3х + у = 13 \)
Окончательный ответ |
|---|
\( (4, 1) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x — 7y = 1 \)
\( 3x + y = 13 \)
Решение
2858 видео решение
Окончательный ответ
\( (4, 1) \)
6

- Постановка задачи
\( x — 2y = -3 \)
\( 3x + y = 5 \)
Окончательный ответ |
|---|
\( (1, 2) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x — 2y = -3 \)
\( 3x + y = 5 \)
Решение
2859 видео решение
Окончательный ответ
\( (1, 2) \)
Лог чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг. |
|---|
\( x — y = 4 \)
\( 2x + y = 2 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( x — y = 4 \)
\( 2x + y = 2 \)
Окончательный ответ |
|---|
\( (2, -2) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x — y = 4 \)
\( 2x + y = 2 \)
Решение
2860 видео решение
Окончательный ответ
\( (2, -2) \)
4 Лог чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг. |
|---|
- Постановка задачи
\( 4x — 2y = 10 \)
\( 3x — 5y = 11 \)
Окончательный ответ |
|---|
\( (2, -1) \)
Решение этой задачи
0 линейная система с использованием правила Крамера.
\( 4x — 2y = 10 \)
\( 3x — 5y = 11 \)
Solution
mattemath — 2861 video solution video by mattemath
Final Answer
\ ( (2, -1) \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
Постановка задачи
\( 2x — 3y = 1 \)
\( x + 2y = 11 \) Окончательный ответ
\( (5, 3) \)
45 Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x — 3y = 1 \)
\( x + 2y = 11 \)
Решение
2862 видео решение
Окончательный ответ
\( (5, 3) \)
6
7 0 in Log чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
Постановка задачи
\( 3x = 2y + 5 \)
\( 4y = 6x — 8 \) Окончательный ответ
нет решения
\( 3x = 2y + 5 \)
\( 4y = 6x — 8 \)
Решение
2863 видео решение
Окончательный ответ
нет решения
900 см. его текущий рейтинг.
Постановка задачи
\( x + 2y = -3 \)
\( -3x — 6y = 9 \) Окончательный ответ
бесконечное число решений Правило.
\( х + 2у = -3 \)
\( -3х — 6у = 9\)
Решение
2864 видео решение
Окончательный ответ
бесконечное количество решений
Войдите, чтобы оценить эту практическую задачу и увидеть ее текущий рейтинг.
\( 3x + 7y = 5 \)
\( -2x + y = -9 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 3x + 7y = 5 \)
\( -2x + y = -9 \)
Окончательный ответ
\( (4, -1) \)
5 Постановка задачи Решите эту линейную систему, используя правило Крамера.
\( 3x + 7y = 5 \)
\( -2x + y = -9 \)
Решение
2865 видеорешение
Окончательный ответ
\( (4, -1) \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
\( 2x + 3y = -4 \)
\( -x + y = 7 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x + 3y = -4 \)
\( -x + y = 7 \)
Окончательный ответ
\( (-5, 2) \)
Постановка задачи Решите эту линейную систему, используя правило Крамера.
\( 2x + 3y = -4 \)
\( -x + y = 7 \)
Решение
2866 видео решение
Окончательный ответ
\( (-5, 2) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
Практика — Системы 3×3
\( 2x+3y+z=2; \) \( -x+2y+3z=-1; \) \( -3x-3y+z=0 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x+3y+z=2; \) \( -x+2y+3z=-1; \) \( -3x-3y+z=0 \)
Окончательный ответ
\( x=4, y=-3, z=3 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x+3y+z=2; \) \( -x+2y+3z=-1; \) \( -3x-3y+z=0 \)
Решение
MIP4U — 1896 видео решение видео MIP4U
Окончательный ответ
\( x=4, y=-3, z=3 \)
9008 и чтобы увидеть его текущий рейтинг.
\( 2x-y-z=2; \) \( 4x+y-z=-5; \) \( 6x-2y+2z=17 \)
Постановка задачи
Решите эту линейную систему используя правило Крамера.
\( 2x-y-z=2; \) \( 4x+y-z=-5; \) \( 6x-2y+2z=17 \)
Окончательный ответ
\( x=1 /2, y=-4, z=3 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x-y-z=2; \) \( 4x+y-z=-5; \) \( 6x-2y+2z=17 \)
Решение
MIP4U — 1902 Видеореал Видео MIP4U
Окончательный ответ
\ (x = 1/2, y = -4, Z = 3 \) 9000
\ (x = 1/2, y = -4, Z = 3 \) 9000
77777 \ (x = 1/2, y = -4, Z = 3 \)8699 \ (x = 1/2, y = -4, Z = 3 \)
869 \ (x = 1/2, y = -4, Z = 3 \)
86 \ (x = 1/2, y = -4, Z = 3 \)
869.
Войдите в систему, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
Постановка задачи
Решите эту линейную систему с помощью Крамера Правило.
\( x+2z=9; \) \( 2y+z=8; \) \( 4x-3y=-2 \)
Окончательный ответ
\( x=1, y =2, z=4 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x+2z=9; \) \( 2y+z=8; \) \( 4x-3y=-2 \)
Решение
PatrickJMT — 1903 видео решение видео от PatrickJMT
Окончательный ответ
\( x=1, y=2, z=4 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
\( x-y+z=4; \) \( 2x+y+z=7; \) \( -x-2y+2z=-1 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x-y+z=4; \) \( 2x+y+z=7; \) \( -x-2y+2z=-1 \)
Окончательный ответ
\(х=3, у=0, г=1 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x-y+z=4; \) \( 2x+y+z=7; \) \( -x-2y+2z=-1 \)
Решение
PatrickJMT — 1904 видео решение видео от PatrickJMT
Окончательный ответ
\( x=3, y=0, z=1 \)
текущие рейтинги и практики, чтобы увидеть эту проблему .
\( -x+2y-3z=1; \) \( 2x+z=0; \) \( 3x-4y+4z=2 \)
Постановка задачи
Решить это линейная система с использованием правила Крамера.
\( -x+2y-3z=1; \) \( 2x+z=0; \) \( 3x-4y+4z=2 \)
Окончательный ответ
\( x=-4/5, y=-3/2, z=-8/5 \)
Постановка задачи
Решите эту линейную систему с помощью правила Крамера.
\( -x+2y-3z=1; \) \( 2x+z=0; \) \( 3x-4y+4z=2 \)
Решение
математика — 1905 видео решение видео от mattemath
Окончательный ответ
\( x=-4/5, y=-3/2, z=-8/5 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
\( x — 3y + 3z = -6 \)
\( -2x + 4y + z = 3 \)
\( 3x — 5y +4z = -9 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\(x — 3y + 3z = -6 \)
\( -2x + 4y + z = 3 \)
\( 3x — 5y +4z = -9 \)
Окончательный ответ
\( (0, 1, -1) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\(x — 3y + 3z = -6 \)
\( -2x + 4y + z = 3 \)
\( 3x — 5y +4z = -9 \)
Решение
Эта задача решается за 2 видео подряд.
2867 решение для видео
2867 решение для видео
Окончательный ответ
\( (0, 1, -1) \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
\( 3x — 2y + z = 2 \)
\( 4x + 3y — 2z = 4 \)
\( 5x — 3y + 3z = 8 \)
Постановка задачи

\( 3x — 2y + z = 2 \)
\( 4x + 3y — 2z = 4 \)
\( 5x — 3y + 3z = 8 \) Окончательный ответ
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 3x — 2y + z = 2 \)
\( 4x + 3y — 2z = 4 \)
\( 5x — 3y + 3z = 8 \)
Решение
2868 видео решение
Окончательный ответ
4 \( (1, 2, 3) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
\( x + y — z = -2 \)
\( 2x — y + z = 0 \)
\( x — 2y + 3z = 1 \)
Постановка задачи

\( x + y — z = -2 \)
\( 2x — y + z = 0 \)
\( x — 2y + 3z = 1 \) Окончательный ответ
\ ( (-2/3, -7/3, -1) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x + y — z = -2 \)
\( 2x — y + z = 0 \)
\( x — 2y + 3z = 1 \)
Решение
2870 видео решение
Окончательный ответ
\( (-2/3, -7/3, -1) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
\( 2x + y — z = 1 \)
\( 3x + 2y + 2z = 13 \)
\( 4x — 2y + 3z = 9 \)
Постановка задачи
32 Решить эту линейную систему с помощью правила Крамера.
\( 2x + y — z = 1 \)
\( 3x + 2y + 2z = 13 \)
\( 4x — 2y + 3z = 9 \) Окончательный ответ
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x + y — z = 1 \)
\( 3x + 2y + 2z = 13 \)
\( 4x — 2y + 3z = 9 \)
Решение
2871 видео решение
Окончательный ответ
4 \( (1, 2, 3) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
\( 2x + 3y — 5z = 1 \)
\( x + y — z = 2 \)
\( 2y + z = 8 \)
Постановка задачи

\( 2x + 3y — 5z = 1 \)
\( x + y — z = 2 \)
\( 2y + z = 8 \) Окончательный ответ
\( (1, 3, 2) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x + 3y — 5z = 1 \)
\( x + y — z = 2 \)
\( 2y + z = 8 \)
Решение
2872 видео решение
Окончательный ответ
\( (1, 3, 2) \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
\( 3x + y — z = 0 \)
\( -2x + 5y + 4z = -1 \)
\( 3x + 2y + z = 1 \)
Постановка задачи
2 9 Решите эту линейную систему, используя правило Крамера.
\( 3x + y — z = 0 \)
\( -2x + 5y + 4z = -1 \)
\( 3x + 2y + z = 1 \)
Окончательный ответ
\( (1/2, -2/3, 5/6) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 3x + y — z = 0 \)
\( -2x + 5y + 4z = -1 \)
\( 3x + 2y + z = 1 \)
Решение
2873 видео решение
Окончательный ответ
\( (1/2, -2/3, 5/6) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
Сеть TTU CAE
Приносим извинения за неудобства, но страница, на которую вы пытались попасть, находится не по этому адресу.
Вы можете использовать приведенные ниже ссылки, чтобы помочь вам найти то, что вы ищете.
Если вы уверены, что у вас правильный веб-адрес, но столкнулись с ошибкой, пожалуйста,
связаться с Администрацией Сайта.
Спасибо.
Возможно, вы искали…



Решающие системы с правилом Крамера – алгебра и тригонометрия OpenStax
Цели обучения
В этом разделе вы:
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2×2
Определитель — это действительное число, которое может быть очень полезным в математике, поскольку оно имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Найдите определитель матрицы 2 × 2
Определитель матрицы [latex]\,2\text{ }×\text{ }2\,[/latex], заданной
[latex]A=\ left[\begin{array}{cc}a& b\\ c& d\end{array}\right][/latex]
определяется как
Обратите внимание на изменение обозначения. Есть несколько способов указать определитель, включая [латекс]\,\mathrm{det}\left(A\right)\,[/latex] и замену скобок в матрице прямыми линиями,[латекс]\,| А|.[/латекс]
Нахождение определителя матрицы 2 × 2
Нахождение определителя заданной матрицы.
[latex]A=\left[\begin{array}{cc}5& 2\\ -6& 3\end{array}\right][/latex]
[reveal-answer q=”1408516″]Show Решение[/reveal-answer][hidden-answer a=”1408516″]
[латекс]\begin{array}{l}\mathrm{det}\left(A\right)=|\begin{array}{ cc}5& 2\\ -6& 3\end{массив}|\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,=5\влево(3\вправо)-\влево(-6\вправо)\влево(2\вправо)\hfill \\ \,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,=27\hfill \end{массив}[/latex][/hidden-answer]
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во Введении к анализу линий алгебры. Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.
Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.
[латекс]\begin{array}{c}{a}_{1}x+{b}_{1}y={c}_{1}\,\,\,\,\left(1\ справа)\\ {a}_{2}x+{b}_{2}y={c}_{2}\,\,\,\,\left(2\right)\end{массив}[/ латекс]
Мы исключаем одну переменную, используя операции со строками, и находим другую. Скажем, что мы хотим найти [латекс]\,х.\,[/латекс]Если уравнение (2) умножить на коэффициент, противоположный [латекс]\,у\,[/латекс]в уравнении (1 ), уравнение (1) умножается на коэффициент [латекс]\,у\,[/латекс] в уравнении (2), и мы добавляем два уравнения, переменная [латекс]\,у\,[/латекс ] будет устранено.
[латекс]\begin{array}{l}\underset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_}{\begin{array}{llll}\hfill & \hfill & \hfill & \hfill \ \ \,\,\,\,{b}_{2}{a}_{1}x+{b}_{2}{b}_{1}y={b}_{2}{c} _{1}\hfill & \hfill & \hfill & \text{Умножить }{R}_{1}\text{ на }{b}_{2}\hfill \\ -{b}_{1}{ a}_{2}x-{b}_{1}{b}_{2}y=-{b}_{1}{c}_{2}\hfill & \hfill & \hfill & \text {Умножить }{R}_{2}\text{ на}-{b}_{1}\hfill \end{array}}\hfill \\ \,\,\,\begin{array}{ll} { b}_{2}{a}_{1}x-{b}_{1}{a}_{2}x={b}_{2}{c}_{1}-{b}_ {1}{c}_{2}\hfill & \hfill \end{массив}\hfill \end{массив}[/latex]
Теперь найдите [латекс]\,x.[/латекс]
[латекс]\begin{array}{l}\,\,\,{b}_{2}{a}_{1} x-{b}_{1}{a}_{2}x={b}_{2}{c}_{1}-{b}_{1}{c}_{2}\hfill \ \ \,\,\,x\left({b}_{2}{a}_{1}-{b}_{1}{a}_{2}\right)={b}_{2 }{c}_{1}-{b}_{1}{c}_{2}\hfill \\ \text{ }x=\frac{{b}_{2}{c}_{1} -{b}_{1}{c}_{2}}{{b}_{2}{a}_{1}-{b}_{1}{a}_{2}}=\frac {\left[\begin{array}{cc}{c}_{1}& {b}_{1}\\ {c}_{2}& {b}_{2}\end{массив}\ right]}{\left[\begin{array}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{ массив}\справа]}\hfill \конец{массив}[/латекс]
Аналогично, чтобы найти [латекс]\,у,[/латекс], мы исключим [латекс]\,х. [/латекс]
[/латекс]
[латекс]\begin{array}{l}\underset{\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_}{\begin{array}{llll}\hfill & \hfill & \hfill & \hfill \\ \,\,\,\,{a}_{2}{a }_{1}x+{a}_{2}{b}_{1}y={a}_{2}{c}_{1}\hfill & \hfill & \hfill & \text{Multiply} {R}_{1}\text{ by }{a}_{2}\hfill \\ -{a}_{1}{a}_{2}x-{a}_{1}{b} _{2}y=-{a}_{1}{c}_{2}\hfill & \hfill & \hfill & \text{Умножить }{R}_{2}\text{ на}-{a }_{1}\hfill \end{массив}}\hfill \\ \,\,\,\,\,\,\begin{массив}{ll}{a}_{2}{b}_{1 }y-{a}_{1}{b}_{2}y={a}_{2}{c}_{1}-{a}_{1}{c}_{2}\hfill & \hfill \end{массив}\hfill \end{массив}[/latex]
Решение для [латекс]\,y\,[/latex] дает
[латекс]\begin{array}{l}{a}_{2}{b}_{1}y-{a}_ {1}{b}_{2}y={a}_{2}{c}_{1}-{a}_{1}{c}_{2}\hfill \\ y\left({ a}_{2}{b}_{1}-{a}_{1}{b}_{2}\right)={a}_{2}{c}_{1}-{a} _{1}{c}_{2}\hfill \\ \text{ }y=\frac{{a}_{2}{c}_{1}-{a}_{1}{c}_ {2}}{{a}_{2}{b}_{1}-{a}_{1}{b}_{2}}=\frac{{a}_{1}{c}_ {2}-{a}_{2}{c}_{1}}{{a}_{1}{b}_{2}-{a}_{2}{b}_{1}} =\frac{|\begin{array}{cc}{a}_{1}& {c}_{1}\\ {a}_{2}& {c}_{2}\end{array} |}{|\begin{array}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{array}| }\hfill \end{массив}[/latex]
Обратите внимание, что знаменатель для [латекс]\,х\,[/латекс]и [латекс]\,у\,[/латекс] является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения [латекс]\,х\,[/латекс]и[латекс]\,у,\,[/латекс], но правило Крамера также вводит новые обозначения:
Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Затем мы можем выразить [латекс]\,х\,[/латекс]и[латекс]\,у\,[/латекс] как частное двух определителей.
Правило Крамера для систем 2×2
Правило Крамера — это метод, использующий детерминанты для решения систем уравнений, в которых число уравнений равно количеству переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
[латекс]\begin{array}{c}{a}_{1}x+{b}_{1}y={c}_{1}\\ {a}_{2}x+{b} _{2}y={c}_{2}\end{array}[/latex]
Решение с использованием правила Крамера задается как
[latex]x=\frac{{D}_{x}} {D}=\frac{|\begin{array}{cc}{c}_{1}& {b}_{1}\\ {c}_{2}& {b}_{2}\end {массив}|}{|\begin{массив}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{ массив}|},\,\,D\ne 0;\,\,\text{}\text{}\,y=\frac{{D}_{y}}{D}=\frac{ |\begin{array}{cc}{a}_{1}& {c}_{1}\\ {a}_{2}& {c}_{2}\end{array}|}{| \begin{массив}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{массив}|},\, \,D\ne 0.[/латекс]
Если мы вычисляем [латекс]\,х,\,[/латекс], то [латекс]\,х\,[/латекс]столбец заменяется столбцом констант. Если мы вычисляем [латекс]\,у,\,[/латекс], то столбец [латекс]\,у\,[/латекс] заменяется столбцом констант.
Использование правила Крамера для решения системы 2 × 2
Решите следующую систему[latex]\,2\text{ }×\text{ }2\,[/latex] с помощью правила Крамера.
[латекс]\begin{array}{c}12x+3y=15\\ \text{ }2x-3y=13\end{array}[/latex]
[reveal-answer q=”fs-id1459617″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1459617″]
Решить для [латекс]\,x. [/латекс]
[/латекс]
[латекс]x=\frac{{D}_{x}}{D}=\frac{|\begin{array}{rr}\ hfill 15& \hfill 3\\ \hfill 13& \hfill -3\end{array}|}{|\begin{array}{rr}\hfill 12& \hfill 3\\ \hfill 2& \hfill -3\end{array }|}=\frac{-45-39}{-36-6}=\frac{-84}{-42}=2[/latex]
Решить для[latex]\,y.[/latex]
[латекс]y=\frac{{D}_{y}}{D}=\frac{|\begin{array}{rr}\hfill 12& \hfill 15\\ \hfill 2& \hfill 13\end {массив}|}{|\begin{массив}{rr}\hfill 12& \hfill 3\\ \hfill 2& \hfill -3\end{массив}|}=\frac{156-30}{-36-6 }=-\frac{126}{42}=-3[/латекс]
Решение:[латекс]\,\влево(2,-3\вправо).[/латекс][/скрытый-ответ]
Попробуйте
Используйте правило Крамера, чтобы решить систему уравнений 2 × 2.
[латекс]\begin{array}{l}\text{ }x+2y=-11\hfill \\ -2x+y=-13\hfill \end{массив}[/latex]
[показать- ответ q=”fs-id1440640″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1440640″]
[латекс]\влево(3,-7\вправо)[/латекс]
[/скрытый-ответ]
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2×2 несложно, но найти определитель матрицы 3×3 сложнее. Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.
Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.
Найдите определитель матрицы 3×3.
[латекс]A=\left[\begin{array}{ccc}{a}_{1}& {b}_{1}& {c}_{1}\\ {a}_{2} & {b}_{2}& {c}_{2}\\ {a}_{3}& {b}_{3}& {c}_{3}\end{массив}\right][ /latex]
Алгебра выглядит следующим образом:
[латекс]|A|={a}_{1}{b}_{2}{c}_{3}+{b}_{1}{c}_ {2}{a}_{3}+{c}_{1}{a}_{2}{b}_{3}-{a}_{3}{b}_{2}{c} _{1}-{b}_{3}{c}_{2}{a}_{1}-{c}_{3}{a}_{2}{b}_{1}[/ латекс]
Нахождение определителя матрицы 3 × 3
Найти определитель заданной матрицы 3 × 3
[латекс]A=\left[\begin{array}{ccc}0& 2& 1\\ 3& — 1& 1\\ 4& 0& 1\end{массив}\right][/latex]
[reveal-answer q=”1570002″]Показать решение[/reveal-answer][hidden-answer a=”1570002″]
Дополните матрицу первыми двумя столбцами и следуйте формуле. Таким образом,
[латекс]\begin{array}{l}|A|=|\begin{array}{ccc}0& 2& 1\\ 3& -1& 1\\ 4& 0& 1\end{array}\,\ ,|\begin{массив}{c}0\\ 3\\ \,\,4\end{массив}\,\,\,\,\begin{массив}{c}2\\ -1\\ 0 \end{массив}|\hfill \\ \,\,\,\,\,\,\,=0\влево(-1\вправо)\влево(1\вправо)+2\влево(1\вправо) \влево(4\вправо)+1\влево(3\вправо)\влево(0\вправо)-4\влево(-1\вправо)\влево(1\вправо)-0\влево(1\вправо)\ влево(0\вправо)-1\влево(3\вправо)\влево(2\вправо)\hfill \\ \,\,\,\,\,\,\,=0+8+0+4-0 -6\hfill \\ \,\,\,\,\,\,\,=6\hfill \end{массив}[/latex][/hidden-answer]
Попробуйте
Найдите определитель матрицы 3 × 3.
[латекс]\mathrm{det}\left(A\right)=|\begin{array}{ccc}1& -3& 7\\ 1& 1& 1\\ 1& -2& 3\end{массив}|[/ латекс]
[ответ на ответ q=”fs-id1643971″]Показать решение[/ответ на ответ]
[скрытый ответ на вопрос a=”fs-id1643971″]
[латекс]-10[/латекс]
[/скрытый-ответ]
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для [латекс]\,2\текст{ }×\текст{ }2\,[/латекс]и [латекс]\,\текст{3}\текст{ }×\текст{ } 3\,[/латекс]матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.
Рассмотрим систему уравнений 3 × 3.
[латекс]x=\frac{{D}_{x}}{D},y=\frac{{D}_{y}}{D},z=\frac{{D}_ {z}}{D},D\ne 0[/latex]
где
Если мы пишем определитель[latex]\,{D}_{x},[/latex]заменяем [ латекс]\,х\,[/латекс]столбец с постоянным столбцом. Если мы записываем детерминант[латекс]{D}_{у},[/латекс] мы заменяем столбец [латекс]\,у\,[/латекс] столбцом констант. Если мы записываем определитель [латекс]\,{D}_{z},[/латекс], мы заменяем столбец [латекс]\,z\,[/латекс] столбцом констант. Всегда проверяйте ответ.
Решение системы 3 × 3 с помощью правила Крамера
Найдите решение данной системы 3 × 3 с помощью правила Крамера.
[латекс]\begin{array}{c}x+y-z=6\\ 3x-2y+z=-5\\ x+3y-2z=14\end{массив}[/latex]
[показать -answer q=”1588465″]Показать решение[/reveal-answer][hidden-answer a=”1588465″]
Использовать правило Крамера.
[латекс]D=|\begin{array}{ccc}1& \,\,1& -1\\ 3& -2& \,\,\,1\\ 1& \,\,3& -2\end{массив }|,{D}_{x}=|\begin{array}{ccc}6& 1& -1\\ -5& -2& \,\,\,1\\ 14& \,\,3& -2\end{ массив}|,{D}_{y}=|\begin{массив}{ccc}1& \,6& -1\\ 3& -5& \,\,1\\ 1& 14& -2\end{массив}|, {D}_{z}=|\begin{array}{ccc}1& \,1& 6\\ 3& -2& -5\\ 1& \,\,3& 14\end{массив}|[/latex]
Затем
[латекс]\begin{array}{l}x=\frac{{D}_{x}}{D}=\frac{-3}{-3}=1\hfill \\ y=\frac{{D}_{y}}{D}=\frac{-9}{-3}=3\hfill \\ z=\frac{{D}_{z}}{D}= \frac{6}{-3}=-2\hfill \end{array}[/latex]
Решение [латекс]\left(1,3,-2\right).[/latex][/ hidden-answer]
Попробуйте
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
[латекс]\begin{array}{r}\hfill x-3y+7z=13\\ \hfill x+y+z=1\,\,\,\\ \hfill x-2y+3z=4 \,\,\,\end{array}[/latex]
[reveal-answer q=”fs-id1405450″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1405450″]
[latex]\left(-2,\frac{3}{5},\frac{12}{5}\right)[/latex]
[/hidden-answer]
Использование правила Крамера для решения Несовместимая система
Решите систему уравнений, используя правило Крамера.
[латекс]\begin{array}{l}3x-2y=4\text{ }\left(1\right)\\ 6x-4y=0\text{ }\left(2\right)\end{ array}[/latex]
[reveal-answer q=”fs-id1464455″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1464455″]
Начнем с нахождения определителей[latex]\,D,{D}_{x},\text{и }{D}_{y}.[/latex]
[latex]D=|\begin{ array}{cc}3& -2\\ 6& -4\end{массив}|=3\left(-4\right)-6\left(-2\right)=0[/latex]
Мы знаем, что определитель нуля означает, что система либо не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
[латекс]\begin{array}{l}\underset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}{\begin {массив}{l}\begin{массив}{l}\hfill \\ -6x+4y\,\,\,\,=-8\hfill \end{массив}\hfill \\ \,\,\, 6x-4y\,\,\,\,\,\,=\,\,\,\,0\hfill \end{массив}}\hfill \\ \,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,=\,-8\hfill \end{массив} [/latex]
Получаем уравнение[латекс]\,0=-8,\,[/латекс], которое неверно. Следовательно, система не имеет решения. График системы показывает две параллельные линии. См. (Рисунок).
Следовательно, система не имеет решения. График системы показывает две параллельные линии. См. (Рисунок).
Рис. 1. [/hidden-answer]
Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным числом решений.
[латекс]\begin{array}{rr}\hfill x-2y+3z=0& \hfill \left(1\right)\\ \hfill 3x+y-2z=0& \hfill \left(2\right) )\\ \hfill 2x-4y+6z=0& \hfill \left(3\right)\end{массив}[/latex]
[reveal-answer q=»fs-id1360831″]Показать решение[/reveal- ответ]
[скрытый ответ a = «fs-id1360831»]
Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.
[латекс]|\begin{array}{rrr}\hfill 1& \hfill -2& \hfill 3\\ \hfill 3& \hfill 1& \hfill -2\\ \hfill 2& \hfill -4& \hfill 6\end {массив}\текст{ }|\текст{ }\begin{массив}{rr}\hfill 1& \hfill -2\\ \hfill 3& \hfill 1\\ \hfill 2& \hfill -4\end{массив}| [/латекс]
Затем
[латекс]1\влево(1\вправо)\влево(6\вправо)+\влево(-2\вправо)\влево(-2\вправо)\влево(2\ вправо)+3\влево(3\вправо)\влево(-4\вправо)-2\влево(1\вправо)\влево(3\вправо)-\влево(-4\вправо)\влево(-2\ вправо)\влево(1\вправо)-6\влево(3\вправо)\влево(-2\вправо)=0[/латекс]
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений. Мы должны выполнить исключение, чтобы узнать.
Мы должны выполнить исключение, чтобы узнать.
Понимание свойств определителей
Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
Свойства определителей
Иллюстрация свойств определителей
Проиллюстрируйте каждое из свойств определителей.
[открыть-ответ q=»fs-id1531880″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1531880″]
Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
[латекс]A=\left[\begin{array}{rrr}\hfill 1& \hfill \,\,2& \hfill 3\\ \hfill 0& \hfill \,\,2& \hfill 1\\ \hfill 0& \hfill \,\,0& \hfill -1\end{array}\right][/latex]
Дополнить[latex]\,A\,[/latex] первыми двумя столбцами.
[латекс]A=\left[\begin{array}{ccc}1& 2& 3\\ 0& 2& 1\\ 0& 0& -1\end{массив}|\,\,\,\begin{массив}{ c}1\\ 0\\ 0\end{массив}\,\,\,\,\begin{массив}{c}2\\ 2\\ 0\end{массив}\right][/latex]
Затем
[латекс]\begin{array}{l}\mathrm{det}\left(A\right)=1\left(2\right)\left(-1\right)+2\left(1\right) \влево(0\вправо)+3\влево(0\вправо)\влево(0\вправо)-0\влево(2\вправо)\влево(3\вправо)-0\влево(1\вправо)\влево (1\правый)+1\левый(0\правый)\левый(2\правый)\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,=-2\hfill \end{array}[/latex]
Свойство 2 утверждает, что перестановка строк меняет знак. Учитывая
Учитывая
[латекс]\begin{array}{l}\begin{array}{l}\\ A=\left[\begin{array}{cc}-1& 5\\ 4&-3\end{array} \right],\,\,\mathrm{det}\left(A\right)=\left(-1\right)\left(-3\right)-\left(4\right)\left(5\ right)=3-20=-17\end{массив}\hfill \\ \hfill \\ B=\left[\begin{массив}{cc}4& -3\\ -1& 5\end{массив}\right ],\,\,\mathrm{det}\left(B\right)=\left(4\right)\left(5\right)-\left(-1\right)\left(-3\right) =20-3=17\hfill\end{массив}[/latex]
Свойство 3 гласит, что если две строки или два столбца идентичны, определитель равен нулю.
[латекс]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,A=\left[\begin{array}{ccc}1& 2& 2\\ 2& 2& 2\\ -1& 2& 2\end{массив}\text{ }|\text{ }\begin{массив}{c}1\\ 2\\ -1\end{массив} \begin{ array}{c}2\\ 2\\ 2\end{массив}\right]\hfill \\ \hfill \\ \mathrm{det}\left(A\right)=1\left(2\right)\ влево(2\вправо)+2\влево(2\вправо)\влево(-1\вправо)+2\влево(2\вправо)\влево(2\вправо)+1\влево(2\вправо)\влево (2\правый)-2\левый(2\правый)\левый(1\правый)-2\левый(2\правый)\левый(2\правый)\hfill \\ \,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,=4-4+8+4-4-8=0\hfill \end{массив}[/latex] 9{-1}\right)=-2\left(-\frac{1}{2}\right)-\left(\frac{3}{2}\right)\left(1\right)=-\ frac{1}{2}\hfill \end{array}[/latex]
Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,
Таким образом,
[латекс]\begin{array}{l}A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],\mathrm{det}\left (A\right)=1\left(4\right)-2\left(3\right)=-2\hfill \\ \hfill \\ B=\left[\begin{array}{cc}2\left (1\правый)& 2\левый(2\правый)\\ 3&4\конец{массив}\правый],\mathrm{det}\левый(B\правый)=2\левый(4\правый)-3 \left(4\right)=-4\hfill \end{массив}[/latex][/hidden-answer]
Использование правила Крамера и свойств определителя для решения системы
Найдите решение данной системы 3 × 3.
[латекс]\begin{array}{ll}2x+4y+4z=2\hfill & \left(1\right)\hfill \\ 3x+7y+7z=-5\hfill & \left(2\ справа)\hfill \\ \text{ }x+2y+2z=4\hfill & \left(3\right)\hfill \end{массив}[/latex]
[reveal-answer q=»fs-id1653554 ″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1653554″]
Используя правило Крамера, мы имеем
[latex]D=|\begin{array}{ccc}2& 4& 4\\ 3& 7& 7\\ 1& 2& 2\end{array}|[/latex]
Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.
Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество. Мы должны выполнить исключение, чтобы узнать.
Получение утверждения, которое является противоречием, означает, что система не имеет решения.[/hidden-answer]
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.
Ключевые понятия
Раздел Упражнения
Вербальный
Объясните, почему мы всегда можем вычислить определитель квадратной матрицы.
[reveal-answer q=”1405260″]Показать решение[/reveal-answer][hidden-answer a=”1405260″]
Определитель – это сумма и произведения элементов матрицы, поэтому вы всегда можете оцените этот продукт, даже если в итоге он будет равен 0,9.0005
[/hidden-answer]
Изучая правило Крамера, объясните, почему нет единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте [латекс]\,2\,×\,2 \,[/латекс]матрица.
Объясните, что в терминах обратной матрицы означает наличие определителя, равного 0.
[открыть-ответ q=»fs-id13
«]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id13
″]
Обратное не существует.
[/скрытый ответ]
Определитель матрицы [латекс]\,2\,×\,2\,[/латекс]матрицы[латекс]\,А\,[/латекс] равен 3. Если поменять местами строки и умножить первую строку на 6 и второй ряд на 2, объясните, как найти определитель и дайте ответ.
Алгебраический
Для следующих упражнений найдите определитель.
[латекс]|\begin{array}{cc}1& 2\\ 3& 4\end{массив}|[/latex]
[reveal-answer q=»fs-id13
″]Показать решение[/reveal- ответ]
[скрытый ответ a = «fs-id13
«]
[латекс]-2[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rr}\hfill -1& \hfill 2\\ \hfill 3& \hfill -4\ end{массив}|[/latex]
[латекс]|\begin{массив}{rr}\hfill 2& \hfill -5\\ \hfill -1& \hfill 6\end{массив}|[/latex]
[reveal-answer q=»fs-id1430900″]Показать решение[/reveal-answer]
[скрытый-ответ a=»fs-id1430900″]
[латекс]7[/латекс]
[/скрытый-ответ]
[латекс]|\begin{массив}{cc}-8& 4\\ -1& 5\end{массив}|[/латекс]
[латекс]|\begin{массив}{rr}\hfill 1& \hfill 0\\ \hfill 3& \hfill -4\end{массив}|[/latex]
[reveal-answer q=»fs- id1395220″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1395220″]
[латекс]-4[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rr}\hfill 10& \hfill 20\\ \hfill 0& \hfill -10\end {array}|[/latex]
[latex]|\begin{array}{cc}10& 0,2\\ 5& 0,1\end{array}|[/latex]
[reveal-answer q=”fs-id1660075 ″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1660075″]
[латекс]0[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rr}\hfill 6& \hfill -3\\ \hfill 8& \hfill 4\end{ array}|[/latex]
[latex]|\begin{array}{rr}\hfill -2& \hfill -3\\ \hfill 3. 1& \hfill 4,000\end{array}|[/latex]
1& \hfill 4,000\end{array}|[/latex]
[reveal-answer q=»fs-id885813″]Показать решение[/reveal-answer]
[hidden-answer a=»fs-id885813″]
[латекс] -7 990,7[/латекс]
[/скрытый ответ]
[латекс]|\begin{массив}{rr}\hfill -1.1& \hfill 0.6\\ \hfill 7.2& \hfill -0.5\end{массив}|[/latex]
[латекс]|\begin {array}{rrr}\hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill -3\end{array}|[/latex]
[reveal-answer q=»fs-id1339464″]Показать решение[/reveal-answer]
[скрытый-ответ a=»fs-id1339464″]
[латекс]3[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rrr}\hfill -1& \hfill 4& \hfill 0\\ \hfill 0& \hfill 2& \hfill 3\\ \hfill 0& \hfill 0& \hfill -3\end{массив}|[/latex]
[латекс]|\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{массив}|[/latex]
[reveal-answer q=”fs-id1601846″ ]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1601846″]
[латекс]-1[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rrr}\hfill 2& \hfill -3& \hfill 1\\ \hfill 3& \hfill -4& \hfill 1\\ \hfill -5& \hfill 6& \hfill 1\end{array}|[/latex]
[latex]|\begin{array}{rrr}\hfill -2& \hfill 1& \hfill 4\\ \hfill -4& \hfill 2& \hfill -8\\ \hfill 2& \hfill -8& \hfill -3\end{массив}|[/latex]
[открыть-ответ q=»fs-id1663783″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1663783″]
[латекс]224[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rrr}\hfill 6& \hfill -1& \hfill 2\\ \hfill -4& \hfill -3& \hfill 5\\ \hfill 1& \hfill 9& \hfill -1\end{array}|[/latex]
[latex]|\begin{array}{rrr}\hfill 5& \hfill 1& \hfill — 1\\ \hfill 2& \hfill 3& \hfill 1\\ \hfill 3& \hfill -6& \hfill -3\end{массив}|[/latex]
[открыть-ответ q=»fs-id1616218″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1616218″]
[латекс]15[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rrr}\hfill 1. 1& \hfill 2& \hfill -1\\ \hfill -4& \ hfill 0& \hfill 0\\ \hfill 4.1& \hfill -0.4& \hfill 2.5\end{array}|[/latex]
1& \hfill 2& \hfill -1\\ \hfill -4& \ hfill 0& \hfill 0\\ \hfill 4.1& \hfill -0.4& \hfill 2.5\end{array}|[/latex]
[latex]|\begin{array}{rrr}\hfill 2& \hfill -1.6 & \hfill 3.1\\ \hfill 1.1& \hfill 3& \hfill -8\\ \hfill -9.3& \hfill 0& \hfill 2\end{массив}|[/latex]
[открыть-ответ q=»fs-id1534877″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1534877″]
[латекс]-17.03[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{ccc}-\frac{1}{2}& \frac{1}{3 }& \frac{1}{4}\\ \frac{1}{5}& -\frac{1}{6}& \frac{1}{7}\\ 0& 0& \frac{1}{8 }\end{array}|[/latex]
В следующих упражнениях решите систему линейных уравнений, используя правило Крамера.
[латекс]\begin{массив}{l}2x-3y=-1\\ 4x+5y=9\end{array}[/latex]
[reveal-answer q=”fs-id1694937″]Показать решение[/reveal-answer]
[hidden-answer a=”fs-id1694937″]
[латекс]\влево(1,1\вправо)[/латекс]
[/скрытый ответ]
[латекс]\begin{array}{r}5x-4y=2\\ -4x+7y =6\end{массив}[/латекс]
[латекс]\begin{массив}{l}\текст{ }6x-3y=2\,\,\,\,\,\hfill \\ -8x+ 9y=-1\hfill \end{array}[/latex]
[reveal-answer q=”fs-id1433846″]Показать решение[/reveal-answer]
[hidden-answer a=”fs-id1433846″]
[латекс]\влево(\фракция{1}{2},\фракция{1}{3}\право)[/латекс]
[/скрытый-ответ]
[латекс]\начало{массив} {l}2x+6y=12\\ 5x-2y=13\end{массив}[/latex]
[латекс]\begin{массив}{l}4x+3y=23\,\,\hfill \\ \text{ }2x-y=-1\hfill \end{массив}[/latex]
[reveal-answer q=”fs-id1516926″]Показать решение[/reveal-answer]
[hidden-answer a= ”fs-id1516926″]
[латекс]\влево(2,5\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{l}10x-6y=2\,\,\, \,\hfill \\ -5x+8y=-1\hfill \end{массив}[/latex]
[латекс]\begin{array}{l}4x-3y=-3\\ 2x+6y=-4\end{массив}[/latex]
[reveal-answer q=”fs-id1615360″] Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1615360″]
[латекс]\left(-1,-\frac{1}{3}\right)[/latex]
[/hidden-answer]
[латекс]\begin{array}{r}4x- 5y=7\\ -3x+9y=0\end{массив}[/latex]
[латекс]\begin{массив}{l}4x+10y=180\,\,\,\,\hfill \\ -3x-5y=-105\hfill \end{массив}[/latex]
[reveal-answer q=”fs-id1530071″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1530071″]
[латекс]\влево(15,12\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{l}\text{ }8x-2y=-3\ hfill \\ -4x+6y=4\,\,\,\,\hfill \end{array}[/latex]
В следующих упражнениях решите систему линейных уравнений, используя правило Крамера.
[латекс]\begin{array}{l}\text{ }x+2y-4z=-1\hfill \\ \text{ }7x+3y+5z=26\,\,\hfill \\ -2x -6y+7z=-6\hfill \end{массив}[/latex]
[reveal-answer q=”fs-id1530969″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1530969″]
[латекс]\влево(1,3,2\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{l}-5x+2y-4z=-47 \hfill \\ \text{ }4x-3y-z=-94\hfill \\ \text{ }3x-3y+2z=94\,\,\,\,\hfill \end{массив}[/latex]
[латекс]\begin{array}{l}\text{ }4x+5y-z=-7\hfill \\ -2x-9y+2z=8\,\,\,\,\hfill \\ \ text{ }5y+7z=21\,\hfill \end{array}[/latex]
[reveal-answer q=”fs-id1699357″]Show Solution[/reveal-answer]
[hidden-answer a= ”fs-id1699357″]
[латекс]\влево(-1,0,3\вправо)[/латекс]
[/скрытый ответ]
[латекс]\begin{array}{r}4x-3y+4z=10\ \ 5x-2z=-2\\ 3x+2y-5z=-9\end{массив}[/latex]
[латекс]\begin{массив}{l}4x-2y+3z=6\,\, \,\hfill \\ \text{ }-6x+y=-2\hfill \\ 2x+7y+8z=24\hfill \end{массив}[/latex]
[reveal-answer q=»fs- id1506671″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1506671″]
[латекс]\влево(\фракция{1}{2},1,2\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{массив}{r}\hfill 5x+2y-z=1\,\,\,\,\,\\ \hfill -7x-8y+3z=1. 5\\ \hfill 6x- 12y+z=7\,\,\,\,\end{массив}[/latex]
5\\ \hfill 6x- 12y+z=7\,\,\,\,\end{массив}[/latex]
[латекс]\begin{массив}{l}\text{ }13x-17y+16z=73\,\, \,\,\hfill \\ -11x+15y+17z=61\,\,\,\,\hfill \\ \text{ }46x+10y-30z=-18\hfill \end{массив}[/latex ]
[reveal-answer q=”1433664″]Показать решение[/reveal-answer][hidden-answer a=”1433664″]
[латекс]\влево(2,1,4\вправо)[/латекс] [/hidden-answer]
[латекс]\begin{array}{l}\begin{array}{l}\hfill \\ -4x-3y-8z=-7\hfill \end{array}\hfill \ \ \text{ }2x-9y+5z=0.5\hfill \\ \text{ }5x-6y-5z=-2\hfill \end{массив}[/latex]
[латекс]\begin{массив}{l}\text{ }4x -6y+8z=10\,\,\hfill \\ -2x+3y-4z=-5\hfill \\ \text{ }x+y+z=1\,\,\,\,\,\hfill \end{array}[/latex]
[reveal-answer q=”fs-id1673950″]Показать решение[/reveal-answer]
[hidden-answer a=”fs-id1673950″]
Бесконечные решения
[/hidden-answer]
[латекс]\begin{array}{r}\hfill 4x-6y+8z=10\,\,\,\,\,\\ \hfill -2x +3y-4z=-5\,\,\,\\ \hfill 12x+18y-24z=-30\end{массив}[/latex]
Технология
В следующих упражнениях используйте функцию определителя в графической утилите.
[латекс]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 8& \hfill 9\\ \hfill 0& \hfill 2& \hfill 1& \hfill 0\\ \hfill 1& \hfill 0& \hfill 3& \hfill 0\\ \hfill 0& \hfill 2& \hfill 4& \hfill 3\end{массив}|[/latex]
[reveal-answer q=»fs-id1597711″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1597711″]
[латекс]24[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 2& \hfill 1\\ \hfill 0& \ hfill -9& \hfill 1& \hfill 3\\ \hfill 3& \hfill 0& \hfill -2& \hfill -1\\ \hfill 0& \hfill 1& \hfill 1& \hfill -2\end{массив}|[/latex]
[латекс]|\begin{array}{rrrr}\hfill \frac{1}{2}& \hfill 1& \hfill 7& \hfill 4\\ \hfill 0& \hfill \frac{1}{2}& \hfill 100& \hfill 5\\ \hfill 0& \hfill 0& \hfill 2& \hfill 2,000\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2\end{массив}|[/latex]
[открыть-ответ q=»fs-id1
5″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id15″] [латекс]1[/латекс]
[/скрытый-ответ]
[латекс]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 2& \ hfill 3& \hfill 0& \hfill 0\\ \hfill 4& \hfill 5& \hfill 6& \hfill 0\\ \hfill 7& \hfill 8& \hfill 9& \hfill 0\end{массив}|[/latex]
Real- World Applications
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем вычислите определитель. Будет ли уникальное решение? Если да, то найти единственное решение.
Затем вычислите определитель. Будет ли уникальное решение? Если да, то найти единственное решение.
Два числа в сумме дают 56. Одно число на 20 меньше другого.
[открыть-ответ q=»fs-id1702584″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1702584″]
Да; 18, 38
[/hidden-answer]
Два числа в сумме дают 104. Если сложить два раза первое число плюс два раза второе число, получится 208
Три числа в сумме дают 106. Первое число на 3 меньше второго числа. Третье число на 4 больше первого числа.
[открыть-ответ q=»fs-id17
″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id17
″]
Да; 33, 36, 37
[/hidden-answer]
Три числа в сумме дают 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше первых двух вместе взятых.
Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера.
Вы инвестируете 10 000 долларов на два счета, на которые начисляются 8% и 5% годовых. В конце года на ваших объединенных счетах было 10 710 долларов. Сколько было вложено в каждый счет?
[открыть-ответ q=»fs-id1354932″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1354932″]
7000 долларов на первый счет, 3000 долларов на второй счет.
[/hidden-answer]
Вы инвестируете 80 000 долларов на два счета, 22 000 долларов на один счет и 58 000 долларов на другой счет. В конце года, при условии простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Каковы процентные ставки для ваших счетов?
Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты стоят 5,95 долл. США, билеты для взрослых — 11,15 долл. США, а общая сумма выручки составила 12 756 долл. США, сколько было продано детских билетов и билетов для взрослых?
США, сколько было продано детских билетов и билетов для взрослых?
[открыть-ответ q=»fs-id1584198″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1584198″]
120 детей, 1080 взрослых
[/hidden-answer]
Концертная площадка продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов. Если общий доход составил $18,090 и было продано 321 билет, сколько одиночных билетов и сколько парных билетов было продано?
Вы решили покрасить кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета вошло в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого цвета стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь?
[открыть-ответ q=»fs-id1584221″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1584221″]
4 галлона желтый, 6 галлонов синий
[/hidden-answer]
Вы продали два вида шарфов на фермерском рынке и хотели бы знать, какой из них более популярен. Всего было продано 56 шарфов, желтый шарф стоил 10 долларов, фиолетовый — 11 долларов. Если ваш общий доход составил 583 доллара, сколько желтых шарфов и сколько фиолетовых шарфов было продано?
Всего было продано 56 шарфов, желтый шарф стоил 10 долларов, фиолетовый — 11 долларов. Если ваш общий доход составил 583 доллара, сколько желтых шарфов и сколько фиолетовых шарфов было продано?
В вашем саду выращивают два вида помидоров, зеленый и красный. Красный весит 10 унций, а зеленый весит 4 унции. У вас есть 30 помидоров общим весом 13 фунтов 14 унций. Сколько у вас помидоров каждого вида?
[открыть-ответ q=»fs-id1699000″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1699000″]
13 зеленых помидоров, 17 красных помидоров
[/hidden-answer]
На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, продажи которой на 5% выше, чем у лука. Какую долю рынка занимает каждый овощ?
На том же рынке три самых популярных фрукта составляют 37% от общего количества продаваемых фруктов. Клубники продают вдвое больше, чем апельсинов, а киви продают на один процент больше, чем апельсинов. Для каждого фрукта найдите процент от общего количества проданных фруктов.
Для каждого фрукта найдите процент от общего количества проданных фруктов.
[открыть-ответ q=»fs-id1648808″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1648808″]
Клубника 18%, апельсины 9%, киви 10%
[/hidden-answer]
Три группы выступили на концертной площадке. Первая группа взимала 15 долларов за билет, вторая группа взимала 45 долларов за билет, а последняя группа взимала 22 доллара за билет. Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй группы, сколько билетов было продано на каждую группу?
Кинотеатр продал билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм — 11 долларов, а на третий фильм — 12 долларов. На первый фильм было продано 100 билетов. Общее количество проданных билетов составило 642, а общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано?
[открыть-ответ q=»fs-id1637286″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1637286″]
100 для фильма 1, 230 для фильма 2, 312 для фильма 3
[/hidden-answer]
Мужчины в возрасте 20–29, 30–39 и 40–49 лет составляли 78% заключенных в тюрьме в прошлом году. В этом году те же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет сократилась до [латекс]\,\frac{3}{4}\,[/latex] своего прежнего населения. Первоначально в возрастной группе 30–39 лет заключенных было на 2% больше, чем в возрастной группе 20–29 лет. Определите процент заключенных для каждой возрастной группы в прошлом году.
В этом году те же возрастные группы составили 82,08% населения. Возрастная группа 20–29 лет увеличилась на 20%, возрастная группа 30–39 лет увеличилась на 2%, а возрастная группа 40–49 лет сократилась до [латекс]\,\frac{3}{4}\,[/latex] своего прежнего населения. Первоначально в возрастной группе 30–39 лет заключенных было на 2% больше, чем в возрастной группе 20–29 лет. Определите процент заключенных для каждой возрастной группы в прошлом году.
В женской тюрьме по дороге общее число заключенных в возрасте от 20 до 49 лет составляло 5525 человек. В этом году возрастная группа 20-29 лет увеличилась на 10%, возрастная группа 30-39 лет уменьшилась на 20%, а возрастная группа 40-49 лет удвоилась. Сейчас там 6040 заключенных. Первоначально в возрастной группе 30–39 лет было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году.
[открыть-ответ q=”fs-id1425394″]Показать решение[/открыть-ответ]
[скрытый-ответ a=”fs-id1425394″]
20–29: 2 100, 30–39: 2 600, 40–49: 825
[/hidden-answer]
Для следующих упражнений используйте следующий сценарий: миндаля, сушеной клюквы и орехов кешью в шоколаде. Информация о пищевой ценности этих продуктов показана на (Рисунок).
Информация о пищевой ценности этих продуктов показана на (Рисунок).
Жир (г) Белок (г) Углеводы (г) Миндаль (10) 6 2 3 Клюква (10) 0,02 0 8 Кешью (10) 7 3,5 5,5
Для специальной смеси «с низким содержанием углеводов» имеется 1000 штук смеси. Общее количество углеводов 425 г, общее количество жиров 570,2 г. Если орехов кешью на 200 штук больше, чем клюквы, сколько штук каждого предмета будет в смеси?
Для смеси «походной» в составе смеси 1000 шт., содержащих 390,8 г жира и 165 г белка. Если миндаля столько же, сколько орехов кешью, то сколько каждого элемента содержится в смеси?
[открыть-ответ q=»fs-id1647224″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1647224″]
300 миндальных орехов, 400 клюквы, 300 орехов кешью
[/hidden-answer]
Для «энергетической» смеси имеется 1000 штук, содержащих 145 г белка и 625 г углеводов. Если количество миндаля и кешью в сумме равно количеству клюквы, сколько каждого элемента содержится в смеси?
Если количество миндаля и кешью в сумме равно количеству клюквы, сколько каждого элемента содержится в смеси?
Повторные упражнения
Системы линейных уравнений: две переменные
В следующих упражнениях определите, является ли упорядоченная пара решением системы уравнений.
[латекс]\begin{массив}{l}3x-y=4\\ x+4y=-3\,\end{массив}[/латекс]и[латекс]\,\слева(-1,1 \right)[/latex]
[reveal-answer q=”fs-id1395131″]Показать решение[/reveal-answer]
[hidden-answer a=”fs-id1395131″]
Нет
[/hidden-answer]
[латекс]\begin{array}{l}6x-2y=24\\ -3x+3y=18\,\end{array}[/latex]и[ латекс]\,\слева(9,15\right)[/latex]
В следующих упражнениях используйте замену для решения системы уравнений.
[латекс]\begin{массив}{l}10x+5y=-5\hfill \\ \,\,\,3x-2y=-12\hfill \end{массив}[/latex]
[показать -answer q=”fs-id1698278″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1698278″]
[латекс]\влево(-2,3\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{l}\frac{4}{7}x+\ frac{1}{5}y=\frac{43}{70}\\ \frac{5}{6}x-\frac{1}{3}y=-\frac{2}{3}\end {массив}[/латекс]
[латекс]\begin{array}{l}5x+6y=14\\ 4x+8y=8\end{массив}[/latex]
[reveal-answer q=»fs-id1428954″]Показать решение [/reveal-answer]
[скрытый-ответ a=”fs-id1428954″]
[латекс]\влево(4,-1\вправо)[/латекс]
[/скрытый ответ]
В следующих упражнениях используйте сложение для решения системы уравнений.
[латекс]\begin{массив}{l}3x+2y=-7\\ 2x+4y=6\end{массив}[/latex]
[латекс]\begin{массив}{r}3x+ 4y=2\\ 9x+12y=3\end{массив}[/латекс]
[открыть-ответ q=»fs-id1584732″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1584732″]
Решений не существует.
[/hidden-answer]
[латекс]\begin{array}{l}8x+4y=2\\ 6x-5y=0.7\end{array}[/latex]
Для следующих упражнений напишите система уравнений для решения каждой задачи. Решите систему уравнений.
Завод имеет себестоимость производства[латекс]\,C\left(x\right)=150x+15\text{,}000\,[/latex]и функцию дохода[латекс]\,R\left (x\right)=200x.\,[/latex]Какова точка безубыточности?
[открыть-ответ q=»fs-id1536207″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1536207″]
[латекс]\влево(300,60,000\вправо)[/латекс]
[/скрытый-ответ]
Исполнитель взимает [латекс]\,С\влево(х\вправо)=50x+10\текст {,}000,\,[/latex], где[latex]\,x\,[/latex] — общее количество посетителей шоу. Заведение берет 75 долларов за билет. После того, как много людей купят билеты, место станет безубыточным, и какова общая стоимость билетов, проданных в этот момент?
Заведение берет 75 долларов за билет. После того, как много людей купят билеты, место станет безубыточным, и какова общая стоимость билетов, проданных в этот момент?
[открыть-ответ q=»fs-id1358367″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1358367″]
[latex]\left(400,30,000\right)[/latex]
[/hidden-answer]
Системы линейных уравнений: три переменные
Для следующих упражнений решите систему из трех уравнений с помощью замены или дополнение.
[латекс]\begin{array}{l}\text{ }0,5x-0,5y=10\hfill \\ \text{ }-0,2y+0,2x=4\hfill \\ \text{ }0,1x +0.1z=2\hfill\end{массив}[/latex]
[открыть-ответ q=»fs-id1513414″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1513414″]
[латекс]\влево(10,-10,10\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\начало{массив}{r}\hfill 5x+3y-z= 5\,\,\,\\ \hfill 3x-2y+4z=13\\ \hfill 4x+3y+5z=22\end{массив}[/latex]
[латекс]\begin{массив}{r }x+y+z=1\\ 2x+2y+2z=1\\ 3x+3y=2\end{массив}[/latex]
[reveal-answer q=»fs-id1366211″]Показать решение[ /показать-ответ]
[скрытый-ответ a=”fs-id1366211″]
Решений не существует.
[/hidden-answer]
[латекс]\begin{array}{l}\text{ }2x-3y+z=-1\hfill \\ \text{ }x+y+z=-4\ hfill \\ \text{ }4x+2y-3z=33\hfill \end{массив}[/latex]
[латекс]\begin{массив}{l}\,\,3x+2y-z=-10 \hfill \\ \,\,\,\,x-y+2z=7\hfill \\ -x+3y+z=-2\hfill \end{массив}[/latex]
[показать-ответить q =”fs-id1409562″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1409562″]
[латекс]\влево(-1,-2,3\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{r}\hfill 3x+4z=-11\\ \hfill x-2y=5\,\,\,\,\,\,\,\\ \hfill 4y- z=-10\end{массив}[/latex]
[латекс]\begin{array}{r}2x-3y+z=0\\ 2x+4y-3z=0\\ 6x-2y-z= 0\end{array}[/latex]
[reveal-answer q=”fs-id1417064″]Показать решение[/reveal-answer]
[hidden-answer a=”fs-id1417064″]
[латекс]\left(x,\frac{8x}{5},\frac{14x}{5}\right)[/latex]
[/hidden-answer]
[латекс]\begin{ array}{r}6x-4y-2z=2\\ 3x+2y-5z=4\\ 6y-7z=5\end{массив}[/latex]
Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.
Решите систему уравнений.
Три нечетных числа в сумме дают 61. Меньшее число на одну треть больше, а среднее число на 16 меньше большего. Какие три числа?
[открыть-ответ q=»fs-id1706459″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1706459″]
11, 17, 33
[/hidden-answer]
Билеты на спектакль в местном театре распроданы. Они продают все 500 билетов на общую сумму 8 070 долларов. Билеты стоили 15 долларов для студентов, 12 долларов для детей и 18 долларов для взрослых. Если группа продала в три раза больше билетов для взрослых, чем билетов для детей, сколько билетов каждого типа было продано? 9{2}}[/latex]
Матрицы и операции с матрицами
В следующих упражнениях выполните запрошенные операции с заданными матрицами.
[латекс]A=\left[\begin{array}{rr}\hfill 4& \hfill -2\\ \hfill 1& \hfill 3\end{array}\right],B=\left[\begin{ array}{rrr}\hfill 6& \hfill 7& \hfill -3\\ \hfill 11& \hfill -2& \hfill 4\end{array}\right],C=\left[\begin{array}{r}\ hfill \begin{массив}{cc}6& 7\\ 11& -2\end{массив}\\ \hfill \begin{массив}{cc}14& 0\end{массив}\end{массив}\right],D =\left[\begin{массив}{rrr}\hfill 1& \hfill -4& \hfill 9\\ \hfill 10& \hfill 5& \hfill -7\\ \hfill 2& \hfill 8& \hfill 5\end{массив}\right],E=\left[\begin{array}{rrr}\hfill 7& \hfill -14& \hfill 3\\ \hfill 2& \hfill -1& \hfill 3\\ \hfill 0& \hfill 1& \hfill 9\end{массив}\right][/latex]
[латекс]-4A[/латекс ]
[открыть-ответ q=»fs-id1615553″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1615553″]
[латекс]\влево[\начало{массив}{cc}-16& 8\\ -4& -12\конец{массив}\вправо][/латекс]
[/hidden-answer]
[latex]10D-6E[/latex]
[latex]B+C[/latex]
[reveal-answer q=»fs-id1706172″]Показать решение[/ раскрыть-ответ]
[скрытый-ответ a=”fs-id1706172″]
не определено; размеры не совпадают
[/hidden-answer]
[latex]AB[/latex]
[latex]BA[/latex]
[reveal-answer q=»fs-id1650879″]Показать решение[/ раскрыть-ответ]
[скрытый-ответ a=”fs-id1650879″]
не определено; внутренние размеры не соответствуют
[/hidden-answer]
[latex]BC[/latex]
[latex]CB[/latex]
[reveal-answer q=»fs-id1647736″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1647736″]
[латекс]\left[\begin{array}{ccc}113& 28& 10\\ 44& 81& -41\\ 84& 98& -42\end{array}\right][/latex]
[/hidden-answer ]
[latex]DE[/latex]
[latex]ED[/latex]
[reveal-answer q=»fs-id16
″]Показать решение[/reveal-answer] 9{3}[/latex] Решение систем с исключением Гаусса
Для следующих упражнений напишите систему линейных уравнений из расширенной матрицы. Укажите, будет ли единственное решение.
Укажите, будет ли единственное решение.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill -3\\ \hfill 0& \hfill 1& \hfill 2\\ \hfill 0& \hfill 0& \hfill 0\end {array}\text{ }|\text{ }\begin{array}{r}\hfill 7\\ \hfill -5\\ \hfill 0\end{array}\right][/latex]
[показать -answer q=»fs-id1637532″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1637532″]
[латекс]\begin{array}{l}x-3z=7\\ y+2z=-5\,\end{массив}[/latex]с бесконечными решениями
[/hidden-answer]
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 5\\ \hfill 0& \hfill 1& \hfill -2\\ \hfill 0& \hfill 0& \hfill 0\end{array }\text{ }|\text{ }\begin{array}{r}\hfill -9\\ \hfill 4\\ \hfill 3\end{array}\right][/latex]
Для следующих упражнений , выпишите расширенную матрицу из системы линейных уравнений.
[латекс]\begin{array}{l}\\ \begin{array}{r}\hfill -2x+2y+z=7\\ \hfill 2x-8y+5z=0\\ \hfill 19x- 10y+22z=3\end{массив}\end{массив}[/latex]
[reveal-answer q=”fs-id1656057″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs -id1656057″]
[латекс]\left[\begin{array}{rrr}\hfill -2& \hfill 2& \hfill 1\\ \hfill 2& \hfill -8& \hfill 5\\ \hfill 19& \hfill -10& \hfill 22 \end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 7\\ \hfill 0\\ \hfill 3\end{массив}\right][/latex]
[/hidden-answer]
[латекс]\begin{array}{l}\,\,\,\,\,4x+2y-3z=14\hfill \\ -12x+3y+z=100 \hfill \\ \,\,\,\,\,9x-6y+2z=31\hfill \end{массив}[/latex]
[латекс]\begin{массив}{r}\hfill x+3z =12\,\\ \hfill -x+4y=0\,\,\,\,\\ \hfill y+2z=-7\end{массив}[/latex]
[reveal-answer q=” fs-id1528512″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1528512″]
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 3\\ \hfill -1& \hfill 4& \hfill 0\\ \hfill 0& \hfill 1& \hfill 2\end {массив}\текст{ }|\текст{ }\begin{массив}{r}\hfill 12\\ \hfill 0\\ \hfill -7\end{массив}\right][/latex]
[/hidden-answer]
Для следующих упражнений решите систему линейных уравнений методом исключения Гаусса.
[латекс]\begin{array}{r}3x-4y=-7\\ -6x+8y=14\end{массив}[/latex]
[латекс]\begin{array}{r}3x -4y=1\\ -6x+8y=6\end{массив}[/latex]
[reveal-answer q=”fs-id1422121″]Показать решение[/reveal-answer]
[hidden-answer a= «fs-id1422121»]
Решений не существует.
[/hidden-answer]
[латекс]\begin{array}{l}\begin{array}{l}\\ -1.1x-2.3y=6.2\end{array}\hfill \\ -5.2 x-4.1y=4.3\hfill \end{массив}[/latex]
[латекс]\begin{массив}{r}\hfill 2x+3y+2z=1\,\,\,\,\,\\ \hfill -4x-6y-4z=-2\\ \hfill 10x +15y+10z=0\,\,\,\,\,\end{массив}[/latex]
[reveal-answer q=”fs-id1455902″]Показать решение[/reveal-answer]
[скрытый -ответ a=”fs-id1455902″]
Решений не существует.
[/hidden-answer]
[латекс]\begin{array}{r}\hfill -x+2y-4z=8\,\,\,\,\\ \hfill 3y+8z=-4\ \ \hfill -7x+y+2z=1\,\,\,\,\end{array}[/latex]
Решение систем с обратными
В следующих упражнениях найдите обратную матрицу.
[латекс]\left[\begin{массив}{rr}\hfill -0.2& \hfill 1.4\\ \hfill 1.2& \hfill -0.4\end{массив}\right][/latex]
[показать -answer q=”fs-id1531734″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1531734″]
[латекс]\frac{1}{8}\left[\begin{array}{cc}2& 7\\ 6& 1\end{array}\right][/latex]
[/hidden-answer]
[латекс]\left[\begin{array}{rr}\hfill \frac{1}{2}& \hfill -\frac{1}{2}\\ \hfill -\frac{1}{4 }& \hfill \frac{3}{4}\end{массив}\right][/latex]
[латекс]\left[\begin{array}{ccc}12& 9& -6\\ -1& 3& 2\\ -4& -3& 2\end{массив}\right][/latex]
[показать- ответ q=”fs-id1514199″]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1514199″]
Обратного не существует.
[/hidden-answer]
[латекс]\left[\begin{array}{ccc}2& 1& 3\\ 1& 2& 3\\ 3& 2& 1\end{массив}\right][/latex]
Для следующих упражнений найдите решения, вычислив обратную матрицу.
[латекс]\begin{array}{l}\,\,\,\,0,3x-0,1y=-10\hfill \\ -0,1x+0,3y=14\hfill \end{array}[/ латекс]
[открыть-ответ q=»fs-id299169″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id299169″]
[латекс]\влево(-20,40\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{l}\,\,\,\,\, \,\,\,0,4x-0,2y=-0,6\hfill \\ -0,1x+0,05y=0,3\hfill \end{массив}[/latex]
[латекс]\begin{массив}{r} 4x+3y-3z=-4,3\\ 5x-4y-z=-6,1\\ x+z=-0,7\end{массив}[/latex]
[открыть-ответ q=»fs-id1531936″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1531936″]
[латекс]\влево(-1,0.2,0.3\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{r}\hfill \begin{array}{ l}\\ -2x-3y+2z=3\end{массив}\\ \hfill -x+2y+4z=-5\\ \hfill -2y+5z=-3\end{массив}[/latex]
Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений.
Учеников попросили принести в класс свои любимые фрукты. 90% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были вдвое менее популярны, чем бананы, а яблоки были на 5% популярнее бананов, каков процент каждого фрукта в отдельности?
[открыть-ответ q=»fs-id1403411″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1403411″]
17% апельсины, 34% бананы, 39% яблоки
[/hidden-answer]
Женское общество устроило распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой. Они оценили пирожные в 2 доллара, а печенье с шоколадной крошкой — в 1 доллар. Они собрали 250 долларов и продали 175 предметов. Сколько пирожных и сколько печенья было продано?
Решение систем с помощью правила Крамера
Для следующих упражнений найдите определитель.
[латекс]|\begin{array}{cc}100& 0\\ 0& 0\end{массив}|[/latex]
[reveal-answer q=»fs-id1504600″]Показать решение[/reveal- ответ]
[скрытый ответ a = «fs-id1504600»]
0
[/hidden-answer]
[латекс]|\begin{array}{cc}0. 2& -0.6\\ 0.7& -1.1\end{массив}|[/latex]
2& -0.6\\ 0.7& -1.1\end{массив}|[/latex]
[латекс] |\begin{массив}{ccc}-1& 4& 3\\ 0& 2& 3\\ 0& 0& -3\end{массив}|[/latex]
[открыть-ответ q=»fs-id1698281″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1698281″]
6
[/hidden-answer]
[латекс]|\begin{array}{ccc}\sqrt{2}& 0& 0\\ 0& \sqrt{2}& 0\\ 0& 0& \sqrt{ 2}\end{array}|[/latex]
В следующих упражнениях используйте правило Крамера для решения линейных систем уравнений.
[латекс]\begin{массив}{r}\hfill 4x-2y=23\,\,\,\,\\ \hfill -5x-10y=-35\end{массив}[/latex]
[reveal-answer q=»fs-id1508832″]Показать решение[/reveal-answer]
[скрытый-ответ a=»fs-id1508832″]
[латекс]\left(6,\frac{1}{2}\right)[/latex]
[/hidden-answer]
[латекс]\begin{array}{l}0,2x-0,1 y=0\\ -0.3x+0.3y=2.5\end{массив}[/латекс]
[латекс]\begin{массив}{r}\hfill -0.5x+0.1y=0.3\,\,\ ,\\ \hfill -0.25x+0. 05y=0.15\end{массив}[/latex]
05y=0.15\end{массив}[/latex]
[reveal-answer q=”fs-id1584180″]Show Solution[/reveal-answer]
[hidden-answer a =”fs-id1584180″]
( x , 5 x + 3)
[/hidden-answer]
[латекс]\begin{array}{l}x+6y+3z=4\\ 2x+y+2z= 3\\ 3x-2y+z=0\end{массив}[/latex]
[латекс]\begin{массив}{r}\hfill 4x-3y+5z=-\frac{5}{2}\ \ \hfill 7x-9y-3z=\frac{3}{2}\,\,\,\,\\ \hfill x-5y-5z=\frac{5}{2}\,\,\,\ ,\end{array}[/latex]
[reveal-answer q=»fs-id1508865″]Показать решение[/reveal-answer]
[hidden-answer a=»fs-id1508865″]
[латекс]\влево(0,0,-\фракция{1}{2}\вправо)[/латекс]
[/hidden-answer]
[латекс]\begin{array}{r}\frac{3}{10}x-\frac{1}{5}y-\frac{3}{10}z =-\frac{1}{50}\\ \frac{1}{10}x-\frac{1}{10}y-\frac{1}{2}z=-\frac{9}{50 }\\ \frac{2}{5}x-\frac{1}{2}y-\frac{3}{5}z=-\frac{1}{5}\end{массив}[/latex ]
Практический тест
Является ли следующая упорядоченная пара решением системы уравнений?
[латекс]\begin{array}{l}\\ \begin{array}{l}-5x-y=12\,\hfill \\ x+4y=9\hfill \end{array}\end{ массив}[/латекс]с[латекс]\,\влево(-3,3\вправо)[/латекс]
[открыть-ответ q=»fs-id1435942″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1435942″]
Да
[/hidden-answer]
Для следующих упражнений решите системы линейных и нелинейных уравнений, используя замену или исключение. Укажите, если решения не существует.
Укажите, если решения не существует.
[латекс]\begin{array}{r}\frac{1}{2}x-\frac{1}{3}y=4\\ \frac{3}{2}x-y=0\end{ array}[/latex]
[latex]\begin{array}{r}\hfill \begin{array}{l}\\ -\frac{1}{2}x-4y=4\end{array} \\ \hfill 2x+16y=2\end{массив}[/latex]
[открыть-ответ q=»fs-id1406246″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1406246″]
Решений не существует.
[/hidden-answer]
[латекс]\begin{array}{r}\hfill 5x-y=1\,\,\,\,\\ \hfill -10x+2y=-2\end{ array}[/latex]
[латекс]\begin{array}{l}4x-6y-2z=\frac{1}{10}\hfill \\ \,\,\,x-7y+5z=- \frac{1}{4}\hfill \\ 3x+6y-9z=\frac{6}{5}\hfill \end{массив}[/latex]
[reveal-answer q=»fs-id1455840″ ]Показать решение[/reveal-answer]
[скрытый-ответ a=”fs-id1455840″]
[латекс]\frac{1}{20}\left(10,5,4\right)[/latex]
[/hidden-answer]
[латекс]\begin{array}{r}x +z=20\\ x+y+z=20\\ x+2y+z=10\end{массив}[/latex]
[латекс]\begin{массив}{r}5x-4y-3z= 0\\ 2x+y+2z=0\\ x-6y-7z=0\end{массив}[/latex]
[reveal-answer q=»fs-id1615810″]Показать решение[/reveal-answer]
[скрытый ответ a=”fs-id1615810″]
[латекс]\left(x,\frac{16x}{5}-\frac{13x}{5}\right)[/latex]
[/hidden-answer]
[латекс]\begin{ array}{l}y={x}^{2}+2x-3\\ y=x-1\end{массив}[/latex] 9{2}}[/latex]
В следующих упражнениях выполните заданные матричные операции.
[латекс]5\влево[\begin{array}{cc}4& 9\\ -2& 3\end{массив}\right]+\frac{1}{2}\left[\begin{array}{ cc}-6& 12\\ 4& -8\end{массив}\right][/latex]
[reveal-answer q=”fs-id16
″]Показать решение[/reveal-answer]
[скрытый-ответ a =”fs-id16″] [латекс]\влево[\begin{array}{cc}17& 51\\ -8& 11\end{массив}\right][/latex]
[/hidden-answer]
9{-1}[/latex] [reveal-answer q=»fs-id1583988″]Показать решение[/reveal-answer]
[hidden-answer a=»fs-id1583988″]
[латекс]\влево[\begin{array}{cc}12& -20\\ -15& 30\end{массив}\right][/latex]
[/hidden-answer]
[латекс]\ mathrm{det}|\begin{array}{cc}0& 0\\ 400& 4\text{,}000\end{array}|[/latex]
[латекс]\mathrm{det}|\begin{array }{rrr}\hfill \frac{1}{2}& \hfill -\frac{1}{2}& \hfill 0\\ \hfill -\frac{1}{2}& \hfill 0& \hfill \ frac{1}{2}\\ \hfill 0& \hfill \frac{1}{2}& \hfill 0\end{массив}|[/latex]
[открыть-ответ q=»fs-id1295612″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1295612″]
[латекс]-\frac{1}{8}[/latex]
[/hidden-answer]
Если[латекс]\,\mathrm{det}\left(A\right)=-6, \,[/latex] какой будет определитель, если поменять местами строки 1 и 3, умножить вторую строку на 12 и взять обратное?
Перепишите систему линейных уравнений в виде расширенной матрицы.
[латекс]\begin{array}{l}14x-2y+13z=140\hfill \\ -2x+3y-6z=-1\hfill \\ x-5y+12z=11\hfill \end{array }[/латекс]
[открыть-ответ q=»fs-id1456561″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1456561″]
[латекс]\left[\begin{array}{rrr}\hfill 14& \hfill -2& \hfill 13\\ \hfill -2& \hfill 3& \hfill -6\\ \hfill 1& \hfill -5& \hfill 12\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 140\\ \hfill -1\\ \hfill 11\end{массив}\right][/latex]
[/hidden-answer]
Перепишите расширенную матрицу в виде системы линейных уравнений.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 3\\ \hfill -2& \hfill 4& \hfill 9\\ \hfill -6& \hfill 1& \hfill 2\end{массив}|\begin{массив}{r}\hfill 12\\ \hfill -5\\ \hfill 8\end{массив}\right][/ латекс]
В следующих упражнениях используйте метод исключения Гаусса для решения систем уравнений.
[латекс]\begin{array}{r}x-6y=4\\ 2x-12y=0\end{массив}[/latex]
[reveal-answer q=»fs-id1518911″]Показать решение [/reveal-answer]
[скрытый-ответ a=”fs-id1518911″]
Решений не существует.
[/hidden-answer]
[латекс]\begin{array}{r}\hfill 2x+y+z=-3\\ \hfill x-2y+3z=6\,\,\,\, \\ \hfill x-y-z=6\,\,\,\,\end{массив}[/latex]
В следующих упражнениях используйте обратную матрицу для решения системы уравнений.
[латекс]\begin{массив}{r}\hfill 4x-5y=-50\\ \hfill -x+2y=80\,\,\,\,\end{массив}[/latex]
[reveal-answer q=»fs-id1440484″]Показать решение[/reveal-answer]
[hidden-answer a=»fs-id1440484″]
[латекс]\влево(100,90\вправо)[/латекс]
[/скрытый-ответ]
[латекс]\begin{array}{r}\hfill \frac{1}{100}x -\frac{3}{100}y+\frac{1}{20}z=-49\\ \hfill \frac{3}{100}x-\frac{7}{100}y-\frac{1 }{100}z=13\,\,\,\,\\ \hfill \frac{9}{100}x-\frac{9}{100}y-\frac{9}{100}z=99\,\,\,\,\end{array}[/latex]
Для следующих упражнений , используйте правило Крамера для решения систем уравнений.
[латекс]\begin{array}{l}200x-300y=2\\ 400x+715y=4\end{массив}[/latex]
[reveal-answer q=»fs-id1703905″]Показать решение [/reveal-answer]
[скрытый-ответ a=”fs-id1703905″]
[латекс]\влево(\frac{1}{100},0\вправо)[/latex]
[/hidden-answer]
[латекс]\begin{array}{l}0,1x+0,1 у-0,1z=-1,2\\ 0,1x-0,2y+0,4z=-1,2\\ 0,5x-0,3y+0,8z=-5,9{2}+160x. \,[/latex]Какой ассортимент сотовых телефонов они должны производить каждый день, чтобы получать прибыль? Округлите до ближайшего числа, приносящего прибыль.
\,[/latex]Какой ассортимент сотовых телефонов они должны производить каждый день, чтобы получать прибыль? Округлите до ближайшего числа, приносящего прибыль.
[открыть-ответ q=»fs-id1598123″]Показать решение[/открыть-ответ]
[скрытый-ответ a=»fs-id1598123″]
32 или более сотовых телефона в день
[/hidden-answer]
Небольшая ярмарка стоит 1,50 доллара для студентов, 1 доллар для детей и 2 доллара для взрослых. За один день пришло в три раза больше детей, чем взрослых. Всего было продано 800 билетов на общую сумму 1050 долларов. Сколько билетов каждого типа было продано?
Глоссарий
Правило Крамера Redux
Вот первый прием использования правила Крамера на матрицах 3 × 3. Это не работает для матриц 4 × 4 и больше, и, конечно, нам это не нужно для 2 × 2.
Это не работает для матриц 4 × 4 и больше, и, конечно, нам это не нужно для 2 × 2.
Допустим, у нас есть маленькая дерзкая матрица 3 × 3, которую мы бы с удовольствием представили нашей подруге Крамер, если бы только она привела с собой свою подругу Детерминант.
Вот что мы делаем, чтобы найти определитель матрицы 3 × 3. Сначала скопируйте левый и центральный столбцы справа от матрицы:
Вы, конечно, помните, что метод Крамера 2 × 2 заставлял нас умножать по диагонали из левого верхнего угла в правый нижний, а затем вычитать из левого нижнего в верхний правый. Это на самом деле очень похоже. Главное — не перепутать столбцы, которые вы копируете повторно. Теперь, когда у нас есть наша матрица и левый и центральный столбцы из нее, скопированные за пределы полос, мы готовы вычислить определитель так же, как мы сделали 2 × 2.
Сначала умножаем из левого верхнего угла в правый нижний, а потом складываем. Мы проделываем это три раза — поэтому снова добавили первые два столбца:
D = aei + bfg + cdh …
Затем снова вычитаем снизу вверх справа, как мы делали раньше:
D = aei + bfg + cdh – gec – hfa – idb
15
540004 Вот и все.
Итак, в ситуации с реальными числами:
Сначала мы скопируем первые два столбца снаружи и справа от полос:
И с этого момента, это в основном plug ‘n’ chug:
D = (4)(1)(4) + (1)(5)(3) + (0)(2)(0) – (3)(1)(0) – (0)(5) (4) – (4)(2)(1)
= 16 + 15 + 0 – 0 – 0 – 8
= 23
Понятно.
Пример задачи
Теперь, поскольку мы знаем, как получить определитель матрицы 3 × 3, вот как мы находим переменные с помощью правила Крамера, когда их три. Вот наши три счастливых холостяка:
2 x + y -3 z = 8
-3 x + 2 y + z = 10
x -3 y + 2
x -3 y + 2 Z Z Z Z = 12 Z .
Первый шаг — найти D , определитель коэффициента. Мы только что узнали, как это сделать для матрицы 3 × 3, так что поехали.
Сначала создайте матрицу коэффициентов:
Ого! Вот оно. Далее находим D :
Далее находим D :
Вспоминаем нашу маленькую хитрость, где мы снова копируем первые два столбца наружу и вправо от матрицы:
Отлично, Смитерс. Теперь умножаем и прибавляем по диагонали сверху слева направо снизу:
D = (2)(2)(2) + (1)(1)(1) + (-3)(-3)(- 3)…
Затем мы умножаем и вычитаем по диагонали снизу слева направо вверх:
D = (2)(2)(2) + (1)(1)(1) + (-3)( -3)(-3) – (1)(2)(-3) – (-3)(1)(2) – (2)(-3)(1)
Итак:
D = 8 + 1 + (-27) – (-6) – (-6) – (-6) = 0
Рух-рох, Лохматый! Когда D = 0, точных значений быть не может! (Вы помните?) Мы подумали, что эти уравнения выглядят подозрительно. Ну как насчет этих?
Проблема выборки
Решите следующую систему уравнений:
3 x — y -4 z = 10
-2 x + 5 y + z =
-3 –3 x + 4 y + 2 z = 8
Сначала мы разбиваем нашу матрицу коэффициентов:
Вы устали от поиска D ? Ага, вы меня знаете:
Копируем первые два столбца прямо снаружи и справа от матрицы:
Затем пришло время умножать и прибавлять по диагонали сверху слева вниз справа и затем умножать и вычитать по диагонали снизу слева направо вверх:
D = (3)(5)(2) + (-1)(1)(-3) + (-4)(-2)(4) – ( -3)(5)(-4) – (4)(1)(3) – (2)(-2)(-1)
Отсюда математическое счастье:
D = 30 + 3 + 32 – 60 – 12 – 4 = -11
Мы знаем, что D = -11, так что теперь мы ищем другие определители. Мы знаем, что эти три вещи верны:
Мы знаем, что эти три вещи верны:
Мы знаем, что способ найти D x состоит в том, чтобы подставить постоянные значения в смесь вместо значений x , а затем используйте наш трюк с копированием столбцов, чтобы получить числа. Время для большего количества подключи и пыхтение. Удалить x -values:
Замените их постоянными значениями:
Скопируйте первые два столбца в нашей модифицированной матрице снаружи и справа:
Умножьте и сложите по диагонали сверху слева к внизу справа, а затем умножить и вычесть по диагонали снизу слева направо вверх:
D x = (10)(5)(2) + (-1)(1)(8) + (-4) (9)(4) – (8)(5)(-4) – (4)(1)(10) – (2)(9)(-1)
= 100 + (-8) + (-144 ) – (-160) – 40 – (-18)
= 86
Далее. Ищем D и .
Вот оно, лишенное всех и -значений. Теперь мы подставляем постоянные значения и прокручиваем оттуда:
Уловка столбца:
Подключи и пыхти:
D y = (3)(9)(2) + (10)( 1)(-3) + (-4)(-2)(8) – (-3)(9)(-4) – (8)(1)(3) – (2)(-2)(10 )
= 54 + (-30) + 64 – 108 – 24 – (-40)
= -4
Решите для y , пока мы здесь:
Мы , так что почти готово.

\( 4x — 2y = 10 \)
\( 3x — 5y = 11 \)
video by mattemath
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг.
\( 2x — 3y = 1 \)
\( x + 2y = 11 \)
Окончательный ответ |
|---|
\( (5, 3) \)
45 Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x — 3y = 1 \)
\( x + 2y = 11 \)
Решение
2862 видео решение
Окончательный ответ
\( (5, 3) \)
6
7 0 in Log чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг.
- Постановка задачи
\( 3x = 2y + 5 \)
\( 4y = 6x — 8 \)
Окончательный ответ |
|---|
нет решения
\( 3x = 2y + 5 \)
\( 4y = 6x — 8 \)
Решение
2863 видео решение
Окончательный ответ
нет решения
- Постановка задачи
\( x + 2y = -3 \)
\( -3x — 6y = 9 \)
Окончательный ответ |
|---|
бесконечное число решений Правило.
\( х + 2у = -3 \)
\( -3х — 6у = 9\)
Решение
2864 видео решение
Окончательный ответ
бесконечное количество решений
Войдите, чтобы оценить эту практическую задачу и увидеть ее текущий рейтинг. |
|---|
\( 3x + 7y = 5 \)
\( -2x + y = -9 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 3x + 7y = 5 \)
\( -2x + y = -9 \)
Окончательный ответ |
|---|
\( (4, -1) \)
5 Постановка задачи Решите эту линейную систему, используя правило Крамера.
\( 3x + 7y = 5 \)
\( -2x + y = -9 \)
Решение
2865 видеорешение
Окончательный ответ
\( (4, -1) \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( 2x + 3y = -4 \)
\( -x + y = 7 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 2x + 3y = -4 \)
\( -x + y = 7 \)
Окончательный ответ |
|---|
\( (-5, 2) \)
Постановка задачи Решите эту линейную систему, используя правило Крамера.
\( 2x + 3y = -4 \)
\( -x + y = 7 \)
Решение
2866 видео решение
Окончательный ответ
\( (-5, 2) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг. |
|---|
Практика — Системы 3×3
\( 2x+3y+z=2; \) \( -x+2y+3z=-1; \) \( -3x-3y+z=0 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( 2x+3y+z=2; \) \( -x+2y+3z=-1; \) \( -3x-3y+z=0 \)
Окончательный ответ |
|---|
\( x=4, y=-3, z=3 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x+3y+z=2; \) \( -x+2y+3z=-1; \) \( -3x-3y+z=0 \)
Решение
MIP4U — 1896 видео решениевидео MIP4U |
|---|
Окончательный ответ
\( x=4, y=-3, z=3 \)
\( 2x-y-z=2; \) \( 4x+y-z=-5; \) \( 6x-2y+2z=17 \)
Постановка задачи |
|---|
Решите эту линейную систему используя правило Крамера.
\( 2x-y-z=2; \) \( 4x+y-z=-5; \) \( 6x-2y+2z=17 \)
Окончательный ответ |
|---|
\( x=1 /2, y=-4, z=3 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( 2x-y-z=2; \) \( 4x+y-z=-5; \) \( 6x-2y+2z=17 \)
Решение
MIP4U — 1902 ВидеореалВидео MIP4U |
|---|
Окончательный ответ
\ (x = 1/2, y = -4, Z = 3 \) 9000
Войдите в систему, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг. |
|---|
Постановка задачи |
|---|
Решите эту линейную систему с помощью Крамера Правило.
\( x+2z=9; \) \( 2y+z=8; \) \( 4x-3y=-2 \)
Окончательный ответ |
|---|
\( x=1, y =2, z=4 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x+2z=9; \) \( 2y+z=8; \) \( 4x-3y=-2 \)
Решение
PatrickJMT — 1903 видео решениевидео от PatrickJMT |
|---|
Окончательный ответ
\( x=1, y=2, z=4 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( x-y+z=4; \) \( 2x+y+z=7; \) \( -x-2y+2z=-1 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\( x-y+z=4; \) \( 2x+y+z=7; \) \( -x-2y+2z=-1 \)
Окончательный ответ |
|---|
\(х=3, у=0, г=1 \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x-y+z=4; \) \( 2x+y+z=7; \) \( -x-2y+2z=-1 \)
Решение
PatrickJMT — 1904 видео решениевидео от PatrickJMT |
|---|
Окончательный ответ
\( x=3, y=0, z=1 \)
. |
|---|
\( -x+2y-3z=1; \) \( 2x+z=0; \) \( 3x-4y+4z=2 \)
Постановка задачи |
|---|
Решить это линейная система с использованием правила Крамера.
\( -x+2y-3z=1; \) \( 2x+z=0; \) \( 3x-4y+4z=2 \)
Окончательный ответ |
|---|
\( x=-4/5, y=-3/2, z=-8/5 \)
Постановка задачи
Решите эту линейную систему с помощью правила Крамера.
\( -x+2y-3z=1; \) \( 2x+z=0; \) \( 3x-4y+4z=2 \)
Решение
математика — 1905 видео решениевидео от mattemath |
|---|
Окончательный ответ
\( x=-4/5, y=-3/2, z=-8/5 \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( x — 3y + 3z = -6 \)
\( -2x + 4y + z = 3 \)
\( 3x — 5y +4z = -9 \)
Постановка задачи |
|---|
Решите эту линейную систему, используя правило Крамера.
\(x — 3y + 3z = -6 \)
\( -2x + 4y + z = 3 \)
\( 3x — 5y +4z = -9 \)
Окончательный ответ |
|---|
\( (0, 1, -1) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\(x — 3y + 3z = -6 \)
\( -2x + 4y + z = 3 \)
\( 3x — 5y +4z = -9 \)
Решение
Эта задача решается за 2 видео подряд.
2867 решение для видео
2867 решение для видео
Окончательный ответ
\( (0, 1, -1) \)
Войдите, чтобы оценить это практическое задание и увидеть его текущий рейтинг. |
|---|
\( 3x — 2y + z = 2 \)
\( 4x + 3y — 2z = 4 \)
\( 5x — 3y + 3z = 8 \)
Постановка задачи | 2 эту линейную систему с помощью правила Крамера.
|---|
Окончательный ответ |
|---|
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг. |
|---|
\( x + y — z = -2 \)
\( 2x — y + z = 0 \)
\( x — 2y + 3z = 1 \)
Постановка задачи |
|---|
Окончательный ответ |
|---|
\ ( (-2/3, -7/3, -1) \)
Постановка задачи
Решите эту линейную систему, используя правило Крамера.
\( x + y — z = -2 \)
\( 2x — y + z = 0 \)
\( x — 2y + 3z = 1 \)
Решение
2870 видео решение
Окончательный ответ
\( (-2/3, -7/3, -1) \)
Войдите, чтобы оценить эту учебную задачу и увидеть ее текущий рейтинг. |
|---|
\( 2x + y — z = 1 \)
\( 3x + 2y + 2z = 13 \)
\( 4x — 2y + 3z = 9 \)
Постановка задачи 32 Решить эту линейную систему с помощью правила Крамера. \( 2x + y — z = 1 \) \( 3x + 2y + 2z = 13 \) \( 4x — 2y + 3z = 9 \)
\( 2x + 3y — 5z = 1 \)
\( (1, 3, 2) \) Постановка задачи Решите эту линейную систему, используя правило Крамера. Решение 2872 видео решениеОкончательный ответ \( (1, 3, 2) \)
\( 3x + y — z = 0 \)
Решите эту линейную систему, используя правило Крамера.
\( (1/2, -2/3, 5/6) \) Постановка задачи Решите эту линейную систему, используя правило Крамера. Решение 2873 видео решениеОкончательный ответ \( (1/2, -2/3, 5/6) \)
Сеть TTU CAEПриносим извинения за неудобства, но страница, на которую вы пытались попасть, находится не по этому адресу. Вы можете использовать приведенные ниже ссылки, чтобы помочь вам найти то, что вы ищете. Если вы уверены, что у вас правильный веб-адрес, но столкнулись с ошибкой, пожалуйста,
связаться с Администрацией Сайта. Спасибо. Возможно, вы искали…   Решающие системы с правилом Крамера – алгебра и тригонометрия OpenStaxЦели обученияВ этом разделе вы: Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений. Вычисление определителя матрицы 2×2 Определитель — это действительное число, которое может быть очень полезным в математике, поскольку оно имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Найдите определитель матрицы 2 × 2Определитель матрицы [latex]\,2\text{ }×\text{ }2\,[/latex], заданной [latex]A=\ left[\begin{array}{cc}a& b\\ c& d\end{array}\right][/latex] определяется как Обратите внимание на изменение обозначения. Есть несколько способов указать определитель, включая [латекс]\,\mathrm{det}\left(A\right)\,[/latex] и замену скобок в матрице прямыми линиями,[латекс]\,| А|.[/латекс] Нахождение определителя матрицы 2 × 2 Нахождение определителя заданной матрицы. [latex]A=\left[\begin{array}{cc}5& 2\\ -6& 3\end{array}\right][/latex] [reveal-answer q=”1408516″]Show Решение[/reveal-answer][hidden-answer a=”1408516″] [латекс]\begin{array}{l}\mathrm{det}\left(A\right)=|\begin{array}{ cc}5& 2\\ -6& 3\end{массив}|\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,=5\влево(3\вправо)-\влево(-6\вправо)\влево(2\вправо)\hfill \\ \,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,=27\hfill \end{массив}[/latex][/hidden-answer] Использование правила Крамера для решения системы двух уравнений с двумя переменными Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера, восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году во Введении к анализу линий алгебры. Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных. Правило Крамера даст нам единственное решение системы уравнений, если она существует. Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение. Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными. [латекс]\begin{array}{c}{a}_{1}x+{b}_{1}y={c}_{1}\,\,\,\,\left(1\ справа)\\ {a}_{2}x+{b}_{2}y={c}_{2}\,\,\,\,\left(2\right)\end{массив}[/ латекс] Мы исключаем одну переменную, используя операции со строками, и находим другую. Скажем, что мы хотим найти [латекс]\,х.\,[/латекс]Если уравнение (2) умножить на коэффициент, противоположный [латекс]\,у\,[/латекс]в уравнении (1 ), уравнение (1) умножается на коэффициент [латекс]\,у\,[/латекс] в уравнении (2), и мы добавляем два уравнения, переменная [латекс]\,у\,[/латекс ] будет устранено. [латекс]\begin{array}{l}\underset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_}{\begin{array}{llll}\hfill & \hfill & \hfill & \hfill \ \ \,\,\,\,{b}_{2}{a}_{1}x+{b}_{2}{b}_{1}y={b}_{2}{c} _{1}\hfill & \hfill & \hfill & \text{Умножить }{R}_{1}\text{ на }{b}_{2}\hfill \\ -{b}_{1}{ a}_{2}x-{b}_{1}{b}_{2}y=-{b}_{1}{c}_{2}\hfill & \hfill & \hfill & \text {Умножить }{R}_{2}\text{ на}-{b}_{1}\hfill \end{array}}\hfill \\ \,\,\,\begin{array}{ll} { b}_{2}{a}_{1}x-{b}_{1}{a}_{2}x={b}_{2}{c}_{1}-{b}_ {1}{c}_{2}\hfill & \hfill \end{массив}\hfill \end{массив}[/latex] Теперь найдите [латекс]\,x.[/латекс] [латекс]\begin{array}{l}\,\,\,{b}_{2}{a}_{1} x-{b}_{1}{a}_{2}x={b}_{2}{c}_{1}-{b}_{1}{c}_{2}\hfill \ \ \,\,\,x\left({b}_{2}{a}_{1}-{b}_{1}{a}_{2}\right)={b}_{2 }{c}_{1}-{b}_{1}{c}_{2}\hfill \\ \text{ }x=\frac{{b}_{2}{c}_{1} -{b}_{1}{c}_{2}}{{b}_{2}{a}_{1}-{b}_{1}{a}_{2}}=\frac {\left[\begin{array}{cc}{c}_{1}& {b}_{1}\\ {c}_{2}& {b}_{2}\end{массив}\ right]}{\left[\begin{array}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{ массив}\справа]}\hfill \конец{массив}[/латекс] Аналогично, чтобы найти [латекс]\,у,[/латекс], мы исключим [латекс]\,х. [латекс]\begin{array}{l}\underset{\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \_\_\_\_\_}{\begin{array}{llll}\hfill & \hfill & \hfill & \hfill \\ \,\,\,\,{a}_{2}{a }_{1}x+{a}_{2}{b}_{1}y={a}_{2}{c}_{1}\hfill & \hfill & \hfill & \text{Multiply} {R}_{1}\text{ by }{a}_{2}\hfill \\ -{a}_{1}{a}_{2}x-{a}_{1}{b} _{2}y=-{a}_{1}{c}_{2}\hfill & \hfill & \hfill & \text{Умножить }{R}_{2}\text{ на}-{a }_{1}\hfill \end{массив}}\hfill \\ \,\,\,\,\,\,\begin{массив}{ll}{a}_{2}{b}_{1 }y-{a}_{1}{b}_{2}y={a}_{2}{c}_{1}-{a}_{1}{c}_{2}\hfill & \hfill \end{массив}\hfill \end{массив}[/latex] Решение для [латекс]\,y\,[/latex] дает [латекс]\begin{array}{l}{a}_{2}{b}_{1}y-{a}_ {1}{b}_{2}y={a}_{2}{c}_{1}-{a}_{1}{c}_{2}\hfill \\ y\left({ a}_{2}{b}_{1}-{a}_{1}{b}_{2}\right)={a}_{2}{c}_{1}-{a} _{1}{c}_{2}\hfill \\ \text{ }y=\frac{{a}_{2}{c}_{1}-{a}_{1}{c}_ {2}}{{a}_{2}{b}_{1}-{a}_{1}{b}_{2}}=\frac{{a}_{1}{c}_ {2}-{a}_{2}{c}_{1}}{{a}_{1}{b}_{2}-{a}_{2}{b}_{1}} =\frac{|\begin{array}{cc}{a}_{1}& {c}_{1}\\ {a}_{2}& {c}_{2}\end{array} |}{|\begin{array}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{array}| }\hfill \end{массив}[/latex] Обратите внимание, что знаменатель для [латекс]\,х\,[/латекс]и [латекс]\,у\,[/латекс] является определителем матрицы коэффициентов. Мы можем использовать эти формулы для решения [латекс]\,х\,[/латекс]и[латекс]\,у,\,[/латекс], но правило Крамера также вводит новые обозначения: Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей. Затем мы можем выразить [латекс]\,х\,[/латекс]и[латекс]\,у\,[/латекс] как частное двух определителей. Правило Крамера для систем 2×2Правило Крамера — это метод, использующий детерминанты для решения систем уравнений, в которых число уравнений равно количеству переменных. Рассмотрим систему двух линейных уравнений с двумя переменными. [латекс]\begin{array}{c}{a}_{1}x+{b}_{1}y={c}_{1}\\ {a}_{2}x+{b} _{2}y={c}_{2}\end{array}[/latex] Решение с использованием правила Крамера задается как [latex]x=\frac{{D}_{x}} {D}=\frac{|\begin{array}{cc}{c}_{1}& {b}_{1}\\ {c}_{2}& {b}_{2}\end {массив}|}{|\begin{массив}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{ массив}|},\,\,D\ne 0;\,\,\text{}\text{}\,y=\frac{{D}_{y}}{D}=\frac{ |\begin{array}{cc}{a}_{1}& {c}_{1}\\ {a}_{2}& {c}_{2}\end{array}|}{| \begin{массив}{cc}{a}_{1}& {b}_{1}\\ {a}_{2}& {b}_{2}\end{массив}|},\, \,D\ne 0.[/латекс] Если мы вычисляем [латекс]\,х,\,[/латекс], то [латекс]\,х\,[/латекс]столбец заменяется столбцом констант. Если мы вычисляем [латекс]\,у,\,[/латекс], то столбец [латекс]\,у\,[/латекс] заменяется столбцом констант. Использование правила Крамера для решения системы 2 × 2Решите следующую систему[latex]\,2\text{ }×\text{ }2\,[/latex] с помощью правила Крамера. [латекс]\begin{array}{c}12x+3y=15\\ \text{ }2x-3y=13\end{array}[/latex] [reveal-answer q=”fs-id1459617″]Показать решение[/reveal-answer] Решить для [латекс]\,x. [латекс]x=\frac{{D}_{x}}{D}=\frac{|\begin{array}{rr}\ hfill 15& \hfill 3\\ \hfill 13& \hfill -3\end{array}|}{|\begin{array}{rr}\hfill 12& \hfill 3\\ \hfill 2& \hfill -3\end{array }|}=\frac{-45-39}{-36-6}=\frac{-84}{-42}=2[/latex] Решить для[latex]\,y.[/latex] [латекс]y=\frac{{D}_{y}}{D}=\frac{|\begin{array}{rr}\hfill 12& \hfill 15\\ \hfill 2& \hfill 13\end {массив}|}{|\begin{массив}{rr}\hfill 12& \hfill 3\\ \hfill 2& \hfill -3\end{массив}|}=\frac{156-30}{-36-6 }=-\frac{126}{42}=-3[/латекс] Решение:[латекс]\,\влево(2,-3\вправо).[/латекс][/скрытый-ответ] ПопробуйтеИспользуйте правило Крамера, чтобы решить систему уравнений 2 × 2. [латекс]\begin{array}{l}\text{ }x+2y=-11\hfill \\ -2x+y=-13\hfill \end{массив}[/latex] [показать- ответ q=”fs-id1440640″]Показать решение[/reveal-answer] [латекс]\влево(3,-7\вправо)[/латекс] [/скрытый-ответ] Вычисление определителя матрицы 3 × 3 Найти определитель матрицы 2×2 несложно, но найти определитель матрицы 3×3 сложнее. Найдите определитель матрицы 3×3. [латекс]A=\left[\begin{array}{ccc}{a}_{1}& {b}_{1}& {c}_{1}\\ {a}_{2} & {b}_{2}& {c}_{2}\\ {a}_{3}& {b}_{3}& {c}_{3}\end{массив}\right][ /latex] Алгебра выглядит следующим образом: [латекс]|A|={a}_{1}{b}_{2}{c}_{3}+{b}_{1}{c}_ {2}{a}_{3}+{c}_{1}{a}_{2}{b}_{3}-{a}_{3}{b}_{2}{c} _{1}-{b}_{3}{c}_{2}{a}_{1}-{c}_{3}{a}_{2}{b}_{1}[/ латекс] Нахождение определителя матрицы 3 × 3Найти определитель заданной матрицы 3 × 3 [латекс]A=\left[\begin{array}{ccc}0& 2& 1\\ 3& — 1& 1\\ 4& 0& 1\end{массив}\right][/latex] [reveal-answer q=”1570002″]Показать решение[/reveal-answer][hidden-answer a=”1570002″] Дополните матрицу первыми двумя столбцами и следуйте формуле. Таким образом, [латекс]\begin{array}{l}|A|=|\begin{array}{ccc}0& 2& 1\\ 3& -1& 1\\ 4& 0& 1\end{array}\,\ ,|\begin{массив}{c}0\\ 3\\ \,\,4\end{массив}\,\,\,\,\begin{массив}{c}2\\ -1\\ 0 \end{массив}|\hfill \\ \,\,\,\,\,\,\,=0\влево(-1\вправо)\влево(1\вправо)+2\влево(1\вправо) \влево(4\вправо)+1\влево(3\вправо)\влево(0\вправо)-4\влево(-1\вправо)\влево(1\вправо)-0\влево(1\вправо)\ влево(0\вправо)-1\влево(3\вправо)\влево(2\вправо)\hfill \\ \,\,\,\,\,\,\,=0+8+0+4-0 -6\hfill \\ \,\,\,\,\,\,\,=6\hfill \end{массив}[/latex][/hidden-answer] Попробуйте Найдите определитель матрицы 3 × 3. [латекс]\mathrm{det}\left(A\right)=|\begin{array}{ccc}1& -3& 7\\ 1& 1& 1\\ 1& -2& 3\end{массив}|[/ латекс] [ответ на ответ q=”fs-id1643971″]Показать решение[/ответ на ответ] [латекс]-10[/латекс] [/скрытый-ответ] Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы? Нет, этот метод работает только для [латекс]\,2\текст{ }×\текст{ }2\,[/латекс]и [латекс]\,\текст{3}\текст{ }×\текст{ } 3\,[/латекс]матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение. Использование правила Крамера для решения системы трех уравнений с тремя переменными Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц 2 × 2. Когда мы вычисляем, что определитель равен нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе. Рассмотрим систему уравнений 3 × 3. [латекс]x=\frac{{D}_{x}}{D},y=\frac{{D}_{y}}{D},z=\frac{{D}_ {z}}{D},D\ne 0[/latex] где Если мы пишем определитель[latex]\,{D}_{x},[/latex]заменяем [ латекс]\,х\,[/латекс]столбец с постоянным столбцом. Если мы записываем детерминант[латекс]{D}_{у},[/латекс] мы заменяем столбец [латекс]\,у\,[/латекс] столбцом констант. Если мы записываем определитель [латекс]\,{D}_{z},[/латекс], мы заменяем столбец [латекс]\,z\,[/латекс] столбцом констант. Всегда проверяйте ответ. Решение системы 3 × 3 с помощью правила КрамераНайдите решение данной системы 3 × 3 с помощью правила Крамера. [латекс]\begin{array}{c}x+y-z=6\\ 3x-2y+z=-5\\ x+3y-2z=14\end{массив}[/latex] [показать -answer q=”1588465″]Показать решение[/reveal-answer][hidden-answer a=”1588465″] Использовать правило Крамера. [латекс]D=|\begin{array}{ccc}1& \,\,1& -1\\ 3& -2& \,\,\,1\\ 1& \,\,3& -2\end{массив }|,{D}_{x}=|\begin{array}{ccc}6& 1& -1\\ -5& -2& \,\,\,1\\ 14& \,\,3& -2\end{ массив}|,{D}_{y}=|\begin{массив}{ccc}1& \,6& -1\\ 3& -5& \,\,1\\ 1& 14& -2\end{массив}|, {D}_{z}=|\begin{array}{ccc}1& \,1& 6\\ 3& -2& -5\\ 1& \,\,3& 14\end{массив}|[/latex] Затем [латекс]\begin{array}{l}x=\frac{{D}_{x}}{D}=\frac{-3}{-3}=1\hfill \\ y=\frac{{D}_{y}}{D}=\frac{-9}{-3}=3\hfill \\ z=\frac{{D}_{z}}{D}= \frac{6}{-3}=-2\hfill \end{array}[/latex] Решение [латекс]\left(1,3,-2\right).[/latex][/ hidden-answer] ПопробуйтеИспользуйте правило Крамера, чтобы решить матрицу 3 × 3. [латекс]\begin{array}{r}\hfill x-3y+7z=13\\ \hfill x+y+z=1\,\,\,\\ \hfill x-2y+3z=4 \,\,\,\end{array}[/latex] [reveal-answer q=”fs-id1405450″]Показать решение[/reveal-answer] [latex]\left(-2,\frac{3}{5},\frac{12}{5}\right)[/latex] [/hidden-answer] Использование правила Крамера для решения Несовместимая система Решите систему уравнений, используя правило Крамера. [латекс]\begin{array}{l}3x-2y=4\text{ }\left(1\right)\\ 6x-4y=0\text{ }\left(2\right)\end{ array}[/latex] [reveal-answer q=”fs-id1464455″]Показать решение[/reveal-answer] Начнем с нахождения определителей[latex]\,D,{D}_{x},\text{и }{D}_{y}.[/latex] [latex]D=|\begin{ array}{cc}3& -2\\ 6& -4\end{массив}|=3\left(-4\right)-6\left(-2\right)=0[/latex] Мы знаем, что определитель нуля означает, что система либо не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных. [латекс]\begin{array}{l}\underset{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}{\begin {массив}{l}\begin{массив}{l}\hfill \\ -6x+4y\,\,\,\,=-8\hfill \end{массив}\hfill \\ \,\,\, 6x-4y\,\,\,\,\,\,=\,\,\,\,0\hfill \end{массив}}\hfill \\ \,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,=\,-8\hfill \end{массив} [/latex] Получаем уравнение[латекс]\,0=-8,\,[/латекс], которое неверно. [/hidden-answer] Использование правила Крамера для решения зависимой системыРешите систему с бесконечным числом решений. [латекс]\begin{array}{rr}\hfill x-2y+3z=0& \hfill \left(1\right)\\ \hfill 3x+y-2z=0& \hfill \left(2\right) )\\ \hfill 2x-4y+6z=0& \hfill \left(3\right)\end{массив}[/latex] [reveal-answer q=»fs-id1360831″]Показать решение[/reveal- ответ] Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами. [латекс]|\begin{array}{rrr}\hfill 1& \hfill -2& \hfill 3\\ \hfill 3& \hfill 1& \hfill -2\\ \hfill 2& \hfill -4& \hfill 6\end {массив}\текст{ }|\текст{ }\begin{массив}{rr}\hfill 1& \hfill -2\\ \hfill 3& \hfill 1\\ \hfill 2& \hfill -4\end{массив}| [/латекс] Затем [латекс]1\влево(1\вправо)\влево(6\вправо)+\влево(-2\вправо)\влево(-2\вправо)\влево(2\ вправо)+3\влево(3\вправо)\влево(-4\вправо)-2\влево(1\вправо)\влево(3\вправо)-\влево(-4\вправо)\влево(-2\ вправо)\влево(1\вправо)-6\влево(3\вправо)\влево(-2\вправо)=0[/латекс] Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений. Понимание свойств определителейЕсть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы. Свойства определителейИллюстрация свойств определителейПроиллюстрируйте каждое из свойств определителей. [открыть-ответ q=»fs-id1531880″]Показать решение[/открыть-ответ] Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали. [латекс]A=\left[\begin{array}{rrr}\hfill 1& \hfill \,\,2& \hfill 3\\ \hfill 0& \hfill \,\,2& \hfill 1\\ \hfill 0& \hfill \,\,0& \hfill -1\end{array}\right][/latex] Дополнить[latex]\,A\,[/latex] первыми двумя столбцами. [латекс]A=\left[\begin{array}{ccc}1& 2& 3\\ 0& 2& 1\\ 0& 0& -1\end{массив}|\,\,\,\begin{массив}{ c}1\\ 0\\ 0\end{массив}\,\,\,\,\begin{массив}{c}2\\ 2\\ 0\end{массив}\right][/latex] Затем [латекс]\begin{array}{l}\mathrm{det}\left(A\right)=1\left(2\right)\left(-1\right)+2\left(1\right) \влево(0\вправо)+3\влево(0\вправо)\влево(0\вправо)-0\влево(2\вправо)\влево(3\вправо)-0\влево(1\вправо)\влево (1\правый)+1\левый(0\правый)\левый(2\правый)\hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,=-2\hfill \end{array}[/latex] Свойство 2 утверждает, что перестановка строк меняет знак. [латекс]\begin{array}{l}\begin{array}{l}\\ A=\left[\begin{array}{cc}-1& 5\\ 4&-3\end{array} \right],\,\,\mathrm{det}\left(A\right)=\left(-1\right)\left(-3\right)-\left(4\right)\left(5\ right)=3-20=-17\end{массив}\hfill \\ \hfill \\ B=\left[\begin{массив}{cc}4& -3\\ -1& 5\end{массив}\right ],\,\,\mathrm{det}\left(B\right)=\left(4\right)\left(5\right)-\left(-1\right)\left(-3\right) =20-3=17\hfill\end{массив}[/latex] Свойство 3 гласит, что если две строки или два столбца идентичны, определитель равен нулю. [латекс]\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,A=\left[\begin{array}{ccc}1& 2& 2\\ 2& 2& 2\\ -1& 2& 2\end{массив}\text{ }|\text{ }\begin{массив}{c}1\\ 2\\ -1\end{массив} \begin{ array}{c}2\\ 2\\ 2\end{массив}\right]\hfill \\ \hfill \\ \mathrm{det}\left(A\right)=1\left(2\right)\ влево(2\вправо)+2\влево(2\вправо)\влево(-1\вправо)+2\влево(2\вправо)\влево(2\вправо)+1\влево(2\вправо)\влево (2\правый)-2\левый(2\правый)\левый(1\правый)-2\левый(2\правый)\левый(2\правый)\hfill \\ \,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,=4-4+8+4-4-8=0\hfill \end{массив}[/latex] 9{-1}\right)=-2\left(-\frac{1}{2}\right)-\left(\frac{3}{2}\right)\left(1\right)=-\ frac{1}{2}\hfill \end{array}[/latex] Свойство 6 гласит, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. [латекс]\begin{array}{l}A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right],\mathrm{det}\left (A\right)=1\left(4\right)-2\left(3\right)=-2\hfill \\ \hfill \\ B=\left[\begin{array}{cc}2\left (1\правый)& 2\левый(2\правый)\\ 3&4\конец{массив}\правый],\mathrm{det}\левый(B\правый)=2\левый(4\правый)-3 \left(4\right)=-4\hfill \end{массив}[/latex][/hidden-answer] Использование правила Крамера и свойств определителя для решения системыНайдите решение данной системы 3 × 3. [латекс]\begin{array}{ll}2x+4y+4z=2\hfill & \left(1\right)\hfill \\ 3x+7y+7z=-5\hfill & \left(2\ справа)\hfill \\ \text{ }x+2y+2z=4\hfill & \left(3\right)\hfill \end{массив}[/latex] [reveal-answer q=»fs-id1653554 ″]Показать решение[/reveal-answer] Используя правило Крамера, мы имеем [latex]D=|\begin{array}{ccc}2& 4& 4\\ 3& 7& 7\\ 1& 2& 2\end{array}|[/latex] Обратите внимание, что второй и третий столбцы идентичны. Получение утверждения, которое является противоречием, означает, что система не имеет решения.[/hidden-answer] Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера. Ключевые понятияРаздел УпражненияВербальныйОбъясните, почему мы всегда можем вычислить определитель квадратной матрицы. [reveal-answer q=”1405260″]Показать решение[/reveal-answer][hidden-answer a=”1405260″] Определитель – это сумма и произведения элементов матрицы, поэтому вы всегда можете оцените этот продукт, даже если в итоге он будет равен 0,9.0005 [/hidden-answer] Изучая правило Крамера, объясните, почему нет единственного решения системы, когда определитель вашей матрицы равен 0. Для простоты используйте [латекс]\,2\,×\,2 \,[/латекс]матрица. Объясните, что в терминах обратной матрицы означает наличие определителя, равного 0. [открыть-ответ q=»fs-id13 «]Показать решение[/открыть-ответ] ″] Обратное не существует. [/скрытый ответ] Определитель матрицы [латекс]\,2\,×\,2\,[/латекс]матрицы[латекс]\,А\,[/латекс] равен 3. Если поменять местами строки и умножить первую строку на 6 и второй ряд на 2, объясните, как найти определитель и дайте ответ. АлгебраическийДля следующих упражнений найдите определитель. [латекс]|\begin{array}{cc}1& 2\\ 3& 4\end{массив}|[/latex] [reveal-answer q=»fs-id13 ″]Показать решение[/reveal- ответ] «] [латекс]-2[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rr}\hfill -1& \hfill 2\\ \hfill 3& \hfill -4\ end{массив}|[/latex] [латекс]|\begin{массив}{rr}\hfill 2& \hfill -5\\ \hfill -1& \hfill 6\end{массив}|[/latex] [reveal-answer q=»fs-id1430900″]Показать решение[/reveal-answer] [латекс]7[/латекс] [/скрытый-ответ] [латекс]|\begin{массив}{cc}-8& 4\\ -1& 5\end{массив}|[/латекс] [латекс]|\begin{массив}{rr}\hfill 1& \hfill 0\\ \hfill 3& \hfill -4\end{массив}|[/latex] [reveal-answer q=»fs- id1395220″]Показать решение[/reveal-answer] [латекс]-4[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rr}\hfill 10& \hfill 20\\ \hfill 0& \hfill -10\end {array}|[/latex] [latex]|\begin{array}{cc}10& 0,2\\ 5& 0,1\end{array}|[/latex] [reveal-answer q=”fs-id1660075 ″]Показать решение[/reveal-answer] [латекс]0[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rr}\hfill 6& \hfill -3\\ \hfill 8& \hfill 4\end{ array}|[/latex] [latex]|\begin{array}{rr}\hfill -2& \hfill -3\\ \hfill 3. [reveal-answer q=»fs-id885813″]Показать решение[/reveal-answer] [латекс] -7 990,7[/латекс] [/скрытый ответ] [латекс]|\begin{массив}{rr}\hfill -1.1& \hfill 0.6\\ \hfill 7.2& \hfill -0.5\end{массив}|[/latex] [латекс]|\begin {array}{rrr}\hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \hfill 0\\ \hfill 0& \hfill 0& \hfill -3\end{array}|[/latex] [reveal-answer q=»fs-id1339464″]Показать решение[/reveal-answer] [латекс]3[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rrr}\hfill -1& \hfill 4& \hfill 0\\ \hfill 0& \hfill 2& \hfill 3\\ \hfill 0& \hfill 0& \hfill -3\end{массив}|[/latex] [латекс]|\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{массив}|[/latex] [reveal-answer q=”fs-id1601846″ ]Показать решение[/reveal-answer] [латекс]-1[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rrr}\hfill 2& \hfill -3& \hfill 1\\ \hfill 3& \hfill -4& \hfill 1\\ \hfill -5& \hfill 6& \hfill 1\end{array}|[/latex] [latex]|\begin{array}{rrr}\hfill -2& \hfill 1& \hfill 4\\ \hfill -4& \hfill 2& \hfill -8\\ \hfill 2& \hfill -8& \hfill -3\end{массив}|[/latex] [открыть-ответ q=»fs-id1663783″]Показать решение[/открыть-ответ] [латекс]224[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rrr}\hfill 6& \hfill -1& \hfill 2\\ \hfill -4& \hfill -3& \hfill 5\\ \hfill 1& \hfill 9& \hfill -1\end{array}|[/latex] [latex]|\begin{array}{rrr}\hfill 5& \hfill 1& \hfill — 1\\ \hfill 2& \hfill 3& \hfill 1\\ \hfill 3& \hfill -6& \hfill -3\end{массив}|[/latex] [открыть-ответ q=»fs-id1616218″]Показать решение[/открыть-ответ] [латекс]15[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rrr}\hfill 1. [latex]|\begin{array}{rrr}\hfill 2& \hfill -1.6 & \hfill 3.1\\ \hfill 1.1& \hfill 3& \hfill -8\\ \hfill -9.3& \hfill 0& \hfill 2\end{массив}|[/latex] [открыть-ответ q=»fs-id1534877″]Показать решение[/открыть-ответ] [латекс]-17.03[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{ccc}-\frac{1}{2}& \frac{1}{3 }& \frac{1}{4}\\ \frac{1}{5}& -\frac{1}{6}& \frac{1}{7}\\ 0& 0& \frac{1}{8 }\end{array}|[/latex] В следующих упражнениях решите систему линейных уравнений, используя правило Крамера. [латекс]\begin{массив}{l}2x-3y=-1\\ 4x+5y=9\end{array}[/latex] [reveal-answer q=”fs-id1694937″]Показать решение[/reveal-answer] [латекс]\влево(1,1\вправо)[/латекс] [/скрытый ответ] [латекс]\begin{array}{r}5x-4y=2\\ -4x+7y =6\end{массив}[/латекс] [латекс]\begin{массив}{l}\текст{ }6x-3y=2\,\,\,\,\,\hfill \\ -8x+ 9y=-1\hfill \end{array}[/latex] [reveal-answer q=”fs-id1433846″]Показать решение[/reveal-answer] [латекс]\влево(\фракция{1}{2},\фракция{1}{3}\право)[/латекс] [/скрытый-ответ] [латекс]\начало{массив} {l}2x+6y=12\\ 5x-2y=13\end{массив}[/latex] [латекс]\begin{массив}{l}4x+3y=23\,\,\hfill \\ \text{ }2x-y=-1\hfill \end{массив}[/latex] [reveal-answer q=”fs-id1516926″]Показать решение[/reveal-answer] [латекс]\влево(2,5\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{l}10x-6y=2\,\,\, \,\hfill \\ -5x+8y=-1\hfill \end{массив}[/latex] [латекс]\begin{array}{l}4x-3y=-3\\ 2x+6y=-4\end{массив}[/latex] [reveal-answer q=”fs-id1615360″] Показать решение[/reveal-answer] [латекс]\left(-1,-\frac{1}{3}\right)[/latex] [/hidden-answer] [латекс]\begin{array}{r}4x- 5y=7\\ -3x+9y=0\end{массив}[/latex] [латекс]\begin{массив}{l}4x+10y=180\,\,\,\,\hfill \\ -3x-5y=-105\hfill \end{массив}[/latex] [reveal-answer q=”fs-id1530071″]Показать решение[/reveal-answer] [латекс]\влево(15,12\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{l}\text{ }8x-2y=-3\ hfill \\ -4x+6y=4\,\,\,\,\hfill \end{array}[/latex] В следующих упражнениях решите систему линейных уравнений, используя правило Крамера. [латекс]\begin{array}{l}\text{ }x+2y-4z=-1\hfill \\ \text{ }7x+3y+5z=26\,\,\hfill \\ -2x -6y+7z=-6\hfill \end{массив}[/latex] [reveal-answer q=”fs-id1530969″]Показать решение[/reveal-answer] [латекс]\влево(1,3,2\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{l}-5x+2y-4z=-47 \hfill \\ \text{ }4x-3y-z=-94\hfill \\ \text{ }3x-3y+2z=94\,\,\,\,\hfill \end{массив}[/latex] [латекс]\begin{array}{l}\text{ }4x+5y-z=-7\hfill \\ -2x-9y+2z=8\,\,\,\,\hfill \\ \ text{ }5y+7z=21\,\hfill \end{array}[/latex] [reveal-answer q=”fs-id1699357″]Show Solution[/reveal-answer] [латекс]\влево(-1,0,3\вправо)[/латекс] [/скрытый ответ] [латекс]\begin{array}{r}4x-3y+4z=10\ \ 5x-2z=-2\\ 3x+2y-5z=-9\end{массив}[/latex] [латекс]\begin{массив}{l}4x-2y+3z=6\,\, \,\hfill \\ \text{ }-6x+y=-2\hfill \\ 2x+7y+8z=24\hfill \end{массив}[/latex] [reveal-answer q=»fs- id1506671″]Показать решение[/reveal-answer] [латекс]\влево(\фракция{1}{2},1,2\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{массив}{r}\hfill 5x+2y-z=1\,\,\,\,\,\\ \hfill -7x-8y+3z=1. [латекс]\begin{массив}{l}\text{ }13x-17y+16z=73\,\, \,\,\hfill \\ -11x+15y+17z=61\,\,\,\,\hfill \\ \text{ }46x+10y-30z=-18\hfill \end{массив}[/latex ] [reveal-answer q=”1433664″]Показать решение[/reveal-answer][hidden-answer a=”1433664″] [латекс]\begin{array}{l}\begin{array}{l}\hfill \\ -4x-3y-8z=-7\hfill \end{array}\hfill \ \ \text{ }2x-9y+5z=0.5\hfill \\ \text{ }5x-6y-5z=-2\hfill \end{массив}[/latex] [латекс]\begin{массив}{l}\text{ }4x -6y+8z=10\,\,\hfill \\ -2x+3y-4z=-5\hfill \\ \text{ }x+y+z=1\,\,\,\,\,\hfill \end{array}[/latex] [reveal-answer q=”fs-id1673950″]Показать решение[/reveal-answer] Бесконечные решения [/hidden-answer] [латекс]\begin{array}{r}\hfill 4x-6y+8z=10\,\,\,\,\,\\ \hfill -2x +3y-4z=-5\,\,\,\\ \hfill 12x+18y-24z=-30\end{массив}[/latex] Технология В следующих упражнениях используйте функцию определителя в графической утилите. [латекс]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 8& \hfill 9\\ \hfill 0& \hfill 2& \hfill 1& \hfill 0\\ \hfill 1& \hfill 0& \hfill 3& \hfill 0\\ \hfill 0& \hfill 2& \hfill 4& \hfill 3\end{массив}|[/latex] [reveal-answer q=»fs-id1597711″]Показать решение[/reveal-answer] [латекс]24[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 2& \hfill 1\\ \hfill 0& \ hfill -9& \hfill 1& \hfill 3\\ \hfill 3& \hfill 0& \hfill -2& \hfill -1\\ \hfill 0& \hfill 1& \hfill 1& \hfill -2\end{массив}|[/latex] [латекс]|\begin{array}{rrrr}\hfill \frac{1}{2}& \hfill 1& \hfill 7& \hfill 4\\ \hfill 0& \hfill \frac{1}{2}& \hfill 100& \hfill 5\\ \hfill 0& \hfill 0& \hfill 2& \hfill 2,000\\ \hfill 0& \hfill 0& \hfill 0& \hfill 2\end{массив}|[/latex] [открыть-ответ q=»fs-id1 5″]Показать решение[/открыть-ответ][скрытый-ответ a=»fs-id15″] [латекс]1[/латекс] [/скрытый-ответ] [латекс]|\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 2& \ hfill 3& \hfill 0& \hfill 0\\ \hfill 4& \hfill 5& \hfill 6& \hfill 0\\ \hfill 7& \hfill 8& \hfill 9& \hfill 0\end{массив}|[/latex] Real- World Applications Для следующих упражнений создайте систему линейных уравнений для описания поведения. Два числа в сумме дают 56. Одно число на 20 меньше другого. [открыть-ответ q=»fs-id1702584″]Показать решение[/открыть-ответ] Да; 18, 38 [/hidden-answer] Два числа в сумме дают 104. Если сложить два раза первое число плюс два раза второе число, получится 208 Три числа в сумме дают 106. Первое число на 3 меньше второго числа. Третье число на 4 больше первого числа. [открыть-ответ q=»fs-id17 ″]Показать решение[/открыть-ответ] ″] Да; 33, 36, 37 [/hidden-answer] Три числа в сумме дают 216. Сумма первых двух чисел равна 112. Третье число на 8 меньше первых двух вместе взятых. Для следующих упражнений создайте систему линейных уравнений для описания поведения. Затем решите систему для всех решений, используя правило Крамера. Вы инвестируете 10 000 долларов на два счета, на которые начисляются 8% и 5% годовых. В конце года на ваших объединенных счетах было 10 710 долларов. Сколько было вложено в каждый счет? [открыть-ответ q=»fs-id1354932″]Показать решение[/открыть-ответ] 7000 долларов на первый счет, 3000 долларов на второй счет. [/hidden-answer] Вы инвестируете 80 000 долларов на два счета, 22 000 долларов на один счет и 58 000 долларов на другой счет. В конце года, при условии простых процентов, вы заработали 2470 долларов в виде процентов. Второй счет получает на полпроцента меньше, чем удвоенный процент по первому счету. Каковы процентные ставки для ваших счетов? Кинотеатру необходимо знать, сколько билетов для взрослых и детей было продано из 1200 билетов. Если детские билеты стоят 5,95 долл. США, билеты для взрослых — 11,15 долл. США, а общая сумма выручки составила 12 756 долл. [открыть-ответ q=»fs-id1584198″]Показать решение[/открыть-ответ] 120 детей, 1080 взрослых [/hidden-answer] Концертная площадка продает одиночные билеты по 40 долларов каждый и билеты для пар по 65 долларов. Если общий доход составил $18,090 и было продано 321 билет, сколько одиночных билетов и сколько парных билетов было продано? Вы решили покрасить кухню в зеленый цвет. Вы создаете цвет краски, смешивая желтую и синюю краски. Вы не можете вспомнить, сколько галлонов каждого цвета вошло в вашу смесь, но вы знаете, что всего было 10 галлонов. Кроме того, вы сохранили квитанцию и знаете, что общая потраченная сумма составила 29,50 долларов США. Если каждый галлон желтого цвета стоит 2,59 доллара, а каждый галлон синего стоит 3,19 доллара, сколько галлонов каждого цвета входит в вашу зеленую смесь? [открыть-ответ q=»fs-id1584221″]Показать решение[/открыть-ответ] 4 галлона желтый, 6 галлонов синий [/hidden-answer] Вы продали два вида шарфов на фермерском рынке и хотели бы знать, какой из них более популярен. В вашем саду выращивают два вида помидоров, зеленый и красный. Красный весит 10 унций, а зеленый весит 4 унции. У вас есть 30 помидоров общим весом 13 фунтов 14 унций. Сколько у вас помидоров каждого вида? [открыть-ответ q=»fs-id1699000″]Показать решение[/открыть-ответ] 13 зеленых помидоров, 17 красных помидоров [/hidden-answer] На рынке три самых популярных овоща составляют 53% продаж овощей. Продажи кукурузы на 4% выше, чем у брокколи, продажи которой на 5% выше, чем у лука. Какую долю рынка занимает каждый овощ? На том же рынке три самых популярных фрукта составляют 37% от общего количества продаваемых фруктов. Клубники продают вдвое больше, чем апельсинов, а киви продают на один процент больше, чем апельсинов. [открыть-ответ q=»fs-id1648808″]Показать решение[/открыть-ответ] Клубника 18%, апельсины 9%, киви 10% [/hidden-answer] Три группы выступили на концертной площадке. Первая группа взимала 15 долларов за билет, вторая группа взимала 45 долларов за билет, а последняя группа взимала 22 доллара за билет. Было продано 510 билетов на общую сумму 12 700 долларов. Если у первой группы было на 40 зрителей больше, чем у второй группы, сколько билетов было продано на каждую группу? Кинотеатр продал билеты на три фильма. Билеты на первый фильм стоили 5 долларов, билеты на второй фильм — 11 долларов, а на третий фильм — 12 долларов. На первый фильм было продано 100 билетов. Общее количество проданных билетов составило 642, а общий доход составил 6 774 доллара. Сколько билетов на каждый фильм было продано? [открыть-ответ q=»fs-id1637286″]Показать решение[/открыть-ответ] 100 для фильма 1, 230 для фильма 2, 312 для фильма 3 [/hidden-answer] Мужчины в возрасте 20–29, 30–39 и 40–49 лет составляли 78% заключенных в тюрьме в прошлом году. В женской тюрьме по дороге общее число заключенных в возрасте от 20 до 49 лет составляло 5525 человек. В этом году возрастная группа 20-29 лет увеличилась на 10%, возрастная группа 30-39 лет уменьшилась на 20%, а возрастная группа 40-49 лет удвоилась. Сейчас там 6040 заключенных. Первоначально в возрастной группе 30–39 лет было на 500 человек больше, чем в возрастной группе 20–29 лет. Определите количество заключенных для каждой возрастной группы в прошлом году. [открыть-ответ q=”fs-id1425394″]Показать решение[/открыть-ответ] 20–29: 2 100, 30–39: 2 600, 40–49: 825 [/hidden-answer] Для следующих упражнений используйте следующий сценарий: миндаля, сушеной клюквы и орехов кешью в шоколаде.
Для специальной смеси «с низким содержанием углеводов» имеется 1000 штук смеси. Общее количество углеводов 425 г, общее количество жиров 570,2 г. Если орехов кешью на 200 штук больше, чем клюквы, сколько штук каждого предмета будет в смеси? Для смеси «походной» в составе смеси 1000 шт., содержащих 390,8 г жира и 165 г белка. Если миндаля столько же, сколько орехов кешью, то сколько каждого элемента содержится в смеси? [открыть-ответ q=»fs-id1647224″]Показать решение[/открыть-ответ] 300 миндальных орехов, 400 клюквы, 300 орехов кешью [/hidden-answer] Для «энергетической» смеси имеется 1000 штук, содержащих 145 г белка и 625 г углеводов. Повторные упражненияСистемы линейных уравнений: две переменныеВ следующих упражнениях определите, является ли упорядоченная пара решением системы уравнений. [латекс]\begin{массив}{l}3x-y=4\\ x+4y=-3\,\end{массив}[/латекс]и[латекс]\,\слева(-1,1 \right)[/latex] [reveal-answer q=”fs-id1395131″]Показать решение[/reveal-answer] Нет [/hidden-answer] [латекс]\begin{array}{l}6x-2y=24\\ -3x+3y=18\,\end{array}[/latex]и[ латекс]\,\слева(9,15\right)[/latex] В следующих упражнениях используйте замену для решения системы уравнений. [латекс]\begin{массив}{l}10x+5y=-5\hfill \\ \,\,\,3x-2y=-12\hfill \end{массив}[/latex] [показать -answer q=”fs-id1698278″]Показать решение[/reveal-answer] [латекс]\влево(-2,3\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{l}\frac{4}{7}x+\ frac{1}{5}y=\frac{43}{70}\\ \frac{5}{6}x-\frac{1}{3}y=-\frac{2}{3}\end {массив}[/латекс] [латекс]\begin{array}{l}5x+6y=14\\ 4x+8y=8\end{массив}[/latex] [reveal-answer q=»fs-id1428954″]Показать решение [/reveal-answer] [латекс]\влево(4,-1\вправо)[/латекс] [/скрытый ответ] В следующих упражнениях используйте сложение для решения системы уравнений. [латекс]\begin{массив}{l}3x+2y=-7\\ 2x+4y=6\end{массив}[/latex] [латекс]\begin{массив}{r}3x+ 4y=2\\ 9x+12y=3\end{массив}[/латекс] [открыть-ответ q=»fs-id1584732″]Показать решение[/открыть-ответ] Решений не существует. [/hidden-answer] [латекс]\begin{array}{l}8x+4y=2\\ 6x-5y=0.7\end{array}[/latex] Для следующих упражнений напишите система уравнений для решения каждой задачи. Решите систему уравнений. Завод имеет себестоимость производства[латекс]\,C\left(x\right)=150x+15\text{,}000\,[/latex]и функцию дохода[латекс]\,R\left (x\right)=200x.\,[/latex]Какова точка безубыточности? [открыть-ответ q=»fs-id1536207″]Показать решение[/открыть-ответ] [латекс]\влево(300,60,000\вправо)[/латекс] [/скрытый-ответ] Исполнитель взимает [латекс]\,С\влево(х\вправо)=50x+10\текст {,}000,\,[/latex], где[latex]\,x\,[/latex] — общее количество посетителей шоу. [открыть-ответ q=»fs-id1358367″]Показать решение[/открыть-ответ] [latex]\left(400,30,000\right)[/latex] [/hidden-answer] Системы линейных уравнений: три переменныеДля следующих упражнений решите систему из трех уравнений с помощью замены или дополнение. [латекс]\begin{array}{l}\text{ }0,5x-0,5y=10\hfill \\ \text{ }-0,2y+0,2x=4\hfill \\ \text{ }0,1x +0.1z=2\hfill\end{массив}[/latex] [открыть-ответ q=»fs-id1513414″]Показать решение[/открыть-ответ] [латекс]\влево(10,-10,10\вправо)[/латекс] [/скрытый-ответ] [латекс]\начало{массив}{r}\hfill 5x+3y-z= 5\,\,\,\\ \hfill 3x-2y+4z=13\\ \hfill 4x+3y+5z=22\end{массив}[/latex] [латекс]\begin{массив}{r }x+y+z=1\\ 2x+2y+2z=1\\ 3x+3y=2\end{массив}[/latex] [reveal-answer q=»fs-id1366211″]Показать решение[ /показать-ответ] Решений не существует. [/hidden-answer] [латекс]\begin{array}{l}\text{ }2x-3y+z=-1\hfill \\ \text{ }x+y+z=-4\ hfill \\ \text{ }4x+2y-3z=33\hfill \end{массив}[/latex] [латекс]\begin{массив}{l}\,\,3x+2y-z=-10 \hfill \\ \,\,\,\,x-y+2z=7\hfill \\ -x+3y+z=-2\hfill \end{массив}[/latex] [показать-ответить q =”fs-id1409562″]Показать решение[/reveal-answer] [латекс]\влево(-1,-2,3\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{r}\hfill 3x+4z=-11\\ \hfill x-2y=5\,\,\,\,\,\,\,\\ \hfill 4y- z=-10\end{массив}[/latex] [латекс]\begin{array}{r}2x-3y+z=0\\ 2x+4y-3z=0\\ 6x-2y-z= 0\end{array}[/latex] [reveal-answer q=”fs-id1417064″]Показать решение[/reveal-answer] [латекс]\left(x,\frac{8x}{5},\frac{14x}{5}\right)[/latex] [/hidden-answer] [латекс]\begin{ array}{r}6x-4y-2z=2\\ 3x+2y-5z=4\\ 6y-7z=5\end{массив}[/latex] Для следующих упражнений напишите систему уравнений для решения каждой задачи. Три нечетных числа в сумме дают 61. Меньшее число на одну треть больше, а среднее число на 16 меньше большего. Какие три числа? [открыть-ответ q=»fs-id1706459″]Показать решение[/открыть-ответ] 11, 17, 33 [/hidden-answer] Билеты на спектакль в местном театре распроданы. Они продают все 500 билетов на общую сумму 8 070 долларов. Билеты стоили 15 долларов для студентов, 12 долларов для детей и 18 долларов для взрослых. Если группа продала в три раза больше билетов для взрослых, чем билетов для детей, сколько билетов каждого типа было продано? 9{2}}[/latex] Матрицы и операции с матрицамиВ следующих упражнениях выполните запрошенные операции с заданными матрицами. [латекс]A=\left[\begin{array}{rr}\hfill 4& \hfill -2\\ \hfill 1& \hfill 3\end{array}\right],B=\left[\begin{ array}{rrr}\hfill 6& \hfill 7& \hfill -3\\ \hfill 11& \hfill -2& \hfill 4\end{array}\right],C=\left[\begin{array}{r}\ hfill \begin{массив}{cc}6& 7\\ 11& -2\end{массив}\\ \hfill \begin{массив}{cc}14& 0\end{массив}\end{массив}\right],D =\left[\begin{массив}{rrr}\hfill 1& \hfill -4& \hfill 9\\ \hfill 10& \hfill 5& \hfill -7\\ \hfill 2& \hfill 8& \hfill 5\end{массив}\right],E=\left[\begin{array}{rrr}\hfill 7& \hfill -14& \hfill 3\\ \hfill 2& \hfill -1& \hfill 3\\ \hfill 0& \hfill 1& \hfill 9\end{массив}\right][/latex] [латекс]-4A[/латекс ] [открыть-ответ q=»fs-id1615553″]Показать решение[/открыть-ответ] [латекс]\влево[\начало{массив}{cc}-16& 8\\ -4& -12\конец{массив}\вправо][/латекс] [/hidden-answer] [latex]10D-6E[/latex] [latex]B+C[/latex] [reveal-answer q=»fs-id1706172″]Показать решение[/ раскрыть-ответ] не определено; размеры не совпадают [/hidden-answer] [latex]AB[/latex] [latex]BA[/latex] [reveal-answer q=»fs-id1650879″]Показать решение[/ раскрыть-ответ] не определено; внутренние размеры не соответствуют [/hidden-answer] [latex]BC[/latex] [latex]CB[/latex] [reveal-answer q=»fs-id1647736″]Показать решение[/reveal-answer] [латекс]\left[\begin{array}{ccc}113& 28& 10\\ 44& 81& -41\\ 84& 98& -42\end{array}\right][/latex] [/hidden-answer ] [latex]DE[/latex] [latex]ED[/latex] [reveal-answer q=»fs-id16 ″]Показать решение[/reveal-answer] 9{3}[/latex]Решение систем с исключением Гаусса Для следующих упражнений напишите систему линейных уравнений из расширенной матрицы. [латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill -3\\ \hfill 0& \hfill 1& \hfill 2\\ \hfill 0& \hfill 0& \hfill 0\end {array}\text{ }|\text{ }\begin{array}{r}\hfill 7\\ \hfill -5\\ \hfill 0\end{array}\right][/latex] [показать -answer q=»fs-id1637532″]Показать решение[/reveal-answer] [латекс]\begin{array}{l}x-3z=7\\ y+2z=-5\,\end{массив}[/latex]с бесконечными решениями [/hidden-answer] [латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 5\\ \hfill 0& \hfill 1& \hfill -2\\ \hfill 0& \hfill 0& \hfill 0\end{array }\text{ }|\text{ }\begin{array}{r}\hfill -9\\ \hfill 4\\ \hfill 3\end{array}\right][/latex] Для следующих упражнений , выпишите расширенную матрицу из системы линейных уравнений. [латекс]\begin{array}{l}\\ \begin{array}{r}\hfill -2x+2y+z=7\\ \hfill 2x-8y+5z=0\\ \hfill 19x- 10y+22z=3\end{массив}\end{массив}[/latex] [reveal-answer q=”fs-id1656057″]Показать решение[/reveal-answer] [латекс]\left[\begin{array}{rrr}\hfill -2& \hfill 2& \hfill 1\\ \hfill 2& \hfill -8& \hfill 5\\ \hfill 19& \hfill -10& \hfill 22 \end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 7\\ \hfill 0\\ \hfill 3\end{массив}\right][/latex] [/hidden-answer] [латекс]\begin{array}{l}\,\,\,\,\,4x+2y-3z=14\hfill \\ -12x+3y+z=100 \hfill \\ \,\,\,\,\,9x-6y+2z=31\hfill \end{массив}[/latex] [латекс]\begin{массив}{r}\hfill x+3z =12\,\\ \hfill -x+4y=0\,\,\,\,\\ \hfill y+2z=-7\end{массив}[/latex] [reveal-answer q=” fs-id1528512″]Показать решение[/reveal-answer] [латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 3\\ \hfill -1& \hfill 4& \hfill 0\\ \hfill 0& \hfill 1& \hfill 2\end {массив}\текст{ }|\текст{ }\begin{массив}{r}\hfill 12\\ \hfill 0\\ \hfill -7\end{массив}\right][/latex] [/hidden-answer] Для следующих упражнений решите систему линейных уравнений методом исключения Гаусса. [латекс]\begin{array}{r}3x-4y=-7\\ -6x+8y=14\end{массив}[/latex] [латекс]\begin{array}{r}3x -4y=1\\ -6x+8y=6\end{массив}[/latex] [reveal-answer q=”fs-id1422121″]Показать решение[/reveal-answer] Решений не существует. [/hidden-answer] [латекс]\begin{array}{l}\begin{array}{l}\\ -1.1x-2.3y=6.2\end{array}\hfill \\ -5.2 x-4.1y=4.3\hfill \end{массив}[/latex] [латекс]\begin{массив}{r}\hfill 2x+3y+2z=1\,\,\,\,\,\\ \hfill -4x-6y-4z=-2\\ \hfill 10x +15y+10z=0\,\,\,\,\,\end{массив}[/latex] [reveal-answer q=”fs-id1455902″]Показать решение[/reveal-answer] Решений не существует. [/hidden-answer] [латекс]\begin{array}{r}\hfill -x+2y-4z=8\,\,\,\,\\ \hfill 3y+8z=-4\ \ \hfill -7x+y+2z=1\,\,\,\,\end{array}[/latex] Решение систем с обратными В следующих упражнениях найдите обратную матрицу. [латекс]\left[\begin{массив}{rr}\hfill -0.2& \hfill 1.4\\ \hfill 1.2& \hfill -0.4\end{массив}\right][/latex] [показать -answer q=”fs-id1531734″]Показать решение[/reveal-answer] [латекс]\frac{1}{8}\left[\begin{array}{cc}2& 7\\ 6& 1\end{array}\right][/latex] [/hidden-answer] [латекс]\left[\begin{array}{rr}\hfill \frac{1}{2}& \hfill -\frac{1}{2}\\ \hfill -\frac{1}{4 }& \hfill \frac{3}{4}\end{массив}\right][/latex] [латекс]\left[\begin{array}{ccc}12& 9& -6\\ -1& 3& 2\\ -4& -3& 2\end{массив}\right][/latex] [показать- ответ q=”fs-id1514199″]Показать решение[/reveal-answer] Обратного не существует. [/hidden-answer] [латекс]\left[\begin{array}{ccc}2& 1& 3\\ 1& 2& 3\\ 3& 2& 1\end{массив}\right][/latex] Для следующих упражнений найдите решения, вычислив обратную матрицу. [латекс]\begin{array}{l}\,\,\,\,0,3x-0,1y=-10\hfill \\ -0,1x+0,3y=14\hfill \end{array}[/ латекс] [открыть-ответ q=»fs-id299169″]Показать решение[/открыть-ответ] [латекс]\влево(-20,40\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{l}\,\,\,\,\, \,\,\,0,4x-0,2y=-0,6\hfill \\ -0,1x+0,05y=0,3\hfill \end{массив}[/latex] [латекс]\begin{массив}{r} 4x+3y-3z=-4,3\\ 5x-4y-z=-6,1\\ x+z=-0,7\end{массив}[/latex] [открыть-ответ q=»fs-id1531936″]Показать решение[/открыть-ответ] [латекс]\влево(-1,0.2,0.3\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{r}\hfill \begin{array}{ l}\\ -2x-3y+2z=3\end{массив}\\ \hfill -x+2y+4z=-5\\ \hfill -2y+5z=-3\end{массив}[/latex] Для следующих упражнений напишите систему уравнений для решения каждой задачи. Решите систему уравнений. Учеников попросили принести в класс свои любимые фрукты. 90% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были вдвое менее популярны, чем бананы, а яблоки были на 5% популярнее бананов, каков процент каждого фрукта в отдельности? [открыть-ответ q=»fs-id1403411″]Показать решение[/открыть-ответ] 17% апельсины, 34% бананы, 39% яблоки [/hidden-answer] Женское общество устроило распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой. Они оценили пирожные в 2 доллара, а печенье с шоколадной крошкой — в 1 доллар. Они собрали 250 долларов и продали 175 предметов. Сколько пирожных и сколько печенья было продано? Решение систем с помощью правила КрамераДля следующих упражнений найдите определитель. [латекс]|\begin{array}{cc}100& 0\\ 0& 0\end{массив}|[/latex] [reveal-answer q=»fs-id1504600″]Показать решение[/reveal- ответ] 0 [/hidden-answer] [латекс]|\begin{array}{cc}0. [латекс] |\begin{массив}{ccc}-1& 4& 3\\ 0& 2& 3\\ 0& 0& -3\end{массив}|[/latex] [открыть-ответ q=»fs-id1698281″]Показать решение[/открыть-ответ] 6 [/hidden-answer] [латекс]|\begin{array}{ccc}\sqrt{2}& 0& 0\\ 0& \sqrt{2}& 0\\ 0& 0& \sqrt{ 2}\end{array}|[/latex] В следующих упражнениях используйте правило Крамера для решения линейных систем уравнений. [латекс]\begin{массив}{r}\hfill 4x-2y=23\,\,\,\,\\ \hfill -5x-10y=-35\end{массив}[/latex] [reveal-answer q=»fs-id1508832″]Показать решение[/reveal-answer] [латекс]\left(6,\frac{1}{2}\right)[/latex] [/hidden-answer] [латекс]\begin{array}{l}0,2x-0,1 y=0\\ -0.3x+0.3y=2.5\end{массив}[/латекс] [латекс]\begin{массив}{r}\hfill -0.5x+0.1y=0.3\,\,\ ,\\ \hfill -0.25x+0. [reveal-answer q=”fs-id1584180″]Show Solution[/reveal-answer] ( x , 5 x + 3) [/hidden-answer] [латекс]\begin{array}{l}x+6y+3z=4\\ 2x+y+2z= 3\\ 3x-2y+z=0\end{массив}[/latex] [латекс]\begin{массив}{r}\hfill 4x-3y+5z=-\frac{5}{2}\ \ \hfill 7x-9y-3z=\frac{3}{2}\,\,\,\,\\ \hfill x-5y-5z=\frac{5}{2}\,\,\,\ ,\end{array}[/latex] [reveal-answer q=»fs-id1508865″]Показать решение[/reveal-answer] [латекс]\влево(0,0,-\фракция{1}{2}\вправо)[/латекс] [/hidden-answer] [латекс]\begin{array}{r}\frac{3}{10}x-\frac{1}{5}y-\frac{3}{10}z =-\frac{1}{50}\\ \frac{1}{10}x-\frac{1}{10}y-\frac{1}{2}z=-\frac{9}{50 }\\ \frac{2}{5}x-\frac{1}{2}y-\frac{3}{5}z=-\frac{1}{5}\end{массив}[/latex ] Практический тестЯвляется ли следующая упорядоченная пара решением системы уравнений? [латекс]\begin{array}{l}\\ \begin{array}{l}-5x-y=12\,\hfill \\ x+4y=9\hfill \end{array}\end{ массив}[/латекс]с[латекс]\,\влево(-3,3\вправо)[/латекс] [открыть-ответ q=»fs-id1435942″]Показать решение[/открыть-ответ] Да [/hidden-answer] Для следующих упражнений решите системы линейных и нелинейных уравнений, используя замену или исключение. [латекс]\begin{array}{r}\frac{1}{2}x-\frac{1}{3}y=4\\ \frac{3}{2}x-y=0\end{ array}[/latex] [latex]\begin{array}{r}\hfill \begin{array}{l}\\ -\frac{1}{2}x-4y=4\end{array} \\ \hfill 2x+16y=2\end{массив}[/latex] [открыть-ответ q=»fs-id1406246″]Показать решение[/открыть-ответ] Решений не существует. [/hidden-answer] [латекс]\begin{array}{r}\hfill 5x-y=1\,\,\,\,\\ \hfill -10x+2y=-2\end{ array}[/latex] [латекс]\begin{array}{l}4x-6y-2z=\frac{1}{10}\hfill \\ \,\,\,x-7y+5z=- \frac{1}{4}\hfill \\ 3x+6y-9z=\frac{6}{5}\hfill \end{массив}[/latex] [reveal-answer q=»fs-id1455840″ ]Показать решение[/reveal-answer] [латекс]\frac{1}{20}\left(10,5,4\right)[/latex] [/hidden-answer] [латекс]\begin{array}{r}x +z=20\\ x+y+z=20\\ x+2y+z=10\end{массив}[/latex] [латекс]\begin{массив}{r}5x-4y-3z= 0\\ 2x+y+2z=0\\ x-6y-7z=0\end{массив}[/latex] [reveal-answer q=»fs-id1615810″]Показать решение[/reveal-answer] [латекс]\left(x,\frac{16x}{5}-\frac{13x}{5}\right)[/latex] [/hidden-answer] [латекс]\begin{ array}{l}y={x}^{2}+2x-3\\ y=x-1\end{массив}[/latex] 9{2}}[/latex] В следующих упражнениях выполните заданные матричные операции. [латекс]5\влево[\begin{array}{cc}4& 9\\ -2& 3\end{массив}\right]+\frac{1}{2}\left[\begin{array}{ cc}-6& 12\\ 4& -8\end{массив}\right][/latex] [reveal-answer q=”fs-id16 ″]Показать решение[/reveal-answer][скрытый-ответ a =”fs-id16″] [латекс]\влево[\begin{array}{cc}17& 51\\ -8& 11\end{массив}\right][/latex] [/hidden-answer] 9{-1}[/latex] [reveal-answer q=»fs-id1583988″]Показать решение[/reveal-answer] [латекс]\влево[\begin{array}{cc}12& -20\\ -15& 30\end{массив}\right][/latex] [/hidden-answer] [латекс]\ mathrm{det}|\begin{array}{cc}0& 0\\ 400& 4\text{,}000\end{array}|[/latex] [латекс]\mathrm{det}|\begin{array }{rrr}\hfill \frac{1}{2}& \hfill -\frac{1}{2}& \hfill 0\\ \hfill -\frac{1}{2}& \hfill 0& \hfill \ frac{1}{2}\\ \hfill 0& \hfill \frac{1}{2}& \hfill 0\end{массив}|[/latex] [открыть-ответ q=»fs-id1295612″]Показать решение[/открыть-ответ] [латекс]-\frac{1}{8}[/latex] [/hidden-answer] Если[латекс]\,\mathrm{det}\left(A\right)=-6, \,[/latex] какой будет определитель, если поменять местами строки 1 и 3, умножить вторую строку на 12 и взять обратное? Перепишите систему линейных уравнений в виде расширенной матрицы. [латекс]\begin{array}{l}14x-2y+13z=140\hfill \\ -2x+3y-6z=-1\hfill \\ x-5y+12z=11\hfill \end{array }[/латекс] [открыть-ответ q=»fs-id1456561″]Показать решение[/открыть-ответ] [латекс]\left[\begin{array}{rrr}\hfill 14& \hfill -2& \hfill 13\\ \hfill -2& \hfill 3& \hfill -6\\ \hfill 1& \hfill -5& \hfill 12\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 140\\ \hfill -1\\ \hfill 11\end{массив}\right][/latex] [/hidden-answer] Перепишите расширенную матрицу в виде системы линейных уравнений. [латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 3\\ \hfill -2& \hfill 4& \hfill 9\\ \hfill -6& \hfill 1& \hfill 2\end{массив}|\begin{массив}{r}\hfill 12\\ \hfill -5\\ \hfill 8\end{массив}\right][/ латекс] В следующих упражнениях используйте метод исключения Гаусса для решения систем уравнений. [латекс]\begin{array}{r}x-6y=4\\ 2x-12y=0\end{массив}[/latex] [reveal-answer q=»fs-id1518911″]Показать решение [/reveal-answer] Решений не существует. [/hidden-answer] [латекс]\begin{array}{r}\hfill 2x+y+z=-3\\ \hfill x-2y+3z=6\,\,\,\, \\ \hfill x-y-z=6\,\,\,\,\end{массив}[/latex] В следующих упражнениях используйте обратную матрицу для решения системы уравнений. [латекс]\begin{массив}{r}\hfill 4x-5y=-50\\ \hfill -x+2y=80\,\,\,\,\end{массив}[/latex] [reveal-answer q=»fs-id1440484″]Показать решение[/reveal-answer] [латекс]\влево(100,90\вправо)[/латекс] [/скрытый-ответ] [латекс]\begin{array}{r}\hfill \frac{1}{100}x -\frac{3}{100}y+\frac{1}{20}z=-49\\ \hfill \frac{3}{100}x-\frac{7}{100}y-\frac{1 }{100}z=13\,\,\,\,\\ \hfill \frac{9}{100}x-\frac{9}{100}y-\frac{9}{100}z=99\,\,\,\,\end{array}[/latex] Для следующих упражнений , используйте правило Крамера для решения систем уравнений. [латекс]\begin{array}{l}200x-300y=2\\ 400x+715y=4\end{массив}[/latex] [reveal-answer q=»fs-id1703905″]Показать решение [/reveal-answer] [латекс]\влево(\frac{1}{100},0\вправо)[/latex] [/hidden-answer] [латекс]\begin{array}{l}0,1x+0,1 у-0,1z=-1,2\\ 0,1x-0,2y+0,4z=-1,2\\ 0,5x-0,3y+0,8z=-5,9{2}+160x. [открыть-ответ q=»fs-id1598123″]Показать решение[/открыть-ответ] 32 или более сотовых телефона в день [/hidden-answer] Небольшая ярмарка стоит 1,50 доллара для студентов, 1 доллар для детей и 2 доллара для взрослых. За один день пришло в три раза больше детей, чем взрослых. Всего было продано 800 билетов на общую сумму 1050 долларов. Сколько билетов каждого типа было продано? ГлоссарийПравило Крамера Redux Вот первый прием использования правила Крамера на матрицах 3 × 3. Допустим, у нас есть маленькая дерзкая матрица 3 × 3, которую мы бы с удовольствием представили нашей подруге Крамер, если бы только она привела с собой свою подругу Детерминант. Вот что мы делаем, чтобы найти определитель матрицы 3 × 3. Сначала скопируйте левый и центральный столбцы справа от матрицы: Вы, конечно, помните, что метод Крамера 2 × 2 заставлял нас умножать по диагонали из левого верхнего угла в правый нижний, а затем вычитать из левого нижнего в верхний правый. Это на самом деле очень похоже. Главное — не перепутать столбцы, которые вы копируете повторно. Теперь, когда у нас есть наша матрица и левый и центральный столбцы из нее, скопированные за пределы полос, мы готовы вычислить определитель так же, как мы сделали 2 × 2. Сначала умножаем из левого верхнего угла в правый нижний, а потом складываем. Мы проделываем это три раза — поэтому снова добавили первые два столбца: D = aei + bfg + cdh … Затем снова вычитаем снизу вверх справа, как мы делали раньше: D = aei + bfg + cdh – gec – hfa – idb 15540004 Вот и все. Итак, в ситуации с реальными числами: Сначала мы скопируем первые два столбца снаружи и справа от полос: И с этого момента, это в основном plug ‘n’ chug: D = (4)(1)(4) + (1)(5)(3) + (0)(2)(0) – (3)(1)(0) – (0)(5) (4) – (4)(2)(1) Понятно. Пример задачиТеперь, поскольку мы знаем, как получить определитель матрицы 3 × 3, вот как мы находим переменные с помощью правила Крамера, когда их три. Вот наши три счастливых холостяка: 2 x + y -3 z = 8 Первый шаг — найти D , определитель коэффициента. Мы только что узнали, как это сделать для матрицы 3 × 3, так что поехали. Сначала создайте матрицу коэффициентов: Ого! Вот оно. Вспоминаем нашу маленькую хитрость, где мы снова копируем первые два столбца наружу и вправо от матрицы: Отлично, Смитерс. Теперь умножаем и прибавляем по диагонали сверху слева направо снизу: D = (2)(2)(2) + (1)(1)(1) + (-3)(-3)(- 3)… Затем мы умножаем и вычитаем по диагонали снизу слева направо вверх: D = (2)(2)(2) + (1)(1)(1) + (-3)( -3)(-3) – (1)(2)(-3) – (-3)(1)(2) – (2)(-3)(1) Итак: D = 8 + 1 + (-27) – (-6) – (-6) – (-6) = 0 Рух-рох, Лохматый! Когда D = 0, точных значений быть не может! (Вы помните?) Мы подумали, что эти уравнения выглядят подозрительно. Ну как насчет этих? Проблема выборкиРешите следующую систему уравнений: 3 x — y -4 z = 10 Сначала мы разбиваем нашу матрицу коэффициентов: Вы устали от поиска D ? Ага, вы меня знаете: Копируем первые два столбца прямо снаружи и справа от матрицы: Затем пришло время умножать и прибавлять по диагонали сверху слева вниз справа и затем умножать и вычитать по диагонали снизу слева направо вверх: D = (3)(5)(2) + (-1)(1)(-3) + (-4)(-2)(4) – ( -3)(5)(-4) – (4)(1)(3) – (2)(-2)(-1) Отсюда математическое счастье: D = 30 + 3 + 32 – 60 – 12 – 4 = -11 Мы знаем, что D = -11, так что теперь мы ищем другие определители. Мы знаем, что способ найти D x состоит в том, чтобы подставить постоянные значения в смесь вместо значений x , а затем используйте наш трюк с копированием столбцов, чтобы получить числа. Время для большего количества подключи и пыхтение. Удалить x -values: Замените их постоянными значениями: Скопируйте первые два столбца в нашей модифицированной матрице снаружи и справа: Умножьте и сложите по диагонали сверху слева к внизу справа, а затем умножить и вычесть по диагонали снизу слева направо вверх: D x = (10)(5)(2) + (-1)(1)(8) + (-4) (9)(4) – (8)(5)(-4) – (4)(1)(10) – (2)(9)(-1) Далее. Ищем D и . Вот оно, лишенное всех и -значений. Теперь мы подставляем постоянные значения и прокручиваем оттуда: Уловка столбца: Подключи и пыхти: D y = (3)(9)(2) + (10)( 1)(-3) + (-4)(-2)(8) – (-3)(9)(-4) – (8)(1)(3) – (2)(-2)(10 ) Решите для y , пока мы здесь: Мы , так что почти готово. |
|---|


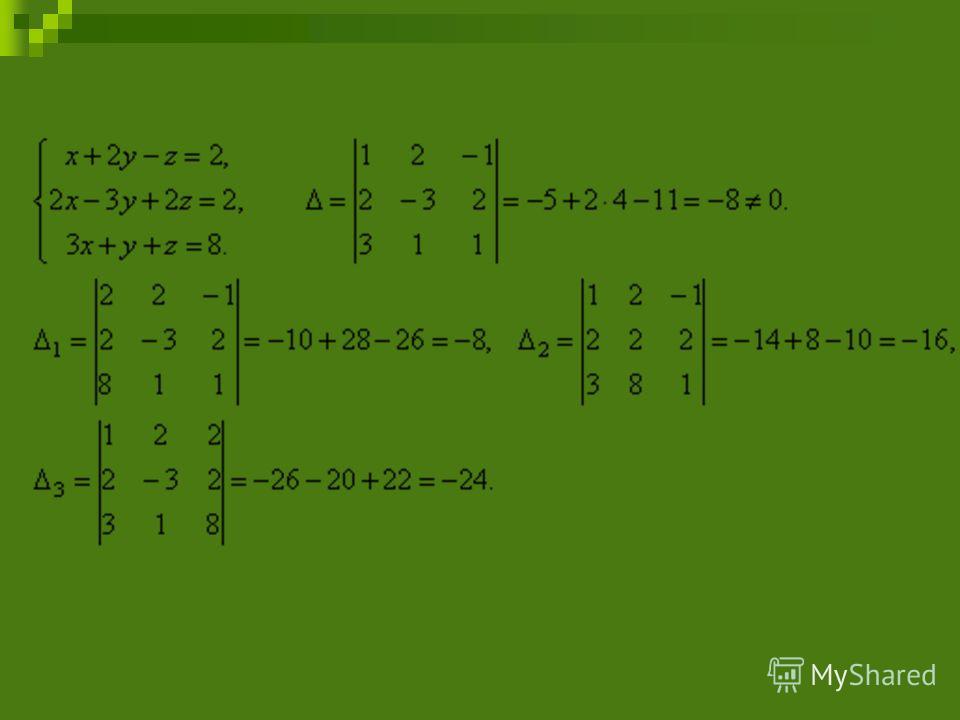

 3
3

 Москва, 2013
Москва, 2013













 Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.


 [/латекс]
[/латекс]

 [/латекс]
[/латекс] Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.
Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
 Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
