Какие интегралы бывают: Виды интегралов — интернет энциклопедия для студентов

{6}(x+y+z) d x d y d z \)

Криволинейные и поверхностные интегралы

ОПРЕДЕЛЕНИЕ

Криволинейный интеграл является интегралом, который вычисляется вдоль кривой в плоскости или в пространстве. Пусть задана кривая $\ c $ и функция $\ f(x ; y) $ непрерывна на этой кривой. Тогда криволинейный интеграл первого вида функции $\ f(x ; y) $ вдоль кривой $\ \mathrm{C} $ называется интегралом $\ \int_{C} f(x ; y) d s $ .

Например. $\ \int_{C}(x+y) d s $ где $\ P(x ; y) $

ОПРЕДЕЛЕНИЕ

Если функции $\ Q(x ; y) $ и $\ \int_{C} P(x ; y) d x+Q(x ; y) d y $ определены на кривой $\ \mathrm{C} $, то криволинейный интеграл второго рода называется интегралом вида $\ \int_{C}(x+y) d x+(x-y) d y $ .

Например: $\ f(x ; y 😉 $

Подробнее о криволинейных интегралах по ссылке.

ОПРЕДЕЛЕНИЕ

Поверхностный интеграл первого вида функции $\ \iint_{S} f(x ; y ; z) d S $ над некоторой поверхностью $\ s $ называется интегралом $\ \iint_{S}(x+y+z) d S $

Например: $\ \iint_{S}(x+y+z) d S $ , где $\ \mathrm{S} $ — часть плоскости $\ x+2 y+3 z=0 $, которая лежит в первом октанте.

{-x} d x \)

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Сходимость несобственных интегралов Интегрирование по частям Интегрирование заменой переменной Внесение под знак дифференциала

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Содержание

Интеграл — Умскул Учебник

На этой странице вы узнаете:

Как связаны Ньютон и Лейбниц?
Почему площадь криволинейной трапеции считается через интеграл?

Интеграл

В топ-5 страшилок по математике неизменно входит интеграл. Так ли он ужасен на самом деле?

Если объяснять простыми словами, интеграл — это площадь фигуры под графиком функции. Например, в геометрии есть формулы, чтобы посчитать площадь прямоугольника или треугольника, а если нужно посчитать площадь фигуры с кривой стороной, заданной функцией, поможет интеграл.

Если у функции y = f(x) есть первообразная y = F(x), тогда множество значений первообразных у = F(x) + С называют неопределенным интегралом функции y = f(x)

Записывается это следующим образом:

$\int f(x)dx = F(x) + C$

Какие бывают интегралы?

Интегралы бывают неопределенные и определенные.

Рассмотрим определенный интеграл. У такого интеграла в отличие от неопределенного есть предел интегрирования, то есть определённый отрезок.

Определенный интеграл функции на отрезке [a; b] – это приращение первообразных

Записывается это следующим образом:

$\int\limits_a^b f(x)dx = F(b) — F(a)$

Для данного интеграла пределом является отрезок от a до b

Как связаны Ньютон и Лейбниц?

И Ньютон, и Лейбниц, бесспорно, являются великими учеными. Как и у обычных людей, у них бывают споры. Именно такой спор и послужил названию одной из формул в математике в честь этих двух замечательных ученых. Формула Ньютона-Лейбница используется для вычисления определенного интеграла. Она была выведена Ньютоном и Лейбницем независимо друг от друга. Есть мнение, что Ньютон свою версию создал раньше Лейбница, но опубликовал позже, из-за этого и случился спор, который завершился только после смерти обоих ученых.

Формула Ньютона-Лейбница

Если функция f(x) непрерывна на промежутке [a; b], то

где F(x) – первообразная для функции f(x),
a – нижний предел интегрирования,
b – верхний предел интегрирования

Данная формула применяется для вычисления определенного интеграла

Пример вычисления определенного интеграла по формуле Ньютона – Лейбница:

Интеграл для нахождения площади фигуры

Представим, что нам нужно посчитать расстояние, пройденное автомобилем с непостоянной скоростью в промежуток времени [a; b]. b f(x)dx\)

Почему площадь криволинейной трапеции считается через интеграл?

Чтобы понять это, разобьем фигуру на конечное число узких прямоугольных столбцов.

Найдем общую площадь, умножив высоту каждого столбика на его ширину и сложив все полученные значения, такая площадь будет приблизительной.

Если разделить данную фигуру на большее количество столбиков, только уже меньших по ширине, получим более точное значение. Повторять такое действие можно до бесконечности, следовательно, ширина будет стремиться к нулю, а количество прямоугольников — к бесконечности.

Сумму такого количества прямоугольников запишем в виде предела при количестве прямоугольников, стремящемся к бесконечности.

При таких условиях рассматриваемая сумма площадей сходится к пределу, описываемому следующим образом

, и равна какому-то числу.

А если фигура расположена под осью абсцисс, для вычисления площади фигуры нужно добавить минус к изначальной формуле. 5 3dx\)

Задание 2.
Вычислите площадь фигуры ограниченной $y = \sin x, x = 0, x = \frac{\pi}{2}$

Задание 3.
Вычислите площадь фигуры ограниченной y = 2x²— 5, x = -1, x = 1

9
$8\frac{2}{3}$
$\frac{20}{3}$
8

Задание 4.
Вычислите площадь фигуры ограниченной y = x² — 3 и y = -2x² + 9

Ответы: 1. – 3; 2. – 1; 3. – 2; 4. – 1

Методы вычисления интегралов, формулы и примеры решений

Содержание:

1. Метод непосредственного интегрирования
2. Внесение под знак дифференциала
3. Интегрирование заменой переменной
4. Интегрирование по частям

1. Метод непосредственного интегрирования

Приведение к табличному виду или метод непосредственного интегрирования.

{\prime}(t) \cdot d t$

Определенный интеграл зависит от переменной интегрирования, поэтому если выполнена замена переменных, то обязательно надо вернуться к первоначальной переменной интегрирования.

Пример

Задание. Найти интеграл $\int \frac{d x}{3-5 x}$

Решение. Заменим знаменатель на переменную $t$ и приведем исходный интеграл к табличному.

$$\int \frac{d x}{3-5 x}\left\|\begin{array}{l} 3-5 x=t \\ -5 d x=d t \\ d x=-\frac{d t}{5} \end{array}\right\|=\int \frac{-\frac{d t}{5}}{t}=-\frac{1}{5} \int \frac{d t}{t}=$$

$=-\frac{1}{5} \ln |t|+C=-\frac{1}{5} \ln |3-5 x|+C$

Ответ. $\int \frac{d x}{3-5 x}=-\frac{1}{5} \ln |3-5 x|+C$

Подробнее о данном методе решении интегралов по ссылке →

4. Интегрирование по частям

Интегрированием по частям называют интегрирование по формуле

$\int u d v=u v-\int v d u$

При нахождении функции $v$ по ее дифференциалу $d v$ можно брать любое значение постоянной интегрирования $C$, так как она в конечный результат не входит.

Поэтому для удобства будем брать $C=0$ .

Использование формулы интегрирования по частям целесообразно в тех случаях, когда дифференцирование упрощает один из сомножителей, в то время как интегрирование не усложняет другой.

Пример

Задание. Найти интеграл $\int x \cos x d x$

Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям.

$$\int x \cos x d x\left\|\begin{array}{ll} u=x & v=\sin x \\ d u=d x & d v=\cos x d x \end{array}\right\|=x \sin x-\int \sin x d x=$$

$=x \sin x+\cos x+C$

Ответ. $\int x \cos x d x=x \sin x+\cos x+C$

Подробнее о данном методе решении интегралов по ссылке →

Читать дальше: метод непосредственного интегрирования.

Чем отличается определенный интеграл от неопределенного

Сегодня слово «Интеграл» можно услышать довольно часто, причем, зачастую, в самых неожиданных местах, например на биржевом канале по телевизору, или по новостям. Нередко мы слышим словосочетание «интегральные показатели» , слово «интегрированный», «интегративный» и тому подобное. Ну, по большому счету, чиновники и телеведущие, вообще, очень любят разные умные слова, правда вряд ли они понимают их истинное значение. А мы сегодня поговорим о том, что же такое интеграл, какие виды интеграла существуют и в чем их отличия.

Что такое интеграл

Интеграл- это латинское слово, которое пришло к нам из античности, и означает оно «Целый», или «Полный». То есть, ясно, что если про некий объект, например, сосуд молока говорили «интегер», это означало, что он полный, и молока в нем сколько было, столько и осталось.

Со временем это слово стали употреблять в совершенно разных дисциплинах- в философии, политике, экономике, в алгебре и геометрии. Но наиболее простую интерпретацию интегралу дает математика.

Определенный интеграл

Итак, интеграл -это некая сумма отдельных частей. Вот наиболее простые примеры для, более четкого понимания сути этого термина:

Предмет — это интеграл(сумма) молекул.
Лист в клетку — это интеграл(сумма) клеток.
Солнечная система — это интеграл(сумма) солнца и планет.
Общество — это интеграл людей.
Отрезок- это интеграл (сумма) метров. Если маленький отрезок, то сантиметров, миллиметров или микроскопических отрезков.
Площадь какой-либо поверхности — это интеграл квадратных метров, квадратных сантиметров или миллиметров, а также микроскопических площадей.

Объем- это интеграл кубических метров или, как их еще называют — литров.

Что такое определенный и неопределенный интегралы?

Начнем с определенного, так как его смысл поддается пониманию легче.

Геометрия изучает площади. Например, если вы хотите поклеить дома обои, вам надо знать площадь стен, чтобы узнать, сколько обоев вы должны купить. Тогда вы просто умножаете длину стены на высоту и получаете ее площадь. В данном случае, эта площадь является интегралом квадратных метров или сантиметров, в зависимости от того, в каких единицах вы ее измеряли. Но поверхности, площадь которых нам требуется вычислить далеко не всегда имеют форму прямоугольника, квадрата, или даже круга. В большинстве случаев — это сложные фигуры с волнистыми сторонами. Наиболее распространенный пример — площадь фигуры под кривой, имеющей уравнение y=1/x . Дело в том, что найти ее площадь при помощи обычных формул, которыми мы находим площадь квадрата, круга или даже сферы — невозможно. Для этой цели был разработан определенный интеграл.

Суть метода в том, что нашу сложную фигуру нужно разбить на очень узкие прямоугольники, настолько узкие, что высота каждых двух соседних практически равна. Ясно, что по сути, можно уменьшать толщину этих прямоугольников бесконечно, поэтому для обозначения их толщины используется размер dx. X — это координата, а приставка d — это обозначение бесконечно уменьшаемой величины. Поэтому, когда мы пишем dx — это значит, что мы берем отрезок по оси x , длина которого очень мала, практически равна нулю.

Итак, мы уже условились, что площадь любой фигуры- это интеграл квадратных метров или любых других фигур с более мелкими площадями. Тогда наша фигура, площадь которой мы ищем, представляет собой интеграл или сумму тех бесконечно тонких прямоугольников, на которые мы ее разбили. А ее площадь- это сумма их площадей. То есть вся наша задача сводится к тому, чтобы найти площадь каждого из этих прямоугольников, а затем их все сложить- это и есть определенный интеграл.

Теперь поговорим о неопределенном интеграле. Только, для того, чтобы понять, что это такое, сначала нужно узнать о производной. Итак, начнем.

Производная — это угол наклона касательной к какому-либо графику в какой-нибудь ее точке. Иными словами — производная — это то, насколько график наклонен в данном его месте. К примеру, прямая линия в любой точке имеет один и тот же наклон, а кривая- разный, но он может повторяться. Для вычисления производной существуют специальные формулы, а процесс ее вычисления называют дифференцированием. Т.е. дифференцирование — это определение угла наклона графика в данной точке.

Таблица основных неопределенных интегралов

А для того, чтобы сделать наоборот — узнать формулу графика по углу ее наклона, прибегают к операции интегрирования, или суммирования данных обо всех точках. Интегрирование и дифференцирование- два взаимообратных процесса. Только здесь уже пользуются не тем интегралом, который был в первом пункте ( для определения площади ), а другим — неопределенным, то есть, не имеющим пределов.

Предположим, что нам известно, что производная некоей функции равна 5. 5 — это угол наклона графика к оси х в данной точке. Тогда, проинтегрировав производную, мы узнаем, что функция этой производной, которую еще называют первообразной — у=5х+с , где с- любое число. Для интегрирования, так же как и для дифференцирования есть специальные формулы, которые можно найти в таблицах.

Заключение

В заключение прорезюмируем, что основное отличие определенного интеграла от неопределенного — в их назначениях. Определенные интегралы используются для вычисления ограниченных параметров, таких как площадь, длина или объем, а неопределенный — при вычислении параметров, не имеющих границ, то есть функций.

Интересное видео на эту тему:

НаукаКомментировать

Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница / Хабр

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

К сожалению, так сложилось, что многим (и мне) она, порой кажется, слишком сложной, недоступной, наукой для избранных. Между тем, так только кажется ! Безусловно, она требует интеллектуального напряжения, памяти, воображения и много чего ещё, как и многие другие интеллектуальные занятия.

Отличительными особенностями её являются:

использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),
логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),
последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),
высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин
Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы
Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т. д.)
Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук
Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными
Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее
Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т. д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Во введении к книге «Развитие понятия интеграла» известный историк математики профессор Фёдор Андреевич Медведев так охарактеризовал сущность интегрирования и процесс его развития в науке «… Интегрирование представляет собой абстрактное выражение разнообразнейших способов измерения величин, и по мере вовлечения в человеческое познание всё новых и новых объектов реальной действительности математики создают всё более и более общие схемы интеграционных процессов с тем, чтобы охватить всё расширяющийся круг объектов, подлежащих измерению» [1].

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

2. Геометрический и аналитико-алгебраический смысл интегрирования

Естественным образом, возникает два вида задач, которые отражают два смысла интегрирования: — геометрический и аналитико-алгебраический. Первый — отыскание площади плоской фигуры под произвольной кривой (квадратура) и отыскание объёма (кубатура). Второй — подсчёт суммарного значения некой переменной величины [2], которая изменяется, принимает различные значения сообразно единицам времени, длины и т.д.

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].
В случае с вещественными числами.
- Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.
- Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.
- В случае с отрицательными числами (-2,3 × 4,3), умножение — сумма произведений и разворот числовой оси или иными словами отражение суммарного значения произведения — в данном случае числа 9,89 относительно начала отсчёта, то есть числа ноль, в результате получаем -9,89.
В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».
Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где а .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

3. Интуитивные способы отыскания значения интеграла

Итак, каким же образом вычислить интегральную сумму ? Можно попробовать несколько способов:

Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

Функция является числовой, то есть область определения и область значений являются числовыми — принимают числовые значения (более точно — вещественные значения).
Функция непрерывна и принимает значения в каждой точке с соответствующим значением переменной (к примеру, в точкесуществует значение функции , а в точке значение
Функция может иметь любое выражение. Мы можем иметь набор значений функции в соответствующих точках в виде таблицы (функция задана таблично). Или функция может быть явно задана в виде аналитического выражения (к примеру, в случае с функцией от одной вещественной переменной — , и т.д.).
Функция может описывать зависимость величины любой природы — физической, биологической, экономической и т.д.

Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

[1]. Медведев Ф.А. Развитие понятия интеграла. — М.: Наука, 1974. С. 4

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для и одно и тоже. Далее, мы покажем, что производная , то есть можно записать или .

[7]. То есть . К примеру, пусть функция задана выражением . Тогда, при , , а значение . Если. Тогда, при , , а значение .

[8]. Пусть имеется точка, число 7 и 10, чтобы найти величину промежутка между этими значениями надо найти разность то есть 10 — 7 = 3.

Неопределенный и определенный интегралы.

Первообразная функции и неопределенный интеграл. Основные свойства неопределенного интеграла.

Первообразная функция.

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:

F(x) = f(x).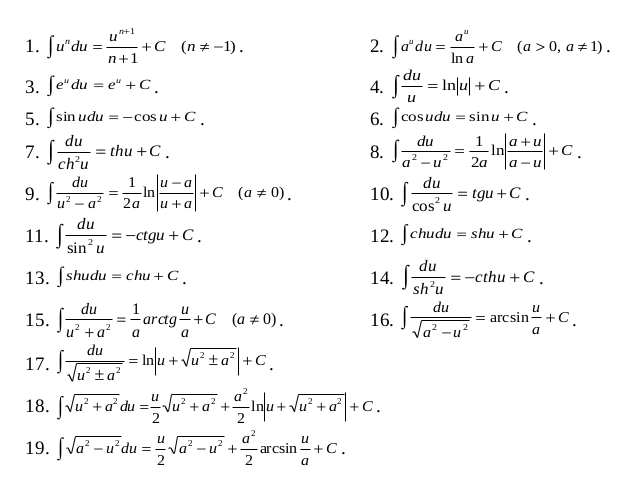

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

F₁(x) = F₂(x) + C.

Неопределенный интеграл.

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

F(x) + C.

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

4. где u, v, w – некоторые функции от х.

Пример:

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.

Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.

Таблица основных формул и правил интегрирования.

Интеграл	Значение	Интеграл	Значение
1	-lncosx+C	9	e^x + C
2	lnsinx+ C	10	sinx + C
3		11	-cosx + C
4		12	tgx + C
5		13	-ctgx + C
6	ln	14	arcsin + C
7		15
8		16

Основные методы интегрирования: непосредственное, замена переменной и по частям.

Методы интегрирования.

Рассмотрим три основных метода интегрирования.

Непосредственное интегрирование.

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.

Рассмотрим применение этого метода на примере:

Требуется найти значение интеграла . На основе известной формулы дифференцирования можно сделать вывод, что искомый интеграл равен , где С – некоторое постоянное число. Однако, с другой стороны . Таким образом, окончательно можно сделать вывод:

Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.

Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.

Способ подстановки (замены переменных).

Теорема: Если требуется найти интеграл , но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:

Доказательство: Продифференцируем предлагаемое равенство:

По рассмотренному выше свойству №2 неопределенного интеграла:

f(x)dx = f[(t)](t)dt

что с учетом введенных обозначений и является исходным предположением. Теорема доказана.

Пример. Найти неопределенный интеграл .

Сделаем замену t = sinx, dt = cosxdt.

Пример.

Замена Получаем:

Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.

Интегрирование по частям.

Способ основан на известной формуле производной произведения:

(uv) = uv + vu

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:

или ;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Пример.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Пример.

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.

Таким образом, интеграл найден вообще без применения таблиц интегралов.

Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.

Пример.

Интегрирование рациональных дробей.

Интегрирование элементарных дробей.

Определение: Элементарными называются дроби следующих четырех типов:

I. III.

II. IV.

m, n – натуральные числа (m  2, n  2) и b² – 4ac <0.

Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

II.

Рассмотрим метод интегрирования элементарных дробей вида III.

Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.

Рассмотрим применение указанной выше формулы на примерах.

Пример.

Вообще говоря, если у трехчлена ax² + bx + c выражение b² – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.

Пример.

Рассмотрим теперь методы интегрирования простейших дробей IV типа.

Сначала рассмотрим частный случай при М = 0, N = 1.

Тогда интеграл вида можно путем выделения в знаменателе полного квадрата представить в виде . Сделаем следующее преобразование:

Второй интеграл, входящий в это равенство, будем брать по частям.

Обозначим:

Для исходного интеграла получаем:

Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл .

Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u² + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.

Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.

Пример:

Интегрирование рациональных дробей.

Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.

Теорема: Если — правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x — a)^…(x — b)^(x²+ px + q)^…(x²+ rx + s)^), то эта дробь может быть разложена на элементарные по следующей схеме:

где A_i, B_i, M_i, N_i, R_i, S_i – некоторые постоянные величины.

При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин A_i, B_i, M_i, N_i, R_i, S_i применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.

Применение этого метода рассмотрим на конкретном примере.

Пример.

Т.к. ( , то

Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

Итого:

Пример.

Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:

6 x⁵ – 8x⁴ – 25x³ + 20x² – 76x – 7 3x³ – 4x² – 17x + 6

6x⁵ – 8x⁴ – 34x³ + 12x² 2x² + 3

9x³ + 8x² – 76x — 7

9x³ – 12x² – 51x +18

20x² – 25x – 25

Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:

3x³ – 4x² – 17x + 6 x — 3

3x³ – 9x² 3x² + 5x — 2

5x² – 17x

5x² – 15x

— 2x + 6

-2x + 6

Таким образом 3x³ – 4x² – 17x + 6 = (x – 3)(3x² + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:

Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

Окончательно получаем:

Пример.

Найдем неопределенные коэффициенты:

Тогда значение заданного интеграла:

Интегрирование тригонометрических выражений.

Интегрирование некоторых тригонометрических

функций.

Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида .

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

Тогда

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Пример.

Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Пример.

Интеграл вида если

функция R является нечетной относительно cosx.

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.

Функция может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.

Пример.

Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.

Интеграл вида если

функция R является нечетной относительно sinx.

По аналогии с рассмотренным выше случаем делается подстановка t = cosx.

Тогда

Пример.

Интеграл вида

функция R четная относительно sinx и cosx.

Для преобразования функции R в рациональную используется подстановка

t = tgx.

Тогда

Пример.

Интеграл произведения синусов и косинусов

различных аргументов.

В зависимости от типа произведения применятся одна из трех формул:

Пример.

Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.

Пример.

Иногда применяются некоторые нестандартные приемы.

Пример.

Итого

Интегрирование некоторых иррациональностей.

Интегрирование некоторых иррациональных функций.

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

Интеграл вида где n— натуральное число.

С помощью подстановки функция рационализируется.

Тогда

Пример.

Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

Проиллюстрируем это на примере.

Пример.

Интегрирование биноминальных дифференциалов.

Определение: Биноминальным дифференциалом называется выражение

x^m(a + bxⁿ)^pdx

где m, n, и p – рациональные числа.

Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:

Если р – целое число, то интеграл рационализируется с помощью подстановки

, где  — общий знаменатель m и n.

Если — целое число, то интеграл рационализируется подстановкой

, где s – знаменатель числа р.

3) Если — целое число, то используется подстановка , где s – знаменатель числа р.

Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.

На рассмотрении этих интегралов остановимся более подробно.

Интегралы вида .

Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.

Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:

Таким образом, интеграл приводится к одному из трех типов:

Интегральное исчисление — формулы, методы, примеры

Интегральное исчисление помогает найти первообразные функции. Эти первообразные также называются интегралами функции. Процесс нахождения первообразной функции называется интегрированием. Обратным процессом нахождения производных является нахождение интегралов. Интеграл функции представляет собой семейство кривых. Нахождение как производных, так и интегралов составляет фундаментальное исчисление. В этом разделе мы рассмотрим основы интегралов и вычисления интегралов.

1.	Что такое интегральное исчисление?
2.	Основные теоремы интегралов
3.	Типы интегралов
4.	Свойства интегралов
5.	Интегральные формулы
6.	Методы интегралов
7.	Применение интегралов
8.	Часто задаваемые вопросы по интегралам

Что такое интегральное исчисление?

Интегралы — это значения функции, найденные в процессе интегрирования. Процесс получения f(x) из f'(x) называется интегрированием. Интегралы присваивают номера функциям таким образом, что описывают задачи перемещения и движения, проблемы площади и объема и т. д., возникающие при объединении всех небольших данных. Зная производную f’ функции f, мы можем определить функцию f. Здесь функция f называется первообразной или интегралом от f’.

Пример: Дано: f(x) = x ² .

Производная f(x) = f'(x) = 2x = g(x)

если g(x) = 2x, то антипроизводная g(x) = ∫ g(x) = x ²

Определение интеграла

F(x) называется первообразной или интегралом Ньютона-Лейбница или примитивной функции f(x) на интервале I. F'(x) = f(x) для каждого значения x в I.

Интеграл представляет площадь области под кривой. Мы аппроксимируем фактическое значение интеграла, рисуя прямоугольники. Определенный интеграл функции можно представить как площадь области, ограниченной ее графиком данной функции между двумя точками прямой. Площадь области находят, разбивая ее на тонкие вертикальные прямоугольники и применяя нижний и верхний пределы, площадь области суммируют. Зададим интеграл функции по интервалу, на котором этот интеграл определен. 9b f(x) dx\) = f(b) — f(a). Это известно как определенный интеграл от f в диапазоне [a,b], где a — нижний предел, а b — верхний предел.

Типы интегралов

Интегральное исчисление используется для решения задач следующих типов.

а) задача о нахождении функции, если задана ее производная.

б) задача нахождения площади, ограниченной графиком функции при заданных условиях. Таким образом, интегральное исчисление делится на два типа.

Определенные интегралы (значения интегралов определенные)
Indefinite Integrals (значение интеграла неопределенно с произвольной константой, C)

Неопределенные интегралы

Это интегралы, которые не имеют ранее существовавшего значения пределов; тем самым делая окончательное значение интеграла неопределенным. ∫g'(x)dx = g(x) + c. Неопределенные интегралы относятся к семейству параллельных кривых.

Определенные интегралы

9b f(x) dx = f(b) — f(a)\)

Свойства интегрального исчисления

Изучим свойства неопределенных интегралов, чтобы работать над ними.

Производная интеграла — это сама подынтегральная функция. ∫ f(x) dx = f(x) +C
Два неопределенных интеграла с одной и той же производной приводят к одному и тому же семейству кривых, поэтому они эквивалентны. ∫ [ f(x) dx -g(x) dx] =0
Интеграл суммы или разности конечного числа функций равен сумме или разности интегралов отдельных функций. ∫ [ f(x) dx+g(x) dx] = ∫ f(x) dx + ∫ g(x) dx
Константа вынесена за знак интеграла. ∫ k f(x) dx = k ∫ f(x) dx, где k ∈ R.
Два предыдущих свойства объединяются, чтобы получить форму: ∫ [k$_1$f$_1$(x) + k$_2$f$_2$(x) +… k $_n$f$_n$(x)] dx = k$_1$∫ f$_1$(x)dx + k$_2$∫ f$_2$(x )dx+ … k$_n$ ∫ f$_n$(x)dx

Интегральные формулы

Мы можем запомнить формулы производных некоторых важных функций. Вот соответствующие интегралы этих функций, которые запоминаются как стандартные формулы интегралов.

∫ x ⁿ dx=x ⁿ⁺¹ /n+1+C, где n ≠ -1
∫ дх =х+С
∫ cosxdx = sinx+C
∫ sinxdx = -cosx+C
∫ сек ² x dx = tanx+C
∫ cosec ² x dx = -cotx+C
∫ сек ² x dx = tanx+C
∫ secx tanxdx = secx+C
∫ cscx cotx dx = -cscx+C
∫1/(√(1-x ² ))= sin ^-1 х + С
∫-1/(√(1-x ²))= cos ^-1 x + C
∫1/(1+x ² )= тангенс ^-1 x + C
∫-1/(1+x ² )= детская кроватка ^-1 x + C
∫1/(x√(x ² -1))= сек ^-1 x + C
∫-1/(x√(x ² -1))= cosec ^-1 x + C
∫ e ^x dx=e ^x + C
∫dx/x=ln|x| + С
∫ ^x dx=a ^x /ln a + C

Методы нахождения интегралов

Существует несколько методов нахождения неопределенных интегралов. Известными методами являются:

Нахождение интегралов путем интегрирования методом подстановки
Нахождение интегралов интегрированием по частям
Нахождение интегралов интегрированием по неполным дробям.

Нахождение интегралов методом подстановки

Несколько интегралов находятся методом подстановки. Если u является функцией x, то u’ = du/dx.

∫ f(u)u’ dx = ∫ f(u)du, где u = g(x).

Нахождение интегралов интегрированием по частям

Если две функции имеют вид произведения, интегралы находятся методом интегрирования по частям.

∫f(x)g(x) dx = f(x)∫ g(x) dx — ∫ (f'(x) ∫g(x) dx) dx.

Нахождение интегралов путем интегрирования дробей

Интегрирование рациональных алгебраических функций, числитель и знаменатель которых содержат положительные целые степени x с постоянными коэффициентами, осуществляется путем их разложения на частные дроби.

Чтобы найти ∫ f(x)/g(x) dx, разложите эту неправильную рациональную функцию в правильную рациональную функцию и затем проинтегрируйте.

∫f(x)/g(x) dx = ∫ p(x)/q(x) + ∫ r(x)/s(x), где g(x) = a(x) . с(х)

Приложения интегрального исчисления

Используя интегрирование, мы можем найти расстояние, зная скорость. Определенные интегралы представляют собой мощный инструмент для нахождения площади под простыми кривыми, площади, ограниченной кривой и линией, площади между двумя кривыми, объема твердых тел. Задачи о перемещении и движении также находят свое применение интегралов. Площадь области, заключенной между двумя кривыми y = f(x) и y = g(x) и линиями x =a, x =b, равна 92)dx\)

= x ² /2- x ³ /3

= 1/2-1/3

= 1/6 кв.

Важные примечания

Примитивное значение функции, найденное в процессе интегрирования, называется интегралом.
Интеграл — это математический объект, который можно интерпретировать как площадь или обобщение площади.
При интегрировании полиномиальной функции степень интеграла увеличивается на 1.

☛ Также проверьте:

Интеграция формулы УФ
Формула определенного интеграла

Часто задаваемые вопросы по интегральному исчислению

Что такое интегралы?

Интегралы — это значения функции, найденные в процессе интегрирования. Интеграл определяется как площадь области под кривой, представленной в виде функции y = f(x).

Как называется символ интеграла?

Целочисленный символ ∫. Это означает, что она ограничена пределом от низшего к высшему и что интегралы представляют собой площадь кривой под графиком функции.

Какие существуют типы интегралов?

Два типа интегралов: определенный интеграл и неопределенный интеграл. Определенные интегралы ограничены пределами. Неопределенные интегралы не привязаны к ранее существовавшим значениям.

Может ли интеграл иметь два ответа?

Да, неопределенный интеграл может иметь бесконечные ответы в зависимости от значения постоянного члена; а определенный интеграл будет постоянной величиной.

Для чего используется двойной интеграл?

Двойной интеграл используется для вычисления площадей областей, нахождения объемов данной поверхности, а также среднего значения любой заданной функции в плоской области.

Как найти интегралы?

Нахождение интегралов — это операция, обратная нахождению производных. Некоторые интегралы запоминаются как формулы. Например, ∫ x ⁿ = x ⁿ⁺¹ / (n+1) + C. Таким образом, x ⁶ = x ⁶⁺¹ / 6+1 = x ⁷ / 7 + C. Некоторые интегралы используют методы интегрирования по частям, интегрирования по неполным дробям, метода подстановки и т.д.

Как использовать интегралы с помощью тригонометрии?

Используйте тригонометрические тождества и упростите функцию до интегрируемой функции, а затем примените формулы и примените процедуры интегрирования, чтобы найти интегралы с помощью тригонометрии.

Что такое интеграл от sin x?

Интеграл от синуса x равен -cos x + C. ∫ sin x dX = -cos x + C.

Для чего используется интегральное исчисление?

Мы используем определенные интегралы, чтобы найти площадь под кривой или между кривыми, которые определяются функциями, мы находим их неопределенные интегралы, используя формулы и методы, а затем находим их разность интегралов, применяя пределы. Мы используем определенные интегралы для вычисления объемов трехмерных тел. Зная скорость, мы можем найти расстояние, так как расстояние является интегралом скорости.

Что такое интеграл? + Пример

В математике мы говорим о двух типах интегралов. Определенные интегралы и неопределенные интегралы .

Как правило, интеграл присваивает числа функциям таким образом, что они могут описывать перемещение, площадь, объем и даже вероятность.

Определенные интегралы

Этот тип интеграла относится к числовым значениям. Он используется в чистой математике, прикладной математике, статистике, естественных науках и многом другом. Однако самое основное понятие определенного интеграла описывает 9b f(x)»d»x#, где

#алмаз f «называется подынтегральной функцией»#
#ромб a и b «являются нижней и верхней границами»#
#ромб x «является фиктивной переменной»#

Вам может быть интересно, что означает #»d»x#. Формально это ничего не значит, а скорее говорит вам, по какой переменной вы дифференцируете, или, в нашем случае, сообщает вам переменную интегрирования.

Когда мы говорим площадь, определяемая функцией #f# с осью x, мы имеем в виду 9n# от #0# до #tau#; Ну, это называется правилом силы. Существует много разных формул для интегралов, которые я не буду рассматривать в этом ответе. Это просто очень общее представление о том, что такое интегралы.

Неопределенные интегралы

Они представлены в виде интегралов с границами. Пусть #I# — неопределенный интеграл от функции #f#.

#I=int f(x)»d»x#

Неопределенные интегралы можно рассматривать как обобщения определенных.

Вместо того, чтобы определяться площадями, объемами или чем-то еще, неопределенные интегралы соотносятся с производными. Неопределенный интеграл функции #f# также называется первообразной и часто обозначается как #F(x)#.

Основная теорема исчисления устраняет разрыв между функцией, ее производной и неопределенным интегралом. По сути, он говорит, что #F# определяется как функция, которая при дифференцировании дает #f#:

#F'(x) = f(x)# 9b f(x) «d»x = F(b)-F(a)#

Надеюсь, этот ответ не был слишком пугающим.

Интегральное значение, определение и функция

Исследуйте интегралы

О боже. Интегралы . Исчисление было недостаточно сложным… теперь у нас есть и эти большие закрученные линии?!

Если это то, что сейчас крутится в вашей голове, вы можете остановить эти мысли на ходу. Интегральное исчисление на самом деле не так страшно, как кажется!

Как только мы углубимся в это, вы можете даже подумать, что интегралы — осмелимся сказать — круто ?

Есть только один способ узнать! Давайте начнем.

Что такое интеграл?

В зависимости от того, на каком этапе обучения вы находитесь, интеграл может представлять собой ответ на несколько разных вопросов. По своей сути в исчислении интегрирование помогает найти антипроизводную функции; другими словами, нахождение интеграла является обратным нахождением производной.

Работая над уроками математического анализа, вы увидите, что существуют различные типы интегралов, в том числе:

Неопределенные интегралы
Определенные интегралы
Несобственные интегралы

Процесс нахождения интеграла называется «интегрированием», поэтому интеграл также можно рассматривать как результат интегрирования. Существует несколько способов вычисления интегралов, таких как метод подстановки или частичное интегрирование.

Поскольку интегрирование является обратной функцией дифференцирования, интегралы легче понять, если вы уже хорошо разбираетесь в производных. Если вам все еще нужна небольшая помощь в сборке деталей, мы можем сначала помочь вам с деривативами!

Определение интеграла

Как мы уже упоминали, существует несколько различных типов интегралов. Это означает, что у нас также будет несколько разных определений.

Вот интегральные определения, которые вам, вероятно, понадобятся (и будут использоваться!) больше всего:

9б f(x)$$

Интегральный тип	Что это?	Как это может выглядеть?
Неопределенный интеграл	Все антипроизводные функции	$${\int f(x) dx = F(x) + C}$$
Несобственный интеграл	$$\text{Если } f \text{ непрерывно на } [a,b\rangle \text{ и разрывно на } b\text{, то интеграл от } f \text{ по } [a,b\ rangle \text{ является неправильным}$$ 9{b}{f(x,y)~dx~dy}$$

Интеграл функции

Поскольку мы сосредоточены на интегральном исчислении, нахождение интеграла функции действительно находится в центре нашего обсуждения. Это основа для всех тех различных типов интегралов и методов, которые мы упоминали ранее.

В зависимости от задачи найти интеграл функции можно несколькими способами:

Подстановка
Частичная интеграция
Интеграция функций абсолютного значения
Интеграция четных или нечетных функций

У вас есть конкретная проблема? Отсканируйте его с помощью приложения Photomath, чтобы узнать, как найти интеграл в этом конкретном сценарии.

Значение интегралов

Мы рассмотрели все определения и предысторию, но что все это на самом деле означает? Опять же, это зависит от контекста задачи, но интеграл может сказать вам:

Площадь под кривой на графике
Область между частью функции и осью $$x$$
Объем воды в ванне в зависимости от расхода воды из крана
Центр масс транспортного средства для точной настройки его функций безопасности
Лучший способ создать 3D-модель

Чем больше вы думаете об этом, тем больше вы начнете видеть вокруг себя все интересные и важные применения интегралов! 9{2}}{2}dx$$

$$a$$ и $$b$$ (или $$-1$$ и $$1$$) — это пределы интегрирования, определяющие интервал, к которому мы ограничены.

В математических терминах мы бы описали определенный интеграл как «интеграл функции $$f(x)$$ по переменной $$x$$ на интервале $$[a, b]$$ ».

Если вы просто посмотрите на все эти математические описания или выражения сразу, это может быть немного ошеломляющим. Разве не легче, когда вы смотрите на каждую часть в отдельности?

Знак интеграла

Эта волнистая, закрученная, изогнутая линия является признаком интеграла, поэтому, когда вы видите ∫ на странице, вы знаете, что имеете дело с интегралом!

Забавный факт: форма знака интеграла на самом деле представляет собой вытянутую букву «S», обозначающую «сумма» (это римская ∫ вместо греческой ∑). «S» для «суммы» основан на идее добавления площади срезов под кривой — чем на большее количество срезов вы разделите всю площадь под кривой, тем более точную сумму вы получите. Интеграл является наиболее точным, потому что «столбцы» срезов становятся бесконечно тонкими. Так круто!

∫

Просто нужно быстро скопировать и вставить сам знак интеграла? Вот: ∫

Вы также можете использовать эти сочетания клавиш!

iOS: [Опция] + [B]
Windows: [Alt] + 8747

Интеграл от dx

В структуре интеграла вы увидите ∫, за которым следует подынтегральная функция, а затем «$$dx$$» в виде точки в конце предложения, например:

$${\int f(x) dx}$$

Этот $$dx$$, известный как дифференциал, говорит нам, что $$x$$ является переменной интегрирования. 2(2x+1)dx$$: 9{2x})dx$$

$$\int\sqrt{2x+6}dx$$

Застряли? Это нормально! Сделайте глубокий вдох и используйте приложение Photomath, чтобы отсканировать проблему, которая доставляет вам неприятности. Мы проведем вас через каждый шаг в удобном для вас темпе и настолько подробно, насколько вам нужно. Никогда не забывайте: вы не одиноки!

Вот как мы решаем первую практическую задачу в приложении:

00:00 / 00:00

FAQ
Каково правило для интегралов?

Существует множество различных правил и свойств для интегралов, в том числе:

Постоянное кратное свойство интегралов	$$\int{(c\times f(x))}dx=c\times \int{f(x)}dx$$
Правило сумм для интегралов	$$\int{(f(x) + g(x))}dx=\int{f(x)}dx + \int{g(x)}dx$$ 9{\ простое число} (t) dt = \ int {f (x)} dx $ $
Сборка по частям	$$\int{u}dv=uv-\int{v}du$$

Какие бывают два типа интегралов?

Существует несколько различных видов интегралов, но два основных типа — это определенные и неопределенные интегралы.

Для чего используются интегралы?

Интегралы используются для нахождения антипроизводной или обратной производной. Это открывает множество различных частей информации, таких как площадь, объем, скорость и многое другое.

Есть домашнее задание по математике?

Зайдите в приложение Photomath, чтобы быстро найти пошаговые решения всех ваших математических задач.

6: Приложения интеграции — Mathematics LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2518

Гилберт Странг и Эдвин «Джед» Герман
OpenStax

В этой главе мы используем определенные интегралы для расчета силы, действующей на плотину, когда водохранилище заполнено, и исследуем, как изменение уровня воды влияет на эту силу. Гидростатическая сила — лишь одно из многих применений определенных интегралов, которые мы исследуем в этой главе. От геометрических приложений, таких как площадь поверхности и объем, до физических приложений, таких как масса и работа, до моделей роста и распада, определенные интегралы являются мощным инструментом, помогающим нам понять и смоделировать мир вокруг нас.

6.0: Прелюдия к приложениям интеграции
Плотина Гувера — чудо инженерной мысли. Когда озеро Мид, водохранилище за плотиной, заполнено, плотина выдерживает большую нагрузку. Однако уровень воды в озере значительно колеблется в результате засух и различных потребностей в воде.
6.1: Площади между кривыми
Точно так же, как определенные интегралы можно использовать для нахождения площади под кривой, их также можно использовать для нахождения площади между двумя кривыми. Чтобы найти площадь между двумя кривыми, заданными функциями, проинтегрируйте разность функций. Если графики функций пересекаются или область сложная, используйте абсолютное значение разности функций. В этом случае может потребоваться вычисление двух или более интегралов.
- 6.1E: Упражнения к разделу 6.1
6.2: Определение объемов путем разрезания
В этом разделе мы используем определенные интегралы для нахождения объемов трехмерных твердых тел. Мы рассматриваем три подхода — срезы, диски и шайбы — для нахождения этих объемов в зависимости от характеристик твердого тела.
- 6.2E: Упражнения к разделу 6.2
6.3: Объемы вращения — цилиндрические оболочки
В этом разделе мы рассмотрим метод цилиндрических оболочек, последний метод нахождения объема тела вращения. Мы можем использовать этот метод для тех же типов твердых тел, что и метод диска или метод шайбы; однако при использовании метода диска и шайбы мы интегрируем по оси координат, параллельной оси вращения. При методе цилиндрических оболочек интегрируем по оси координат, перпендикулярной оси вращения.
- 6.3E: Упражнения к разделу 6.3
6.4: Длина дуги кривой и площадь поверхности
Длину дуги кривой можно рассчитать с помощью определенного интеграла. Длина дуги сначала аппроксимируется с использованием отрезков прямой, что приводит к сумме Римана. Принятие предела дает нам формулу определенного интеграла. Тот же процесс можно применить к функциям от y. Понятия, используемые для расчета длины дуги, можно обобщить, чтобы найти площадь поверхности вращения. Интегралы, полученные по формулам длины дуги и площади поверхности, часто трудно оценить.
- 6.4E: Упражнения к разделу 6.4
6.5: Физические приложения интеграции
В этом разделе мы рассмотрим некоторые физические приложения интеграции. Несколько физических приложений определенного интеграла распространены в технике и физике. Определенные интегралы можно использовать для определения массы объекта, если известна его функция плотности. Работу также можно рассчитать путем интегрирования силовой функции или при противодействии силе тяжести, как в задаче о насосе. Определенные интегралы также можно использовать для расчета силы, действующей на объект, погруженный в жидкость.
- 6.5E: Упражнения к разделу 6.5
6.6: Моменты и центры масс
В этом разделе мы рассматриваем центры масс (также называемые центроидами) и центроиды при определенных условиях. Основная идея центра масс — это понятие точки баланса. Многие из нас видели исполнителей, которые крутят тарелки на концах палочек. Артисты стараются, чтобы несколько из них вращались, не позволяя ни одному из них упасть. Математически эта точка наилучшего восприятия называется центром масс тарелки. 96.6E: Упражнения к разделу 6.6 Тем не менее, мы упустили некоторые ключевые детали в предыдущих обсуждениях. Например, мы не изучали, как обращаться с экспоненциальными функциями с иррациональными показателями. Определение числа e — еще одна область, в которой предыдущее развитие было несколько неполным. Теперь у нас есть инструменты для работы с этими понятиями более математически строгим способом, и мы делаем это в этом разделе.
- 6.7E: Упражнения к разделу 6.7
6.8: Экспоненциальный рост и спад
Одно из наиболее распространенных применений экспоненциальных функций связано с моделями роста и убывания. Экспоненциальный рост и затухание проявляются во множестве естественных приложений. От роста населения и постоянного начисления процентов до радиоактивного распада и закона охлаждения Ньютона — экспоненциальные функции встречаются в природе повсеместно. В этом разделе мы исследуем экспоненциальный рост и затухание в контексте некоторых из этих приложений.
- 6.8E: Упражнения к разделу 6. 8
6.9: Вычисление гиперболических функций
Мы познакомились с некоторыми их основными свойствами гиперболических функций в разделе «Введение в функции и график». В этом разделе мы рассмотрим формулы дифференцирования и интегрирования для гиперболических функций и их обратных функций.
- 6.9E: Упражнения для раздела 6.9
6.10: Обзорные упражнения главы 6

Миниатюра: область между двумя функциями.

Эта страница под названием 6: Applications of Integration распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Странгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Глава
Автор
ОпенСтакс
Лицензия
CC BY-NC-SA
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать страницу Содержание
нет
Теги
1. автор @ Эдвин «Джед» Герман
2. автор@Гилберт Странг
3. источник@https://openstax. org/details/books/calculus-volume-1

Функции, определяемые интегралами, часть 1

Функции, определяемые интегралами

Часть 1: Функция

F(x) и его производная

Многие полезные функции естественным образом описываются интегрированием известных функций. Иногда эти недавно определенные функции оказываются функциями, которые мы уже знаем в каком-то другом контексте, а иногда они действительно новые. В этой части мы определяем функцию F(x) путем интегрирования заданной непрерывной функции f(x) , а затем изучаем производную новой функции F(x) .

Для нашего первоначального примера мы начинаем с функции

график которого представляет собой четверть окружности радиуса 5 :

Мы определяем новую функцию F(x) , установив ее значение в виде положительного числа x как интеграл от f от 0 до x :

Обратите внимание, что, поскольку x используется для представления независимой переменной для функции F , другая переменная t используется для переменной интегрирования.

Что означает это определение функции? Поскольку определенный интеграл положительной функции f представляет собой площадь под графиком f , мы можем думать о F(x) как о площади под графиком f(t) между t = 0 и t = x . Проиллюстрируем это на следующем рисунке.

Посмотреть построение функции F динамически, нажмите на одну из следующих анимаций. Но сначала прочтите эти инструкции.

Каждая анимация появляется в новом окне браузера. Чтобы вернуться на эту страницу, закройте окно анимации.
Чтобы запустить анимацию, щелкните в любом месте окна. Вы можете делать это столько раз, сколько захотите.
Если у вашей мыши есть правая кнопка, щелчок правой кнопкой мыши вызовет параметры для приостановки анимации, покадрового перемещения и т. д.
Если ваш компьютер подключен к Интернету напрямую, выберите самую плавную анимацию. Если вы используете коммутируемый доступ, обратите внимание на размеры файлов — время загрузки пропорционально размеру файла.
Горизонтальные масштабы графиков f и F одинаковы: от x = 0 до x = 5 . Но обратите внимание, что вертикальные масштабы разные.

Варианты анимации F(x): Наименее гладкий (93K), более гладкий (316K), самый гладкий (762K).

Используйте определение F(x) в своем рабочем листе, чтобы построить собственный график F(x) . Изучите график и объясните, почему он имеет именно такую форму.
Составьте таблицу значений F(x) для x в диапазоне от 0 до 5 . (Не ограничивайтесь только целочисленными значениями x .) Убедитесь, что полученные значения соответствуют вашему графику F(x) .

Обратимся теперь сначала к оценке, а затем к вычислению производной Ф(х) . В целях оценки мы рассчитаем коэффициенты разности

с разницей = 0,001 . (Подойдет любое разумно малое значение — вы можете поэкспериментировать с другими значениями в своем рабочем листе.)

Вычислите приближенную производную F (разностное частное) и соответствующее значение f для каждого из Значения x , указанные на вашем листе. Заполняйте таблицу в своем рабочем листе по ходу дела.

Ваши результаты на шаге 3 должны убедительно свидетельствовать о связи между F'(x) и f(x) . Однако горстки примерно равных пар чисел недостаточно для установления равенства. Теперь мы рассмотрим, почему это кажущееся равенство на самом деле может быть истинным .

Сначала мы рассмотрим изменение в значениях функции F , когда x увеличивается на:

по определению F и свойство определенных интегралов. Таким образом, изменение F представляет собой площадь под графиком f между x и x + . [Примечание: мы неявно используем тот факт, что f(x) неотрицательно, когда мы ссылаемся на площадь. Однако вывод остается верным для любой непрерывной функции, если использовать понятие «площадь со знаком».]

О каком свойстве интегралов говорится в предыдущем абзаце?
Опишите в геометрических терминах, почему изменение F составляет указанную площадь. [Подсказка: интерпретируйте определение F с точки зрения площади. ]

Мы иллюстрируем интерпретацию площади изменения F на следующей паре рисунков, используя x = 3 и = 0,001 . На левом рисунке показана область под графиком f между 3 и 3,001 , заштрихованная зеленым цветом. Поскольку интервал настолько мал, заштрихованная область больше похожа на линию. На правом рисунке мы оставили прежним масштаб по вертикали, но значительно расширили масштаб по горизонтали. Опять площадь под графиком f между 3 и 3.001 затенен зеленым цветом.

Почему график f на [3, 3.001] кажется горизонтальной линией?
Дайте быструю оценку заштрихованной области.
Для произвольного x и произвольного (маленького) дайте быструю оценку площади под графиком f на интервале [x, x + ] .
Объясните оценку разностного отношения:
Обратите внимание, что ваша оценка разностного отношения
- улучшает по мере уменьшения, а
- является независимым от .
Объясните следующий расчет мгновенной скорости изменения F :
Для нашего конкретного примера
используйте вспомогательное приложение, чтобы подтвердить формулу на шаге 10. То есть запросите у системы компьютерной алгебры символьную формулу для F(x) . Затем запросите производную этой формулы и подтвердите, что результат эквивалентен формуле для f(x) .
(необязательно) Объясните, почему F является решением задачи о начальных значениях

модули на math.

duke.edu

Интегрирование и взятие интеграла

Интегрирование — это алгебраический метод нахождения интеграла функции в любой точке графика.
Нахождение интеграла
функции по х означает нахождение площади по оси х по кривой.
Интеграл обычно называют антипроизводной
, потому что интегрирование — это процесс, обратный дифференцированию.
Фундаментальная теорема исчисления показывает, что антидифференцирование — это то же самое, что и интегрирование.

Физическое понятие интеграла аналогично производной.
Для производной мотивация состояла в том, чтобы найти скорость в любой момент времени
при заданном положении объекта. Если мы знаем скорость объекта в определенное время, интеграл даст нам положение объекта в это время.
Точно так же, как производная дает мгновенную скорость изменения, интеграл
дает общее расстояние в любой момент времени.

Интеграл получается не только при попытке найти процесс, обратный взятию производной
, но и при попытке решить область проблема , а также. Точно так же, как процесс
дифференцирования используется для нахождения наклона в любой точке графика, процесс
интегрирования находит площадь кривой до любой точки графика.

Интеграция Римана

До того, как была разработана интеграция, мы могли только приблизить площадь функций
, разделив пространство на прямоугольники и добавив площади.

Мы можем приблизить площадь к оси x, увеличив количество прямоугольников
под кривой. Площадь этих прямоугольников была рассчитана путем умножения длины на
ширины, или х умноженных на изменение х . После вычисления площади сумма 90 394 прямоугольников будет аппроксимировать площадь. Чем больше прямоугольников, тем лучше будет аппроксимация 90 394.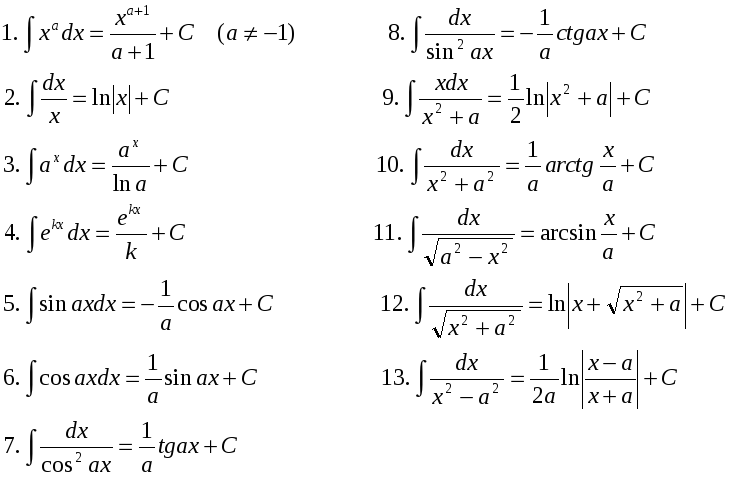 Это формула для суммы Римана,
, где i — любое начальное значение x, а n — количество прямоугольников:

Это был утомительный процесс и никогда не давал точной площади кривой. К счастью,
Ньютон и Лейбниц разработали метод интегрирования, который позволил им найти
точную площадь кривой в любой точке.

Подобно тому, как процесс дифференцирования находит функцию наклона
по мере того, как расстояние между двумя точками становится бесконечно малым, процесс интегрирования
находит площадь под кривой как количество разбиений прямоугольников под
кривая становится бесконечно большой.

Определение интеграла от f(x) из [a,b]

Интеграл функции x от a до b представляет собой сумму прямоугольников кривой
на каждом интервале изменения x по мере того, как число прямоугольников стремится к бесконечности.

Обозначения в левой части обозначают определенный интеграл от f(x)
от а до б. Когда мы вычисляем интеграл из интервала [a,b], мы подставляем a к
интегральной функции и вычитаем его из b в интегральной функции:

где F обозначает интегрированную функцию. Это точно вычисляет площадь под
любой непрерывной функцией.

Общее правило мощности для интеграции

Для проведения интегрирования важно знать общее правило мощности. это
полная противоположность степенному правилу дифференцирования.

Давайте посмотрим на общую функцию

Когда мы берем интеграл от функции, мы сначала прибавляем 1 к показателю степени, а затем
делим член на сумму показателя степени и 1.

После того, как мы сделали это с каждым термином, мы добавляем константу в конце. Напомним, что
, взяв производную от константы, уберет ее, поэтому взятие интеграла от
функция даст нам константу. Мы помечаем его C, потому что константа неизвестна
— это может быть любое число! Поскольку у нас может быть бесконечно много возможных функций
для интеграла, мы называем его неопределенным интегралом.

Сделаем пример.

Найдите интеграл от

Начнем с первого термина. Мы смотрим на показатель степени 2 и увеличиваем его на 1,
, затем делим член на полученный показатель степени 3.

Затем мы смотрим на следующий член и делаем то же самое. Поскольку его показатель степени равен
1, результирующий показатель степени будет равен 2, поэтому мы делим весь член на 2.

Последний член имеет значение x, но мы его просто не видим. Мы можем представить последний член
как -3x ⁰ . Это эквивалентно -3(1). Если мы используем степенное правило интегрирования,
, мы добавляем 1 к показателю степени, чтобы возвести его в первую степень, а затем делим
срок по 1.

Все, что нам нужно сделать, это добавить константу в конце, и все готово.

Эта формула степени для интегрирования работает для всех значений n , кроме для n = -1 (поскольку
нельзя делить на 0). Мы можем взять обратную производную от логарифмической функции
, чтобы решить эти случаи.

В общем

Итоги интегрирования

Мы должны понимать

Определенный интеграл как предел сумм Римана
Определенный интеграл как изменение количества над интегралом
как интегралы представляются графически, численно и аналитически
как они интерпретируются как положение объекта при заданной скорости.
No related posts.

Интеграл — Умскул Учебник

Методы вычисления интегралов, формулы и примеры решений

1. Метод непосредственного интегрирования

4. Интегрирование по частям

Чем отличается определенный интеграл от неопределенного

Что такое интеграл

Что такое определенный и неопределенный интегралы?

Заключение

Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница / Хабр

0. Предисловие

1. Предпосылки возникновения интегрирования

2. Геометрический и аналитико-алгебраический смысл интегрирования

3. Интуитивные способы отыскания значения интеграла

4. Отыскание значения интеграла через отыскание первообразной

Неопределенный и определенный интегралы.

Интегральное исчисление — формулы, методы, примеры

Что такое интегральное исчисление?

Определение интеграла

Типы интегралов

Неопределенные интегралы

Определенные интегралы

Свойства интегрального исчисления

Интегральные формулы

Методы нахождения интегралов

Нахождение интегралов методом подстановки

Нахождение интегралов интегрированием по частям

Нахождение интегралов путем интегрирования дробей

Приложения интегрального исчисления

Часто задаваемые вопросы по интегральному исчислению

Что такое интегралы?

Как называется символ интеграла?

Какие существуют типы интегралов?

Может ли интеграл иметь два ответа?

Для чего используется двойной интеграл?

Как найти интегралы?

Как использовать интегралы с помощью тригонометрии?

Что такое интеграл от sin x?

Для чего используется интегральное исчисление?

Что такое интеграл? + Пример

Интегральное значение, определение и функция

Что такое интеграл?

Определение интеграла

Интеграл функции

Значение интегралов

Знак интеграла

∫

Интеграл от dx

Есть домашнее задание по математике?

6: Приложения интеграции — Mathematics LibreTexts

Функции, определяемые интегралами, часть 1

Функции, определяемые интегралами

Часть 1: Функция

Интегрирование и взятие интеграла

Интеграция Римана

Общее правило мощности для интеграции

Итоги интегрирования

Добавить комментарий Отменить ответ