Как решать параболу: Парабола, квадратичная функция. Как решаются квадратные уравнения?

2+bx+c=0\)

 

4) Найти точку пересечения с осью Оу, решив уравнение y=a*0+b*0+c

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Елизавета Бимбетовна Тулемисова

Репетитор по математике

Стаж (лет)

Образование:

Астраханский государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Алина Владимировна Ваулина

Репетитор по математике

Стаж (лет)

Образование:

Уральский федеральный университет им. Б.Н.Ельцина

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Татьяна Михайловна Столят

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный педагогический университет им. М. Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Физика
• Химия
• Русский язык
• Английский язык
• Обществознание
• История России
• Биология
• География
• Информатика

Специализации

• Репетитор по геометрии
• Подготовка к ЕГЭ по математике (профильный уровень)
• Подготовка к олимпиадам по химии
• Подготовка к олимпиадам по физике
• Подготовка к ЕГЭ по русскому языку
• Подготовка к ОГЭ по русскому языку
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Репетитор для подготовки к ВПР по русскому языку
• Репетитор по обществознанию для подготовки к ОГЭ
• Программирование Pascal

Похожие статьи

• Теорема Виета
• Периметр ромба
• Вычитание пересекая десятки
• Как перевести центнеры в килограммы?
• ЕГЭ по математике, профильный уровень. Рациональные уравнения
• Геометрическая прогрессия
• Интеграл с переменным верхним пределом
• Как животные помогали людям во время ВОВ

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Девятое задание тестовой части ЕГЭ по профильной математике

Автор: Ерохин Алексей Дмитриевич

Научный руководитель: Михеенко Дарья Сергеевна

Рубрика: Математика: алгебра и начала анализа, геометрия

Опубликовано в Юный учёный №4 (56) апрель 2022 г.

Дата публикации: 04.03.2022 2022-03-04

Статья просмотрена: 79 раз

Скачать электронную версию

Библиографическое описание:

Ерохин, А. Д. Девятое задание тестовой части ЕГЭ по профильной математике / А. Д. Ерохин, Д. С. Михеенко. — Текст : непосредственный // Юный ученый. — 2022. — № 4 (56). — С. 75-77. — URL: https://moluch.ru/young/archive/56/2845/ (дата обращения: 28.11.2022).



Статья посвящена новому заданию тестовой части ЕГЭ по профильной математике. В статье указаны несколько способов решения этого задания. Содержание статьи будет полезным преподавателям и студентам.

Ключевые слова : задача, парабола, решение, дополнительная система координат, способ решения, уравнение параболы.

В 2022 году в демоверсии ЕГЭ была представлена новая задача под номером девять. Она не сложна, но при этом может отнять немало времени на решение. Рассмотрим несколько методов решение этой задачи и найти самый быстрый из них.

Условие задачи. На рисунке изображён график функции вид где числа a, b и c — целые. Найдите значение .

Как же это решать? Ну, если пойти самым очевидным и простым методом, то внимательно посмотрев на график, необходимо выбрать три любые целочисленные точки. Допустим это будут точки: . Теперь просто подставим значения и в исходное уравнение функции. Получаем систему из трёх линейных уравнений:

И теперь задача сводится к нахождению a, b и c. Есть три уравнения и три неизвестные. Начнём с ними работать. Вычтем последнее уравнение из первых двух. Тогда получаем:

Заметим, что верхнее уравнение можно сократить на 2. В итоге у нас получается:

Дальше остаётся только вычесть из верхнего уравнения нижнее, после чего получаем значение a:

Ну и теперь подставляем это значение в любое из уравнений получаем что:

Теперь, зная все коэффициенты функции и понимая, что изначальная функция выглядит так, запишем уравнение исходной параболы:

Зная это, уже вполне окончательно можно решить задачу:

Данный способ решения самый простой и не вызывает трудностей в решении.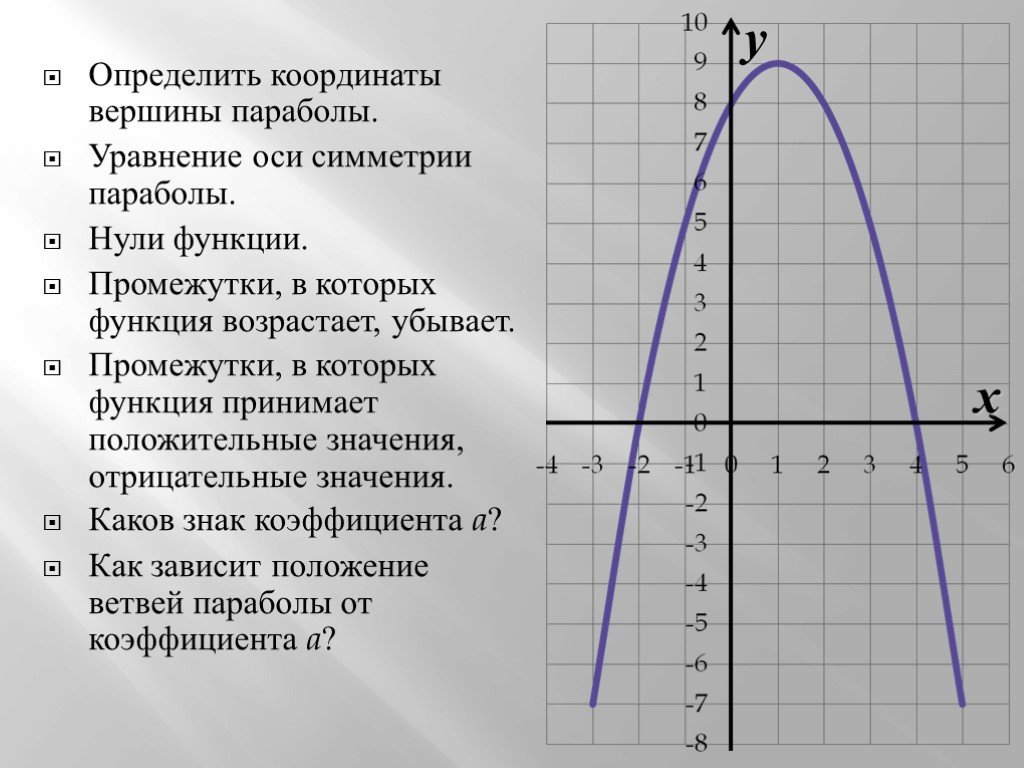 Но на самом деле, если чуть-чуть подумать, можно сильно сократить рассуждения, даже в этом решении. Вспомним как устроена парабола около её вершины. Построим дополнительную систему координат, началом отсчёта которой будет являться вершина этой параболы. Тогда можно заметить, что это парабола вида но с небольшим сдвигом. Понимая, что при движении параболы её старший коэффициент не меняется, то получаем значение . И всё решение по -итогу сводится к решению системы линейных уравнений, но уже с двумя неизвестными. Решение будет схожим, но только быстрее, ведь пропускается одно из преобразований.

Вторым шагом, способным упростить решение, является понимание, что вершина любой параболы находится в точке :

Уже зная, что получим:

Но, посмотрев на график, становится понятно, что . Тогда:

;

А зная значение , для решения нам потребуется всего лишь одно уравнение, подставив полученные значения в которое, находим значение .

Эти методы решения связаны с понимаем того, как ведёт себя парабола при её движении по координатной плоскости.

Но существует ещё более быстрый способ решения. Для этого необходимо знать, как ведёт себя уравнение параболы при её сдвиге. Если изначально была парабола , то чтобы получит график параболы, показанный на рисунке, эту параболы необходимо сдвинуть на 4 влево и на 3 вниз. То есть уравнение необходимой нам параболы принимает форму:

Получилось, что при понимании того, как меняется уравнение параболы при её движении, можно без дополнительных точек решить данную задачу:

.

Но существует, самый быстрый способ решения данной задачи. Если вспомнить, что уже есть дополнительная система координат, понимаем, что парабола в этой новой системе будет вести себя также, как и парабола вида в изначальной. Если вернуться к условию и понять, что спрашивают, какое значение примет функция при , то, рассмотрев эту задачу в новой системе координат, то понимаем, что на самом деле необходимо найти значение функции при , ведь график смещён на 4 влево. Но необходимо помнить, что парабола также смещена ещё и на 3 вниз, следовательно задача обретает вид:

Это решение будет самым быстрым, но не самым лёгким. Первый способ решения подходит для любой новой задачи под номером 9, но чтобы решать её быстрее, необходимо глубже понимать геометрию разных графиков функций. Поэтому данная задача и хороша, ведь способ и скорость её решения зависит исключительно от набора знаний ученика, и только от него зависит, сколько времени он на неё потратит.

задача, решение, парабола, дополнительная система координат, способ решения, уравнение параболы

задача, парабола, решение, дополнительная система координат, способ решения, уравнение параболы

• Как издать спецвыпуск?
• Правила оформления статей
• Оплата и скидки

How To Find the Vertex of a Parabola

How To Find the Vertex of a Parabola

Andrew Lee

February 25, 2021

Online Tutoring

,

Geometry

,

Mathematics

To найти вершину параболы, вам сначала нужно знать, как построить квадратные уравнения.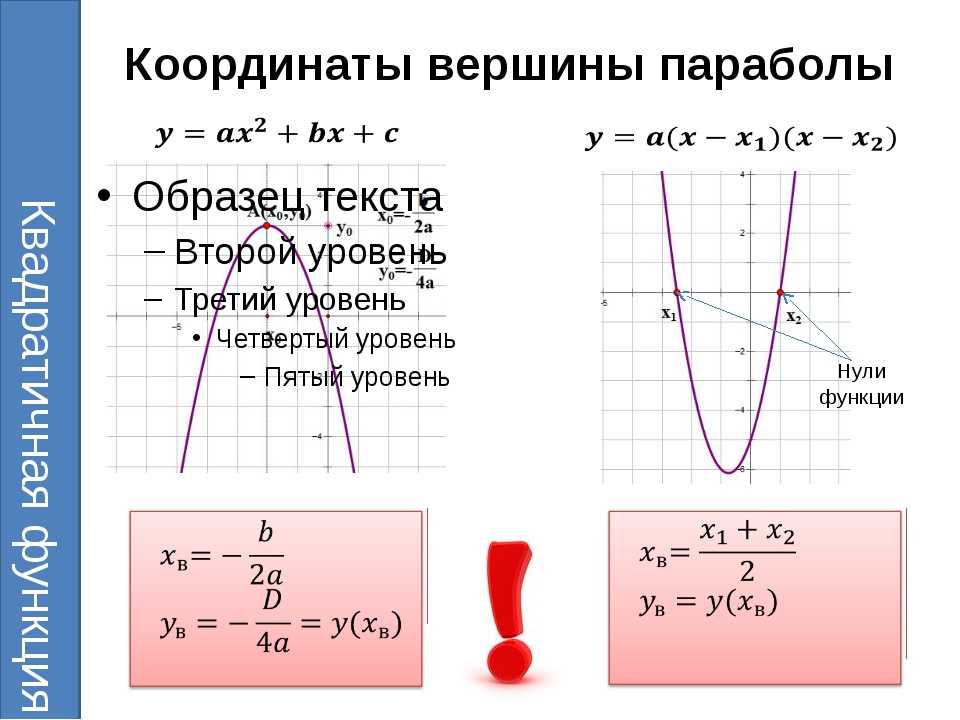 При их построении помните, что любую квадратичную функцию можно представить в стандартной форме (подробнее об этом позже). Это позволяет вам найти старший коэффициент и решить для x-перехватов. Точки пересечения x и y — это точки на графике, где парабола пересекает ось x или ось y.

Представление квадратичной функции в стандартной форме также позволит вам найти ось симметрии, линию, которая проходит через вершину и делит параболу пополам. Затем вы можете найти координату x и координату y вершины, которая является самой высокой или самой низкой точкой на параболе.

Определение параболы

Парабола — это набор точек, находящихся на одинаковом расстоянии от фокуса (фиксированной точки) и директрисы (фиксированной линии). Это форма «u», которая образуется, когда кто-то рисует квадратное уравнение или квадратичную функцию.

В зависимости от коэффициентов исходного уравнения парабола открывается вправо, влево, вверх или вниз.

Ось симметрии параболы

Прежде чем найти вершину параболы, рассмотрим ось симметрии.

Помните, в параболе каждая точка представляет собой x и y , которые решают квадратичную функцию.

Ось симметрии — это вертикальная линия, проходящая через вершину параболы. Вершина параболы – это точка максимума или минимума на графике квадратичной функции.

Помните, что любую квадратичную функцию можно записать в стандартной форме.

Уравнение для оси симметрии параболы может быть выражено как:

Нахождение вершины параболы

Чтобы найти координаты вершины параболы, вы должны сначала использовать уравнение для нахождения оси симметрии. Затем подставьте найденное значение x обратно в исходный вопрос, чтобы получить значение y.

Найдем ось симметрии, когда a = 1 и b = -4.

Теперь мы знаем, что x = 2. Теперь подставим это обратно в исходное квадратное уравнение.

Решение дает y = -1. Теперь мы знаем, что вершина параболы имеет координату (2, -1). Нахождение вершины параболы не может быть проще, если вы знаете эти шаги!

Найти вершину параболы за короткое время

Чтобы найти вершину параболы, сначала нужно найти x (или y , если ваша парабола расположена сбоку) через формулу для оси симметрии. Затем вы будете использовать это значение для решения х (или х , если ваша парабола выходит в сторону) с помощью квадратного уравнения. Эти две координаты являются вершиной вашей параболы.

Дополнительная помощь по домашнему заданию по математике

• Как использовать тест ведущего коэффициента для построения графика конечного поведения
• Однозначные функции: правило исключительной геометрии
• Как освоить квадратичную регрессию
• Как найти ось симметрии параболы

Параболы с вершинами не в начале координат

Результаты обучения

• Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки фокального диаметра, используя уравнение параболы в стандартной форме.
• Найдите уравнение объекта параболической формы с заданными размерами.

Как и другие графики, с которыми мы работали, график параболы можно транслировать. Если парабола сдвинута [latex]h[/latex] единиц по горизонтали и [latex]k[/latex] единиц по вертикали, вершина будет [latex]\left(h,k\right)[/latex]. Этот перевод приводит к стандартной форме уравнения, которое мы видели ранее, с заменой [латекс]x[/латекс] на [латекс]\left(x-h\right)[/латекс] и [латекс]y[/латекс] на [ латекс]\влево(у-к\вправо)[/латекс]. 9{2}=4p\left(yk\right)[/latex] для парабол, ось симметрии которых параллельна оси y . Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.

Общее примечание: стандартные формы парабол с вершиной (

h , k )

В таблице приведены стандартные характеристики парабол с вершиной в точке [латекс]\влево(ч,к\вправо)[ /латекс].

9{2}=4p\влево(yk\вправо)[/латекс]

Ось симметрии

[латекс]\влево(ч,\текст{}k+p\вправо)[/латекс]

[латекс]у=к-п[/латекс]

[латекс]\влево(ч\пм 2п,\текст{ }к+п\вправо)[/латекс]

(a) Когда [latex]p>0[/latex], парабола открывается вправо. (b) Когда [латекс]p<0[/латекс], парабола открывается влево. (c) Когда [латекс]p>0[/латекс], парабола раскрывается. (d) Когда [латекс]p<0[/латекс], парабола раскрывается вниз.

Как: Имея уравнение стандартной формы для параболы с центром в точке ( 9{2}=4p\влево(x-h\вправо)[/латекс], тогда:

• используйте данное уравнение для определения [латекс]h[/латекс] и [латекс]k[/латекс] для вершины, [латекс]\влево(ч,к\вправо)[/латекс]
• использовать значение [латекс]k[/латекс] для определения оси симметрии, [латекс]у=к[/латекс]
• установите [латекс]4p[/латекс] равным коэффициенту [латекс]\левый(х-ч\правый)[/латекс] в данном уравнении для решения для [латекс]p[/латекс]. Если [latex]p>0[/latex], парабола открывается вправо. Если [latex]p<0[/latex], парабола открывается влево. 9{2}=4p\влево(y-k\вправо)[/латекс], тогда:
  • используйте данное уравнение для определения [латекс]h[/латекс] и [латекс]k[/латекс] для вершины, [латекс]\влево(ч,к\вправо)[/латекс]
  • использовать значение [latex]h[/latex] для определения оси симметрии, [latex]x=h[/latex]
  • установить [латекс]4p[/латекс] равным коэффициенту [латекс]\левый(у-к\правый)[/латекс] в данном уравнении для решения для [латекс]p[/латекс]. Если [latex]p>0[/latex], парабола раскрывается. Если [latex]p<0[/latex], парабола направлена ​​вниз.
  • используйте [latex]h,k[/latex] и [latex]p[/latex], чтобы найти координаты фокуса, [latex]\left(h,\text{ }k+p\right)[/ латекс]
  • используйте [latex]k[/latex] и [latex]p[/latex], чтобы найти уравнение директрисы, [latex]y=k-p[/latex]
  • используйте [латекс]h,k[/латекс] и [латекс]p[/латекс], чтобы найти конечные точки фокусного диаметра, [латекс]\left(h\pm 2p,\text{ }k+p\ справа)[/латекс]
• Нанесите вершину, ось симметрии, фокус, директрису и фокальный диаметр и нарисуйте плавную кривую, чтобы сформировать параболу. 9{2}=-20\влево(у — 3\вправо)[/латекс]. Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки фокального диаметра.

  Показать решение

  Решение прикладных задач, связанных с параболами

  Как мы упоминали в начале раздела, параболы используются для проектирования многих объектов, которые мы используем каждый день, таких как телескопы, подвесные мосты, микрофоны и радиолокационное оборудование. Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света параллельны параболе оси симметрии направлены в сторону любой поверхности зеркала, свет отражается прямо в фокус. Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.

  Отражающее свойство парабол

  Параболические зеркала обладают способностью фокусировать солнечную энергию в одной точке, повышая температуру на сотни градусов за считанные секунды. Таким образом, параболические зеркала используются во многих недорогих и энергоэффективных солнечных продуктах, таких как солнечные плиты, солнечные обогреватели и даже разжигатели огня, предназначенные для путешествий.

  Пример: Решение прикладных задач, связанных с параболами

  Поперечное сечение конструкции переносного солнечного зажигалки. Солнечные лучи отражаются от параболического зеркала к объекту, прикрепленному к воспламенителю.

  No related posts.