Квадратичные формы.
Определение. Однородный многочлен второй степени относительно переменных х1 и х2
Ф(х1, х2) = а11 ,
не содержащий свободного члена и неизвестных в первой степени, называется квадратичной формой переменных х1 и х2.
Определение. Однородный многочлен второй степени относительно переменных х1, х2 и х3
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1, х2 и х3.
Рассмотрим
квадратичную форму двух переменных.
Пусть на плоскости задан ортогональный базис . Каждая точка плоскости имеет в этом базисе координаты х1, х2.
Если задана квадратичная форма Ф(х1, х2) = а11 , то ее можно рассматривать как функцию от переменных х1 и х2.
Кривые второго порядка на плоскости (окружность, эллипс, гипербола, парабола).
Определение. Кривой второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка
где — вещественные числа, и хотя бы одно из чисел отлично от нуля.
Определение. Окружностью
называется геометрическое место точек
плоскости, равноудаленных от фиксированной
точки, называемой центром
окружности.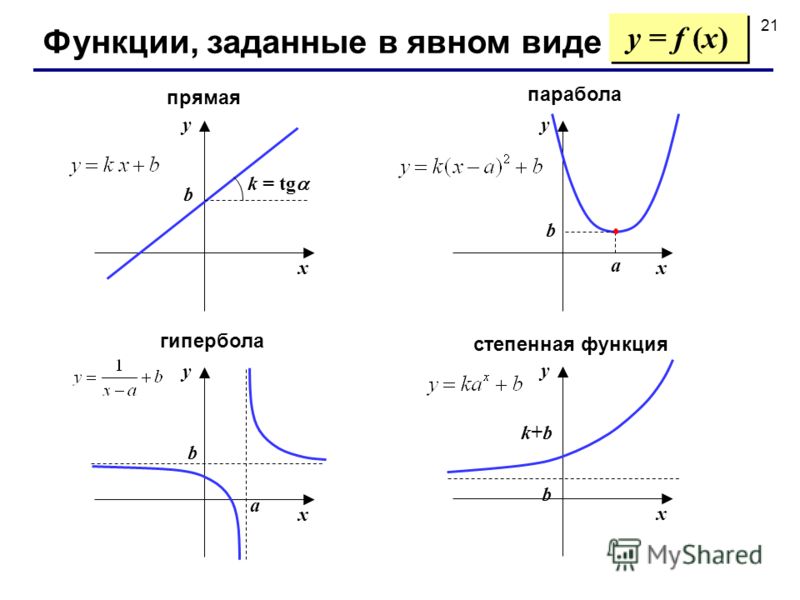
Получим уравнение окружности, если известны ее центр и радиус.
Окружность радиуса с центром в точке имеет уравнение:
(8.1.)
Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.
Пусть и — фокусы эллипса. Начало системы координат расположим на середине отрезка . Ось направим вдоль этого отрезка, ось — перпендикулярно к этому отрезку (рис. 8.2).
Пусть сумма расстояний от точки эллипса до фокусов равна , а расстояние между фокусами — . Тогда в выбранной системе координат эллипс имеет уравнение: (8.2)
где
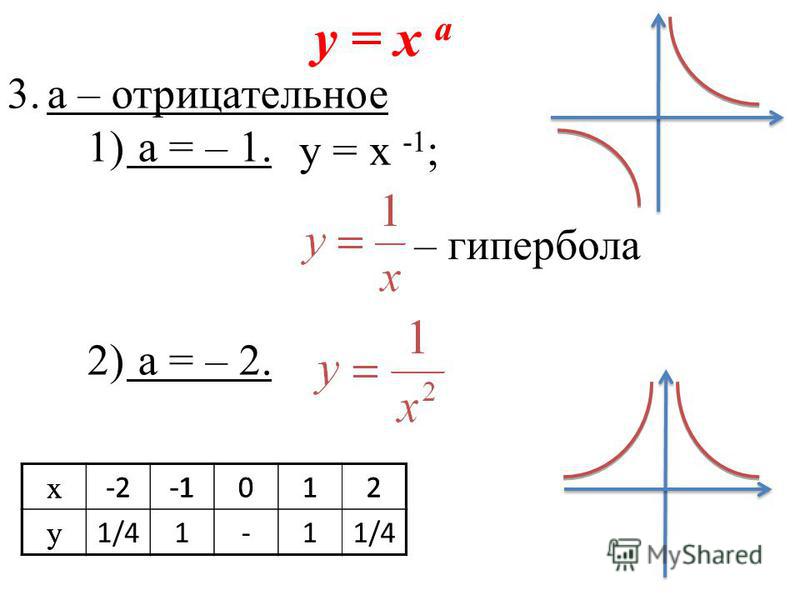8.2.Уравнение (8.2) называется каноническим уравнением эллипса.
Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Для получения уравнения гиперболы выберем систему координат. Начало координат расположим на середине отрезка между фокусами, ось направим вдоль этого отрезка, а ось ординат — перпендикулярно к нему (рис. 8.3).
Рис. 8.3.
Пусть расстояние между фокусами и гиперболы равно , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна . Тогда гипербола в выбранной выше системе координат имеет уравнение: (8.3)
где
Уравнение (8.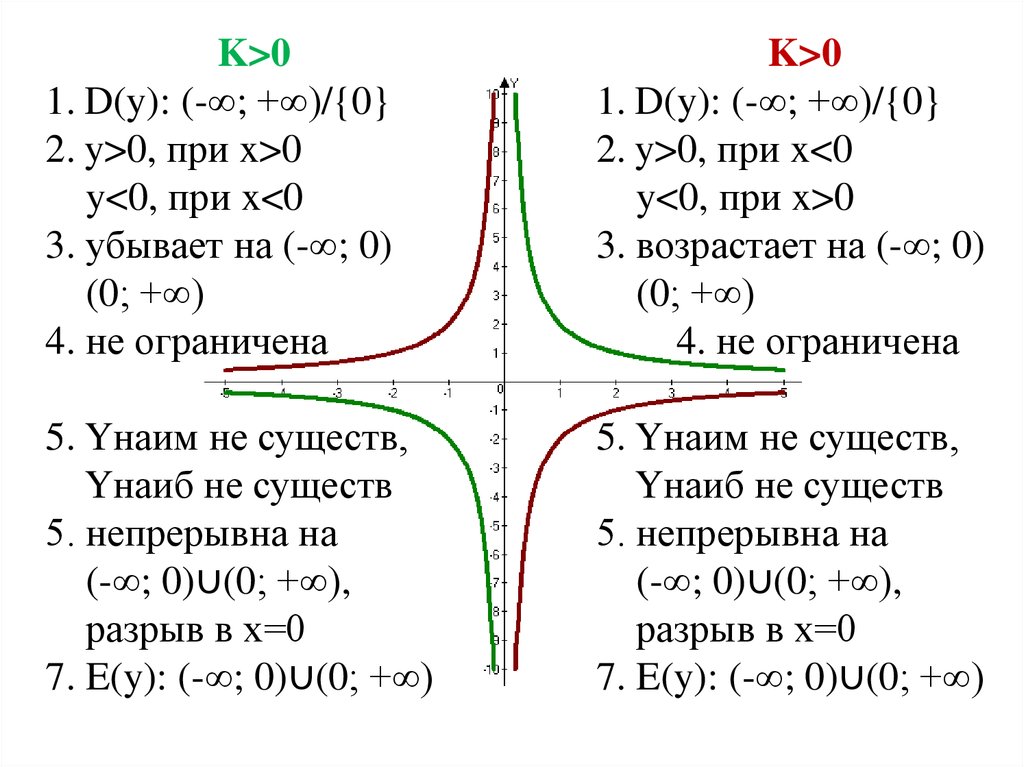
3)
называется каноническим уравнением
гиперболы.
Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой, параболы.
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса опустим перпендикуляр на директрису . Начало координат расположим на середине отрезка , ось направим вдоль отрезка так, чтобы ее направление совпадало с направлением вектора . Ось проведем перпендикулярно оси (рис. 8.4).
Рис. 8.4.
Пусть расстояние между фокусом и директрисой параболы равно . Тогда в выбранной системе координат парабола имеет уравнение
(8.
4)
Уравнение (8.4) называется каноническим уравнением параболы.
Асимптотика точки уравнения гиперболы, граф, угол, текст, другие png
Асимптотика точки уравнения гиперболы, граф, угол, текст, другие pngтеги
- угол,
- текст,
- другие,
- симметрия,
- график функции,
- график,
- параллель,
- асимптота,
- точка,
- линия,
- гипербола,
- область,
- уравнение,
- загрузка,
- диаграмма,
- круг,
- граф,
- png,
- прозрачный,
- бесплатная загрузка
Об этом PNG
- Размер изображения
- 803x615px
- Размер файла
- 70.96KB
- MIME тип
- Image/png
изменить размер PNG
ширина(px)
высота(px)
Лицензия
Некоммерческое использование, DMCA Contact Us
org/ImageGallery» align=»middle»>
org/ImageObject»> Шаблонные рамки, арабески, Разное, угол, белый png
5000x3750px
276.5KB
org/ImageObject»> зеленая стрелка графическая диаграмма, диаграмма компьютер значки диаграммы статистика, аналитика, стрелка, диаграмма, график, рост, отчет, значок статистики, разное, угол, текст png
512x512px
19.77KB
15KB
org/ImageObject»> Линейный график Гистограмма, график, разное, инфографика, угол png
512x512px
12.59KB
37KB
53KB
81KB
org/ImageObject»> Круговая диаграмма Гистограмма Круговой график, Математический график с, компьютерные обои, сфера, график функции png
600x484px
114.53KBOpenAlgebra.
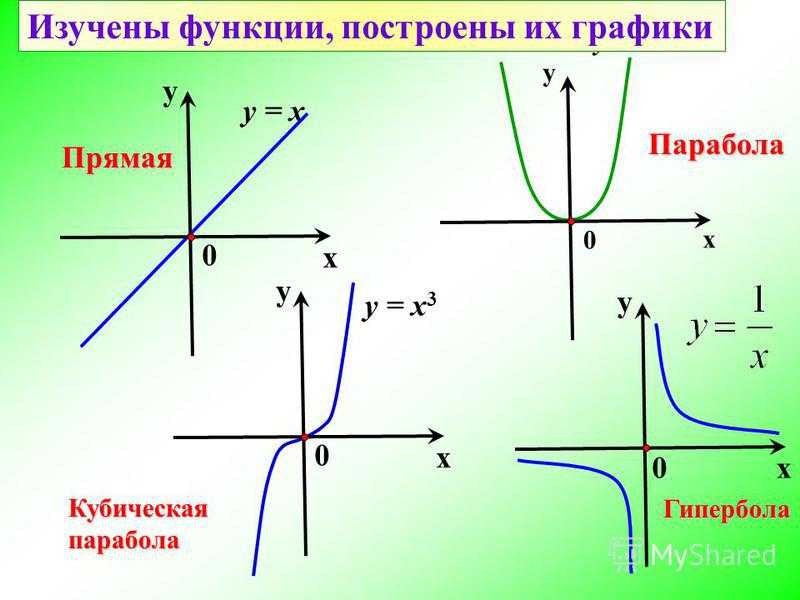com: ГиперболыГипербола — это множество всех точек, расстояния которых до двух фиксированных точек вычитаются из одной и той же константы. В этом разделе мы сосредоточимся на уравнении гиперболы.
Ось, которая содержит вершины, называется поперечной осью, а ось, не содержащая вершин, называется сопряженной осью. Также обратите внимание, что форма сильно отличается от формы параболы, гиперболы асимптотичны к следующим линиям:
Мы будем использовать эти асимптоты для построения графиков гипербол.
[ Интерактивный : Гипербола ]
Чтобы легко построить график асимптот гиперболы, используйте следующий процесс.
Шаг 1 : Определите центр ( h , k ) из стандартной формы.
Шаг 2 : Точки графика a единиц слева и справа от центра.
Шаг 3 : Точки графика b 92 член отрицателен, тогда гипербола открывается вверх и вниз.
Сравните эту гиперболу с предыдущей и обратите внимание на разницу в стандартной форме. Прямоугольник и асимптоты на самом деле не являются частью графика. Мы используем их для получения более точного эскиза. При построении графика в графической утилите результат выглядит следующим образом.
Нарисуйте график гиперболы и приведите уравнения асимптот.
Следующие примеры требуют, чтобы мы завершили квадрат, чтобы получить стандартную форму. Не забудьте вынести старший коэффициент из каждой группы переменных перед использованием ( 92, чтобы завершить квадрат.
youtube.com/embed/s4F6IZLgVhs»> Постройте график гиперболы, х — и у — точки пересечения, и приведите уравнения асимптот.
Когда мы завершили квадрат, обратите внимание, что мы добавили 64 и вычли 225, чтобы сбалансировать уравнение. На первый взгляд может показаться, что мы добавили 16 и 25 в левую часть. Но на самом деле после распределения 4 и -9 мы прибавляли и вычитали большие значения.
Когда поперечная ось вертикальна, будьте осторожны с центром. Распространенной ошибкой является использование (-2, 1) для центра в приведенном выше примере, потому что сначала идет переменная y , а мы привыкли читать ее слева направо. Это было бы неправильно, поэтому позаботьтесь о том, чтобы использовать правильные h и k .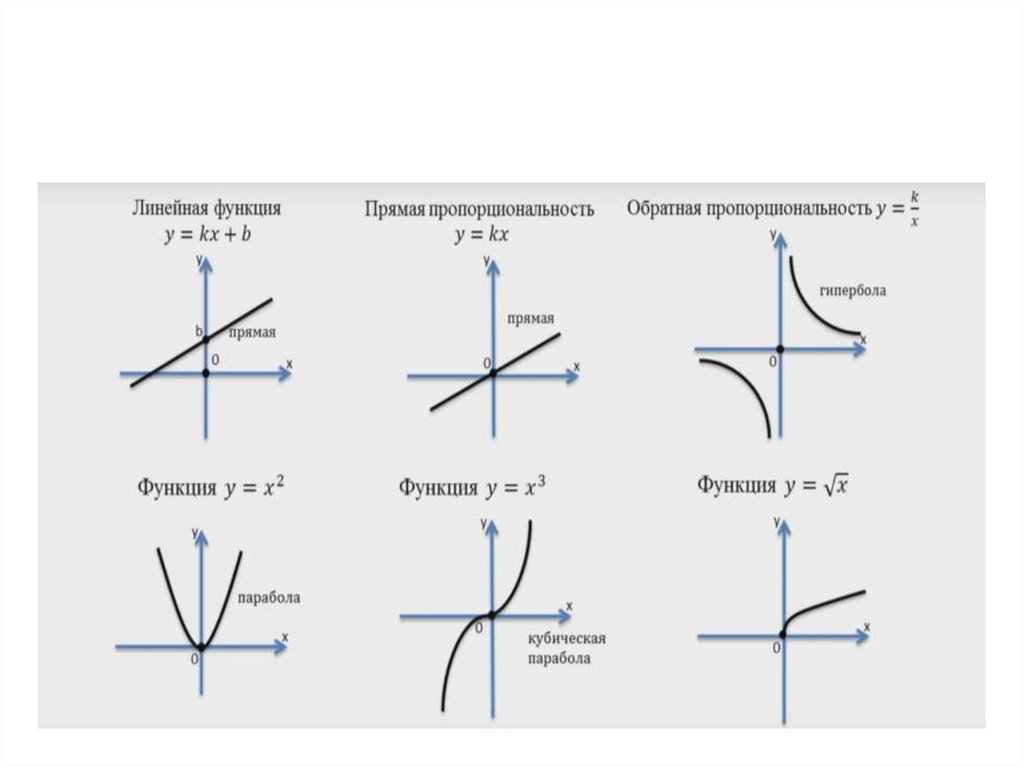
Пример : Найдите уравнение гиперболы с центром в точке (-3, 1), где a = 2, b = 3, и с вертикальной поперечной осью. График это.
Пример : Найдите уравнение гиперболы с вершинами (3,0) и (-3,0), горизонтальной поперечной осью и сопряженной осью длиной 4 единицы.
Пример : Найдите уравнение гиперболы с центром (2, -5), вертикальной поперечной осью, измеряющей 10 единиц, и сопряженной осью, измеряющей 6 единиц.
Видео на YouTube : Нажмите на проблему, чтобы увидеть, как она решена.
—
Гипербола
A Гипербола — это множество всех точек на плоскости, для которых абсолютное значение разности расстояний между двумя фиксированными точками остается постоянным. Две данные точки являются фокусами гиперболы, а середина отрезка, соединяющего фокусы, является центром гиперболы.
Гипербола выглядит как две противоположные U-образные кривые, как показано на рисунке 1.
Рис. 1. Свойства гипербол.
Гипербола имеет две оси симметрии (см. рис. 1). Ось в направлении раскрытия гиперболы называется 9.0011 поперечная ось. Сопряженная ось проходит через центр гиперболы и перпендикулярна поперечной оси. Точки пересечения гиперболы и поперечной оси называются вершинами (единственное число, вершина ) гиперболы.
Гипербола с центром в точке (0, 0), поперечная ось которой проходит вдоль оси x , имеет стандартную форму следующего уравнения.
где ( a , 0) и (– a , 0) — вершины, а ( c , 0) и (– c , 0) — его фокусы.
В гиперболе . Не путайте это с формулой эллипса, .
По мере того, как точки гиперболы удаляются от ее центра, они становятся все ближе и ближе к двум линиям, называемым линиями асимптоты. Линии асимптот используются в качестве ориентиров при построении графика гиперболы.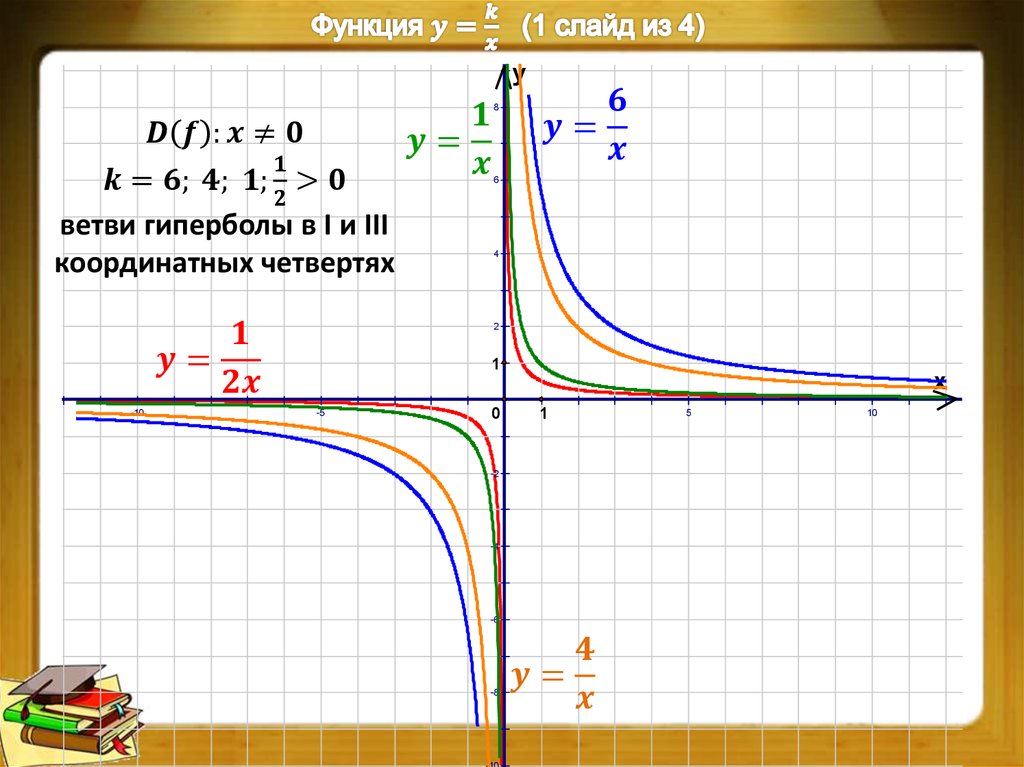
Чтобы построить линии асимптот, сформируйте прямоугольник, используя точки (– a , b ), (– a , – b ), ( a , b ) и ( a , – b ) и нарисуйте их диагонали в виде расширенных линий.
Для гиперболы с центром в точке (0, 0), поперечная ось которой проходит вдоль оси x , уравнение асимптоты принимает вид
Пример 1
Нарисуйте следующую гиперболу. Найдите его центр, вершины, фокусы и уравнения его асимптот.
Это гипербола с центром в точке (0, 0), а ее поперечная ось проходит вдоль оси x .
Вершины: (–4, 0) (4, 0)
Очаги:
Уравнения асимптот:
График этой гиперболы показан на рисунке 2.
Гипербола с центром в точке (0, 0), поперечная ось которой проходит вдоль оси y , имеет стандартную форму следующего уравнения.
Вершины теперь (0, и ) и (0, – и ). Фокусы находятся в точках (0, c ) и (0, – c ) с c 2 = a 2 + b 2 . Линии асимптоты имеют уравнения
В общем, когда гипербола записывается в стандартной форме, поперечная ось проходит вдоль или параллельно оси переменной, которая не вычитается.
Рис. 2. Центр, асимптоты, фокусы и вершины.
Пример 2
Нарисуйте следующую гиперболу и найдите ее центр, вершины, фокусы и уравнения асимптот.
Это гипербола с центром в точке (0, 0) и поперечной осью вдоль оси y , поскольку переменная y не вычитается.
Вершины: (0, 2), (0, –2)
Очаги: ,
Уравнения асимптот:
График этой гиперболы показан на рисунке 3.
Гипербола с центром в точке ( h , k ) будет иметь следующие стандартные уравнения:
Если поперечная ось горизонтальна, то
В этом случае вершины находятся в точках ( h + a , k ) и ( h – a , k ). Фокусы находятся в точках ( h + c , k ) и ( h – c , k ), где .
Если поперечная ось вертикальна,
Вершины составляют ( H , K + A ) и ( H , K — A ), а фокусы ( H , K + C . ) и ( h , k – c ), где c 2 = a 2 + b 2 .
Рис. 3. График примера.
Пример 3
График.
Центр: (2, –3)
Поперечная ось горизонтальна.
вершин:
Найдите координаты углов прямоугольника, чтобы построить линии асимптоты.
График этой гиперболы показан на рисунке 4.
Уравнение xy = 16 также представляет собой гиперболу. Центр этой гиперболы находится в точке (0, 0), а ее поперечной осью является линия y = х . Асимптотами являются оси x и y . Его вершины находятся в и . График этой гиперболы показан на рисунке 5.
Рис. 4. График Примера.
Рис.