Как научиться решать простые и сложные уравнения
Как научиться решать простые и сложные уравнения
Уважаемые родители!
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для многих смежных дисциплин. В послешкольной жизни реальной необходимостью становится непрерывное образование, что требует базовой общешкольной подготовки, в том числе и математической.
В начальной школе закладываются не только знания по основным темам, но и развивается логическое мышление, воображение и пространственные представления, а также формируется интерес к данному предмету.
Соблюдая принцип преемственности, мы сделаем упор на важнейшую тему, а именно «Взаимосвязь компонентов действий при решении составных уравнений».
С помощью данного урока можно без труда научиться решать усложненные уравнения. На уроке вы подробно познакомитесь с пошаговой инструкцией решения усложненных уравнений.
Многих, родителей ставит в тупик вопрос – как же заставить детей научиться решать простые и сложные уравнения. Если уравнения простые — это еще пол беды, но ведь бывают и сложные – например интегральные. Кстати, для сведения, есть и такие уравнения, над решением которых бьются лучшие умы нашей планеты и за решение которых выдаются очень весомые денежные премии. Например, если вспомнить Перельмана и невостребованную им денежную премию в размере нескольких миллионов.
Однако вернемся для начала к простым математическим уравнениям и повторим виды уравнений и названия компонентов. Небольшая разминка:
_________________________________________________________________________
РАЗМИНКА
Найди лишнее число в каждом столбике:
2) Какого слова не хватает в каждом столбике?
3) Соедините слова из первого столбика со словами из 2 столбика.
«Уравнение» «Равенство»
4) Как вы объясните, что такое «равенство»?
5) А «уравнение»? Это равенство? Что в нем особенного?
слагаемое сумма
уменьшаемое разность
вычитаемое произведение
множитель равенство
делимое
уравнение
Вывод: Уравнение – это равенство с переменной, значение которой надо найти.
_______________________________________________________________________
Предлагаю каждой группе написать на листке фломастером уравнения: (на доску)
1 группе — с неизвестным слагаемым; 2 группе — с неизвестным уменьшаемым; 3 группе – с неизвестным вычитаемым; 4 группе – с неизвестным делителем; 5 группе – с неизвестным делимым; 6 группе – с неизвестным множителем. | 1 группа х + 8 = 15 2 группа х – 8 = 7 3 группа 48 – х = 36 4 группа 540 : х = 9 5 группа х : 15 = 9 6 группа х * 10 = 360 |
Один из группы должен на математическом языке прочитать свое уравнение и прокомментировать их решение, т.
е. проговорить выполняемую операцию с известными компонентами действий (алгоритм).
Вывод: Умеем решать простые уравнения всех видов по алгоритму, читать и записывать буквенные выражения.
_____________________________________________________________________________
Предлагаю решить задачу, в которой появляется новый тип уравнений.
Х + 2кг 5кг и 3 кг | С какой величиной связан рисунок? Составьте и запишите по этому рисунку уравнение: Подберите для полученного уравнения подходящее уравнение: х + а = в а : х = в х : а = в х * а = в х – а = в а – х = в |
Вывод: Познакомились с решением уравнений, в одной из частей которых содержится числовое выражение, значение которого надо найти и получить простое уравнение.
________________________________________________________________________
Рассмотрим еще один вариант уравнения, решение которого сводится к решению цепочки простых уравнений. Вот один из введения составных уравнений.
а + в * с (х – у) : 3 2 * d + (m – n) Являются ли уравнениями записи? Почему? Как называют такие действия? Прочитайте их, называя последнее действие: | Нет. Это не уравнения, т. к. в уравнении должен быть знак «=». Выражения а + в * с — сумма числа а и произведения чисел в и с; (х – у) : 3 — частное разности чисел х и у; 2 * d + (m – n) — сумма удвоенного числа d и разности чисел m и n. |
Предлагаю каждому записать на математическом языке предложение:
Произведение разности чисел х и 4 и числа 3 равно 15.
Запишите на математическом языке предложение: произведение разности чисел х и 4 и числа 3 равно 15 | (х – 4) * 3 = 15 |
ВЫВОД: Возникшая проблемная ситуация мотивирует постановку цели урока: научиться решать уравнения в которых неизвестный компонент является выражением. Такие уравнения являются составными уравнениями.
__________________________________________________________________________
А может нам помогут уже изученные виды уравнений? (алгоритмы)
На какое из известных уравнений похоже наше уравнение? Х * а = в
ОЧЕНЬ ВАЖНЫЙ ВОПРОС: Чем является выражение в левой части – суммой, разностью, произведением или частным?
(х – 4) * 3 = 15 (Произведением)
Почему? (т.к. последнее действие – умножение)
Вывод: Такие уравнения еще не рассматривались. Но можно решить, если на выражение х – 4 наложить карточку (у — игрек), и получится уравнение, которое легко можно решить, используя простой алгоритм нахождения неизвестного компонента.
При решении составных уравнений необходимо на каждом шаге осуществлять выбор действия на автоматизированном уровне, комментируя, называя компоненты действия.
↓
↓
↓
↓
| (у – 5) * 4 = 28 |
Вывод: В классах с разной подготовкой эта работа может быть организована по-разному.
В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.
_____________________________________________________________________________
ЗАКЛЮЧЕНИЕ:
Когда речь идёт о чём-нибудь очень простом, понятном, мы часто говорим: «Дело ясно, как дважды два — четыре!».
А ведь прежде чем додуматься до того, что дважды два — четыре, людям пришлось учиться много, много тысяч лет.
Многие правила из школьных учебников арифметики и геометрии были известны древним грекам две с лишним тысячи лет назад.
Всюду, где надо что-то считать, измерять, сравнивать, без математики не обойтись.
А чем дальше, тем больше и точнее нужно было считать. С каждым десятилетием математика становилась всё нужнее людям.
Трудно представить, как жили бы люди, если бы не умели считать, измерять, сравнивать. Этому учит математика.
Сегодня Вы окунулись в школьную жизнь, побывали в роли учеников и я предлагаю Вам, уважаемые родители, оценить свои умения по шкале.
Мои умения | Дата и оценка |
Компоненты действий. | |
Составление уравнения с неизвестным компонентом. | |
Чтение и запись выражений. | |
Находить корень уравнения в простом уравнении. | |
Находить корень уравнения, в одной из частей которых содержится числовое выражение. | |
Находить корень уравнения, в которых неизвестный компонент действия является выражением. |
Как научить ребенка решать уравнения
Одна и самых сложных тем в начальной школе — решение уравнений.
Усложняется она двумя фактами:
Во-первых, дети не понимают смысл уравнения. Зачем цифру заменили буквой и что это вообще такое?
Во-вторых, объяснение, которое предлагается детям в школьной программе, непонятно в большинстве случаев даже взрослому:
Для того чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Для того чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Для того чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
И вот, придя домой ребенок чуть ли не плачет.
На помощь приходят родители.
И посмотрев в учебник, решают научить ребенка решать «проще».
Нужно же всего лишь перекинуть на одну сторону цифры, поменяв знак на противоположный, понимаешь?
Смотри, х-3=7
Минус три переносим с плюсом к семерке, считаем и получается х=10
В этом месте у детей обычно происходит сбой программы.
Знак? Поменять? Перенести? Что?
— Мама, папа! Вы ничего не понимате! Нам в школе по-другому объясняли!!!
— Тогда и решай как объясняли!
А в школе, тем временем, продолжается тренировка темы.
1. Вначале нужно определить какой компонент действия нужно найти
5+х=17 — нужно найти неизвестное слагаемое.
х-3=7 — нужно найти неизвестное уменьшаемое.
10-х=4 — нужно найти неизвестное вычитаемое.
2. Теперь нужно вспомнить правило, упомянутое выше
Для того чтобы найти неизвестное слагаемое, нужно…
Как Вы думаете, трудно ли маленькому ученику все это запомнить?
А еще нужно добавить сюда тот факт, что с каждым классом уравнения становятся все сложнее и больше.
В итоге и получается что уравнения для детей одна из самых сложных тем математики в начальной школе.
И даже если ребенок уже в четвертом классе, но у него трудности с решением уравнениями, скорее всего у него проблема с пониманием сути уравнения. И надо просто вернуться назад, к основам.
Сделать это можно за 2 простых шага:
Шаг первый — Надо научить детей понимать уравнения.
Нам потребуется простая кружка.
Напишите пример 3 + 5 = 8
А на дне кружки «х». И, перевернув кружку, закройте цифру «5»
Что под кружкой?
Уверены, ребенок сразу угадает!
Теперь закройте цифру «5». Что под кружкой?
Так можно писать примеры на разные действия и играть. У ребенка происходи понимание, что х = это не просто непонятный знак, а «спрятанная цифра»
Подробнее о технике — в видео
Шаг второй — Научите определять, х в уравнении является целым или частью? Самым большим или «маленьким»?
Для этого нам подойдет техника «Яблоко»
Задайте ребенку вопрос, где в данном уравнении самое большое?
5+х=17
Ребенок ответит «17».
Отлично! Это будет наше яблоко!
Самое большое число — это всегда целое яблоко. Обведем в кружок.
А целое всегда состоит из частей. Давай подчеркнем части.
5 и х — части яблока.
А раз х — это часть. Она больше или меньше? х большое — или маленькое? Как его найти?
Важно отметить, что в таком случае ребенок думает, и понимает, почему, чтобы найти х в данном примере, нужно из 17 вычесть 5.
Умничка!
После того, как ребенок поймет, что ключем к правильному решению уравнений является определить, х — целое или часть, он легко будет решать уравнения.
Потому что запомнить правило, когда понимаешь его гораздо проще, чем наоборот: вызубрить и учиться применять.
Данные техники «Кружка» и «Яблоко» позволяют научить ребенка понимать, что он делает и зачем.
Когда ребенок понимает предмет, он у него начинает получаться.
Когда у ребенка получается, ему это нравится.
Когда нравится, появляется интерес, желание и мотивация.
Когда появляется мотивация — ребенок учится сам.
Учите ребенка понимать программу и тогда процесс учебы станет отнимать у Вас значительно меньше времени и сил.
Вам понравилось объяснение данной темы?
Именно так, просто и легко, мы учим родителей объяснять школьную программу в «Школе умных детей».
Хотите научиться объяснять материалы ребенку также доступно и легко, как в этой статье?
Тогда регистрируйтесь бесплатно на 40 уроков школы умных детей прямо сейчас по кнопке ниже.
Получить 40 уроков Школы умных детей бесплатно>>
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Корякова Людмила Николаевна, учитель начальных классов Урок математики в 4 классе Тема: Решение уравнений нового вида. Цель: Способствовать развитию умения решать сложные уравнения, где неизвестное выражено суммой или разностью чисел. Задачи: · формировать умения решать сложные уравнения, где неизвестное выражено суммой или разностью чисел; · развивать логическое мышление и умение анализировать; · применять элементы здоровьесберегающих технологий на уроке; ·
воспитывать
коллективизм, взаимопомощь. Оборудование: Карточки уравнений; карточка с геометрическим материалом; доска; учебник. Ход урока: I. Организационный момент: 1. Приветствие гостей. 2. Упражнение на развитие внимания, памяти: Я покажу вам карточку и буду держать её 5 секунд. Назовите по порядку, какие вы запомнили предметы. Сколько их? (на карточке треугольник, квадрат, круг, прямоугольник, овал) 3. Я желаю получить такую оценку каждому из вас на уроке. А для этого надо отгадать эти анаграммы и вы узнаете, чем мы будем заниматься сегодня на уроке. Анаграммы: ЕШАРЬТТОАГЫДАВЬТМСЕТЬАК (решать)(отгадывать)(смекать) II. Актуализация знаний. Устный счет. 1. — Назови компоненты при сложении. Как найти неизвестное слагаемое? Как называются компоненты при вычитании? Как найти уменьшаемое? Вычитаемое? 2. Задание: расставь действия в выражениях a + b – (d + k ) : m – n 34125 500 – (280 + 120) = 100 (600 – 327) + 27 = 300 3. Реши задачи: А) К неизвестному числу прибавить 700 и получится сумма 1800 1. Составь уравнение. Х + 700 = 1800 Х = 1100 Б) Из неизвестного числа вычли 60 и получили разность 150 1. Составь уравнение. 2. Чему равно неизвестное число? Х – 60 = 150 Х = 210 III. Решение уравнений. Мы с вами повторили решение простых уравнений, теперь переходим к решению более сложных. У доски: 120 + Х = 200 – 75 120 + Х = 125 Х = 125 – 120 Х = 5 120 + 5 = 200 – 75 125 = 125 IV. Физминутка «Близнецы» Дети встают между партами, кладут друг другу руки на
плечи и закрывают глаза. · присесть · встать · встать на пальчики, опуститься · наклониться влево · наклониться вправо · прогнуться назад · постоять на правой ноге, согнув левую ногу в колене · постоять на левой ноге, согнув правую ногу в колене · открыть глаза и тихо сесть Задание на ошибку: (х + 29) – 48 = 90 Диалог: · Что случилось? · Что вы увидели нового для себя? · Какая возникла проблема? · Давайте попробуем её решить? Составление плана решения уравнения: 1. Расставим порядок действий. Если бы это был пример, с чего бы вы начали его решение? (х + 29) – 48 = 90 2. Установим название компонентов по последнему действию. Где находится неизвестное число? (х + 29) – 48 = 90 3. Вырази чему равен неизвестный компонент? Х + 29 = 90 + 48 – такое уравнение мы умеем решать? Х + 29 = 138 – получили простое уравнение. Х = 138 – 29 Х = 109 (109 + 29) – 48 = 90 90 = 90 4. Так чем мы будем заниматься сегодня на уроке? (Решать уравнения нового вида, где неизвестное выражено суммой или разностью) V. Еще раз назовите тему нашего урока? (Решение уравнений нового вида) Повторим алгоритм решения уравнений: 1. Расстановка порядка действий. 2. Установление названия компонентов по последнему действию. 3. Найди уменьшаемое, вычитаемое, слагаемое. 4. Проверка (порядок действий). VI. Цель: Да, сегодня мы научимся решать эти уравнения, где неизвестное будет выражено суммой или разностью. VII. Закрепление нового материала (у доски)
Физминутка «Клоуны» Дети свободно стоят между партами; по моей команде: · брови свести и развести; · глаза прищурить, затем широко открыть; · губы максимально открыть в импровизированной улыбке, а затем поджать; · шею вытянуть, затем опустить; ·
руками обнять
себя, погладить и пожелать успехов в учебе. VIII. Работа в парах сменного состава. (Каждому ребенку раздать карточки с уравнением вида: 100 – (х + 25) = 52) Что главное при работе в паре? (Помочь своему товарищу) IX. Объясни как решал уравнение? (Устно) Физминутка для глаз: · обведи глазами синий кружок по часовой стрелке; · красный – против часовой стрелке; (Повторить 2-3 раза) X. Самостоятельная работа (Разноуровневые задания) 1 уровень на «3»: 189 – (х – 80) = 39 х – 80 = 189 – 39 2 уровень на «4»: 350 – (45 + а) = 60 3 уровень на «5»: Составь по задаче уравнение и реши его: Из числа 280 вычесть сумму чисел х и 40 равно 80 280 – (х + 40) = 80 х + 40 = 280 – 80 х + 40 = 200 х = 200 – 40 х = 160 ________________ 280 – (160 + 40) = 80 80 = 80 XI. Проверка разноуровневых заданий (по образцу): 1 уровень: 189 – (х – 80) = 39 х – 80 = 189 – 39 х – 80 = 150 х = 150 +80 х = 230 _________________ 189 – (230 – 80) = 39 39 = 39 2 уровень: 350 – (45 + а) = 60 45 + а = 350 – 60 45 +а = 290 а = 290 – 45 а = 245 __________________ 350 – (45 + 245) = 60 60 = 60 3 уровень: 280 – (х + 40) = 80 х + 40 = 280 – 80 х + 40 = 200 х = 200 – 40 х = 160 ________________ 280 – (160 + 40) = 80 80 = 80 XII. XIII. Рефлексия урока. Как вы себя чувствовали сегодня на уроке? Комфортно Тревожно Покажите мне карточками, чтобы я увидела всех. Почему? С чем связана твоя тревога? XIV. Домашнее задание. 1 уровень на «3»: стр. 92 № 9 2 уровень на 4»: стр. 93 № 14 3 уровень на «5»: стр. 96 на смекалку: Подумай и попробуй исследовать и решить это уравнение самостоятельно 60х + 180 = 420, составь план решения. |
Корень уравнения при этом должен остаться прежним. (два ученика у доски)
Найдите среди них с таким порядком действий, которое уже встречалось сегодня.
Какое уравнение отнесем к сложным? Почему?
Даны
выражения, подумайте с чего начинается решение выражений, где больше чем одно
действие (с порядка действий) :
По моему сигналу они выполняют следующие команды:
Оцениваю
детей.
Скажем, мы имеем дело со следующим уравнением: -4x + 7 = 15.
В этом примере коэффициент -4. Чтобы от него избавиться нужно разделить обе части уравнения на -4.
Получаем -6х = -12
Cегодня разберёмся, как эти линейные уравнения решать.
Г. Петерсон в 3-х частях, часть вторая, М.: Издательство «Ювента», 2008 г.
Слайд № 7 
Как решить уравнение?
В математике вы наверняка встречали слово «уравнения». Вы, должно быть, читали такие вопросы, как «Решите уравнение 2x + 12 = 33, чтобы найти значение x». Но каково значение термина уравнение? Уравнения в математике — это утверждения. Эти операторы часто имеют два связанных выражения со знаком «равно».
Уравнения могут даже иметь более двух выражений. Математикам удалось решить некоторые уравнения, имеющие более двух выражений до определенного уровня. Кроме того, даже они оказываются беспомощными. Но нам не нужно беспокоиться об этих сложных уравнениях. В этой статье мы изучим фундаментальные понятия каждого уравнения, известного человечеству. Мы изучим, что такое уравнение и сколько типов уравнений существует в этом мире.
Определение уравнений
Уравнения очень легко идентифицировать. Везде, где вы видите два алгебраических выражения слева и справа от знака равенства «=», вы нашли уравнение. Таким образом, мы можем сказать, что утверждения со знаком «равно» между ними известны как уравнения. Если между выражениями нет знака равенства, они не считаются уравнением. В следующем разделе этой статьи мы увидим разницу между уравнениями и выражениями. А пока посмотрите на примеры, приведенные ниже:
Пример 1: Является ли x + y = 13 уравнением?
Решение: Да, x + y = 13 является уравнением, потому что оно имеет знак «равно» между x + y и 13.
Пример 2: Является ли – 24 + 13y уравнением?
Решение: Нет! a – 24 + 13y не является уравнением, потому что не имеет знака равенства.
Пример 3: Является ли 66 – 12 = 34 – 3 уравнением?
Решение: Действительно, это уравнение, потому что между числами 66 – 12 и 34 – 3 стоит знак «равно».
Уравнения используются в математике для определения значений неизвестных величин. Они используются при решении текстовых задач и многих повседневных задач, связанных со временем и расстоянием, работой, прибылями и убытками и многим другим. Давайте теперь узнаем основную разницу между уравнением и выражением.
Уравнение против. Expression
Уравнения и выражения — это две разные вещи. Студенты часто путают эти два понятия и делают много ошибок. См. приведенную ниже таблицу, чтобы прояснить разницу между уравнением и выражением.
| Уравнение | Выражение |
В математике уравнение формируется, когда два выражения имеют одинаковое значение и соединяются вместе со знаком «равно» посередине. | Это математическое выражение, состоящее как минимум из одного слова и нескольких терминов, связанных операторами. |
| Рядом с ним стоит символ «=». | Символ равенства «=» не появляется в выражении. |
| Можно решить, чтобы определить значение неизвестной величины. | Максимум можно уменьшить до самой простой формы. |
| Например: 7x – 2a = 34, 4a + 22 = 3c + b и т. д. | Например: 34x – 3z + 2y, a + 3k и т. д. |
Части уравнения 90
В каждом уравнении левая часть должна быть равна правой. Обе стороны должны быть равны. Коэффициенты, переменные, операторы, константы, термины, выражения и знак «=» — все это важные компоненты уравнения. Уравнение может иметь любой один или все эти термины, вращающиеся вокруг знака «=». Давайте изучим эти термины по отдельности:
- Термин: Любая числовая или алгебраическая единица, присутствующая вокруг операторов, называется термином.
- Переменные: Все алфавитные члены, присутствующие в уравнении, значение которого неизвестно, называются переменными.
- Константы: Все числовые члены уравнения называются константами.
- Коэффициенты: Постоянные члены, находящиеся непосредственно перед переменными, являются коэффициентами.
- Операторы: Арифметические операторы, такие как знак сложения, знак вычитания, знак равенства и т. д., известны как операторы.
Уравнение может содержать только числовые члены, алгебраические члены или и то, и другое. Мы изучим шаги для решения уравнения в следующем модуле.
Как решить уравнение?
Вы можете представить уравнение как весы. Обе части уравнения дают одно и то же значение, поэтому весы уравновешиваются. Оно остается в силе независимо от того, добавляем мы или удаляем одно и то же количество из обеих частей уравнения. То же самое остается верным независимо от того, умножаем мы или делим одно и то же целое число на обе части уравнения.
Любая операция, которую вы выполняете в левой части уравнения, должна быть реализована и в правой части уравнения. Это делается для сохранения баланса уравнения. Давайте возьмем пример, чтобы понять эту концепцию.
Рассмотрим уравнение x + 3y = 2a + b. Это сбалансированное уравнение. Допустим, мы хотим добавить 20 к левой части. Левая часть меняется на x + 3y + 20. Но теперь уравнение нарушено. Нам нужно добавить 20 к правой стороне, чтобы сбалансировать ее. Следовательно, новое уравнение будет иметь вид x + 3y + 20 = 2a + b + 20,9.0003
Давайте теперь научимся решать уравнение:
- Шаг 1: Всегда держите переменные с одной стороны символа «=», а константы с другой стороны символа «=». Обычно переменные располагаются слева, а константы — справа от знака «=».
- Шаг 2: Выполните необходимые операции с такими же терминами, как сложение или вычитание. Не оперируйте одинаковыми терминами с непохожими терминами. Если вы сделаете это, вы будете следовать неправильному подходу.
Если вы сделаете это, вы будете следовать неправильному подходу.- Шаг 3: Упростите уравнение и получите желаемый ответ.
Посмотрите на приведенный ниже пример:
Пример 1: Решите уравнение a + 34b – 22 = b + 18
Решение:
Из шага 2: a + 33b = 40
Из шага 3: Это уравнение нельзя упростить, следовательно, a + 33b = 40 — это решение этого уравнения.
Пример 2: Решите уравнение 4x + 3 = x + 27
Решение:
Из шага 1: 4x – x = 27 – 3
Из шага 2: 3x = 24
Из шага 3: x = 24/3 , поэтому значение x и решение этого уравнения равны 8.
Типы уравнений
Уравнения классифицируются на основе степени переменных. Степень означает мощность, присвоенную любой переменной. Переменные, имеющие степень 1, известны как линейные переменные. Точно так же переменные, имеющие степень два, известны как квадратичные переменные, а степени три известны как кубические переменные и так далее.
Уравнения классифицируются как линейные уравнения, квадратные уравнения, кубические уравнения и т. д. Изучим их подробно.
Линейные уравнения: Уравнения, в которых все переменные степени равны единице, называются линейными уравнениями. Например, x + 2y = 11, x + 5 = 0 и т. д. Далее они классифицируются как линейные уравнения с одной переменной, линейные уравнения с двумя переменными и т. д. Стандартная форма линейного уравнения: kx + ly – m = 0, где x и y — переменные, а k, l и m — константы.
Квадратные уравнения: Уравнения, имеющие хотя бы одну переменную второй степени, называются квадратными уравнениями. Например, х 2 + a = 22, k 2 – m 2 – n = 0 и т. д. kx 2 + lx + m = 0 – стандартная форма квадратного уравнения.
Кубические уравнения: Уравнения, имеющие хотя бы одну переменную степени 3, называются кубическими уравнениями. Например, x 3 – x 2 + 2 = 31y, k 3 – m 2 + n 3 = 19 и т.
д. Стандартная форма записи кубического уравнения – kx 3 + лк 2 + mx + n = 0,
Во всех приведенных выше случаях k коэффициенты при x, x 2 и x 3 никогда не могут быть равны нулю. Если k = 0, то члены, содержащие степень, будут удалены, что сделает уравнение недействительным.
Например, если в уравнении kx 2 + lx + m = 0, если k = 0, то уравнение принимает вид lx +m = 0, что является не квадратным, а линейным уравнением.
Ключевые примечания к уравнениям
- Решение или корень уравнения относится к значениям переменной, которые делают уравнение верным.
- Когда одно и то же число суммируется, вычитается, умножается или делится на обе части уравнения, решение остается неизменным.
- Прямая линия изображает линейное уравнение с одной или двумя переменными, а парабола изображает квадратное уравнение.
1.
Как написать полное уравнение? Вы можете написать полное уравнение, добавив знак равенства в начало уравнения, а затем записав все переменные, числа или символы, которые появляются по обе стороны от него.
Например, x + 2 = 5 В этом примере «x» стоит с одной стороны знака равенства, а «2» — с другой.
2.
Как написать полное уравнение?Чтобы написать полное уравнение, вам нужно знать, как решать по одной переменной за раз.
Допустим, у нас есть уравнение:
x + y = 12
Чтобы найти x, нам нужно изолировать его, вычитая y из обеих частей уравнения:
x + y – y = 12 – y
x = 12 – y
Теперь, если мы хотим найти y, мы просто делаем то же самое: вычитаем x из обеих частей, а затем делим на 2.
3.
Как решить уравнение?Начнем с простого уравнения:
x² + 3x + 2 = 0
Чтобы решить это уравнение, нам нужно выделить член x. Мы можем сделать это, добавляя или вычитая кратные одному и тому же числу обе части уравнения.
Мы упростим себе жизнь, добавив 6 к обеим частям уравнения. Это дает нам:
x² + 3x + 2 = 0 + 6 (прибавьте 6)
x² + 3x + 8 = 6 (вычтите 6)
Теперь у нас есть уравнение, в котором мы можем выделить наш член x:
(x² + 3x) – 8 = 0 (вычесть 8 с обеих сторон)
Теперь мы можем найти x: разделить обе части на (x² + 3x):
1/2(x² + 3x) – 8/2 = 0 => 1/ 2(1+3*(-8)) -8/2 => 1/2(-11) -8/2 => 1/2(-11) – (-8/2) => 1/2( -11 – 16) => 1/2(-17)=> x=-17
4.
Какие шаги в уравнении?Уравнение — это математическое утверждение о том, что две вещи равны. Есть четыре шага, чтобы решить уравнение:
1. Найдите значение одной части уравнения отдельно. Например, если у вас 3+2=5, то 5=3+2.
2. Решите переменную через другие переменные в уравнении, вычитая или разделяя обе части уравнения на что-то. Например, если у вас 3x+2=5, то 3x-5/3=0 или -5/3 x = 0, поэтому x = -1/3 или 1/3.
3. Подставьте свой ответ обратно в исходное уравнение и решите для другой переменной через все остальные; это даст вам еще одно решение для проверки.
Например, если x = 1/3 и y = -1/3 (из шага 2), то 3(-1/3)+2(-1/3)=5(-1/3). Если сложить их вместе, получится -4/9.2 + bx + c = 0,
* Уравнения абсолютного значения имеют вид |x|.
* Рациональные выражения имеют вид p/q, где p и q — многочлены без общих множителей и q ≠ 0.
Решение линейных уравнений — Полный курс алгебры
Навыки
в
A L G E B R A
Содержание | Дом
9
Закон обратного
Четыре формы уравнений
Транспонирование
Логическая последовательность операторов
Транспонирование по сравнению с заменой сторон
Форма ах = 0
Раздел 2 :
Отмена
Неизвестность с обеих сторон
Уравнения простых дробей
УРАВНЕНИЕ – это алгебраическое выражение, в котором глагол равен «равно» = . Уравнение включает неизвестное число, обычно называемое 9.0321 х . Вот простой пример:
х + 4 = 10.
«Некоторое число плюс 4 равно 10.»
Мы говорим, что уравнение имеет две стороны: левая сторона, x + 4, и правая сторона, 10.
Поскольку x является в первой степени, мы называем это линейным уравнением. Линейное уравнение также называют уравнением первой степени.
Степенью любого уравнения является наивысший показатель степени, встречающийся у неизвестного числа. Уравнение первой степени называется линейный , потому что, как мы увидим много позже, его график представляет собой прямую линию .
Уравнение — это утверждение — станет истинным только тогда, когда неизвестное имеет определенное значение, которое мы называем решением уравнения.
Решение этого уравнения, очевидно, 6:
6 + 4 = 10.
6 — это единственное значение x , для которого утверждение « x + 4 = 10» будет верным. Мы говорим, что x = 6 удовлетворяет уравнению.
Теперь алгебра зависит от того, как все выглядит.
Что касается того, как все выглядит, то мы будем знать, что решили уравнение, когда мы изолируем x слева.
Почему слева? Потому что так мы читаем, слева направо. « x равно…»
В стандартной форме линейного уравнения — x + b = 0 — x отображается слева.
На самом деле, мы видели, что для любого уравнения, которое выглядит так:
| x + и | = | б , |
| решение всегда будет выглядеть так: | ||
| x | = | б − а . |
| Если | |||
| х + 4 | = | 10, | |
| затем | |||
| х | = | 10 − 4 | |
| = | 6. | ||
Закон обратного
Есть две пары обратных операций. Сложение и вычитание, умножение и деление.
Формально, чтобы решить уравнение, мы должны изолировать неизвестное с одной стороны уравнения.
ось − б + в = д .
Мы должны переместить a, b , c на другую сторону, чтобы x было одно.
Вопрос:
Как переложить число из одной части уравнения
в другую?
Ответ:
Записав его на другой стороне с обратной операцией.
Это закон обратного. Это следует из двух правил урока 5.
Пример 1. Решите это уравнение:
| а х − б + в | = | д . |
| Решение. Поскольку b — это – 90 322 слева, мы прибавим 90 321 к 90 322 справа: 90 044 | ||
| a x + c | = | д + б . |
| Поскольку c равно , прибавив слева, мы вычтем из справа: | ||
| топор | = | д + б — в . |
| И, наконец, с на умножаем слева, делим на справа: | ||
| x | = | d + b − c a |
Мы решили уравнение.
Четыре формы уравнений
Таким образом, решение любого линейного уравнения будет состоять из четырех форм, соответствующих четырем арифметическим операциям. Ниже приведены основные правила решения любого линейного уравнения. В каждом случае мы будем сдвигать и на другую сторону.
1. Если x + a = b , то x = b − a .
«Если к числу добавить в одной части уравнения,
мы можем вычесть из другой стороны.»
2. Если x − a = b , то x = b + a .
«Если число равно вычесть с одной стороны уравнения,
мы можем прибавить к другой стороне уравнения».
| 3. Если x = b , то x = | б а | . | |
«Если число умножить на одну часть уравнения,
мы можем разделить его с другой стороны.»
| 4. Если | x и | = b , тогда x = ab . |
«Если число делит с одной стороны уравнения,
мы можем умножить с другой стороны.»
В любом случае и были сдвинуты на другую сторону с помощью обратной операции.
Любое линейное уравнение можно будет решить, применяя одно или несколько из этих правил.
Транспонирование
Когда используются операции сложения или вычитания (Формы 1 и 2), мы называем это транспонированием.
Мы можем переместить член в другую часть уравнения
, изменив его знак .
+ a переходит на другую сторону как − и .
− a переходит на другую сторону как + a .
Транспонирование — одна из наиболее характерных операций алгебры, и считается, что это значение слова алгебра арабского происхождения. (Арабские математики изучили алгебру в Индии, откуда они привезли ее в Европу.) Транспонирование — это метод тех, кто действительно использует алгебру в науке и математике, потому что это искусно. И, как мы сейчас увидим, он сохраняет четкую логическую последовательность утверждений. Более того, это подчеркивает, что вы делаете алгебру глазами. Когда ты увидишь
| х + и | = | б , |
| тогда вы сразу видите что + a идет на другую сторону как — a : | ||
| x | = | б − а . |
Однако часто учат писать — a с обеих сторон, рисовать линию и добавлять.
Во-первых, вы никогда не увидите этого ни в одном тексте по исчислению. То, что вы увидите, — это логическая последовательность утверждений, к которой мы вот-вот придем.
Более того, мы доказали, что можем просто транспонировать. Нет необходимости доказывать это снова каждый раз, когда вы решаете уравнение.
(Вы должны доказывать теорему Пифагора каждый раз, когда применяете ее? Нет, не нужно.)
Если вы хотите представить, что вы вычли из с обеих сторон, прекрасно. Но приходиться писать не умело.
Вот что вы увидите в своем тексте исчисления.
Логическая последовательность операторов
Рассмотрим снова уравнение примера 1.
ось − б + в = д .
Это алгебраическое предложение — это утверждение — будет логически влечь за собой другие утверждения.
Теперь мы увидим логическую последовательность, ведущую к последнему утверждению, которое является решением.
| (1) | топор − б + в | = | д | |
| подразумевает | (2) | топор | = | г + б − в |
| подразумевает | (3) | х | = | г + б − в . и |
Исходное уравнение (1) «трансформируется» путем перестановки членов. Утверждение (1) подразумевает утверждение (2).
Затем этот оператор преобразуется путем деления на 9.0321 и . Из утверждения (2) следует утверждение (3), которое является решением.
Таким образом, мы решаем уравнение, преобразовывая его — изменяя его внешний вид — оператор за оператором, строка за строкой в соответствии с правилами алгебры, пока x , наконец, не будет изолировано слева. Так пишутся книги по математике (но, к сожалению, не книги по алгебре!). Каждая строка — это собственное читаемое утверждение, которое следует из строки выше — без зачеркивания.
Другими словами, что такое расчет? Это дискретное преобразование символов. В арифметике мы преобразуем «19 + 5» в «24». В алгебре мы преобразуем x + a = b в x = b − a .
Задача 1. Напишите логическую последовательность утверждений, которые будут решать это уравнение для x :
абвх − д + e − f = 0
Чтобы увидеть ответ, проведите мышью слева направо
по цветной области.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
| (1) | abcx − d + e − f | = | 0 | |
| подразумевает | (2) | абс | = | д − д + ж |
| подразумевает | (3) | х | = | d − e + f . абв |
Сначала транспонируйте термы . Линия (2).
Не нужно писать термин 0 справа.
Затем разделите на коэффициент x .
Задача 2. Напишите логическую последовательность утверждений, которые будут решать это уравнение для x :
| (1) | 2 х + 5 | = | 27 | |
| подразумевает | (2) | 2 х | = | 27 — 5 = 22 |
| подразумевает | (3) | х | = | 22 2 |
| подразумевает | (4) | х | = | 11. |
В задачах 3, 4 и 5 дано только решение. Студент должен написать логическую последовательность утверждений, которая приводит к этому.
Задача 3. Решите для x : ( p − q ) x + r = с
| х = | s − r p − q |
Задача 4. Решить для x :
аб ( с + г ) х — е + е = 0
| х = | e − f ab ( c + d ) |
Задача 5. Решите для x : 2 x + 1 = 0
х = -½
Каждое из приведенных выше уравнений имеет стандартную форму, а именно:
ax + b = 0,
не означает .
Это означает коэффициент x . И b не означает b . Это означает любые условия.
Вот почему это называется формой. Что бы ни выглядело как .
| Проблема 6 . Решите: | топор + б | = | 0. | |
| х | = | — | б а | |
Это простое уравнение иллюстрирует выполнение алгебры глазами. Студент должен немедленно увидеть решение. Вы должны увидеть , что b пойдет на другую сторону как − b , а на поделится.
Это навык в алгебре.
Задача 7. Решите для x : x = 0 ( a 0).
Теперь, когда произведение двух чисел равно 0, то хотя бы одно из них должно быть 0. (Урок 6.) Поэтому любое уравнение такой формы имеет решение,
х = 0,
Мы могли бы решить это формально, конечно, разделив на и .
| x = | 0 и | = 0, |
| (Урок 6.) | ||
Задача 8. Решите для x :
| 4 х − 2 | = | −2 |
| 4 x | = | -2 + 2 = 0 |
| x | = | 0. |
Задача 9. Напишите последовательность утверждений, которые будут решать это уравнение:
| (1) | 6 − х | = | 9 |
| (2) | − х | = | 9 − 6 |
| (3) | − х | = | 3 |
| (4) | х | = | −3. |
Когда мы переходим от строки (1) к строке (2), слева остается x . Ибо члены в строке (1) равны 6 и − x .
Мы «решили» уравнение, когда выделили x — а не — x — слева. Поэтому переходим от строки (3) к строке (4), меняя знаки с обеих сторон. (Урок 5.)
В качестве альтернативы мы могли бы исключить − x слева, немедленно изменив все знаки:
| (1) | 6 − х | = | 9 |
| (2) | −6 + х | = | −9 |
| (3) | х | = | -9 + 6 = -3. |
| Задача 10. Решите для x : | 3 − х | = | −5 |
| х | = | 8. | |
Задача 11. Решить для x :
| 4 − (2 x − 1) | = | −11. |
| 4 − 2 x + 1 | = | −11. |
| 5 − 2 x | = | −11 |
| −2 x | = | −11 − 5 |
| 2 x | = | 16 |
| x | = | 8. |
Задача 12. Решить для x :
| 3 x − 15 2x + 1 | = 0, |
( Подсказка : Сравните Урок 6, Задача 18.
)
х = 5,
Транспонирование по сравнению с заменой сторон
| Пример 2. | а + б = в — х |
Мы легко можем решить это — в одну строку — просто переставив x влево, а то, что слева, вправо:
x = c − a − б .
| Пример 3. | а + б = в + х |
В этом примере + x находится справа. Так как мы хотим + x слева, мы можем добиться этого, поменяв местами стороны:
в + х = а + б
Примечание: Когда мы поменяемся сторонами, знаки не изменятся.
При перестановке c решение легко следует:
с + х = а + б — с .
Таким образом, когда − x находится справа, его удобно просто транспонировать. Но когда + x справа, мы можем поменяться сторонами.
Задача 13. Решите для х :
| р + кв | = | г − x − с | |
| Транспонировать: | |||
| х | = | r − s − p − q | |
Задача 14. Решите для x :
| р − к + р | = | с + х | |
| Стороны обмена: | |||
| с + х | = | р − к + р | |
| х | = | р − к + р − с | |
Задача 15.
Решите для x :
| 0 | = | пикс. + кв | |
| пикс. + q | = | 0 | |
| пикселей | = | — | q |
| x | = | — | q p |
Задача 16. Решите для x :
| −2 | = | −5 x + 1 |
| 5 x | = | 1 + 2 = 3 |
| x | = | 3 5 |
Задача 17.
Решите для x :
| р | = | q − топор . |
| топор | = | − |
| x | = | q − p и |
Задача 18. Найти cos θ («косинус thay -ta»).
| А | = | 8 − 2 потому что θ. |
Следует заметить, что это уравнение имеет точно такую же форму , что и задача 17. cos θ — неизвестное. Вы решите ее точно так же, как задачу 17.
| 2 cos θ | = | 8 − А |
| cos θ | = | 8 − А 2 |
Алгебра состоит в распознавании формы.
А их только конечное число.
Раздел 2 :
Отмена
Неизвестность с обеих сторон
Уравнения простых дробей
Содержание | Дом
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Уроки факторинга — Уроки Византа
Несколько предыдущих уроков объясняют методы, используемые для факторизации выражений. Этот урок посвящен важному применению этих методов — решению уравнений.
Зачем решать факторингом?
Самыми основными инструментами для решения уравнений являются сложение, вычитание, умножение и деление. Эти методы хорошо работают для таких уравнений, как x + 2 = 10 – 2x и 2(x – 4) = 0.
А как быть с уравнениями, в которых переменная имеет показатель степени, например x 2 + 3x = 8x – 6? Вот здесь и приходит на помощь факторинг. Мы будем использовать это уравнение в первом примере.
Процесс «Решение с помощью факторинга» потребует четырех основных шагов:
- Переместите все члены в одну часть уравнения, обычно в левую, с помощью сложения или вычитания.
- Полностью разложите уравнение на множители.
- Приравняйте каждый множитель к нулю и решите.
- Перечислите каждое решение из шага 3 как решение исходного уравнения.
Первый пример
x 2 + 3x = 8x – 6
Шаг 1
Первый шаг — переместить все члены влево, используя сложение и вычитание. Сначала мы вычтем 8x с каждой стороны.
x 2 + 3x – 8x = 8x – 8x – 6
x
2 – 5x = -6
Теперь добавим по 6 к каждой стороне.
x 2 – 5x + 6 = -6 + 6
x
2 – 5x + 6 = 0
Со всеми членами в левой части переходим к шагу 2.
Шаг 2
5
5 идентифицируйте левый как трехчлен и разложите его соответственно:
(x – 2)(x – 3) = 0
Теперь у нас есть два множителя, (x – 2) и (x – 3).
Шаг 3
Теперь мы устанавливаем каждый фактор равным нулю. Результатом являются две подзадачи:
x – 2 = 0
и
x – 3 = 0
Решение первой подзадачи, x – 2 = 0, дает x = 2. Решение второй подзадачи, x – 3 = 0, дает х = 3.
Шаг 4
Последний шаг состоит в объединении двух предыдущих решений, x = 2 и x = 3, в одно решение исходной задачи.
x 2 + 3x = 8x – 6
x = 2, 3
Решите факторингом: Почему это работает?
Изучите приведенное ниже уравнение:
ab = 0
Если вы принимаете a = 3, то логически b должно равняться 0. Точно так же, если вы допускаете b = 10, тогда a должно равняться 0.
Теперь попробуйте сделать так, чтобы и были каким-то другим ненулевым числом. Вы должны заметить, что пока a не равно 0,
b должны быть равны нулю.
Чтобы сформулировать наблюдение в более общем виде: «Если ab = 0, то либо a = 0, либо b = 0».
Это важное свойство нуля, которое мы используем при решении с помощью факторизации.
Когда пример был разложен на (x – 2)(x – 3) = 0, это свойство применялось для определения того, что либо (x – 2) должно равняться нулю, либо (x – 3) должно равняться нулю. Таким образом, мы смогли создать два уравнения и определить два решения из этого наблюдения.
Второй пример
5x 3 = 45x
Шаг 1
Переместите все члены в левую часть уравнения. Мы делаем это, вычитая 45x с каждой стороны.
5x 3 – 45x = 45x – 45x
5x
3 – 45x = 0.
Шаг 2
Следующим шагом будет полная факторизация левой стороны. Прежде всего заметим, что два члена слева имеют наибольший общий делитель 5x.
5x(x 2 – 9) = 0
Теперь (x 2 – 9) можно разложить на множители как разницу между двумя квадратами.
5x(x + 3)(x – 3) = 0
У нас осталось три множителя: 5x, (x + 3) и (x – 3).
Как объяснялось в разделе «Почему это работает?» разделе, хотя бы один из трех множителей должен быть равен нулю.
Шаг 3
Создайте три подзадачи, установив каждый фактор равным нулю.
1. 5x = 0
2. x + 3 = 0
3. x – 3 = 0
Решение первого уравнения дает x = 0. Решение второго уравнения дает x = -3. И решение третьего уравнения дает x = 3.
Шаг 4
Окончательное решение формируется из решений трех подзадач.
x = -3, 0, 3
Третий пример
3x 4 – 288x 2 – 1200 = 0
Шаги 1 и 2
Все три члена уже находятся в левой части уравнения, так что мы можем начать разложение. Во-первых, мы выносим за скобки наибольший общий делитель числа 3.
3(x 4 – 96x 2 – 400) = 0
Затем мы факторизуем трехчлен.
3(x 2 + 4)(x 2 – 100) = 0
Наконец, мы факторизуем бином (x 2 – 100) как разницу между двумя квадратами.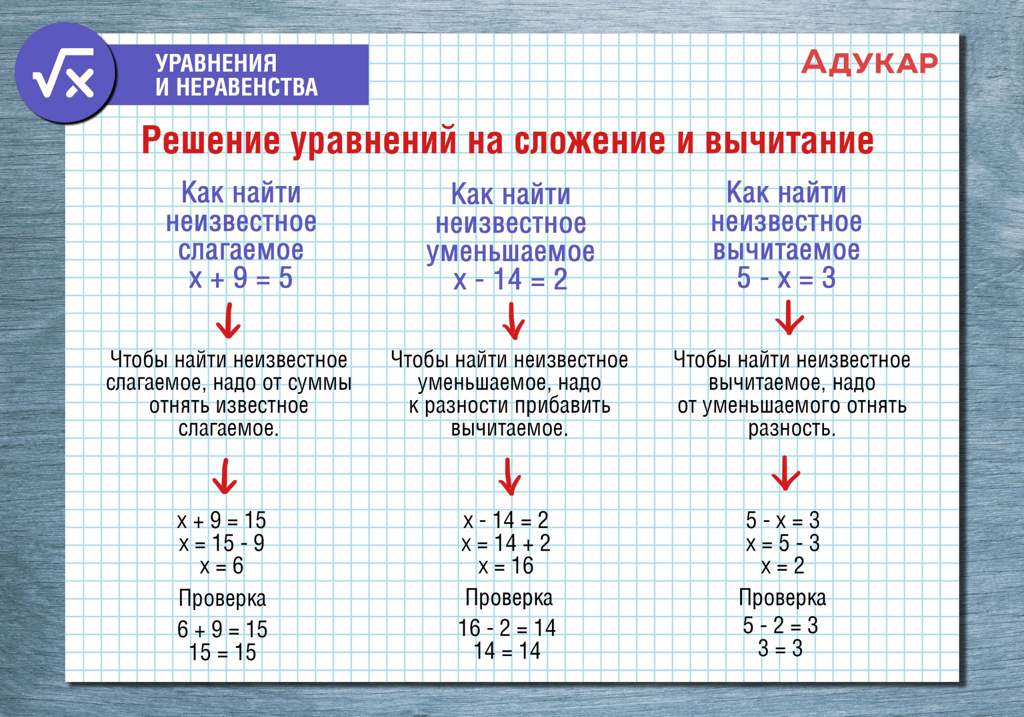
3(х 2 + 4)(x + 10)(x – 10) = 0
Шаг 3
Далее мы устанавливаем каждый из четырех коэффициентов равными нулю, что приводит к четырем новым уравнениям.
1. 3 = 0
2. x 2 + 4 = 0
3. x + 10 = 0
4. x – 10 = 0
Первое уравнение неверно и не дает решения. Второе уравнение не может быть решено с помощью основных методов. (x 2 + 4 = 0 на самом деле имеет два решения для мнимых чисел, но мы прибережем мнимые числа для другого урока!) Уравнение
3 имеет решение x = -10, а уравнение 4 имеет решение x = 10.
Шаг 4
Теперь мы включаем все найденные решения в одно решение исходной задачи:
x = -10, 10
Это может быть сокращено как
x = ±10
Решить с помощью фактора ресурсов
Калькулятор уравнений – Решить с помощью факторинга |
