Матричные уравнения как решать: Матричные уравнения и их решение

Содержание

Как записать простейшее матричное уравнение

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

Обратные матрицы используются при решении матричных уравнений.

Простейшими матричными уравнениями называются соотношения вида: АХ=В и ХА=В, где А,В— известные матрицы, Х – неизвестная.

Если дано уравнение вида АХ=В, то решение выглядит так Х=А -1 В.

Если уравнение вида ХА=В, то Х=ВА -1 .

Непосредственной подстановкой легко установить, что найденное Х является решением соответствующего уравнения.

ПРИМЕРЫ: Решить матричные уравнения.

РЕШЕНИЕ:

Тогда нам дано уравнение вида ХА=В, следовательно Х=ВА -1 . Найдем A -1 .

Тогда нам дано уравнение вида АX=В, следовательно Х=А -1 B. Найдем A -1 .

Как вычислить определитель смотреть здесь.

Как умножать матрицы можно посмотреть здесь.

Как найти обратную матрицу можно посмотреть здесь.

Упражнения к уроку:

Решить матричные уравнения:

Автор: Аникина Анна

Комментарии к этой заметке:

Как можно решить логарифм матрицы простейшем способом?

все очень хорошо. Мог бы переслать Вам ,разработанный мной калькулятор для решения матричных уравнений, но не знаю как это исполнить.Хочется узнать Ваше мнение о нем

А как решить уравнение вроде ХА=В+2Х. Вот что делать с 2Х?

Доброго времени суток, Юлия! Необходимо представить 2Х=Х2Е (Е-единичная матрица соответствующего размера). А далее использовать свойства действий с матрицами.

Решение матричных уравнений: как это делается

Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,

где x — неизвестное.

А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.

Итак, матричным уравнением называется уравнение вида

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Решение матричных уравнений: примеры

Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:

Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Найдём матрицу, обратную матрице B .

Сначала найдём определитель матрицы B :

Найдём алгебраические дополнения матрицы B :

Составим матрицу алгебраических дополнений матрицы B :

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

Находим матрицу, обратную матрице B :

; ;

Причем элементы матриц А и В заданы, а Х₁, Х₂, Х₃ – неизвестные.

Тогда уравнение А × Х = В называется простейшим матричным уравнением.

Чтобы его решить, т.е. найти элементы матрицы неизвестных Х, поступим следующим образом:

1. Умножим обе части уравнения на матрицу А -1 , обратную для матрицы А, слева:

А -1 (А × Х) = А -1 × В

2. Используя свойство умножения матриц, запишем

(А -1 × А) Х = А -1 × В

3. Из определения обратной матрицы

(А -1 × А = Е) имеем Е × Х = А -1 × В.

4. Используя свойство единичной матрицы (Е × Х = Х), окончательно получим Х = А -1 × В

Замечание. Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С -1 справа.

Пример. Решить матричное уравнение

Решение. Введем обозначения

А = ; В = ,

Их определения умножения матриц с учетом размерностей А и В матрица неизвестных Х будет иметь вид

Х =

С учетом введенных обозначений имеем

А × Х = В откуда Х = А -1 × В

Найдем А -1 по алгоритму построения обратной матрицы

Тогда для Х получим

Х = откуда х₁ = 3, х₂ = 2

Ранг матрицы

Рассмотрим матрицу А размера (m x n)

Минором к-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых К строк и любых К столбцов. Очевидно, к £ min (m, n).

Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.

Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором.

Определение. Матрицы, имеющие одинаковые ранги, называются эквивалентными.

Вычисление ранга матрицы

Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках.

Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга:

— умножение всех элементов ряда матрицы на число l ¹ 0;

— замена строк столбцами и наоборот;

— перестановка местами параллельных рядов;

— вычеркивание нулевого ряда;

— прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число.

Пример. Вычислить ранг матрицы

А =

Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (-3).

К четвертой строке прибавим третью.

Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно r(А) = 3.

Системы n линейных уравнений с n неизвестными.

Методы их решения

Рассмотрим систему n линейных уравнений с n неизвестными.

а₁₁х₁ + а₁₂х₂ + … + а₁_nx_n = b₁

Определение: Решением системы (1) называется совокупность чисел (х₁, х₂, …, х_n), которая обращает каждое уравнение системы в верное равенство.

Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1).

A =

Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей.

В =

Матричный метод

Х = — матрица неизвестных;

С = — матрица свободных членов системы (1).

Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения

Решение уравнения (2) изложено выше, то есть Х = А -1 × С, где А -1 – обратная матрица для основной матрицы системы (1).

Метод Крамера

Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:

где D = det А – определитель основной матрицы А системы (1), который называется главным, Dх_i получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т.е.

D = ;

Dх₁ = ;

Dх₂ = ; … ;

Dх_n = ;

Пример. Решить систему уравнений методом Крамера

2х₁ + 3х₂ + 4х₃ = 15

Решение.

Вычислим определитель основной матрицы системы

D = det A = = 44 ¹ 0

Вычислим вспомогательные определители

Dх₁ = = 0;

Dх₂ = = 44;

Dх₃ = = 132.

По формулам Крамера найдем неизвестные

; ; .

Метод Гаусса

Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. в приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы и она приобретает также треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.

Пример. Решить систему уравнений методом Гаусса

3х₁ + 2х₂ + х₃ = 17

Решение. Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.

В =

Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях

Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид:

После умножения второй строки на и сложения ее с третьей строкой матрица А примет треугольный вид. Однако чтобы упростить вычисления можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:

Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим:

Восстановим из полученной матрицы В систему уравнений, равносильную данной

х₁ + 4х₂ — 3х₃ = 9

Из последнего уравнения находим Найденное значение х₃ = 1 подставим во второе уравнение системы, из которого х₂ = 2х₃ = 2 × 1 = 2.

После подстановки х₃ = 1 и х₂ = 2 в первое уравнение для х₁ получим х₁ = 9 — 4х₂ + 3х₃ = 9 — 4 × 2 + 3 × 1 = 4.

Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.

3 × 4 + 2 × 2 + 1 = 17 верно

1.4. Решение матричных уравнений

Систему n линейных уравнений с n неизвестными:

a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n=b₂

. . . . . . . . . . . . . . . . . . .

a_n1x₁+a_n2x_n+…+a_nnx_n=b_n

можно записать в матричной форме ( в виде матричного уравнения), если матрицу из коэффициентов при неизвестных обозначить через А, матрицу-столбец из неизвестных – через X и матрицу столбец свободных членов – через В, т. е.

А·Х=В. (1)

Пусть определитель матрицы А не равен 0.Чтобы решить уравнение (1), то есть найти неизвестную матрицу Х, умножим его на А

-1 слева:

А^-1·А·Х= А^-1·В.

Так как А^-1·А=Е и ЕХ=Х, то получаем решение матричного уравнения (1) в виде

Х= А^-1·В.

Таким же образом можно решать любые матричные уравнения, если соответствующие обратные матрицы существуют.

Пример. Найти неизвестную матрицу Х из уравнения:

Х =.

Решение. Обозначим данные матрицы соответственно буквами А, В и С. В результате получим следующее матричное уравнение:

А·Х·В=С.

Предположим, что А^-1 и В^—¹ существуют.

Чтобы найти матрицу Х, умножим данное уравнение на А^-1 слева:

А^-1·А·Х·В= А^-1·С, или Х·В= А^-1·С.

Далее умножим полученное уравнение на обратную матрицу В^-1 справа. В результате получаем решение:

Х= А^-1·С·В^—¹.

Находим обратные матрицы для А и В:

А^-1= , B^-1=

Полученные обратные матрицы А^-1 и В^-1 подставляем в равенство:

Х= А^-1^.С^. B^-1:

Х= А^-1^.С^. B^-1===

Следовательно, Х= .

Проверку можно осуществить, подставляя матрицу Х в исходное уравнение:

=, т. е. =.

Упражнения.

Записать систему линейных уравнений в виде матричного уравнения и решить его:

2х₁-x₂-x₃=4 x₁+2x₂+4x₃=31

1.4.1. 3x₁+4x₂-2x₃=11 1.4.2. 5x₁+x₂+2x₃=29

3x₁-2x₂+4x₃=11 3x₁-x₂+x₃=10

x₁+x₂+x₃+x₄=2 2x₁+x₂=1

x₁

+2x₂+3x₃+4x₄=3 3x₁+2x₂=1

1.4.3. x₁+4x₂+9x₃+16x₄=3 1.4.4. x₁+х₂+3x₃+4x₄=1

x₁+8x₂+27x₃+64x₄=-9 2x₁-x₂+2x₃+3x₄=1

Найти неизвестную матрицу Х из уравнений:

1. 4.5.Х= 1.4.6.Х=

1.4.7.Х=

1.4.8. Х=

1.4.9.Х=

1.4.10.Формулы поворота осей координат на угол имеют вид:

x₂=x₁cos-y₁sin

y₂=x₁sin+y₁cos

Найти обратные соотношения, записав систему уравнений в матричной форме и разрешив полученное уравнение относительно х

1 и у₁.

Найти результат последовательного выполнения двух линейных преобразований с помощью произведения соответствующих матриц:

1.4.11. x₁=3y₁-y₂ y₂=4z₁+z₂

x₂=2y₁+3y₂ y₂=-2z₁+z₂

1.4.12. z₁= 2x₁-x₂ x₁=y₁+2y₁

z₂=x₁+3x₂ x₂=-3y₁+y₂

x₁=3y₁-y₂ y₁=2z₁+z₂-3z₃

4.13. x₂=y₁+2y₂-y₃ y2=z₁+2z₂

x₃=3y₂+2y₃ y3=z₁+4z₁

z₁=x₁+3x₃ x₁=-y₁+y₂-y₃

1.4.14. z₂=2x₁-x₂ x₂=2y₁+3y₂

z₃=x₁+x₂+x₃ x₃=4y₁

Найти линейные преобразования, обратные следующим преобразованиям:

1.4.15. x₁=y₁+2y₂y₁=2x₁+2x₂+3x₃

x₂=3y₁+4y₂

1.4.6y₂=x₁-x₂

y₃=-x₁+2x₂+x₃

x₁=y₁+y₃

1. 4.17. x₂=y₂

x₃=2y₂+2y₃

1.6. Матричные уравнения. Матричная запись СЛАУ. Формулы Крамера

1.6. Матричные уравнения. Матричная запись СЛАУ. Формулы Крамера

Высшая математика > 1. Элементы линейной алгебры > 1.6. Матричные уравнения. Матричная запись СЛАУ. Формулы Крамера

Рассмотрим два типа матричных уравнений:
1.

Теорема 1

Для матричного уравнения: решение находится по формуле: .

Доказательство

Пусть — невырожденная матрица, то есть , из этого следует, что существует обратная матрица Умножим матричное уравнение слева на , получим: , , откуда: .

Пусть дана СЛАУ -ого порядка: .

Рассмотрим следующие матрицы: матрицу системы: , столбец неизвестных: и столбец свободных членов: .

Теорема 2
Матричная запись СЛАУ имеет вид: .
Доказательство
Перемножим матрицы: .

Замечание 1
Очевидно, что матричная запись СЛАУ это частный случай 1-ого типа матричных уравнений (при ), поэтому ее решение также находится по формуле: .

Пример 1
Решить матричным методом СЛАУ: .
Замечание 2
Решение этой системы мы уже находили по формулам Крамера.
Решение
Выпишем матрицу системы: , столбец неизвестных: и столбец свободных членов: . Определитель системы: . Находим обратную матрицу: . Тогда решение системы в матричной форме имеет вид: , следовательно: .

Вернемся к теореме 4 из пункта 1.2. Ранее эта теорема была оставлена без доказательства, теперь мы уже можем ее доказать.

Теорема 1.2.4

Если определитель СЛАУ -ого порядка отличен от нуля , то системе имеет, и притом единственное, решение, которое может быть найдено по формулам Крамера: , ,:,.

Доказательство

При решение системы может быть найдено матричным методом, то есть: .

Вспомним, что в формулах Крамера вспомогательные определители получаются из определителя системы заменой столбца коэффициентов при неизвестном столбцом свободных членов, то есть: , где . Разложим эти определители по элементам -ого столбца: и подставим эти разложения в решение системы, получим: , где — определитель системы. Отсюда следует, что решение системы действительно может быть найдено по формулам Крамера: , ,:,, при .

2. .

Теорема 3
Для матричного уравнения решение находится по формуле: .
Доказательство
Пусть — невырожденная матрица, то есть , из этого следует, что существует обратная матрица . Умножим матричное уравнение справа на , получим: , , откуда: .

Пример 2
Решить матричное уравнение: .
Решение
, . Так как , то существует обратная матрица . Тогда решение матричного уравнения имеет вид: .

gif»>

16.5: Решение систем уравнений с матрицами

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 55335

Jacob Moore & Contributors
Pennsylvania State University Mont Alto via Mechanics Map

Система уравнений — это любой набор уравнений, которые имеют общие переменные. Линейное уравнение — это уравнение, полностью состоящее из констант и простых переменных. Эти переменные можно умножать только на константу, их нельзя умножать вместе, возводить в степень, использовать для логарифмических или квадратных корней или выполнять другие, более сложные математические функции. Ниже приведен пример системы линейных уравнений.

\[ F_{AX} + F_{BX} = 0 \]

\[ F_{AY} — 8 = 0 \]

\[-16 + 4 F_{AY} + 8 F_{AX} = 0 \]

В таких курсах, как статика и динамика, мы часто сталкиваемся с системой линейных уравнений и должны найти неизвестные в этих уравнениях. Когда в нашей системе всего несколько уравнений, мы обычно решаем уравнения вручную, используя алгебраические методы, такие как подстановка или исключение, сложение или вычитание. Для более крупных и сложных задач мы можем столкнуться с более крупными системами уравнений, и в какой-то момент математику может стать трудно обрабатывать вручную. Для этих больших систем линейных уравнений самый простой способ найти неизвестные — это преобразовать систему уравнений в одно матричное уравнение, а затем использовать компьютерные инструменты для решения матричного уравнения для неизвестных. Некоторые компьютерные инструменты позволяют вам вводить систему уравнений вручную, но в фоновом режиме компьютер, вероятно, просто преобразует ее в матричное уравнение в фоновом режиме. По этой причине может быть полезно понять этот процесс.

Что касается предположений, важно отметить, что этот метод будет работать только с системами из линейных уравнений , а чтобы получить разрешимое матричное уравнение, нам потребуется столько же уравнений, сколько и неизвестных переменных . Например, выше у нас есть система уравнений с тремя уравнениями и тремя неизвестными переменными. Если эти числа не совпадают, мы не сможем решить матричное уравнение описанным ниже методом.

Преобразование системы уравнений в матричное уравнение:

Первым шагом в преобразовании системы уравнений в матричное уравнение является преобразование уравнений в согласованный формат. Обычно мы помещаем все переменные с их коэффициентами на одну сторону уравнения, а константы — на другую сторону уравнения. Кроме того, лучше всего перечислять переменные в одном и том же порядке в каждом уравнении. Этот процесс перестановки уравнений в дальнейшем облегчит преобразование.

Рисунок \(\PageIndex{1}\): Чтобы преобразовать систему уравнений в одно матричное уравнение, мы сначала переставим уравнения в определенном порядке. Затем выпишем коэффициентную (\(A\)), переменную (\(X\)) и постоянную (\(B)\) матрицы.

Далее мы начнем процесс записи трех матриц, составляющих матричное уравнение. Этими тремя матрицами являются матрица коэффициентов (часто называемая матрицей \(A\)), матрица переменных (часто называемая матрицей \(X\)) и постоянная матрица (часто называемая матрицей \( Б\) матрица).

Матрица коэффициентов (или матрица \(A\)) представляет собой матрицу \(N \times N\) (где \(N\) — количество уравнений / количество неизвестных переменных), которая содержит все коэффициенты для переменных. Каждая строка матрицы представляет собой одно уравнение, а каждый столбец представляет одну переменную (иногда полезно записывать переменную вверху каждого столбца). Для случаев, когда переменная не фигурирует в уравнении, мы принимаем коэффициент равным 0,9.0010
Матрица переменных (или матрица \(X\)) представляет собой матрицу \(N \times 1\), которая содержит все неизвестные переменные. Важно, чтобы порядок переменных в матрице коэффициентов соответствовал порядку переменных в матрице переменных.
Наконец, с другой стороны знака равенства мы имеем константную матрицу (или матрицу \(B\)). Это матрица \(N \times 1\), содержащая все константы из правой части уравнений. Важно, чтобы порядок констант соответствовал порядку уравнений в матрице коэффициентов.

После настройки трех матриц мы готовы найти неизвестные в матрице переменных.

Решение матричного уравнения:

Начиная с наших матриц \(A\), \(X\) и \(B\) в матричном уравнении ниже, мы ищем решения для значений неизвестных переменных, которые содержатся в нашей матрице \(X\).

\[ [A][X] = [B] \]

Для скалярного уравнения мы бы просто сделали это, разделив обе части на \(A\), где значение для \(X\) будет \(Б/А\). Вместо этого с матричным уравнением нам нужно будет умножить обе части уравнения на обратную матрицу \(A\). Это отменит матрицу \(A\) в левой части, оставив только искомую матрицу \(X\). Слева у нас будет обратная матрица \(A\), умноженная на матрицу \(B\). Результатом этой операции будет матрица \(N \times 1\), содержащая решение для всех переменных. Значение в каждой строке решения будет соответствовать переменной, указанной в той же строке матрицы \(X\). 9{-1} [B] \]

Можно найти обратную матрицу \(A\) вручную, а затем умножить ее на матрицу \(B\), но этот процесс займет больше времени, чем просто решение уравнения с помощью алгебры. Истинная сила метода заключается в том, что компьютерные инструменты, такие как MATLAB или Wolfram Alpha, могут выполнять обращение и умножение матриц за вас.

Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром.

Источник YouTube: https://youtu.be/ZLaeFbqR9QU.

Пример \(\PageIndex{1}\)

Уравнения равновесия тела, показанного ниже, перечислены справа. Преобразуйте систему уравнений в одно матричное уравнение и найдите неизвестные.

Рисунок \(\PageIndex{2}\): схема проблемы для примера \(\PageIndex{1}\). Система уравнений для решения сил, действующих на вертикальный столб, прикрепленный к земле.

Решение:: Видео \(\PageIndex{2}\): рабочее решение примера проблемы \(\PageIndex{1}\), предоставленное доктором Джейкобом Муром. Источник YouTube: https://youtu.be/QX-hJhXTEe0.

Эта страница под названием 16.5: Решение систем уравнений с матрицами распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) посредством исходного содержимого, которое было отредактировано для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Джейкоб Мур и авторы
Лицензия
CC BY-SA
Версия лицензии
4,0
Показать оглавление
нет
Теги
1. источник@http://mechanicsmap.psu.edu

Объяснение урока: Решение системы двух уравнений с использованием обратной матрицы

В этом пояснении мы научимся решать систему двух линейных уравнений используя обратную матрицу коэффициентов.

Мы можем решить систему двух линейных уравнений, которые также называются одновременных уравнений, используя методы замены или исключения, так что это справедливо спросить, почему нам нужно изучать другой метод для решения той же системы. Фактически, использование обратной матрицы для решения системы двух линейных уравнений более сложный, чем предыдущие два метода, что еще больше оправдывает это вопрос. Мы изучаем этот метод как модель для понимания взаимосвязи между системой линейных уравнений и матрицами. Поскольку система двух линейные уравнения — это простейшая модель, связывающая систему уравнений с матрицы, имеет смысл начать отсюда.

Метод, который мы изучим в этом объяснении, может быть использован для системы, содержащей большее количество линейных уравнений и неизвестных переменных, хотя мы не будем обсуждайте большие системы здесь. Хотя не так уж сложно решить систему два линейных уравнения без использования матриц, сделать это сложнее когда у нас есть три или более уравнений. Понимание отношений между системой линейных уравнений и матриц позволяет организовать заданную систему уравнений в краткое матричное уравнение, которое можно решить с помощью метод, аналогичный тому, что мы обсудим здесь.

Прежде чем мы обсудим, как решать одновременные уравнения с использованием матриц, нам нужно понять, как решить матричное уравнение. Вспомните обратную матрицу.

Определение: обратные матрицы

Для квадратной матрицы 𝐴 обратная матрица 𝐴 — квадратная матрица тот же заказ удовлетворяет 𝐴𝐴=𝐴𝐴=𝐼, где 𝐼 — единичная матрица того же порядка. Если такая матрица существует, мы говорим, что матрица 𝐴 обратима.

Рассмотрим матричное уравнение 𝐴𝑋=𝐵, где 𝐴 и 𝐵 известны 𝑛×𝑛 и матрицы 𝑛×𝑘 соответственно и 𝑋 — неизвестная матрица 𝑛×𝑘. Мы далее предполагаем, что 𝐴 — обратимая матрица. Мы знаем, что для умножения пара матриц, количество столбцов первой матрицы должно быть равно количество строк второй матрицы. Мы видим, что умножение матриц 𝐴𝑋 хорошо определен.

Поскольку матрица 𝐴 обратима, существует 𝑛×𝑛 обратная матрица 𝐴. Умножая слева на 𝐴 с обеих сторон уравнения 𝐴𝑋=𝐵 получаем

𝐴𝐴𝑋=𝐴𝐵.

(1)

В левой части уравнения мы знаем, что 𝐴𝐴=𝐼, где 𝐼 — мультипликатив личность. Следовательно, 𝐴𝐴𝑋=𝐼𝑋=𝑋.

Подставляя это выражение в левую часть уравнения (1), мы можем написать 𝑋=𝐴𝐵.

Обе матрицы 𝐴 и 𝐵 известны; следовательно, это дает решение матричного уравнения 𝐴𝑋=𝐵.

Практическое руководство. Решение матричных уравнений

Пусть 𝐴 — обратимая матрица, а 𝐵 — матрица такое, что умножение 𝐴𝐵 определено. Матрица 𝑋 удовлетворяющее уравнению 𝐴𝑋=𝐵 определяется выражением 𝑋=𝐴𝐵.

Этот метод позволяет решить любое матричное уравнение вида 𝐴𝑋=𝐵, если матрица 𝐴 обратима. Однако этот метод нельзя использовать, если 𝐴 необратима. Это может произойти, если 𝐴 не является квадратной матрицей или если 𝐴 является квадратным и det𝐴=0. В таких случаях, матричное уравнение либо имеет бесконечное число решений, либо не имеет решения. В качестве простого примера мы можем представить случай, когда 𝐴=𝑂, где 𝑂 — нулевая матрица.

Мы знаем, что 𝑂 необратима, так как дет𝑂=0. Матричное уравнение 𝑂𝑋=𝐵 имеет нет решения, если 𝐵 ненулевая матрица, так как умножение нулевой матрицы любой матрицей приводит к нулевой матрице. С другой стороны, если 𝐵 — нулевая матрица естественного порядка, полученная из этого умножение матриц, любая матрица 𝑋 удовлетворяет уравнению 𝑂𝑋=𝑂. Это означает, что данное матричное уравнение имеет бесконечный количество решений.

В нашем первом примере мы будем решать матричное уравнение, используя обратную матрицу.

Пример 1. Решение уравнений матриц с использованием их обратных значений

Учитывая, что 𝐴=2−5−8−9,𝐴𝑥𝑦=−28, каково значение 𝑦?

Ответ

В этом примере нам дано матричное уравнение. Матрица 𝑥𝑦 неизвестно матрица. Если мы найдем эту матрицу, мы можем найти значение 𝑦.

Пример не дает нам, что такое матрица 𝐴, но это дает нам обратную этой матрице 𝐴. Напомним, что обратная квадратная матрица 𝐴, если она существует, является матрица, удовлетворяющая 𝐴𝐴=𝐴𝐴=𝐼, где 𝐼 — единичная матрица. Мы можем умножить из слева от 𝐴 по обе стороны данного уравнения к получать 𝐴𝐴𝑥𝑦=𝐴−28.

Мы знаем, что 𝐴𝐴=𝐼, что является мультипликативным тождество, поэтому мы можем пренебречь множителем 𝐴𝐴 и заполнить в представленном выражении для 𝐴 справа сторона, чтобы написать 𝑥𝑦=2−5−8−9−28.

Вычисляя это умножение матриц, получаем 𝑥𝑦=2×(−2)+(−5)×8(−8)×(−2)+(−9)×8=−44−56.

Это приводит к неизвестной матрице. Мы знаем, что две матрицы равны если каждая пара соответствующих элементов в матрицах равны.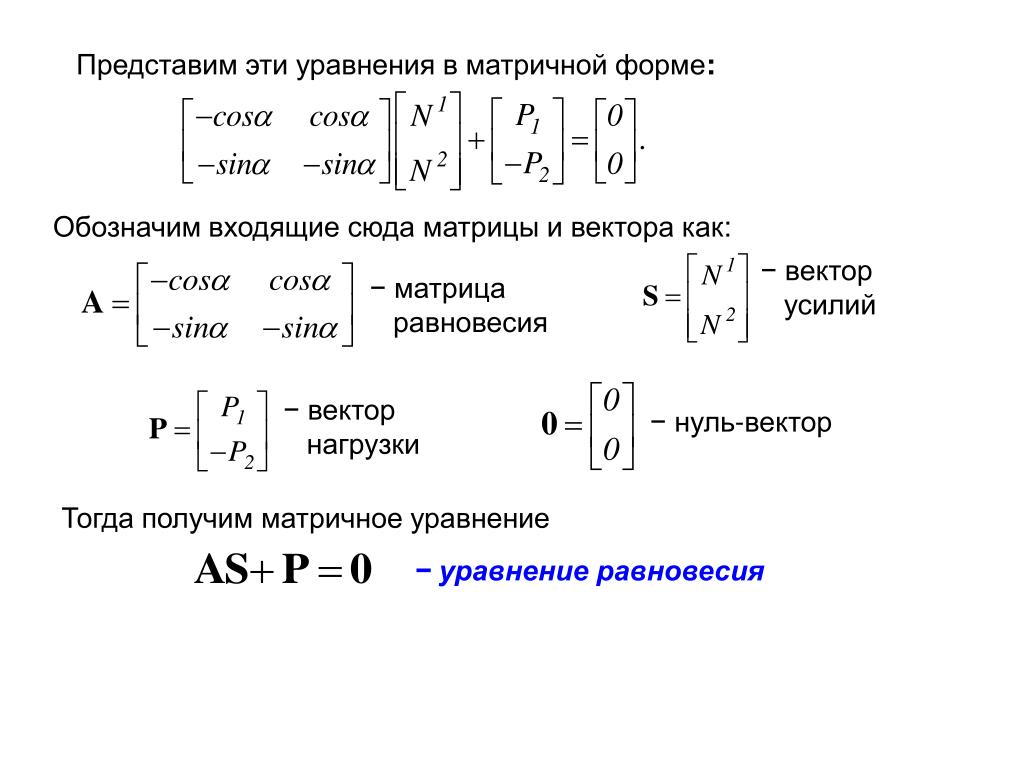 Следовательно, это приводит к 𝑥=−44, 𝑦=−56.

В частности, в примере запрашивается значение 𝑦, которое равно 𝑦=−56.

В предыдущем примере мы решили матричное уравнение, когда нам дали обратная матрица 𝐴. Если нам не задано выражение для 𝐴 мы можем найти обратную матрицу, используя следующей формуле, если det𝐴≠0.

Формула: обратная матрица 2 × 2

Пусть 𝐴=𝑎𝑏𝑐𝑑 такой, что det𝐴≠0. Затем, 𝐴=1𝐴𝑑−𝑏−𝑐𝑎,det где det𝐴=𝑎𝑑−𝑏𝑐. Если det𝐴=0, матрица 𝐴 не является обратимым.

Рассмотрим пример, в котором мы решаем матричное уравнение сначала найти обратную матрицу 2×2.

Пример 2. Решение уравнений матриц с использованием их обратных значений

Учитывая, что 581−8𝑥𝑦=−431, определить значения 𝑥 и 𝑦.

Ответ

В этом примере нам дано матричное уравнение. Матрица 𝑥𝑦 неизвестно матрица. Если мы найдем эту матрицу, мы можем найти значения 𝑥 и 𝑦.

Напомним, что для заданных матриц 𝐴 и 𝐵 неизвестная матрица 𝑋, удовлетворяющая уравнению 𝐴𝑋=𝐵 дается 𝑋=𝐴𝐵, если существует обратная матрица 𝐴 и матрица умножение 𝐴𝐵 может быть определено. В нашем задании например, эта матрица 𝐴 соответствует Матрица 2×2 581−8. Следовательно, это можно записать как

𝑥𝑦=581−8−431,

(2)

если обратная матрица существует и умножение матриц корректно определено. Следовательно, нам нужно начать с нахождения обратной этой матрицы, если она существуют.

Мы знаем, что обратная квадратная матрица существует, если ее определитель не равен до нуля. Сначала вычислим определитель этой матрицы. Мы знаем это дет𝑎𝑏𝑐𝑑=𝑎𝑑−𝑏𝑐.

Применяя эту формулу к заданной матрице 2×2, det581−8=5×(−8)−8×1=−48.

Поскольку определитель отличен от нуля, мы можем перейти к поиску его обратного. Мы вспомните формулу обратной матрицы 2 × 2: 𝐴=1𝐴𝑑−𝑏−𝑐𝑎.det

Следовательно, используя найденный ранее определитель матрицы, 581−8=1−48−8−8−15.

Подставив это выражение в уравнение (2), 𝑥𝑦=1−48−8−8−15−431.

Мы знаем, что для умножения пары матриц количество столбцов первой матрицы должно быть равно количеству строк второй матрицы. Вычисляя это матричное умножение, мы получаем 𝑥𝑦=1−48(−8)×(−43)+(−8)×1(−1)×(−43)+5×1=1−4833648.

Наконец, вычислив скалярное умножение, 𝑥𝑦=⎛⎜⎜⎝336−4848−48⎞⎟⎟⎠=−7−1.

Это приводит к неизвестной матрице. Мы знаем, что пары матриц равны, если каждая пара соответствующих элементов в матрицах равны. Следовательно, это приводит к 𝑥=−7,𝑦=−1.

До сих пор мы рассмотрели несколько примеров решения матричных уравнений используя обратную матрицу. Обратим внимание на систему двух линейных уравнения.

Практическое руководство. Представление систем двух уравнений в виде матричных уравнений

Рассмотрим систему уравнений, заданную формулой 𝑎𝑥+𝑏𝑦=𝑒,𝑐𝑥+𝑑𝑦=𝑓, для некоторых известных констант 𝑎, 𝑏, 𝑐, 𝑑, 𝑒, 𝑓. Мы можем написать эту систему двух уравнения как одно матричное уравнение 𝑎𝑏𝑐𝑑𝑥𝑦=𝑒𝑓.

Если мы выполним умножение матриц в левой части матричного уравнения, это будет то же самое, что и 𝑎𝑥+𝑏𝑦𝑐𝑥+𝑑𝑦=𝑒𝑓.

Приравнивание соответствующих элементов матриц с обеих сторон этой уравнение приводит обратно к системе двух линейных уравнений. Следовательно, эта матрица уравнение эквивалентно системе двух линейных уравнений. Поскольку мы можем написать система уравнений в виде матричного уравнения, мы можем решить эту систему, используя обратная матрица.

Мы видим, что коэффициенты 𝑥 и 𝑦 в системе уравнений стала матрицей 2×2 в матричное уравнение. Это называется матрицей коэффициентов, потому что ее элементы получаются из коэффициентов совместных уравнений. При написании матрица коэффициентов, нам нужно быть осторожным с порядком элементов. Поскольку переменная матрица имеет 𝑥 в качестве первого элемента, коэффициенты 𝑥 идут в первом столбце. Следовательно, тот же матрица коэффициентов используется, даже если первое уравнение в системе написано как 𝑏𝑦+𝑎𝑥=𝑒. Вместо того, чтобы следовать порядку написания коэффициентов в данном уравнении нужно рассмотреть, какой переменной является коэффициент из.

Отметим также, что матрица-столбец в правой части матрицы уравнение содержит постоянные члены из правых частей одновременные уравнения. Порядок этих констант должен соответствовать матрица коэффициентов. Поскольку коэффициенты первого уравнения 𝑎𝑥+𝑏𝑦=𝑒, записываются в первой строке коэффициента матрица, константа 𝑒 из этого уравнения также должна появиться в первой строке этого матричного уравнения.

Как мы обсуждали при решении матричных уравнений, это также означает, что система уравнений либо не имеет решения, либо имеет бесконечное число решений, когда матрица коэффициентов необратима.

В следующем примере мы запишем пару одновременных уравнений в матричное уравнение, а затем решить матричное уравнение, используя обратную матрицу.

Пример 3. Решение пары одновременных уравнений с использованием матриц

Рассмотрим одновременные уравнения 4𝑥−2𝑦=0,3𝑦+5𝑥=−11.

Выразите данные одновременные уравнения в виде матричного уравнения.
Запишите обратную матрицу коэффициентов.
Умножьте на обратное в левой части, чтобы решить матричное уравнение.

Ответ

Часть 1

Напомним, что пара одновременных уравнений, заданная формулой 𝑎𝑥+𝑏𝑦=𝑒,𝑐𝑥+𝑑𝑦=𝑓 можно записать в виде матричного уравнения 𝑎𝑏𝑐𝑑𝑥𝑦=𝑒𝑓.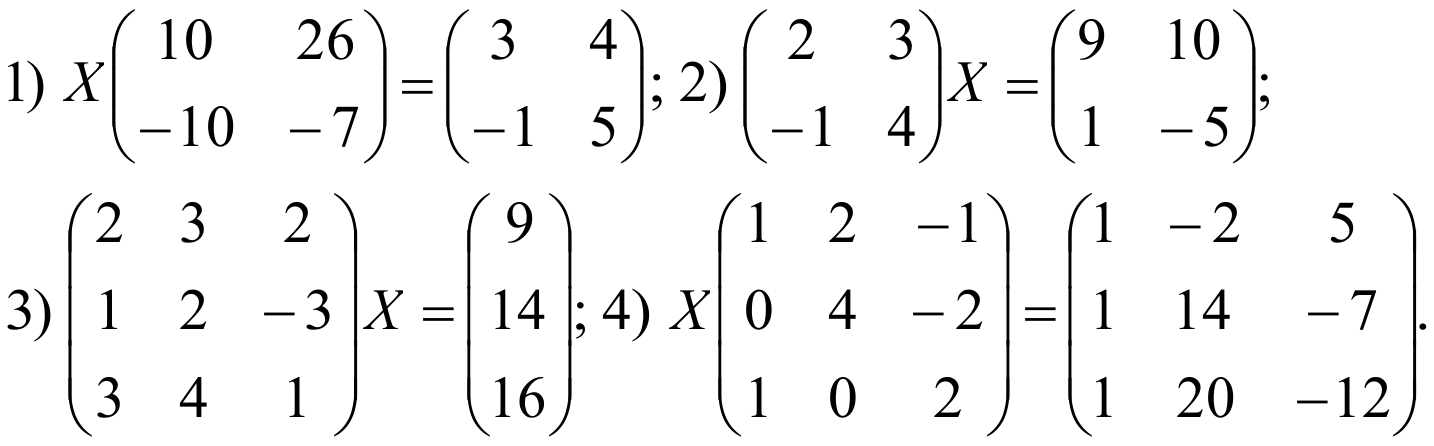

Здесь важно отметить, что матрица коэффициентов 𝑎𝑏𝑐𝑑 — коэффициент одновременные уравнения в порядке, указанном в переменной матрице 𝑥𝑦. Это означает, что первый столбец матрица коэффициентов содержит коэффициенты переменной 𝑥, а второй столбец содержит коэффициенты переменной 𝑦. В частности, мы должны сначала заметить, что 5𝑥 и 3𝑦 записываются наоборот заказ. Мы можем изменить эту пару одновременных уравнений, чтобы сказать 4𝑥−2𝑦=0,5𝑥+3𝑦=−11.

Тогда мы можем написать 4−253𝑥𝑦=0−11.

Часть 2

В этой части нам нужно найти обратную матрицу коэффициентов. в предыдущей части мы нашли матрицу коэффициентов 4−253. Мы знаем, что обратная квадратная матрица существует, если ее определитель не равен до нуля. Сначала вычислим определитель этой матрицы. Мы знаем это дет𝑎𝑏𝑐𝑑=𝑎𝑑−𝑏𝑐.

Применяя эту формулу к матрице коэффициентов, det4−253=4×3−(−2)×5=22.

Поскольку определитель отличен от нуля, мы можем перейти к поиску его обратного. Напомним формулу обратной матрицы 2×2: 𝐴=1𝐴𝑑−𝑏−𝑐𝑎.det

Следовательно, используя найденный ранее определитель матрицы, 4−253=12232−54.

Часть 3

В этой части нам нужно умножить на обратный слева сторону и решить матричное уравнение. Начнем с матричного уравнения 4−253𝑥𝑦=0−11.

Умножение обеих частей уравнения на обратный коэффициент матрица, у нас есть 4−2534−253𝑥𝑦=4−2530−11.

В левой части этого уравнения обратный коэффициент матрица умножается на матрицу коэффициентов. Напомним, что для любого обратимая матрица 𝐴, имеем 𝐴𝐴=𝐼, где 𝐼 — единичная матрица. Это означает 4−2534−253=𝐼.

Поскольку 𝐼 — единичная матрица, которая умножается на переменная матрица, этим членом можно пренебречь. Это ведет к 𝑥𝑦=4−2530−11. 

Теперь мы можем заменить обратную матрицу из предыдущей части: 𝑥𝑦=12232−540−11.

Вычисляя это умножение матриц, получаем 𝑥𝑦=1223×0+2×(−11)−5×0+4×(−11)=122−22−44.

Наконец, вычислив скалярное умножение, 𝑥𝑦=⎛⎜⎜⎝−2222−4422⎞⎟⎟⎠=−1−2.

Следовательно, решение матричного уравнения есть 𝑥𝑦=−1−2.

В предыдущем примере мы решили матричное уравнение, соответствующее заданному пара одновременных уравнений. Хотя мы не проверяли это явно, это можно показать, что значения, которые мы нашли для 𝑥 и 𝑦 удовлетворяют заданным совместным уравнениям. В следующий задачу, мы решим пару одновременных уравнений с помощью матриц.

Пример 4. Решение системы двух уравнений с использованием матриц

Использование матриц для решения системы −𝑥+5𝑦=8,−3𝑥+𝑦=8.

Ответ

В этом примере нам нужно решить систему двух линейных уравнений по формуле с помощью матриц. Мы знаем, что можем написать систему двух линейных уравнения в эквивалентное матричное уравнение. Вспомним этот процесс. Учитывая систему уравнений 𝑎𝑥+𝑏𝑦=𝑒,𝑐𝑥+𝑑𝑦=𝑓, мы можем написать эквивалентное матричное уравнение 𝑎𝑏𝑐𝑑𝑥𝑦=𝑒𝑓.

Здесь важно отметить, что матрица коэффициентов 𝑎𝑏𝑐𝑑 — коэффициент одновременных уравнений в порядке, указанном в переменной матрица 𝑥𝑦. Это означает, что первый столбец коэффициента матрица содержит коэффициенты переменной 𝑥, а вторая столбец содержит коэффициенты переменной 𝑦.

Заметим, что переменная 𝑥 в первом уравнении есть только сопровождается отрицательным знаком. Это свидетельствует о том, что коэффициент 𝑥 в этом уравнении равно −1. Так же переменная 𝑦 во втором уравнении не отображает никаких означает, что его коэффициент равен 1. Мы можем переписать эта пара одновременных уравнений с этой информацией: −1𝑥+5𝑦=8, −3𝑥+1𝑦=8.

Тогда мы можем написать матричное уравнение

−15−31𝑥𝑦=88.

(3)

Это матричное уравнение можно решить, умножив слева обратное матрицы коэффициентов −15−31, если она существует. Мы знаем, что обратная квадратная матрица существует, если ее определитель не равен нулю. Позволь нам сначала вычислить определитель этой матрицы. Мы знаем это дет𝑎𝑏𝑐𝑑=𝑎𝑑−𝑏𝑐.

Применяя эту формулу к матрице коэффициентов, det−15−31=(−1)×1−5×(−3)=14.

Следовательно, используя найденный ранее определитель матрицы, −15−31=1141−53−1.

Напомним, что для любой обратимой матрицы 𝐴 имеем 𝐴𝐴=𝐼, где 𝐼 — единичная матрица. Это означает, что мы будем иметь возможность удалить матрицу коэффициентов из левой части уравнения (3) путем умножения слева обратная матрица коэффициентов. Умножение обеих частей уравнения обратной матрице коэффициентов, имеем 𝑥𝑦=1141−53−188.

Мы знаем, что для перемножения пары матриц необходимо количество столбцы первой матрицы должны быть равны количеству строк второй матрица. Мы видим, что умножение матриц в правой части приведенного выше уравнения корректно определено. Вычисляя это матричное умножение, мы получаем 𝑥𝑦=1141×8+(−5)×83×8+(−1)×8=114−3216.

Наконец, вычислив скалярное умножение, 𝑥𝑦=⎛⎜⎜⎝−32141614⎞⎟⎟⎠=⎛⎜⎜⎝−16787⎞⎟⎟⎠.

Это дает нам решение матричного уравнения 𝑥𝑦=⎛⎜⎜⎝−16787⎞⎟⎟⎠.

Мы знаем, что пара матриц равна, если каждая пара соответствующих записи равны. Отсюда получаем решение заданной системы уравнения 𝑥=−167, 𝑦=87.

В нашем последнем примере мы решим реальную задачу, связанную с системой два уравнения с использованием матриц.

Пример 5.

Решение двух уравнений с двумя неизвестными с использованием матриц

Длина прямоугольника на 6 см больше его ширины и длины в два раза. на 39 см больше чем его ширина. Учитывая это, используйте матрицы для определения периметра прямоугольника.

Ответ

В этом примере нам нужно найти периметр прямоугольника, длина и ширина соотносятся согласно данному описанию. Мы знаем что периметр прямоугольника равен удвоенной сумме его длин и ширина. Начнем с обозначения длины и ширины прямоугольника неизвестными константами 𝑥 и 𝑦 соответственно. Затем, периметр=2(𝑥+𝑦).

Давайте начнем с записи отношения между 𝑥 и 𝑦 в виде уравнений. Во-первых, нам дано, что длина прямоугольника 6 см более чем в два раза его ширина. Это можно записать как 𝑥=2𝑦+6.

Во-вторых, нам известно, что удвоенная длина равна на 39 см больше своего ширина. Это можно записать как 2𝑥=39+𝑦.

Переформулируем эти уравнения так, чтобы левые части уравнения содержат переменные, а правые части содержат константы: 𝑥−2𝑦=6,2𝑥−𝑦=39.

Теперь решим эту систему уравнений с помощью матриц. Напомним, что система уравнений 𝑎𝑥+𝑏𝑦=𝑒,𝑐𝑥+𝑑𝑦=𝑓 можно записать в виде матричного уравнения 𝑎𝑏𝑐𝑑𝑥𝑦=𝑒𝑓.

Следовательно, мы можем записать нашу систему уравнений в виде

1−22−1𝑥𝑦=639.

(4)

Это матричное уравнение можно решить, умножив слева обратное матрицы коэффициентов 1−22−1, если она существует. Мы знаем, что обратное квадратной матрицы существует, если ее определитель не равен нулю. Давайте сначала вычислить определитель этой матрицы. Мы знаем это дет𝑎𝑏𝑐𝑑=𝑎𝑑−𝑏𝑐.

Применяя эту формулу к матрице коэффициентов, det1−22−1=1×(−1)−(−2)×2=3.

Поскольку определитель отличен от нуля, мы можем перейти к поиску его обратного. Мы вспоминаем формула обратной матрицы 2 × 2: 𝐴=1𝐴𝑑−𝑏−𝑐𝑎.det

Следовательно, используя найденный ранее определитель матрицы, 1−22−1=13−12−21.

Напомним, что для любой обратимой матрицы 𝐴 имеем 𝐴𝐴=𝐼, где 𝐼 — единичная матрица. Это означает, что мы будем иметь возможность удалить матрицу коэффициентов из левой части уравнение (4) путем умножения слева обратной матрица коэффициентов. Умножая обе части уравнения на обратная матрица коэффициентов, имеем 𝑥𝑦=13−12−21639.

Наконец, вычислив скалярное умножение, 𝑥𝑦=⎛⎜⎜⎝723273⎞⎟⎟⎠=249.

Мы знаем, что пара матриц равна, если каждая пара соответствующих элементов равный. Отсюда получаем решение заданной системы уравнений 𝑥=24,𝑦=9.

Это ведет к периметру прямоугольника: 2(𝑥+𝑦)=2(24+9)=66.cm

Наконец, отметим, что матрицы и их мультипликативные обратные могут применяться в области криптографии. В этом контексте цель состоит в том, чтобы закодировать сообщение до его передачи, чтобы предотвратить его понимание, если оно будет перехвачено во время передачи. Затем сообщение может быть декодировано, как только оно достигнет желаемого адресата.

В качестве иллюстрации мы можем захотеть передать сообщение « help ». Начнем с того, что представим каждую букву в виде числа, используя следующую простую алфавитную таблицу.

A: 1
B: 2
C: 3
D: 4
E: 5
F: 6
G: 7

H: 8
I: 9
J: 1044444444.

l: 12
m: 13
n: 14

o: 15
p: 16
q: 17
r: 18
s: 19
t: 20
u: 9 9 9 4 v 50445 x: 24
y: 25
z: 26

Затем, беря наше сообщение по две буквы за раз, мы записываем каждую двухбуквенную секцию в виде матрицы 2×1: help=85,=1216. Затем, чтобы закодировать наше сообщение, мы выбираем обратимую матрицу 2 × 2 в качестве нашей матрицы кодирования 𝐶 и умножьте каждую из приведенных выше матриц 2 × 1 слева на 𝐶. Например, выбрав 𝐶=1245, наше сообщение кодируется как 124585=1857,12451216=44128.

Поэтому мы передаем сообщение 185744128.

Теперь напомним, что для матрицы 𝐶=𝑎𝑏𝑐𝑑 с det𝐶≠0 ее мультипликативная обратная дается выражением 𝐶=1𝐶𝑑−𝑏−𝑐𝑎,det где det𝐶=𝑎𝑑−𝑏𝑐. В этом случае мы имеем det𝐶=(1×5)−(2×4)=−3, поэтому 𝐶=1−35−2−41=⎛⎜⎜⎝−532343−13⎞⎟⎟⎠. После того, как сообщение 185744128 было получено, чтобы расшифровать его, мы должны умножить каждый из этих 2×1 матрицы слева на 𝐶. Это «отменит» эффект 𝐶 и вернуть нам исходную пару 2×1 матрицы 851216. Мы можем тогда прочтите сообщение «помощь» по этим четырем числам, найдя соответствующие буквы в алфавитной таблице.

Давайте закончим повторением нескольких важных понятий из объяснения.

Ключевые моменты

Пусть 𝐴 — обратимая матрица, а 𝐵 — матрица такая, что умножение 𝐴𝐵 определено. Матрица 𝑋, удовлетворяющая уравнению 𝐴𝑋=𝐵, есть данный 𝑋=𝐴𝐵.
Если матрица 𝐴 необратима, матричное уравнение 𝐴𝑋=𝐵 имеет либо бесконечное число решений, либо не имеет решение.
Рассмотрим систему уравнений, заданную формулой 𝑎𝑥+𝑏𝑦=𝑒,𝑐𝑥+𝑑𝑦=𝑓 для некоторых известных констант 𝑎, 𝑏, 𝑐, 𝑑, 𝑒, 𝑓. Мы можем записать эту систему двух уравнений как одно матричное уравнение 𝑎𝑏𝑐𝑑𝑥𝑦=𝑒𝑓. Затем это уравнение можно решить с помощью обратной матрицы: 𝑥𝑦=𝑎𝑏𝑐𝑑𝑒𝑓. 

решение матричных уравнений

решение матричных уравнений

В этом руководстве вы узнаете, как решать различные виды уравнений с матрицами и векторами.

Для матрицы A и вектора y типы уравнений, которые мы хотели бы решить, имеют форму y = A·x , где A и y даны. Задача состоит в том, чтобы найти вектор x . Первые два подраздела показывают, как работать с этим уравнением без ограничений на вектор решения x . В разделе 4 показано, как действовать в ситуации, когда вектор решения x ограничен.

В приведенном выше уравнении матрица и векторы должны совпадать. Это означает, что количество строк A должно равняться размеру вектора y и размеру вектора решения x всегда будет равно количеству столбцов A .

Примечание. В сценариях Praat мы не различаем в обозначениях вектор и его транспонирование.

1. Матрица А квадратная

В этом случае точное решение для x возможно, потому что, если A «хорошо себя ведет», мы можем вычислить его обратное, и решение будет x = A ^-1 · y . Функция solve# (a##, y#) предназначена для этого типа задач.

В следующем примере показана точно решаемая система, поскольку A является квадратной матрицей и «хорошо себя ведет»:

 а## = {{0, 2, 0, 1},

 ... {2, 2, 3, 2},

 ... {4,-3, 0, 1},

 ... {6, 1,-6,-5}}

 у# = {0,-2,-7,6}

 x# = решить# (a##, y#)

 writeInfoLine: x#

В моем информационном окне отображается:

-0,49999999999999967 1,000000000000001 0,33333333333333344 -2,00000000000000027

В качестве проверки мы можем вычислить норму разности между y и A·x , которая должна быть равна нулю для идеального решения.

 appendInfoLine: норма (y# - mul# (a##, x#))

Мое информационное окно показывает 1.0777744118960794e-14, что почти равно нулю (это не совсем ноль из-за ошибок округления, потому что реальные числа не могут быть точно представлены в компьютере.

2. В матрице A строк больше, чем столбцов 90 176

Если в матрице строк больше, чем столбцов, точное решение, как правило, невозможно, и лучшее, что мы можем сделать, это найти вектор решения x , что минимизирует квадрат расстояния между векторами y и A·x . Задача теперь может быть поставлена так: найти вектор x , который минимизирует || г — А·х || ² . Это проблема регрессии, которую можно решить с помощью разложения по сингулярным значениям.

В следующем примере показана матрица 5×2 A . Таким образом, решение представляет собой вектор с двумя элементами.

 а## = {{-0,84,-0,184},

 . .. {0,09, 1,26},

 ... {0,62,-0,20},

 ... {-1.48,-1.03},

 ... {1,29, 0,03}}

 у# = {-0,19, -0,90, -1,53, -2,30, 0,58}

 x# = решить# (a##, y#)

 writeInfoLine: x#

В моем информационном окне отображается:

0,5881230621928452 0,21643159712237164

Мы можем вычислить норму разности:

 appendInfoLine: норма (y# - mul# (a##, x#))

В моем информационном окне отображается:

2,556992185298919

Это означает, что нельзя найти другой вектор x , который имеет || г — А·х || < 2,556992185298919!

3. В матрице A столбцов больше, чем строк 90 176.

Если количество столбцов больше количества строк, то система в целом недоопределена, т. е. мы не можем определить полный вектор решения.

4. Вектор x

ограничен
Если есть дополнительные ограничения на вектор x , мы можем обрабатывать три разных случая:
4.
1 Ограничения на квадрат нормы решения x
Их можно выразить в следующей форме: минимизировать || г — А·х || ² + α( x′x — δ) для некоторых α > 0 и δ ≥ 0. Здесь ограничение на квадрат нормы x′x для x накладывается добавлением штрафной функции с весовым коэффициентом а.
Используемая функция: solveWeaklyConstrained# ( a ##, y #, альфа , дельта )
Функция называется «слабо ограниченной», потому что штрафная функция запрещает относительно большое отклонение x′x от δ. Если мы позволим α уйти в бесконечность, мы получим задачу регрессии методом наименьших квадратов с ограничениями минимизации || г — А·х || ² при условии х’х = δ. Реализованный нами алгоритм описан Ten Berge (1991).
4.1.1 Пример из цитируемой статьи с матрицей 6×2
A а## = {{4, 1, 0,5}, . .. {4,-1,-0,5}, ... {-4, 1,-0,5}, ... {-4,-1, 0,5}, ... {2, 0, 0}, ... {-2, 0, 0}} у# = {-1,-1,-1,-1,-1,1} альфа = 6,0 дельта = 2 / 3 x# = решитьWeaklyConstrained#(a##, y#, альфа, дельта) writeInfoLine: x#
В моем информационном окне отображается:
-0,05633802816 -3,341667830688472e-17 0,7616819283108669
4.1.2 Решение регрессии без ограничения
Никаких ограничений не будет, если мы установим α = 0
x# = решитьWeaklyConstrained#(a##, y#, 0.0, дельта) writeInfoLine: x#
В моем информационном окне отображается:
-0,05555555555555557 -5,696494054485392e-17 3,0458443711512004e-16
Такое же решение появилось бы, если бы мы использовали следующий код:
. x# = решить#(a##, y#) writeInfoLine: x#
4.
1.3. Для принудительного применения решения, где норма решения равна единице
Мы выбираем очень большое значение для α и устанавливаем δ равным 1,0.
x# = решитьWeaklyConstrained#(a##, y#, 1e100, 1.0) writeInfoLine: x#
В моем информационном окне отображается:
-0,056338028161 -3,341667830688472e-17 0,9984117520251988
4.2. Ограничение неотрицательности решения
Здесь мы ограничиваем элементы решения неотрицательностью. Задача формулируется как минимизировать || г — А · x || ² где все x _i ≥ 0.
Эта проблема может быть решена с помощью итеративного альтернативного метода наименьших квадратов, описанного Боргом и Грёненом (19).97). Используемая функция: solvNonegative# (a##, y# [x#], maxNumberOfIterations , допуск , infoLevel )
Параметры имеют следующее значение:
а##, у#
матрица A и вектор y .
[х#]
необязательный вектор для запуска итераций. Если не указано, процедура начинается с нулевого вектора.
максимальное количество итераций
максимальное количество итераций, которое должно быть выполнено, если критерий допуска не выполняется.
допуск
— это значение критерия, которое необходимо для принятия решения о остановке итераций. Если d ( n ) есть квадрат ошибки аппроксимации на n -м шаге итерации, т.е. d ( n ) = || y — A·x ( n )|| ² , где x ( n ) — приближение x на шаге n , то итерация останавливается, если либо d(n) == 0, либо
| д ( н ) — д ( н -1)| / || и || ² < допуск .
информационный уровень
определяет количество информации, которая записывается в информационное окно во время итераций. Информация не записывается, если значение равно нулю.
В качестве примера рассмотрим:
а## = {{-4, 2, 2}, {2, 4, 2}, {1, 1, 1}, { 2,-1, 3}} у#= {1,2,1,3} результат# = решитьНеотрицательный# (a##, y#, 100, 1e-17, 0) writeInfoLine: результат#
В моем информационном окне отображается:
0,17687074830212887 0 0,8594104308385341
Тот же ### и y# с дополнительным выводом и всего тремя итерациями:
результат# = решитьНеотрицательный# (a##, y#, 3, 1e-17, 2) writeInfoLine: результат#
Теперь мое информационное окно показывает:
Итерация: 1, ошибка: 2.7083144168962345
Итерация: 2, ошибка: 0,22835187182198863
Итерация: 3, ошибка: 0,019415103584264275
Количество итераций: 3; Минимум: 0,019415103584264275
0,18686771227425772 0,0063553925295192215 0,85421349654
Решение не достигается только после 3 итераций. Используем найденное решение для запуска новой итерации:
результат# = решитьНеотрицательный# (a##, y#, результат#, 100, 1e-17, 1) writeInfoLine: результат#
В моем информационном окне отображается
.
Количество итераций: 6; Минимум: 0,011337868480725613
0,17687074830212887 0 0,8594104308385341
Окончательное решение было достигнуто после 6 дополнительных итераций.
4.3 Ограничения на разреженность решения
Как мы видели выше, если количество столбцов больше количества строк, то единственного решения, вообще говоря, не существует, потому что количество неизвестных больше, чем количество уравнений. Однако есть исключение:
Если матрица A имеет некоторые специальные свойства и , то вектор решения должен быть разреженным, т.е. большинство его значений равны нулю, тогда мы можем найти x , который минимизирует || г — А·х || ² .
В общем случае для минимизации необходима итерационная процедура. Мы реализовали один на основе итеративной жесткой пороговой обработки , описанной Blumensath & Davies (2010).
solveSparse# (a##, y# [x#], maxNumberOfNonzeros , maxNumberOfIterations , допуск , info )
Параметры имеют следующее значение:
а##, у#
матрица A и вектор y .
[х#]
необязательный вектор для запуска итераций. Если не указано, процедура начинается с нулевого вектора.
максимальное числоNumberOfNonzeros
максимальное количество ненулевых элементов в векторе решения, т. е. разреженность.
максимальное количество итераций
максимальное количество итераций, которое должно быть выполнено, если критерий допуска не выполняется.
допуск
— это значение критерия, которое необходимо для принятия решения о остановке итераций. Если d ( n ) есть квадрат ошибки аппроксимации на n -м шаге итерации, т. е. d ( n ) = || y — A·x ( n )|| ² , где x ( n ) — приближение x на шаге n , то итерация останавливается, если
| д ( н ) — д ( н -1)|/|| и || ² < допуск .
информационный уровень
определяет количество информации, которая записывается в информационное окно во время итераций. Информация не записывается, если значение равно нулю.
В следующем примере мы сначала создаем разреженный вектор x со случайными числами от 0,1 до 10 и случайную гауссову матрицу A . Из этих двух мы строим наши и . Затем мы решаем разреженную систему и сравниваем ее решение x с построенным x .
ряд = 100 nкол = 1000 x# = ноль# (ncol) для размера i (x#) x# [i] = если randomUniform (0,1) < 0,005, то randomUniform (0,1, 10), иначе 0,0 fi конец для # В среднем в x# 5 из 1000 будут не равны нулю.No related posts.