| New Page 1 Понятие множества Множество — это совокупность некоторых объектов. Какие
могут быть множества? Во первых, конечные или бесконечные. Например, множество
спичек в коробке — это конечное множество, их можно взять и сосчитать.
Количество песчинок на пляже сосчитать гораздо труднее, но, в принципе,
возможно. И это количество выражается каким то конечным числом. Так что
множество песчинок на пляже тоже конечно. А вот множество точек на прямо это
множество бесконечное. Так как во первых, прямая сама по себе бесконечная и на
ней можно поставить сколько угодно точек. Множество точек отрезка прямой тоже
бесконечное. Потому что теоретически точка может быть сколь угодно маленькая.
Конечно, мы физически не сможем нарисовать точку, размером, например, меньше
размера атома, но, с точки зрения математики точка не имеет размера. Ее размер
равен нулю. А что получается, если разделить на нуль какое то число? Правильно,
бесконечность. Рассмотрим пример. Пусть у нас имеется два множества. Первое
— совокупность все точек на прямой. Второе — совокупность всех точек на отрезке
прямой. Почему они не равны? Во первых, отрезок и прямая могут даже не
пересекаться. Тогда они уж точно не равны, так как содержат в себе абсолютно
разные точки. Если они пересекаются, то у них только одна общая точка. Все
остальные так же разные. А если отрезок лежит на прямой? Тогда все точки отрезка
являются и точками прямой. Но не все точки прямой являются точками отрезка. Так
что и в этом случае множества нельзя считать равными (одинаковыми). Каждое множество задается правилом, которое однозначно определяет, принадлежит элемент к этому множеству или нет. Какие могут быть эти правила? Например, если множество конечное, можно тупо перечислить все его объекты. Можно задать диапазон. Например, все целые числа от 1 до 10. Это будет тоже конечное множество, но тут мы не перечисляем его элементы, а формулируем правило. Или неравенство, к примеру, все числа, больше 10. Это будет уже бесконечное множество, поскольку нельзя назвать самое большое число — какие бы число мы не называли, всегда есть это число плюс 1. Как правило, множества обозначаются прописными буквами
латинского алфавита A, B, C
и так далее. Если
множество состоит из конкретных элементов и мы хотим задать его списком этих
элементов, то мы можем заключить этот список в фигурные скобки, например
A={a, b, c, d}.
Если a является элемент
множества A, то это записывают следующим образом: a Î A . Если же a
не является элементом множества A, то пишут a
Ï
A. Определение 1 (определение равенства множеств). Множества А и B равны, если они состоят из одних и тех же элементов, то есть, если из x Î A следует x Î B и обратно, из x Î B следует x Î A. Формально равенство двух множеств записывается следующим образом: (А=В ) := » x (( x Î A ) Û (x Î B )), Это означает, что для любого объекта x соотношения x Î A и x Î B равносильны. Здесь » – квантор всеобщности (» x читается как «для каждого x «). Определение 2 (определение подмножества). Множество А является подмножеством множества В , если любое х принадлежащее множеству А , принадлежит множеству В. Формальное это можно представить в виде выражения: (A Ì B ) := » x ((x Î A ) Þ (x Î B )) Если A
Ì
B, но A
¹
B, то A – собственное
подмножество множества В. Замечание. Пустое множество является подмножеством любого множества. Операции над множествами Над множествами возможны следующие операции: Объединение. Суть этой операции состоит в том, что бы два множества объединить в одно, содержащее элементы каждого из объединяемых множеств. Формально это выглядит так: C=A È B: = {x:x Î A или x Î B } Пример. Решим неравенство | 2 x + 3 | > 7. Из него следует либо неравенство 2x+3 >7, для 2x+3 ≥0, тогда x>2 либо неравенство 2x+3 Множеством решений данного неравенство является
объединения множеств (-∞,-5) È (2,
∞). Давайте проверим. Посчитаем значение выражение | 2 x + 3 | для нескольких точек, лежащих и не лежащих в данном диапазоне:
Как видим, все решено правильно (красным обозначены пограничные диапазоны). Пересечение. Пересечением называется операция создания нового
множества из двух, содержащих элементы, которые входят в оба этих множества. Формально операция пересечения множеств записывается так: C=A Ç B := {x: x Î A и x Î B } Пример. Пусть у нас есть множество Тогда C=A Ç B = {5,6,7} Вычитание. Вычитание множеств — это исключение из вычитаемого множества тех элементах, которые содержатся в вычитаемом и вычитателе: Формально вычитание множества записывается так: A \ B: = {x:x Î A и x Ï B } Пример. Пусть у нас есть множество A={1,2,3,4,5,6,7}, B={5,6,7,8,9,10}. Тогда C=A \ B = { 1,2,3,4} Дополнение. Дополнение — это унарная операция (операция не над двумя,
а над одним множеством). Эта операция является результатом вычитания данного
множества из полного универсального множества (множества, которое включает в
себя все остальные множества). A : = {x:x Î U и x Ï A} = U \ A Графически это можно изобразить в виде: Симметричная разность. В отличии от обычной разности при симметричной разности множеств элементы остаются только те, что присутствуют либо в одном, либо в другом множестве. Или, говоря простым языком, из двух множеств создается, но из него исключаются те элементы, которые есть и в том и в другом множестве: Математически это можно выразить так: A D B:= (A \ B ) È (B \ A ) = (A È B ) \ (A Ç B ) Свойства операций над множествами.Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами:
A È B=B È A
(A È B )
È C=A È
(B È C ) |
| Пример 1 |
| Вычислить а) $ \lim_{x \to 0} \frac{1}{x} $; б)$ \lim_{x \to \infty} \frac{1}{x} $ |
| Решение |
а) $$ \lim \limits_{x \to 0} \frac{1}{x} = \infty $$ б)$$ \lim_{x \to \infty} \frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ \text{a)} \lim \limits_{x \to 0} \frac{1}{x} = \infty \text{ б)}\lim \limits_{x \to \infty} \frac{1}{x} = 0 $$ |
Что делать с неопределенностью вида: $ \bigg [\frac{0}{0} \bigg ] $
| Пример 3 |
| Решить $ \lim \limits_{x \to -1} \frac{x^2-1}{x+1} $ |
| Решение |
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: «ноль делить на ноль» или «бесконечность делить на бесконечность» и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность «ноль делить на ноль» нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность «бесконечность делить на бесконечность», тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!
Предел в бесконечности Задачи с квадратными корнями — Matheno.com
Обновление: По состоянию на сентябрь 2022 года у нас есть гораздо дополнительных интерактивных способов узнать об основополагающей концепции пределов в бесконечности, широко используя графики Desmos калькуляторы. Пожалуйста, посетите наш Введение в Пределы в Бесконечности, чтобы начать действительно получить этот материал для себя. Все это бесплатно и предназначено для того, чтобы помочь вам преуспеть в вашем курсе.
Если вам сейчас просто нужно попрактиковаться в решении проблем с ограничениями, предыдущие ученики сочли нижеприведенную информацию очень полезной. А если у вас есть вопросы, задавайте их на нашем форуме! 92}$ в любой задаче, где $x \to\, -\infty$, поскольку тогда вы автоматически просматриваете отрицательные значения x .
Для более полного обсуждения этого важного вопроса, пожалуйста, посетите экран «Предел в бесконечности с квадратными корнями» в нашей главе «Пределы», посвященной этой теме. У нас также есть специально разработанные интерактивные графические калькуляторы Desmos, которые помогут вам понять, что вы делаете, когда вычисляете эти пределы.
Приведенные ниже задачи иллюстрируют, начиная с части (b) первой. 92}}}{1} \\[8px]
&= \lim_{x \to \infty} \sqrt{5 + \dfrac{2}{x}} \\[8px]
&= \sqrt{\lim_{x \to \infty} 5 + \cancelto{0}{\lim_{x \to \infty}\left( \dfrac{2}{x}\right)}} \\[ 8px]
&= \sqrt{5} \quad \cmark
\end{align*} \]
Обратите внимание, что на последнем шаге мы использовали тот факт, что $\displaystyle{\lim_{x \to \infty}\frac{ 2}{х} = 0}$.
Мы можем проверить результат, взглянув на график функции. Обратите внимание, что горизонтальная линия $y = \sqrt{5}$ является горизонтальной асимптотой для этого графика. 92\left( 5 + \frac{2}{x} \right)}}{x}$, числитель всегда будет положительным из-за квадратного корня. Знаменатель, с другой стороны, всегда будет отрицательным, потому что мы рассматриваем постоянно увеличивающиеся отрицательные значения для x . Следовательно, поскольку $x \to\, -\infty$, дробь всегда будет иметь отрицательное значение , и поэтому, если мы найдем число в качестве предела, мы ожидаем, что оно будет отрицательным. Это быстрое начальное рассуждение является хорошей проверкой нашего окончательного результата.
Чтобы получить этот результат, мы снова используем наш обычный «трюк» деления числителя и знаменателя на 92}}}{1} \\[8px]
&= \lim_{x \to\, -\infty} -\sqrt{5 + \dfrac{2}{x}} \\[8px]
&= -\sqrt{5} \quad \cmark
\end{align*} \]
Обратите внимание, что на последнем шаге мы использовали тот факт, что $\displaystyle{\lim_{x \to\, -\infty}\frac {2}{x} = 0}$.
Обратите внимание, что в качестве ответа мы получили отрицательное число, что соответствует нашим быстрым первоначальным рассуждениям выше.
Мы можем проверить результат, взглянув на график функции. Обратите внимание, что горизонтальная линия $y = -\sqrt{5}$ является горизонтальной асимптотой для этого графика. 92 + x} – x \\[8px]
f(10) &= \sqrt{100 + 10} – 10 \приблизительно 10,488 – 10 = 0,488 \\[8px]
f(20) &= \sqrt{400 + 20} – 20 \приблизительно 20,494 – 20 = 0,494 \\[8px]
f(100) &= \sqrt{10,000 + 100} – 100 \приблизительно 100,499 -100 = 0,499
\end{align*} \]
[свернуть]
Практическая задача №3
Эта задача предоставлена по запросу учащегося. У него есть другой (тот же самый) классный, неожиданный результат.
Найти $\displaystyle{\lim_{x \to \infty}\left(\sqrt{x + \sqrt{x}} – \sqrt{x} \right)}$.
Нажмите, чтобы просмотреть решение исчисления
По мере того, как $x$ растет и растет, как $\sqrt{x + \sqrt{x}}$, так и $\sqrt{x}$ растут и растут. Таким образом, мы не сразу знаем, в чем разница между двумя терминами. $(“\infty – \infty”$ может быть чем угодно — это «неопределенное выражение», означающее, что у нас есть еще работа.)
Чтобы продолжить, мы будем использовать тот же подход, который мы использовали ранее при оценке пределов, которые имели в них квадратные корни: мы рационализируем выражение, умножив его на сопряженное $\sqrt{x + \sqrt{x}} + \sqrt{x}$, деленное само на себя: 92}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty} \frac{\left(x + \sqrt{x } \right) – x}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{x }}{\sqrt{x + \sqrt{x}} + \sqrt{x}} \\[8px]
\end{align*} \]
Теперь воспользуемся нашим обычным приемом деления числителя и знаменателя на самая большая степень в знаменателе . Эта мощность равна $\sqrt{x}.$
Эта мощность равна $\sqrt{x}.$
\[ \begin{align*}
&= \lim_{x \to \infty}\frac{\dfrac{\sqrt{x}}{\sqrt{x} }}{\dfrac{\sqrt{x + \sqrt{x}}+ \sqrt{x}}{\sqrt{x}}} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\dfrac{\sqrt{x + \sqrt{x}}}{\sqrt{x}}+ \dfrac{\sqrt{x}} {\sqrt{x}}} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\sqrt{\dfrac{x + \sqrt{x}}{x}}+ 1} \\[8px]
&= \lim_{x \to \infty}\frac{1}{\sqrt{1 + \dfrac{1}{\sqrt{x}}}+ 1} \\[8px ]
&= \frac{1}{\sqrt{1 + \cancelto{0}{\dfrac{1}{\sqrt{x}}}}+ 1} \\[8px]
&= \frac{1 }{\sqrt{1}+ 1} \\[8px]
&= \dfrac{1}{2} \quad \cmark
\end{align*} \]
Обратите внимание, что ближе к концу мы использовали тот факт, что $\displaystyle{\lim_{x \to\, \infty}\frac{1}{\sqrt{x}} = 0}$.
Этот предел неожиданный, по крайней мере для нас! Но вы можете проверить несколько чисел, чтобы увидеть, как это работает:
\[ \begin{align*}
f(x) &= \sqrt{x + \sqrt{x}} – \sqrt{x} \\[8px ]
f(100) &= \sqrt{100 + \sqrt{100}} – \sqrt{100} \приблизительно 10,48 – 10 = 0,48 \\[8px]
f(10000) &= \sqrt{10000 + 100 } – 100 \приблизительно 100,499 – 100 = 0,499 \\[8px]
\end{align*} \]
[свернуть]
Практическая задача № 4
Это обобщенная версия задачи № 2 выше . 2 + ax}$, деленное само на себя: 92}}}\\[8px]
2 + ax}$, деленное само на себя: 92}}}\\[8px]
&= \lim_{x \to\, -\infty}\frac{-a}{1 + \sqrt{1 + \frac{a}{x}}} \\ [8px]
&= \frac{-a}{1 + \sqrt{1}} \\[8px]
&= \frac{-a}{2} \quad \cmark
\end{align*} \ ]
Обратите внимание, что в предпоследней строке мы использовали тот факт, что $\displaystyle{\lim_{x \to\, -\infty} \frac{a}{x} = 0 }.$
[ свернуть]
Практическая задача #7
Учащийся разместил этот вопрос в комментариях ниже.
Найти $\displaystyle{\lim_{x \to \infty}\big[\sqrt{x}\sqrt{x}\sqrt{x} – \sqrt{x} \big]}.$ 93}} = \infty$ и $ \displaystyle{\lim_{x \to \infty}\sqrt{x}} = \infty,$ имеем $”\infty – \infty”$, что неопределенно: мы не Мы не знаем, каков на самом деле предел, но у нас есть еще много работы.
Как это часто бывает, разложение на множители обеспечивает путь вперед: обратите внимание, что мы можем извлечь $\sqrt{x}$ из обоих членов:
\begin{align*}
\sqrt{x}\sqrt{ x}\sqrt{x} – \sqrt{x} &= \sqrt{x} \big( \sqrt{x}\sqrt{x} – 1 \big) \\[8px]
&= \sqrt{x }(х – 1)
\end{выравнивание*}
Как только мы это сделали, предел становится ясным:
\begin{align*}
\lim_{x \to \infty}\big[\sqrt{x}\sqrt{x}\sqrt{x} – \ sqrt{x} \big] &= \lim_{x \to \infty}\big[\sqrt{x}(x – 1)\big] \\[8px]
&= \big[\lim_{x \ к \infty}\sqrt{x} \big] \cdot \big[\lim_{x \to \infty}(x – 1)\big] \\[8px]
&= \infty \cdot \infty \\ [8px]
&= \infty \quad \cmark
\end{align*}
[свернуть]
Практическая задача №8
Учащийся разместил этот вопрос в комментариях ниже.
Найти $\displaystyle{ \lim_{x \to \infty}\sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x} }$.
Нажмите, чтобы просмотреть решение исчисления
Есть два основных шага, чтобы найти этот предел.
Шаг 1 : Как и в предыдущих задачах, мы умножаем выражение на его сопряженное деление на себя:
\begin{align*}
\lim_{x \to \infty}\left( \sqrt{x + \sqrt{x + \sqrt{x}}} — \sqrt{x}\right) &= \lim_{x \to \infty}\left(\sqrt{x + \sqrt{x + \sqrt{x) }}} – \sqrt{x} \right)\cdot \frac{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x}}{\sqrt{x + \sqrt{ х + \sqrt{x}}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty} \frac{\left(\sqrt{x + \sqrt{x + \sqrt{x}}}\right)\left(\sqrt{x + \sqrt{x) + \sqrt{x}}} \right) + \cancel{\left(\sqrt{x + \sqrt{x + \sqrt{x}}} — \sqrt{x} \right)\left(\sqrt{ x} \right)} – \cancel{\left(\sqrt{x}\right)\left(\sqrt{x + \sqrt{x + \sqrt{x}}} – \sqrt{x} \right) } + \left( -\sqrt{x}\right)\left(\sqrt{x} \right) }{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x} }\\[8px]
&=\lim_{x \to \infty} \frac{\left(x + \sqrt{x + \sqrt{x}} \right) -x}{\sqrt{x + \ sqrt{x + \sqrt{x}}} + \sqrt{x}} \\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x}}}{\sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x }}
\end{align*}
С этим переписанным выражением вы можете посмотреть на него и увидеть, что в числителе преобладает (первый) член $\sqrt{x}$, в то время как числитель преобладает в равной степени на два множителя $\sqrt{x}$, поэтому предел будет $\dfrac{1}{2}. $
$
Но если вы этого не видите (поскольку вы еще не сделали 10 000 такие типы задач), или вам нужно это доказать, мы переходим к нашему обычному подходу Шаг 2 : Разделите числитель и знаменатель на наибольший множитель в знаменателе, который равен $\sqrt{x}.$ Итак, давайте умножим и числитель, и знаменатель на $\dfrac{1}{\sqrt{x} } $:
\begin{align*}
\lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x}}}{\sqrt{x + \sqrt{x + \sqrt{x }}} + \sqrt{x}}
&= \lim_{x \to \infty}\frac{\frac{1}{\sqrt{x}}\sqrt{x + \sqrt{x}}}{ \frac{1}{\sqrt{x}}\left( \sqrt{x + \sqrt{x + \sqrt{x}}} + \sqrt{x}\right)} \\[8px]
&= \ lim_ {x \ to \ infty} \ frac {\ sqrt {\ frac {x + \ sqrt {x}} {x}}} {\ sqrt {\ frac {x + \ sqrt {x + \ sqrt {x} }}{x}} + \frac{\sqrt{x}}{\sqrt{x}}}\\[8px]
&= \lim_{x \to \infty}\frac{\sqrt{1 + \frac{1}{\sqrt{x}}}}{\sqrt{1 + \frac{\sqrt{x + \sqrt {x}}}{x}}+1} \\[8px]
&= \frac{\sqrt{1 + \cancelto{0}{\left( \lim_{x \to \infty}\frac{1 }{\sqrt{x}}\right)}}}{\sqrt{1 + \cancelto{0}{\left( \lim_{x \to \infty}\frac{\sqrt{x + \sqrt{x }}}{x}\right)}}+1} \\[8px]
&= \frac{\sqrt{1}}{\sqrt{1} + 1} \\[8px]
&= \frac {1}{2} \quad \cmark
\end{align*}
Ого! : )
[свернуть]
Хотите доступ к все наших проблем исчисления и решения? Войдите бесплатно с помощью своей учетной записи Google, Facebook или Apple или с помощью специальной учетной записи Matheno (которую вы можете создать за 60 секунд). Затем посетите наш главный экран исчисления.
Затем посетите наш главный экран исчисления.
И если у вас есть вопрос о проблеме с ограничениями, с которыми вам может понадобиться помощь, или о ограничениях в целом, пожалуйста, зайдите на наш форум и оставьте сообщение. Будем рады помочь!
По состоянию на сентябрь 2022 года мы используем наш форум для комментариев и обсуждения этой темы, а также для любых математических вопросов. Будем рады вас видеть и помочь! Нажмите, чтобы посетить наш форум: community.matheno.com.
Войти
Вы можете бесплатно войти в систему, чтобы получить доступ ко всем нашим материалам, с помощью своей учетной записи Facebook, Google или Apple ИЛИ с помощью специальной учетной записи Matheno. (У вас нет специальной учетной записи Matheno, но вы хотели бы ее создать? Создайте ее за 60 секунд здесь.)
Заметки по исчислению I, раздел 2–5
Пределы, включающие бесконечность
В этой функции у нас есть два примера ограничений
с участием бесконечности. | |
| Здесь задействована бесконечность, поскольку мы находим предел
работает как x стремится к нулю слева. На самом деле, когда ответ на предел
проблема
бесконечность, мы действительно говорим, что нет предела. Отрицательный
бесконечный ответ говорит нам, что значение функции является
очень сильно
большое количество. Это лучше, чем просто сказать, что нет предела. Примечание: когда то график функция должна иметь вертикальную асимптоту. | |
| В этом случае мы видим, что правый предел как x стремится к нулю, положительная бесконечность. Теперь мы знаем, что официально: потому что левша и правые пределы не совпадают. | |
Вот еще один способ трактовки бесконечности в
пределы. Мы можем принять ограничения как . При взятии лимита
type: и ответ – константа.
Тогда функция имеет горизонтальную асимптоту
по значению функции. При взятии лимита
type: и ответ – константа.
Тогда функция имеет горизонтальную асимптоту
по значению функции. |
Многочлен ведет себя
как его термин высшей степени
как . Этот
можно увидеть в следующем примере:
| превосходит все остальное в этом выражении как x приближается к бесконечности. Следовательно, предел этого выражения должен быть бесконечность. |
При превышении лимита
рациональное выражение и
наибольшая степень числителя равна наибольшей степени
знаменатель, то предел выражения как x подходы
бесконечность — это отношение коэффициентов членов высшей степени
в числителе и знаменателе.
В этой предельной задаче наибольшая степень
числитель и член с наивысшей степенью в
знаменатель . С
это члены с наивысшей степенью, они доминируют в предельной проблеме, и
мы можем игнорировать другие члены при определении предела. Мы видим, что
предел представляет собой частное коэффициентов высших степеней. С
это члены с наивысшей степенью, они доминируют в предельной проблеме, и
мы можем игнорировать другие члены при определении предела. Мы видим, что
предел представляет собой частное коэффициентов высших степеней. |
При превышении лимита
рациональное выражение и
наибольшая степень числителя или знаменателя больше, чем
высшую силу другого, то следуйте этому совету:
| Поскольку наибольшая степень числителя больше, чем знаменатель наибольшая степень, член числителя с наибольшей степенью принимает это выражение когда x приближается к бесконечности. Поэтому предел этого типа выражения должна быть положительная бесконечность. | |
Поскольку наибольшая степень знаменателя больше, чем
наибольшая степень числителя, наибольшая степень знаменателя
принимает это выражение по мере приближения к x бесконечность. |

 Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
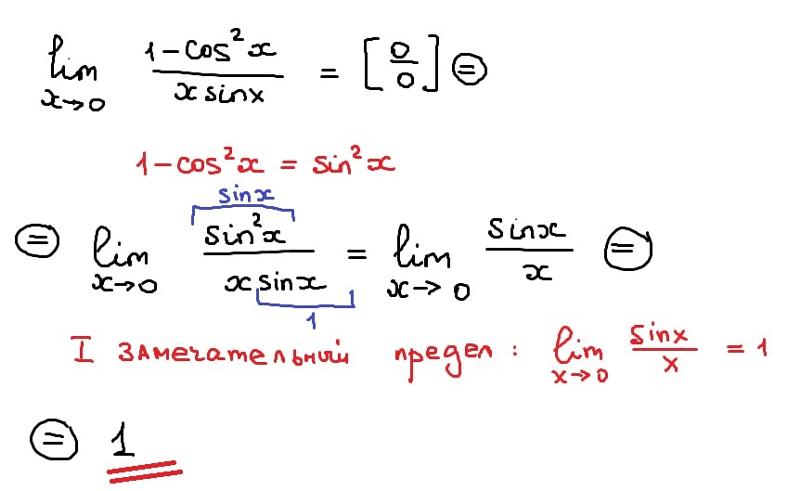 Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на
Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на 
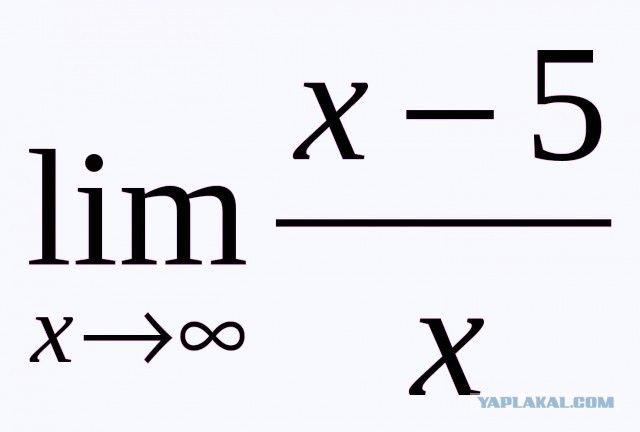
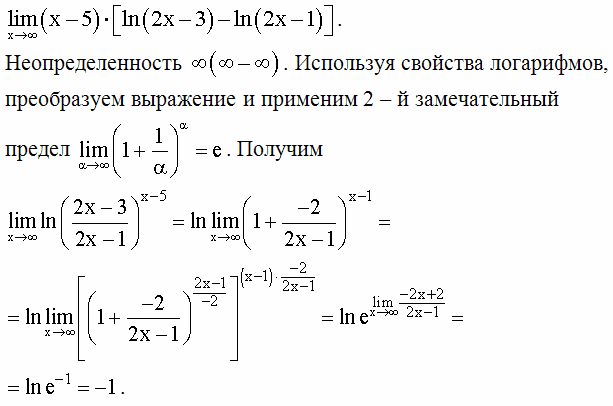

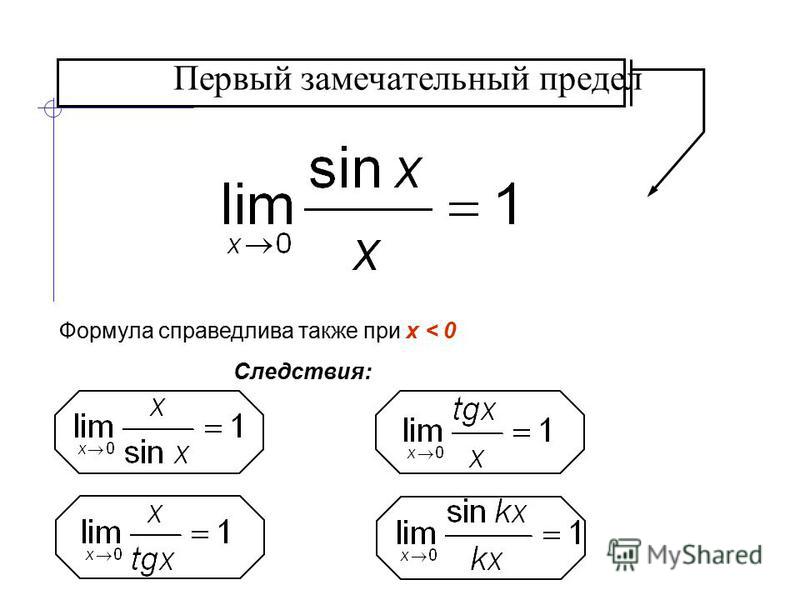 Одним из важных множеств является множество N всех натуральных чисел N={1,2,3,…,}
. Существует также специальное, так называемое пустое множество, которое не
содержит ни одного элемента. Пустое множество обозначается символом
Æ
.
Одним из важных множеств является множество N всех натуральных чисел N={1,2,3,…,}
. Существует также специальное, так называемое пустое множество, которое не
содержит ни одного элемента. Пустое множество обозначается символом
Æ
. В качестве примера можно привести опять же
прямую и отрезок. Если отрезок лежит на прямой, то множество его точек являются
подмножеством точек этой прямой. Или, другой пример. Множество целых чисел,
которые делятся без остатка на 3, является подмножеством множества целых чисел.
В качестве примера можно привести опять же
прямую и отрезок. Если отрезок лежит на прямой, то множество его точек являются
подмножеством точек этой прямой. Или, другой пример. Множество целых чисел,
которые делятся без остатка на 3, является подмножеством множества целых чисел.
 Что бы изобразить это наглядно, давайте представим, что у нас есть два множества
точек на плоскости, а именно фигура A
и фигура
B.
Их пересечение обозначает фигуру
C —
это и есть результа операции пересечения множеств:
Что бы изобразить это наглядно, давайте представим, что у нас есть два множества
точек на плоскости, а именно фигура A
и фигура
B.
Их пересечение обозначает фигуру
C —
это и есть результа операции пересечения множеств:
 Математический анализ – это совокупность разделов математики, которые занимаются изучением функций и их обобщений методами дифференциального и интегрального исчисления. Сюда относятся: функциональный анализ, включая теорию интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, теория рядов и многомерных интегралов, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, векторный анализ, а также вариационное исчисление. Изучение математического анализа по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Математический анализ Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по математическому анализу приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения!
Математический анализ – это совокупность разделов математики, которые занимаются изучением функций и их обобщений методами дифференциального и интегрального исчисления. Сюда относятся: функциональный анализ, включая теорию интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, теория рядов и многомерных интегралов, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, векторный анализ, а также вариационное исчисление. Изучение математического анализа по видео урокам будет полезно как для начинающих, так и для более опытных математиков. Видеоуроки из рубрики Математический анализ Вы можете смотреть бесплатно в любое удобное время. К некоторым видео урокам по математическому анализу приложены дополнительные материалы, которые можно скачать. Приятного Вам обучения! В этом видео я не буду учить тебя формулам, а объясню смысл производной на пальцах так, чтобы даже круглому чайнику было понятно. Но сначала тебе лучше посмотреть мое предыдущее видео, где я так же доступно рассказываю о функции. В этом видеоуроке мы просто, понятно и наглядных жизненных примерах…
В этом видео я не буду учить тебя формулам, а объясню смысл производной на пальцах так, чтобы даже круглому чайнику было понятно. Но сначала тебе лучше посмотреть мое предыдущее видео, где я так же доступно рассказываю о функции. В этом видеоуроке мы просто, понятно и наглядных жизненных примерах… Большинство элементов исследования функций опираются на базовое понятие предела функции. Здесь будет рассмотрен предел функции в точке на простом примере, после чего будет дано строгое определение предела функции в точке с подробной иллюстрацией на графике для лучшего усвоения материала. На данном занятии также рассматриваются другие примеры, и сформулировано строгое определение односторонних…
Большинство элементов исследования функций опираются на базовое понятие предела функции. Здесь будет рассмотрен предел функции в точке на простом примере, после чего будет дано строгое определение предела функции в точке с подробной иллюстрацией на графике для лучшего усвоения материала. На данном занятии также рассматриваются другие примеры, и сформулировано строгое определение односторонних…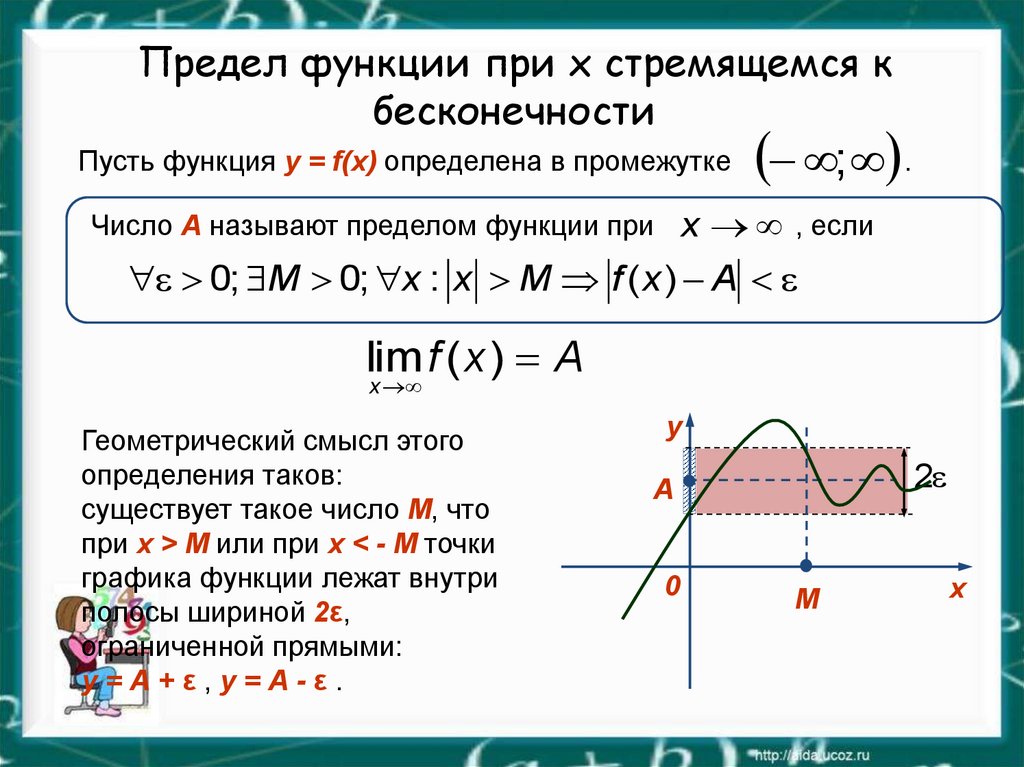 На самом деле ты про нее и так уже почти все знаешь, если посмотрел мои предыдущие видео, и нам осталось только расставить точки над i. Первообразная — это «родительская» функция для производной. Найти первообразную — это значит ответить на вопрос: а чей ребенок? Если известна дочка, то мы должны найти маму. Раньше мы наоборот искали дочку по заданной маме. Сейчас мы делаем обратный переход — от…
На самом деле ты про нее и так уже почти все знаешь, если посмотрел мои предыдущие видео, и нам осталось только расставить точки над i. Первообразная — это «родительская» функция для производной. Найти первообразную — это значит ответить на вопрос: а чей ребенок? Если известна дочка, то мы должны найти маму. Раньше мы наоборот искали дочку по заданной маме. Сейчас мы делаем обратный переход — от… Вы увидите, что зависимость, которая показывает, как одна величина связана с другой величиной, называется функцией. Любая функция — это связь между величинами…
Вы увидите, что зависимость, которая показывает, как одна величина связана с другой величиной, называется функцией. Любая функция — это связь между величинами…
 2-1}{x+1} = \infty $$
2-1}{x+1} = \infty $$