Как решать примеры с целыми и дробями: Как решать дробные примеры с целыми числами. Правила арифметических действий над обыкновенными дробям. Порядок выполнения действий с дробями

Содержание

Как объяснить дроби ребенку?

Дроби – сложная для понимания тема, проблемы с которой возникают не только у детей, но и у взрослых. Но избежать знакомства с ней никак не получится: начиная с 5 класса, редкий урок математики будет обходиться без решения примеров и задач с дробными числами. Представьте себя на месте ребенка, который никогда не видел (а если и видел, то не понимал смысла)дробей. Конечно же, он не сможет выполнить с ними даже самых простейших математических действий.

Но если школьника подготовить заранее,процесс изучения дробей не вызовет сложностей. Главное – найти правильный подход и запастись терпением. А ещё важно подобрать правильную методику,которая поможет быстрее разобраться с дробями.

Дроби: с чего начать?

Начать нужно с повторения предыдущего материала. Если быть точнее – нужно вспомнить основные математические действия с целыми числами: сложение, вычитание, умножение, деление. Все эти знания формируются в дошкольном и младшем школьном возрасте, и без них решать примеры с дробями не представляется возможным. Если с этими действиями проблем нет, то нужно объяснить ученику, чем вообще являются дроби.

Говоря доступным для ребёнка языком, дробь – это часть чего-либо. Это самое «что-либо» может быть всем, чем угодно: тортиком, апельсином, начерченным на бумаге кругом. Иногда часть какого-то предмета называют долей. Но при этом суть понятия не меняется: этот самый предмет дробят, делят на части.

Понять значение этого действия гораздо проще на наглядных примерах. Так, можно взять пирог и разрезать (то есть разделить) его на несколько равных частей. Один кусок будет считаться одной долей от целого пирога. Если пирог разделён на четыре части, то один кусочек – это одна четвертая. Если на восемь, то одна восьмая часть.

Помните мультик, где герои делили апельсин?

«Мы делили апельсин.

Много нас, а он один.

Эта долька для ежа, эта долька для чижа…»

В этой нехитрой песенке как раз объясняется принцип деления на доли, или дробление. То же самое можно проделать с яблоком, плиткой шоколада или конфетами из вазы. Общее количество конфет – это целое, а одна конфетка – это часть.

Всё, что нужно знать о дробях

Есть несколько важных понятий, которые следует запомнить:

1. Дробь не является целым числом, а обозначает количество частей целого.

2. Дробное число всегда меньше целого.

3. Чем на большее количество долей поделено целое, тем эти части меньше. И наоборот: чем меньше количество долей, тем они больше. Понять этот принцип будет проще по всё тому же пирогу. Если поделить его поровну между четырьмя друзьями, каждому достанется крупный кусочек. А если друзей не четверо, а, например, шестеро, то кусочки уже будут не такими крупными.

4. Складывать и вычитать дроби можно только тогда, когда у них одинаковый знаменатель. Математические действия – сложение и вычитание – выполняется с числителями, а знаменатель остаётся неизменным.

Дроби: как это оформить?

Обыкновенная дробь –

это понятие будет регулярно встречаться школьникам почти на каждом уроке математики, поэтому нужно сразу разобраться с тем, что оно обозначает и как используется на практике. Начнём со второй части: обыкновенная дробь используется для записи любого количества долей. Выглядит она как «двухэтажная» конструкция из двух чисел, разделённых горизонтальной чертой. Эта черта называется дробной и обозначает, что число разделили.

Верхний «этаж» называется числителем,

нижний – знаменателем.

Числитель – это число взятых частей от целого, а знаменатель – количество частей, на которое разделили целое. Кстати, знаменатель можно записывать не только внизу, но и справа от числителя после дробной черты. Например: 1/3 или 2/6 или 4/8.

А теперь снова вернёмся к нашему вкусному пирогу. Уже понятно, что разделить его можно между любым количеством друзей. Соответственно, число всех нарезанных кусочков мы запишем в знаменатель. А количество кусков, доставшихся, например, Пете, мы запишем в верхней части, то есть в числителе. Если пирог порезали на восемь частей, а Петя съел два из них, то запись будет выглядеть так: 2/8. А если поделить яблоко между двумя товарищами, то каждому достанется по одной второй, или ½.

Правильные и неправильные дроби

Наверное, вы уже обратили внимание, что во всех приведённых примерах числитель меньше знаменателя. Это называется правильной дробью.

Но ведь бывают и другие ситуации. Например, к Маше пришла в гости подруга Лена, и мама Маши решила угостить девочек фруктами. Одна достала из холодильника два яблока и, чтобы им было удобнее, разрезала каждое пополам. Получается следующее: одно яблоко разделено на две части, значит в знаменателе будет два. Один кусочек этого самого яблока – это одна вторая. То же самое и со вторым яблоком. А всего на тарелке лежит четыре кусочка.

Но только вот Лена не очень любит яблоки. Она съела всего лишь один кусок, а все остальные достались Маше. Получается, что на долю Лены пришлась ½ часть, а у Маши 3/2. Это и есть неправильная дробь,

то есть та, в которой числитель больше знаменателя.

Иногда в математических примерах могут встретиться ещё более странные записи: 1/1, 3/3, 5/5. Это тоже неправильные дроби, которые по сути не совсем соответствуют определению дробных чисел.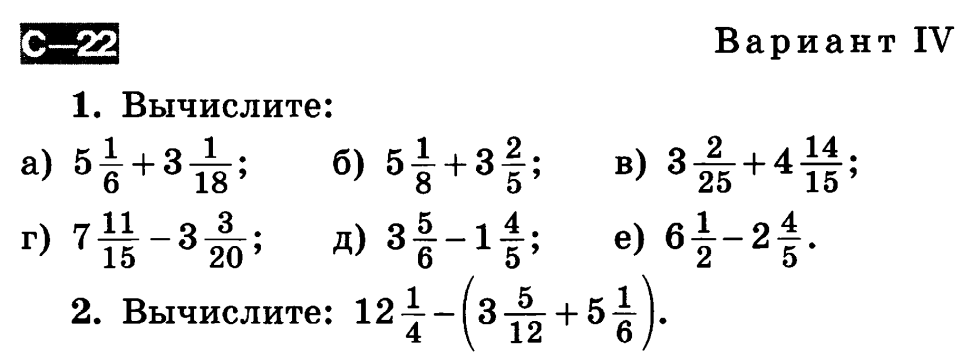 И снова вернёмся к сочному и спелому яблоку и рассмотрим на его примере число 2/2. Знаменатель указывает на то, что яблоко разделено на две части, а числитель говорит о том, что Маша съела обе. То есть она съела всё яблоко, а это значит, что дробное число 2/2 = 1. Если пирог разделён на три части и все они достались Пете, то он смог полакомиться целым пирогом: 3/3 = 1.

Действия с дробями

В самом начале мы говорили, что горизонтальная черта в записи дроби означает деление. То есть числитель можно разделить на знаменатель. Рассмотрим пример с неправильной дробью 6/3. Мы 6 делим на 3 и получаем в ответе 2. Ещё один пример – 8/4: 8 делим на 4 и получаем 2.

В этих примерах в итоге получается целое число без остатка. Но бывает и по-другому, и называется это действие «выделение целой части».

Выделение у дроби целой части

Для примера возьмём неправильную дробь 7/2 и попробуем её разделить:

7 : 2 = 3 и 1 в остатке.

Выполним обратное действие и проверим правильность решения:

3 х 2 + 1 = 7

Теперь осталось записать. А делается это очень просто: целая часть записывается крупно слева от дроби, а сама дробь будет выглядеть как остаток в числителе и количество частей в знаменателе: 3 ½

Кстати, то, что мы сейчас получили, называется смешанной дробью. У неё есть целая и дробная часть. Но подобные действия можно выполнить только с неправильными дробями, у которых числитель больше знаменателя. В математике используется и обратное действие: перевод смешанной дроби в неправильную. Но эти действия, скорее всего, вы будете изучать позже – в 6 классе.

Сравнение дробей

А на данном этапе сосредоточимся на более простых задачках. Например, научимся сравнивать дроби. Сравнить их можно только, если они имеют одинаковый знаменатель. По правилам математики сравниваются числители.

Что больше – 1/5 или 4/5? Сравним числители и увидим, что 1 < 4, а значит 1/5 < 4/5.

А если в примере дробные числа с разными знаменателями? Тогда их сначала нужно привести к общему, а потом сравнить. Но это более сложная тема, требующая детального разбора. Как и другие примеры с умножением, делением, сокращением. А пока достаточно общего представления о дробях.

‍

Как прибавлять дробные числа. Вычитание дробей с разными знаменателями

Одной из важнейших наук, применение которой можно увидеть в таких дисциплинах, как химия, физика и даже биология, является математика. Изучение этой науки позволяет развить некоторые умственные качества, улучшить и способность концентрироваться. Одна из тем, которые заслуживают отдельного внимания в курсе «Математика» — сложение и вычитание дробей. У многих учеников ее изучение вызывает затруднение. Возможно, наша статья поможет лучше понять эту тему.

Как вычесть дроби, знаменатели которых одинаковые

Дроби — это те же числа, с которыми можно производить различные действия. Их отличие от целых чисел заключается в присутствии знаменателя. Именно поэтому при выполнении действий с дробями нужно изучить некоторые их особенности и правила. Наиболее простым случаем является вычитание обыкновенных дробей, знаменатели которых представлены в виде одинакового числа. Выполнить это действие не составит особого труда, если знать простое правило:

Для того чтобы из одной дроби вычесть вторую, необходимо из числителя уменьшаемой дроби вычесть числитель вычитаемой дроби. Это число записываем в числитель разницы, а знаменатель оставляем тот же: k/m — b/m = (k-b)/m.

Примеры вычитания дробей, знаменатели которых одинаковы

7/19 — 3/19 = (7 — 3)/19 = 4/19.

От числителя уменьшаемой дроби «7» отнимаем числитель вычитаемой дроби «3», получаем «4». Это число мы записываем в числитель ответа, а в знаменатель ставим то же число, что было в знаменателях первой и второй дроби — «19».

На картинке ниже приведено еще несколько подобных примеров.

Рассмотрим более сложный пример, где произведено вычитание дробей с одинаковыми знаменателями:

29/47 — 3/47 — 8/47 — 2/47 — 7/47 = (29 — 3 — 8 — 2 — 7)/47 = 9/47.

От числителя уменьшаемой дроби «29» отниманием по очереди числители всех последующих дробей — «3», «8», «2», «7». В итоге получаем результат «9», который записываем в числитель ответа, а в знаменатель записываем то число, которое находится в знаменателях всех этих дробей, — «47».

Сложение дробей, имеющих одинаковый знаменатель

Сложение и вычитание обыкновенных дробей осуществляется по одному и тому же принципу.

Для того чтобы сложить дроби, знаменатели которых одинаковы, необходимо числители сложить. Полученное число — числитель суммы, а знаменатель останется тот же: k/m + b/m = (k + b)/m.

Рассмотрим, как это выглядит на примере:

1/4 + 2/4 = 3/4.

К числителю первой слагаемой дроби — «1» — добавляем числитель второй слагаемой дроби — «2». Результат — «3» — записываем в числитель суммы, а знаменатель оставляем тот же, что присутствовал в дробях, — «4».

Дроби с различными знаменателями и их вычитание

Действие с дробями, которые имеют одинаковый знаменатель, мы уже рассмотрели. Как видим, зная простые правила, решить подобные примеры достаточно легко. Но что делать, если необходимо произвести действие с дробями, которые имеют различные знаменатели? Многие учащиеся средних школ приходят в затруднение перед такими примерами. Но и здесь, если знать принцип решения, примеры уже не будут представлять для вас сложности. Здесь также существует правило, без которого решение подобных дробей просто невозможно.

Чтобы произвести вычитание дробей с разными знаменателями, необходимо их привести к одинаковому наименьшему знаменателю.

О том, как это сделать, мы поговорим подробнее.

Свойство дроби

Для того чтобы несколько дробей привести к одинаковому знаменателю, нужно использовать в решении главное свойство дроби: после деления или умножения числителя и знаменателя на одинаковое число получится дробь, равная данной.

Так, например, дробь 2/3 может иметь такие знаменатели, как «6», «9», «12» и т. д., то есть она может иметь вид любого числа, которое кратно «3». После того как числитель и знаменатель мы умножим на «2», получится дробь 4/6.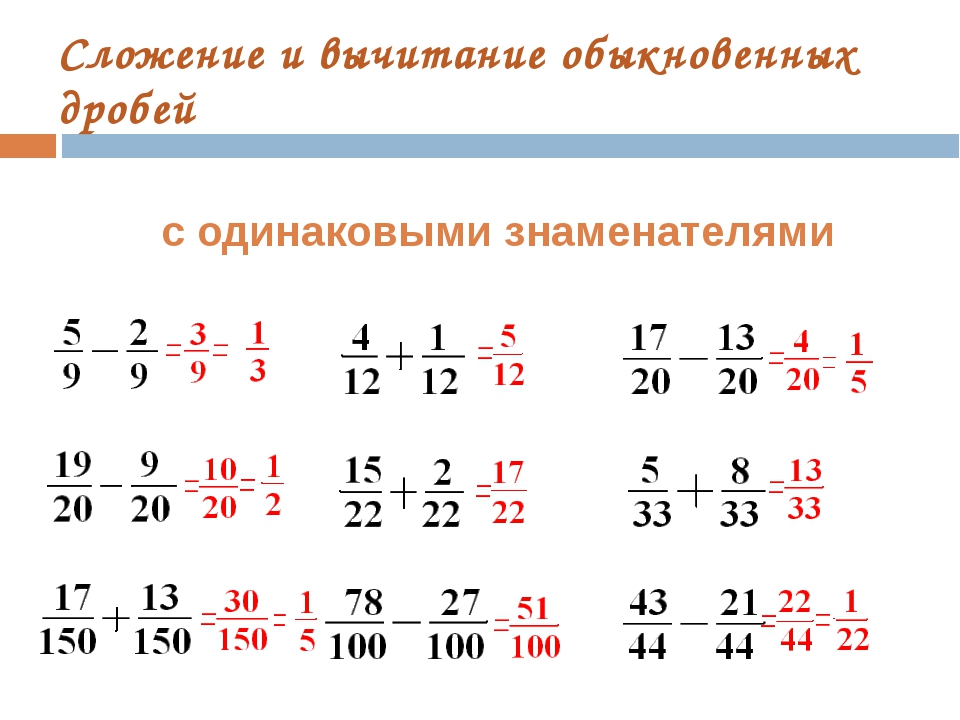 После того как числитель и знаменатель исходной дроби мы умножим на «3», получим 6/9, а если аналогичное действие произвести с цифрой «4», получим 8/12. Одним равенством это можно записать так:

2/3 = 4/6 = 6/9 = 8/12…

Как привести несколько дробей к одному и тому же знаменателю

Рассмотрим, как привести несколько дробей к одному и тому же знаменателю. Для примера возьмем дроби, приведенные на картинке ниже. Для начала необходимо определить, какое число может стать знаменателем для их всех. Для облегчения разложим имеющиеся знаменатели на множители.

Знаменатель дроби 1/2 и дроби 2/3 на множители разложить нельзя. Знаменатель 7/9 имеет два множителя 7/9 = 7/(3 х 3), знаменатель дроби 5/6 = 5/(2 х 3). Теперь необходимо определить, какие же множители будут наименьшими для всех этих четырех дробей. Так как в первой дроби в знаменателе имеется число «2», значит, оно должно присутствовать во всех знаменателях, в дроби 7/9 присутствуют две тройки, значит, они также обе должны присутствовать в знаменателе.

Рассмотрим первую дробь — 1/2. В ее знаменателе имеется «2», но нет ни одной цифры «3», а должно быть две. Для этого мы знаменатель умножаем на две тройки, но, согласно свойству дроби, мы и числитель должны умножить на две тройки:
1/2 = (1 х 3 х 3)/(2 х 3 х 3) = 9/18.

Аналогично производим действия с оставшимися дробями.

2/3 — в знаменателе не хватает одной тройки и одной двойки:
2/3 = (2 х 3 х 2)/(3 х 3 х 2) = 12/18.
7/9 или 7/(3 х 3) — в знаменателе не хватает двойки:
7/9 = (7 х 2)/(9 х 2) = 14/18.

5/6 или 5/(2 х 3) — в знаменателе не хватает тройки:
5/6 = (5 х 3)/(6 х 3) = 15/18.

Все вместе это выглядит так:

Как вычесть и сложить дроби, имеющие различные знаменатели

Как уже говорилось выше, для того чтобы произвести сложение или вычитание дробей, имеющих различные знаменатели, их необходимо привести к одному знаменателю, а дальше воспользоваться правилами вычитания дробей, имеющих одинаковый знаменатель, о котором уже рассказывалось.

Рассмотрим это на примере: 4/18 — 3/15.

Находим кратное чисел 18 и 15:

Число 18 состоит из 3 х 2 х 3.
Число 15 состоит из 5 х 3.
Общее кратное будет состоять из следующих множителей 5 х 3 х 3 х 2 = 90.

После того как знаменатель будет найден, необходимо вычислить множитель, который будет отличным для каждой дроби, то есть то число, на которое необходимо будет умножить не только знаменатель, но и числитель. Для этого число, которое мы нашли (общее кратное), делим на знаменатель той дроби, у которой нужно определить дополнительные множители.

90 поделить на 15. Полученное число «6» будет множителем для 3/15.
90 поделить на 18. Полученное число «5» будет множителем для 4/18.

Следующий этап нашего решения — приведение каждой дроби к знаменателю «90».

Как это делается, мы уже говорили. Рассмотрим, как это записывается в примере:

(4 х 5)/(18 х 5) — (3 х 6)/(15 х 6) = 20/90 — 18/90 = 2/90 = 1/45.

Если дроби с маленькими числами, то можно общий знаменатель определить, как в примере, приведенном на картинке ниже.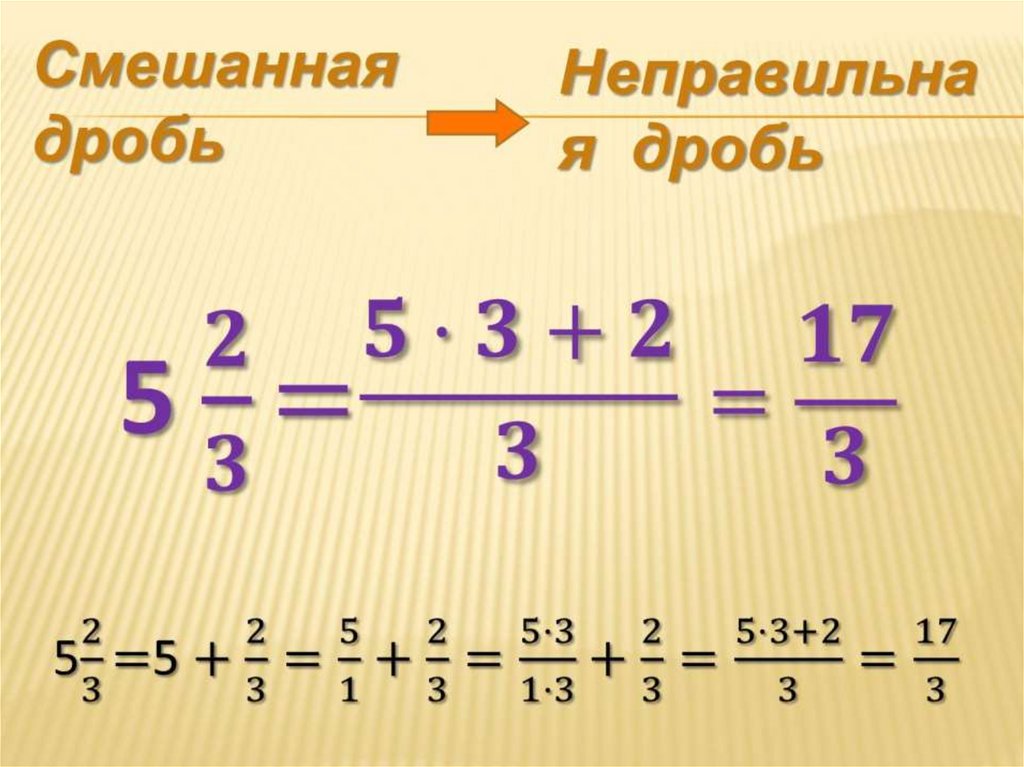

Аналогично производится и имеющих различные знаменатели.

Вычитание и имеющих целые части

Вычитание дробей и их сложение мы уже детально разобрали. Но как произвести вычитание, если у дроби есть целая часть? Опять же, воспользуемся несколькими правилами:

Все дроби, имеющие целую часть, перевести в неправильные. Говоря простыми словами, убрать целую часть. Для этого число целой части умножаем на знаменатель дроби, полученное произведение добавляем к числителю. То число, которое получится после этих действий, — числитель неправильной дроби. Знаменатель же остается неизменным.
Если дроби имеют различные знаменатели, следует привести их к одинаковому.
Произвести сложение или вычитание с одинаковыми знаменателями.
При получении неправильной дроби выделить целую часть.

Есть и иной способ, при помощи которого можно осуществить сложение и вычитание дробей с целыми частями. Для этого производятся отдельно действия с целыми частями, и отдельно действия с дробями, а результаты записываются вместе.

Приведенный пример состоит из дробей, которые имеют одинаковый знаменатель. В том случае, когда знаменатели различны, их необходимо привести к одинаковому, а далее выполнить действия, как показано на примере.

Вычитание дробей из целого числа

Еще одной из разновидностей действий с дробями является тот случай, когда дробь необходимо отнять от На первый взгляд подобный пример кажется трудно решаемым. Однако здесь все довольно просто. Для его решения необходимо перевести целое число в дробь, причем с таким знаменателем, который имеется в вычитаемой дроби. Далее производим вычитание, аналогичное вычитанию с одинаковыми знаменателями. На примере это выглядит так:

7 — 4/9 = (7 х 9)/9 — 4/9 = 53/9 — 4/9 = 49/9.

Приведенное в этой статье вычитание дробей (6 класс) является основой для решения более сложных примеров, которые рассматриваются в последующих классах. Знания этой темы используются впоследствии для решения функций, производных и так далее. Поэтому очень важно разобраться и понять действия с дробями, рассматриваемые выше.

Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.

Сложение дробей с одинаковыми знаменателями.

На примере посмотрим, как складывать дроби с общим знаменателем.

Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac{1}{5}\) от всего пути. Во второй день они прошли от точки B до D или \(\frac{2}{5}\) от всего пути. Какое расстояние они прошли от начала пути до точки D?

Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac{1}{5} + \frac{2}{5}\).

Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.

\(\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}\)

В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:

\(\bf \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)

Ответ: туристы прошли \(\frac{3}{5}\) всего пути.

Сложение дробей с разными знаменателями.

Рассмотрим пример:

Нужно сложить две дроби \(\frac{3}{4}\) и \(\frac{2}{7}\).

Чтобы сложить дроби с разными знаменателями нужно сначала найти , а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.

Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac{3}{4}\) нужно умножить на 7. Вторую дробь \(\frac{2}{7}\) нужно умножить на 4.

\(\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}\)

В буквенном виде получаем такую формулу:

\(\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}\)

Сложение смешанных чисел или смешанных дробей.

Сложение происходит по закону сложения.

У смешанных дробей складываем целые части с целыми и дробные части с дробными.

Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.

Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).

\(3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}\)

Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.

Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).

Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.

\(7\frac{1}{8} + 2\frac{1}{6} = 7\frac{1 \times \color{red} {3}}{8 \times \color{red} {3}} = 2\frac{1 \times \color{red} {4}}{6 \times \color{red} {4}} =7\frac{3}{24} + 2\frac{4}{24} = 9\frac{7}{24}\)

Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби.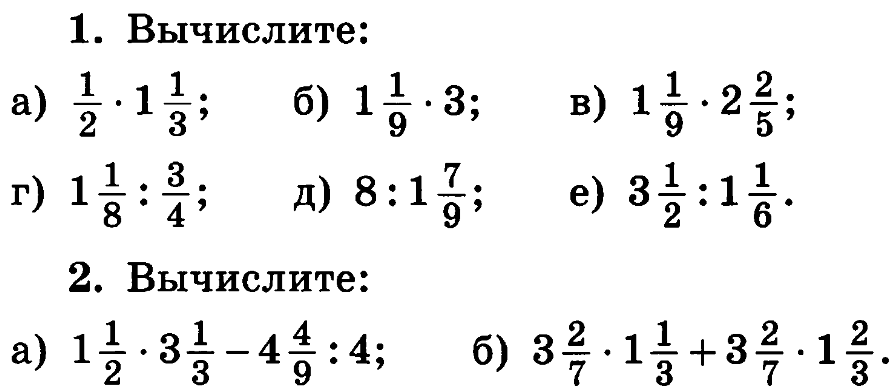 В зависимости от типа выражения переходим к алгоритму решения.

Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.

Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.

Пример №1:
Может ли сумма двух в результате получить правильную дробь? Неправильную дробь? Приведите примеры.

\(\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}\)

Дробь \(\frac{5}{7}\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac{2}{7}\) и \(\frac{3}{7}\).

\(\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}\)

Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).

Ответ: на оба вопроса ответ да.

Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\) б) \(\frac{1}{3} + \frac{2}{9}\).

а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)

б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)

Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\) б) \(5\frac{1}{3}\)

а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)

б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)

Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\) б) \(2\frac{9}{13} + \frac{2}{13}\) в) \(7\frac{2}{5} + 3\frac{4}{15}\)

а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)

б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)

в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)

Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\).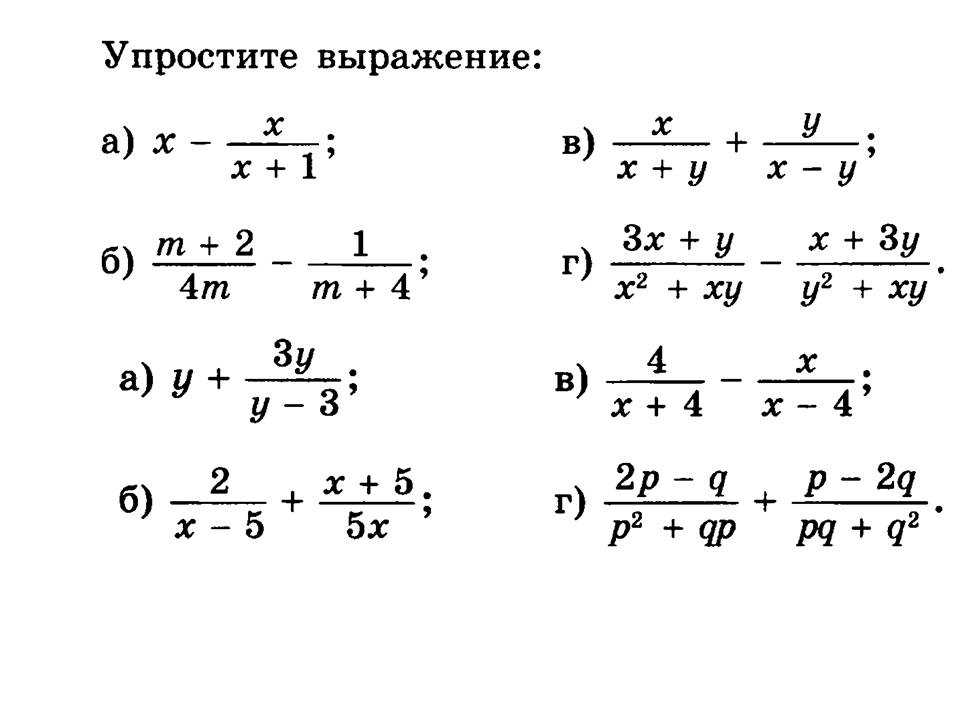 Как вы думаете торт полностью съели или нет?

Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.

\(\frac{8}{11} + \frac{3}{11} = \frac{11}{11} = 1\)

Ответ: весь торт съели.

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.

Вычитание дробей с одинаковыми знаменателями, примеры:

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей — правильной из целого числа (натурального числа) :

Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

найти НОК для всех знаменателей;
поставить для всех дробей дополнительные множители;
умножить все числители на дополнительный множитель;
полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Например:

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Например:

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример:

Т. к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:

Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.

Yandex.RTB R-A-339285-1

Как найти разность дробей с одинаковыми знаменателями

Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:

В итоге у нас осталось 3 восьмых доли, поскольку 5 − 2 = 3 . Получается, что 5 8 — 2 8 = 3 8 .

Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.

Определение 1

Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде a b — c b = a — c b .

Такую формулу мы будем использовать и в дальнейшем.

Возьмем конкретные примеры.

Пример 1

Вычтите из дроби 24 15 обыкновенную дробь 17 15 .

Решение

Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24 . Мы получаем 7 и дописываем к ней знаменатель, получаем 7 15 .

Наши подсчеты можно записать так: 24 15 — 17 15 = 24 — 17 15 = 7 15

Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.

Пример 2

Найдите разность 37 12 — 15 12 .

Решение

Воспользуемся описанной выше формулой и подсчитаем: 37 12 — 15 12 = 37 — 15 12 = 22 12

Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 11 6 . Это неправильная дробь, из которой мы выделим целую часть: 11 6 = 1 5 6 .

Как найти разность дробей с разными знаменателями

Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:

Определение 2

Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.

Рассмотрим на примере, как это делается.

Пример 3

Вычтите из 2 9 дробь 1 15 .

Решение

Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45 . Для первой дроби необходим дополнительный множитель 5 , а для второй – 3 .

Подсчитаем: 2 9 = 2 · 5 9 · 5 = 10 45 1 15 = 1 · 3 15 · 3 = 3 45

У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 10 45 — 3 45 = 10 — 3 45 = 7 45

Краткая запись решения выглядит так: 2 9 — 1 15 = 10 45 — 3 45 = 10 — 3 45 = 7 45 .

Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.

Пример 4

Найдите разность 19 9 — 7 36 .

Решение

Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 76 9 и 7 36 .

Считаем ответ: 76 36 — 7 36 = 76 — 7 36 = 69 36

Результат можно сократить на 3 и получить 23 12 . Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 1 11 12 .

Краткая запись всего решения — 19 9 — 7 36 = 1 11 12 .

Как вычесть из обыкновенной дроби натуральное число

Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.

Пример 5

Найдите разность 83 21 – 3 .

Решение

3 – то же самое, что и 3 1 . Тогда можно подсчитать так: 83 21 — 3 = 20 21 .

Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.

Из дроби 83 21 при выделении целой части получится 83 21 = 3 20 21 .

Теперь просто вычтем 3 из него: 3 20 21 — 3 = 20 21 .

Как вычесть обыкновенную дробь из натурального числа

Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.

Пример 6

Найдите разность: 7 — 5 3 .

Решение

Сделаем 7 дробью 7 1 . Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7 — 5 3 = 5 1 3 .

Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.

Определение 3

Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1 . После этого нужно вычесть нужную дробь из единицы и получить ответ.

Пример 7

Вычислите разность 1 065 — 13 62 .

Решение

Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065 — 13 62 = (1064 + 1) — 13 62

Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064 + 1 — 13 62 . Подсчитаем разность в скобках. Для этого единицу представим как дробь 1 1 .

Получается, что 1 — 13 62 = 1 1 — 13 62 = 62 62 — 13 62 = 49 62 .

Теперь вспомним про 1064 и сформулируем ответ: 1064 49 62 .

Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:

1065 — 13 62 = 1065 1 — 13 62 = 1065 · 62 1 · 62 — 13 62 = 66030 62 — 13 62 = = 66030 — 13 62 = 66017 62 = 1064 4 6

Ответ тот же, но подсчеты, очевидно, более громоздкие.

Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.

Пример 8

Вычислите разность 644 — 73 5 .

Решение

Вторая дробь – неправильная, и от нее надо отделить целую часть.

Теперь вычисляем аналогично предыдущему примеру: 630 — 3 5 = (629 + 1) — 3 5 = 629 + 1 — 3 5 = 629 + 2 5 = 629 2 5

Свойства вычитания при работе с дробями

Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.

Пример 9

Найдите разность 24 4 — 3 2 — 5 6 .

Решение

Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 25 4 — 3 2 , а потом отнимем от нее последнюю дробь:

25 4 — 3 2 = 24 4 — 6 4 = 19 4 19 4 — 5 6 = 57 12 — 10 12 = 47 12

Преобразуем ответ, выделив из него целую часть. Итог — 3 11 12 .

Краткая запись всего решения:

25 4 — 3 2 — 5 6 = 25 4 — 3 2 — 5 6 = 25 4 — 6 4 — 5 6 = = 19 4 — 5 6 = 57 12 — 10 12 = 47 12 = 3 11 12

Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.

Пример 10

Н айдите разность 98 + 17 20 — 5 + 3 5 .

Решение

Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98 + 17 20 — 5 + 3 5 = 98 + 17 20 — 5 — 3 5 = 98 — 5 + 17 20 — 3 5

Завершим расчеты: 98 — 5 + 17 20 — 3 5 = 93 + 17 20 — 12 20 = 93 + 5 20 = 93 + 1 4 = 93 1 4

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Правила сложения дробей с разными знаменателями очень простые.

Рассмотрим правила сложения дробей с разными знаменателями по шагам:

1. Найти НОК (наименьшее общее кратное) знаменателей. Полученный НОК будет общим знаменателем дробей;

2. Привести дроби к общему знаменателю;

3. Сложить дроби, приведенные к общему знаменателю.

На простом примере научимся применять правила сложения дробей с разными знаменателями.

Пример

Пример сложения дробей с разными знаменателями.

Сложить дроби с разными знаменателями:

1	+	5
6	+	12

Будем решать по шагам.

1. Найти НОК (наименьшее общее кратное) знаменателей.

Число 12 делится на 6.

Отсюда делаем вывод, что 12 есть наименьшее общее кратное чисел 6 и 12.

Ответ: нок чисел 6 и 12 равен 12:

НОК(6, 12) = 12

Полученный НОК и будет общим знаменателем двух дробей 1/6 и 5/12.

2. Привести дроби к общему знаменателю.

В нашем примере привести к общему знаменателю 12 нужно только первую дробь, ведь у второй дроби знаменатель уже равен 12.

Разделим общий знаменатель 12 на знаменатель первой дроби:

2 есть дополнительный множитель.

Умножим числитель и знаменатель первой дроби (1/6) на дополнительный множитель 2.

3.5 Решение уравнений с использованием целых чисел; The Division Property of Equality — Preалгебра 2e

Цели обучения

К концу этого раздела вы сможете:

Определить, является ли целое число решением уравнения
Решите уравнения с целыми числами, используя свойства сложения и вычитания равенства
Модель Свойства Разделения Равенства
Решите уравнения, используя свойство деления равенства
Перевести в уравнение и решить

Приготовься 3.10

Прежде чем начать, пройдите этот тест на готовность.

Evaluatex+4whenx=-4.Evaluatex+4whenx=-4.
Если вы пропустили эту проблему, просмотрите пример 3.22.

Приготовься 3.11

Решить:y-6=10.Решить:y-6=10.
Если вы пропустили эту проблему, просмотрите пример 2.33.

Приготовься 3.12

Перевести в алгебраическое выражение 55 меньше х.х.
Если вы пропустили эту проблему, просмотрите Таблицу 1.3.

Определить, является ли число решением уравнения

В разделе «Решение уравнений со свойствами равенства вычитания и сложения» мы увидели, что решение уравнения — это значение переменной, которая дает истинное утверждение при подстановке в это уравнение. В этом разделе мы нашли решения, которые были целыми числами. Теперь, когда мы работали с целыми числами, мы найдем целочисленные решения уравнений.

Шаги, которые мы предпринимаем, чтобы определить, является ли число решением уравнения, одинаковы независимо от того, является ли решение целым или целым числом.

Как

Как определить, является ли число решением уравнения.

Шаг 1. Подставьте число вместо переменной в уравнении.
Шаг 2. Упростите выражения в обеих частях уравнения.
Шаг 3. Определить, верно ли полученное уравнение.
- Если это правда, число является решением.
- Если это не так, число не является решением.

Пример 3,60

Определите, является ли каждое из следующих решений решением уравнения 2x−5=−13:2x−5=−13:

ⓐx=4x=4
ⓑх=-4х=-4
ⓒx=-9.x=-9.

Решение

ⓐ Подставьте 4 вместо x в уравнении, чтобы определить, верно ли оно.


Умножить.
Вычесть.

Поскольку x=4x=4 не дает истинного уравнения, 44 не является решением уравнения.

ⓑ Подставьте -4 вместо x в уравнении, чтобы определить, верно ли оно.

Умножить.
Вычесть.

Поскольку x=−4x=−4 дает истинное уравнение, −4−4 является решением уравнения.

ⓒ Подставьте -9 вместо x в уравнении, чтобы определить, верно ли оно.

Замените x на −9.
Умножить.
Вычесть.

Поскольку x=−9x=−9 не дает истинного уравнения, −9−9 не является решением уравнения.

Попробуй 3.119

Определите, является ли каждое из следующих решений решением уравнения 2x−8=−14:2x−8=−14:

ⓐx=−11x=−11
ⓑх=11х=11
ⓒx=−3x=−3

Попробуй 3.

120

Определите, является ли каждое из следующих решений решением уравнения 2y+3=-11:2y+3=-11:

ⓐy=4y=4
ⓑу=-4у=-4
ⓒу=-7у=-7

Решите уравнения с целыми числами, используя свойства сложения и вычитания равенства

В разделе «Решение уравнений со свойствами равенства на вычитание и сложение» мы решили уравнения, подобные двум показанным здесь, с использованием свойств равенства на вычитание и сложение. Теперь мы можем снова использовать их с целыми числами.

Когда вы добавляете или вычитаете одно и то же количество из обеих частей уравнения, вы все равно получаете равенство.

Свойства равенств

Свойство равенства вычитания	Добавление свойства равенства
Для любых чисел a,b,c, Для любых чисел a,b,c, ifa=bthena-c=b-c. ifa=bthena-c=b-c.	Для любых чисел a,b,c, Для любых чисел a,b,c, ifa=bthena+c=b+c.ifa=bthena+c=b+c.

Пример 3,61

Решить: у+9=5.у+9=5.

Решение


Вычтите 9 с каждой стороны, чтобы отменить сложение.
Упрощение.

Проверьте результат, подставив -4−4 в исходное уравнение.

	у+9=5у+9=5
Замените -4 на y	−4+9=?5−4+9=?5
	5=5✓5=5✓

Поскольку y=−4y=−4 делает y+9=5y+9=5 истинным утверждением, мы нашли решение этого уравнения.

Попробуй 3.121

Решить:

у+11=7у+11=7

Попробуй 3.122

Решить:

y+15=-4y+15=-4

Пример 3,62

Решить: a−6=−8a−6=−8

Решение


Добавьте 6 с каждой стороны, чтобы отменить вычитание.
Упрощение.
Проверьте результат, подставив −2−2 в исходное уравнение:
Замените -2-2 на aa

Решение a−6=−8a−6=−8 равно −2,−2.

Поскольку a=-2a=-2 делает утверждение a-6=-8a-6=-8 верным, мы нашли решение этого уравнения.

Попробуй 3.123

Решите:

a−2=−8a−2=−8

Попробуй 3.124

Решить:

n−4=−8n−4=−8

Моделирование свойства деления равенства

Все уравнения, которые мы решали до сих пор, имели вид x+a=bx+a=b или x−a=b. x−a=b. Мы смогли изолировать переменную, добавив или вычтя постоянный член. Теперь мы посмотрим, как решать уравнения, включающие деление.

Мы смоделируем уравнение с огибающими и счетчиками на рис. 3.21.

Рисунок 3.21

Здесь есть два одинаковых конверта с одинаковым количеством счетчиков. Помните, что левая сторона рабочего пространства должна равняться правой стороне, но счетчики с левой стороны «спрятаны» в конвертах. Итак, сколько фишек в каждом конверте?

Чтобы определить число, разделите жетоны с правой стороны на 22 группы одинакового размера. Таким образом, 66 счетчиков, разделенных на 22 группы, означают, что в каждой группе должно быть 33 счетчика (поскольку 6÷2=3).6÷2=3).

Какое уравнение моделирует ситуацию, показанную на рис. 3.22? Есть два конверта, и каждый содержит xx счетчиков. Вместе два конверта должны содержать в общей сложности 66 жетонов. Таким образом, уравнение, моделирующее ситуацию, имеет вид 2x=6,2x=6.

Рисунок 3. 22

Мы можем разделить обе части уравнения на 22, как мы это сделали с конвертами и счетчиками.

Мы обнаружили, что каждый конверт содержит 3 счетчика. 3 счетчика. Это проверяет? Мы знаем, что 2·3=6,2·3=6, так что это работает. Три фишки в каждом из двух конвертов равняются шести.

На рис. 3.23 показан другой пример.

Рисунок 3.23

Теперь у нас есть 33 одинаковых конверта и 12 фишек. 12 фишек. Сколько фишек в каждом конверте? Мы должны разделить 12 счетчиков12 счетчиков на 3 группы.3 группы. Поскольку 12÷3=4,12÷3=4, в каждом конверте должно быть 4 счетчика4 счетчика. См. Рисунок 3.24.

Рисунок 3.24

Уравнение, моделирующее ситуацию, имеет вид 3x=12,3x=12. Мы можем разделить обе части уравнения на 3,3.

Это проверка? Это так, потому что 3·4=12,3·4=12.

Манипулятивная математика

Выполнение задания по манипулятивной математике «Свойство равенства деления» поможет вам лучше понять, как решать уравнения с использованием свойства равенства деления.

Пример 3,63

Напишите уравнение, моделируемое огибающими и счетчиками, а затем решите его.

Решение

4 конверта, 4 конверта или 44 неизвестных значения слева соответствуют 8 счетчикам8 счетчикам справа. Назовем неизвестную величину в конвертах х.х.

Напишите уравнение.
Разделите обе стороны на 4.
Упрощение.

В каждом конверте 2 фишки2 фишки.

Попробуй 3.125

Напишите уравнение, моделируемое конвертами и счетчиками. Тогда решите это.

Попробуй 3.126

Напишите уравнение, моделируемое конвертами и счетчиками. Тогда решите это.

Решение уравнений с использованием свойства деления равенства

Предыдущие примеры приводят к свойству разделения на равенство. Когда вы делите обе части уравнения на любое ненулевое число, вы все равно получаете равенство.

Раздел имущества равенства

Для любых чисел a,b,c и c≠0, Ifa=bthenac=bc. Для любых чисел a,b,c и c≠0, Ifa=bthenac=bc.

Пример 3,64

Решить:7x=-49. Решить:7x=-49.

Решение

Чтобы изолировать x,x, нам нужно отменить умножение.


Разделите каждую сторону на 7.
Упрощение.

Проверьте решение.

	7х=-497х=-49
Замените x на −7.	7(-7)=?-497(-7)=?-49
	−49=−49✓−49=−49✓

Таким образом, −7−7 является решением уравнения.

Попробуй 3.127

Решить:

8a=568a=56

Попробуй 3.128

Решить:

11n=12111n=121

Пример 3,65

Решите: −3y=63.−3y=63.

Решение

Чтобы изолировать y,y, нам нужно отменить умножение.


Разделите каждую сторону на −3.
Упрощение

Проверьте решение.

	−3y=63−3y=63
Замените -21 на y.	-3(-21)=?63-3(-21)=?63
	63=63✓63=63✓

Поскольку это верное утверждение, y=−21y=−21 является решением уравнения.

Попробуй 3.129

Решить:

−8p=96−8p=96

Попробуй 3.130

Решите:

−12m=108−12m=108

Перевести в уравнение и решить

В предыдущих примерах нам дали уравнение, содержащее переменную. В следующих нескольких примерах нам нужно будет сначала перевести словесные предложения в уравнения с переменными, а затем решить уравнения.

Пример 3,66

Переведите и решите: на пять больше xx равно −3,−3.

Решение

	на пять больше xx равно −3−3
Перевести	х+5=-3х+5=-3
Вычтите 55 с обеих сторон.	х+5-5=-3-5х+5-5=-3-5
Упрощение.	х=-8х=-8

Проверьте ответ, подставив его в исходное уравнение.

х+5=-3-8+5=?-3-3=-3✓х+5=-3-8+5=?-3-3=-3✓

Попробуй 3.131

Переведите и решите:

Семь больше xx равно −2−2.

Попробуй 3.132

Переведите и решите:

На одиннадцать больше, чем y, равно 2. На одиннадцать больше, чем y, равно 2.

Пример 3,67

Переведите и решите: разница nn и 66 равна −10,−10.

Решение

	разница между nn и 66 составляет −10−10
Перевести.	n−6=−10n−6=−10
Добавьте по 66 с каждой стороны.	n−6+6=−10+6n−6+6=−10+6
Упрощение.	н=-4n=-4

Проверьте ответ, подставив его в исходное уравнение.

n−6=−10−4−6=?−10−10=−10✓n−6=−10−4−6=?−10−10=−10✓

Попробуй 3.

133

Переведите и решите:

Разница между pp и 22 составляет −4−4.

Попробуй 3.134

Переведите и решите:

Разница qq и 77 равна −3−3.

Пример 3,68

Переведите и решите: число 108108 есть произведение −9−9 и гг.

Решение

	число 108108 является произведением −9−9 и yy
Перевести.	108=-9y108=-9y
Разделить на −9−9.	108−9=−9y−9108−9=−9y−9
Упрощение.	−12=у−12=у

Проверьте ответ, подставив его в исходное уравнение.

108=-9y108=?-9(-12)108=108✓108=-9y108=?-9(-12)108=108✓

Попробуй 3.135

Переведите и решите:

Число 132132 является произведением −12−12 и yy.

Попробуй 3.

136

Переведите и решите:

Число 117117 является произведением −13−13 и zz.

СМИ

ДОСТУП К ДОПОЛНИТЕЛЬНЫМ ОНЛАЙН-РЕСУРСАМ

Одношаговые уравнения со сложением или вычитанием
Одношаговые уравнения с умножением или делением

Раздел 3.5 Упражнения

Практика ведет к совершенству

Определение того, является ли число решением уравнения

В следующих упражнениях определите, является ли каждое число решением данного уравнения.

285.

4x−2=64x−2=6

ⓐx=−2x=−2
ⓑх=-1х=-1
ⓒx=2x=2

286.

4y-10=-144y-10=-14

ⓐy=-6y=-6
ⓑу=-1у=-1
ⓒу=1у=1

287.

9а+27=-639а+27=-63

ⓐа=6а=6
ⓑа=-6а=-6
ⓒа=-10а=-10

288.

7c+42=-567c+42=-56

ⓐ c=2c=2
ⓑ с=-2с=-2
ⓒ с=-14с=-14

Решите уравнения, используя свойства сложения и вычитания равенства

В следующих упражнениях найдите неизвестное.

289.

n+12=5n+12=5

290.

м+16=2м+16=2

291.

р+9=-8р+9=-8

292.

д+5=-6д+5=-6

293.

и-3=-7и-3=-7

294.

v−7=−8v−7=−8

295.

ч-10=-4ч-10=-4

296.

k−9=−5k−9=−5

297.

х+(-2)=-18х+(-2)=-18

298.

у+(-3)=-10у+(-3)=-10

299.

r-(-5)=-9r-(-5)=-9

300.

с-(-2)=-11с-(-2)=-11

Модель Свойства Разделения Равенства

В следующих упражнениях напишите уравнение, моделируемое огибающими и счетчиками, а затем решите его.

301.

302.

303.

304.

Решите уравнения, используя свойство равенства деления

В следующих упражнениях решите каждое уравнение, используя свойство равенства деления, и проверьте решение.

305.

5x=455x=45

306.

4р=644р=64

307.

−7c=56−7c=56

308.

−9x=54−9x=54

309.

−14p=−42−14p=−42

310.

−8м=−40−8м=−40

311.

−120=10q−120=10q

312.

−75=15 лет−75=15 лет

313.

24x=48024x=480

314.

18n=54018n=540

315.

−3z=0−3z=0

316.

4u=04u=0

Переведите в уравнение и решите

В следующих упражнениях переведите и решите.

317.

Четыре больше, чем nn равно 1.

318.

Девять больше, чем мм равно 5.

319.

Сумма восьми и pp равна −3−3.

320.

Сумма двух и qq равна −7−7.

321.

Разница между aa и three составляет −14−14.

322.

Разница между bb и 55 составляет −2−2.

323.

Число -42 является произведением -7 и хх.

324.

Число -54 является произведением -9 и yy.

325.

Произведение -15 и ff равно 75.

326.

Произведение −18 и gg равно 36.

327.

−6 плюс куб. см равно 4.

328.

−2 плюс дд равно 1.

329.

Девять меньше мм равно −4.

330.

Тринадцать меньше nn равно −10−10.

Смешанная практика

В следующих упражнениях решите.

331.

ⓐx+2=10x+2=10
ⓑ2x=102x=10

332.

ⓐу+6=12у+6=12
ⓑ6у=126у=12

333.

ⓐ−3p=27−3p=27
ⓑp−3=27p−3=27

334.

ⓐ−2q=34−2q=34
ⓑq−2=34q−2=34

335.

а-4=16а-4=16

336.

б-1=11б-1=11

337.

−8m=−56−8m=−56

338.

−6n=−48−6n=−48

339.

−39=и+13−39=и+13

340.

−100=v+25−100=v+25

341.

11r=-9911r=-99

342.

15с=-30015с=-300

343.

100=20д100=20д

344.

250=25n250=25n

345.

−49=x−7−49=x−7

346.

64=у-464=у-4

Математика на каждый день

347.

Упаковка печенья Пакет из 51 печенья51 печенье имеет 33 одинаковых ряда печенья. Найдите количество файлов cookie в каждой строке, c, c, решив уравнение 3c=51,3c=51.

348.

Детский сад 9 класс0767 В детском саду Конни 24 ребенка. 24 ребенка. Она хочет, чтобы они попали в 44 равные группы. Найдите количество детей в каждой группе, g,g, решив уравнение 4g=24,4g=24.

Письменные упражнения

349.

Помогает ли моделирование свойства деления равенства с конвертами и счетчиками понять, как решить уравнение 3x=15?3x=15? Объясните, почему да или почему нет.

350.

Предположим, вы используете конверты и счетчики для моделирования решения уравнений x+4=12x+4=12 и 4x=12,4x=12. Объясните, как вы будете решать каждое уравнение.

351.

Фрида начала решать уравнение −3x=36−3x=36, прибавив 33 к обеим частям. Объясните, почему метод Фриды не решит уравнение.

352.

Рауль начал решать уравнение 4y=404y=40, вычитая 44 из обеих частей. Объясните, почему метод Рауля не решает уравнение.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.

ⓑ В целом, после просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующей главе? Почему или почему нет?

Целочисленная формула | Как вычислять целые числа (с помощью целочисленных правил)

Целочисленная формула (Содержание)

Целочисленная формула
Примеры целочисленной формулы

Любое число, которое можно записать без дробей, называется целым числом. Таким образом, целые числа — это в основном целые числа, которые могут быть положительными, нулевыми или отрицательными, но не дробными. Набор целых чисел обозначается Z, что может быть записано как Z = {…-5,-4,-3,-2,-1, 0, 1, 2, 3, 4, 5…….}. Здесь Z — множество, обладающее свойством счетности, которое, по сути, говорит нам, что, хотя в Z существует бесконечное число элементов, эти значения счетны и могут быть идентифицированы в множестве. Действительное число включает в себя все числа, включая дроби, и действительное число может быть преобразовано в целые числа путем округления числа до ближайшего целого числа. Например, 1, 34, 9890, 340945 и т. д. — все являются целыми числами, а 9,4, 34,56, 803,45 — действительными числами, которые можно округлить до целых чисел 9, 35 и 803.

Формула для целого числа:

Не существует конкретной формулы для целого числа, так как это не что иное, как набор чисел. Но есть определенные правила, когда мы выполняем любые математические операции, такие как сложение, вычитание и т. д. над целыми числами:

Сложение двух положительных целых чисел всегда дает положительное целое число.
Сложение двух отрицательных целых чисел всегда приводит к отрицательному целому числу.
Сложение одного положительного и одного отрицательного целых чисел приведет к
Положительное число, если положительное целое число больше
Отрицательное число, если отрицательное целое больше

Примеры целочисленной формулы
Давайте рассмотрим пример, чтобы лучше понять вычисление целочисленной формулы.
Целочисленная формула – Пример №1
Допустим, у нас есть набор целых чисел, заданный как Z = {2,3,-3,-4,9}
Решение:
Попробуем разобраться в правилах, о которых мы говорили выше.
Сложение двух положительных целых чисел всегда дает положительное целое число.
Итак, давайте возьмем 2 положительных целых числа из набора: 2, 9.
Итак, 2+9 = 11, что является положительным целым числом.
Сложение двух отрицательных целых чисел всегда дает отрицательное целое число.
Итак, возьмем 2 отрицательных целых числа из набора: -3, -4.
Итак, -3-4 = -7, что является отрицательным целым числом.
Сложение одного положительного и одного отрицательного целых чисел даст
1. Положительное число, если положительное целое число больше.
Итак, давайте возьмем одно положительное и одно отрицательное целое число из набора: -3, 9.
Итак, -3+9 = 6, что является положительным целым числом.
2. Отрицательное число, если отрицательное целое больше.
Итак, возьмем одно положительное и одно отрицательное целое число из набора: -3, 2.
Итак, -3+2 = -1, что является отрицательным целым числом.
Целочисленная формула – пример #2
Допустим, вы решаете какое-то математическое уравнение, где вы знаете, что сумма двух последовательных целых чисел равна 97. Теперь вы хотите узнать, что это за числа.
Решение:
Предположим, что целое число 1 ^st равно x.
Целое число 2 ^и будет x + 1.
Итак,
x + (x + 1) = 97
2x + 1 = 97
2x = 97 – 1
2x = 96
х = 96 / 2
х = 48
Таким образом, целое число 1 ^st равно 48
, а целое число 2 ^nd равно 48 + 1 = 49
, которое в основном содержит целое число, как объяснено выше,
3 900. кроме дробных чисел. Целые числа могут быть положительными или отрицательными, даже 0 также является целым числом. Кроме того, как мы видели в приведенных выше примерах, сложение, вычитание и умножение двух или более целых чисел всегда дают целое число, но это не относится к функции деления. Использование деления может привести к целому числу или дроби. Например, если мы разделим 10 на 2, мы получим 5, что является целым числом, но если 10 разделить на 4, то получится 2,5, что не является целым числом.
Актуальность и использование целочисленной формулы
Целые числа используются в языках программирования и кодировании, потому что эти системы понимают только двоичные числа, т. е. 1 или 0. Таким образом, все, что делает компьютерная система, сначала преобразует это в двоичные числа. Целые числа используются в математике, финансах, статистических инструментах и т. д. По сути, они являются основным элементом всех этих областей. Целые числа действительно важны не только в статистических инструментах и математических операциях, но и в реальной жизни. Если вы хотите подсчитать, сколько денег у вас в кошельке, это целое число. Если вы хотите подсчитать, сколько учеников в классе, снова целое число. Количество деревьев на вашем заднем дворе, количество автомобилей, количество лет вашего опыта и т. д. — все это целые числа. Таким образом, целые числа интенсивности в реальной жизни настолько велики, что их невозможно измерить. Одной строкой мы можем сказать, что целые числа есть везде.
No related posts.