§ Как решать уравнения с пропорцией
Решение линейных уравнений Как решать уравнения с пропорцией Как решать уравнения с неизвестным в дроби
Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию. Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или, как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке «Пропорции». В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Запомните!
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции, то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции. Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и решим уравнение до конца. В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Важно!
Если в члене пропорции присутствуют знаки «+» или «−», обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда будете использовать правило пропорции.
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции для дальнейшего решения.
Теперь раскроем скобки с помощью правила раскрытия скобок.
Из урока «Решение линейных уравнений» используем правило переноса и правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
Другие примеры решения уравнений с пропорцией
- =
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число - =
0,21 6,8 3x · 6,8 = 0,21 · 1,7
20,4 x=
·20
x =21 · 17 100 · 10
=204 · x 10 21 · 17 100 · 10 204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
21 · 17 · 10 204 · 1000 x =
21 · 17 204 · 100 x =
7 · 17 68 · 100 x =
119 : 17 6800 : 17 x =
Ответ: x =
Решение линейных уравнений Как решать уравнения с пропорцией Как решать уравнения с неизвестным в дроби
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
Уравнение пропорции. Решить уравнение пропорцией.
- Альфашкола
- Статьи
- Как решать уравнения с помощью пропорции?
Дарим в подарок бесплатный вводный урок!
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ОГЭ по математике
- Репетитор по олимпиадной математике
- Репетитор для подготовки к ЕГЭ по физике
- Подготовка к олимпиадам по физике
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по грамматике английского языка
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по биологии для подготовки к ЕГЭ
- Репетитор по географии для подготовки к ОГЭ
- Scratch
Существует правило для решения уравнений пропорцией. Вспомним основное свойство пропорции:
Вспомним основное свойство пропорции:
Напомним, что такое крайние и средние члены пропорции:
Пример 1. Найдите \(x\) из уравнения:
Решение:
\(\frac{x}{12} =\frac{2}{6} \)
Переможим крест накрест:
\(x*6=12*2\)
\(6x=24\)
\(x = 24:6\)
\(x =4\)
Ответ: \(x=4 \).
Пример 2. Найдите \(x\) из уравнения:
\(\frac{1}{5} =\frac{7}{x} \)
\(1*x=5*7\)
\(x=35\)
Ответ: \(x=35.\).
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Виктория Анатольевна Шилова
Репетитор по математике
Стаж (лет)
Образование:
Северо-Казахстанский государственный университет имени Козыбаева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Татьяна Сергеевна Вахнина
Репетитор по математике
Стаж (лет)
Образование:
Орский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Анна Петровна Беляцкая
Репетитор по математике
Стаж (лет)
Образование:
Белорусский национальный технический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Похожие статьи
- Объём параллелепипеда
- Углы правильного многоугольника.
 Формулы
Формулы - Площадь поверхности конуса
- Как сокращать дроби
- Признак делимости на 17
- Как написать каноническое и параметрическое уравнение прямой, образованной пересечением плоскостей
- ЕГЭ по математике, базовый уровень. Задачи на совместную работу (вариант 4)
- Что делать, если родители против выбранной профессии?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как решить пропорцию
Сопутствующие ресурсы: Proportions Google Activity, Учебное пособие для печати, карты Proportions Boom (цифровые карточки с заданиями), Ratio and Proportions Mazes Что такое пропорция? Существует несколько различных способов определения пропорции. Как решить пропорцию? Пропорцию можно решить несколькими способами. Один из способов — умножить на . Есть свойство, которое вы можете использовать, называемое свойством экстремумов средних. Он говорит, что перекрестные произведения пропорции будут равны. | Добро пожаловать на уроки математики у Кейт! Учителя: обязательно ознакомьтесь с пособиями и заданиями. |
Почему это свойство называется средним пределом? Пропорция также может быть записана через двоеточие как a:b = c:d. Крайние значения — это термины, наиболее удаленные друг от друга снаружи: a и d. Средства — это термины внутри: b и c. Это свойство говорит, что произведение средних равно произведению крайних значений: ad = bc.
Крайние значения — это термины, наиболее удаленные друг от друга снаружи: a и d. Средства — это термины внутри: b и c. Это свойство говорит, что произведение средних равно произведению крайних значений: ad = bc.
Если у вас есть переменная в вашей пропорции, вы можете перекрестно умножить и получить уравнение, которое намного проще решить.
Пример 1
Найдите x.
Эту пропорцию можно решить несколькими способами. Чтобы решить ее перекрестным умножением, вы умножаете по диагонали и устанавливаете два перекрестных произведения равными друг другу. Перемножьте x и 3 вместе и установите его равным тому, что вы получите, когда вы умножите 2 и 9 вместе.
Пример 2Найдите x. Если промежуточные шаги не имели для вас смысла, вы можете проверить урок по решению уравнений с переменными с обеих сторон для освежения. Следующие два примера решить немного сложнее. Пример 3Найдите x. Пример 4Найдите x. ПрактикаГотов попробовать решить пропорцию самостоятельно? Пройдите практический тест ниже: Работает на |
Решить пропорции: определение, примеры решения
Вам когда-нибудь приходилось делить печенье с другом? Если это так, вы использовали концепцию решения пропорций, даже не осознавая этого! Пропорции, представляющие собой математические отношения, являются прекрасными примерами арифметики в реальном мире. Покупка продуктов, приготовление пищи и путешествие из одного места в другое — это характерные сценарии реальной жизни, в которых соотношения являются обычными и необходимыми для надлежащей и рентабельной работы.
Покупка продуктов, приготовление пищи и путешествие из одного места в другое — это характерные сценарии реальной жизни, в которых соотношения являются обычными и необходимыми для надлежащей и рентабельной работы.
Эта статья поможет вам понять, как решать пропорции и различные формулы, которые вы можете использовать.
Что такое пропорция?
Пропорция может быть определена различными способами. Согласно одному определению, пропорция — это уравнение, имеющее два равных отношения. Другими словами, процент — это когда две дроби соединены в центре знаком равенства. Переменные могут быть найдены в одной или обеих дробях в пропорциях.
Отдельно, доля или количество, рассматриваемое по сравнению с общей суммой, обычно называют пропорцией. Когда два отношения равны, они пропорциональны в соответствии с определением пропорции. Если две величины увеличиваются или уменьшаются в одном и том же отношении, говорят, что отношения прямо пропорциональны друг другу. Символы «::» или «=» используются для представления пропорций.
Пример пропорции
Когда два отношения равны, говорят, что они пропорциональны. Например, время, которое требуется поезду, чтобы пройти 50 километров в час, равно времени, которое требуется, чтобы пройти 250 километров за 5 часов. Его можно выразить как 50 км/ч = 250 км/5 часов.
Соотношение и пропорция, в чем разница?
Многие студенты часто используют термины «отношение» и «пропорция» как синонимы. Термин пропорция относится к пропорциональным отношениям между двумя или более соотношениями. Различия между отношением и пропорцией, приведенные в таблице, могут помочь вам лучше понять концепцию.
| Отношение | Пропорция |
| Отношение используется для сравнения размеров двух объектов, имеющих одинаковые единицы измерения. | Пропорция выражает отношение между двумя отношениями. |
| Записывается через двоеточие (:) или косую черту (/). | Записывается через двойное двоеточие (::) или знак равенства (=). |
Типы пропорций
Пропорции можно классифицировать по разным типам в зависимости от типа взаимосвязи между двумя величинами. Существует два типа пропорций.
- Прямая пропорция
- Обратная пропорция
Прямая пропорция
Если существует прямая зависимость между двумя физическими величинами, то она известна как прямая зависимость. Другими словами, вы можете называть количества прямо пропорциональными, если одно количество увеличивается, другое количество также увеличивается, и наоборот. Например, если скорость автомобиля увеличивается, он преодолевает большее расстояние за фиксированный промежуток времени. Прямая пропорция записывается как y ∝ x.
Обратная пропорция
Этот тип описывает косвенную зависимость, т. е. между двумя физическими величинами нет связи. Две физические величины называются косвенно пропорциональными, если одна из них увеличивается, а другая уменьшается, и наоборот. В обозначениях обратная пропорция записывается как y ∝ 1/x. Например, при увеличении скорости автомобиля он сможет преодолевать большее расстояние за меньшее время.
В обозначениях обратная пропорция записывается как y ∝ 1/x. Например, при увеличении скорости автомобиля он сможет преодолевать большее расстояние за меньшее время.
Как решить пропорцию?
Перекрестное умножение — один из методов решения пропорций. Свойство Means Extremes — это свойство, которое вы можете использовать. В нем говорится, что перекрестные произведения пропорции будут равны.
Утверждается, что если ab = cd, то ad = bc.
Итак, что такое свойство Means Extremes и почему оно так называется? Пропорция может быть выражена как a:b = c:d с использованием двоеточия. С внешней стороны крайними являются термины, которые находятся дальше всего друг от друга: а и d. Термины внутри означают: b и c.
Давайте рассмотрим тот же пример:
x:9 :: 2:3
Чтобы решить уравнение пропорции с помощью перекрестного умножения, сначала вам нужно умножить по диагонали. Умножьте x и 3 вместе, затем установите результат равным результату умножения 2 и 9.
Это дает нам:
x(3)/3=18/3
x =
Теперь разделите обе части на 3, чтобы получить x отдельно. 6
Как решать пропорции с переменными
Что такое переменная в математике? Переменная — это буква, обозначающая неизвестное число, значение или количество. Например, в случае алгебраических выражений используются переменные. x+9=4 — линейное уравнение, в котором x — переменная, а 9 и 4 — константы. Так как же решить пропорции с переменными?
Пример:
(x+1):5 :: (x-3):3
Найдите x.
Решение:
Сначала выполните перекрестное умножение. При упрощении каждой стороны будьте осторожны. Убедитесь, что 5 и 3 равномерно распределены.
Убедитесь, что 5 и 3 равномерно распределены.
3(x+ 1) = 5(x- 3)
Раскройте скобки и упростите уравнение.
3x+ 3 = 5x-15
Сдвиньте все переменные в одну сторону, а константы в другую.
3 + 15 = 5x – 3x
18 = 2x
Разделите обе части на 2, чтобы получить x отдельно.
18/2 = 2x/2
x = 9
Практические вопросы для решения пропорций
Q1. Решите для х.
x:9 :: 4:x
Ответ: Когда вы умножаете один х на другой, результат равен х в квадрате.
(x) (x) = (9) (4)
x 2 = 36
Чтобы удалить квадрат, нам нужно извлечь квадратный корень из обеих сторон.
√x 2 = √36
х = 6
Q2. Решите для х.
(x+3):8 :: 5:(x+9)
Ответ: Когда (x+3) умножается на (x+9), это называется биномиальным умножением. Вам нужно использовать метод FOIL. (Сначала снаружи, внутри последним).
(x+3)(x+9) = (8) (5)
Используйте ФОЛЬГУ, чтобы упростить левую сторону.
x 2 +9x +3x + 27 = 40
x 2 +12x + 27 = 40
Теперь нам нужно приравнять это квадратное уравнение к нулю.
x 2 +12x + 27 = 40
-40 = -40
x 2 +12x -13 = 06 Вы можете факторизовать, дополнить квадрат или использовать квадратную формулу, чтобы ответить на проблему. В этом случае мы будем использовать метод факторинга для решения.
x 2 +12x -13 = 0
(x + 13) (x – 1) = 0
Разделите множители и приравняйте их к нулю.
x + 13 = 0 или x – 1 = 0
Таким образом, два значения x равны -13 и x = + 1
Q3. Металлический стержень длиной десять футов весит 128 фунтов. Каков вес сравнимого бруска длиной два фута четыре дюйма?
Ответ:
Мы должны начать с преобразования «два фута четыре дюйма» в измерение только в футах. Четыре дюйма составляют одну треть фута, потому что в одном футе двенадцать дюймов. Таким образом, только в футах длина будет следующей:
Четыре дюйма составляют одну треть фута, потому что в одном футе двенадцать дюймов. Таким образом, только в футах длина будет следующей:
2 фута + 0,333 фута
= 2,333 фута
Отношение длины к весу стержня определяется как длина (футы) вес (фунты)
Соотношение двух сравнимых стержней может быть выражено как 10:128 :: 2,333:w
w — неизвестный вес, который мы должны найти.
(10) (w) = (128) (2,333)
w = 128 * 2,333 / 10
= 29,8624 фунта
Q4. Один отрезок трубы длиной 21 метр необходимо разрезать на два отрезка в соотношении длин отрезков 2:5. Какова длина кусков?
Ответ:
Длина короткого отрезка будет обозначаться буквой «s». Таким образом, более длинный кусок после отсечения метров должен иметь длину 21 с. Тогда отношение будет выражено следующим образом:
короткая часть длинная часть: 25 = s21 – s
Решая пропорцию перекрестным умножением,
2 (21 – s) = (5) (s)
42 – 2s = 5s
42 = 7s
s = 6
Из исходного утверждения мы видим, что длина длинного куска равна
21 – s = 21 – 6 = 15
Итак, две части трубы имеют длину 6 см и 15 см.
Q5. Вычислите, сколько сантиметров в тридцати дюймах, если двенадцать дюймов равны 30,48 сантиметра.
Ответ:
Мы можем начать наши отношения с «дюймов» вверху, а затем использовать букву «с», чтобы представить требуемое значение в сантиметрах. Уравнение будет выглядеть следующим образом:
дюймов сантиметров : 12:30,48 :: 30:c
Решая пропорцию перекрестным умножением,
12 (c) = (30) (30,48)
c = 914,412
c = 76,2
Следовательно, в тридцати дюймах 76,2 сантиметра.
Q6. У вас есть водосточные желоба, установленные на задней части вашего дома. Согласно инструкции, желоба должны опускаться на 14 дюймов на каждые четыре фута бокового потока. Тридцать семь футов будут покрыты водостоками. Насколько наклонным должен быть нижний конец водосточных желобов по сравнению с начальной точкой?
Ответ: Водосточные желоба должны иметь наклон вниз, чтобы дождевая вода направлялась к концу. Водосточные желоба должны снижаться на 14 дюймов на каждые четыре фута длины по мере продвижения от верхнего конца к нижнему. Итак, насколько должны испортиться водосточные желоба при пролете в тридцать семь футов? В пропорции мы возьмем «d» как расстояние, которое нам нужно обнаружить.
Водосточные желоба должны снижаться на 14 дюймов на каждые четыре фута длины по мере продвижения от верхнего конца к нижнему. Итак, насколько должны испортиться водосточные желоба при пролете в тридцать семь футов? В пропорции мы возьмем «d» как расстояние, которое нам нужно обнаружить.
склонение (дюймы) Длина (футы) : 1/44 = d37
d = (37) )(1/4)4
= (37/4)4= 9,254
d = 2,31256 Нижний1 конец должен быть на 2,3125 или 2 615 дюймов ниже, чем верхний конец.
Часто задаваемые вопросы
1. Как решить пропорцию?
Чтобы решить пропорцию, нужно выполнить три шага:
- Запишите пропорцию в виде уравнения
- Настройте уравнение
- Решите уравнение
2. Что означает решение пропорций?
Решение пропорций — это процесс нахождения значения по двум другим значениям. Например, если у вас есть число, и вы хотите найти другое число, эквивалентное ему, вы можете найти это второе число, составив пропорцию.

 Формулы
Формулы Один из способов описать пропорцию состоит в том, что это уравнение с двумя равными отношениями . Другими словами, пропорция — это когда у вас есть две дроби со знаком равенства посередине. В некоторых пропорциях просто две дроби установлены равными друг другу. Пропорции также могут иметь переменные в одной или обеих дробях. Этот урок покажет вам, как найти переменную в пропорции.
Один из способов описать пропорцию состоит в том, что это уравнение с двумя равными отношениями . Другими словами, пропорция — это когда у вас есть две дроби со знаком равенства посередине. В некоторых пропорциях просто две дроби установлены равными друг другу. Пропорции также могут иметь переменные в одной или обеих дробях. Этот урок покажет вам, как найти переменную в пропорции.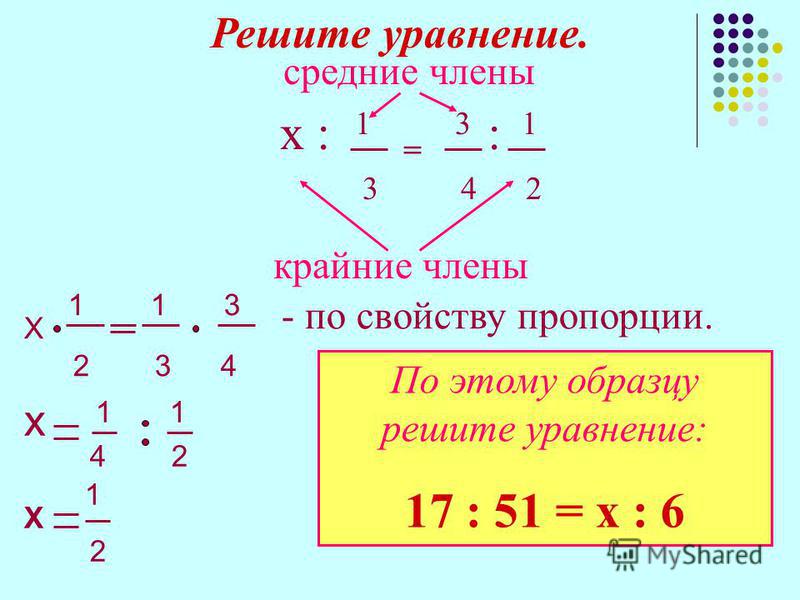 Если вы решаете уравнение, и ваш знак равенства исчез, у вас проблема!
Если вы решаете уравнение, и ваш знак равенства исчез, у вас проблема! Мы можем извлечь квадратный корень из обеих частей, но нужно помнить, что калькулятор даст только положительное решение. 6 в квадрате равно 36, но -6 умножить на -6 также равно положительному числу 36. Вы можете найти аналогичные уравнения в уроке по заполнению квадрата, если у вас есть дополнительные вопросы на этом этапе.
Мы можем извлечь квадратный корень из обеих частей, но нужно помнить, что калькулятор даст только положительное решение. 6 в квадрате равно 36, но -6 умножить на -6 также равно положительному числу 36. Вы можете найти аналогичные уравнения в уроке по заполнению квадрата, если у вас есть дополнительные вопросы на этом этапе. Обычно быстрее всего попытаться учесть факторы, если можете, поэтому мы рекомендуем всегда сначала пытаться учитывать факторы. В этом случае квадратичное выражение, которое мы имеем в левой части, можно разложить на множители. После того, как вы разложили его на множители, установите каждый фактор равным 0 и решите.
Обычно быстрее всего попытаться учесть факторы, если можете, поэтому мы рекомендуем всегда сначала пытаться учитывать факторы. В этом случае квадратичное выражение, которое мы имеем в левой части, можно разложить на множители. После того, как вы разложили его на множители, установите каждый фактор равным 0 и решите.