Транспортная задача: метод аппроксимации Фогеля
Среди четырех, чаще всего применяющихся на практике, методов формирования опорного плана в транспортной задаче самый необычный — метод аппроксимации Фогеля. Последовательность действий при его использовании совершенно иная, чем при заполнении транспортной таблицы методом «Северо-Западного угла» или методом «Минимального элемента».
На первый взгляд аппроксимация Фогеля сложнее, но это ложное впечатление. Метод простой и позволяет получить опорный план более приближенный к оптимальному решению, чем в случае применения других методов (за исключением разве что метода «Двойного предпочтения»).
Сущность аппроксимации Фогеля в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем строка или столбец с наибольшей разностью заполняются в направлении от клетки с минимальным тарифом к клетке с максимальным. Подробнее далее.
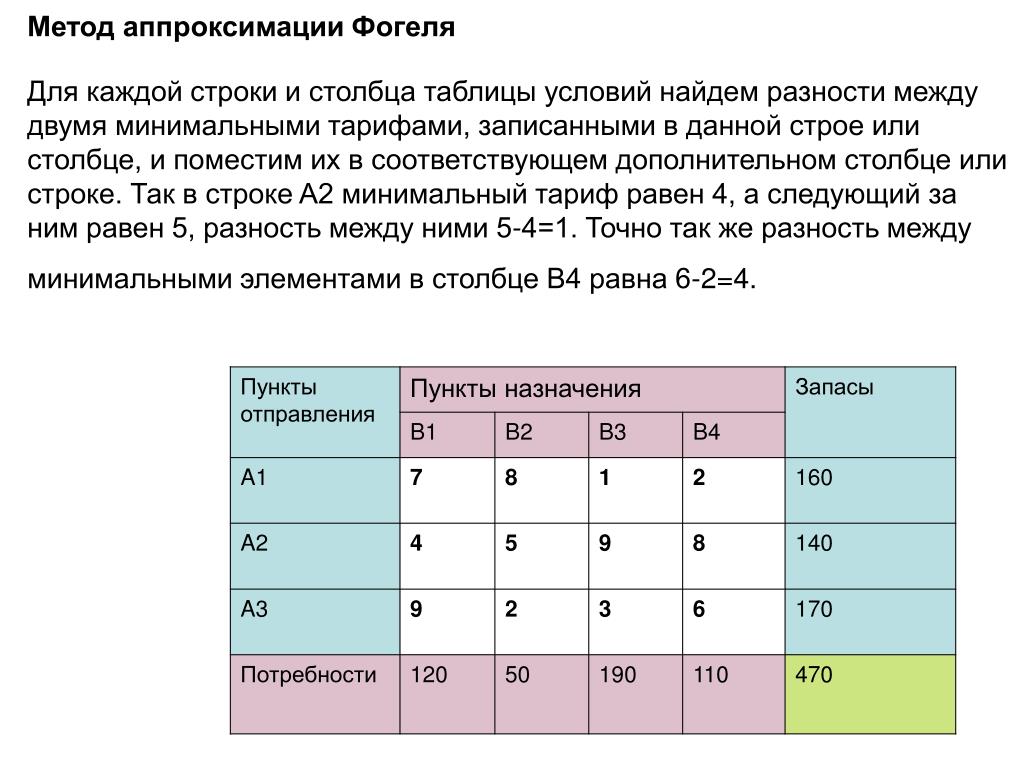
Первым делом находим для каждой строки транспортной таблицы абсолютные разности (по модулю, т. е. без знака) между двумя минимальными тарифами в этой строке. То же самое делаем и для каждого столбца: ищем в нем два минимальных тарифа и находим их разность по модулю.
е. без знака) между двумя минимальными тарифами в этой строке. То же самое делаем и для каждого столбца: ищем в нем два минимальных тарифа и находим их разность по модулю.
Если в строке/столбце две клетки с одинаковыми и минимальными значениями тарифов, то берем именно их. Тогда разность будет равна 0.
Найденные разности выписываем в добавочный столбец (Δi) и добавочную строку (Δj).
Среди вычисленных разностей (и по строкам, и по столбцам!) выбираем наибольшую.
Затем в строке или столбце, которому соответствует максимальная разность, ищем клетку с минимальным тарифом. Заполняем ее максимально возможным объемом грузоперевозки.
Если клеток с минимальным тарифом несколько, то заполняем ту из них, которой соответствует наибольшая разность (Δj — если выбираем по строке, или Δi — если выбираем по столбцу).
Затем повторяем все вышеописанные действия снова, только уже не учитывая заполненные клетки и выбранные ранее разности (Δi и Δj). И так до тех пор, пока не будет полностью найден опорный план.
И так до тех пор, пока не будет полностью найден опорный план.
Оставшиеся ячейки транспортной матрицы уже и так очевидно каким образом следует заполнить:
В результате мы получаем опорный план:
Зачастую опорный план, полученный аппроксимацией Фогеля, оказывается либо сразу оптимальным (как в этом примере), либо очень близким к нему. Но именно часто, а не всегда!
Галяутдинов Р.Р.
Источники
- Аппроксимация Фогеля // Викиучебник. URL: http://ru.wikibooks.org/wiki/Аппроксимация_Фогеля (дата обращения: 5.03.2014)
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Если понравилась статья, поделитесь с друзьями и подпишитесь на обновления:
Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.
Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р. Р. Транспортная задача: метод аппроксимации Фогеля // Сайт преподавателя экономики. [2014]. URL: https://galyautdinov.ru/post/approksimaciya-fogelya (дата обращения: 03.04.2023).
Р. Транспортная задача: метод аппроксимации Фогеля // Сайт преподавателя экономики. [2014]. URL: https://galyautdinov.ru/post/approksimaciya-fogelya (дата обращения: 03.04.2023).
Алгоритм метода Фогеля.
В каждой строке находят разность между двумя наименьшими стоимостями и записывают ее около соответствующей строки справа;
В каждом столбце находят разность между двумя наименьшими стоимостями и записывают ее под соответствующим столбцом;
Среди всех полученных разностей находят максимальную и распределяют объем перевозки в клетку строки или столбца с наименьшей стоимостью;
Исключают из рассмотрения строку или столбец с распределенными поставками и возвращаются к пункту 1. Процесс продолжается до тех пор, пока все запасы не будут вывезены, а потребности удовлетворены;
Когда план построен, рассчитываются транспортные расходы.

Методы решения задач математического программирования Алгоритм метода двойного предпочтения.
В таблице в каждом столбце отмечают галочкой клетку с наименьшей стоимостью и в каждой строке отмечают галочкой клетку с наименьшей стоимостью;
В клетки с двумя галочками записывают максимально возможные объемы перевозок, каждый раз, исключая соответствующий столбец или строку;
Распределяют перевозки по клеткам с одной галочкой;
В оставшейся части таблицы перевозки распределяют в клетки с наименьшей стоимостью.
Когда план построен, рассчитываются транспортные расходы.
Алгоритм метода северо-западного угла.
Пользуясь таблицей 9 распределяют груз, начиная с левой верхней, условно называемой северо-западной, клетки (1,1). Необходимо удовлетворить потребности В1 за счет поставщика А1;
а).
 Если b 1>a1,
в клетку (1,1) записывают a1 и строку 1 вычеркивают из рассмотрения;
Если b 1>a1,
в клетку (1,1) записывают a1 и строку 1 вычеркивают из рассмотрения;
b). Если a1>b1, в клетку (1,1) записывают b1 и столбец 1 вычеркивают из рассмотрения;
а). Если b1>a1, ∆= b1 — a1 – неудовлетворенные потребности. Спускаются на клетку вниз и сравнивают ∆ с a2;
b). Если a1>b1, ∆=a1 — b1 – не вывезенные запасы. Двигаются по строке вправо и сравнивают ∆ с b2;
Необходимо вернуться к пункту 2;
Рассчитываются транспортные расходы.
Алгоритм метода потенциалов.
проверяется тип модели транспортной задачи и в случае открытой модели сводим ее к закрытой;
проверяем план (таблицу) на удовлетворение системе уравнений и на невыражденность; в случае вырождения плана добавляем условно заполненные клетки с помощью « 0 »;
для опорного плана определяются потенциалы ui и vj, соответствующие базисным клеткам, по условию:
ui + vj = cij
Таких
уравнений будет m
n
1 , а переменных будет m
n. Для их определения одну из переменных
полагают равной любому постоянному
значению. Обычно принимают u1 = 0.
Для их определения одну из переменных
полагают равной любому постоянному
значению. Обычно принимают u1 = 0.
После этого для небазисных клеток опорного плана определяются оценки ,
где
При этом если 0, то опорный план оптимален, если же среди окажется хотя бы один положительный элемент, то опорный план можно улучшить.Улучшение опорного плана осуществляется путем целенаправленного переноса из клетки в клетку транспортной таблицы отдельных перевозок без нарушения баланса по некоторому замкнутому циклу.
Циклом транспортной таблицы называется последовательное соединение замкнутой ломаной линией некоторых клеток, расположенных в одном ряду (строке, столбце), причем число клеток в одном ряду должно быть равно двум.
Каждый цикл имеет
четное число вершин, одна из которых в
клетке с небазисной переменной, другие
вершины в клетках с базисными переменными.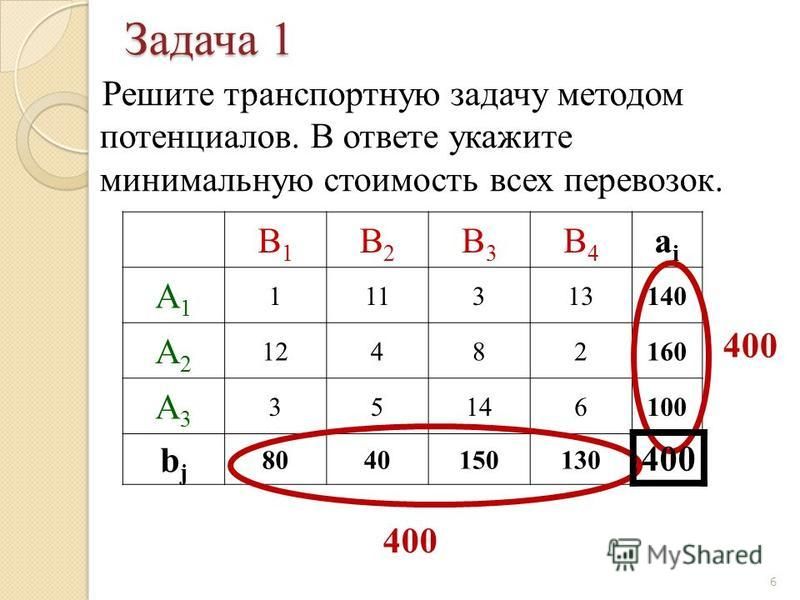 Клетки отмечаются знаком «+», если
перевозки в данной клетке увеличиваются
и знаком «–» в противном случае. Цикл
начинается и заканчивается на выбранной
небазисной переменной и отмечается
знаком «+». Далее знаки чередуются.
Клетки отмечаются знаком «+», если
перевозки в данной клетке увеличиваются
и знаком «–» в противном случае. Цикл
начинается и заканчивается на выбранной
небазисной переменной и отмечается
знаком «+». Далее знаки чередуются.
Количество единиц продукта, перемещаемого из клетки в клетку по циклу, постоянно, поэтому сумма перевозок в каждой строке и в каждом столбце остаются неизменными. Стоимость всего плана изменяется на цену цикла.
Цена цикла – это стоимость перевозки единицы продукта по циклу с учетом знаков вершин.
Улучшение опорного плана осуществляется путем нахождения цикла с отрицательной ценой.
Если критерий оптимальности не выполняется, то переходим к следующему шагу. Для этого:
а) в качестве начальной небазисной переменной принимается та, у которой оценка имеет максимальное значение;
б) составляется цикл пересчета;
в) находится число перерасчета по циклу: число X=min{Xij}, где Xij— числа в заполненных клетках со знаком « — »;
г) составляется новая таблица, добавляя X в плюсовые клетки и отнимая X из минусовых клеток цикла;
Возвращаются к пункту 3 и т.
 д.
д.Через конечное число шагов (циклов) обязательно приходят к ответу, так как транспортная задача всегда имеет решение.
Метод приближения Фогеля (VAM) | метод решения транспортной задачи | Транспортная модель
Метод аппроксимации Фогеля (VAM) является одним из методов получения допустимого решения транспортной задачи. Мы уже знаем метод наименьших затрат и метод северо-западного угла | метод решения транспортной задачи | Транспортная модель транспортной задачи для получения допустимого решения.
Метод аппроксимации Фогеля (VAM) Метод работает на концепции альтернативной или штрафной стоимости.
Альтернативная стоимость — это штраф за неправильный выбор ячейки для распределения.
Мы узнаем, как найти альтернативную стоимость, только позже в этом примечании, проходя различные этапы численного представления, представленного здесь.
Чтобы понять метод аппроксимации Фогеля, мы пройдемся по численному представлению следующим образом (то же численное значение, которое мы использовали в методе северо-западного угла | методе решения транспортной задачи | транспортной модели и методе наименьших затрат:
ЧисловойКомпания по производству мобильных телефонов имеет три филиала, расположенных в трех разных регионах, скажем, в Джайпуре, Удайпуре и Мумбаи.
 Компания должна доставить мобильные телефоны в три пункта назначения, например, в Канпур, Пуну и Дели. Доступность из Джайпура, Удайпура и Мумбаи составляет 40, 60 и 70 единиц соответственно. Спрос в Канпуре, Пуне и Дели составляет 70, 40 и 60 соответственно. Стоимость перевозки указана в матрице ниже (в рублях). Используйте метод аппроксимации Фогеля, чтобы найти базовое допустимое решение (BFS).
Компания должна доставить мобильные телефоны в три пункта назначения, например, в Канпур, Пуну и Дели. Доступность из Джайпура, Удайпура и Мумбаи составляет 40, 60 и 70 единиц соответственно. Спрос в Канпуре, Пуне и Дели составляет 70, 40 и 60 соответственно. Стоимость перевозки указана в матрице ниже (в рублях). Используйте метод аппроксимации Фогеля, чтобы найти базовое допустимое решение (BFS). Обратите внимание, что все пояснения даны в «ГОЛУБОМ» цвете. Вы должны написать на экзамене единственное, что дано этим обычным цветом под каждым шагом (если есть), иначе вы можете напрямую решить матрицу задачи, как описано здесь.
Решение:
Шаг 1: Сбалансируйте проблему
Сбалансируйте проблему, что означает, что мы должны проверить, что если;
Σ Предложение=Σ Спрос\цвет{#32c5d4} \Sigma \text { Предложение} = \Sigma \text { Спрос} Σ Предложение=Σ Спрос
Если это так, то будем рассматривать данную задачу как сбалансированную.
Что, если он не сбалансирован?
т. е. Σ Предложение≠Σ Спрос\цвет{#32c5d4} \text {т.е. } \Sigma \text { Предложение} \not = \Sigma \text { Спрос}т.е. Σ Предложение=Σ Спрос
Если такое условие возникает, то мы должны добавить фиктивный источник или рынок; в зависимости от того, что делает проблему сбалансированной.
Вы можете посмотреть это видео о несбалансированных транспортных задачах для таких чисел.
→\to→ Данная транспортная задача сбалансирована.
Шаг 2: Найдите разницу между строками и столбцами
Теперь мы найдем разницу в строках и столбцах предоставленной матрицы.
Примечание. Разница между строками и столбцами называется возможностью или штрафными издержками. Таким образом, обнаружив разницу в каждой строке и столбце, мы находим здесь альтернативную стоимость.
Чем больше значение разницы, тем выше будет штраф за размещение во второй наименьшей ячейке затрат вместо наименьшей ячейки затрат этой конкретной строки/столбца в матрице.
Таким образом, это указывает на штраф за неправильное распределение.
Для того же мы решим это следующим образом:
Здесь, как вы можете видеть в первой строке, нам нужно найти ячейку, содержащую наименьшее значение (можно сказать наименьшую стоимость), а затем из оставшихся двух значений найти наименьшее.
Следовательно, мы находим 1 и 4 как наименьшие значения в первой строке.
Возьмите разность этих двух чисел, то есть (4−1)=3(4-1) = 3(4−1)=3.
Точно так же найдите различия для всех строк, как показано выше.
Найти разницу для всех столбцов одним и тем же способом.
Шаг 3. Выберите строку/столбец с наибольшей разницей
Как видно выше, наибольшее значение разницы равно 4 для последней строки.
Итак, мы выберем эту строку и узнаем минимальную стоимость в этой строке.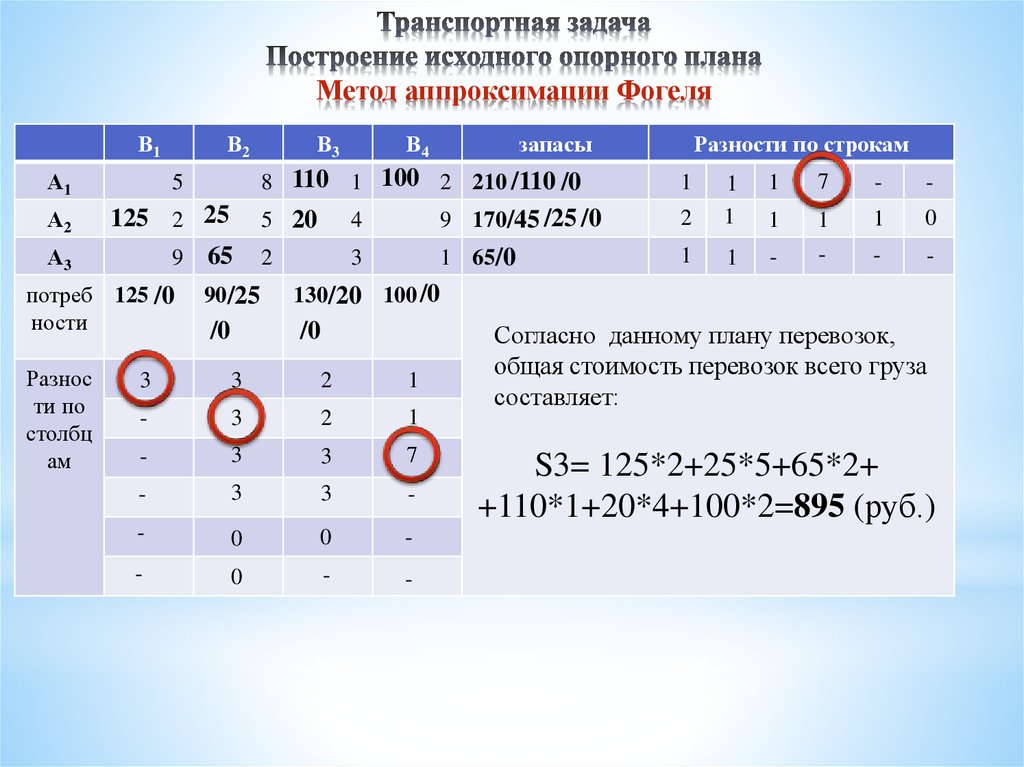
Вы обнаружите, что минимальная стоимость 2.
Теперь сравним спрос и предложение для этой строки и столбца соответственно.
Мы обнаруживаем, что у нас есть предложение 70 и спрос 40 для выбранной ячейки.
Сравнение обоих и выбор минимального из них для размещения в ячейке, как показано ниже.
Проверить столбец, требование которого выполнено.
Шаг 4. Удалите строку/столбец, чей спрос или предложение удовлетворены, подготовьте новую матрицу и повторите ту же процедуру
Как видите, теперь у нас есть новая матрица с удаленным вторым столбцом (поскольку его требование было 40 и оно выполнено)
Теперь мы будем повторять ту же процедуру, пока не закончим со всеми распределениями.
т. е.
- Найти разницу между строками и столбцами.
- Выберите наибольшую разницу.
- Выделить ячейку с минимальной стоимостью, связанной с выбранной самой высокой разницей в строке или столбце.

- Проверить строку/столбец, если спрос или предложение удовлетворены.
Совет:
→ Как вы можете видеть на последнем шаге выше, разница между строками и столбцами не предусмотрена.
→ Это потому, что у нас осталось только две ячейки, и вы можете сначала выбрать любую из этих ячеек, это не имеет значения.
→ Кроме того, если вы найдете разницу и выполните ту же процедуру, это приведет вас к тому же ответу.Это поможет сэкономить время на экзамене.
Шаг 5: После того, как все распределения сделаны, запишите все распределения в матрицу и найдите Транспортные расходы
Теперь у нас есть все распределения с соответствующей ячейкой.
Найдите транспортные расходы следующим образом:
→ Транспортные стоимости=(1×40)+(3×40)+(3×20)+(6×30)+(2×40)=480 рупий\begin{aligned } \to \\text {Транспортные расходы} &= (1 \times 40) + (3 \times 40) + (3 \times 20) + (6 \times 30) + (2 \times 40) \\ &= \text {рупий} 480 \end{выровнено}→ Транспортные стоимости=(1×40)+(3×40)+(3×20)+(6×30)+(2×40)=480 рупий
Вы можете найти решение этого числа с помощью VAM и метода наименьших затрат, как то же самое Rs 480\text {Rs } 480Rs 480 , но это не всегда возможно.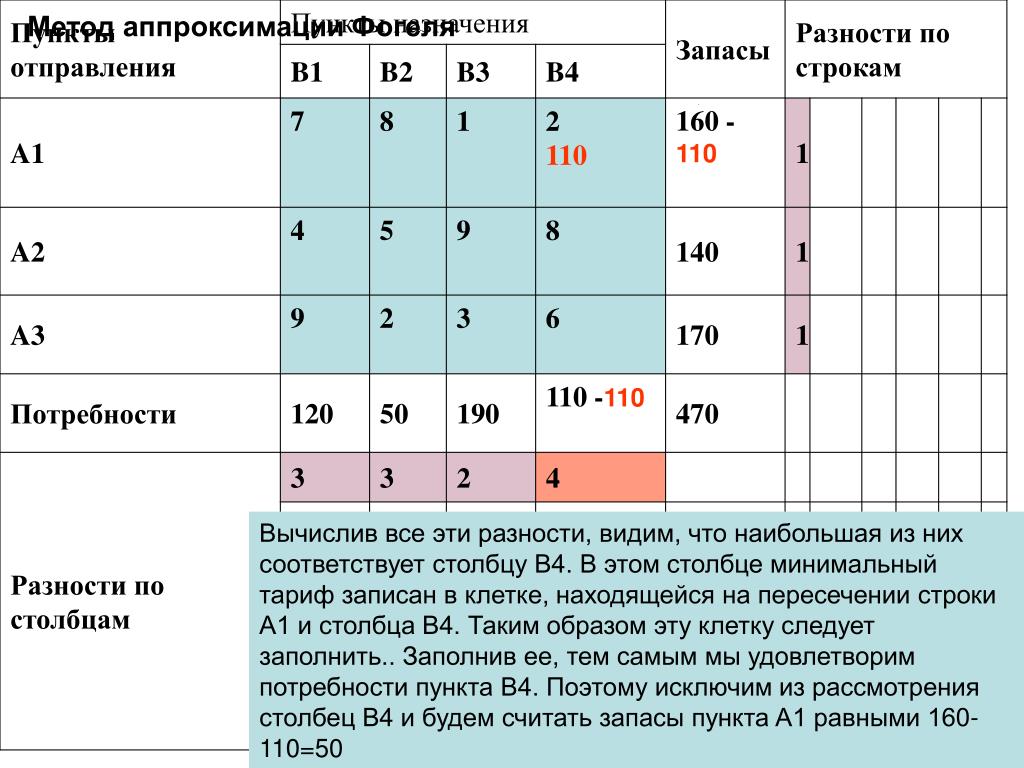
Фактически, VAM является более эффективным методом, чем два других ( Метод наименьших затрат и Метод северо-западного угла | Метод решения транспортной проблемы | Транспортная модель ).
Если в вопросе не указан конкретный метод, мы рекомендуем использовать метод приближения Фогеля.
Интересно, а что, если есть ничья при выборе ячейки разницы или распределения ???
Посмотрите это видео для того же — Связь при выборе строки и столбца — Метод аппроксимации Фогеля (VAM), также скоро будут загружены примечания для того же самого. Подпишитесь на уведомления, чтобы получать уведомления о последних обновлениях на веб-сайте EL.
Теперь доступны примечания к вышеупомянутому видео — Связь при выборе строки и столбца (метод аппроксимации Фогеля — VAM) | Числовой | Решение транспортной проблемы | Транспортная модель
Найти решение того же числа по:
Метод наименьшей стоимости
Метод северо-западного угла | метод решения транспортной задачи | Транспортная модель
Открытый доступ SCIRP
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.

- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Подача статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp.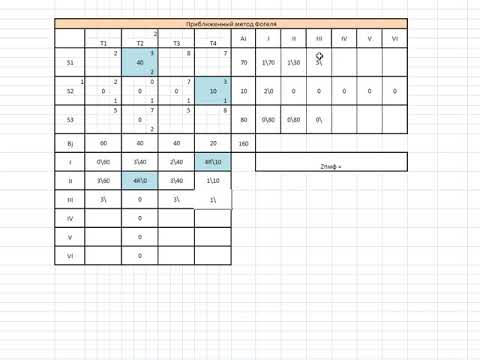 org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Анализ подотчетности политики и программ, ориентированных на питание, в Буркина-Фасо()
Исса Сомби
Социология разума Том 13 № 2, 3 апреля 2023 г.

DOI: 10.4236/см.2023.132005 9Загрузки 86 просмотров
Антиэритроцитарная аллоиммунизация в системе резус-фактора при хронической болезни почек: частота у пациентов клинической больницы Университета Яунде I()
Хосуэ Симо Луокдом, Ромарик Де Манфуо Туоно, Кевин Нелли Деджо, Приска Ингрид Меупия Текам, Футсе Йимта, Пеги Марсьяль Мбианда Чуесси, Мэрилин Сеуко Ньопвоу, Пьер Рене Фоцинг Кветче
Журнал библиотеки открытого доступа Том 10 № 3, 31 марта 2023 г.
DOI: 10.4236/oalib.1109932 8 загрузок 58 просмотров
Воздействие прогрессивной обрезки на листового минера ( Coelaenomenodera lameensis ) Распространенность и урожайность масличной пальмы ( Elaeis guineensis )
— Пример плантации масличных пальм Benso, Adum Banso Estate, Гана()Исаак Аддо, Эммануэль Ака, Самуэль Аваала Авоннеа, Кваси Баах Офори, Виктор Тетте Зутах, Джеффри Смит Одуро, Эстер Фоби Донкор, Квадво Гьяси Санто
Американский журнал наук о растениях Том 14 № 3, 31 марта 2023 г.

DOI: 10.4236/ajps.2023.143025 4 загрузки 49 просмотров
Эксклюзивный остеосинтез малоберцовой кости для лечения открытых переломов Gustillo I-III B дистальной половины костей голени в условиях ограниченных ресурсов()
Жорж Куигва Тоха, Пол Мунгуаконква Будема, Она Лонгомбе Ахука, Акинджа Битум Увонда, Жан Мари Вианни Кабангу Чимбила
Открытый журнал ортопедии Том 13 № 3, 31 марта 2023 г.
DOI: 10.4236/ojo.2023.133012 2 загрузки 27 просмотров
Вопрос об основном праве на материальное равенство: оправдывают ли исключительные случаи ультралиберальную меритократию? ()
Жоао Маурисио Лейтао Адеодато, Жоао Витор Крус де Кастро
Beijing Law Review Vol.



 Если b 1>a1,
в клетку (1,1) записывают a1 и строку 1 вычеркивают из рассмотрения;
Если b 1>a1,
в клетку (1,1) записывают a1 и строку 1 вычеркивают из рассмотрения; д.
д.




