Как решать уравнения в маткаде: Решение уравнений в MathCad 13, 14, 15 на примерах. Методы Given

7. РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MATHCAD

Информатика и вычислительная техника / Программные средства / 7. РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MATHCAD

Постановка задачи

Задача ставится следующим образом:

Пусть имеется алгебраическое уравнение  с одним неизвестным х или система алгебраических уравнений

,

где f₁(x₁, …, x_m) и f_n(x₁, … , x_m) – некоторые функции.

Требуется решить данное уравнение или систему уравнений, т.е. найти те значения х, в которых уравнения превращаются в верное равенство.

Отыскание корней численными методами связано с несколькими задачами:

Ø Исследование существования корней в принципе, определение их количества и примерного расположения;

Ø Отыскание корней с заданной погрешностью

Всевозможные функции MathCAD нацелены на решение второй задачи, т.е. предполагается, что корни уже приблизительно локализированы. Выбор встроенных функций для решения уравнений и систем уравнений осуществляется в зависимости от специфики уравнения.

Решение одного уравнения с одним неизвестным

Рассмотрим алгебраическое уравнение f(x)=0 с одним неизвестным х, например, sin(x)=0.

Для решения таких уравнений MathCAD имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.

Мнемоника команды выглядит следующим образом:

root (f(x), x) или root (f(x), x, a, b),

где f(х) – скалярная функция, определяющая уравнение; х – скалярная переменная, относительно которой решается уравнение; а, b – границы интервала, внутри которого происходит поиск корня.

Первый тип функции root требует дополнительного задания начального значе

ния переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.

Приведем пример решения очень простого уравнения sin(x)=0, корни которого известны заранее (рис. 38).

Обратите внимание, что, хотя уравнение имеет бесконечное количество корней MathCAD находит (с заданной точностью) только один из них, х₀, лежащий наиболее близко к х = 0,5. Если задать другое начальное значение, например х = 3, то решением будет другой корень уравнения х₁ = π и т.д. Таким образом, для поиска корня средствами MathCAD требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих.

Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в область локального экстремума. В этом случае секущая может иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого корня. Для решения таких уравнений лучше применять функцию Minerr.

Рис. 7.1. Функция Minerr

Примечание: Для решения уравнения с одним неизвестным применимы и градиентные методы, относящиеся в MathCAD к системам уравнений.

Иногда удобнее задавать не начальное приближение к корню, а интервал [а, b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нуж

но. Поиск корня будет осуществлен в промежутке между а и b альтернативным численным методом (Риддера или Брента). Явный вид функции f(x) может быть определен непосредственно в теле функции root (рис. 39).

Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:

Ø внутри интервала [а, b] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно;

Ø значения f(а) и f(b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

Если уравнение не имеет действительных корней, но имеет мнимые, то их также можно найти. Например, уравнение х²+1=0, имеющее два чисто мнимых корня, решается два раза с разными начальными значениями (рис. 40).

При задании начального значения 0,5 численный метод отыскивает первый корень (отрицательную мнимую единицу –i), а при начальном значении –0,5 находится и второй корень i.

Для решения этого уравнения второй вид функции root (с четырьмя, а не с двумя аргументами) неприменим, поскольку f(х) является положительно определенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.

Нахождение корней полинома

Если функция f(x) является полиномом, то все его корни можно определить, использую встроенную функцию polyroots(v), где v – вектор, составленный из коэффициентов полинома.

Поскольку полином n-й степени имеет ровно n корней (некоторые из них могут быть кратными), вектор v должен состоять из n+1 элемента. Результатом действия функции polyroots является вектор, составленный из n корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root.

Например, найдем корни полинома четвертой степени f(x)=х⁴-6х³+12х²-10х+3 с

помощью функции polyroots (рис. 41).

Рис. 7.2. Функция Polyroots

Запишем коэффициенты рассматриваемого в примере полинома в виде вектора. Первым в векторе должен идти свободный член полинома, вторым – коэффициент при х

1 и т.д. Соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени x^N.

Совет: Иногда исходный полином имеется не в развернутом виде, а, например, как произведение нескольких полиномов. В этом случае определить все его коэффициенты можно, выделив его и выбрав в меню Symbolics (Символика) пункт Expand (Разложить). В результате символьный процессор MathCAD сам преобразует полином в нужную форму, пользователю надо будет только корректно ввести ее в аргументы функции polyroots.

Далее показано действие функции polyroots. Обратите внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. Просто нужно помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня.

Для функции polyroots можно выбрать один из двух численных методов – метод полиномов Лаггера (он установлен по умолчанию) или метод парной матрицы.

Решение системы линейных алгебраических уравнений

Рассмотрим систему уравнений вида

                                                    (1)

В матричной форме СЛАУ записывается в эквивалентном виде:

А∙Х=В, (2)

где А – матрица коэффициентов СЛАУ размерности n×n; x – вектор неизвестных; В – вектор правых частей уравнений.

Рис.

7.3. Матрица

СЛАУ имеет единственное решение, если матрица А является невырожденной, т. е. ее определитель не равен нулю. С вычислительной точки зрения, решение СЛАУ не представляет трудностей, если матрица А не очень велика.

В MathCAD СЛАУ можно решить как в более наглядной форме (1), так и в более удобной для записи форме (2). Для первого способа следует использовать вычислительный блок Given/Find, а для второго – встроенную функцию решения системы линейных уравнений lsolve. Мнемоника написания команды следующая:

lsoive (А, В),

где А – матрица коэффициентов системы; В – вектор правых частей.

Применение функции lsolve показано на рис. 42.

В некоторых случаях, для большей наглядности представления СЛАУ, его можно решить точно так же, как систему нелинейных уравнений. Не забывайте, что при численном решении всем неизвестным требуется присвоить начальные значения (это сделано в первой строке листинга) (рис. 43). Они могут быть произвольными, так как решение СЛАУ с невырожденной матрицей единственно.

Решение системы нелинейных уравнений

Рис. 7.4. Решение системы

Рассмотрим решение системы N нелинейных уравнений с m неизвестными

Здесь f_i(x₁, … , x_m) – некоторые скалярные функции от скалярных переменных x₁, x₂, …, х_m и, возможно, от еще каких-либо переменных. Уравнений может быть как больше, так и меньше числа переменных. Заметим, что систему можно формально переписать в виде f(x)=0, где х – вектор, составленный из переменных x₁, x₂, …, х_m; f(x) – соответствующая векторная функция.

Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:

1) Given – ключевое слово;

2) Система, записанная логическими операторами в виде равенств и, возможно, неравенств;

3) Find (х₁, …, х_m) – встроенная функция для решения системы относительно переменных х₁, …, х

m.

Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Если вы предпочитаете ввод с клавиатуры помните, что логический  знак равенства вводится сочетанием  клавиш <Ctrl> + <=>. Блок Given/Find используется для  поиска решения итерационные  методы, поэтому, как и для функции root, требуется задать начальные значения для всех х₁, …, х_m. Сделать это необходимо до ключевого слова Given. Значение функции Find есть вектор, составленный из решения по каждой переменной. Таким образом, число элементов вектора

Find равно числу аргументов.

Рис. 7.5. Система

В листинге (рис 44) приведен пример решения системы двух уравнений.

В первой строке листинга переменным х и у, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, содержащая вектор решения. Первый элемент вектора есть первый аргумент функции Find, второй элемент – ее второй аргумент.

Совет: Часто бывает очень полезно проверить точность решения уравнений, вычислив значения образующих их функций в найденных вычислительным процессором корнях.

Рис. 7.6. Точность

В листинге найдено только одно из двух решений – находящееся в правой нижней части графика (рис. 45). Чтобы отыскать и второе решение, следует повторить вычисления, изменив начальные значения так, чтоб они лежали ближе к другой точке пересечения графиков, например, х=–1,  y=–1.

Пока мы рассмотрели пример системы из двух уравнений и таким же числом

неизвестных, что встречается наиболее часто. Но число уравнений и неизвестных может и не совпадать. Более того, в вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, введение ограничения на поиск только отрицательных значений х (рис. 46).

Рис. 7.7. Ограничение на поиск

Обратите внимание, что, несмотря на те же начальные значения, что и в предыдущем листинге  мы получили  другой корень. Это произошло именно благодаря введению дополнительного неравенства, которое определено в блоке Given в предпоследней строке.

Если предпринять попытку решить несовместную систему, MathCAD выдаст сообщение  об ошибке, гласящее, что ни одного решения не найдено, и предложение попробовать поменять начальные значения или значение погрешности.

Примечание: Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Другая константа TOL определяет условие прекращения итераций численным алгоритмом. Значение CTOL может быть задано пользователем, так же как и TOL, например, CTOL:=0,01. По умолчанию принято, что CTOL=TOL=0,001, но по желанию можно переопределить их.

Рис. 7.8. Переопределение

Вычислительным блоком с функцией Find можно найти и корень уравнения с одним неизвестным. Действие Find в этом случае совершенно аналогично уже рас

смотренным в данном разделе примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа  возвращаемого функцией Find (рис 47).

Символьное решение уравнений

Некоторые уравнения можно решить точно с помощью символьного процессора MathCAD. Делается это очень похоже на численное решение уравнений с применением вычислительного блока. Присваивать неизвестным начальные значения нет необходимости. Рассмотрим листинги символьного решение уравнения с одним неизвестным и системы двух уравнений с двумя неизвестными.

Как видно, вместо знака равенства после функции Find в листингах (рис. 48) следует знак символьных вычислений, который можно ввести с панели Symbolic, или, нажав клавиши <Ctrl>+<. >.

Рис. 7.9. Пример вычисления

Не забывайте, что сами уравнения должны иметь вид логических выражений, т.е. знаки равенства нужно вводить с помощью панели Booleans (Булевы операторы). Обратите внимание, что во втором листинге вычислены как два первых действительных корня, которые мы уже находили численным методом, так и два других мнимых корня. Эти два последних корня чисто мнимые, так как множитель

MathCAD — это просто! Часть 2. Уравнения

Решение уравнений на бумаге — это задача, с которой каждый знаком еще со школьной скамьи. Сначала мы учились решать простые линейные уравнения, деля а на b и получая x, потом — системы уравнений, затем переходили к квадратным уравнениям. Находим дискриминант, извлекаем корень, делим, складываем… Все это вам знакомо, не так ли? Знакомы, наверное, и трансцендентные уравнения: тригонометрические, логарифмические (они же показательные), смешанные…

Системы трансцендентных уравнений — это вообще песня, причем песня из серии «этот стон у нас песней зовется». Люди давно уже пришли к выводу, что решать уравнения с помощью компьютера — отнюдь не роскошь, а вполне разумный подход к делу. Только раньше каждый, кто желал решить уравнение, должен был уметь программировать и владеть при этом какими-нибудь численными методами — например, методом Гаусса для решения систем линейных уравнений или методом Зейделя для решения трансцендентных. Сейчас эти все методы, конечно, тоже используются, но большая часть пользователей могут забыть их как страшный сон — все эти вычисления возможны в MathCAD’е, и именно о том, как их выполнять в этом замечательном математическом пакете, я сейчас и расскажу.

Аналитическое решение уравнений

Довольно значительное число уравнений поддаются аналитическому решению — т.е. решению в обобщенном виде, когда корни уравнения представляются в виде какой-то формулы, выражающей их зависимость от входящих в уравнение функций и различных коэффициентов перед ними. При этом, однако, надо заметить, что такой подход применим отнюдь не ко всем уравнениям — большая часть трансцендентных уравнений не может быть решена аналитически. Поэтому мы сейчас будем говорить преимущественно о полиномиальных уравнениях, известных также под названием алгебраических. Алгебраическим называется уравнение, которое можно преобразовать так, что в левой части будет многочлен от одной или нескольких неизвестных, а в правой — нуль. Степень многочлена называется степенью уравнения. Простейшие алгебраические уравнения: линейное уравнение — уравнение 1-й степени с одним неизвестным ax + b = 0, имеющее один действительный корень; квадратное уравнение — уравнение 2-й степени ax2 + bx + c = 0, которое в зависимости от значения коэффициентов может иметь либо два различных, либо два совпадающих действительных корня либо не иметь действительных корней. Вообще алгебраическое уравнение степени n не может иметь более n корней, что доказывается в рамках основной теоремы алгебры, которую в ВУЗах проходят в курсе математического анализа.

Что ж, давайте, пожалуй, перейдем к практике. То есть запустим MathCAD, включим панель символьных вычислений (Symbolic) — о том, как это сделать, уже было рассказано ранее в первой статье про MathCAD. На этой панели нам с вами понадобится оператор solve — именно он отвечает за аналитическое решение уравнений. Общий вид этого оператора такой: уравнение solve, переменная > решение. Здесь уравнение — это именно то уравнение, решение которого мы хотим найти в общем виде, а переменная — это символ, обозначающий в нашем уравнении переменную величину. Его нужно указывать для того, чтобы MathCAD (не такой уж он умный, как иногда кажется!) мог отличить переменную от коэффициентов. Давайте попробуем найти решение обычного квадратного уравнения ax2 + bx + c = 0. Для этого нажмите на кнопку Solve на панели инструментов символьных вычислений и на то место, где должно быть записано уравнение, введите наше квадратное уравнение. Здесь есть два тонких момента. Во-первых, чтобы записать «x2», нужно после x нажать Shift + 6 — тогда вы перейдете от записи переменных к записи показателя степени. Чтобы затем переключиться в режим записи других слагаемых в уравнении, достаточно нажать на клавиатуре стрелку вправо.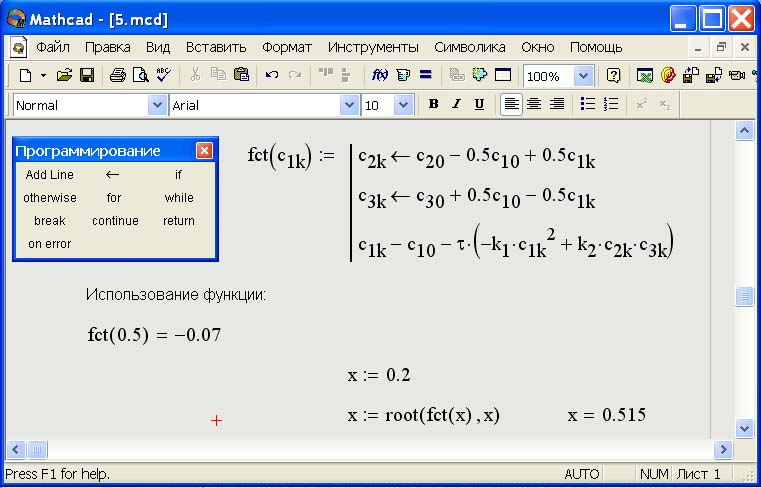 Вообще навигация по записям в MathCAD при помощи стрелок вполне прозрачная — вы передвигаетесь стабильно в том направлении, куда указывает стрелка, и перескакиваете в показатели степени и индексы автоматически. Во-вторых, при записи уравнения в операторе solve «равно» нужно не обычное, а логическое — оно записывается с клавиатуры комбинацией Ctrl + =. При этом, если правая часть вашего уравнения равна нулю, то и ноль, и знак равенства можно опускать — MathCAD посчитает, что уравнение записано в стандартном виде, и успешно (если это, конечно, возможно) решит его. Итак, давайте посмотрим, что получилось от «скармливания» оператору solve нашего с вами квадратного уравнения.

Как видите, ничего неожиданного не произошло: MathCAD честно воспользовался известными всем еще из школьного курса алгебры формулами Виета, а решения уравнения записал в виде вектора-столбца. Несложно самостоятельно убедиться в том, что MathCAD знает и формулы Кордано для решения кубических уравнений — их он также может решать с произвольными коэффициентами. Правда, конечно, решения получаются несравненно более громоздкими, а потому я их здесь не буду приводить. Это же справедливо и для уравнений четвертой степени, для которых также существуют аналитические решения. Решение других видов уравнений (например, показательных) в аналитическом виде также вполне возможно. Например, если мы запишем уравнение eax + b = 0, то MathCAD совершенно справедливо сообщит, что решением этого уравнения будет выражение ln(-b)/a. Точно так же можно решать простые тригонометрические уравнения.

Численное решение уравнений с помощью функции solve

Но, конечно, такие красивые результаты в максимально обобщенной форме мы сможем получать далеко не всегда. Уже на уравнениях пятой степени MathCAD спотыкается, и произвольные коэффициенты приходится заменять постоянными. Впрочем, в этом ничего страшного нет — даже уравнения третьей степени со всеми произвольными коэффициентами решать вряд ли имеет смысл, поскольку гораздо проще подставить коэффициенты и получить нормальные числа в решении — в конце концов, общие формулы для решения алгебраических выражений используются именно из-за того, что живому человеку гораздо проще подставить числа в готовую формулу, чем подбирать каждый раз корни уравнения. С компьютерами дело обстоит в большинстве случаев с точностью до наоборот — получить численное решение уравнения зачастую гораздо проще, чем аналитическое. Оператор solve умеет находить и численные решения уравнений. Если аналитическое решение получить не удается, он автоматически подключает систему нахождения численных решений уравнений. Так что, если мы запишем совершенно невообразимое для нормального человека уравнение x25 + sin(x) + ln(x) + ex + 1/x = 0, то MathCAD, и глазом не моргнув, выдаст нам результат вычислений.

Но численное решение уравнений с помощью функции solve — честно говоря, не лучшая идея. Некоторые виды уравнений она решает из рук вон плохо — в первую очередь, конечно же, это относится к уравнениям тригонометрическим. Начнем с того, что эта функция выдает решение только для одного периода в то время, как большая часть решений тригонометрических уравнений описывается с помощью специального целочисленного параметра, выражающего номер периода. Но это, в общем-то, не самое худшее, поскольку иногда использование solve приводит к получению совершенно неверного результата, который при подстановке его в уравнение дает совершенно неверное значение. Конечно, это является минусом MathCAD’а, но положение дел совсем не фатально. Если использовать специальные методы решения трансцендентных уравнений, то численные результаты будут совершенно адекватными. Можно также пойти по другому пути, например, преобразуя выражения с помощью символьного процессора MathCAD (о том, как это делается, я еще расскажу в дальнейшем), а затем уже решая с помощью solve более простые уравнения, получившиеся в результате этих преобразований. Численное решение уравнений требует от пользователя понимания того, что он ожидает в результате этого решения получить. Поэтому прежде, чем приступать к рассказу о самом процессе численного решения, я расскажу об одной полезной функции, которая пригодится для численного решения простых трансцендентных уравнений.

Решение уравнений с помощью функции root

Эта очень хорошая и полезная во всех смыслах функция имеет лишь одно ограничение — она может найти всего один корень. К сожалению, несущественным это ограничение назвать, честно говоря, сложно. Впрочем, вы увидите, что и его запросто можно обойти — разработчики MathCAD, по крайней мере, предусмотрели такую возможность, и ею вполне можно воспользоваться, если, конечно, в этом есть необходимость. Функция root имеет следующий вид: root(функция, переменная). Функция — это фактически левая часть уравнения в стандартном виде, т.е. уравнения, в котором левая часть равна нулю. Переменная — это, конечно же, тот символ, который обозначает в функции переменную величину. Для использования функции root нужно задать начальное приближение — то есть число, отталкиваясь от которого, функция root будет искать корни нашего уравнения. От начального приближения может весьма существенно зависеть и сам результат работы функции root, особенно если искомые корни уравнения находятся сравнительно близко. Начальное приближение задается очень просто: набираем имя нашей переменной до функции root, ставим двоеточие (MathCAD самостоятельно преобразует его в знак присвоения «:=»), пишем число, соответствующее нашему начальному приближению.

В принципе, вместо начального приближения можно задать интервал, в пределах которого должно лежать решение, отыскиваемое нами с помощью функции root. Для этого после имени переменной в списке параметров функции нужно (через запятую, конечно же) указать начало и конец интервала, на котором должно располагаться решение. У этого способа есть только одно существенное но: числа, определяющие начало и конец этого интервала, должны иметь разные знаки. При этом, если уравнение не имеет действительных корней, то и интервал нужно задавать в комплексной форме. Мнимая единица при этом записывается как i или как j.

Как видите, для численного нахождения уравнений с помощью функции root необходимо довольно точно представлять, где именно должны располагаться корни уравнения — сделать это можно, например, с помощью графика функции, на котором с помощью трассировки можно определить нули функции. Но о том, как строить графики и как ими потом пользоваться, как-нибудь в другой раз.

SF, spaceflyer@tut.by

Компьютерная газета. Статья была опубликована в номере 14 за 2008 год в рубрике soft

Как записать систему уравнений в mathcad

Содержание

• MathCad | ANSYS CFX | MS Office
• Поиск по сайту
• Выбор языка
• Решение систем уравнений в MathCad

Mathcad дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно пятидесяти. В первой части этого раздела описаны процедуры решения систем уравнений. В заключительной части приведены примеры и проведено обсуждение некоторых часто встречающихся ошибок. Результатом решения системы будет численное значение искомого корня. Для символьного решения уравнений необходимо использовать блоки символьного решения уравнений. При символьном решении уравнений искомый корень выражается через другие переменные и константы.

Для решения системы уравнений выполните следующее:

• Задайте начальные приближения для всех неизвестных, входящих в систему уравнений. Mathcad решает уравнения при помощи итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению.
• Напечатайте ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений. При печати слова Given можно использовать любой шрифт, прописные и строчные буквы. Убедитесь, что при этом Вы не находитесь в текстовой области или параграфе.
• Введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями уравнений стоит символ =. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов , , и .
• Введите любое выражение, которое включает функцию Find. При печати слова Find можно использовать шрифт любого размера, произвольный стиль, прописные и строчные буквы.

Find(z1, z2, z3, . . . )

Возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных.

Функция Find возвращает найденное решение следующим образом:

• Если функция Find имеет только один аргумент, то она возвращает решение уравнения, расположенного между ключевым словом Given и функцией Find.
• Если функция Find имеет более одного аргумента, то она возвращает ответ в виде вектора. Например, Find(z1, z2) возвращает вектор, содержащий значения z1 и z2 , являющиеся решением системы уравнений.

Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называются блоком решения уравнений.

На Рисунке 5 показан рабочий документ, который использует блок решения уравнений для решения одного уравнения с одним неизвестным. Так как имеется только одно уравнение, то только одно уравнение появляется между ключевым словом Given и формулой, включающей функцию Find. Так как уравнение имеет одно неизвестное, то функция Find имеет только один аргумент. Для решения одного уравнения с одним неизвестным можно также использовать функцию root, как показано ниже:

Рисунок 5: Блок решения уравнений для одного уравнения с одним неизвестным.

Между ключевым словом Given и функцией Find в блоке решения уравнений могут появляться выражения строго определенного типа. Ниже приведен список всех выражений, которые могут быть использованы в блоке решения уравнений. Использование других выражений не допускается. Эти выражения часто называются ограничениями. В таблице, приведенной ниже, через x и y обозначены вещественнозначные скалярные выражения, а через z и w обозначены любые скалярные выражения.

Условие	Как ввести	Описание
w = z	[Ctrl] =	Булево равенство возвращает 1, если операнды равны; иначе 0
x > y	>	Больше чем.
x

Следующие выражения недопустимы внутри блока решения уравнений:

• Ограничения со знаком .
• Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
• Неравенства вида a -15 .

Причиной появления этого сообщения об ошибке может быть следующее:

• Поставленная задача может не иметь решения.
• Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число. Если решение задачи комплексное, то оно не будет найдено, если только в качестве начального приближения не взято также комплексное число. На Рисунке 11 приведен соответствующий пример.
• В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Метод поиска решения, который используется в Mathcad, не позволяет в этом случае построить следующее приближение, которое бы уменьшало невязку. Для поиска искомого решения пробуйте использовать различные начальные приближения или добавьте ограничения на переменные в виде неравенств, чтобы обойти точку локального минимума.
• В процессе поиска решения получена точка, которая не является точкой локального минимума, но из которой метод минимизации не может определить дальнейшее направление движения. Метод преодоления этой проблемы — такой же, как для точки локального минимума: измените начальное приближение или добавьте ограничения в виде неравенств, чтобы миновать нежелательную точку остановки.
• Возможно, поставленная задача не может быть решена с заданной точностью. Если значение встроенной переменной TOL слишком мало, то Mathcad может достигнуть точки, находящейся достаточно близко к решению задачи, но уравнения и ограничения при этом не будут выполнены с точностью, задаваемой переменной TOL. Попробуйте увеличить значение TOL где-нибудь выше блока решения уравнений.

Что делать, когда имеется слишком мало ограничений

Если количество ограничений меньше, чем количество переменных, Mathcad вообще не может выполнить блок решения уравнений. Mathcad помечает в этом случае функцию Find сообщением об ошибке “слишком мало ограничений”.

Задача, аналогичная той, которая приведена на Рисунке 12, называется недоопределенной. Ограничений в ней меньше, чем переменных. Поэтому ограничения не содержат достаточной информации для поиска решения. Поскольку функция Find имеет пять аргументов, Mathcad определяет, что требуется решить два уравнения с пятью неизвестными. Вообще говоря, такая задача обычно имеет бесконечное число решений.

При использовании блока решения уравнений в Mathcad необходимо задать количество уравнений по крайней мере не меньшее, чем число искомых неизвестных. Если зафиксировать значения некоторых переменных, удастся решить уравнения относительно оставшихся переменных. На Рисунке 13 показано, как, зафиксировав часть переменных, решить недоопределенную задачу из Рисунка 12. Поскольку функция Find содержит только два аргумента, z и w, Mathcad определяет переменные x, y и v как имеющие фиксированные значения 10, 50 и 0 соответственно. Блок решения уравнений становится в этом случае корректно определенным, потому что теперь имеются только две неизвестных, z и w, и два уравнения.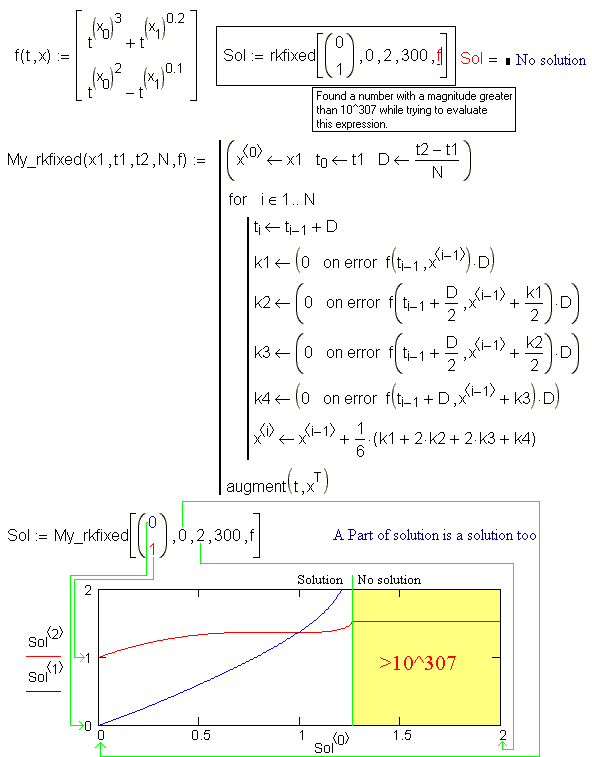

Рисунок 12: Функция Find имеет пять аргументов, поэтому Mathcad определяет, что требуется решить два уравнения с пятью неизвестными.

Рисунок 13: Проблема может быть решена, если уменьшить количество аргументов функции Find.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ

4 Решение уравнений и систем средствами Mathcad

Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.

Функция root, блоки Given…Find, Given…Minerr

В ходе численного решения обычно выделяют два этапа:

• отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
• уточнение корней – нахождение численного значения корня с указанной точностью.

Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 .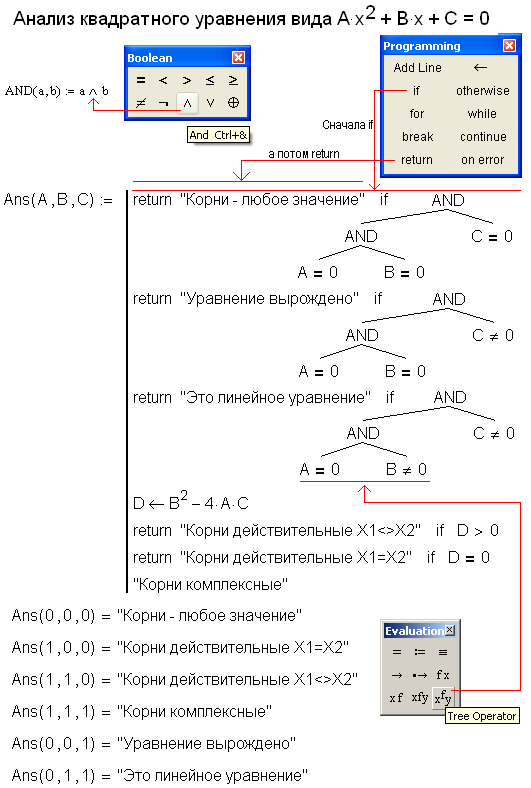 Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.

Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается

root(f(x), x, [a, b])

и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:

• f(x) – функция левой части уравнения f(x) = 0;
• x – переменная, относительно которой требуется решить уравнение;
• a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде

Этот прием используется в Mathcad так:

1. задается матрица коэффициентов при неизвестных системы A;
2. задается столбец свободных членов b;
3. вводится формула для нахождения решения системы X:=A -1 b;
4. выводится вектор решений системы X=.

Кроме того, пакет Mathcad имеет встроенную функцию

lsolve(A, b),

возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).

Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.

Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.

Порядок выполнения лабораторной работы

1. Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
2. Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
3. Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:

Лабораторная работа № 4
Решение уравнений и систем в Mathcad.

1. В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
2. Выполнить задание 1.

Задание 1. Решить уравнение .

Решение.

Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.

Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:

Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:

Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).

Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).

Для появления графика щелкнем левой клавишей мыши вне графической области.

Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.

Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.

После указанных преобразований график функции f(x) будет выглядеть следующим образом:

Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.

Этап отделения корней завершен.

Уточним теперь корни уравнения с помощью функции root.

Присвоим начальное приближение переменной x и укажем точность поиска корня:

Уточним заданное приближение к значению корня с помощью функции root:

Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:

Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:

Задание 2. Решить уравнение .

Решение.

Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:

Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.

Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.

Для получения результата напечатаем polyroots(v) =:

Задание 3. Решить систему линейных уравнений Сделать проверку.

Решение.

1-й способ. Использование блока Given … Find.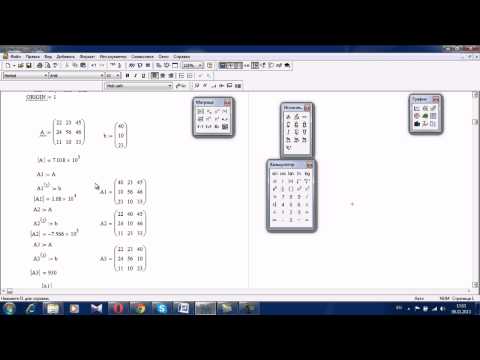

Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:

Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).

После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:

Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом

После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.

2-й способ. Использование блока Given…Minerr.

Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:

3-й способ. Решение системы линейных уравнений матричным способом.

Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:

Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:

Решим систему матричным способом по формуле

Решим систему с помощью функции lsolve:

Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:

MathCad | ANSYS CFX | MS Office

Поиск по сайту

Выбор языка

Решение систем уравнений в MathCad

Часто в курсовом проекте либо в лабораторной работе (да и вообще по жизни) возникает необходимость в решении больших и громоздких систем уравнений. Методы решения систем уравнений применяются те же, что и при решении уравнений: это вычислительный блок Given — Find и метод solve

Способ №1: использование вычислительного блока Given — Find:

Вычислительный блок Given — Find хорош тем, что он способен предоставить результат решения системы уравнений в двух видах: численном и символьном. Рассмотрим каждый из них подробнее.
Численный метод применяется в том случае если инженеру или студенту, необходимо получить только лишь численные результаты своей работы. В этом случае необходимо изначально задать значения всех «букв» и переменных(!). Переменные нужно задать в качестве начальных приближений. Эти начальные приближения нужны для корректной работы численных методов MathCad (см. подробнее в Решение уравнений). При этом, если начальное приближение не задано или задано не верно, то высока вероятность, что решение найдено не будет. Далее через «жирное» равно записывается список уравнений Вашей системы, а после него Find(x,y,z. )→ либо «=».
Символьный метод применяют для нахождения выражения искомой переменной из данной системы. В этом случае не обязательно задавать все величины входящие в систему. Достаточно просто записать все уравнения по порядку и затем найти решения в виде выражений с помощью оператора Find(x,y,z. )→. Нужно отметить, что не всегда удается получить символьное выражение для переменной, ввиду сложности преобразований.

Чтобы опустить нудное разъяснение синтаксиса MathCad, ниже приводятся примеры решения систем уравнений с помощью блоков Given — Find как численном так и в символьном виде, которые наглядно продемонстрируют правила оформления решения.

Пример №1. Решение системы уравнений в MathCad с помощью блока Given — Find численно: Скачать

Пример №2. Решение системы уравнений в MathCad с помощью блока Given — Find символьно: Скачать

Способ №2: Применение метода solve:

Этот метод очень хорошо подходит для получения корня в символьном виде. Записывается он так же как и для уравнений, с тем лишь отличием, что уравнения записываются в матрицу-столбец (см. рис. 1).
Рис. 1. Панель «Матрица»
После заполнения матрицы уравнениями, нажимаем кнопку с надписью solve на панели Symbolic (см. рис. 2) и перечисляем через запятую все искомые переменные.
Рис. 2. Панель «Символьные»
Форма записи представлена в примере.

Пример №3. Решение системы уравнений в MathCad с помощью solve: Скачать

Символьное решение уравнений » MathCadHelp.com » Номер 1 в назначениях MathCad

В этом разделе обсуждается, как использовать ключевые слова или команды меню из символического меню для символьного решения уравнения для переменной, поиска символических корней выражения и решения система уравнений символически. Большинство примеров в этом разделе демонстрируют «живое» решение с использованием ключевых слов-символов, но вы можете применять команды из меню «Символы» к выражениям в каждом конкретном случае, если хотите. Имейте в виду, что, в отличие от выражений с измененными ключевыми словами, выражения, измененные с помощью команд из меню «Символика», не обновляются автоматически, как описано в разделе «Использование меню «Символика»» на странице 360.

Решать уравнения символически намного сложнее, чем решать их численно. Вы можете обнаружить, что символьный решатель не дает решения. Это может произойти по разным причинам, описанным в разделе «Ограничения обработки символов» .

Решение уравнения для переменной

Чтобы символически решить уравнение для переменной, используйте ключевое словоsolve:

• Введите уравнение. Убедитесь, что вы используете [Ctrl]= для создания знака равенства.
• Нажмите [Ctrl] [Shift 1 • (удерживая нажатыми клавиши управления и Shift, введите точку). Mathcad отображает местозаполнитель слева от стрелки «→»
• В заполнителе введите решить, затем запятую и переменную, для которой нужно решить.
• Нажмите [Enter], чтобы увидеть результат.

Mathcad найдет переменную и вставит результат справа от «→». Обратите внимание: если переменная была возведена в квадрат в исходном уравнении, при решении вы можете получить два ответа. Mathcad отображает их в векторе. На рис. 17-17 показан пример.

Другой способ найти переменную — ввести уравнение, щелкнуть переменную, для которой нужно решить уравнение, и выбрать «Переменная⇒Решить» в меню «Символика».

Примеры решения уравнений, решения неравенств и поиска корней

Вы также можете решить неравенство, введенное с помощью символов <, >, ≤ и ≥. Решения неравенств будут отображаться в терминах логических выражений Mathcad. Если существует несколько решений, Mathcad помещает их в вектор. Логическое выражение Mathcad, такое как x < 2, имеет значение 1, если оно истинно, и 0, если оно ложно. Таким образом, решение «x меньше 2 и больше -2» будет представлено выражением (x < 2) . (-2 < х).

Поиск корней выражения

Вы можете использовать ключевое слово решения, чтобы найти корни выражения способом, аналогичным решению уравнения с переменной:

• Введите выражение.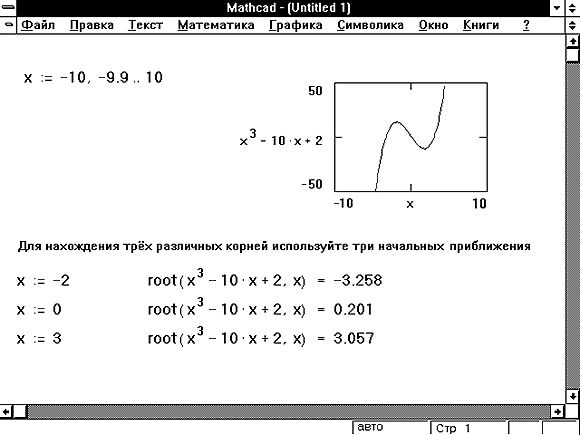
• Нажмите [Ctrl] [Shift 1 • (удерживая нажатыми клавиши управления и Shift, введите точку). Mathcad отображает заполнитель слева от стрелки «→».
• В заполнителе введите решить, поставьте запятую и переменную, для которой нужно найти решение.
• Нажмите [Enter], чтобы увидеть результат.

Обратите внимание, что нет необходимости устанавливать выражение равным нулю. Когда Mathcad не находит знака равенства, предполагается, что вы хотите установить выражение равным нулю.

Символьное решение системы уравнений: ключевое слово «решить»

Один из способов символьного решения системы уравнений — использовать то же ключевое слово, которое используется для решения одного уравнения с одним неизвестным. Чтобы решить систему из n уравнений для n неизвестных:

• Нажмите [Ctrl] M, чтобы создать вектор, состоящий из n строк и 1 столбца.
• Заполните каждый заполнитель вектора одним из n уравнений, составляющих систему. Убедитесь, что вы используете [Ctrl]= для создания знака равенства.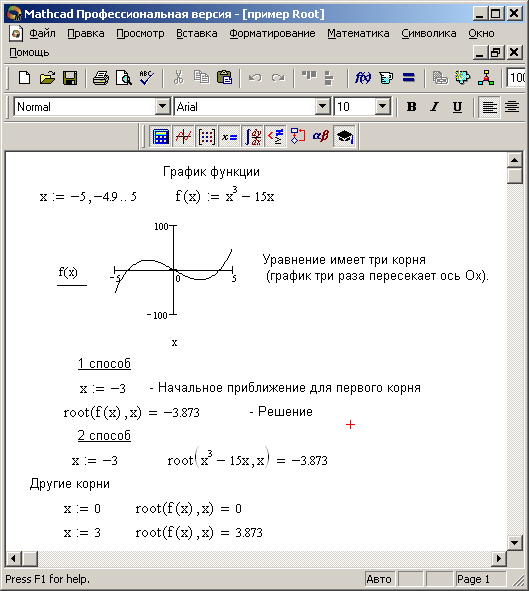
• Нажмите [Ctrl] [Shift 1 • (удерживая нажатыми клавиши управления и Shift, введите точку). Mathcad отображает заполнитель слева от стрелки «→».
• В заполнителе введите решить, а затем запятую.
• Нажмите [Ctrl] M, чтобы создать вектор, состоящий из n строк и 1 столбца.
• Нажмите [Enter], чтобы увидеть результат.

Mathcad отображает n решений системы уравнений справа от стрелки.

Символьное решение системы уравнений: Блок решения

Еще один способ символьного решения системы уравнений — использовать блок решения, аналогичный блокам численного решения, описанным в разделе «Решение уравнений».

• Введите слово «Дано». Это говорит Mathcad, что далее следует система уравнений. Вы можете набирать Given любым сочетанием прописных и строчных букв и любым шрифтом. Просто убедитесь, что вы не вводите его в текстовой области или абзаце.
• Теперь введите уравнения в любом порядке после слова «Дано». Убедитесь, что вы нажимаете [Ctrl]=, чтобы ввести «=».
• Введите функцию поиска в соответствии с вашей системой уравнений. Эта функция описана в разделе «Системы уравнений». Аргументы функции – это переменные, для которых вы решаете.
• Нажмите [Ctrl]. (клавиша управления, за которой следует точка). Mathcad отображает символический знак равенства.
• Щелкните за пределами функции поиска.

Mathcad отображает решения системы уравнений справа от стрелки. Если функция поиска имеет один аргумент, Mathcad возвращает один результат. Если функция поиска имеет более одного аргумента, Mathcad возвращает вектор результатов. Например, Find(x, y) возвращает
вектор, содержащий выражения для x и y, которые решают систему уравнений. Обратите внимание: если ваша система является переопределенной линейной системой, функция поиска не вернет решение. Используйте функцию Minerr вместо Find. Minerr вернет ответ, который минимизирует ошибки в ограничениях.

Большинство рекомендаций по блокам решения, описанных в разделе «Решение уравнений», относятся к символьному решению систем уравнений.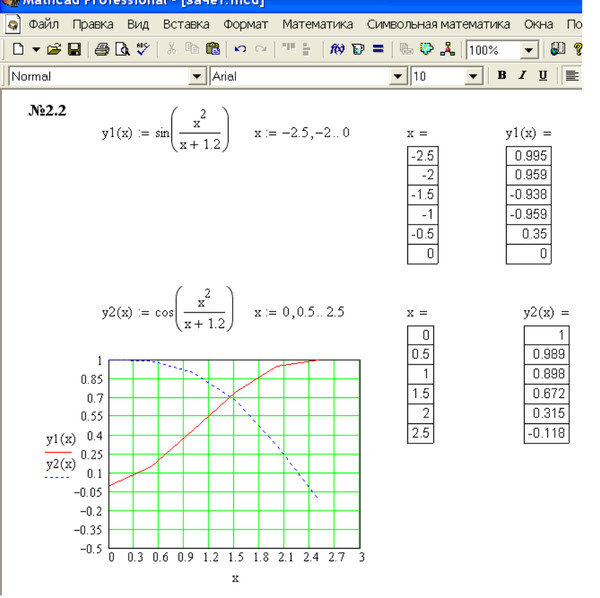 Основное отличие состоит в том, что при символическом решении уравнений вам не нужно вводить приблизительные значения для решений.

На рис. 17-18 показан пример блока решения, используемого для символического решения системы уравнений. Дополнительные сведения о блоках решения см. в разделе «Решение уравнений».

Решение системы уравнений в символьном виде.

Решение уравнений » MathCadHelp.com » Номер 1 в заданиях MathCad

В этой главе описывается, как решать уравнения от одного уравнения
с одним неизвестным до систем, содержащих до пятидесяти уравнений с пятьюдесятью неизвестными. Описанные здесь методы генерируют числовые решения. «Символическое вычисление» описывает различные методы символического решения уравнений.

Следующие секции составляют

Решение одного уравнения
Как использовать функцию корня Mathcad для численного решения одного уравнения с одним неизвестным.

Системы уравнений
Как использовать «блоки решения» для решения систем из n уравнений с n неизвестными.

Эффективное использование решателя
Примеры эффективного решения систем уравнений для различных значений параметра.

Решение одного уравнения

Чтобы решить одно уравнение с одним неизвестным, используйте функцию корня. Эта функция принимает выражение и одну из переменных выражения. Затем он изменяет эту переменную до тех пор, пока выражение не станет равным нулю. После этого функция возвращает значение, при котором выражение становится равным нулю.

Возвращает значение z, при котором выражение или функцияj(z) равно 0. Оба аргумента этой функции должны быть скалярными. Функция возвращает скаляр

Первый аргумент — это либо функция, определенная в другом месте листа, либо выражение. Он должен возвращать скалярное значение.

Второй аргумент — это имя переменной, которое появляется в выражении. Именно эту переменную Mathcad будет изменять, чтобы выражение стремилось к нулю. Вы должны присвоить номер этой переменной, прежде чем использовать корневую функцию. Mathcad использует это как начальное значение при поиске решения.

Например, чтобы определить a как решение уравнения <Вставьте уравнение здесь>, выполните следующие действия: 9.0003

• Определите предполагаемое значение для x. Введите x: 3. Ваш выбор значения приближения определяет, какой корень Mathcad возвращает. используйте корневую функцию.

• Для выражений с несколькими корнями, например, x2 – 1 = 0, ваше предполагаемое значение определяет, какой корень будет возвращен Mathcad. На рис. 15-1 показан пример, в котором корневая функция возвращает несколько разных значений, каждое из которых зависит от начального предполагаемого значения.

• Mathcad найдет комплексные корни так же, как и действительные корни. Чтобы найти сложный корень, вы должны начать с комплексного значения для начального предположения.

• Решение уравнения вида f(x) = g(x) эквивалентно использованию корневой функции следующим образом:

решение уравнения

Корневая функция может решить только одно уравнение с одним неизвестным. Чтобы решить несколько уравнений одновременно, используйте технику, описанную в следующем разделе «Системы уравнений». Чтобы решить уравнение с помощью символов или найти точный числовой ответ с точки зрения элементарных функций, выберите «Решить для переменной» в меню «Символические» или используйте ключевое слово решения. См. главу 17, «Вычисление символов 9».0003

Использование графика и корневой функции для поиска корней выражения.

Что делать, если функция корня не сходится

Mathcad вычисляет функцию корня, используя метод секущих. Предположительное значение, которое вы указываете для x, становится отправной точкой для последовательных приближений к корневому значению. Когда величина j(x), оцененная в предложенном корне, меньше значения предопределенной переменной TOL, корневая функция возвращает результат.

Если после многих приближений Mathcad все еще не может найти приемлемый ответ, он помечает корневую функцию сообщением об ошибке, указывающим на ее неспособность сходиться к результату. Эта ошибка может быть вызвана любой из следующих причин:

• Выражение не имеет корней.
• Корни выражения далеки от первоначального предположения.
• Выражение имеет локальные максимумы или минимумы между начальным предположением и корнями.
• Выражение имеет разрывы между начальным предположением и корнями.
• Выражение имеет комплексный корень, но первоначальная догадка была реальной (или наоборот).

Чтобы найти причину ошибки, попробуйте построить выражение. Это поможет определить, пересекает ли выражение ось X, и если да, то примерно, где это происходит. Как правило, чем ближе ваше первоначальное предположение к точке пересечения выражения с осью X, тем быстрее корневая функция будет сходиться к приемлемому результату.

Советы по использованию корневой функции

Вот несколько советов по максимальному использованию корневой функции:

• Чтобы изменить точность корневой функции, измените значение встроенной переменной TaL. Если вы увеличите TaL, корневая функция будет сходиться быстрее, но ответ будет менее точным. Если вы уменьшите TaL, корневая функция будет сходиться медленнее, но ответ будет более точным. Чтобы изменить TaL в указанной точке рабочего листа, включите определение, например TOL := 0,01 . Чтобы изменить TaL для всего листа, выберите «Параметры» в меню «Математика», перейдите на вкладку «Встроенные переменные» и замените число в текстовом поле рядом с «TaL». После того, как вы нажмете «ОК», выберите «Рассчитать рабочий лист» в меню «Математика», чтобы обновить весь рабочий лист, используя новое значение TaL.

• Если выражение имеет несколько корней, попробуйте найти их с разными значениями предположений. Построение графика функции – это хороший способ определить, сколько существует корней, где они находятся и какие первоначальные догадки могут их найти. На рис. 15-1 показан пример этого. Если два корня расположены близко друг к другу, возможно, вам придется сократить TaL, чтобы различить
между ними.

• Если fix) имеет небольшой наклон около корня, то root(f(x), x) может сходиться к значению r, которое относительно далеко от фактического корня. В таких случаях, даже если It( r)1 < TO L , r может быть далеко от точки, где f( r) = O. Чтобы найти более точный корень, уменьшите значение TaL. Или попробуйте найти root(g(x),x), где

Советы по использованию корневой функции

• Для выраженияfix) с известным корнем a, нахождение дополнительных корней fix) эквивалентно поиску корней hex) = (f(x))/(x – a ). Разделение известных корней подобным образом . эффективен для разрешения двух корней, которые могут быть расположены близко друг к другу. Часто проще искать корни шестнадцатеричного числа, как определено здесь, чем пытаться найти другие корни для исправления) с различными предположениями

Многократное решение уравнения

Предположим, вы хотите решить уравнение много раз, варьируя один из параметров в уравнении. Например, предположим, что вы хотите решить уравнение eX = a · x2 для нескольких различных значений параметра a.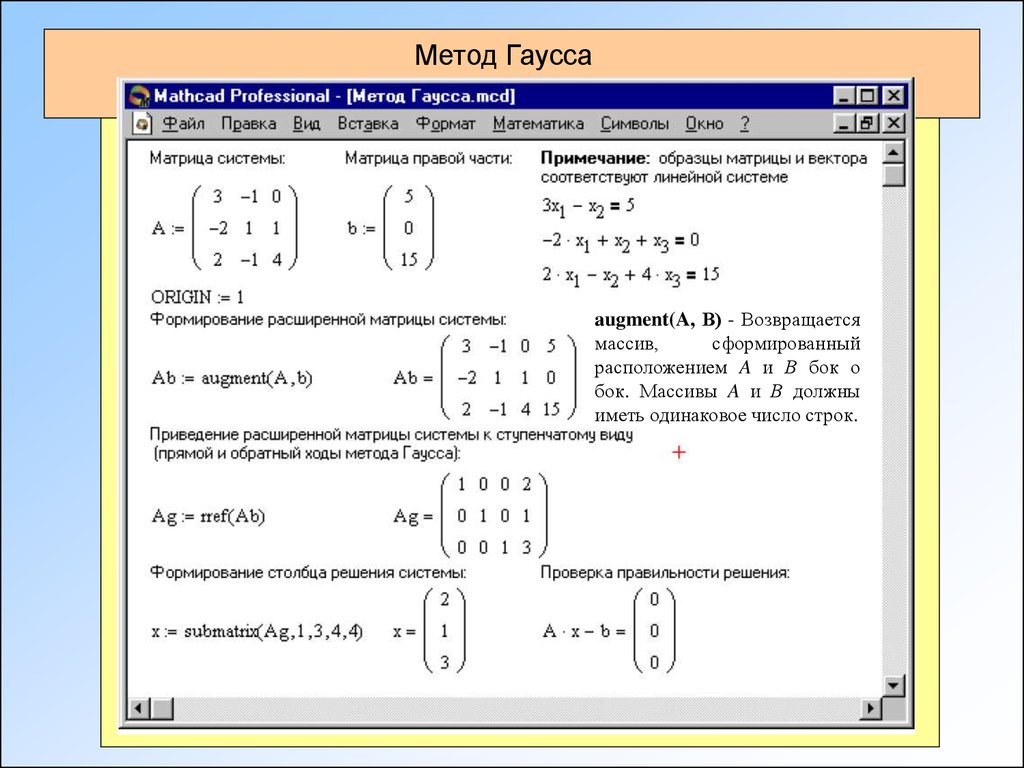 Самый простой способ сделать это — определить функцию:

Повторное решение уравнения

Чтобы решить уравнение для определенного значения a, укажите как a, так и предполагаемое значение x в качестве аргументов для этой функции. Затем оцените помазание, набрав f (a, x) =.

На рис. 15-2 показан пример того, как такую ​​функцию можно использовать для поиска нескольких решений корневой функции. Обратите внимание, что поскольку предполагаемое значение x передается в саму функцию, нет необходимости определять его где-либо еще на листе.

Определение пользовательской функции с корневой функцией.

Нахождение корней многочлена

Чтобы найти корни выражения, имеющего форму:

Нахождение корней многочлена

, вы можете использовать функцию поликорней, а не функцию корня. В отличие от корня, для поликорня не требуется приблизительное значение. Более того, многокорень возвращает сразу все корни, действительные или сложные. На Рисунке 15-3 и Рисунке 15-4 показаны примеры.

Использование поликорней для выполнения примера, показанного в

Функция поликорней всегда возвращает числовые значения корней многочлена. Чтобы найти корни символически, используйте символическое ключевое слово решения или выберите «Решить для переменной» в меню «Символический». См. главу 17, «Вычисление символов».

Использование поликорней для нахождения корней многочлена.

Основы ускорительной физики и техники

PTC Mathcad (PTC 2018) — мощный программный вычислительный инструмент. Это позволяет пользователю создавать, решать и анализировать различные математические задачи. Здесь мы познакомим вас с некоторыми базовыми возможностями Mathcad , а затем применим их для расчета некоторых реальных параметров ускорителя.

Упражнение 1. Редактирование основных уравнений, расчеты и построение графиков 92}{13} = 11,841 \]

2. Создадим две переменные и решим одно и то же уравнение. Скопируйте уравнение, которое вы только что создали, в другое место на рабочем листе. Вы можете сделать это, щелкнув в любом месте поля уравнения, нажимая клавишу пробела, пока все уравнение не окажется внутри синих линий редактирования, а затем используйте функции копирования и вставки. Замените «7» на переменную, скажем «a», а «13» на другую, например «\(\beta\)» в уравнении, напечатав их. Один из способов вставить бета-версию греческого символа — выбрать «Панели инструментов» в меню «Вид», удерживать нажатой кнопку мыши и отпустить ее, когда курсор находится на греческом языке, а затем выбрать нужный символ. Далее, где-то над уравнением, введите 92}{\beta} = 11,841 \] Попробуйте ввести разные значения для a и \(\beta\).

   3. Mathcad выполняет итерационные вычисления с использованием переменных диапазона . Всякий раз, когда Mathcad встречает переменную диапазона , он вычисляет уравнение для каждого значения этой специальной переменной.

      Скопируйте наше существующее уравнение и переменную ‘\(\beta\)’ и вставьте их в другую область. Теперь превратите «a» в переменную диапазона, набрав a:7,14;70 . Matchcad должен ответить

   \[ a := 7,14..70 \]

   Теперь Mathcad определил ‘a’ так, чтобы он имел значения 7, 14, 21, … 70. Теперь наше уравнение вычисляется для каждого значения ‘a ‘ и результаты приведены ниже. Двойной щелчок в таблице ответов открывает окно параметров отображения. Поэкспериментируйте с ними, чтобы увидеть, на что способен Mathcad.

   4. В Mathcad вы можете определить функцию и решить ее. Еще раз давайте воспользуемся нашим выражением выше. Начните с определения функции А(а): . Заполнитель появляется справа от того, что было напечатано. Либо введите, либо вставьте уравнение, которое мы использовали. Нам также нужно выбрать некоторые значения для «а», чтобы мы могли снова ввести a: 7, 14; 70 . Наконец, нам нужно вычислить некоторые решения нашей функции, поэтому введите A(a)= . Вы должны увидеть что-то вроде:

   Другой способ решения этой функции — просто поместить значение «а», которое вы хотите найти, в скобки:

   93 \]
   5. Matchad также имеет графические возможности. Давайте построим график значения A(a) в зависимости от «а». Выберите Graph из меню Insert и выберите X-Y Plot . Заполнители отображаются для осей X и Y. Введите или скопируйте/вставьте a для оси X и A(a) для оси Y. Должен получиться график, подобный приведенному ниже:

   Двойной щелчок в поле графика открывает окно параметров настройки. Проверь их. Поэкспериментируйте с другими особенностями поля графика.

   Упражнение 2. Матрицы

   1. Нажмите View > Toolbars > Matrix , чтобы открыть панель инструментов Matrix. Чтобы создать матрицу, щелкните значок матрицы на панели инструментов (левый верхний угол) или введите Ctrl-M . Создайте следующую матрицу 2X2:
   2. Mathcad может выполнять различные операции с матрицей. Откройте панели инструментов Matrix и Symbolic. Чтобы транспонировать матрицу, используйте пробел, чтобы заключить всю матрицу в рамки редактирования. Выберите Символическая матрица Транспонируйте значок (нижний левый угол) на панели инструментов символов, затем нажмите Введите . Вы должны получить:
   3. Чтобы инвертировать матрицу, выполните ту же процедуру еще раз. На этот раз выберите значок Symbolic Matrix inverse (нижний правый угол) на панели инструментов Symbolic. Mathcad должен произвести:
   4. Чтобы найти определитель, выполните ту же процедуру, но выберите определитель символьной матрицы (нижний правый угол) на панели инструментов Symbolic. Mathcad должен выдать:
   5. Создайте еще одну матрицу М и выполните над ней арифметические операции. Например:
   6. Наконец, Mathcad также позволяет создавать и выполнять математические функции над векторами. Чтобы создать вектор, просто сделайте матрицу из одного столбца:

   Настройте Mathcad , чтобы сделать следующее:

   Полезные советы

   Ниже приведены некоторые полезные советы и подсказки при использовании Mathcad :

   • Чтобы изменить параметр, просто щелкайте по нему, пока справа от него не появится курсор, а затем удалите или измените его по своему усмотрению.

     No related posts.