Обыкновенные дроби – понятие, примеры (5 класс, математика)
4.6
Средняя оценка: 4.6
Всего получено оценок: 162.
4.6
Средняя оценка: 4.6
Всего получено оценок: 162.
Обыкновенные дроби это основа всех действии с дробями. Без понимания этой темы не получится вникнуть в десятичные дроби, без которых не обходится ни одно вычисление. Чтобы не путаться в простейших вопросах разберем в подробностях тему обыкновенных дробей в рамках математики 5 класса.
Обыкновенная дробь
Обыкновенная дробь представляет собой дробь, у которой числитель равен знаменателю.
Такую дробь еще называют правильной. Если же числитель больше знаменателя, то дробь неправильная. Если числитель равен знаменателю, то это уже не дробь, а единица
Обыкновенная дробь всегда записывается с помощью дробной черты. Знаменатель показывает количество частей, на которые разделили целое. Числитель показывает, сколько таких частей взяли для расчета. Черту дроби всегда можно заменить знаком делении.
Черту дроби всегда можно заменить знаком делении.
Сложение и вычитание обыкновенных дробей
Сложение и вычитание обыкновенных дробей производится по одному и тому же принципу. Поэтому эти действия всегда объединяют в одну группу. Обязательным условием сложения или вычитания дробей является одинаковый знаменатель. Если у двух дробей разные знаменатели, то требуется привести дроби к одному знаменателю и выполнить требуемые действия.
В буквенной записи сложение дробей выглядит так:
$${а\over{с}}+{в\over{с}}={{а+в}\over{с}}$$
Умножение обыкновенных дробей
Умножение любых дробей, записанных с помощью дробной черты, осуществляется по одному и тому же принципу: «каждый на каждый». Числитель умножается на числитель, а знаменатель умножается на знаменатель.
Почти любую обыкновенную дробь можно перевести в десятичную. Для этого нужно числитель поделить на знаменатель без остатка.
Деление обыкновенных дробей
Деление обыкновенных дробей осуществляется с помощью переворота делителя.
- Перевернуть делитель, то есть поставить числитель на место знаменателя, а знаменатель на место числителя.
- Умножить делимое на перевернутый делитель
- Записать результат
Сравнение обыкновенных дробей
Сравнивать обыкновенные дроби можно благодаря возможности замены дробной черты на знак деления. Разберемся подробнее.
- Если у дробей одинаковые числители, но разные знаменатели, то больше та дробь, знаменатель которой меньше.
- Если у дробей одинаковые знаменатели, но разные числители, то больше та дробь, числитель которой больше.
- Если у дробей разные числители и разные знаменатели, то дроби приводят к одному знаменателю, а из двух дробей с одинаковым знаменателем больше та дробь, числитель которой больше.
Что мы узнали?
Мы рассмотрели понятие обыкновенной дроби. Сказали, что обыкновенные и правильные дроби это одно и то же. Вспомнили, как правильно складывать, вычитать, умножать и делить обыкновенные дроби.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 162.
А какая ваша оценка?
Сложение и вычитание обыкновенных дробей
Давайте разберемся, как складывать и вычитать обыкновенные дроби. Данный навык необходим для решения множества задач как и в школьном курсе, так и при сдаче ОГЭ или ЕГЭ по математике. Итак, перейдем к рассмотрению различных примеров.
Сложение и вычитание дробей с одинаковыми знаменателями
Начнем с рассмотрения самого простого примера – сложения и вычитания дробей с одинаковыми знаменателями. В данном случае необходимо просто произвести действия с числителями – сложить их или вычесть.
При сложении и вычитании дробей с одинаковыми знаменателями знаменатель не изменяется!
Главное не производить никакие операции сложения и вычитания в знаменателе, но некоторые школьники забывают об этом.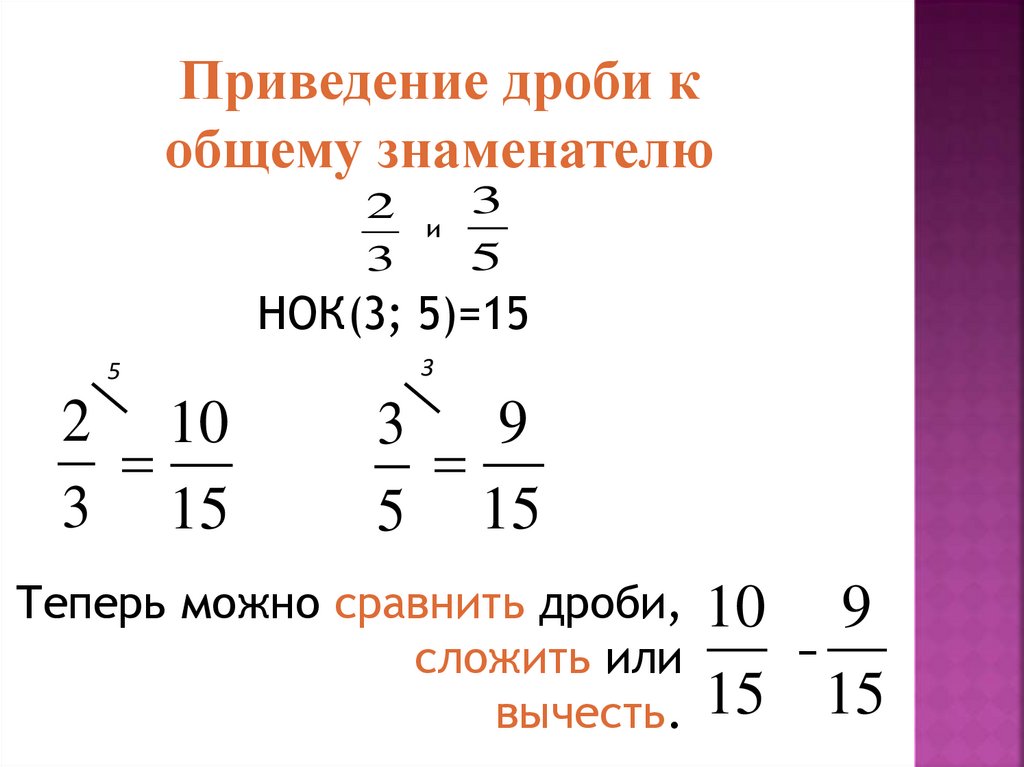 Чтобы лучше понять это правило, прибегнем к принципу визуализации, или говоря простыми словами, рассмотрим жизненный пример:
Чтобы лучше понять это правило, прибегнем к принципу визуализации, или говоря простыми словами, рассмотрим жизненный пример:
У Вас есть половина яблока – это ½ от всего яблока. Вам дают еще одну половину, то есть еще ½. Очевидно, что теперь у Вас целое яблоко (не считая, что оно разрезано 🙂 ). Поэтому ½ + ½ = 1, а не что-то другое, как, например, 2/4. Или же у Вас забирают эту половину: ½ – ½ = 0. В случае вычитания с одинаковыми знаменателями получается вообще особый случай – при вычитании одинаковых знаменателей, мы получим 0, а на 0 делить нельзя, и данная дробь не будет иметь смысла.
Приведем напоследок пример:
Сложение и вычитание дробей с разными знаменателями
Что же делать, если знаменатели разные? Для этого нам необходимо вначале привести дроби к одному знаменателю, а затем действовать как я указал выше.
Приводить дробь к общему знаменателю можно двумя способами. Во всех способах используется одно правило – при умножении числителя и знаменателя на одно и то же число дробь не изменяется.
Существует два способа. Первый – самый простой – так называемый “крест-накрест”. Он заключается в том, что первую дробь мы умножаем на знаменатель второй дроби (и числитель и знаменатель), а вторую дробь умножаем на знаменатель первой (аналогично и числитель и знаменатель). После этого действуем как в случае с одинаковыми знаменателями – теперь они действительно одинаковые!
Пример:
Предыдущий способ универсален, однако в большинстве случаев у дробей знаменателей можно найти наименьшее общее кратное – число, на которое делится и первый знаменатель и второй, причем самое маленькое. В данном методе нужно уметь видеть такие НОКи, потому что специальный поиск их достаточно ёмкий и уступает по скорости методу “крест-накрест”. Но в большинстве случаев НОКи довольно хороши видны, если набить глаз и достаточно тренироваться.
Пример:
Надеюсь, что теперь Вы в совершенстве владеете методами сложения и вычитания дробей!
Даниил Романович | Просмотров: 1. 7k
7k
дробей | Начальная алгебра
Цели обучения
- Сложение и вычитание дробей
- Найдите общий знаменатель двух или более дробей
- Используйте общий знаменатель для сложения или вычитания дробей
- Упростить дробь до минимума
- Умножение дробей
- Умножение двух или более дробей
- Умножить дробь на целое число
- Разделить дроби
- Найдите обратное число
- Разделить дробь на целое число
- Разделить дробь на дробь
Введение
Прежде чем мы начнем, вот несколько важных терминов, которые помогут вам понять принципы работы с дробями в этом разделе.
- произведение: результат умножения
- коэффициент: что-то умножается — для [latex]3 \cdot 2 = 6[/latex] , и 3, и 2 являются множителями 6
- числитель: верхняя часть дроби – числитель дроби [latex]\frac{2}{3}[/latex] равен 2
- знаменатель: нижняя часть дроби – знаменатель дроби [латекс]\фракция{2}{3}[/латекс] равен 3
Примечание об инструкциях
В учебниках по математике и учителями используется много разных слов, чтобы дать учащимся инструкции о том, что они должны делать с данной задачей.
| Инструкция | Интерпретация |
|---|---|
| Найти | Выполните указанные математические действия, которые могут включать сложение, вычитание, умножение, деление. |
| Упрощение | 1) Выполнить указанные математические действия, включая сложение, вычитание, умножение, деление 2) Запишите математическую формулировку в наименьших терминах, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций |
| Оценка | Выполнение указанных математических операций, включая сложение, вычитание, умножение, деление |
| Уменьшить | Напишите математическое выражение в наименьшем или минимальном выражении, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением |
Сложение и вычитание дробей
Сложение дробей
Когда вам нужно складывать или вычитать дроби, сначала нужно убедиться, что дроби имеют одинаковый знаменатель. Знаменатель говорит вам, на сколько частей разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Знаменатель говорит вам, на сколько частей разбито целое, а числитель говорит вам, сколько из этих частей вы используете.
Концепция «части целого» может быть смоделирована с помощью пиццы и кусочков пиццы. Например, представьте, что пиццу разрезают на 4 части, и кто-то берет 1 часть. Теперь [latex]\frac{1}{4}[/latex] из пиццы исчез, а [latex]\frac{3}{4}[/latex] остался. Обратите внимание, что обе эти дроби имеют знаменатель 4, который относится к количеству ломтиков, на которые была разрезана вся пицца. Что, если у вас есть еще одна пицца, разрезанная на 8 равных частей, и 3 из этих частей исчезли, оставив [латекс]\frac{5}{8}[/latex]?
Как можно описать общее количество оставшейся пиццы одним числом, а не двумя разными дробями? Вам нужен общий знаменатель, технически называемый наименьшим общим кратным . Помните, что если число кратно другому, вы можете разделить их и не получить остатка.
Один из способов найти наименьшее общее кратное двух или более чисел – сначала умножить каждое из них на 1, 2, 3, 4 и т. д. Например, найти наименьшее общее кратное 2 и 5.
д. Например, найти наименьшее общее кратное 2 и 5.
| Затем перечислите все числа, кратные 5: | |
| [латекс]2\cdot 1 = 2[/латекс] | [латекс]5\cdot 1 = 5[/латекс] |
| [латекс]2\cdot 2 = 4[/латекс] | [латекс]5\cdot 2 = 10[/латекс] |
| [латекс]2\cdot 3 = 6[/латекс] | [латекс]5\cdot 3 = 15[/латекс] |
| [латекс]2\cdot 4 = 8[/латекс] | [латекс]5\cdot 4 = 20[/латекс] |
| [латекс]2\cdot 5 = 10[/латекс] | [латекс]5\cdot 5 = 25[/латекс] |
Наименьшее их общее кратное будет общим знаменателем для них двоих!
Чтобы сложить дроби с разными знаменателями, сначала перепишите их с одинаковыми знаменателями. Тогда вы знаете, что делать! Шаги показаны ниже.
Сложение дробей с разными знаменателями
- Найдите общий знаменатель.

- Перепишите каждую дробь, используя общий знаменатель.
- Теперь, когда дроби имеют общий знаменатель, можно сложить числители.
- Упростите, убрав все общие множители в числителе и знаменателе.
Упрощение дроби
Часто, если ответом на задачу является дробь, вас попросят записать ее в наименьших выражениях. Это общепринятое соглашение, используемое в математике, аналогично тому, как предложение начинается с заглавной буквы и заканчивается точкой. В этом курсе мы не будем вдаваться в подробности методов сокращения дробей, потому что их много. Процесс упрощения дроби часто называют уменьшение дроби . Мы можем упростить, сократив (разделив) общие множители в числителе и знаменателе дроби. Мы можем это сделать, потому что дробь представляет собой деление.
Например, чтобы упростить [латекс]\frac{6}{9}[/latex], вы можете переписать 6 и 9, используя наименьшие возможные коэффициенты, следующим образом:
[латекс]\frac{6}{9}= \frac{2\cdot3}{3\cdot3}[/latex]
Поскольку 3 есть и в числителе, и в знаменателе, а дроби можно считать делением, мы можем разделить 3 в верхней части на 3 в нижней снизу уменьшить до 1.
[латекс]\frac{6}{9}=\frac{2\cdot\cancel{3}}{3\cdot\cancel{3}}=\frac{2\cdot1}{3}=\frac {2}{3}[/latex]
Переписывание дробей с наименьшими возможными множителями часто называется простой факторизацией.
В следующем примере показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.
Вы можете найти общий знаменатель, найдя общие кратные знаменателей. Наименьшее общее кратное является самым простым в использовании.
В следующем видео вы увидите пример сложения двух дробей с разными знаменателями.
Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти LCM.
Подумай об этом
Добавить [латекс] \frac{3}{4}+\frac{1}{6}+\frac{5}{8}[/latex]. Упростите ответ и запишите в виде смешанного числа.
Упростите ответ и запишите в виде смешанного числа.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы сложили вместе три дроби с разными знаменателями.
Показать раствор
Вычитание дробей
Когда вы вычитаете дроби, вы должны думать о том, есть ли у них общий знаменатель, как и при сложении дробей. Ниже приведены примеры вычитания дробей, знаменатели которых не совпадают.
В приведенном ниже примере показано, как использовать кратные для нахождения наименьшего общего кратного, которое будет являться наименьшим общим знаменателем.
В следующем видео вы увидите пример вычитания дробей с разными знаменателями.
Умножение дробей
Точно так же, как сложение, вычитание, умножение и деление при работе с целыми числами, вы также используете эти операции при работе с дробями. Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.
Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.
Когда вы умножаете дробь на дробь, вы получаете «долю дроби». Предположим, у вас есть [latex]\frac{3}{4}[/latex] конфеты, и вы хотите найти [latex]\frac{1}{2}[/latex] [latex]\frac{ 3}{4}[/латекс]:
Разделив каждую четвертую пополам, можно разделить шоколадный батончик на восьмые части.
Затем выберите половину из них, чтобы получить [латекс]\фрак{3}{8}[/латекс].
В обоих приведенных выше случаях, чтобы найти ответ, вы можете перемножить числители вместе и знаменатели вместе.
Умножение двух дробей
[латекс] \frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b\cdot d}=\frac{\text{ произведение числителей}}{\text{произведение знаменателей}}[/latex]
Умножение более двух дробей
[латекс] \frac{a}{b}\cdot \frac{c}{d}\cdot \frac{e}{f}=\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex]
Повторим: если дробь имеет общие делители в числителе и знаменателе, мы можем привести дробь к ее упрощенной форме, удалив общие делители.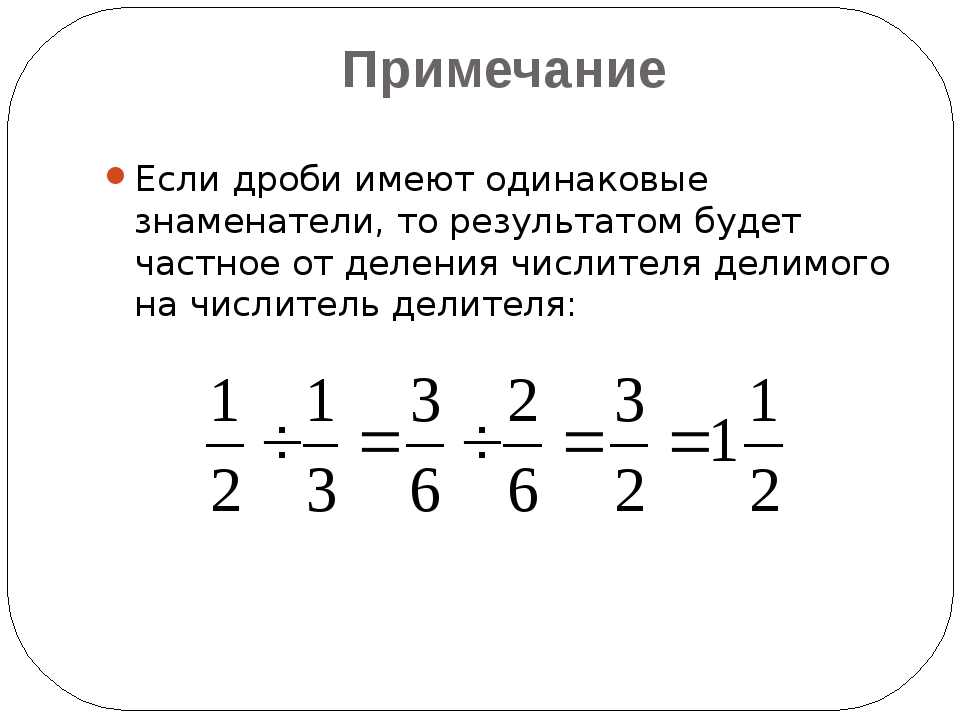
Например,
- Учитывая [латекс] \frac{8}{15}[/latex], множители 8: 1, 2, 4, 8, а множители 15: 1, 3, 5 , 15. [latex] \frac{8}{15}[/latex] упрощено, поскольку нет общих делителей 8 и 15.
- Учитывая [латекс] \frac{10}{15}[/latex], множители 10: 1, 2, 5, 10, а множители 15: 1, 3, 5, 15. [латекс] \frac {10}{15}[/latex] не является упрощенным, поскольку 5 – общий делитель 10 и 15.
Вы можете сначала упростить, прежде чем умножать две дроби, чтобы облегчить себе работу. Это позволяет вам работать с меньшими числами при умножении.
В следующем видео вы увидите пример как умножить две дроби, а затем упростить ответ.
Подумайте об этом
Умножьте [латекс] \frac{2}{3}\cdot \frac{1}{4}\cdot\frac{3}{5}[/latex]. Упростите ответ.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби.
Показать раствор
Разделение дробей
Бывают случаи, когда вам нужно использовать деление для решения проблемы. Например, если для нанесения одного слоя краски на стены комнаты требуется 3 литра краски, а у вас есть ведро с 6 литрами краски, сколько слоев краски вы можете нанести на стены? Вы делите 6 на 3 для ответа 2 пальто. Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].
Прежде чем мы начнем делить дроби, давайте рассмотрим некоторые важные термины.
- обратное: две дроби являются обратными, если их произведение равно 1 (не волнуйтесь, мы покажем вам примеры того, что это означает.)
- частное: результат деления
Для деления дробей необходимо использовать обратное число или дробь. Если вы умножаете два числа вместе и в результате получаете 1, то эти два числа являются обратными. Вот несколько примеров взаимного обмена:
Если вы умножаете два числа вместе и в результате получаете 1, то эти два числа являются обратными. Вот несколько примеров взаимного обмена:
| Оригинальный номер | Обратный | Продукт |
|---|---|---|
| [латекс] \frac{3}{4}[/латекс] | [латекс] \frac{4}{3}[/латекс] | [латекс] \frac{3}{4}\cdot \frac{4}{3}=\frac{3\cdot 4}{4\cdot 3}=\frac{12}{12}=1[/ латекс] |
| [латекс] \frac{1}{2}[/латекс] | [латекс] \frac{2}{1}[/латекс] | [латекс]\frac{1}{2}\cdot\frac{2}{1}=\frac{1\cdot}{2\cdot1}=\frac{2}{2}=1[/latex] |
| [латекс] 3=\frac{3}{1}[/латекс] | [латекс] \frac{1}{3}[/латекс] | [латекс] \frac{3}{1}\cdot \frac{1}{3}=\frac{3\cdot 1}{1\cdot 3}=\frac{3}{3}=1[/ латекс] |
| [латекс]2\frac{1}{3}=\frac{7}{3}[/latex] | [латекс] \frac{3}{7}[/латекс] | [латекс]\frac{7}{3}\cdot\frac{3}{7}=\frac{7\cdot3}{3\cdot7}=\frac{21}{21}=1[/latex] |
Иногда мы называем обратное число «переворотом» другого числа: переверните [латекс] \frac{2}{5}[/latex], чтобы получить обратное [латекс]\frac{5}{2}[ /латекс].
Деление на ноль
Вы знаете, что значит делить на 2 или делить на 10, но что значит делить количество на 0? Это вообще возможно? Можно ли разделить 0 на число? Рассмотрим дробь
[латекс]\frac{0}{8}[/latex]
. Мы можем прочитать это как «ноль разделить на восемь». Поскольку умножение обратно делению, мы могли бы переписать это как задачу на умножение.
[латекс]\текст{?}\cdot{8}=0[/латекс].
Мы можем сделать вывод, что неизвестное должно быть равно 0, так как это единственное число, которое дает 0 при умножении на 8.
Теперь рассмотрим обратную величину [латекс]\фрак{0}{8}[/латекс], которая будет [латекс]\фрак{8}{0}[/латекс]. Если мы перепишем это как задачу на умножение, то получим
[латекс]\текст{?}\cdot{0}=8[/латекс].
Это не имеет никакого смысла. Не существует чисел, которые можно умножить на ноль, чтобы получить результат 8. Обратная величина [латекс]\фракция{8}{0}[/латекс] не определена, и фактически любое деление на ноль не определено.
Внимание! Деление на ноль не определено, как и обратная величина любой дроби с нулем в числителе. Для любого действительного числа а [латекс]\фракция{а}{0}[/латекс] не определена. Кроме того, обратная величина [latex]\frac{0}{a}[/latex] всегда будет неопределенной.
Деление дроби на целое число
При делении на целое число вы умножаете его на обратное. В примере покраски, где вам нужно 3 литра краски для слоя и у вас есть 6 литров краски, вы можете найти общее количество слоев, которые можно покрасить, разделив 6 на 3, [латекс]6\div3=2[/латекс ]. Вы также можете умножить 6 на обратную величину 3, то есть [латекс] \frac{1}{3}[/latex], поэтому задача умножения будет выглядеть так:
[латекс] \frac{6}{1}\cdot \ frac{1}{3}=\frac{6}{3}=2[/latex].
Деление – это умножение на обратное число
Для любого деления вы можете превратить операцию в умножение, используя обратное число. Деление равносильно умножению на обратное.
Та же идея будет работать, когда делитель (вещь, которую делят) является дробью. Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты:
[латекс] \frac{1}{5}\text{ of }\frac{3}{4}=\frac{1}{5}\cdot \frac{3}{4}= \frac{3}{20}[/латекс]
Каждый человек получает [латекс]\фрак{3}{20}[/латекс] целого шоколадного батончика.
Если у вас есть рецепт, который нужно разделить пополам, вы можете разделить каждый ингредиент на 2 или умножить каждый ингредиент на [латекс]\frac{1}{2}[/latex] , чтобы найти новое количество .
Например, деление на 6 равносильно умножению на обратную величину 6, то есть [латекс]\frac{1}{6}[/латекс]. Посмотрите на схему двух пицц ниже. Как можно справедливо разделить то, что осталось (область, заштрихованная красным), между 6 людьми?
Каждый человек получает один кусок, поэтому каждый человек получает [латекс] \frac{1}{4}[/latex] пиццы.
Деление дроби на целое — это то же самое, что и умножение на обратную, поэтому вы всегда можете использовать умножение дробей для решения задач на деление.
Разделить дробь на дробь
Иногда вам нужно решить задачу, требующую деления на дробь. Предположим, у вас есть пицца, которая уже разрезана на 4 куска. Сколько существует фрагментов [latex]\frac{1}{2}[/latex]?
8 ломтиков. Вы видите, что деление 4 на [latex] \frac{1}{2}[/latex] дает тот же результат, что и умножение 4 на 2.
Что произойдет, если вам нужно разделить каждый срез на трети?
У вас получится 12 частей, что равносильно умножению 4 на 3.
Деление дробями
- Найдите обратную величину числа, следующего за символом деления.
- Умножьте первое число (то, что перед знаком деления) на величину, обратную второму числу (после знака деления).
Самый простой способ запомнить, как делить дроби, — это фраза «сохранить, изменить, перевернуть». Это означает СОХРАНИТЬ первое число, ИЗМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.
Это означает СОХРАНИТЬ первое число, ИЗМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.
Зачем повторять темы из предыдущих уроков математики?
Опять остатки?
Вы были в классе весь день, бегая, забирая своих детей из детского сада, и после долгой, жестокой дороги вы возвращаетесь домой и понимаете, что не подумали о том, что приготовить на ужин. Вы подходите к холодильнику, и все, что вы видите, это остатки, беспорядочные кусочки прошлых блюд. Несмотря на усталость, вам удается приготовить еду, которую все охотно съедят, и продолжить свой вечер.
В этом разделе вам может показаться, что темы представляют собой смесь объедков. Цель состоит в том, чтобы напомнить вам о некоторых навыках и темах из предыдущих уроков математики, которые, как и коробка с остатками в задней части вашего холодильника, легко забываются большинством людей. Потому что иногда мы просто забываем, как работают эти понятия.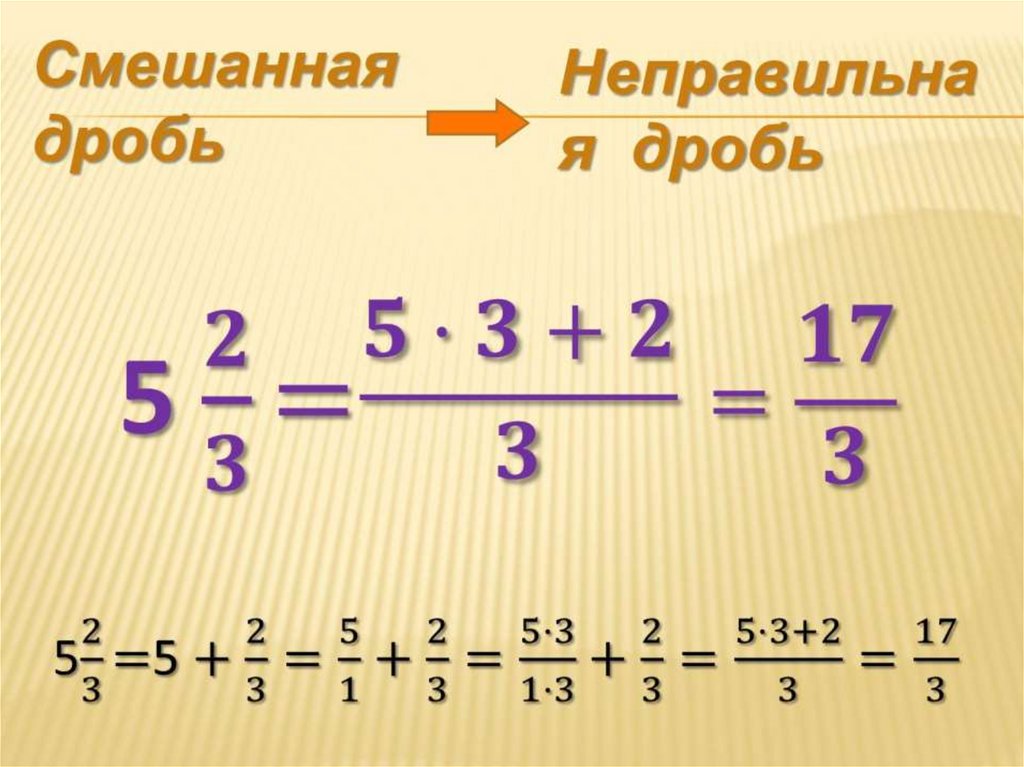 . . пока они нам снова не понадобятся.
. . пока они нам снова не понадобятся.
Результаты обучения
Свойства действительных чисел
- Определение действительных чисел и подмножеств действительных чисел
- Определить свойства действительных чисел и использовать их для вычисления алгебраических выражений
Многошаговые уравнения
- Использование свойств действительных чисел для решения многошаговых линейных уравнений
- Определение и использование распределительного свойства для решения линейных уравнений
- Классифицировать решения уравнений
Решение проблем
- Составление уравнений из описаний задач
- Использование формул для решения прикладных задач
Работая с остальными разделами этого курса, вернитесь к этому обзору, если вы чувствуете, что вам нужно напоминание о затронутых темах. Эти темы были выбраны потому, что о них часто забывают и они широко используются на протяжении всего курса. Не волнуйтесь, как и кетчуп, у этих концепций долгий срок годности.
Не волнуйтесь, как и кетчуп, у этих концепций долгий срок годности.
4.4 Сложение и вычитание дробей с общим знаменателем — Предварительная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Добавление дроби модели
- Сложение дробей с общим знаменателем
- Вычитание дроби модели
- Вычитание дробей с общим знаменателем
Приготовься 4.9
Прежде чем приступить к работе, пройдите этот тест на готовность.
Упрощение: 2x+9+3x−4,2x+9+3x−4.
Если вы пропустили эту проблему, просмотрите пример 2.22.
Приготовься 4.10
Нарисуйте модель дроби 34.34.
Если вы пропустили эту проблему, просмотрите пример 4.2.
Приготовься 4.11
Упрощение: 3+26,3+26.
Если вы пропустили эту проблему, просмотрите пример 4.48.
Добавление дроби к модели
Сколько четвертей изображено? Одна четверть плюс 22 четверти равно 33 четвертям.
Помните, что четверти — это доли доллара. Четверти — это еще один способ сказать четверти. Итак, на изображении монет видно, что
142434одна четверть+две четверти=три четверти142434одна четверть+две четверти=три четверти
Давайте воспользуемся дробными кругами для моделирования того же примера, 14+24,14+24.
| Начните с одной детали 1414. | ||
| Добавьте еще две 1414 шт. | ||
| Результат 3434. |
Итак, мы снова видим, что
14+24=3414+24=34
Манипулятивная математика
Выполнение упражнения по манипулятивной математике «Сложение дробей модели» поможет вам лучше понять сложение дробей
Пример 4,52
Используйте модель, чтобы найти сумму 38+28,38+28.
Решение
Начните с трех деталей 1818. | ||
| Добавьте две детали 1818. | ||
| Сколько штук 1818? |
Есть пять штук 1818 или пять восьмых. Модель показывает, что 38+28=58,38+28=58.
Попробуй 4.103
Используйте модель, чтобы найти каждую сумму. Покажите схему, иллюстрирующую вашу модель.
18+4818+48
Попробуй 4.104
Используйте модель, чтобы найти каждую сумму. Покажите схему, иллюстрирующую вашу модель.
16+4616+46
Сложение дробей с общим знаменателем
В примере 4.52 показано, что для сложения частей одинакового размера — это означает, что дроби имеют одинаковый знаменатель — мы просто складываем количество частей.
Добавление дроби
Если a,b,a,b и cc числа, где c≠0,c≠0, то
ac+bc=a+bcac+bc=a+bc
Чтобы сложить дроби с общим знаменателем, сложите числители и поместите сумму над общим знаменателем.
Пример 4,53
Найдите сумму: 35+15,35+15.
Решение
| 35+1535+15 | |
| Сложите числители и поместите сумму над общим знаменателем. | 3+153+15 |
| Упрощение. | 4545 |
Попробуй 4.105
Найдите каждую сумму: 36+26,36+26.
Попробуй 4.106
Найдите каждую сумму: 310+710,310+710.
Пример 4,54
Найдите сумму: x3+23.x3+23.
Решение
| х3+23х3+23 | |
| Сложите числители и поместите сумму над общим знаменателем. | х+23х+23 |
Обратите внимание, что мы не можем больше упрощать эту дробь. Поскольку хх и 22 не похожи друг на друга, мы не можем их комбинировать.
Поскольку хх и 22 не похожи друг на друга, мы не можем их комбинировать.
Попробуй 4.107
Найдите сумму: x4+34.x4+34.
Попробуй 4.108
Найдите сумму: y8+58.y8+58.
Пример 4,55
Найдите сумму: −9d+3d.−9d+3d.
Решение
Начнем с того, что перепишем первую дробь со знаком минус в числителе.
−ab=−ab−ab=−ab
| −9d+3d−9d+3d | |
| Перепишите первую дробь с минусом в числителе. | −9d+3d−9d+3d |
| Сложите числители и поместите сумму над общим знаменателем. | −9+3d−9+3d |
| Упростите числитель. | −6d−6d |
| Переписать со знаком минус перед дробью. | −6d−6d |
Попробуй 4.109
Найдите сумму: −7d+8d. −7d+8d.
−7d+8d.
Попробуй 4.110
Найдите сумму: −6m+9м.−6м+9м.
Пример 4,56
Найдите сумму: 2n11+5n11.2n11+5n11.
Решение
| 2n11+5n112n11+5n11 | |
| Сложите числители и поместите сумму над общим знаменателем. | 2н+5н112н+5н11 |
| Объедините похожие термины. | 7н117н11 |
Попробуй 4.111
Найдите сумму: 3p8+6p8.3p8+6p8.
Попробуй 4.112
Найдите сумму: 2q5+7q5.2q5+7q5.
Пример 4,57
Найдите сумму: −312+(−512).−312+(−512).
Решение
| −312+(−512)−312+(−512) | |
Сложите числители и поместите сумму над общим знаменателем. | −3+(−5)12−3+(−5)12 |
| Доп. | −812−812 |
| Упростите дробь. | −23−23 |
Попробуй 4.113
Найдите каждую сумму: −415+(−615).−415+(−615).
Попробуй 4.114
Найдите каждую сумму: −521+(−921).−521+(−921).
Модель Вычитание дробей
Вычитание двух дробей с общими знаменателями очень похоже на сложение дробей. Представьте себе пиццу, нарезанную на 1212 кусочков. Предположим, что за ужином съедено пять штук. Это означает, что после обеда в коробке осталось семь кусков (или 712712 пиццы). Если Леонардо съест 22 оставшихся куска (или 212212 пиццы), сколько останется? Осталось бы 55 штук (или 512512 пиццы).
712−212=512712−212=512
Давайте воспользуемся дробными кругами для моделирования того же примера, 712−212,712−212.
Начните с семи 112112 штук. Уберите два 112112 штук. Сколько двенадцатых осталось?
Сколько двенадцатых осталось?
Опять же, у нас есть пять двенадцатых, 512,512.
Манипулятивная математика
Выполнение упражнения по манипулятивной математике «Модель вычитания дробей» поможет вам лучше понять вычитание дробей.
Пример 4,58
Используйте дробные круги, чтобы найти разницу: 45−15,45−15.
Решение
Начните с четырех 1515 штук. Уберите одну 1515 штуку. Посчитайте, сколько пятых осталось. Осталось три 1515 штуки.
Попробуй 4.115
Используйте модель, чтобы найти каждую разницу. Покажите схему, иллюстрирующую вашу модель.
78-4878-48
Попробуй 4.116
Используйте модель, чтобы найти каждую разницу. Покажите схему, иллюстрирующую вашу модель.
56-4656-46
Вычитание дробей с общим знаменателем
Мы вычитаем дроби с общим знаменателем почти так же, как складываем дроби с общим знаменателем.
Вычитание дроби
Если a,b,a,b и cc числа, где c≠0,c≠0, то
ac-bc=a-bcac-bc=a-bc
Чтобы вычесть дроби с общим знаменателем, мы вычитаем числители и помещаем разницу над общим знаменателем.
Пример 4,59
Найдите разницу: 2324−1424,2324−1424.
Решение
| 2324−14242324−1424 | |
| Вычтите числители и поместите разницу над общим знаменателем. | 23−142423−1424 |
| Упростите числитель. | 924924 |
| Упростите дробь, удалив общие множители. | 3838 |
Попробуй 4.117
Найдите разницу: 1928−728.1928−728.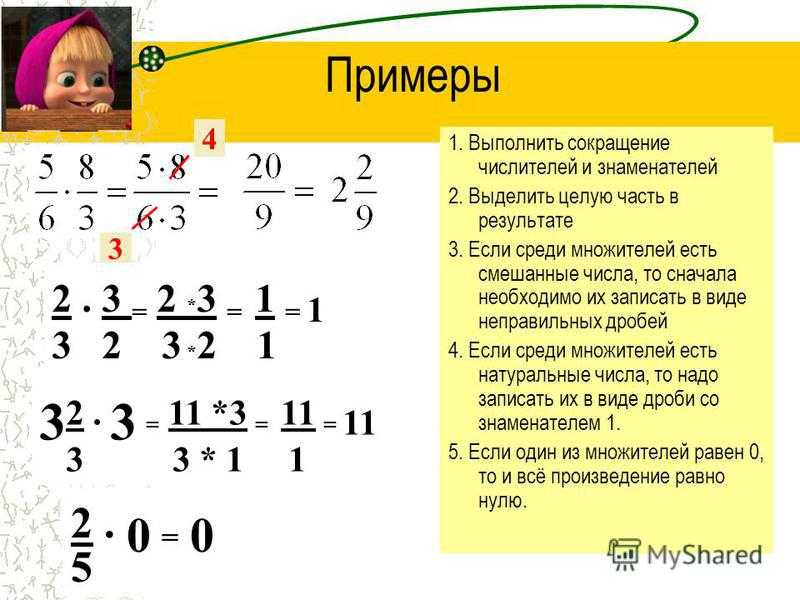
Попробуй 4.118
Найдите разницу: 2732−1132,2732−1132.
Пример 4,60
Найдите разницу: y6−16.y6−16.
Решение
| y6−16y6−16 | |
| Вычтите числители и поместите разницу над общим знаменателем. | г-16г-16 |
Дробь упрощена, потому что мы не можем объединять члены в числителе.
Попробуй 4.119
Найдите разницу: x7-27.x7-27.
Попробуй 4.120
Найдите разницу: y14-1314.y14-1314.
Пример 4,61
Найдите разницу: −10x−4x.−10x−4x.
Решение
Помните, что дробь -10x-10x может быть записана как -10x.-10x.
| −10x−4x−10x−4x | |
Вычесть числители. | −10−4x−10−4x |
| Упрощение. | −14x−14x |
| Перепишите со знаком минус перед дробью. | −14x−14x |
Попробуй 4.121
Найдите разницу: −9x−7x.−9x−7x.
Попробуй 4.122
Найдите разницу: −17a−5a.−17a−5a.
Теперь давайте сделаем пример, включающий сложение и вычитание.
Пример 4,62
Упрощение: 38+(−58)−18,38+(−58)−18.
Решение
| 38+(-58)-1838+(-58)-18 | |
| Приведите числители к общему знаменателю. | 3+(−5)−183+(−5)−18 |
| Упростите числитель слева направо. | −2−18−2−18 |
| Вычтите члены в числителе. | −38−38 |
Перепишите со знаком минус перед дробью. | −38−38 |
Попробуй 4.123
Упрощение: 25+(−45)−35,25+(−45)−35.
Попробуй 4.124
Упрощение: 59+(−49)−79,59+(−49)−79.
Раздел 4.4 Упражнения
Практика ведет к совершенству
Модель Дробь Дополнение
В следующих упражнениях используйте модель для сложения дробей. Покажите схему, иллюстрирующую вашу модель.
254.
25+1525+15
255.
310+410310+410
256.
16+3616+36
257.
38+3838+38
Сложение дробей с общим знаменателем
В следующих упражнениях найдите каждую сумму.
258.
49+1949+19
259.
29+5929+59
260.
613+713613+713
261.
915+715915+715
262.
х4+34х4+34
263.
у3+23у3+23
264.
7п+9п7п+9п
265.
8q+6q8q+6q
266.
8b9+3b98b9+3b9
267.
5а7+4а75а7+4а7
268.
−12y8+3y8−12y8+3y8
269.
−11×5+7×5−11×5+7×5
270.
−18+(−38)−18+(−38)
271.
−18+(−58)−18+(−58)
272.
−316+(−716)−316+(−716)
273.
−516+(−916)−516+(−916)
274.
−817+1517−817+1517
275.
−919+1719−919+1719
276.
613+(-1013)+(-1213)613+(-1013)+(-1213)
277.
512+(-712)+(-1112)512+(-712)+(-1112)
Модель вычитания дробей
В следующих упражнениях используйте модель для вычитания дробей. Покажите схему, иллюстрирующую вашу модель.
278.
58−2858−28
279.
56−2656−26
Вычитание дробей с общим знаменателем
В следующих упражнениях найдите разницу.
280.
45−1545−15
281.
45−3545−35
282.
1115−7151115−715
283.
913−413913−413
284.
1112−5121112−512
285.
712−512712−512
286.
421−1921421−1921
287.
−89−169−89−169
288.
y17−917y17−917
289.
x19-819×19-819
290.
5y8−785y8−78
291.
11z13−81311z13−813
292.
−8d−3d−8d−3d
293.
−7c−7c−7c−7c
294.
−23u−15u−23u−15u
295.
−29v−26v−29v−26v
296.
6c7−5c76c7−5c7
297.
12d11−9d1112d11−9d11
298.
−4r13−5r13−4r13−5r13
299.
−7s3−7s3−7s3−7s3
300.
−35−(−45)−35−(−45)
301.
−37−(−57)−37−(−57)
302.
−79−(−59)−79−(−59)
303.
−811−(−511)−811−(−511)
Смешанная практика
В следующих упражнениях выполните указанную операцию и запишите свои ответы в упрощенной форме.
304.
−518·910−518·910
305.
−314·712−314·712
306.
n5−45n5−45
307.
611-с11611-с11
308.
−724+224−724+224
309.
−518+118−518+118
310.
815÷125815÷125
311.
712÷928712÷928
Математика на каждый день
312.
Смесь Trail Джейкоб смешивает орехи и изюм, чтобы приготовить смесь Trail. У него есть 610610 фунтов орехов и 310310 фунтов изюма. Сколько трейл микса он может сделать?
313.
Выпечка Джанет нужно 5858 чашек муки для рецепта, который она готовит. У нее всего 3838 чашек муки, а остальное она попросит одолжить у соседки. Сколько муки она должна занять?
Письменные упражнения
314.
Грег уронил свой ящик со сверлами, и три сверла выпали. В корпусе есть прорези для сверл, причем прорези расположены в порядке от меньшего к большему. Грегу нужно положить выпавшие биты обратно в кейс в пустые слоты.

