Как решить неравенство дробные: Дробные неравенства и их решение

alexxlab / / Разное

Решение неравенств методом интервалов

Разделы: Математика, Внеклассная работа

Цели:

  1. Обобщить использование метода интервалов для решения неравенств,
  2. Показать широкие возможности этого метода для решения неравенств, содержащих переменные под знаком log, , и тригонометрические функции.

Мы будем рассматривать неравенства, правая часть которых равна нулю, а левая часть представлена в виде произведения или частного функций.

Идея метода: Знак произведения или частного определяется знаком сомножителей.

Рис.1

Линейная функция с ненулевым угловым коэффициентом меняет знак при переходе через нуль функции, причём справа от нуля знак функции совпадает со знаком углового коэффициента.

Рис.2

Квадратный трёхчлен с D>0 при переходе через каждый нуль функции меняет свой знак, причём правее большего корня знак квадратного трёхчлена совпадает со знаком его старшего коэффициента. [1]

Эти соображения приводят к следующей схеме решения неравенства:

Пример 1:[1]

  1. Найдём нули числителя: , , .
  2. Найдём нули знаменателя: .
  3. Наносим найденные нули на числовую ось. Т.к. неравенство строгое, то все нули изображаем выколотыми точками, которые разбивают числовую ось на интервалы:

Рис. 3

На самом правом из них знак каждого сомножителя совпадает со знаком его старшего коэффициента:

Следовательно, дробь на этом промежутке тоже отрицательна.

  1. При переходе через каждый из отмеченных нулей, один и только один из сомножителей меняет знак, и поэтому каждый раз меняется знак дроби. Учитывая это, расставляем в интервалах знаки (как показано на Рис.3).
  2. Выбираем интервалы, на которых дробь отрицательна.
  3. Записываем ответ: .

В рассмотренном примере 1, знаки в промежутках знакопостоянства функции чередуются. Однако делать обобщение, что так будет происходить всегда, разумеется, не следует.

Пример 2:

  1. нули числителя:

    -2 – нуль второй кратности

  2. нули знаменателя:
  3. наносим найденные нули на числовую ось, т.к. неравенство не строгое, то нули числителя изображаем заштрихованными точками, а нуль знаменателя мы выкалываем, т.к. это число не входит в область определения неравенства:

Рис.4

Обозначим нуль второй кратности галочкой, чтобы не забыть. Т.к. числитель всегда принимает положительные значения, то на правом крайнем промежутке знак будет зависеть от знака старшего коэффициента знаменателя, т. е. «+». Левее «1» знаменатель будет отрицательным, а числитель положительным, поэтому при переходе через число -2 знак не меняется:

Рис.5

Это поможет понять следующая геометрическая картинка (Рис.6):

Рис.6

  1. Для записи ответа выбираем промежуток, где стоит знак «+» и заштрихованную точку , при которой дробь обращается в нуль.
    Ответ:

Вывод: при переходе через нуль чётной кратности, знак не меняется.

Решить по вариантам, с последующим обсуждением у доски.

I вариант

Пример 3:

  1. нули числителя:

    ;
  1. нули знаменателя:

    ;
    — нуль второй кратности

Рис.7

Ответ:

II вариант

Пример 4:

  1. нули числителя:
    — нуль второй кратности
  2. нули знаменателя:

    ;
    — нуль третьей кратности

Рис. 8

Ответ:

Применение метода интервалов не ограничивается решением рациональных неравенств.

Универсальность метода основана на достаточно наглядном свойстве непрерывных функций:

«Если на интервале (a;b) функция f(x) непрерывна и не обращается в нуль, то на этом интервале она сохраняет знак».

Пример 5: [1] ,

Будем решать это неравенство по той же схеме, но не на всей оси, а на области определения логарифмической функции, т.е. на промежутке (*):

  1. нули числителя:

    ; — не входит в (*)
  2. нули знаменателя:

    ;

Рис. 9

  1. на самом правом промежутке
    , ,

Следовательно на этом промежутке левая часть неравенства отрицательна

  1. при переходе через каждый корень меняет знак один и только один из сомножителей. Учитывая это, расставляем знаки на остальных промежутках.

Ответ: .

Пример 6:

  1. нули числителя:


    корней нет
  2. нули знаменателя:
  3. решение изображаем на рис. 10:

Рис.10

Квадратный трёхчлен в числителе не имеет корней и не меняет свой знак. Его знак совпадает со знаком старшего коэффициента, т.е. «+».

Ответ:.

Пример 7: ОДЗ:

Приведём неравенство к такому виду, чтобы в правой части был «0»:

  1. нули числителя:

;;;

  1. нули знаменателя:
  2. решение изображаем на рис. 11:

Рис.11

Ответ:.

Пример 8:

ОДЗ:

Рис.12

  1. нули числителя:
  2. нули знаменателя:

, но ОДЗ удовлетворяет только

  1. решение изображаем на рис. 13:

Рис.13

Ответ:.

Задание на дом: (Решение предоставлено в Приложении1)

  1. Ответ:.
  2. Ответ:.
  3. Ответ:.
  4. Ответ: .
  5. Ответ:.

Задания для факультативный занятий предоставлены в Приложении2.

Вывод: Как известно, линейная, квадратичная, степенная, показательная, логарифмическая и тригонометрические функции, а так же их композиции и функции, получаемые из них с помощью арифметических действий, непрерывны в своей области определения. Поэтому метод интервалов можно применять при решении практически всех неравенств школьного курса. Метод интервалов позволяет представить множество решений неравенства в виде объединения промежутков, границы которых либо корни соответствующего уравнения, либо граничные точки области определения.


Список литературы:

[1] «Метод интервалов» //Журнал «Квант» No12, 1985 г.

Дробно-рациональные неравенства — примеры с решением

Рациональным называется неравенство, в левой и правой частях которого — рациональные выражения.

Содержание:

Задача:

Лодка прошла по течению реки 5 км и вернулась обратно, затратив на весь путь не больше 1 ч. Какова наименьшая возможная скорость лодки, если скорость течения реки равна

Решение:

Обозначим через

По условию задачи на весь путь лодка затратила не больше 1 ч. Составим математическую модель:

Полученное в ходе решения задачи неравенство является рациональным.

Рассмотрим один из методов решения рациональных неравенств — метод интервалов. Этот метод основан на использовании графика функции.

Предположим, что нужно решить неравенство где — функция, график которой изображен на рисунке 80. Тогда для решения неравенства достаточно указать значения аргумента, при которых значения функции неотрицательны, т. е. при которых график функции лежит не ниже оси абсцисс. Это промежутки [-6; -2] и [2; 8]. Следовательно, все решения неравенства — это все

Рис. 80

Рис. 81

значения переменной принадлежащие объединению множеств

Заметим, что такие же решения имеет неравенство — функция, график которой изображен на рисунке 81, так как значения функции неотрицательны при тех же значениях переменной, что у функции .

Таким образом, для применения метода интервалов к решению неравенства достаточно построить схему графика функции, на которой отражены только некоторые (необходимые для решения неравенства) свойства функции, а именно ее область определения, нули и промежутки знакопостоянства.

Примеры с решением

Пример №1

Решите неравенство

Решение:

Рассмотрим функцию Построим схему графика этой функции, по которой определим ее промежутки знакопостоянства. Для этого найдем точки пересечения графика с осью абсцисс, т. е. нули этой функции: при

Отметим нули функции на оси абсцисс (рис. 82). Так как данное неравенство строгое, то нули функции отметим на оси пустыми точками.

Нули функции разбили ось на четыре промежутка. Определим, выше или ниже оси абсцисс расположен график функции в каждом из полученных промежутков.

Поскольку правее точки 4 каждый из трех множителей произведения принимает положительные значения, то при график функции расположен выше оси абсцисс.

При переходе через каждую из отмеченных точек знак функции а значит, и положение графика относительно оси абсцисс меняется, так как меняется знак одного из множителей.

Построим схему графика функции (рис. 83).

Рис. 83

При построенная кривая лежит ниже оси абсцисс. Это объединение интервалов является множеством решений данного неравенства.

Ответ:

Пример №2

Решите неравенство

Решение:

Рассмотрим функцию Найдем ее нули: при Так как неравенство нестрогое, то нули функции являются решениями данного неравенства, поэтому включим их во множество решений неравенства и отметим на оси абсцисс закрашенными точками (рис. 84).

Затем определим положение графика функции в каждом из четырех полученных промежутков. Правее точки 3 каждый из трех множителей произведения принимает положительные значения, значит, график функции расположен выше оси абсцисс. При переходе через точки 3 и 2 положение графика меняется, так как меняется знак одного из множителей или При переходе через точку -9 положение графика не меняется, так как множитель принимает неотрицательные значения при всех

Рис. 84

Построим схему графика функции (см. рис. 84) и запишем решение неравенства в соответствии с его знаком:

Ответ:

Если во множителе число — четное, то при переходе через точку а положение графика относительно оси абсцисс не меняется, а если число — нечетное, то меняется.

Пример №3

Решите неравенство

Решение:

Рассмотрим функцию

Отметим на оси абсцисс нули этой функции (числа -3 и 1) и те значения переменной, которые не входят в область определения функции (это числа -2 и 4 — значения переменной, при которых знаменатель дроби обращается в нуль (нули знаменателя) (рис.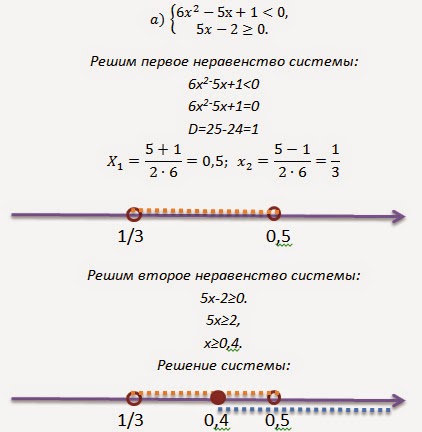 85).

Рис. 85

Рис. 86

Так как неравенство нестрогое, то нули функции являются решениями неравенства (на оси абсцисс — закрашенные точки -3 и 1). Нули знаменателя не являются решениями неравенства (на оси абсцисс — пустые точки -2 и 4).

Построим схему графика (рис. 86). Положение графика относительно оси абсцисс меняется при переходе через каждую точку. По схеме графика в соответствии со знаком неравенства запишем его решение:

Ответ:

Для того чтобы решить рациональное неравенство методом интервалов, нужно:

  1. Привести неравенство к виду или
  2. Найти и отметить на оси абсцисс нули функции и те значения переменной, при которых значения функции не существуют (нули знаменателя).
  3. Построить схему графика функции.
  4. Записать ответ в соответствии со знаком неравенства.

Решите неравенство

Решение:

(1) Неравенство имеет вид где

(2)

(3)

(4) Ответ:

Пример №4

Решите неравенство

Решение:

(1) Неравенство имеет вид где

(2) Найдем нули функции (числа 0; 2) и, поскольку знак неравенства строгий, отметим их на оси абсцисс пустыми точками.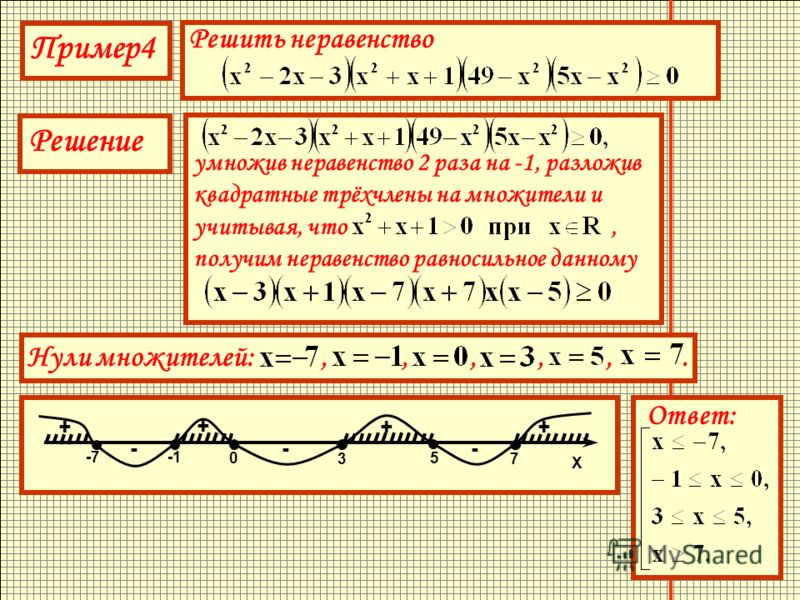 Найдем значение переменной, при котором значения функции не существуют, — нуль знаменателя (число -1) и отметим его на оси абсцисс пустой точкой (рис. 87).

(3) Построим схему графика функции, при этом учтем, что при переходе через точку -1 положение графика относительно оси не меняется, а при переходе через точки 0 и 2 меняется (рис. 88).

(4) Ответ:

Для того чтобы положение графика в первом правом промежутке было выше оси абсцисс, нужно умножением обеих частей неравенства на -1 добиться положительных коэффициентов перед переменной в линейных множителях.

  • Заказать решение задач по высшей математике
Пример №5

Решите неравенство

Решение:

Для того чтобы все коэффициенты перед переменными в линейных множителях были положительными, умножим обе части неравенства на -1 и получим неравенство

(1) Неравенство имеем вид где

(2) Найдем нули функции (числа 3 и 4) и, поскольку знак неравенства нестрогий, отметим их на оси абсцисс закрашенными точками. Найдем значение переменной, при котором значение функции не существует (число -1), и отметим его на оси абсцисс пустой точкой (рис. 89).

Рис. 89

Рис. 90

(3) Построим схему графика функции, при этом учтем, что при переходе через точку 4 положение графика относительно оси не меняется, а при переходе через точки -1 и 3 меняется (рис. 90).

(4) Ответ:

Пример №6

Какие из следующих неравенств являются рациональными:

а)

б)

в)

г)

Решение:

Неравенства а), б), г) — рациональные, так как в левой и правой частях этих неравенств — рациональные выражения. Неравенство в) не является рациональным, так как содержит иррациональные выражения с переменной.

Пример №7

Решите неравенство:

а)

б)

Решение:

а) (1) Неравенство имеет вид , где

(2) Нулями функции являются числа -8; —1 и 2. Поскольку знак неравенства строгий, отметим их на оси абсцисс пустыми точками.

(3) Построим схему графика функции. При переходе через каждую из точек -8; -1 и 2 положение графика относительно оси меняется.

(4) Ответ:

б) Умножим обе части данного неравенства на -1 и получим неравенство которое запишем в виде Нулями функции являются числа -3; 1 и 3. Так как знак неравенства нестрогий, то на оси абсцисс числа -3; 1 и 3 отметим закрашенными точками. Построим схему графика функции.

При переходе через точку 1 положение графика относительно оси не меняется, а при переходе через точки -3 и 3 — меняется.

Ответ:

Пример №8

Решите неравенство:

а)

б)

Решение:

а) Нулями функции являются числа -2,5 и 7. Так как знак неравенства нестрогий, то отметим их на оси абсцисс закрашенными точками. Нулем знаменателя является число -4. Отметим его пустой точкой. Построим схему графика функции.

Ответ:

б) Умножим обе части неравенства на и получим неравенство Нулями функции являются числа 1 и 4. Так как знак неравенства нестрогий, то отметим их на оси абсцисс закрашенными точками. Нулем знаменателя является число -2. Отметим его пустой точкой. Построим схему графика функции. При переходе через точку 4 положение графика относительно оси не меняется.

Ответ:

Пример №9

Решите неравенство

Решение:

Запишем неравенство в виде:

Нулем функции является число -2,75. Так как знак неравенства строгий, то отметим его на оси абсцисс пустой точкой. Нулем знаменателя является число 2. Отметим его на оси абсцисс пустой точкой. Построим схему графика функции.

Ответ:

Пример №10

Решите неравенство

Решение:

Приведем неравенство к виду:

Отметим на оси абсцисс нуль функции

т. е. и те значения переменной, при которых значения функции не существуют: х = 2 и х = 3. Построим схему графика функции.

Ответ:

Пример №11

Найдите область определения функции

Решение:

Так как функция определена для , то решим неравенство Данное неравенство равносильно неравенству

Для нахождения нулей функции используем условие равенства дроби нулю:

При значение функции не существует. Построим схему графика функции. При переходе через точку 4 положение графика относительно оси не меняется, так как множитель входит и в числитель, и в знаменатель, а при переходе через точки 0 и 3 положение графика меняется.

Пример №12

Решите систему неравенств

Решение:

Отметим на оси абсцисс множество решений первого неравенства системы.

Отметим на этой же оси множество решений второго неравенства системы.

Найдем пересечение множеств решений.

Ответ:

Пример №13

Найдите решение совокупности неравенств

Решение:

Отметим на оси абсцисс множество решений первого неравенства совокупности.

Отметим на этой же оси множество решений второго неравенства совокупности.

Найдем объединение множеств решений.

Ответ:

Рациональные неравенства и их система. Дробные рациональные неравенства

>>Математика:Рациональные неравенства

Рациональное неравенство с одной переменной х — это неравенство вида — рациональные выражения, т. е. алгебраические выражения, составленные из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в натуральную степень . Разумеется, переменная может быть обозначена любой другой буквой, но в математике чаще всего предпочтение отдается букве х.

При решении рациональных неравенств используются те три правила, которые были сформулированы выше в § 1. С помощью этих правил обычно преобразуют заданное рациональное неравенство к виду / (ж) > 0, где / (х) — алгебраическая дробь (или многочлен). Далее разлагают числитель и знаменатель дроби f (х) на множители вида х — а (если, конечно, это возможно) и применяют метод интервалов, который мы уже упоминали выше (см. в предыдущем параграфе пример 3).

Пример 1. Решить неравенство (х — 1) (х + 1) (х — 2) > 0.

Решение. Рассмотрим выражение f(х) = (х-1)(х + 1)(х-2).

Оно обращается в 0 в точках 1,-1,2; отметим эти точки на числовой прямой. Числовая прямая разбивается указанными точками на четыре промежутка (рис.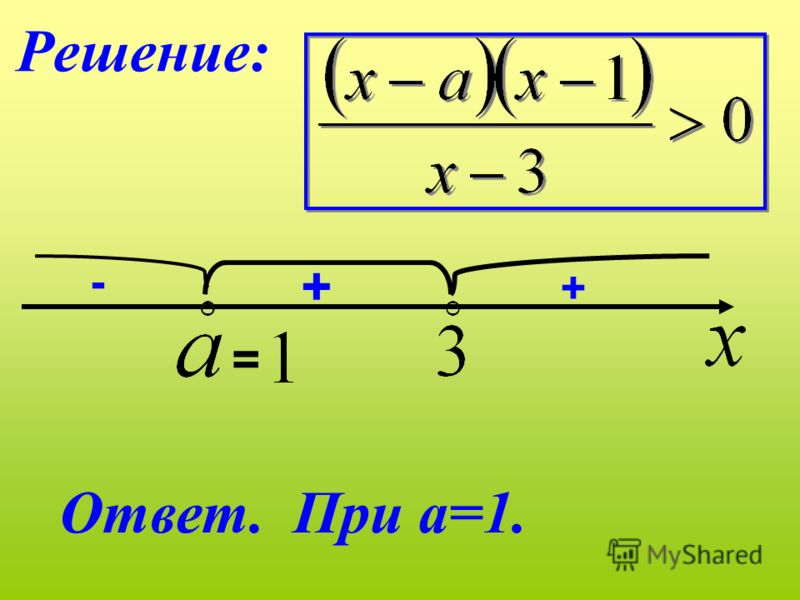 6), на каждом из которых выражение f (x) сохраняет постоянный знак. Чтобы в этом убедиться, проведем четыре рассуждения (для каждого из указанных промежутков в отдельности).

Возьмем любую точку х из промежутка (2, Эта точка расположена на числовой прямой правее точки -1, правее точки 1 и правее точки 2. Это значит, что х > -1, х >1, х > 2 (рис. 7). Но тогда x-1>0, х+1>0, х — 2 > 0, а значит, и f (х) > 0 (как произведение рациональное неравенство трех положительных чисел). Итак, на всем промежутке выполняется неравенство f (x) > 0.


Возьмем любую точку х из интервала (1,2). Эта точка расположена на числовой прямой правее точки-1, правее точки 1, но левее точки 2. Значит, х > -1, х > 1, но х 0,x-1>0,x-2


Возьмем любую точку х из интервала (-1,1). Эта точка расположена на числовой прямой правее точки -1, левее точки 1 и левее точки 2. Значит, х >-1, но х 0, х -1 0 (как произведение двух отрицательных и одного положительного числа). Итак, на промежутке (-1,1) выполняется неравенство f (x)> 0.


Возьмем, наконец, любую точку х из открытого луча (-оо, -1). Эта точка расположена на числовой прямой левее точки -1, левее точки 1 и левее точки 2. Это значит, что x


Подведем итоги. Знаки выражения f (x) в выделенных промежутках таковы, как показано на рис. 11. Нас интересуют те из них, на которых выполняется неравенство f (x) > 0. С помощью геометрической модели , представленной на рис. 11, устанавливаем, что неравенство f (x) > 0 выполняется на интервале (-1, 1) или на открытом луче
О т в е т: -1 2.


Пример 2. Решить неравенство
Решение. Как и в предыдущем примере, почерпнем необходимую информацию из рис. 11, но с двумя изменениями по сравнению с примером 1. Во-первых, поскольку нас интересует, при каких значениях х выполняется неравенство f (x) Во-вторых, нас устраивают и те точки, в которых выполняется равенство f (x) = 0. Это точки -1, 1, 2, отметим их на рисунке темными кружочками и включим в ответ.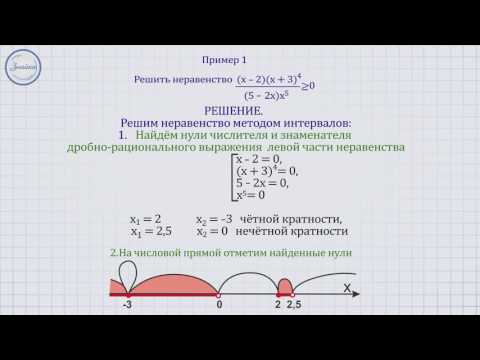 На рис. 12 представлена геометрическая модель ответа, от которой нетрудно перейти к аналитической записи.
Ответ:
П р и м е р 3. Решить неравенство
Решение . Разложим на множители числитель и знаменатель алгебраической дроби fх, содержащейся в левой части неравенства. В числителе имеем х 2 — х = х(х — 1).

Чтобы разложить на множители квадратный трехчлен х 2 — bх ~ 6, содержащийся в знаменателе дроби, найдем его корни. Из уравнения х 2 — 5х — 6 = 0 находим х 1 = -1, х 2 = 6. Значит, (мы воспользовались формулой разложения на множители квадратного трехчлена: ах 2 + bх + с = а(х — х 1 — х 2)).
Тем самым мы преобразовали заданное неравенство к виду


Рассмотрим выражение:


Числитель этой дроби обращается в 0 в точках 0 и 1, а обращается в 0 в точках -1 и 6. Отметим эти точки на числовой прямой (рис. 13). Числовая прямая разбивается указанными точками на пять промежутков, причем на каждом промежутке выражение fх) сохраняет постоянный знак. Рассуждая так же, как в примере 1, приходим к выводу, что знаки выражения fх) в выделенных промежутках таковы, как показано на рис. 13. Нас интересует, где выполняется неравенство f (x)

0твет: -1


Пример 4. Решить неравенство


Решение. При решении рациональных неравенств, как правило, предпочитают оставлять в правой части неравенства только число 0. Поэтому преобразуем неравенство к виду


Далее:


Как показывает опыт, если в правой части не(ра-венства содержится лишь число 0, удобнее проводить рассуждения, когда в левой его части и числитель и знаменатель имеют положительный старший коэффициент . А что у нас? У нас в знаменателе дроби в этом смысле все в порядке (старший коэффициент, т.е. коэффициент при х 2 , равен 6 — положительное число), но в числителе не все в порядке — старший коэффициент (коэффициент при х) равен -4 (отрицательное число). Умножив обе части неравенства на -1 и изменив при этом знак неравенства на противоположный, получим равносильное ему неравенство


Разложим числитель и знаменатель алгебраической дроби на множители. В числителе все просто:
Чтобы разложить на множители содержащийся в знаменателе дроби квадратный трехчлен

(мы снова воспользовались формулой разложения на множители квадратного трехчлена).
Тем самым заданное неравенство мы привели к виду


Рассмотрим выражение


Числитель этой дроби обращается в 0 в точке а знаменатель — в точках Отметим эти точки на числовой прямой (рис. 14), которая разбивается указанными точками на четыре промежутка, причем на каждом промежутке выражение f (х) сохраняет постоянный знак (эти знаки указаны на рис. 14). Нас интересуют те промежутки, на которых выполняется неравенство fх


Во всех рассмотренных примерах мы преобразовывали заданное неравенство в равносильное ему неравенство вида f {х) > 0 или f (x)
При этом количество множителей в числителе и знаменателе дроби может быть любым. Затем отмечали на числовой прямой точки а,Ь,с,д. и определяли знаки выражения f (х) на выделенных промежутках. Заметили, что на самом правом из выделенных промежутков выполняется неравенство f (х) > 0, а далее по промежуткам знаки выражения f (х) чередуются (см. рис. 16а). Это чередование удобно иллюстрировать с помощью волнообразной кривой, которая чертится справа налево и сверху вниз (рис. 166). На тех промежутках, где эта кривая (ее иногда называют кривой знаков) расположена выше оси х, выполняется неравенство f (х) > 0; где эта кривая расположена ниже оси х, выполняется неравенство f (х)


Пример 5. Решить неравенство


Решение. Имеем


(обе части предыдущего неравенства умножили на 6).
Чтобы воспользоваться методом интервалов, отметим на числовой прямой точки (в этих точках числитель дроби, содержащейся в левой части неравенства, обращается в нуль) и точки (в этих точках знаменатель указанной дроби обращается в нуль). Обычно точки отмечают схематически, учитывая порядок их следования (какое — правее, какое — левее) и не особенно обращая внимания на соблюдение масштаба. Ясно, что Сложнее обстоит дело с числами Первая прикидка показывает, что и то и другое число чуть больше, чем 2,6, откуда нельзя сделать вывод о том, какое из указанных чисел больше, а какое — меньше.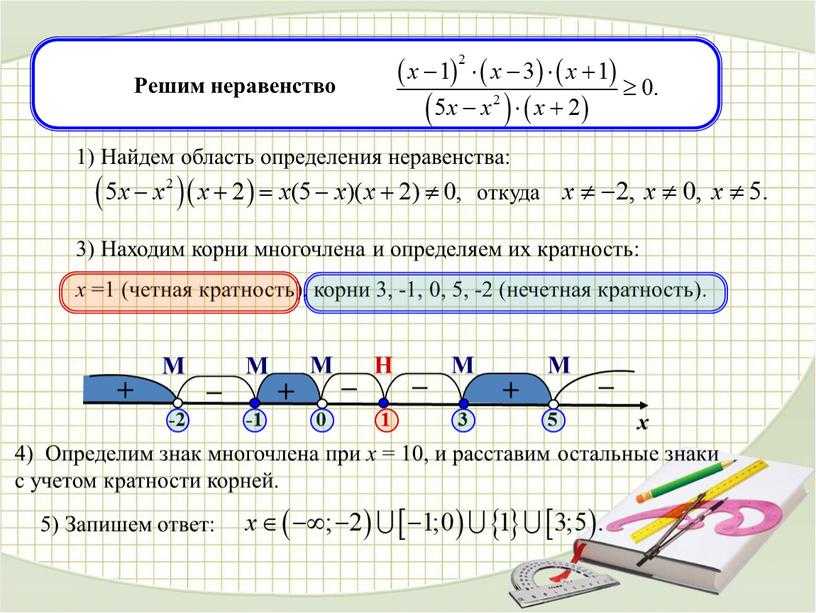 2-5x}{x+1}\) .

При решении дробных рациональных неравенств используется метод интервалов. Поэтому если алгоритм, приведенный ниже, вызовет у вас затруднения, посмотрите статью по .

Алгоритм решения дробно-рациональных неравенств.

    Примеры:

    Расставьте знаки на интервалах числовой оси. Напомню правила расстановки знаков:

    Определяем знак в самом крайнем правом интервале — берем число с этого интервала и подставляем его в неравенство вместо икса. После этого определяем знаки в скобках и результат перемножения этих знаков;

    Примеры:


    Выделите нужные промежутки. Если есть отдельно стоящий корень, то отметьте его флажком, чтоб не забыть внести его в ответ (см. пример ниже).

    Примеры:

    Запишите в ответ выделенные промежутки и корни, отмеченные флажком (если они есть).

    Примеры:
    Ответ: \((-∞;-1)∪(-1;1,2]∪}

Алгебра: решение рациональных неравенств

В конце книги «Квадратные уравнения и неравенства» я показал вам, как решать и изображать квадратные неравенства с одной переменной. Вы помните процесс? По сути, вы разложили квадратное число на множители, нашли критические числа, разбили числовую прямую на интервалы на основе этих критических чисел, а затем проверили эти интервалы, чтобы увидеть, какие из них являются решениями неравенства.

Вы будете использовать очень похожий процесс для решения рациональных неравенств. На самом деле, если быть до конца честным, процесс точно такой же, просто я тогда не дал вам абсолютно точного определения того, что такое критическое число. Не то чтобы я не хотел тебе говорить; Я только что обнаружил, что студенты, изучающие алгебру, лучше всего работают, руководствуясь принципом «необходимо знать». Вам действительно не нужно было знать полное определение в «Квадратных уравнениях и неравенствах», но для решения рациональных неравенств вам нужно.

Talk the Talk

Критическое число либо приводит к тому, что функция становится равной 0, либо делает ее неопределенной.

Я уже упоминал, что критическое число — это значение x , которое делает выражение равным 0. Однако есть и другой способ, которым значения получают классификацию «критического числа», когда они делают функцию неопределенной.

Если вы выполните следующие действия, решение рациональных неравенств станет проще простого:

  1. Переформулируйте неравенство так, чтобы в правой части остался только 0 . Это означает, что вы должны добавлять и вычитать члены с обеих сторон, чтобы все переместилось влево.
  2. При необходимости создайте одну фракцию слева . Используйте общие знаменатели, чтобы объединить любые термины в одну дробь.
  3. Разложите числитель и знаменатель на множители . Это делает нахождение критических чисел чрезвычайно простым.
  4. Установите каждый множитель в числителе равным 0 и решите . Отметьте эти критические числа на числовой прямой, используя открытую точку (если символ неравенства ) или закрытую точку (если символ неравенства ¤ или ¥).
  5. Приравняйте каждый множитель в знаменателе к 0 и решите . Это тоже критические числа, но их всегда следует помечать открытой точкой на числовой прямой, поскольку они представляют собой значения, которые делают рациональную функцию неопределенной. (Помните, 0 в знаменателе — плохая новость, поскольку деление на 0 запрещено.)
  6. Выберите контрольные точки, чтобы найти интервалы решения . После того, как вы нашли критические числа, процесс будет идентичен шагам, которые вы выполняли в разделе «Квадратные уравнения и неравенства».

Будьте особенно осторожны с точками, которые вы ставите на числовой строке. Если вы поставите неправильную точку, вы получите неправильные знаки неравенства в своем окончательном ответе, не говоря уже о том, что график также будет неточным.

Пример 5 : Решите неравенство и нарисуйте его решение.

Решение . Начните с переноса этого — x в левую часть неравенства, добавив x к обеим частям. только одну дробь в левой части неравенства, сложив все вместе. Наименьший общий знаменатель этих двух членов равен x + 4, поэтому умножьте вновь перемещенные x 1 числитель и знаменатель члена на это значение и объедините дроби.

Разложить числитель на множители.

Установите каждый множитель числителя равным 0 и решите, чтобы получить два критических числа.

Рисунок 18.4 Критические точки, соответствующим образом отмеченные на числовой прямой.

Рисунок 18.5 График решения задачи 2x + 5 x + 4 ¥ -x.

  • x + 1 = 0 или x + 5 = 0
  • x = -1 или x = -5
У вас есть проблемы

Задача 5. Решите неравенство и нарисуйте его график числовая строка с сплошными точками, поскольку знак неравенства ¥ допускает равенство, как показано на рис. 18.4. Окончательное критическое число получается путем установки коэффициента знаменателя равным 0.

  • x + 4 = 0
  • x = -4

Не забудьте использовать открытую точку для x = -4, поскольку ее значение исходит из знаменателя.

Теперь выберите контрольные точки из каждого интервала (я предлагаю x = -6, x = -4,5, x = -2 и x = 0). И x = -4,5, и x = 0 делают неравенство верным, поэтому их интервалы составляют решение: -5 ¤x x ¥-1. Затемните эти интервалы на числовой прямой, чтобы получился график, показанный на рис. 18.5.

Выдержки из Полное руководство по алгебре для идиотов © 2004, У. Майкл Келли. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

Вы можете приобрести эту книгу на Amazon.com и в Barnes & Noble.

Аналитическое решение рациональных неравенств

Аналитическое решение рациональных неравенств

В этом разделе предполагается, что вы знаете, как решить полиномиальные неравенства аналитически.

Рациональная функция — это частное двух многочленов. Давайте посмотрим на неравенство


в качестве примера неравенства с рациональной функцией. Вот график

Ключевой вопрос, на который мы должны ответить, чтобы решить наше неравенство: Где функция f ( x ) меняет знак?

Как и в случае полиномов, f ( x ) может менять знак, где f ( x )=0. (В нашем случае это происходит, когда x = 0.) Обратите внимание, что f ( x ) = 0, если числитель числа f ( x ) равен 0.

Но, как видите, функция f ( x ) тоже довольно резко меняет знак при x =1. Что происходит в х = 1? Знаменатель числа f ( x ) равен 0 при x = 1. В частности, f (1) не определено, так как нельзя делить на 0. Почти во всех случаях это означает, что график f ( x ) имеет вертикальную асимптоту в точках, где знаменатель равен 0. На вертикальной асимптоте знак f ( x ) может измениться с «» на «» или наоборот.

Это предлагает следующий метод решения рациональных неравенств:

Шаг 1. Найдите все точки x , где числитель f ( x ) равен 0, и найдите все точки x , где знаменатель f ( x ) равен 0 изображение оси x и отметьте эти точки. (Я буду обозначать точки, в которых числитель равен 0, желтыми точками, а точки, в которых знаменатель равен 0, — зелеными точками. Ваш учитель может назвать этот набор критических точек неравенства.

Шаг 2. Остальная часть процедуры более или менее идентична той, которую мы использовали для полиномиальных неравенств. Наши критические точки делят ось x на три интервала. Выберите точку (на ваш выбор!) в каждом интервале. Возьмем х = -1, х = 1/2 и х = 2. Вычислите f ( x ) для этих точек:


Эти три точки представляют то, что происходит в интервалах, в которых они содержатся:

Поскольку f (-1)>0, f ( x ) будет положительным для всех x в интервале . Аналогично, поскольку f (1/2)<0, f ( x ) будет отрицательным для , все x в интервале (0,1). Поскольку f (2)>0, f ( x ) будет положительным для все x в интервале . Вы можете указать это на оси x , вставив знаки плюс или минус на оси x . Вместо этого я использую цветовое кодирование: синий для положительного, красный для отрицательного:

Шаг 3. Мы хотим решить неравенство


поэтому мы ищем все x такие, что . Следовательно, набор

содержит все решения неравенства. С f (0)=0, x =0 является решением неравенства , поэтому мы включаем его в набор решений. x = 1, с другой стороны, является , а не решением. Вы даже не можете вставить x =1 в f ( x ), чтобы проверить, является ли это решением. «Зеленые точки» (знаменатель равен 0) и никогда не будут частью набора решений.

Предупреждение! Я знаю, что математики все усложняют, но упрощение, которое вы можете придумать, приводит к неправильным ответам. Мы хотели решить неравенство


Почему бы нам просто не умножить обе части на знаменатель x -1, чтобы получить

(Обратите внимание, что этот ответ неверен!) Мы можем умножить неравенство на число только в том случае, если мы знаем его знак . Вы помните, почему? Но секунду назад мы умножили на х -1. Является ли x -1 положительным или отрицательным, зависит от неизвестной переменной x .

Вот еще один пример: Найдите решения неравенства


Шаг 1. Числитель равен 0, когда x = -3 и когда x = 3. Знаменатель равен 0, когда x = -1 и когда x = 1. Нарисуйте изображение оси x и отметьте эти точки. Я буду обозначать точки, где числитель равен 0, желтыми точками, а точки, где знаменатель равен 0, зелеными точками.

Шаг 2. Наши критические точки разделяют x — ось на пять интервалов. Выберите точку (на ваш выбор!) в каждом интервале. Позвольте мне взять, и х = 0. Вычислите f ( x ) для этих точек:


Эти пять точек представляют собой то, что происходит в интервалах, в которых они содержатся:

Так как f (-4)>0, f ( x ) будет положительным для все x в интервале . Аналогично, поскольку f (-2)<0, f ( x ) будет отрицательным для всех x в интервале (-3,-1). Поскольку f (0)>0, f ( x ) будет положительным для всех x в интервале (-1,1). Поскольку f (2)<0, f ( x ) будут отрицательными для , все x в интервале (1,3). Поскольку f (4)>0, f ( x ) будет положительным для всех x в интервале . Вы можете указать это на оси x , вставив знаки плюс или минус на оси x . Вместо этого я использую цветовое кодирование: синий для положительного, красный для отрицательного:

Шаг 3. Мы хотим решить неравенство


поэтому мы ищем все x такие, что f ( x ) < 0. Следовательно, набор

содержит все решения неравенства. Ни одна из конечных точек интервала не будет включена, поскольку наше неравенство было «строгим».

(Вы заметили, что наша функция в левой части неравенства — четная функция? Следовательно, множество решений будет симметрично относительно x = 0.)

Вот наш следующий пример: Найдите решения неравенства


Для работы нашего метода необходимо, чтобы одна сторона неравенства равнялась нулю! Итак, давайте изменим наше неравенство на


Затем мы объединяем термины слева:

Шаг 1 . Я уже разложил числитель на множители, чтобы было легко увидеть, что числитель будет равен 0, когда x = -3 и когда x = 2. Знаменатель обращается в нуль при x = -2. Нарисуйте изображение оси x и отметьте эти точки. Я буду обозначать точки, где числитель равен 0, желтыми точками, а точки, где знаменатель равен 0, зелеными точками.

Шаг 2. Наши критические точки разделяют x — ось на четыре интервала. Выберите точку (на ваш выбор!) в каждом интервале. Возьмем х = — 4, х = -2,5, х = 0 и х = 3. Вычислить


для этих точек:

Эти точки являются репрезентативными для того, что происходит в интервалах, в которых они содержатся:

Поскольку f (-4)<0, f ( x ) будет отрицательным для , все x в интервале . Точно так же с f (-2.5)>0, f ( x ) будет положительным для всех x в интервале (-3,-2). Поскольку f (0)<0, f ( x ) будут отрицательными для , все x в интервале (-2,2). Так как f (3)>0, f ( x ) будет положительным для все x в интервале . Вы можете указать это на оси x , вставив знаки плюс или минус на x — ось. Вместо этого я использую цветовое кодирование: синий для положительного, красный для отрицательного:

Шаг 3. Мы хотим решить неравенство


поэтому мы ищем все x такие, что . Следовательно, набор

содержит все решения неравенства. Оба x = -3 и x = 2 включены, поскольку они делают числитель и, таким образом, f ( x ) равны нулю; x = -2 исключено, поскольку оно делает знаменатель f ( x ) равным нулю, и, таким образом, само f ( x ) не определено.

Пора попробовать самому:

Упражнение 1.
Найдите решения неравенства

Отвечать.
Упражнение 2.
Найдите решения неравенства

Отвечать.
Упражнение 3.
Найдите решения неравенства

Отвечать.
Упражнение 4.
Найдите решения неравенства

Отвечать.
Упражнение 5.
Найдите решения неравенства

Отвечать.
[Назад]
[Алгебра] [Тригонометрия] [Комплексные переменные]
[Исчисление] [Дифференциальные уравнения] [Матричная алгебра]
Домашняя страница S.O.S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

Гельмут Кнауст
Copyright 1999-2022 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час

Решение рациональных неравенств — различные способы решения, пример решения и часто задаваемые вопросы

Ключевой подход к решению рациональных неравенств зависит от определения критических значений рационального выражения, которое делит числовую прямую на характерные открытые интервалы. Критические значения — это нули (0) как числителя, так и знаменателя. Обратите внимание, что нули знаменателя делают рациональное выражение неопределенным, поэтому их следует немедленно исключить или отбросить как вероятное решение. Однако нули числителей также требуют проверки на предмет возможного включения во все решение.

Не знаете, как найти рациональное неравенство? Что ж! Существуют различные способы решения рациональных неравенств:

  • Алгебраическое решение рациональных неравенств.

  • Решение неравенств с рациональными выражениями.

  • Решение рациональных неравенств графическим способом.

Как решать рациональные неравенства

Ниже приведены шаги, необходимые для поиска рациональных неравенств и их решения.

Шаг 1: Запишите выражение неравенства в виде одного частного слева и нуля (0) справа.

Шаг 2: определите критические точки — точки, в которых рациональное выражение будет неопределенным или равным нулю.

Шаг 3: Используйте критические точки для разделения числовой прямой на интервалы.

Шаг 4. Проверьте значение каждого интервала. Числовая строка отображает знак каждого фактора числителя, а также знаменателя в каждом интервале. Числовая линия также показывает знак частного.

Шаг 5: определите интервалы, в которых допустимо неравенство.

Шаг 6: Запишите решение в виде интервальной записи.

Рациональное

Вот как выглядит рациональное выражение, имеющее отношение двух многочленов.

(Изображение будет загружено в ближайшее время)

Иногда нам нужно решать рациональные неравенства, подобные этим:0003

Example

>

greater than

(x + 1)/(3 − x) > 2

<

less than

x/(x + 7) <−3

≥

больше, чем или равна

(x — 1)/(5– x) x

(x-1)/(5– x) x) x

(X -1)/(5– x) x) x

(x-1)/(5– x) x) x) x) x) x).

≤

меньше или равно

(3 − 2x)/(x − 1) ≤ 2

Пример решения

Пример: Решить и упростить данное рациональное неравенство: — 3x — 4 )/(x 2 — 8x + 16) < 0

Решение:

Шаг 1: Вынесите на множители числитель и знаменатель, чтобы найти их нули. В факторизованном виде получим:

(x+1) (x — 4) / (x — 4) (x — 4) < 0

Шаг 2: определить нули рационального неравенства, установив каждый множитель равным до нуля

Шаг 3: Найдите x. Получаем:

Нули числителей: –1 и 4

Нули знаменателей: 4

Шаг 4: Рассмотрим принятие нулей в качестве критических чисел, чтобы разделить числовую прямую на отдельные интервалы.

Шаг 5: Проверьте достоверность каждого интервала, выбрав проверочное значение и оценив их в исходное рациональное неравенство.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *