Как решить правильно уравнение: Решение уравнений — урок. Математика, 6 класс.

Как решить уравнение?

Этап урока. Технология проведения	Деятельность учеников	Деятельность учителя	Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов	Планируемые результаты УУД
				Предметные	УУД
I. Мотивация к учебной деятельности (3 мин) Цели: — актуализировать требования к ученику со стороны учебной деятельности; — создать условия для возникновения у учеников внутренней потребности включения в учебную деятельность; -установить тематические рамки; — уточнить тип урока и наметить шаги учебной деятельности.	Проговаривают стихотворение – правила поведения на уроке, объясняют, для чего нужно выполнять эти правила. Проговаривают девиз урока. Проговаривают тип урока и называют шаги учебной деятельности. Слушают и смотрят картинку с данным этапом. Проговаривают название этапа с учителем.	Организует актуализацию требований к ученику со стороны учебной деятельности. Создаёт условия для возникновения у учеников внутренней потребности включения в учебную деятельность. Устанавливает тематические рамки. Организует уточнение типа урока и называние шагов учебной деятельности. Затруднение: учитель просит учащихся найти букву / картинку, которая добавилась или исчезла. Показывает данный этап на доске.	1. Громко прозвенел звонок. Начинается урок. Наши ушки – на макушке, Глазки широко открыты. Слушаем, запоминаем, Ни минуты не теряем. 2. — Какие математические записи мы знаем? Назовите их. 4 + 5, 6 — 3 (выражения) — Как прочитать эти выражения? (сумма чисел …, первое слагаемое…, второе слагаемое…; разность чисел …, уменьшаемое …, вычитаемое …) 3 , 10 6 (неравенства) — прочитайте их 2 + 8 = 9 (равенство) — Верное это равенство? (Нет) — Превратите это равенство в верное. — Какие ещё есть математические равенства, знаете? — Хотите узнать? 3. Девиз урока: «Знаешь – говори, не знаешь – слушай». — Значит, чему будет посвящён наш урок? (Открытию нового знания) — Какие мы делаем шаги при открытии нового знания? («Что я не знаю?», «Сам найду способ»)	Уметь читать математические выражения, неравенства, равенства.	Уметь совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД). Уметь оформлять свои мысли в устной форме (Коммуникативные УУД). Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя (Познавательные УУД). Умение слушать и понимать речь других (Коммуникативные УУД).
II. Актуализация и фиксирование индивидуального затруднения в пробном действии (10 мин) Цели: — организовать актуализацию умений задачи на нахождение целого или частей; — организовать выполнение учащимися пробного учебного действия; — организовать фиксирование учащимися индивидуального затруднения.	Слушают и смотрят картинку с данным этапом. Проговаривают название этапа с учителем. Выполняют задание на индивидуальных досках. Проговаривают, что повторили. Слушают и смотрят картинку с данным этапом. Проговаривают название этапа с учителем. Слушают и смотрят картинку с данным этапом. Проговаривают название этапа с учителем. Выполняют задание устно. Фиксируют индивидуальное затруднение (Я не знаю). Проговаривают название этапа с учителем. Проговаривают название следующего этапа с учителем.	Показывает картинку следующего этапа. Называет этап. Организует актуализацию умений решать задачи на нахождение целого или частей. Пример с яблоком, мешочками, стаканом с водой Организует обобщение актуализированных знаний. Показывает картинку следующего этапа. Показывает картинку следующего этапа. Называет этап. Предлагает задание для пробного действия. Показывает картинку следующего этапа. Называет этап. Организует выполнение учащимися пробного учебного действия. Организует фиксирование индивидуального затруднения. Показывает картинку следующего этапа. Называет этап. Организует уточнение следующего этапа учебной деятельности	1. — А теперь переходим к следующему этапу (2). — Что мы будем делать? (Повторять). 2. — Прочитайте текст. Является ли он задачей? Докажите. — Заполните схему и запишите решение. Фронтальная проверка, выбор верного решения. Решение обратных задач. Фронтальная работа. 3. – Что мы повторили? (Решение задач на нахождение целого и частей). — Мы находимся на этапе 3. 4. Задание для пробного действия. — А теперь мы переходим к этапу 5. Получаем задание для пробного действия. Х + 4 = 9 8 – у = 5 (обсуждение в парах данных неравенств) 6. Выполнение пробного действия — А что сейчас будем делать? — Мы переходим к этапу 5 и будем выполнять задание: — Как называются данные математические записи? (Равенства) — Как ещё можно назвать эти записи? Фронтальная проверка. 7. Фиксация индивидуального затруднения. — У нас получились разные варианты. — А почему (назвать по имени) вы не предлагаете свои варианты? (Мы не знаем) — Мы были на этапе 6 (затруднение). 8. — Какой наш следующий этап? (Этап 7 — Что я не знаю?)	Знать структуру задачи. Уметь решать задачи на нахождение целого или частей.	Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь преобразовывать информацию из одной формы в другую (Познавательные УУД). Уметь оформлять свои мысли в устной форме (Коммуникативное УУД). Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь проговаривать последовательность действий на уроке; высказывать своё предположение (Регулятивные УУД). Уметь оформлять мысли в устной и письменной форме (Коммуникативные УУД).
III. Выявление места и причины затруднения (2 мин) Цели: — выявить место (шаг, операция) затруднения; — зафиксировать во внешней речи причину затруднения.	Под руководством учителя выявляют место затруднения. Проговаривают причину затруднения с помощью учителя.	Организует выявление места затруднения. Организует фиксирование во внешней речи причины затруднения.	— В каком месте возникло затруднение? (При назывании математических записей). — Почему возникло затруднение? (Не знаем, что это за записи).		Уметь оформлять свои мысли в устной форме (Коммуникативные УУД). Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя (Познавательные УУД).
IV. Построение проекта выхода из затруднения (3 мин) Цели: — организовать постановку цели урока; — организовать составление совместного плана действий; — определить средства.	Проговаривают следующий шаг учебной деятельности. С помощью учителя проговаривают называют следующий этап, ставят цель урока. С помощью учителя проговаривают название следующего этапа. Составляют и проговаривают план действий с помощью учителя. Называют средства.	Организует уточнение следующего шага учебной деятельности. Показывает картинку следующего этапа. Называет этап. Организует постановку цели урока. Показывает картинку следующего этапа. Называет этап. Организует составление совместного плана действий. Организует определение средств.	1. — Какой следующий шаг учебной деятельности? (Сам найду способ) 2. — Какой наш следующий этап? (Этап 8. Постановка цели) — Какую цель ставим? (Узнать, как называется эта математические записи). 3. – А какое наше действие следующее? (Составить план. Этап 9) — Наметим наш план действий: 1. Сами попробуем выполнить задание: узнать, что такое … 2. Сопоставим свои предположения с учебником, спросим у учителя. 3. Устраним затруднение. 4. Применим новое знание. — Что нам поможет? (свой опыт, учебник, учитель) Физкультминутка		Уметь проговаривать последовательность действий на уроке; (Регулятивные УУД). Уметь оформлять свои мысли в устной форме; слушать и понимать речь других (Коммуникативные УУД). Уметь определять и формулировать цель на уроке с помощью учителя (Регулятивные УУД). Уметь проговаривать последовательность действий на уроке (Регулятивные УУД).
V.Реализация построенного проекта (10 мин) Цели: -реализовать построенный проект в соответствии с планом; — зафиксировать новое знание в речи и знаках; -организовать устранение и фиксирование преодоления затруднения; — уточнить тему урока.	С помощью учителя проговаривают название следующего этапа. Под руководством учителя выполняет составленный план действий. Отвечают на вопросы учителя. С помощью учителя проговаривают название следующего этапа. Фиксируют новое знание в речи и знаках. Под руководством учителя формулируют тему урока.	Показывает картинку следующего этапа. Называет этап. Организует реализацию построенного проекта в соответствии с планом. Организует подводящий диалог. Показывает картинку следующего этапа. Называет этап. Организует фиксирование нового знания в речи и знаках. Организует уточнение темы урока.	1. — Какой наш следующий этап? (Этап 10. Выполняем по плану действия) 2. Подводящий диалог: — Посмотрите на эти равенства. — Что здесь необычного? (Какие-то иностранные буквы). — Что обозначают данные буквы? (Наверное, какие-то числа). — Вы знаете, какие числа нужно подставить вместо букв, чтобы получилось верное равенство? 3. — Давайте сформулируем понятие такого равенства. Введение понятий: «уравнение», «решить уравнение». Стр. 20, 3 Оформление решения. 4. – Какой следующий этап? (Этап 11. Фиксируем новое знание в речи и знаках). Устранение затруднения. — Какая тема урока сегодня? (Уравнение).		Уметь добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД). Уметь оформлять свои мысли в устной форме; слушать и понимать речь других (Коммуникативные УУД). Уметь работать по коллективно составленному плану (Регулятивные УУД).
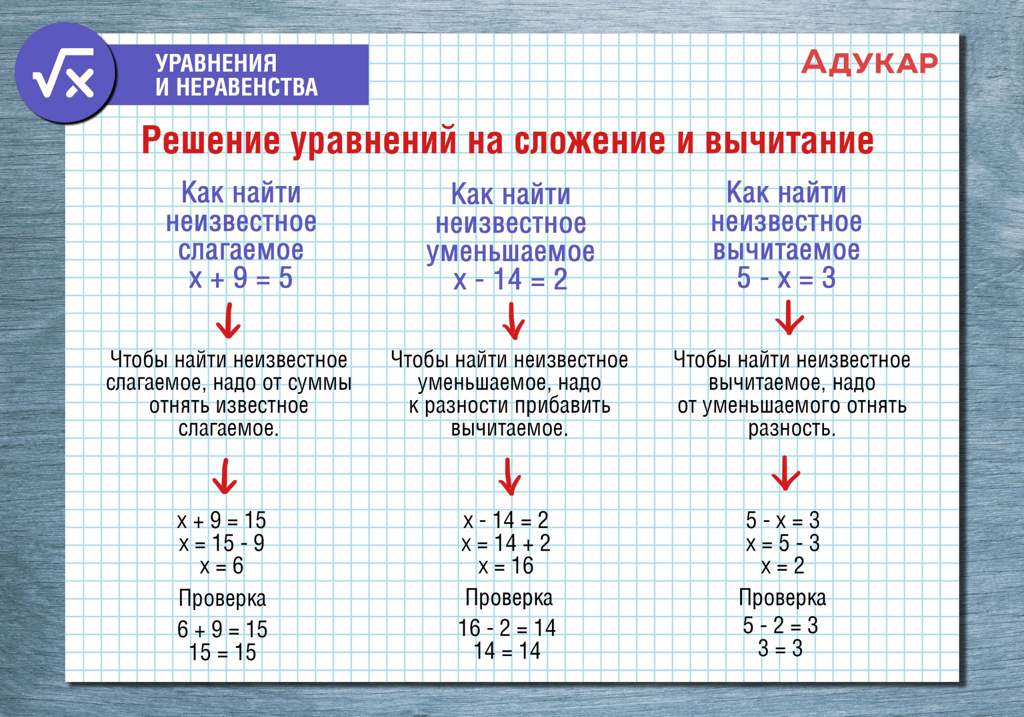
VI.Первичное закрепление с проговариванием во внешней речи (7 мин) Цель: — организовать усвоение учениками нового способа действий с проговариванием во внешней речи.	С помощью учителя проговаривают название следующего этапа. Выполняют задание на доске.	Показывает картинку следующего этапа. Называет этап. Организует усвоение учениками нового способа действий с проговариванием во внешней речи.	— Переходим к этапу 12. Закрепление. Оформить решение уравнений в тетради (фронтальная работа) х + 4 = 9 8 – у = 5 х – 4 = 6	Уметь решать уравнения вида а ± х = b, х – а = b на основе взаимосвязи между частью и целым	Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь оформлять свои мысли в устной и письменной форме; слушать и понимать речь других (Коммуникативные УУД).
VII. Самостоятельная работа с самопроверкой по эталону (7 мин) Цели: — организовать выполнение учащимися самостоятельной работы на новое знание; — организовать самопроверку по эталону, самооценку; — организовать выявление места и причины затруднений, работу над ошибками.	С помощью учителя проговаривают название следующего этапа. Выполняют задание самостоятельно в тетради. Выполняют самопроверку по эталону. Называют с помощью учителя место своего затруднения, причину исправляют ошибки. Выполняют самооценку по алгоритму.	Показывает картинку следующего этапа. Называет этап. Организует выполнение учащимися самостоятельной работы на новое знание. Организует самопроверку по эталону. Организует выявление места и причины затруднений, работу над ошибками. Организует самооценку (методика Цукерман)	— Какой наш следующий этап? (Этап 13. Самостоятельная работа с проверкой по эталону) Стр. 21 № 5 (б, в) Решите уравнения: 1 + Х=5 3+Х=9 Эталон для самопроверки. — У кого всё правильно? — У кого есть ошибки? — В каком слове ошибки? — В чём причина? Самооценка по алгоритму.	Уметь решать уравнения вида а ± х = b, х – а = b на основе взаимосвязи между частью и целым.	Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь выполнять работу по предложенному плану (Регулятивные УУД). Уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок (Регулятивные УУД). Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД).
VIII. Рефлексия учебной деятельности на уроке (3 мин) Цели: — зафиксировать новое содержание урока; — организовать рефлексию и самооценку учениками собственной учебной деятельности.	С помощью учителя проговаривают название следующего этапа. Отвечают на вопросы учителя. По схеме рассказывают, что узнали, знают, смогли. Делают самооценку в блокноте.	Показывает картинку следующего этапа. Называет этап. Организует фиксирование нового содержания. Организует рефлексию. Организует самооценку учебной деятельности.	— Мы переходим к последнему этапу 15. Подводим итог работы на уроке. — Какую цель ставили? Достигли цели? — Какая тема урока была? Расскажите по схеме, чему научились на уроке. — Оцените свою деятельность на уроке, поставьте мячик-попрыгунчик на нужную ступеньку. Если вам урок был понятен и интересен, нарисуйте ему улыбку.		Уметь проговаривать последовательность действий на уроке (Регулятивные УУД). Уметь оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки. (Регулятивные УУД). Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД).

ГДЗ по математике 2 класс учебник Моро, Волкова 2 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бельтюкова Г. В.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

Решебник — страница 19Готовое домашнее задание

Номер 1.

1) Вычисли с устным объяснением.
2) Проверь вычитание любым способом.

Ответ:

Пишу десятки под десятками, а единицы под единицами. Вычитаю единицы: из 0 нельзя вычесть 2. Беру 1 дес. из 7 дес. (чтобы не забыть, ставлю точку над цифрой 7. 1 дес. = 10 ед. 10 − 2 = 8 Пишу под единицами 8. Вычитаю десятки: Было 7 дес., но 1 дес. взяли при вычитании единиц. Осталось 6 дес. 6 − 3 = 3 Пишу 3 под десятками. Читаю ответ: разность чисел 70 и 32 равна 38.

Пишу десятки под десятками, а единицы под единицами. Вычитаю единицы: из 0 нельзя вычесть 7. Беру 1 дес. из 6 дес. (чтобы не забыть, ставлю точку над цифрой 6. 1 дес. = 10 ед. 10 − 7 = 3 Пишу под единицами 3. Вычитаю десятки: Было 6 дес., но 1 дес. взяли при вычитании единиц. Осталось 5 дес. 5 − 1 = 4 Пишу 4 под десятками. Читаю ответ: разность чисел 60 и 17 равна 43.
Пишу десятки под десятками, а единицы под единицами. Складываю единицы: 8 + 2 = 10 10 ед. − это 1 дес. и 0 ед. Пишу под единицами 0, а 1 дес. запомню и прибавлю к десяткам. Складываю десятки: 3 + 2 = 5, да еще 1: 5 + 1 = 6 Пишу под десятками 6 Читаю ответ: сумма чисел 38 и 22 равна 60.
Пишу десятки под десятками, а единицы под единицами. Вычитаю единицы: 6 − 5 = 1 Пишу под единицами 1. Вычитаю десятки: 7 − 4 = 3 Пишу 3 под десятками. Читаю ответ: разность чисел 76 и 45 равна 31.
Пишу десятки под десятками, а единицы под единицами. Вычитаю единицы: из 0 нельзя вычесть 6. Беру 1 дес. из 9 дес. (чтобы не забыть, ставлю точку над цифрой 9. 1 дес. = 10 ед. 10 − 6 = 4 Пишу под единицами 4. Вычитаю десятки: Было 9 дес., но 1 дес. взяли при вычитании единиц. Осталось 8 дес. 8 − 5 = 3 Пишу 3 под десятками. Читаю ответ: разность чисел 90 и 56 равна 34.

Номер 2.

В ателье сшили 26 платьев, костюмов на 4 больше, чем платьев, а брюк на 10 меньше, чем костюмов. Сколько брюк сшили в ателье?

Ответ:

Номер 3.

Проверь, правильно ли решены уравнения.

Ответ:

х − 20 = 7 9 − 20 = 7 Неверно решено уравнение х = 20 + 7 х = 27

у + 9 = 17 8 + 9 = 17 Верно решено уравнение у = 17 − 9 у = 8

Номер 4.

Ответ:

100 − (20 + 40) = 100 – 60 = 40 90 − (16 + 4) = 90 – 20 = 70
37 − 8 = 29 62 − 6 = 56
43 + 7 − 9 = 50 – 9 = 41 52 + 8 − 7 = 60 – 7 = 53

Задание внизу страницы

На одной улице 20 фонарей, а на другой 18 фонарей. Из них 4 неисправны. Сколько исправных фонарей на этих улицах?

Ответ:

Первая улица – 20 ф. Вторая улица – 18 ф. Неисправны – 4 ф. Исправны – ? ф. (20 + 18) − 4 = 34 (ф.) – исправных на улицах. Ответ: 34 фонаря.

Задание на полях страницы

Вычисли. Найди лишнее выражение

Ответ:

37 – 7 = 30 20 + 10 = 30 70 – 40 = 30 100 – 70 = 30 48 – 18 = 30 62 – 32 = 30 76 – 36 = 40 – лишнее выражение

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Ваше сообщение отправлено!

+

Распространенные математические ошибки

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т.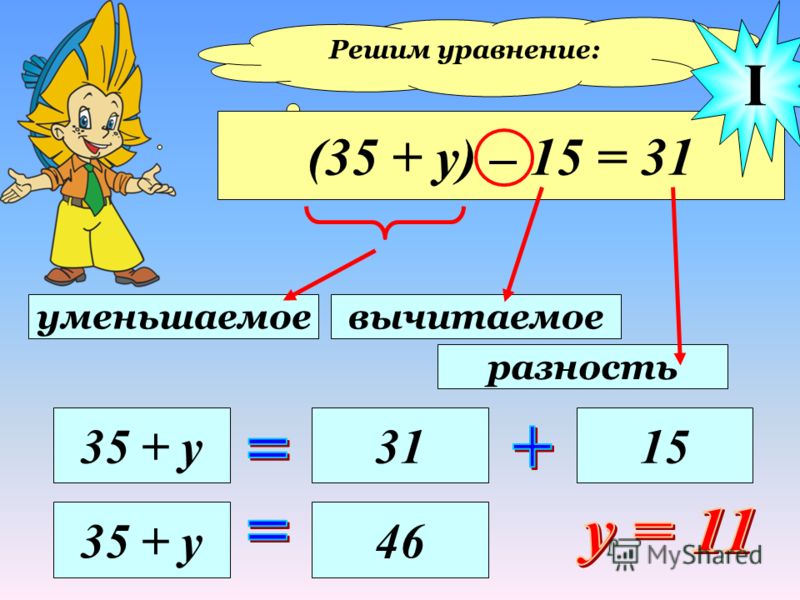 е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Здесь рассматриваются ошибки, которые учащиеся часто допускают при выполнении алгебры, а не только ошибки, обычно допускаемые на уроках алгебры. Я видел каждую из этих ошибок, сделанных учениками всех уровней, от уроков алгебры до выпускных классов по математике! На самом деле, несколько примеров в этом разделе на самом деле взяты из исчисления.

Если вы не занимались исчислением, вы можете игнорировать эти примеры. В каждом случае, когда я приводил примеры, я пытался включить примеры из класса алгебры, а также случайный пример из курсов более высокого уровня, таких как исчисление.

Я убежден, что многие из приведенных здесь ошибок вызваны тем, что люди ленятся или спешат и не обращают внимания на то, что они делают. Замедляясь, обращая внимание на то, что вы делаете, и обращая внимание на правильные обозначения, вы можете избежать подавляющего большинства этих ошибок!

Деление на ноль

Все знают, что \(\frac{0}{2} = 0\) проблема в том, что слишком много людей также говорят, что \(\frac{2}{0} = 0\) или \(\frac{2}{0} = 2\)! Помните, что деление на ноль не определено! Вы просто не можете делить на ноль, так что не делайте этого!

Вот очень хороший пример хаоса, который может возникнуть при делении на ноль. Посмотрите, сможете ли вы найти ошибку, которую я допустил в приведенной ниже работе.

1. \(a = b\)Начнем считать, что это правда. 92}\) с обеих сторон.
2. \(b\left( {a — b} \right) = \left( {a + b} \right)\left( {a — b} \right)\) Фактор обеих сторон.
3. \(b = a + b\) Разделите обе части на \(a — b\).
4. \(b = 2b\)Вспомним, что мы начали с предположения \(a = b\).
5. \(1 = 2\) Разделите обе части на b .

Итак, нам удалось доказать, что 1 = 2! Теперь мы знаем, что это не так, поэтому ясно, что где-то ошиблись. Вы видите, где была допущена ошибка?

Ошибка была на шаге 5. Вспомним, что мы начали с предположения \(a = b\). Однако, если это так, то мы имеем \(a — b = 0\)! Итак, на шаге 5 мы действительно делим на ноль!

Эта простая ошибка привела нас к чему-то, что, как мы знали, было неправдой, однако в большинстве случаев ваш ответ не будет явно неправильным. Не всегда будет понятно, что вы делите на ноль, как это было в этом примере. Вы должны быть в поиске такого рода вещи.

Помните, что делить на ноль НЕЛЬЗЯ!

Плохая/потерянная/предполагаемая скобка

Вероятно, это ошибка, которую я считаю самой неприятной. Есть несколько ошибок, которые люди обычно делают здесь.

Первая ошибка заключается в том, что люди ленятся и решают, что скобки не нужны на определенных шагах или что они могут помнить, что скобки должны быть там. Конечно, проблема здесь в том, что они часто забывают о них уже на следующем этапе!

Другая ошибка заключается в том, что учащиеся иногда не понимают, насколько на самом деле важны круглые скобки. Это часто наблюдается в ошибках, допущенных при возведении в степень, как показывают мои первые несколько примеров. 92}\)

Обратите внимание на очень важную разницу между этими двумя! Имея дело с показателями степени, помните, что показатель степени получает только количество непосредственно слева от показателя степени. Итак, в неправильном случае x — это величина сразу слева от экспоненты, поэтому мы возводим в квадрат только x , а 4 не возводится в квадрат. В правильном случае скобка находится сразу слева от показателя степени, поэтому это означает, что все, что находится внутри скобки, должно быть возведено в квадрат! 92} = — \left( 3 \right)\left( 3 \right) = — 9\)

Этот вариант похож на предыдущий, но имеет одну тонкость, которая иногда вызывает проблемы. Помните, что только количество слева от экспоненты получает экспоненту. Итак, в неправильном случае ТОЛЬКО 3 находится слева от показателя степени, и поэтому ТОЛЬКО 3 возводится в квадрат!

Многие люди знают, что технически они должны возвести в квадрат -3, но они ленятся и не записывают скобки, полагая, что вспомнят их, когда придет время реально оценить. Однако удивительно, как многие из этих людей тут же забывают о скобках и записывают -9.2} — x — 10\)

Будьте внимательны и обратите внимание на разницу между ними! В первом случае я поставил скобки вокруг \(4x — 5\), а во втором — нет. Поскольку мы вычитаем многочлен, нам нужно убедиться, что мы вычитаем весь многочлен! Единственный способ убедиться, что мы делаем это правильно, — это заключить его в круглые скобки.

Опять же, это одна из тех ошибок, когда люди знают, что технически скобки должны быть там, но они не вставляют их и тут же забывают, что они там были, и неправильно выполняют вычитание. 92} — 180x + 225\end{eqnarray*}\)

Помните, что возведение в степень должно быть выполнено ДО того, как вы распределите какие-либо коэффициенты через скобки!

Аддитивные предположения

Я не знал, как еще это назвать, но это ошибка, которую допускают многие студенты. 2}\] \[\sqrt {x + y} \ne \sqrt x + \sqrt y \] \[\frac{1}{{x + y}} \ne \frac{1}{x} + \frac{1}{y}\] \[\cos \left( {x + y} \right) \ne \cos x + \cos y\] 92} & \ne & 1 + 9\\16 & \ne & 10\end{eqnarray*}\]

Вы найдете случайный набор чисел, для которых одно из этих правил будет работать, но они не работают почти для любой случайно выбранной пары чисел.

Обратите внимание, что существует гораздо больше примеров, когда это дополнение предположение не работает, чем то, что я перечислил здесь. Я просто записал те, которые вижу чаще всего. Кроме того, пару из тех, что я перечислил, можно было бы сделать более общими. Например, 92} — 1\]

Обратите внимание: чтобы убрать \(x\) из знаменателя, я сначала вынес \(x\) из числителя. Вы можете что-то отменить только в том случае, если оно умножается на ЦЕЛЫЙ числитель и знаменатель, или если ЯВЛЯЕТСЯ целым числителем или знаменателем (как в случае со знаменателем в нашем примере).

Сравните это со следующим примером, который содержит очень распространенную ошибку, которую допускают студенты. 3} — x}}{x}\) (сделано неправильно). 93} — 1\]

Другими словами, они сокращают \(x\) в знаменателе против только одного из \(x\) в числителе ( т.е. сокращают \(x\) только из первого члена или только со второго срока). ЭТОГО НЕВОЗМОЖНО!!!!! Чтобы сделать эту отмену, вы ДОЛЖНЫ иметь \(x\) в обоих терминах.

Чтобы убедиться, что такая отмена неверна, рассмотрим следующий пример с числами.

Пример 3. Упростить \(\frac{{8 — 3}}{2}\).

Это легко сделать, просто выполнив следующие арифметические действия

\[\frac{{8 — 3}}{2} = \frac{5}{2} = 2,5\]

Однако давайте сделаем неправильную отмену, как в предыдущем примере. Сначала мы сократим двойку в знаменателе на восьмерку в числителе. Это НЕПРАВИЛЬНО, но отражает отмену, которая была неправильно выполнена в предыдущем примере. Это дает,

\[\frac{{8 — 3}}{2} = 4 — 3 = 1\] 92} = х\) (сделано неправильно).

Слишком многие ученики привыкли просто отменять (то есть упрощать) вещи, чтобы облегчить себе жизнь. Таким образом, самая большая ошибка при решении такого рода уравнений состоит в том, чтобы сократить \(x\) с обеих сторон, чтобы получить

\[2x = 1 \hspace{0,25 дюйма} \Rightarrow \hspace{0,25in} x = \frac{1}{2}\]

Хотя \(x = \frac{1}{2}\) является решением, есть еще одно решение, которое мы упустили. Вы видите, что это такое? Взгляните на следующий пример, чтобы увидеть, что это такое. 92} — x & = & 0\\ x\left( {2x — 1} \right) & = & 0\end{eqnarray*}\]

Отсюда видно, что либо

\[x = 0 \hspace{0,5 дюйма} \mbox{ИЛИ} \hspace{0,5 дюйма} 2x — 1 = 0\]

Во втором случае мы получаем \(x = \frac{1}{2}\), которое мы получили в первой попытке, но в первом случае мы также получаем \(x = 0\), которого не было получить с первой попытки. Ясно, что \(x = 0\) будет работать в уравнении, как и решение!

Мы пропустили \(x = 0\) в первой попытке, потому что пытались облегчить себе жизнь, «упростив» уравнение перед решением. Хотя некоторое упрощение — вещь хорошая и необходимая, НИКОГДА не следует делить термин, как мы это делали в первой попытке при решении. Если вы сделаете это, вы потеряете решения.

Правильное использование квадратного корня

Кажется, существует очень большое заблуждение об использовании квадратных корней. Студенты, похоже, ошибочно полагают, что

\[\sqrt {16} = \pm \,4\]

Однако это неверно. Квадратные корни ВСЕГДА положительны или равны нулю! Таким образом, правильное значение

\[\кварт {16} = 4\]

Это ЕДИНСТВЕННОЕ значение квадратного корня! Если мы хотим -4, то делаем следующее

\[ — \ sqrt {16} = — \ влево ( {\ sqrt {16} } \ вправо) = — \ влево ( 4 \ вправо) = — 4 \]

Обратите внимание, что я использовал круглые скобки только для того, чтобы подчеркнуть, как именно появляется знак минус! Как правило, два средних шага опускаются. Итак, если мы хотим получить отрицательное значение, мы должны поставить знак минус! 92} & = & 16\\x & = & \pm \sqrt {16} \\x & = & \pm \,4\end{eqnarray*}\]

Обратите внимание, что \( \pm \) появляется на втором шаге до того, как мы действительно найдем значение квадратного корня! Он не появляется как часть извлечения квадратного корня.

Я чувствую, что должен указать, что многие инструкторы (включая меня иногда) не помогают делу тем, что они часто опускают второй шаг и тем самым, кажется, подразумевают, что \( \pm \) показывает вверх из-за квадратного корня.

Итак, помните, что квадратные корни ВСЕГДА возвращают положительный ответ или ноль. Если вы хотите получить отрицательный результат, вам нужно поставить его со знаком минус ДО того, как вы возьмете квадратный корень.

Неоднозначные дроби

Это больше вопрос обозначений, чем вопрос алгебры. Я решил поместить это здесь, потому что слишком много студентов заканчивают занятия по алгебре, не понимая этого момента. На самом деле есть три вида «плохих» обозначений, которые люди часто используют с дробями, что может привести к ошибкам в работе.

Первый использует «/» для обозначения дроби, например 2/3. В этом случае действительно нет проблем с использованием «/», но как насчет 2/3\(x\)? Это может быть любая из двух следующих дробей.

\[\frac{2}{3}x \hspace{0,5 дюйма} \mbox{ИЛИ} \hspace{0,5 дюйма} \frac{2}{{3x}}\]

Из 2/3\(х\) непонятно, какое из этих двух должно быть! Вы, как ученик, можете знать, какое из двух значений вы намеревались использовать, но оценщик — нет. Кроме того, хотя вы можете знать, какую из двух задач вы имели в виду, когда записывали ее, будете ли вы знать, какую из двух, когда вернетесь к проблеме во время изучения?

Вы должны использовать «/» для дробей только тогда, когда всем, а не только вам, будет ясно и очевидно, как следует интерпретировать дробь.

Следующая проблема с обозначениями, с которой я довольно часто сталкиваюсь, это люди, которые пишут,

\[\frac{2}{3}\,\,\begin{массив}{*{20}{c}}{}\\ x\end{массив}\]

Из этого не ясно, принадлежит ли \(x\) знаменателю дроби или нет. Студенты часто пишут такие дроби, и обычно они имеют в виду, что \(x\) не должно быть в знаменателе. Проблема в том, что на первый взгляд часто кажется, что он должен быть в знаменателе, а ученик просто недостаточно далеко перевел черту дроби.

Если вы хотите, чтобы \(x\) было в знаменателе, запишите его таким образом, \(\frac{2}{{3x}}\), т. е. убедитесь, что вы рисуете дробь черта на ВЕСЬ знаменатель. Если вы не хотите, чтобы он был в знаменателе, не оставляйте никаких сомнений! Запишите это как \(\frac{2}{3}x\).

Последняя проблема с обозначениями, которую я вижу, связана с использованием «/» для обозначения дроби, но на самом деле это проблема со скобками. Это включает в себя такие дроби, как

\[\frac{{a + b}}{{c + d}}\]

Часто учащиеся, которые используют «/» для обозначения дробей, пишут, что это дробь, как

\[а + б/с + г\]

Эти ученики знают, что записывают исходную дробь. Однако почти все остальные увидят следующие

\[а + \фракция {b}{с} + г\]

Это определенно НЕ исходная фракция. Итак, если вы ДОЛЖНЫ использовать «/» для обозначения дробей, используйте круглые скобки, чтобы было ясно, что такое числитель и что такое знаменатель. Итак, вы должны написать это как

\[\слева(а + б \справа) / \слева( с + г \справа)\]

Часто задаваемые вопросы: решить дифференциальное уравнение? — Общее использование

ZhouZhuofei 4 ноября 2020 г., 17:25

#1

Здесь у меня есть функция:

\frac{dx}{dt} = kx(N-x) — lx(1-\alpha\frac{x}{N}) + \sigma k x \xi(t)

\xi(t) — случайный член возмущения, \sigma — его дисперсия,
k,l,N, \alpha является константой.

 с использованием графиков
используя дифференциальные уравнения
к, л, N, а = 0,02, 0,01, 1,0, 0,2
f(u,p,t)=k*u*(N-u) - l*u * (1 - α * u/N)
и₀ = 0,001
tspan = (0,0,100,0)
prob = ODEProblem(f,u₀,tspan)
res = решить(вероятность,Tsit5(), reltol=1e-8, abstol=1e-8)
сюжет (разрешение)
 

как добавить \xi(t) в эту функцию и решить?

Доубартон 4 ноября 2020 г., 19:31

#2

На самом деле это стохастическое дифференциальное уравнение, а не обыкновенное дифференциальное уравнение. Взгляните на Stochastic Differential Equations · DifferentialEquations.jl, чтобы узнать, как их решать с помощью DifferentialEquations.jl.

1 Нравится

ЭлОкеанографо 4 ноября 2020 г. , 19:34

#3

Как сказал @dawbarton, это SDE — в основном, вы определяете вторую функцию для стохастического члена и создаете SDEPProblem вместо ODEProblem . Если я правильно понимаю ваше уравнение, оно должно выглядеть так:

 f(u, p, t) = k*u*(N-u) - l*u * (1 - α * u/N)
g(u, p, t) = k * σ * u
prob = SDEProblem(f, g, u₀, tspan)
res = решить (проблема)
 

В качестве примечания: ваши уравнения будут решаться быстрее, если вы избегаете глобальных переменных, передавая параметры в виде именованного кортежа:

 params = (k=0,02, l=0,01, N=1,0, α=0,2, σ= 1.0)
f(u, p, t) = p.k*u*(p.N-u) - p.l*u * (1 - p.α * u/p.N)
g(u, p, t) = p.k * p.σ * u
prob = SDEProblem(f, g, u₀, tspan, params)
@time res = решить (проблема)
 

3 лайков

ЧжоуЧжуофэй 5 ноября 2020 г. , 5:31

#4

em, поэтому g(u, p, t) = k*σ*u равно σkx , dW = \frac{d(\xi(t))}{dt}, верно?

если я хочу изменить дисперсию (\xi(t)), как это сделать?

Циренберг 5 ноября 2020 г., 7:44

#5

В DifferentialEquations.jl полное уравнение имеет вид du = f(u,p,t)dt + g(u,p,t)dW , так что g(u,p,t) является предфактором винеровского процесса dW как вы правильно говорите. Этот префактор напрямую устанавливает дисперсию винеровского процесса, в вашем случае это \sigma k x согласно вашему первому уравнению. Поэтому, если вы говорите, что для вашей задачи \sigma является дисперсией \xi, вам следует просто изменить \sigma, чтобы изменить дисперсию.