Графический способ решения уравнений с модулем | Элективный курс по алгебре (10 класс) по теме:
Конспект занятия элективных курсов по теме
«Графический способ решения уравнений с модулем»
Учитель: Акимова Марина Васильевна
Урок обобщения, систематизации знаний и применение этих знаний к решению уравнений графическим способом.
Цель:
систематизировать знания по построению графиков функций и отработать навыки решения уравнений графическим способом.
Задачи:
- систематизация теоретических знаний учащихся, связанных с понятием график функции (с модулем, тригонометрических функций)
- формирование практических навыков и умений у учащихся при построении графиков функций и решении уравнений, содержащих модуль, графическим способом;
- формирование творческого мышления;
- развитие внимательности, мобильности, коммуникативности.
Оборудование: интерактивная доска, карточки – задания, сигнальные карты.
Ход урока.
Шерлок Холмс говорил: «Самый совершенный мозг ржавеет без дела» Нам сегодня это не грозит, т.к. работы будет много!
Немногие умы гибнут от износа, по большей части они ржавеют от неупотребления.
Кристин Боуви
План урока таков:
1.Разминка (повторение)
2.Защита презентаций
3.Математический бой
4.Подведение итогов.
5.Релаксация
Класс разбит на две команды , победит та, которая наберёт большее количество баллов. Нам помогут наши гости.
Активность команды оценивается в 1 балл. Каждый верный ответ – 1 балл, неверный ответ – 0 баллов. У каждого из вас набор из карточек. Зная ответ на мой вопрос, вы поднимаете зелёную, если сомневаетесь – жёлтую, если не знаете — красную!
1.Разминка.
1)Презентация ученика «отгадай функцию»
Дан график, запиши аналитическую модель этой функции) – с помощью сигнальных карточек (красный, жёлтый, зелёный цвет).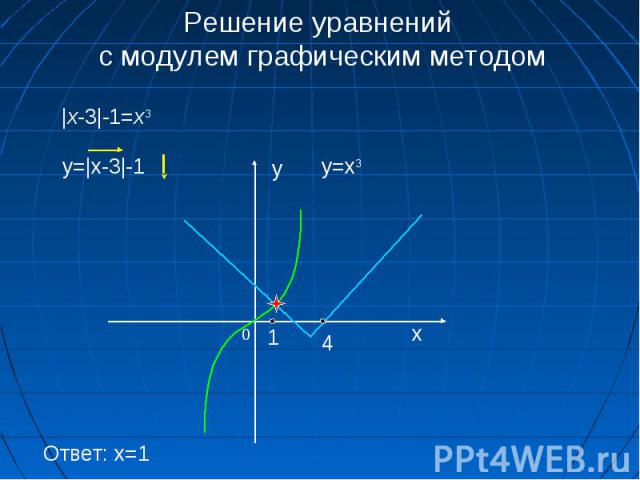
3 мин.
Молодцы! Наиболее активной была команда -…
Следующий этап – защита презентаций: вспомним правила построения графиков функций, содержащих знак модуля.
2.Защита презентаций
Презентация ученика «Построение графика функции у = f(ΙхΙ), если известен график функции у = f(х).» 3 мин.
Правило построения:
1. Построим график функции y=f(x), для х≥0
2. Достроим левую часть графика, симметричную построенной правой части относительно оси ординат.
Практические задания.
1. Построить график функции Y=|x|²-4|x|+3
2. Построить график функции у = sin|x|
3. Построить график функции y=cos|x|
4. Построить график функции y= cos|x|+2
Презентация «Построение графика функции у = Ιf(х)Ι, если известен график функции у = f(х).» 3 мин.
Правило построения:
1.Построить график y=f(x)
2.Сохранить без изменения части графика y=f(x), расположенные выше оси OX.
3.Отобразить симметрично оси OX части графика y=f(x), расположенные ниже оси OX.
Практические задания.
1).построить график функции Y=|3x+2|
2) Построить график функции Y=|X²-4x+3|
3) Построить график функции y=|cosx|
4)построить график функции y=|sinx|-4
3.Математический бой.
Итак, мы с вами вспомнили способы построения графиков функций, содержащих знак модуля. Знаем графики элементарных функций. Эти знания сейчас будем применять при решении уравнений.
-Какие способы решения уравнений с модулем вы знаете?
(алгебраический, графический, введение новой переменной)
Сегодня мы рассмотрим решение уравнений графическим способом.
-В чём суть этого способа сейчас посмотрим на следующем слайде.
А теперь приступим к работе.
Класс разбит на две команды. Каждой выдаётся задание — 6 одинаковых уравнений. Капитан распределяет между членами команды по 1 уравнению. Их надо решить максимум за 10 мин.
Реши уравнение графическим способом
а) |x-1|=2;
б) x2 = |x| ;
в) |соsx| = х2 + 1; или sin|x| = -x2
г) |x-1|= |x|-1;
д) 3|x|=4 — х2 (МФТИ, 2000г)
е)|x2-3x|=2x-4 (МГУ, 2000г)
Затем каждая команда представляет своё решение.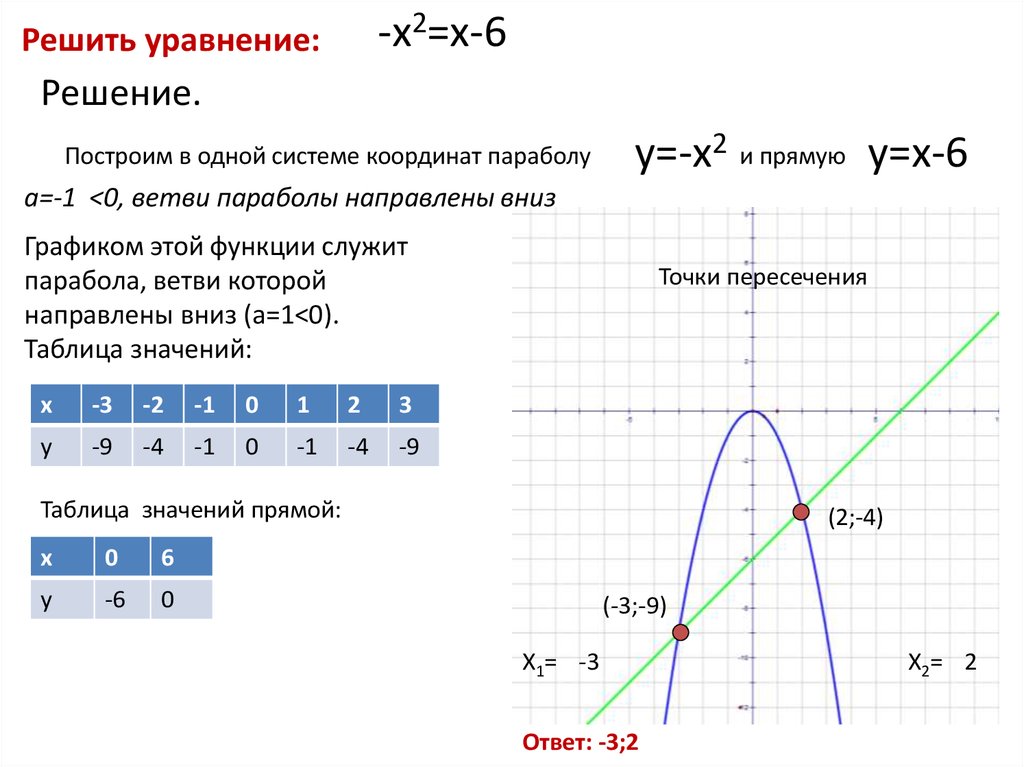
Оппоненты комментируют. (В одном уравнении координаты точек точно не определяются)10 мин.
По окончании работы учитель задаёт учащимся вопросы:
-Какие способы решения уравнений вы знаете?
-Какое преимущество графического способа решения уравнений?
-В чём недостатки решения уравнений графическим способом?
4.Подведение итогов.
а)Результаты работы каждой команды оценивает учитель , заполняя на доске таблицу.
б)Свою работу оценивают учащиеся с помощью сигнальных карточек (30 сек.)
5.Релаксация Предмет математики столь серьёзен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль)
а) Историческая справка про модуль. ( проект учащегося -2 мин.)
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц (1646-1716) тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.
б)Математики шутят – слайды – картинки
На этой позитивной ноте заканчиваем наше занятие, листочки с работами сдайте учителю.
Чтобы переварить знания, надо поглощать их с аппетитом!
«Решение уравнений с модулем».
Алгебраическое и графическое решение уравнений, содержащих модули
2017 г.
Определение.
Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна –а, если а меньше нуля:
а, если а0;
lаl= о, если а = 0;
-а, если а
Способы решения уравнений, содержащих модуль.
Решим аналитически и графически уравнение:
lх-2l=3
Аналитическое решение
1-й способ
Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т.е. х-20 или х-2=0 , тогда оно «выйдет» из-под знака модуля со знаком «плюс» и уравнение примет вид: х-2=3 . Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: -(х-2)=3 или х-2=-3 .
Таким образом, получаем, либо х-2=3, либо
х-2=-3.
Решая полученные уравнения, находим: х 1 =5, х 2 =-1. Ответ: х 1 =5, х 2 =-1.
2-й способ
Установим, при каких значениях х, модуль равен нулю: х-2=0, х=2. Получим два промежутка, на каждом из которых решим уравнение. 2 Х
Получим две смешанные системы: х2, -(х-2)=3 х-2=3 Решим каждую систему: х2 х=-1 х=5 Ответ: х 1 =-1, х 2 =5.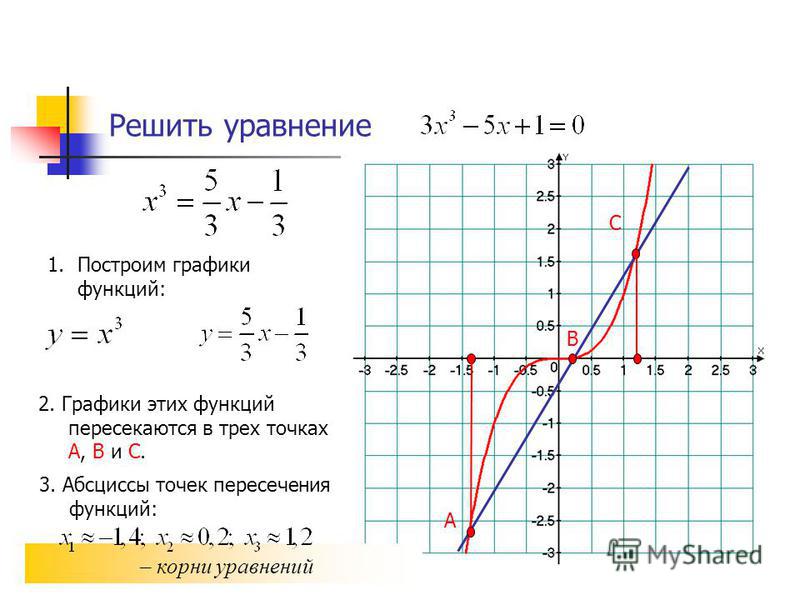
Графическое решение.
Для решения уравнения графическим способом, надо построить графики функций у=lх-2l и у=3.
у
у=3 у=lх-2l
3
2
-1 0 2 5 х
Ответ: х 1 =-1, х 2 =5.
Решим аналитически и графически уравнение
1+lхl=0,5
Аналитическое решение:
1+lхl=0,5,
lхl=0,5-1,
lхl=-0,5
Ответ: решений нет.
Графическое решение:
Преобразуем уравнение 1+ lхl=0,5.
Получим lхl=-0,5
Графиком функции у= lхl являются лучи – биссектрисы 1-го и 2-го координатных углов.
Ответ: решений нет.
Решение при помощи зависимостей между числами а и b, их модулями и квадратами этих чисел.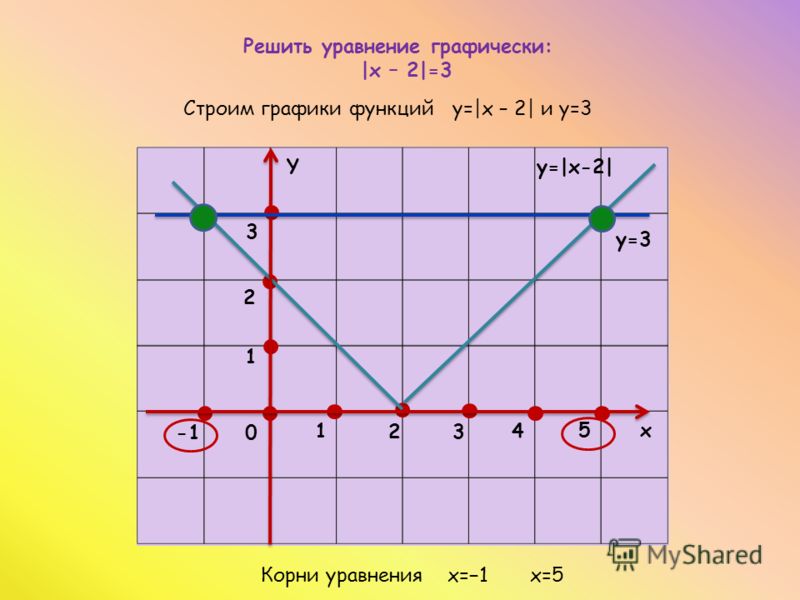
l a l = l b l a=b или a=-b = a=b или a=-b
Решим уравнение l x+1 l = l 2x-5 l двумя различными способами.
1-й способ
Учитывая первое соотношение получим:
Х+1=2х-5 х+1=-2х+5
х-2х=-5-1 х+2х=5-1
-х=-6 3х=4
х=6 х=1
Таким образом корни уравнения: х 1 =6, х 2 = 1
2-й способ В силу второго соотношения имеем = Решив это уравнение, получим: х 1 = 1 , х 2 =6
Ответ: х 1 = 1 , х 2 =6
Графики простейших функций, содержащих знак абсолютной величины
Алгебраическая сумма модулей n линейных выражений представляет собой кусочно-линейную функцию, график которой состоит из n+1 прямолинейного отрезка.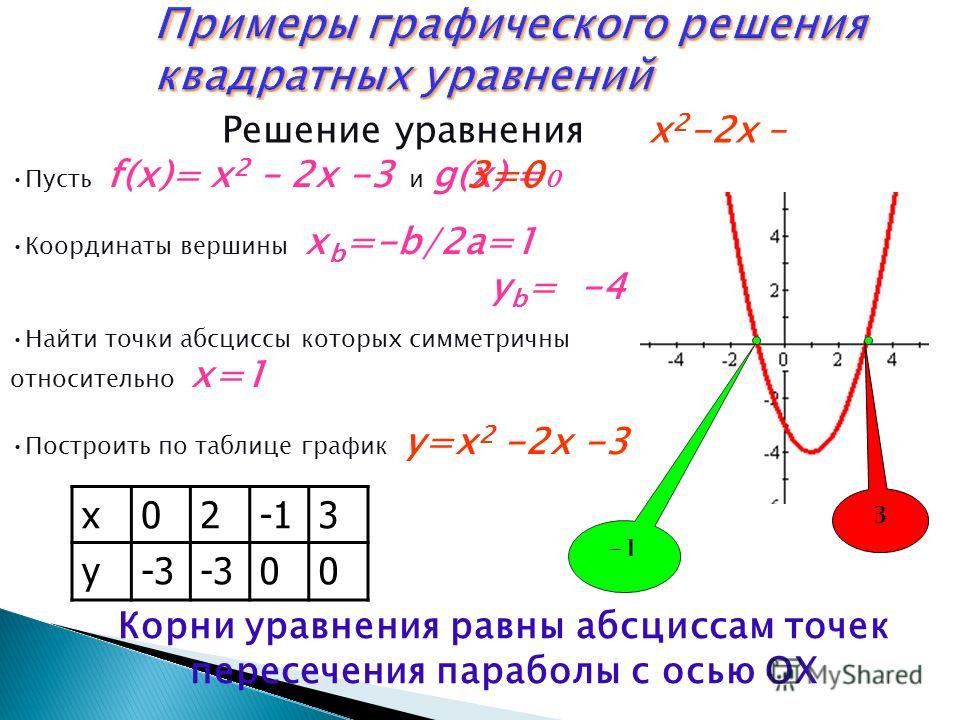
Тогда график может быть построен по n+2 точками, n из которых представляют собой корни внутримодульных выражений, ещё одна произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя – с абсциссой, большей большего из этих корней.
f(x)= l x-1 l
у
0 1 2 х
f(x)= l x-1 l + l x-2 l
у
0 1 2 3 4 х
f(x)=lx-1l+ lx-2l+ lx-3l
у
0 1 2 3 4 х
f(x)=lx-1l- lx-2l
у
0 1 2 3 4 х
конец
Уравнения абсолютного значения — MathBootCamps
Решение уравнений абсолютного значения основано на идее, что абсолютное значение представляет собой расстояние между точкой на числовой прямой и нулем. В этом уроке мы рассмотрим несколько примеров, чтобы понять, как решать эти уравнения, а также немного взглянем на эту идею расстояния применительно к решению уравнений абсолютного значения.
Содержание
- Этапы решения уравнений абсолютного значения
- Пошаговые примеры
- Уравнения с абсолютной величиной без решений или с одним решением
- Почему наш метод работает?
- Другая перспектива
реклама
Этапы решения уравнений с абсолютными значениями
При наличии уравнения с абсолютными значениями сначала необходимо выделить часть уравнения с абсолютными значениями. Затем вы напишете два уравнения, основанных на определении абсолютного значения (хотя иногда в конечном итоге будет только одно уравнение). Это звучит сложно, но это всего на один или два шага больше, чем решение типичного линейного уравнения.
Давайте попробуем выполнить эти шаги на нескольких примерах!
Примеры
В этом первом примере абсолютная часть уравнения уже изолирована, поэтому применим только второй шаг. Независимо от того, применим ли этот первый шаг или нет, у вас всегда будет ноль, одно или два решения любого уравнения абсолютного значения.
Пример
Решите уравнение:
\(|5x – 2| = 13\)
Решение
Как уже упоминалось, часть абсолютного значения уже изолирована. Поэтому мы решим два уравнения без абсолютного значения: одно, где 13 положительное, а другое, где 13 отрицательное.
Уравнение 1:
\(\begin{align}5x – 2 &= 13\\ 5x &= 15\\ x &= 3\end{align}\)
Уравнение 2:
\(\begin{align}5x – 2 &= -13\\ 5x &= -11 \\ x &= -\dfrac{11}{5}\end{align}\)
Итак, у этого уравнения есть два решения:
\(x = \bbox[border: 1px сплошной черный; padding: 2px]{3, -\dfrac{11}{5}}\)
Далее например, будет немного больше работы, так как часть уравнения с абсолютным значением не изолирована. В этой ситуации вам всегда нужно будет изолировать этот термин, прежде чем писать два уравнения, иначе вы получите неверные ответы.
Пример
Решите уравнение:
\(4 + 3|х – 5| = 16\)
Решение
Первым шагом здесь будет использование алгебры для выделения абсолютной части уравнения.
\(4 + 3|х – 5| = 16\)
Вычтите 4 с обеих сторон.
\(3|х – 5| = 12\)
Разделите обе части на 3.
\(|х – 5| = 4\)
Теперь вы можете написать и решить два уравнения, в одном из которых 4 отрицательное, а в другом 4 положительное. Не забудьте убрать символ абсолютного значения на этом шаге.
Уравнение 1:
\(\begin{align}x – 5 &= 4\\ x &= 9\end{align}\)
Уравнение 2:
\(\begin{align}x – 5 &= -4\\ x &= 1\end{align}\)
Еще раз, есть два решения уравнения:
\(x = \bbox[border: 1px сплошной черный; padding: 2px]{1, 9}\)
Уравнения с абсолютной величиной с одним решением или без решений
В обоих приведенных выше примерах было два решения, поэтому вы можете подумать, что это всегда так. Хотя это часто правильно, бывают случаи, когда есть только одно решение и даже когда его нет. Следующие два примера покажут, когда это произойдет.
Пример – одно решение
Решите уравнение:
\(6|x – 2| – 1 = -1\)
Решение
Как обычно, мы сначала выделим уравнение абсолютного значения.
\(6|х – 2| – 1 = -1\)
Добавьте по 1 с обеих сторон.
\(6|х – 2| = 0\)
Разделите обе части на 6.
\(|х – 2| = 0\)
Обычно на этом этапе мы пишем два уравнения без полос абсолютного значения, но запись 0 с положительным или отрицательным значением — это то же самое. Итак, у нас есть только одно уравнение:
\(х – 2 = 0\)
Добавление 2 к обеим сторонам дает единственное решение.
\(x = \bbox[граница: 1px сплошной черный; отступ: 2px]{2}\)
Мы более подробно рассмотрим, почему это происходит, но сначала давайте посмотрим, как вы можете остаться без решений.
Пример – нет решений
Решите уравнение:
\(|10x – 1| + 3 = -8\)
Решение
Чтобы выделить абсолютное значение, вычтите 3 из обеих частей.
\(|10х – 1| = -11\)
На этом шаге можно определить, что решений уравнения нет. Почему? Абсолютное значение любого числа положительно. Здесь у нас абсолютное значение чего-то отрицательное.
Ответ : Нет решений
Абсолютное значение любого числа всегда положительно. Используйте это, чтобы определить, когда нет решений уравнения абсолютного значения.
Обратите внимание, что в обоих примерах шаги были такими же, как и раньше. Вы всегда будете следовать этим двум шагам при решении любого уравнения абсолютного значения.
Почему это работает?
Вы можете думать об абсолютном значении любого числа как о том, насколько далеко оно от нуля на числовой прямой. Рассмотрим \(|3|\) и \(|–3|\) ниже.
Вот почему абсолютное значение всегда положительное — оно представляет расстояние. Теперь подумайте об уравнении, в котором часть абсолютного значения изолирована, например \(|5x + 1| = 2\). Если абсолютное значение равно 2, то все, что вы знаете, это то, что \(5x + 1\) — это 2 единицы от нуля на числовой прямой.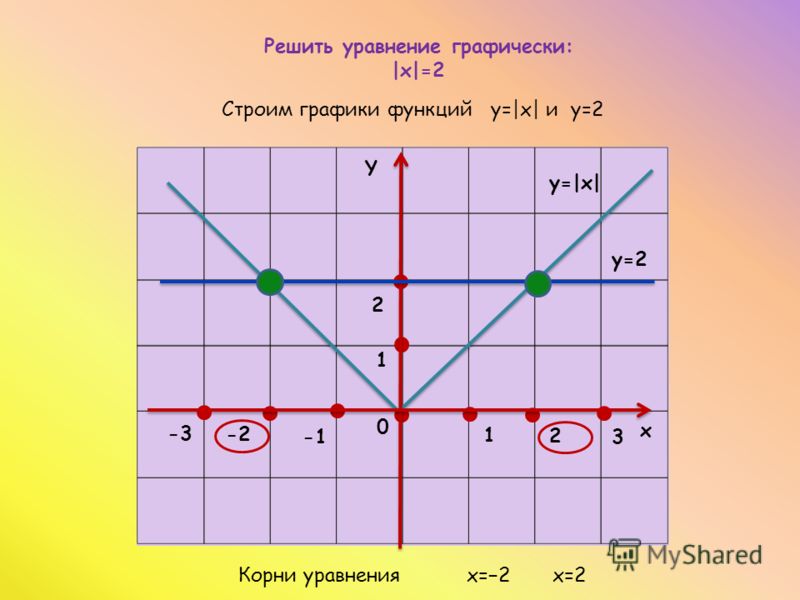
Это дает две возможности:
Вот почему мы получаем два разных уравнения. В случае только одного решения вы получите выражение абсолютного значения, равное нулю. Поскольку это означает, что расстояние от нуля на числовой прямой равно нулю, вы получите только одно уравнение.
Другая перспектива
Когда вы изучаете графики уравнений абсолютного значения, вы можете графически увидеть три случая: одно решение, отсутствие решения и два решения. Это связано с формой графика функции абсолютного значения. Это немного выходит за рамки данного урока, но на графике ниже вы можете увидеть график \(y = |x – 1|\) и \(y = 2\). Обратите внимание, что два графика пересекаются в двух точках. Они представляют два решения уравнения \(|x – 1| = 2\).
Вероятно, вы видите, как горизонтальная линия пересекает график ровно в одной точке (одно решение) или ни в одной точке (нет решений). Это будет просто изменение числа в правой части уравнения.
Сводка
Уравнения абсолютного значения всегда решаются с помощью одних и тех же шагов: выделить член абсолютного значения, а затем написать уравнения на основе определения абсолютного значения.
В итоге может получиться два решения, одно решение или ни одного решения. Чтобы поймать, когда решения нет, всегда помните, что абсолютные значения должны быть положительными, но не забывайте применять эту идею только после того, как член абсолютного значения будет выделен.
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и наборы задач.
Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), сообщающие о новинках!
Как построить график функции абсолютного значения
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по алгебре 1
10 диагностических тестов 557 практических тестов Вопрос дня Карточки Учитесь по концепции
Алгебра 1 Помощь » Функции и линии » График » Как построить график функции абсолютного значения
Какое из этих уравнений, скорее всего, будет уравнением, соответствующим приведенному выше графику?
Возможные ответы:
Правильный ответ:
Объяснение:
Это график абсолютного значения.
Его уравнение принимает вид , в котором представлено количество единиц, на которое базовый граф переводится вправо и вверх соответственно.
Поскольку график переведен на две единицы вправо и на одну единицу вниз, и , уравнение будет таким: функции
Возможные ответы:
Граф не имеет -перехватов.
Правильный ответ:
Объяснение:
Чтобы найти -перехват(ы) графика, установите и решите для .
Rewrite this as the compound equation:
or
Solve each separately:
Есть два -перехвата:
Сообщить об ошибке
Какое из этих уравнений, скорее всего, соответствует приведенному выше графику?
Возможные ответы:
Правильный ответ:
Объяснение:
Это график абсолютного значения.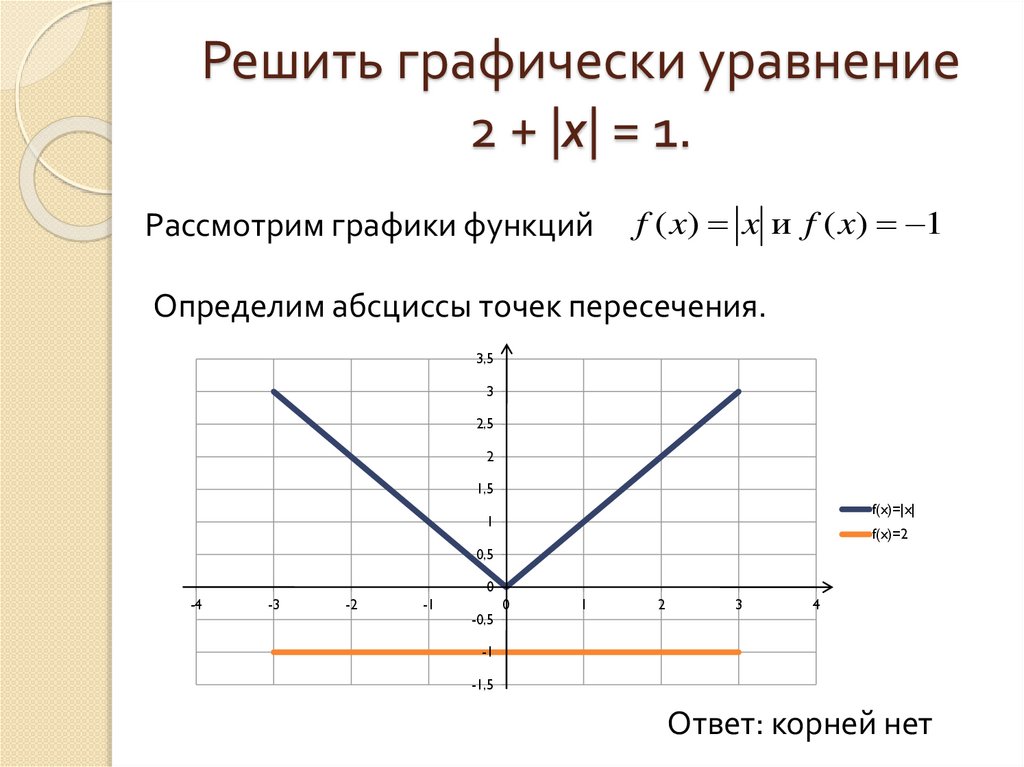
Его уравнение принимает вид , в котором представлено количество единиц, на которое базовый граф переводится вправо и вверх соответственно.
Поскольку график переводится на три единицы влево и на шесть единиц вниз, и .
Подключите эти значения в общую форму уравнения:
Упрощение:
Отчет о ошибке
Возможные ответы:
Правильный ответ:
Правильный ответ:
. Объяснение:
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Уведомление об авторских правах
Просмотреть преподавателей алгебры
Джордж
Сертифицированный преподаватель
Главный кампус государственного университета Оклахомы, бакалавр наук, химическая инженерия.