Сложение дробей — как складывать дроби 🤔
Поможем понять и полюбить математику
Начать учиться
187.3K
Тема дробей — одна из самых объемных в математике. Начиная с пятого класса и до самого выпуска из школы эти правила будут пригождаться вновь и вновь. В этой статье разберемся со сложением. Поехали!
Понятие дроби
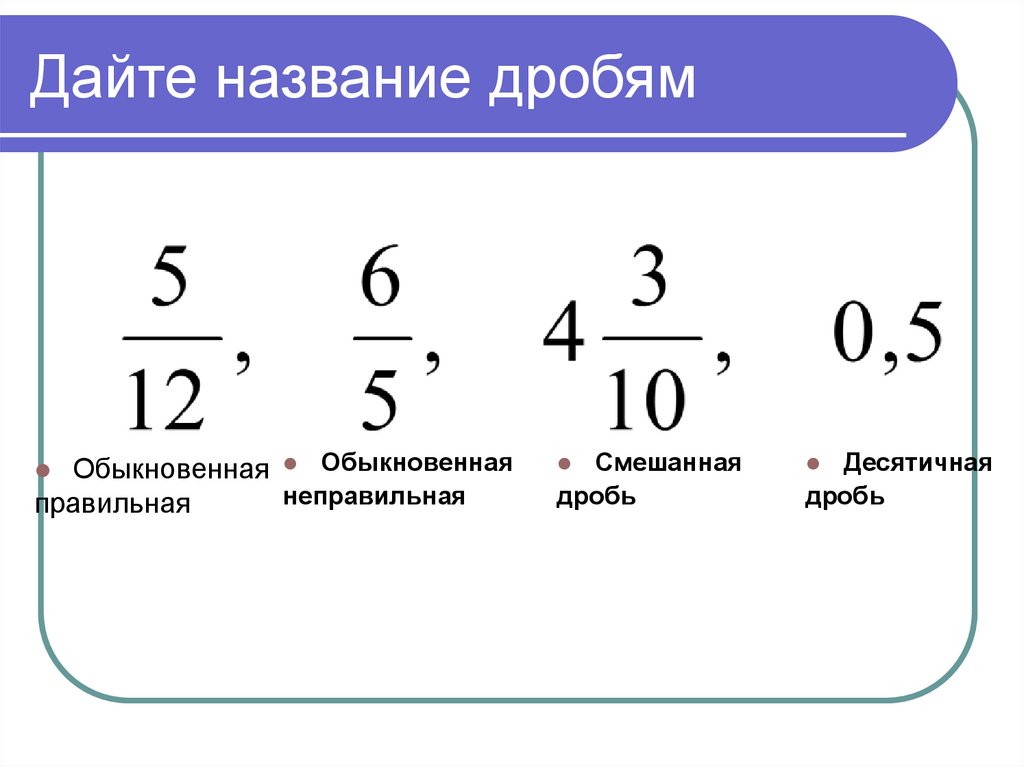
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Черта между ними означает деление.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 − 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x − y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной называют такую дробь, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1/4.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.
- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).

- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить сумму двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное знаменателей (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в произведении дают значения знаменателей складываемых дробей.
НОК (15, 18) = 3 × 2 × 3 × 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
- 90 : 15 = 6,
- 90 : 18 = 5.
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, тренируйтесь решать примеры на сложение дробей как можно чаще.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Как решать систему неравенств
К следующей статье
197. 3K
3K
Деление дробей: теория и практика
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Вычитание дробей, формулы и примеры решений
Содержание:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
- Вычитание смешанных дробей
Определение
Вычитание дробей является действием, обратным к сложению. Вычесть из одной дроби другую — это означает найти такую третью дробь, которая в сумме со второй дробью дает первую.
Вычитание дробей с одинаковыми знаменателями
Чтобы вычесть дроби с одинаковыми знаменателями, нужно от
числителя первой дроби отнять числитель второй, а
знаменатель оставить без изменений.
Пример
Задание. Найти разность дробей $\frac{10}{11}$ и $\frac{7}{11}$
$$\frac{10}{11}-\frac{7}{11}=\frac{10-7}{11}=\frac{3}{11}$$
Ответ. $\frac{10}{11}-\frac{7}{11}=\frac{3}{11}$
Вычитание дробей с разными знаменателями
Чтобы вычислить дроби с разными знаменателями, нужно вначале привести их к наименьшему общему знаменателю, а затем отнимать их как дроби с одинаковым знаменателем.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычесть дроби $\frac{2}{5}$ и $\frac{1}{3}$
Решение. Заданные дроби имеют разные знаменатели, приводим их к общему, который равен 15 (как НОК знаменателей 5 и 3),
тогда дополнительные множители соответственно к первой дроби —
$15:5=3$ , ко второй — $15:3=5$ .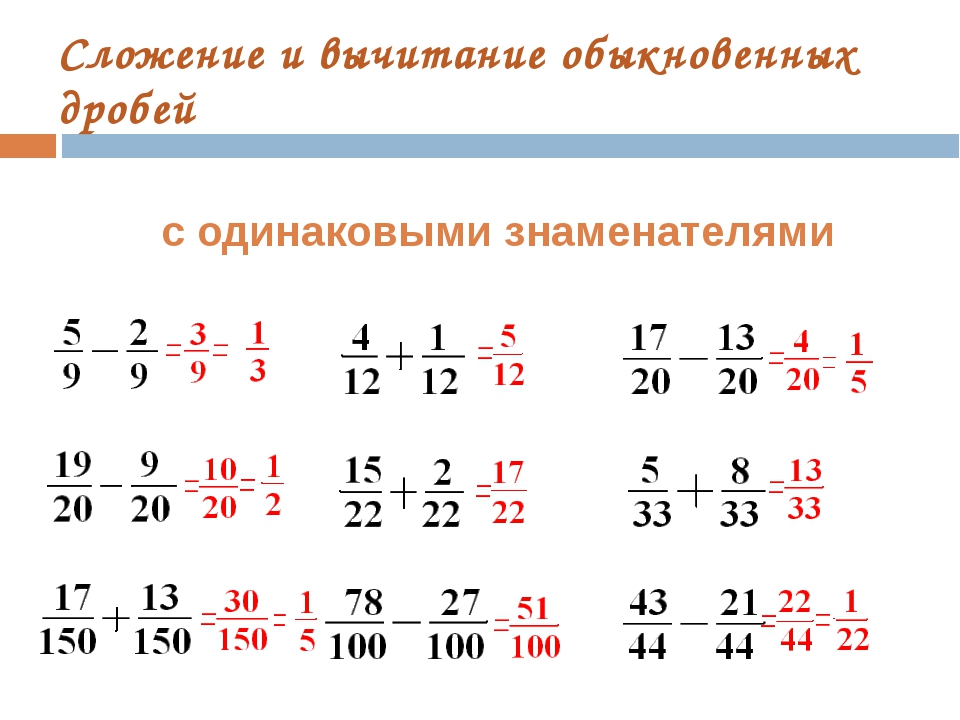 {2}}{11}-\frac{1}{22}\right)=$$
$$=4+\frac{7 \cdot 2-1 \cdot 1}{22}=4+\frac{14-1}{22}=4+\frac{13}{22}=4 \frac{13}{22}$$
{2}}{11}-\frac{1}{22}\right)=$$
$$=4+\frac{7 \cdot 2-1 \cdot 1}{22}=4+\frac{14-1}{22}=4+\frac{13}{22}=4 \frac{13}{22}$$
Ответ. $6 \frac{7}{11}-2 \frac{1}{22}=4 \frac{13}{22}$
В случае, когда дробь вычитаемого больше, чем дробь уменьшаемого, поступают следующим образом: берут одну единицу (целое) из целого числа уменьшаемого, записывают его как неправильную дробь, числитель и знаменатель которой равны между собой и равны знаменателю дробной части, и прибавляют к дробной части, далее отнимают две смешанные дроби, как описано выше.
Пример
Задание. Выполнить вычитание $5 \frac{4}{9}-1 \frac{11}{12}$
Решение. Дробь $\frac{4}{9}$ меньше ( сравнение дробей ), чем дробь $\frac{11}{12}$ (так как $4 \cdot 12 = 36 < 9 \cdot 11 = 99$ ), тогда
$$5 \frac{4}{9}-1 \frac{11}{12}=5+\frac{4}{9}-1 \frac{11}{12}=4+1+\frac{4}{9}-1 \frac{11}{12}=$$ $$=4+\frac{9}{9}+\frac{4}{9}-1 \frac{11}{12}=4 \frac{9+4}{9}-1 \frac{11}{12}=4 \frac{13}{9}-1 \frac{11}{12}=$$ $$=(4-1)+\left(\frac{13^{4}}{9}-\frac{11^{3}}{12}\right)=3+\frac{13 \cdot 4-11 \cdot 3}{36}=$$ $$=3+\frac{52-33}{36}=3+\frac{19}{36}=3 \frac{19}{36}$$
Ответ. $5 \frac{4}{9}-1 \frac{11}{12}=3 \frac{19}{36}$
$5 \frac{4}{9}-1 \frac{11}{12}=3 \frac{19}{36}$
Аналогичным образом поступают, когда надо вычесть из целого числа дробное.
Пример
Задание. Найти разность $4-3 \frac{3}{5}$
Решение. Выполним вычитание дробей по описанному выше правилу
$$4-3 \frac{3}{5}=3+1-3 \frac{3}{5}=3+\frac{5}{5}-3 \frac{3}{5}=3 \frac{5}{5}-3 \frac{3}{5}=$$ $$=(3-3)+\left(\frac{5}{5}-\frac{3}{5}\right)=0+\frac{5-3}{5}=\frac{2}{5}$$
Ответ. $4-3 \frac{3}{5}=\frac{2}{5}$
Замечание. Производить операции со смешанными числами можно и иначе: записать смешанное число в виде неправильной дроби и уже работать далее как с обыкновенными дробями.
Читать следующую тему: умножение дробей.
Пошаговое руководство — Психометрический успех
Обновлено 16 февраля 2023 г.
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби
Дроби состоят из двух чисел, одно над и одно под разделительной чертой.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числительные, то есть числа, определяющие положение, например «третье» или «четвертое».
Верхнее число дроби называется числителем и указывает на то, со сколькими частями целого мы имеем дело.
Самый простой способ определить дробь — представить себе круг, разделенный поровну на шесть частей.
Сам пирог представляет собой единое целое, а отдельные ломтики — его части. Поскольку у нас есть шесть равных частей одного целого, наш знаменатель здесь равен 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Само по себе это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о фракциях
Чтобы понять, как вычислять дроби, важно усвоить основы. Во-первых, давайте рассмотрим три разных типа дробей:
Определения и примеры дробей
Правильная дробь – Правильная дробь – это дробь, в которой числитель меньше знаменателя. 1/2, 10/15 и 85/100 — все это примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
Неправильная дробь – В неправильной дроби значение числителя больше значения знаменателя. 6/3, 25/18 и 50/20 — все это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.
Смешанные дроби – Смешанная дробь представлена целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝.
 Смешанные дроби также известны как смешанные числа.
Смешанные дроби также известны как смешанные числа.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
Эквивалентные дроби – это дроби, которые кажутся разными, но имеют одинаковое значение. Например, 2/3 равно 4/6.
Упрощенные дроби – это дроби, приведенные к наименьшей форме. По сути, низший эквивалент высшей дроби. Итак, в приведенном выше примере 2/3 — это упрощенная версия 4/6.
Обратные числа — Здесь дробь переворачивается путем размещения знаменателя над числителем. Например, обратное 2/3 равно 3/2. Обратные числа используются при делении и умножении дробей (5 ÷ 1/5 равно 5 х 5/1 или 5 х 5).
Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы рассмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
Мы рассмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
10 простых дробей и способы их решения
Ниже приведены десять примеров дробных уравнений и рекомендации по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную дробь в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число. В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
При запросе на преобразование смешанной дроби в неправильную:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и добавьте его к числителю дроби.
- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над первоначальным знаменателем. Это дает вам неправильную дробь.
Пример:
Пример вопроса
Преобразуйте 7⅘ в неправильную дробь.
2. Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Пример вопроса
Преобразование 3/10 в десятичную дробь.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
3. Как преобразовать дробь в проценты
Существует три простых способа преобразования дроби в проценты. Мы рассмотрим их все здесь, используя одну и ту же дробь 7/20.
Первый метод:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
Умножить числитель на 100, затем разделить полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35% атор и двигаться десятичная точка вашего ответа на два знака вправо:
7 ÷ 20 = 0,35
Перемещение десятичной точки дает преобразование 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак %.
Если вам нужно подготовиться к ряду различных тестов при приеме на работу и вы хотите перехитрить конкурентов, выберите Премиум-членство от JobTestPrep .
Вы получите доступ к трем пакетам PrepPack на ваш выбор из базы данных, которая охватывает всех основных поставщиков тестов и работодателей, а также специализированные пакеты профессий.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
4. Как складывать дроби
Процесс сложения дробей прост при условии, что знаменатели совпадают.
В качестве базового примера возьмем 1/6 + 3/6. В этом случае у вас равные знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, в которых меньшие числа не совпадают, вам сначала нужно найти наименьший общий знаменатель . Это наименьшее число, которое полностью делится на оба существующих знаменателя.
Это наименьшее число, которое полностью делится на оба существующих знаменателя.
Пример:
Пример вопроса
1/4 + 2/3
5. Как вычитать дроби
Как и в случае сложения, вычитание дробей легко, когда знаменатели одинаковы. Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.
Пример:
Пример Вопрос
4/7 – 3/7.
Теперь давайте посмотрим на вычитание дробей с различными знаменателями .
Пример:
Пример вопроса
4/5 – 2/3
6. Как делить дроби
Чтобы разделить одну дробь на другую, сначала нужно превратить делимую дробь в обратную, переключив знаменатель и числитель.
Пример:
Пример Вопрос
Возьмем пример 1/2 ÷ 1/5, последняя дробь как обратная 5/1.
Теперь умножьте первую дробь на обратную:
1/2 x 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Итак, 1/2 x 5/1 = 5/2
7.
 Как умножать дроби
Как умножать дробиПроцесс вычисления дробей путем умножения друг на друга прост:
- Умножить ваши числители
- Умножьте ваши знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Пример вопроса
Используя пример уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Как сделать Упростить дробь
Упростить дробь означает привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся и числитель, и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
Пример вопроса
- Множители 32: 1, 2, 4, 8, 16, 32
- Коэффициенты 48: 1, 2, 3, 4, 8, 12, 16, 24, 48
Наибольший общий множитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислять дроби величин
Когда вам представят количество и попросят вычислить дробную часть, просто разделите данное количество на знаменатель дроби, а затем умножьте это число на числитель.
Пример:
Пример вопроса
У вас есть 55 конфет, две пятых из которых вы хотите отдать соседу, чтобы он забрал его домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте это число на числитель: 11 x 2 = 22
другой, либо умножить, либо разделить обе части одной дроби на одно и то же целое число.
Если ваши ответы также являются целыми числами, то дробь сохраняет свое значение и эквивалентна.
Пример:
Пример Вопрос
Чтобы определить, эквивалентно ли 12/15 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Поскольку у вас нет целую цифру в качестве ответа здесь, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 x 3 = 12
5 x 3 = 15
По существу, если одна дробь является упрощенной версией другой, то они эквивалентны.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
Резюме
Дроби — это числовые величины, которые помогают нам измерять равные части целого.
Они бывают в виде правильных, неправильных и смешанных дробей и могут быть легко преобразованы в десятичные точки и проценты.
Методы, используемые в дробных уравнениях, различаются в зависимости от решаемой задачи, и каждый из них необходимо практиковать с осторожностью, убедившись, что вы полностью понимаете вопрос, и показывая свою работу в процессе.
Хотя поначалу они могут показаться пугающими, время, потраченное на понимание основных правил, должно помочь вам научиться с легкостью вычислять дроби.
Пошаговое руководство — Психометрический успех
Обновлено 16 февраля 2023 г.
Что такое дроби?
Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:
- Половина (1/2)
- Одна пятая (1/5)
- Две трети (2/3)
Дроби
Дроби состоят из двух чисел, одно над и одно под разделительной чертой.
Нижнее число известно как знаменатель и относится к отдельным частям целого.
Когда мы говорим о знаменателе, мы используем порядковые числительные, то есть числа, определяющие положение, например «третье» или «четвертое».
Верхнее число дроби называется числитель и указывает на то, со сколькими частями целого мы имеем дело.
Самый простой способ определить дробь — представить себе круг, разделенный поровну на шесть частей.
Сам пирог представляет собой единое целое, а отдельные кусочки являются его частями. Поскольку у нас есть шесть равных частей одного целого, наш знаменатель здесь равен 6.
Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.
Само по себе это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.
Ключевые факты о дробях
Чтобы понять, как вычислять дроби, важно разобраться с основами. Во-первых, давайте рассмотрим три разных типа дробей:
Во-первых, давайте рассмотрим три разных типа дробей:
Определения и примеры дробей
Правильная дробь – Правильная дробь – это дробь, в которой числитель меньше знаменателя. 1/2, 10/15 и 85/100 — все это примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
Неправильная дробь – В неправильной дроби значение числителя больше значения знаменателя. 6/3, 25/18 и 50/20 — все это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.
Смешанные дроби – Смешанная дробь представлена целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные дроби также известны как смешанные числа.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
Ключевые термины
Теперь, когда мы знаем различные типы дробей, давайте посмотрим на некоторые другие ключевые термины и фразы:
Эквивалентные дроби – это дроби, которые кажутся разными, но имеют одинаковое значение.
 Например, 2/3 равно 4/6.
Например, 2/3 равно 4/6.Упрощенные дроби – это дроби, приведенные к наименьшей форме. По сути, низший эквивалент высшей дроби. Итак, в приведенном выше примере 2/3 — это упрощенная версия 4/6.
Обратные числа — Здесь дробь переворачивается путем размещения знаменателя над числителем. Например, обратное 2/3 равно 3/2. Обратные числа используются при делении и умножении дробей (5 ÷ 1/5 равно 5 х 5/1 или 5 х 5).
Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы рассмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.
10 простых дробей и способы их решения
Ниже приведены десять примеров дробных уравнений и рекомендации по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.
1. Как преобразовать смешанную дробь в неправильную дробь
Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число. В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.
При запросе на преобразование смешанной дроби в неправильную:
- Сначала умножьте целое число на знаменатель дробной части.
- Возьмите полученное число и добавьте его к числителю дроби.
- Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над первоначальным знаменателем. Это дает вам неправильную дробь.
Пример:
Пример вопроса
Преобразуйте 7⅘ в неправильную дробь.
2. Как преобразовать дробь в десятичную
Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.
Метод, используемый для преобразования дроби в десятичную, представляет собой простое деление: вы просто делите числитель на знаменатель.
Пример:
Пример вопроса
Преобразование 3/10 в десятичную дробь.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
3. Как преобразовать дробь в проценты
Существует три простых способа преобразования дроби в проценты. Мы рассмотрим их все здесь, используя одну и ту же дробь 7/20.
Первый метод:
Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:
7 ÷ 20 = 0,35
Умножить числитель на 100, затем разделить полученное число на знаменатель:
7 x 100 = 700
700 ÷ 20 = 35% атор и двигаться десятичная точка вашего ответа на два знака вправо:
7 ÷ 20 = 0,35
Перемещение десятичной точки дает преобразование 35%.
При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак %.
Если вам нужно подготовиться к ряду различных тестов при приеме на работу и вы хотите перехитрить конкурентов, выберите Премиум-членство от JobTestPrep .
Вы получите доступ к трем пакетам PrepPack на ваш выбор из базы данных, которая охватывает всех основных поставщиков тестов и работодателей, а также специализированные пакеты профессий.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
4. Как складывать дроби
Процесс сложения дробей прост при условии, что знаменатели совпадают.
В качестве базового примера возьмем 1/6 + 3/6. В этом случае у вас равные знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:
1 + 3 = 4
Итак, 1/6 + 3/6 = 4/6
При сложении дробей, в которых меньшие числа не совпадают, вам сначала нужно найти наименьший общий знаменатель . Это наименьшее число, которое полностью делится на оба существующих знаменателя.
Пример:
Пример вопроса
1/4 + 2/3
5. Как вычитать дроби
Как и в случае сложения, вычитание дробей легко, когда знаменатели одинаковы. Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.
Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.
Пример:
Пример Вопрос
4/7 – 3/7.
Теперь давайте посмотрим на вычитание дробей с различными знаменателями .
Пример:
Пример вопроса
4/5 – 2/3
6. Как делить дроби
Чтобы разделить одну дробь на другую, сначала нужно превратить делимую дробь в обратную, переключив знаменатель и числитель.
Пример:
Пример Вопрос
Возьмем пример 1/2 ÷ 1/5, последняя дробь как обратная 5/1.
Теперь умножьте первую дробь на обратную:
1/2 x 5/1
Для этого умножьте числители и знаменатели:
1 x 5 = 5 (числители)
2 x 1 = 2 (знаменатели)
Итак, 1/2 x 5/1 = 5/2
7. Как умножать дроби
Процесс вычисления дробей путем умножения друг на друга прост:
- Умножить ваши числители
- Умножьте ваши знаменатели
- Напишите новый числитель над новым знаменателем
Пример:
Пример вопроса
Используя пример уравнения 1/2 x 1/6:
1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)
Как сделать Упростить дробь
Упростить дробь означает привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.
По сути, найти наименьшую возможную эквивалентную дробь.
Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся и числитель, и знаменатель.
Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:
Пример вопроса
- Множители 32: 1, 2, 4, 8, 16, 32
- Коэффициенты 48: 1, 2, 3, 4, 8, 12, 16, 24, 48
Наибольший общий множитель здесь: 16
Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:
32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)
Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ до наименьшей возможной формы.
9. Как вычислять дроби величин
Когда вам представят количество и попросят вычислить дробную часть, просто разделите данное количество на знаменатель дроби, а затем умножьте это число на числитель.
Пример:
Пример вопроса
У вас есть 55 конфет, две пятых из которых вы хотите отдать соседу, чтобы он забрал его домой. Сколько конфет она возьмет?
Разделите полученную сумму на знаменатель дроби: 55 ÷ 5 = 11
Умножьте это число на числитель: 11 x 2 = 22
другой, либо умножить, либо разделить обе части одной дроби на одно и то же целое число.
Если ваши ответы также являются целыми числами, то дробь сохраняет свое значение и эквивалентна.
Пример:
Пример Вопрос
Чтобы определить, эквивалентно ли 12/15 4/5, разделите 12 и 15 на целое число:
12 ÷ 2 = 6
15 ÷ 2 = 7,5
Поскольку у вас нет целую цифру в качестве ответа здесь, перейдите к следующему основному числу:
12 ÷ 3 = 4
15 ÷ 3 = 5
Вы также можете сделать это в обратном порядке, умножив обе части младшей дроби:
4 x 3 = 12
5 x 3 = 15
По существу, если одна дробь является упрощенной версией другой, то они эквивалентны.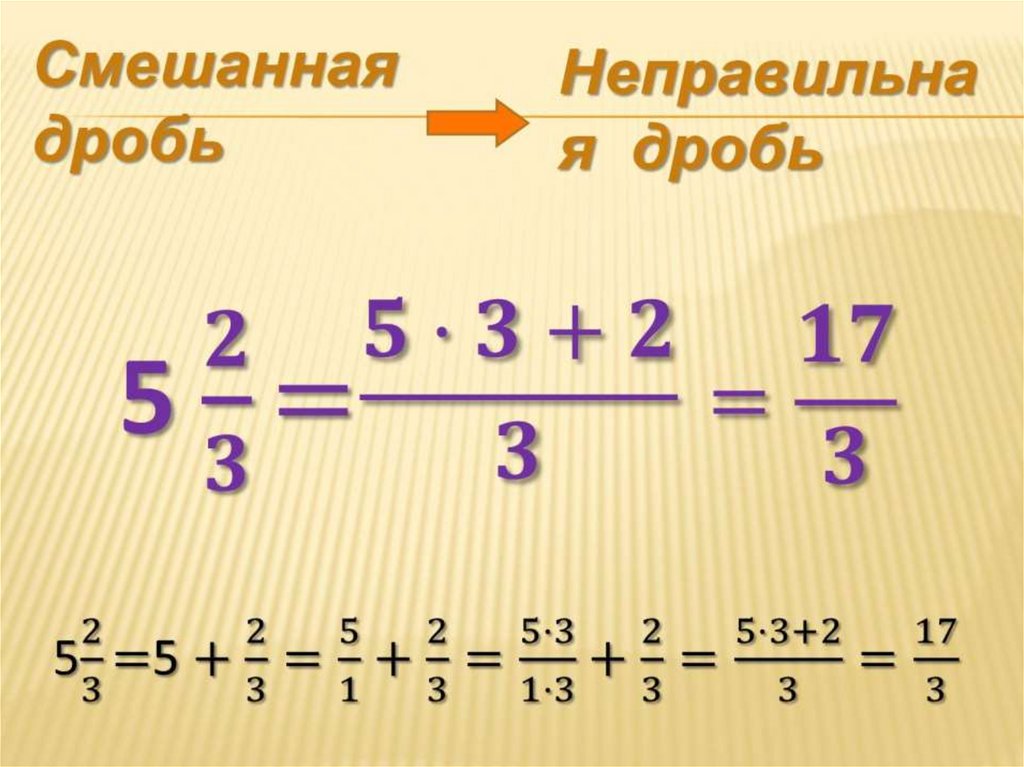


 Смешанные дроби также известны как смешанные числа.
Смешанные дроби также известны как смешанные числа. Например, 2/3 равно 4/6.
Например, 2/3 равно 4/6.