Дополнительный материал
7.
8.
9.
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Натуральный логарифм Логарифм степени Логарифм частного, разность логарифмов Логарифм произведения, сумма логарифмов
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Логарифм числа.
 Свойство логарифмов
Свойство логарифмовМуниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа рабочего поселка Мухен района имени лазо хабаровского края»
Методическая разработка
урока математики в 10 классе
по теме
«Логарифм числа. Свойства логарифмов»
Кушнарь Лариса Александровна
учитель математики I категории
МБОУ СОШ р.п. Мухен
2018г
Аннотация
Методическая разработка урока математики
«Логарифм числа и его свойства» с применением технологии проблемного обучения. Данная разработка предназначена для изучения темы «Логарифм числа и его
свойства» для учащихся10-11 классов общеобразовательных учреждений. Материал
будет полезен учителям математики, преподающих математику в старших классах.
Урок построен с применением методов проблемного обучения.
Данная разработка предназначена для изучения темы «Логарифм числа и его
свойства» для учащихся10-11 классов общеобразовательных учреждений. Материал
будет полезен учителям математики, преподающих математику в старших классах.
Урок построен с применением методов проблемного обучения.
Для того, чтобы установить связи преемственности в изучении нового материала с изученным, включить новые знания в систему ранее усвоенных, повторяется тема «Показательная функция», которая подготавливает детей к восприятию нового материала.
Исходя из целей
урока ,были спланированы следующие моменты: исторический материал и связь с
окружающим миром – для развития интереса к предмету; повторение – как
теоретическая основа ранее изученного материала; изучение нового материала
базируется на определении и свойствах показательной функции; усвоение нового
материала идет самостоятельно, через создание проблемной ситуации; задания
дифференцированные, составленные для групп учащихся, что способствует
созданию ситуации выбора, успеха, сотрудничества друг с другом, учебной
самостоятельности, для учащихся с различными каналами восприятия использованы
разнообразные задания и иллюстративный материал; группы формируются по уровню
развития и способностей, используя диагностику учебных возможностей.
Цели урока: научиться находить логарифм по основанию а числа, представленного в виде степени с основанием а, записывать числа в виде логарифма с основанием а, упрощать выражения пользуясь основными логарифмическими тождествами, а также логарифмировать выражения по указанному основанию.
Задачи урока:
Образовательные: повторить знания, полученные на предыдущих занятиях по теме «Показательная функция»; познакомить с понятием логарифма и его свойствами; установить связи преемственности в изучении нового материала с изученным, включить новые знания в систему ранее усвоенных; закрепить изученный на этом уроке материал «Логарифмы и их свойства».
Воспитательные: воспитывать стремление к достижению цели, умение доводить дело до конца; воспитывать личную ответственность за порученное дело, добросовестное выполнение своих обязанностей; воспитывать дисциплинированность, организованность, общественную активность; формировать культурные потребности;
Развивающие: развивать умственные силы и познавательные
способности учащихся; развивать потребность в образовании,
самообразовании, постоянном пополнении своих знаний, расширении общего
кругозора; развивать творческое мышление.
Обучающийся должен знать: обозначение определение логарифма числа, основное логарифмическое тождество; три основных свойства логарифма.
Обучающийся должен уметь: выполнять преобразования выражений, содержащих логарифмы; находить логарифм числа, применять свойства логарифмов при логарифмировании.
Тип урока: комбинированный, урок изучения нового учебного материала. Форма проведения урока: фронтальная , работа в парах.
Основные методы обучения: фронтальный, проблемный, частично-поисковый, наглядно-иллюстративный, информационно-коммуникационная технология.
Оборудование: компьютер, проектор, презентация к уроку, раздаточный материал.
Структура урока:
1Организационный момент.
2Актуализация опорных знаний.
3Мотивация учебной деятельности, сообщение темы, цели урока.
4. Изучение нового материала.
5. Физминутка для глаз.
6.Э тап закрепления знаний.
7.
8.Домашнее задание.
9.Рефлексия.
Ход урока.
1. Организационный момент (приветствие; проверка отсутствующих; проверка готовности к уроку)
Французский писатель Анатоль Франс (1844-1924 гг) заметил: «Что учиться можно только весело….Чтобы переварить знания, надо поглощать их с аппетитом».
Последуем совету писателя: будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они скоро нам понадобятся для успешной сдачи экзамена.
2. Актуализация опорных знаний.
Проводится фронтальный опрос (обучающиеся работают в парах): математическое лото по теме «Решение показательных уравнений»
(приложение 1)
3. Мотивация учебной деятельности, сообщение темы, цели урока
Мотивация может быть основана на необходимости решения уравнения вида
ax=b при условии, что правая часть не представима в виде степени.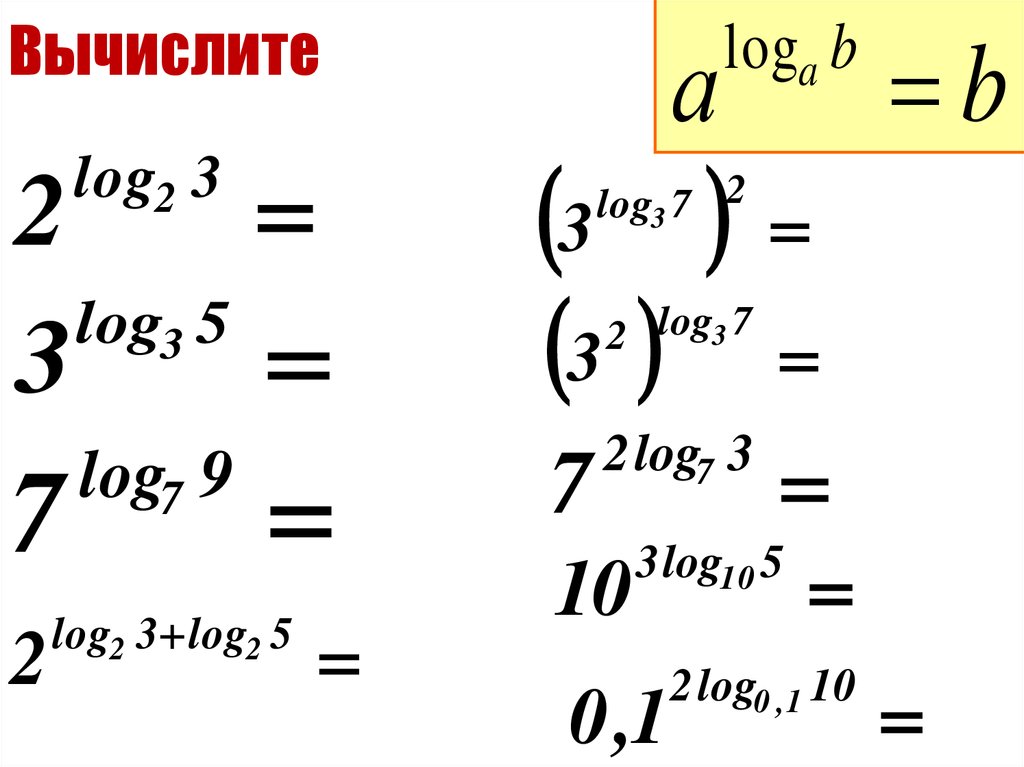 Такие уравнения могут быть получены при решении
следующих задач:
Такие уравнения могут быть получены при решении
следующих задач:1. Однолетнее растение дает 100 семян, из которых на следующий год прорастает половина. Через сколько лет прорастут 10000 семян?
2. Банк начисляет на вклад 10% в год. Через какое время вклад вырастет в 10 раз?
Математические модели данных задач имеют следующий вид: 50x=10000; 1,1x = 10
Проблема, которую предстоит решить, можно сформулировать следующим образом: «Как с достаточной степенью точности решить уравнение вида ax=b?».
Тема нашего урока «Логарифм числа. Свойства логарифмов». Почему обращение к данной теме является актуальным на этапе итогового повторения?
Возможные ответы:( логарифмы широко представлены в материалах ЕГЭ, знания окажутся востребованы для дальнейшего обучения в высших учебных заведениях).
Давайте вместе с вами определим цели нашего урока.
Цель урока: научиться
находить логарифм по основанию а числа, представленного в виде
степени с основанием а, записывать числа в виде логарифма с
основанием а, упрощать выражения пользуясь основными логарифмическими
тождествами, а также логарифмировать выражения по указанному основанию.
4. Изучение нового материала
Эвристическая беседа с использованием наглядных материалов :
Решаем показательное уравнение 2x =8 . Так как 8 = 23, то 2х = 23. Уравнение имеет единственное решение х=3. А теперь рассмотрим аналогичное уравнение 2x =6.
Учащиеся с преподавателем ищут ответы на следующие вопросы:
— Что представляет собой левая часть уравнения?
— Что представляет собой правая часть уравнения?
— Какие способы решения уравнений известны?
— В чем заключается графический способ решения уравнения?
Применяя графический способ решения, по чертежу устанавливаем, что уравнение так же имеет единственное решение (по чертежу видим, что он заключен в промежутке от 2 до 3). Однако в отличие от предыдущего уравнения это решение является числом иррациональным. Поэтому для обозначения такого корня вводится новое понятие и новый символ – логарифм.
Очень часто приходится решать подобную задачу: известно,
что ax=b. Необходимо найти показатель степени х, то есть решать задачу, обратную возведению
числа в степень. При нахождении этого показателя степени х и возникает понятие
логарифма числа b по основанию а. Обозначается x
= logab. Даем определение логарифма.
Необходимо найти показатель степени х, то есть решать задачу, обратную возведению
числа в степень. При нахождении этого показателя степени х и возникает понятие
логарифма числа b по основанию а. Обозначается x
= logab. Даем определение логарифма.
Далее, анализируя общий вид уравнения ax=b, устанавливаем, каким условиям должны удовлетворять параметры а и b?
Определение: Логарифмом числа по основанию называется показатель степени, в которую надо возвести основание а, чтобы получить число b. Это число обозначается символом logab .
Из определения следует основное логарифмическое тождество .
Это равенство называется основным логарифмическим тождеством.
Операцию нахождения логарифма числа называют логарифмированием.
Предлагается обучающимся прочитать определение логарифма вслух и про себя. Далее предлагается вернуться к проблемной ситуации и решить задачи, используя понятие логарифма.
Объяснение свойств логарифмов
Рассмотрим основные
свойства логарифмов.
1.
Пример:
2.
Пример:
3.
Пример:
4. Логарифм произведения положительных чисел равен сумме логарифмов множителей.
где а > 0, а≠ 0, b>0,c>0.
На примере посмотрим ,как применяется данное свойство.
1).
2)
Рассмотрим свойство:
5. Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя.
, где a>0,a ≠ 0, b>0, c> 0.
Примеры:
1) .
6) .
6. Логарифм степени с положительным основанием равен показателю степени, умноженному на логарифм основания.
, где a > 0, a ≠ 0, b >0 ,
5. Физминутка для глаз.
6. Этап закрепления знаний.(Решение задач с целью усвоения понятия логарифма)
1)Установите соответствие между первым и вторым столбцами, во 2 столбике есть ошибки, которые нужно устранить
Проверка по образцу. За каждый правильный ответ 1 балл.
За каждый правильный ответ 1 балл.
Ответы.
2)Историческая справка.Вычисление логарифмов.(заранее подготовленное сообщение одного из учащихся)
Более 300 лет логарифмы использовались для облегчения вычислений. Их основное достоинство — способность сводить умножение к сложению. Были составлены обширные таблицы логарифмов чисел, с помощью которых можно легко переходить от чисел к их логарифмам и обратно.
Все таблицы логарифмов до 1950 г. являлись перепечаткой или сокращением таблиц Генри Бриггса (1561 —1630)
За 300 лет не нашлось никого, кто повторил бы эту работу..
Любопытно, что немного раньше Бриггса таблицу натуральных логарифмов составил Джон Непер (1550—1617)
Изобретатель первых логарифмических таблиц, Непер, так говорит о своих побуждениях : « Я старался, насколько мог и умел, отделяться от трудности и скуки вычислений, докучность которых отпугивает весьма многих от изучения математики»
В самом деле,
логарифмы чрезвычайно облегчают и ускоряют вычисления, не говоря уже о том,
что они дают возможность производить такие операции, выполнение которых
без их помощи очень затруднительно (извлечение корня любой степени).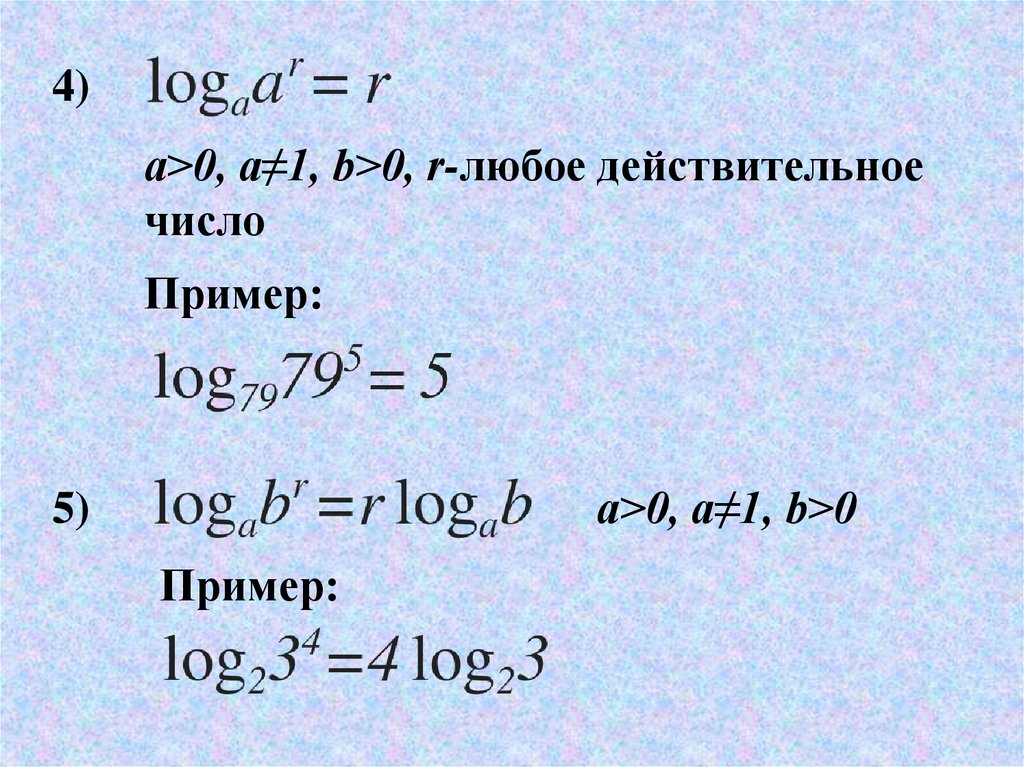
Не без основания писал Лаплас, что «изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов». Великий математик говорит об астрономах, так как им приходится делать особенно сложные и утомительные вычисления. Но слова его с полным правом могут быть отнесены ко всем вообще, кому приходится иметь дело с числовыми выкладками.
3) Записать следующие равенства в виде показательных:
При выполнении задания мы встретились с логарифмом, имеющим основанием число 10. Такие логарифмы называются десятичными и имеют специальное обозначение lg. Например: lg100 = 2, .
4) Записать числа -3, -1, 0, 1, 3 в виде логарифма с основанием 2.
5) Найдите х:
Решение задач с целью усвоения свойств логарифма.
Найдите значение выражения:
Для тех, кто быстро и верно решает, подготовлены дополнительные задания на карточках:
Вычислите:
6) Это интересно.
Этой головоломкой развлекались математики в Одессе. Предлагается задача: любое данное число записать с помощью трех двоек и математических символов.
Решение. Возьмем , например, число , так как
Аналогично,
7.Итоги урока.
· Что называется логарифмом?
· Что называется логарифмированием?
· Чему равен логарифм произведения?
· Назовите формулу перехода от логарифма по одному основанию к логарифму по другому основанию.
· Чему равен логарифм частного?
· Чему равен логарифм степени?
· Назовите основное логарифмическое тождество.
· Что называется десятичным логарифмом?
· Объясните смысл формулы .
8. Домашнее задание
1. Выучить определение логарифма и его свойства. По учебнику выполнить: Глава VII, стр.232 № 14 (1,3,5), стр. 235 № 32(1,3).
2. Подготовить
исторический материал о понятии логарифма, о применении логарифмов в науке и
практике (по желанию).
7. Рефлексия
“Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
а математика способна достичь всех этих целей”.
Так сказал американский математик Морис Клайн.
Ответьте на вопросы:
- Что понравилось, запомнилось на уроке?
- Достигли ли вы поставленной цели?
- Над чем еще нужно поработать?
Выводы по уроку:
Результаты проведенного урока позволяют сделать вывод о правильности
выбора целей, определения задач урока и формы его проведения. В ходе урока были
изучены и закреплены: определение логарифма, свойства логарифмов. Обсуждение
выбора методов решения способствовало развитию у учащихся математического вкуса
и интуиции; формированию логики мышления. Форма проведения урока
способствовала развитию культуры учебных взаимоотношений между учениками и
учителем. Обсуждения решения заставляли учащихся осознать необходимость умения
вести дискуссию и излагать свои идеи, грамотно ссылаясь на математические факты
и понятия.
Обсуждения решения заставляли учащихся осознать необходимость умения
вести дискуссию и излагать свои идеи, грамотно ссылаясь на математические факты
и понятия.
Используемые ресурсы:
http://pedsovet.su/
http://festival.1september.ru/
http://nsportal.ru/
1. Основные логарифмы
Основы акустики
1. Основные логарифмы
2. Шкала в белах и децибелах
3. Интенсивность звука и давление
4. Закон обратных квадратов
5. Добавление интенсивности звука
6. Уровень спектра
7. Объединение звуковой энергии во времени
8. Определения
1. Основные логарифмы
Цели
Понять, что такое логарифмическая шкала и основные правила использования логов.
1. Что такое логарифм
Если мы подумаем о числе, скажем, 10 000 000, то мы можем представить это номер несколькими различными способами — мы можем использовать стандартный формат, поскольку мы только что сделали. В качестве альтернативы мы могли бы использовать научную запись 1,0 x 10 7 , что просто означает 1,0, умноженное на 10 миллионов. Преимущество научное представление состоит в том, что мы можем представлять очень большие или очень маленькие числа, не беспокоясь о неправильном подсчете количества нулей или десятичные знаки. Именно так большинство калькуляторов представляют очень большие или очень маленькие цифры.
Другой способ выразить то же число, сказав, что это то же самое, что и 10 возводится в степень определенного значения. Для этого примера 10000000 = 10 7 . В этом примере 10 называется основанием, а 7 — показателем степени.
Этот пример относительно прост, но мы можем расширить его, чтобы использовать показатели степени, которые не обязательно являются целыми числами, например. 0,005 = 10 -2,301 [ используйте свой калькулятор для продемонстрировать , что дело обстоит именно так ]. Здесь у нас отрицательный показатель степени, потому что наше число меньше 1,0 (но > 0 — см. ниже). [примечание, 1 = 1 0 ].
0,005 = 10 -2,301 [ используйте свой калькулятор для продемонстрировать , что дело обстоит именно так ]. Здесь у нас отрицательный показатель степени, потому что наше число меньше 1,0 (но > 0 — см. ниже). [примечание, 1 = 1 0 ].
А логарифм — это просто значение показателя степени само по себе. Таким образом, для например, логарифм (по основанию 10) 0,005 равен -2,301. Точно так же логарифм 10 миллионов равен 7. Обычно мы выражаем логарифмы числа x в виде журнала ( x ), который относится к «логарифму по основанию 10» — это кнопка «лог» на вашем калькуляторе. Вы также можете увидеть log 10 (x) , что означает то же самое, но явно указывает, что такое база.
Активность
Используйте свой калькулятор, чтобы найти логарифм (по основанию 10) следующего:
- 2,0
- 20,0
- 200,0
- -2,0
- -20,0
Видите ли вы появление закономерности? Как вы думаете, почему это так?
2. Антилоги
Антилоги
если у нас есть логарифмическое значение (т.е. показатель степени), мы можем взять обратный процесс, просто возведя 10 в степень этого экспонента. Так, например, если log 10 (x) = -2,301 , то x = 10 -2,301 = 0,005
Итак, в общем: если y = log 10 (x) , то x = 10 y
3. Умножение, деление и логарифмы
Если у нас есть простой пример, где мы хотим умножить 10000 на 100 мы получаем 1000 000. Если мы запишем эти три в экспоненциальной форме, мы получим:
| 10 4 x 10 2 = 10 6 |
то есть Чтобы умножить эти числа, нам просто нужно сложить показатели. Мы можем расширить это, чтобы показать, как мы можем использовать логарифмы в умножение двух чисел.
Предположим, у нас есть два числа A и B, мы можем представить их оба в экспоненциальной форме: A=10 log(A) и B=10 log(B) , если мы хотим умножить эти два:
| A x B = 10 log(A) x 10 log(B) = 10 log(A)+log(B) |
В более общем виде мы можем написать:
| журнал (A x B) = журнал (A) + журнал (B) | (1. 1) 1) |
Мы можем следовать аналогичным аргументам, если хотим разделить два числа A и B:
Или в более общем плане:
| (1.2) |
Активность
1. С помощью калькулятора покажите, что log10(2 + 5) = log 10 (2) + log 10 (5) = 1
2. Теперь используйте кнопку антилогарифма на вашем калькуляторе (обычно shift+log), чтобы показать, что антилогарифм 1 равен 10. Как вы думаете, почему это так — подсказка, что такое 2 x 5?
4. Зачем нужны логарифмы?
Есть несколько причин, по которым мы используем логарифмы в аудиологии/акустике. Вот несколько из них:
- логарифмы позволяют относительно легко оперировать с очень большими или маленькими числами
- ухо реагирует на изменение интенсивности звука нелинейным образом — просто заметные изменения интенсивности звука для громких звуков включают в себя много большие изменения звукового давления, чем для тихих звуков (т.
 е. восприятие интенсивности звука больше похожа на логарифмическую шкалу)
е. восприятие интенсивности звука больше похожа на логарифмическую шкалу) - восприятие звуковой частоты (высоты) происходит в логарифмическом масштабе — например увеличение высоты тона на одну октаву влечет за собой двукратное увеличение частота.
5. Основные правила логарифмирования
Помимо правил умножения и деления, приведенных выше, следует помнить и другие важные правила:
- Логарифм 1 равен нулю.
- Логарифмирование 0 невозможно — невозможно возвести 10 в степень значения и получить 0.
- Точно так же нельзя логарифмировать отрицательные числа.
- Логарифм числа меньше единицы (но > 0) отрицателен, а логарифм числа больше 1 положителен.
- Сложение двух значений НЕ равносильно сложению их логарифмов.
6. Некоторые полезные значения
Хотя логарифмы можно легко получить на калькуляторах, есть различные значения, которые полезно запомнить:
| Номер | Журнал 10 (Номер) |
| 1,0 | 0 |
| 2,0 | 0,3010 |
| 3,0 | 0,4771 |
| 4,0 | 0,6021 |
| 10 | 1,0 |
Обратите внимание: если мы знаем, что log(2,0) = 0,3010, мы можем легко получить log(20), поскольку 2=10×2, и, таким образом, мы можем использовать уравнение (1. 1):
1):
| логарифм 10 (20) = логарифм 10 (10 x 2) = логарифм 10 (10) + логарифм 10 (2) = 1+ 0,3010 = 1,3010 |
Мы можем использовать тот же метод, чтобы найти логарифм 0,2, попробуйте сами.
« Предыдущая | Далее »
unix — Как рассчитать логарифм числа с помощью bc?
спросил
Изменено 8 месяцев назад
Просмотрено 44к раз
Я впервые использую bc. Я хочу рассчитать журнал (база 10) числа. Как мне это?
- unix
- до н.э.
2
Вызвать bc с опцией -l (чтобы включить математическую библиотеку) примерно так:
$ echo 'l(100)/l(10)' | до н.э. -l 2.000000000000000000000
Используйте функцию l , которая представляет собой натуральный логарифм. Возьмите логарифм интересующего вас числа и разделите на натуральный логарифм 10.
6
логарифм x по основанию b можно вычислить по любой логарифмической функции по произвольному основанию k — это действительно здорово!
log_b(x) = log_k(x) / log_k(b)
напр.
log_b(x) = ln(x) / ln(b)
если b=10:
log_10(x) = ln(x) / ln(10)
и -l в bc включает математическую библиотеку
, вот почему это работает:
# bc -l л(100) / л(10) 2.000000000000000000000
1
Если запустить bc с ключом -l , то появится функция l() , которая вычисляет натуральный логарифм своего аргумента.
bc напрямую не дает логарифм, кроме как за исключением или другими способами, используя bc, мы можем вычислить только ln(x). Итак, чтобы получить любой другой логарифм с основанием, разумно запомнить некоторые тождества. Базовый —
Итак, чтобы получить любой другой логарифм с основанием, разумно запомнить некоторые тождества. Базовый —
логарифмическая база 10 (x) = логарифмическая база e (x) / логарифмическая база e (10)
Вот несколько примеров различных базовых логарифмов —
totan@Home-Computer ~ $ bc -l до н.э. 1.06.95 Авторское право 1991–1994, 1997, 1998, 2000, 2004, 2006 Free Software Foundation, Inc. Это бесплатное программное обеспечение АБСОЛЮТНО БЕЗ ГАРАНТИЙ. Для получения подробной информации введите «гарантия». л(8)/л(2) 3.000000000000000000002 л(1000)/л(10) 3.000000000000000000000 л(100000)/л(100) 2,500000000000000000000 л(100000)/л(10) 5.000000000000000000001 л(81)/л(3) 4.000000000000000000001 л(64)/л(4) 3.000000000000000000000 покидать() totan@Домашний-Компьютер ~ $
Надеюсь, это поможет вам.
1
бк-л л(____)
(заполните поле своим номером)
Я нашел учебники по адресу:
http://unix-simple.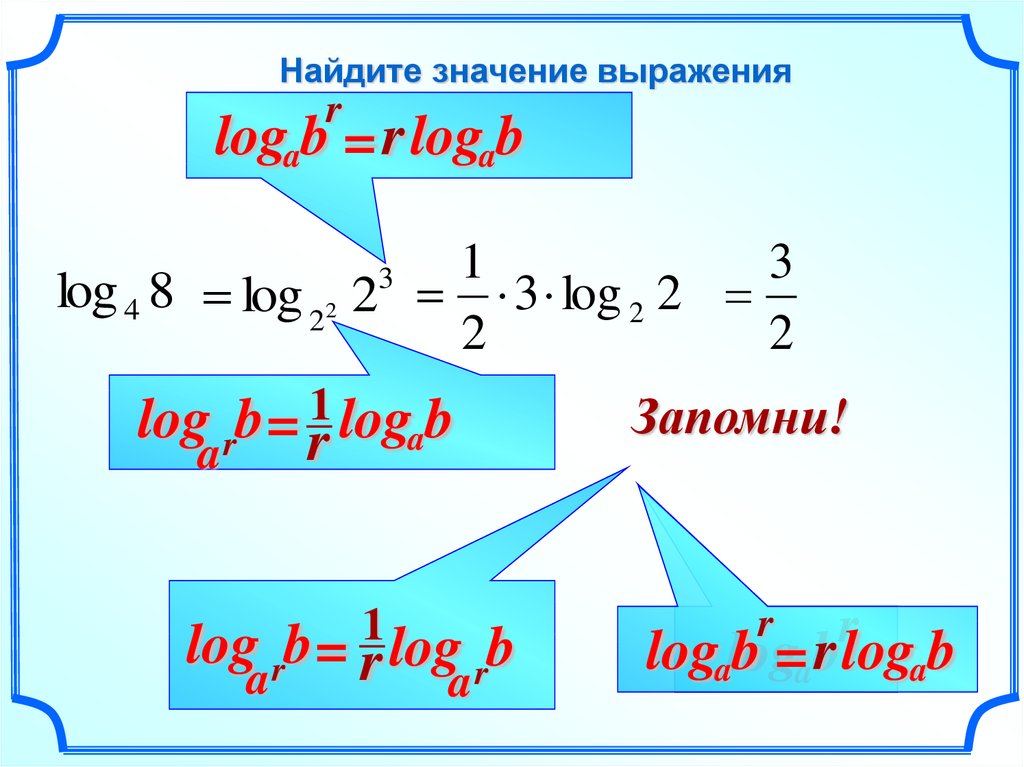 blogspot.com/2006/10/unix-basic-calculator.html
blogspot.com/2006/10/unix-basic-calculator.html
и
http ://unix-simple.blogspot.com/2006/10/taking-roots-with-unix-basic.html
3
Плакат специально запрошенный журнал 10.
У меня bc 1.06.95 на Ubuntu 12.10. «l(x)» в этой версии БК не основание 10. Это натуральный логарифм (основание e). Это подтверждается здесь, и БК имеет с некоторых пор работал так:
http://linux.about.com/od/commands/l/blcmdl1_bc.htm
Я подозреваю, что вам нужно, чтобы лог базы 10 работал, это расширение BC:
http: //x-bc.sourceforge.net/extensions_bc.html
Не уверен, что это правильный способ установки, и получил ошибки при попытке опубликовать его здесь.
Доминик-Люк Уэбб
1
Как указывали многие другие, bc , вызываемый с параметром -l , будет включать стандартные математические библиотеки и предлагать их функциональные возможности через расширения.

 е. восприятие интенсивности звука больше похожа на логарифмическую шкалу)
е. восприятие интенсивности звука больше похожа на логарифмическую шкалу)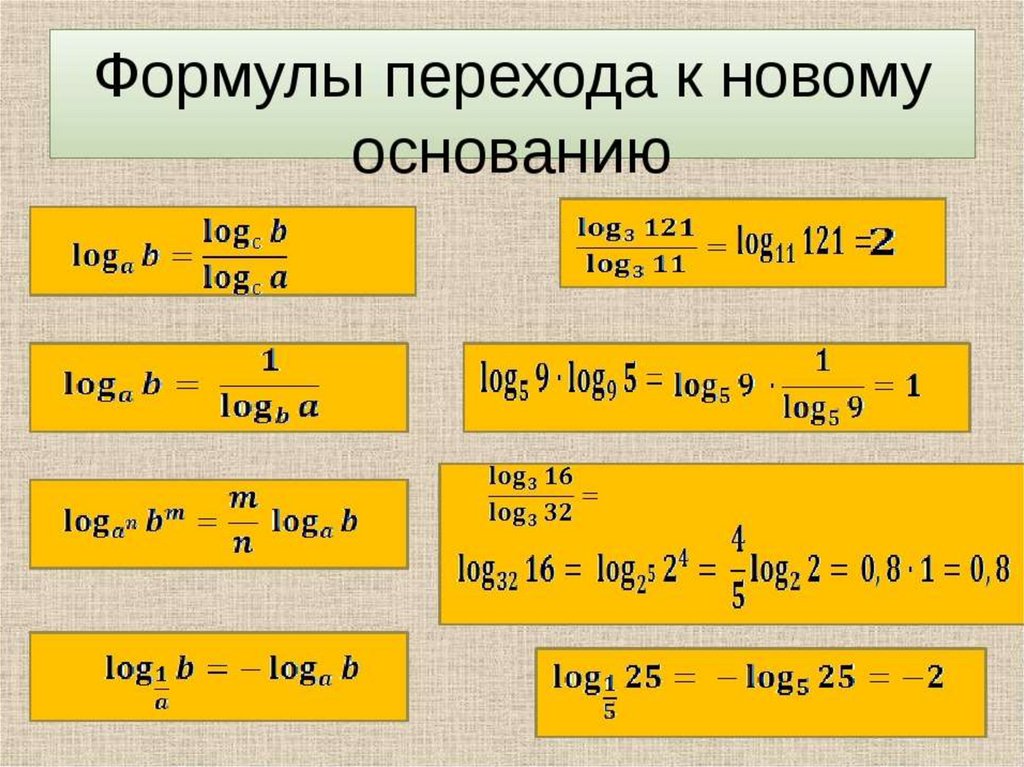 э. -l
2.000000000000000000000
э. -l
2.000000000000000000000