Как сложить все трехзначные числа: Как сложить все трехзначные числа? Нужны решение и ответ. Решение должно быть коротким.

alexxlab / / Разное

Задача 12 — Виленкин Математика 5 класс гдз

Задача 12 — Виленкин Математика 5 класс гдз
 
  Задача 12



Запишите все трехзначные числа, для записи которых употребляются только цифры 0 и 7. Найдите сумму этих чисел и разделите ее на 211.

В данной задаче мы должны записать все трехзначные числа в записи которых есть только цифры ноль и семь. Но число не может начинаться с нуля, поэтому первая цифра всегда должна быть семеркой, первая цифра это в данном случае число сотен.

Тогда мы можем подобрать следующие комбинации это 700, 707, 770, 777. Таких чисел оказалось всего четыре. Чтобы решить задачу до конца нужно эти четыре числа сложить между собой и полученный результат разделить на двести одиннадцать. Подробное решение вы можете посмотреть в видео уроке.

Контактный Email:
avcevceru @ g m a i l . c o m

Контент опубликованный на сайте vcevce.ru защищен законом об авторском праве. Любое частичное или полное копирование опубликованной информации запрещено. ©

Алгоритм сложения трехзначных чисел

Трехзначные числа – это те числа, в записи которых используется три знака. Например, 112, 655, 452 и им подобные числа. При убавлении и прибавлении одного знака получаются двухзначные и трехзначные числа соответственно. Одной из математических тем, которую проходят в третьем классе, является «Алгоритм сложения трехзначных чисел».

Интересный метод сложения трехзначных чисел поможет ученикам разобраться в теме. Знакомство с письменным методом суммирования трехзначных чисел с переходом через разрядную единицу вычислением в столбик оттачивает образовательные навыки учеников 3 класса.

Для успешного сложения чисел такого вида необходимо повторить сложение двухзначных.

К примеру, в задании нужно вычислить следующий пример: 22 + 15 + 55 + 28.

Первый шаг – сложение всех встречающихся в примере десятков: 2 + 1 + 5 + 2. Получилось 10 десятков.

Второй шаг – сложение всех встречающихся единиц: 2 + 5 + 5 + 8, что равняется 20.

10 десятков – это 100. 100 + 20 = 120.

Решение примеров сложения двухзначных чисел с помощью этого метода происходит куда быстрее, чем сложение привычным способом, где: 22+15, потом добавлять 55 и складывать с 28.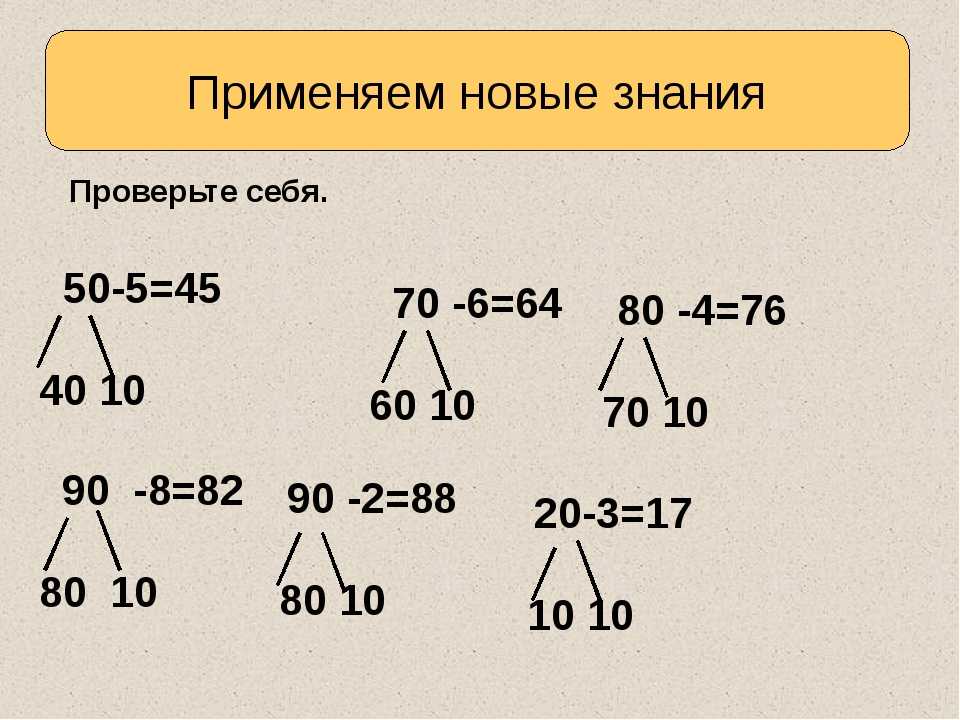

Навыки сложения таким способом двухзначных чисел являются хорошей почвой для суммирования трехзначных. В тестовых работах есть возможность получить новую информацию. Например, в заданиях, результатом вычислений которых является сумма больше десяти, используется сложение с переходом через разряд.

Если при сложении получается ответ меньше десяти, то используется сложение неразрядного перехода.

Подготавливая учеников к решению более сложных задач, учитель использует математические примеры на сложение чисел, сумма которых в конечном итоге равняется больше 100.

Аналогично таким методом решаются и примеры с трехзначными числами.

Например: 335 + 44 + 456 + 20.

Первое действие – сложение десятков: 33 + 4 + 45 + 2 = (33 + 45) + (4 + 2)= 78 + 6=84.

Второе действие – сложение единиц: 5 + 4 + 6 + 0=(5+0) + (4+6)=15.

84 десятка – это 840 сложить с 15, что даёт в сумме 855.

Не менее интересный метод для сложения трехзначных чисел упростит решение задачи ученикам 3 класса.

Суть метода заключена в сложении слева направо, что облегчает получение результата самых важных цифр будущего ответа.

Пример, отражающий стратегию сложения трехзначных чисел:

275+347.

Первое действие сводится к сложению 275 + 300. Далее необходимо прибавить 40, после чего добавить 7. После прибавления первых трех сотен, задание подходит к сложению 40. Далее пример облегчается тем, что остаётся добавить лишь 7.

Этот процесс решения показан следующей схемой:

Задачи на устное сложение трехзначных чисел можно решать таким способом до тех пор, пока не наступит время для прибавления однозначного числа. Легкость этого метода заключена в том, что сложение 275 и 347 требует запомнить все шесть цифр, однако 575 и 47, 615 и 7 – требует не забывать всего лишь о пяти и четырех цифрах соответственно.

Решать упрощенную задачу в разы легче, чем ту, которая представлена в изначальном сложном варианте.

В любом примере на сложение метод слева направо имеет следующую последовательность:

  • сложение сотен
  • сложение десятков
  • сложение сотен и десятков вместе.

Решая в уме подобные задачи, цифры необходимо именно слышать, а не использовать метод визуального воспроизведения чисел. Подкрепление звуками помогает освоить данный способ гораздо быстрее.

Но не всем ученикам 3 класса подойдет слуховое восприятие задач.

Использование графических презентаций – один из легкодоступных способов проведения урока по данной теме.

Отображенные с помощью интересных рисунков, правила сложения легче усваиваются учениками, нежели скучно поданная информация.

Кроме того, можно преподнести математические занятия в виде интересных исторических фактов.

Традиционным способом, который используется во многих школах, является сложение столбиком.

Пример 1:

Первым делом нужно складывать единицы. 1+7= 8.

Далее складывают десятки. 1+6=7.

Третий шаг – сложение сотен. 2+3=5

Пример 2:

Первый шаг – сложение единиц. 8+2=10. Когда складывают единицы, в сумме дающие десяток либо другое двухзначное число, то последнюю цифру (хвостик двухзначного числа) записывают, а десяток запоминают.

Во втором шаге складывают десятки, прибавляя тот десяток, который получился при сложении единиц. В данном случае это приобретает следующий вид:

На третьем этапе складывают сотни, прибавляя к ним ту сотню, получившуюся при сложении десятков, то есть:

Такой метод суммирования хорошо применяется в письме, когда можно записать все числа, которые не вошли в единицы и остатки.

Маленькие таблички с алгоритмом суммирования чисел из трех знаков нужно оформить красочно, на каждый пункт приводить пример. Сначала пишут единицы под единицами, далее десятки под десятками, на очереди сложение сотен. Заканчивается ответом.

Метод, когда числа складывают столбиком, делается поэтапно. Всегда складывают цифры, которые соответствуют друг другу в разряде. Идет сложение от наименьшего к большему. То есть единица с единицей, сотня с сотней и так далее. Сложение таким образом цифр называют арабским методом, так как суммируются в порядке справа на лево.

Много примеров, когда при суммировании двух или более знаков в ответе выходит сумма, больше 10. Здесь единицу относят к последующему разряду. А на месте вопросительного знака пишут цифру на десяток меньше выведенного результата. Например, нужно сложить 9 и 4. Получилось 13. Цифру 3 нужно поставить на место вопроса, а 1 прибавляем к сумме чисел следующего (большего) разряда.

Знание алгоритма пригодится для решения уравнения, неравенства, выражения, при решении задач с несколькими неизвестными.

При сложении трехзначных чисел полезным будет знать, что такое целое и частное и как их найти.

Например, 250 + 430=680. Целое – это сумма двух чисел, в данном случае 680.

Частное в данном случае 250 и 430.

Чтобы найти неизвестную часть, нужно из целого вычесть известную.

Для проверки сложения производят вычитание, а для проверки вычитания – сложение.

На уроке, посвященном суммированию чисел, состоящим из трех знаков, ученикам будет полезно узнать некоторые факты о них.

Интересным числом является 999. Оно не только самое большое из трехзначных чисел, но и в перевернутом виде превращается в другое число – 666.

Самое маленькое трехзначное число – 100.

Уровень подготовки учеников можно проверить с помощью учебника М.И.Моро. Кроме заданий учебник содержит ответы и правила, с помощью которых решаются математические упражнения.

Работа с трехзначными числами помогает ученикам развивать мыслительную активность, воспитывать внимательность к окружающим действиям и явлениям.

Математические примеры приучают детей к самостоятельному решению проблемы, изначально проанализировав ситуацию.

В интернете огромной популярностью пользуются онлайн тренажеры, с помощью которых легко усвоить алгоритм сложения трехзначных чисел в третьем классе. Они несут в себе большую пользу для детей начальной школы, развивая навыки и мелкую моторику, внимательность, анализ действий.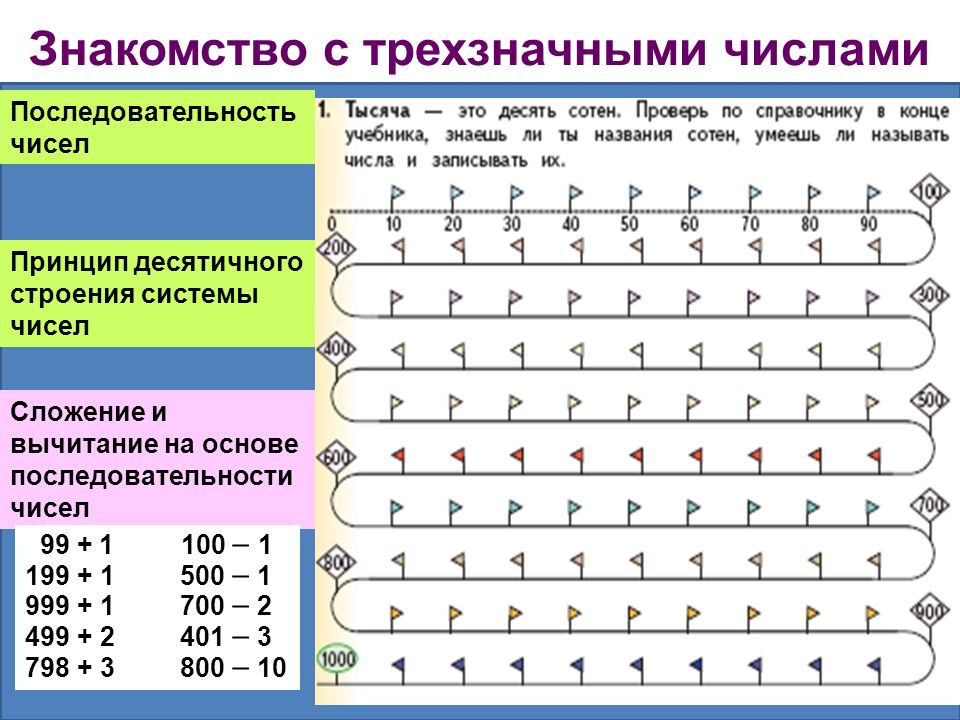

Для успеха в упражнениях, связанных с решением методом столбика, определяющим фактором является постоянная мозговая тренировка. Достичь высоких показателей на скорость решения возможно лишь при каждодневных занятиях.

NumberNut.com: Арифметика: Сложение: Трехзначные числа

Числа и подсчет| Арифметика |Дроби и десятичные дроби|Предварительная алгебра|Карта сайта

Цифры становятся больше. Теперь, когда у вас под контролем однозначное и двузначное сложение, вам нужно двигаться вверх и начать работать со значениями в столбце сотен (трехзначные числа). Запомните процесс и работайте справа налево. Вместо того, чтобы останавливаться на столбце десятков, у вас будет еще один столбец для работы. Давайте рассмотрим несколько примеров без ношения.

456 + 123 = 579
281 + 715 = 996
809 + 150 = 959

И в вертикальном формате. ..

462
+ 516
978

Эти примеры дали вам меньше тысячи (1000) ответов. Должно быть очевидно, что многие из сложенных вами трехзначных чисел дадут вам сумму , которая больше 1000. Как ты доехал? Верните эти навыки ношения/перегруппировки.

Когда общее количество столбцов превышает «9» вам нужно будет перенести «1» в следующий столбец слева. Сумма из столбца единиц , которая больше «9», перенесет «1» в столбец десятков . Если вы получите если в столбце десятков больше 9, то в столбце сотен появится 1. От сотен вы перейдете к тысячам . Это тот же процесс, что и с двузначными числами. Если вам кажется, что это слишком сложно, просто помните, что вы складываете только однозначные числа. Мы не просим вас складывать все числа за один раз.

Разбейте задачу на несколько простых шагов. В математике есть правила, позволяющие делать вещи. очень просто.

Пример:
573 + 769 = ?
Шаги для решения:
• Колонка единиц: 3 + 9 = 12
• Напишите «2» и перенесите «1».
• Столбец десятков: 1 (переносится) + 7 + 6 = 14
• Напишите «4» и перенесите «1».
• Столбец сотен: 1 (перенесено) + 5 + 7 = 13
• Напишите «13», и ваш окончательный ответ будет «1342».
Ответ:
573 + 769 = 1342

Разбейте на этапы…

573
+ 769
?		 1  
573
+ 769
2
1 1  
573
+ 769
4 2		 573
+ 769
13 42

Теперь, когда вы знаете основы перехода от одного столбца к другому, вы сможете складывать вместе любые два значения. Вы всегда будете использовать один и тот же процесс: начните с крайнего правого столбца (столбца единиц) и двигайтесь влево. Когда вы достигнете чисел, называемых десятичными, правила останутся прежними. Но с десятичными знаками вам нужно выровнять десятичные точки, прежде чем начать.

С имеющимися у вас навыками вы легко справитесь с этими задачами.

1234 + 4231 = 5465

20 567 + 35 411 = 55 978

И в вертикальном формате:

65 872
+ 2 781
68 653

Разбейте его на этапы…

65 872
+ 2 781
3 		1    
65 872
+ 2 781
5 3		 1 1    
65 872
+ 2 781
6 53		 1 1    
65 872
+ 2 781
68 653

Помните, что это только один столбец за раз. После некоторой практики это будет намного легче.

► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ

► Или выполните поиск на сайтах…



  • Обзор
  • Операции
  • Дополнение
    • от 1 до 10
    • Переноска
    • 2-значные номера
    • Трехзначные номера
    • Несколько дополнений
    • Целые числа
    • Рабочие тетради
  • Вычитание
  • Умножение
  • Подразделение
  • Мероприятия

Википедия:
https://en.wikipedia.org/wiki/arithmetic
Encyclopædia Britannica:
22229303. com:
http://www.

encyclopedia.com/topic/arithmetic.aspx

Программа Python для суммирования цифр заданного числа

Улучшить статью

Сохранить статью

  • Уровень сложности: Легко
  • Последнее обновление: 11 авг, 2021

  • Читать
  • Обсудить

    • Улучшить статью

    Сохранить статью

    Дано число и задача состоит в том, чтобы найти сумму цифр этого числа в Python.
    Примеры:

    Ввод: n = 87
    Вывод: 15
    Ввод: n = 111
    Вывод: 3
    Метод-1: использование методов str() и int(). : Метод str() используется для преобразования числа в строку. Метод int() используется для преобразования цифры строки в целое число.

    Преобразовать число в строку и перебрать каждую цифру в строке, а после преобразования каждой цифры в целое число добавить к сумме цифр в каждой итерации.

    Python3

    DEF GETAM (N):

    8797

    78777777777977

    877787979797977

    97

    97

    97

    0288 sum = 0

         for digit in str (n): 

           sum + = int ( digit)      

         return sum

        

    n = 12345

    print (getSum(n))

    Вывод: 

     15

    Метод-2: Использование методов sum(). : Метод sum() используется для суммирования чисел в списке.

    Преобразование числа в строку с помощью str(), удаление строки и преобразование в список чисел с помощью методов strip() и map() соответственно. Затем найдите сумму, используя метод sum().

    Python3

        

    def getSum(n):

          

         strr = str (n)

         list_of_number = list ( map ( int , strr.strip()))

         return sum (list_of_number)

        

    n = 12345

    Печать (getsum (n))

    GET: 

     15

    MEDECTION: Следствие. Следствие. переменная для хранения суммы и установите ее на 0

  • Повторите следующие два шага, пока число не будет равно 0
  • Получите крайнюю правую цифру числа с помощью оператора остатка '%', разделив его на 10 и прибавив к сумма.
  • Divide the number by 10 with help of '//' operator
  • Print or return the sum

    • A. Iterative Approach:

    Python3

        

    def getSum (n):

    Сумма = 0

    ,

    ,

    (n !287 (n !287 . 0287 ):

            

             sum = sum + (n % 10 )

             n = n / / 10

            

         return sum

        

    n = 12345

    print (getSum(n))

    Output: 

     15

    B. Recursive Approach:

    Python3

    DEF SUMDIGITS (NO):

    возврат 0 , если NO 888888 , если NO 8888 , если NO 8888 , если NO Если NO Если NO Если NO .0287 else int (no % 10 ) + sumDigits( int (no / 10 )) 

        

    N =

    12345

    Печать (Sumdigits (N))

    .

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *