Уравнение касательной к графику функции
Похожие презентации:
Уравнение касательной к графику функции
Уравнение касательной к графику функции
Уравнение касательной к графику функции. 10 класс
Касательная к графику функции
Уравнение касательной. Условие касания
Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал
Уравнение касательной к графику функции
Касательная к графику функции
Производная сложной функции
Касательная. Уравнение касательной
1. Уравнение касательной к графику функции
2. Верно ли определение?
Касательная – это прямая,имеющая с данной кривой
одну общую точку.
3. Пусть дана и две прямые и , имеющая с данной параболой одну общую точку М (1;1).
Пуст ь дана y x 2 и две прямые x 1 и y 2 x 1 ,имеющая с данной параболой одну общую т очку М
(1;1).
x 1
4. На данном уроке:
1. выясним, что же такое касательная к
выясним, что же такое касательная кграфику функции в точке, как составить
уравнение касательной;
2. рассмотрим основные задачи на
составление уравнения касательной.
Для этого:
вспомним общий вид уравнения прямой
условия параллельности прямых
определение производной
правила дифференцирования
Формулы дифференцирования
5. Определение производной
Пусть функция y f (x) определена внекотором интервале, содержащем внутри
себя точку x0 . Дадим аргументу x
приращение такое, чтобы не выйти из этого
интервала. Найдем соответствующее
приращение y функции и составим
y
отношение x .Если существует предел
отношения при x 0 , то указанный предел
называют производной функции
y f (x)
‘
в точке x0 и обозначают f ( x0 ) .
y
lim
f ‘ ( x0 )
x 0 x
6. Правила дифференцирования
1. Производная суммы равна сумме производных.f x g x ‘ f ‘ x g ‘ x
2. Постоянный множитель можно вынести за знак
производной.

‘
‘
kf x kf x
3. Производная произведения двух функций равна сумме
двух слагаемых; первое слагаемое есть произведение
производной первой функции на вторую функцию, а второе
слагаемое есть произведение первой функции на
производную второй функции.
f x g x f ‘ x g x f x g ‘ x
‘
4. Производная частного
f x f ‘ x g x f x g ‘ x
2
x
g
x
g
‘
7. Основные формулы дифференцирования
f (x)С
1
x
x
x
‘
f ( x)
‘
f (x)
f ( x)
0
sin x
cos x
1
2
x
cos x
sin x
1
2 x
x
1
tgx
ctgx
1
cos 2 x
1
2
sin x
8. Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны
Параллельны ли прямые:a ) y 2 x 1;
б) y 2 x 2;
в) y 3 x 1.
9. Пусть дан график функции y=f(x). На нем выбрана точка M(a;f(a)), в этой точке к графику функции проведена касательная (мы предполагаем, что она суще
Пусть дан график функции y=f(x). На нем выбрана точка
На нем выбрана точкаM(a;f(a)), в этой точке к графику функции проведена касательная
(мы предполагаем, что она существует). Найти угловой
коэффициент касательной.
y f x , M a; f a
k сек
y
x
k кас lim kcек
x 0
k кас
y
lim
x 0 x
10. Геометрический смысл производной
Если к графику функции y = f (x) в точкеx a можно провести касательную,
непараллельную оси у, то f ‘ (a)
выражает угловой коэффициент
касательной
kкас
y
f (a x) f (a)
‘
lim
lim
f a
x 0 x
x a
(a x) a
11. Геометрический смысл производной
Производная в точкеx x0 равна
угловому коэффициенту
касательной к
графику функции
y = f(x) в этой точке.
.
Т.е.
f ( x0 ) tg
‘
Причем, если :
1. f ‘ ( x0 ) tg 0, то острый
2. f ‘ ( x0 ) tg 0, то развернутый
3. f ‘ ( x0 ) tg 0, то тупой
12. Вывод уравнения касательной
y kx m, M a; f aПусть прямая задана уравнением:
k f ‘ (a)
f a ka m
m f a ka
y kx f a ka
y f a f
‘
a x a
уравнение касательной к
графику функции
y f (x)
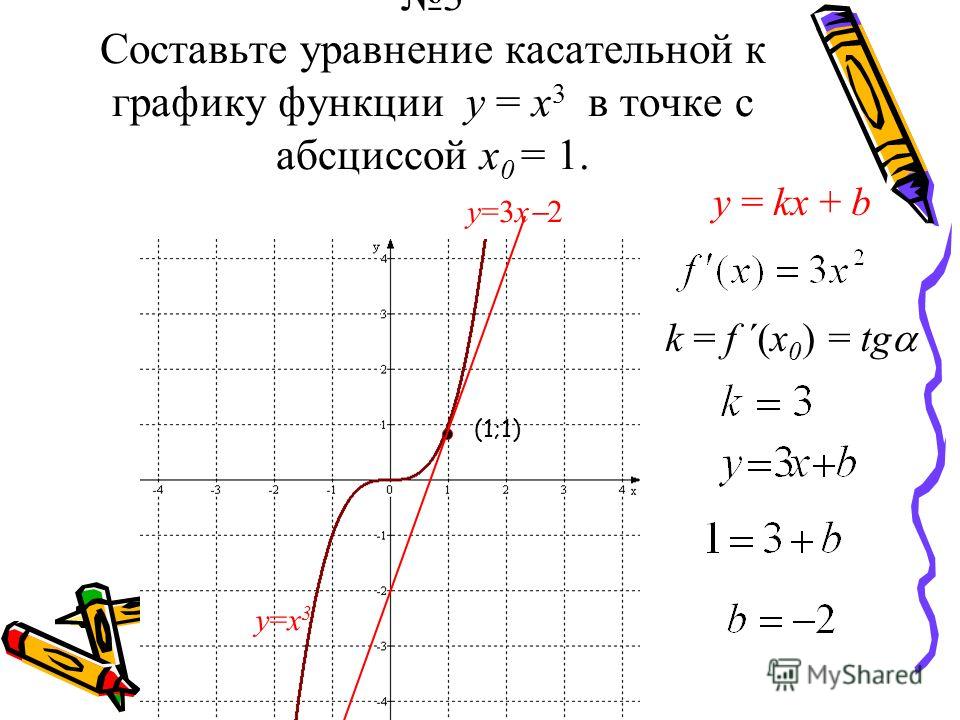
13.
 Составить уравнение касательной:к графику функции
Составить уравнение касательной:к графику функцииM 1;1
f (1) 12 1
f ‘ ( x) 2 x
f ‘ (1) 2 1 2
y f (a ) f ‘ (a )( x a )
y 1 2 ( x 1)
y 1 2x 2
y 2x 1
f ( x) x
2
в точке
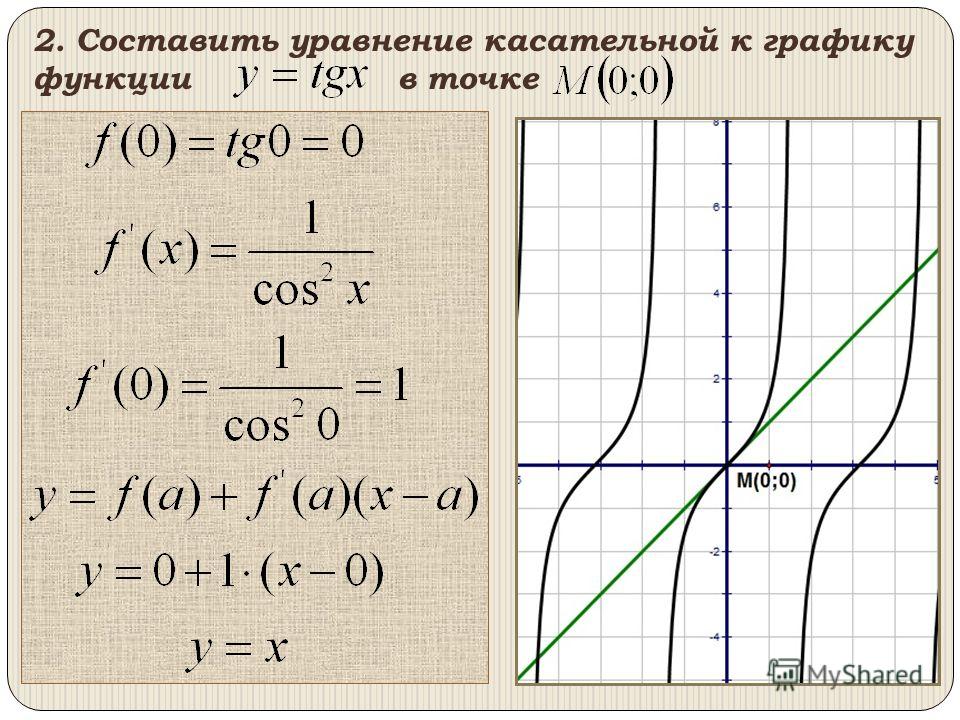
14. Составить уравнение касательной:
к графику функцииf (0) tg 0 0
1
‘
f ( x)
cos 2 x
1
‘
f ( 0)
1
2
cos 0
y f (a ) f ‘ (a )( x a )
y 0 1 ( x 0)
y x
y tgx
в точке M 0;0
15. Алгоритм нахождения уравнения касательной к графику функции y=f(x).
1. Обозначим абсциссу точки касания буквойx=a.
2. Вычислим f (a ) .
3. Найдем f ‘ ( x) и f ‘ (a) .
4. Подставим найденные числа a , в формулу
y f a f a x a .
‘
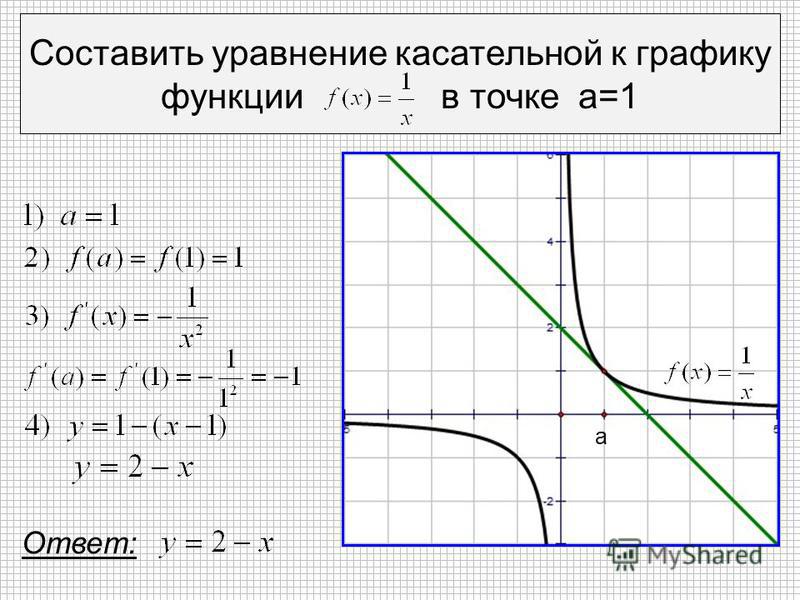
16. Составить уравнение касательной к графику функции в точке .
Составить уравнение касательной к1
графику функции y в точке x 1 .
x
1
f ( x)
x
1) a 1
2) f (a) f (1) 1
1
‘
3) f ( x) 2
x
1
f (a) f (1) 2 1
1
‘
‘
4) y 1 ( x 1)
y 2 x
Ответ
y 2 x
:
17.
 К графику функции провести касательную так, чтобы она была параллельна прямой .x3
К графику функции провести касательную так, чтобы она была параллельна прямой .x3К графику функции y 3
провести касательную так,
чтобы она была параллельна прямой y 4 x 5 .
kкас 4, k кас f ‘ ( x) f ‘ ( x) 4
x
f ( x)
3
‘
1
3 x 2 x 2
3
f ‘ (a) a 2 a 2 4,
3
‘
.
1) a1 2, a2 2
3
(
2
)
8
2
8 , f (a )
2) f (a1 )
2
3
3
3 3
3
3) f ‘ (a1 ) f ‘ (a2 ) 4
16
16
4) y 4 x
, y 4x
3
3
,
y
lim
f ‘ ( x0 )
x 0 x
f ‘ ( x0 ) tg
острый tg 0
f ‘ ( x0 )
Ответ : f (2) 0,5
2 1
0,5
4 2
19. Самостоятельная работа
f ( 1) 1,520. Номера из учебника
• № 29.3 (а,в)а) Ответ : f ‘ (2) 0 острый; в) Ответ : f ‘ ( 3) 0 тупой
• № 29.12 (б,г)
б ) Ответ : y 2 x; г ) Ответ : y 7
• № 29.18
Ответ : y 5 x 16, y 5 x 1,
• № 29.23 (а)
8
4
а) Ответ : y x , y x ,
3
3
21.
 Ответьте на вопросы:1. Что называется касательной к графику
Ответьте на вопросы:1. Что называется касательной к графикуфункции в точке?
2. В чем заключается геометрический
смысл производной?
3. Сформулируйте алгоритм нахождения
уравнения касательной?
22. Домашняя работа
№ 29.3 (б,г)№ 29.12 (а,в)
№ 29.19
№ 29.23 (б)
23. Литература
1.2.
3.
4.
Алгебра и начала математического анализа: Учеб. Для 10-11
кл. для учащихся общеобразовательных учреждений
(базовый уровень) / Под редакцией А.Г. Мордковича. – М.:
Мнемозина, 2009.
Алгебра и начала математического анализа: Задачник, Для
10-11 кл. для учащихся общеобразовательных учреждений
(базовый уровень) / Под редакцией А.Г. Мордковича. – М.:
Мнемозина, 2009.
Алгебра и начала анализа. Самостоятельные и контрольные
работы для 10-11 классов. / Ершова А.П., Голобородько В.В. –
М.: ИЛЕКСА, 2010
ЕГЭ 2010. Математика. Задача В8. Рабочая тетрадь / Под
редакцией А.Л.Семенова и И.В.Ященко – M.
 2-4 а)составьте уравнение касательной к графику данн… — Учеба и наука
2-4 а)составьте уравнение касательной к графику данн… — Учеба и наукаЛучший ответ по мнению автора
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
в зоопарке живут крокодилы и страусы. 2)<=8
2)<=8
6.4 Уравнение касательной к кривой | Дифференциальное исчисление
Предыдущий 6.3 Правила дифференциации | Следующий 6,5 Вторая производная |
6.4 Уравнение касательной к кривой (EMCH8)
temp textВ данной точке кривой градиент кривой равен градиенту касательной к изгиб.
Производная (или функция градиента) описывает градиент кривой в любой точке кривой.
Точно так же он также описывает градиент касательной к кривой в любой точке кривой.
Чтобы определить уравнение касательной к кривой:
- Найдите производную по правилам дифференцирования.
- Подставьте \(x\)-координату данной точки в производную, чтобы вычислить градиент касательной.
- Подставить градиент касательной и координаты заданной точки в
соответствующую форму уравнения прямой. 9{2} \\
& \\
\поэтому \frac{dy}{dx} &= 3 \left( 2x \right) \\
&= 6x
\конец{выравнивание*}
Вычислить градиент касательной
Чтобы определить градиент касательной в точке \(\left(1;3\right)\), мы подставьте \(х\)-значение в уравнение для производной.
\начать{выравнивать*} \frac{dy}{dx} &= 6x \\ \поэтому m &= 6(1) \\ &= 6 \конец{выравнивание*}
Определить уравнение касательной
Подставить градиент касательной и координаты заданной точки в форма точки градиента уравнения прямой линии.

\начать{выравнивать*} y-{y}_{1} & = m\left(x-{x}_{1}\right) \\ у-3 & = 6\влево(х-1\вправо) \\ у & = 6х-6+3 \\ у & = 6x-3 \конец{выравнивание*}
Эскиз кривой и касательной
Рабочий пример 14: Нахождение уравнения касательной к кривой 9{2} + 24(-1) + 9 \\ \поэтому m &= 12 — 24 + 9 \\ &= -3 \конец{выравнивание*}
Определить уравнение касательной
Подставить градиент касательной и координаты точки в градиентно-точечная форма уравнения прямой линии.
\начать{выравнивать*} y-{y}_{1} & = m\left(x-{x}_{1}\right) \\ y-1 & = -3\влево(x-(-1)\вправо) \\ у & = -3х — 3 + 1 \ у & = -3x — 2 \конец{выравнивание*}
Рабочий пример 15: Нахождение уравнения нормали к кривой
- Определить уравнение нормали к кривой \(xy = -4\) в точке
\(\влево(-1;4\вправо)\).

- Нарисуйте грубый набросок.
Найдите производную
Сделайте \(y\) предметом формулы и продифференцируйте по \(x\): 9{2}} \\ \поэтому m &= 4 \конец{выравнивание*}
Используйте градиент касательной для вычисления градиента нормали:
\начать{выравнивать*} m_{\text{тангенс}} \times m_{\text{нормаль}} &= -1 \\ 4 \times m_{\text{нормаль}} &= -1 \\ \поэтому m_{\text{нормаль}} &= -\frac{1}{4} \конец{выравнивание*}
Найти уравнение нормали
Подставить градиент нормали и координаты заданной точки в уравнение градиентно-точечная форма уравнения прямой линии.

\начать{выравнивать*} y-{y}_{1} & = m\left(x-{x}_{1}\right) \\ y-4 & = -\frac{1}{4}\left(x-(-1)\right) \\ y & = -\frac{1}{4}x — \frac{1}{4} + 4\\ y & = -\frac{1}{4}x + \frac{15}{4} \конец{выравнивание*} 9{2} + (4)(2) -7 \\ &=13 \\ \поэтому \text{Касательная: } y &=13x +c \конец{выравнивание*}
где \(c\) — точка пересечения \(y\).
Касательная пересекает \(F(x)\) в точке \((2;F(2))\)
\начать{выравнивать*} F(2) &=(2)^{3} + 2(2)^{2} — 7(2) +1 \\ &=8+8-14+1\ &=3 \\ \text{Касательная: } 3 &=13(2) + c \\ \поэтому с &= — 23 \\ у & = 13x — 23 \конец{выравнивание*} 9{2}\) равно \(\text{5}\).
 {2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\).
{2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\).\begin{выравнивание*} \text{Градиент касательной } = g'(x) = \frac{2}{3}x+2 \\ \поэтому \frac{2}{3}x+2 &=0 \\ \frac{2}{3}x &= -2\\ \поэтому x&=-2 \times \frac{3}{2} \\ &=-3 \\ \text{И} g(-3) &= \frac{1}{3}(-3)^{2}+2(-3)+1 \\ &= \фракция{1}{3}(9)-6+1\ &= 3-6+1 \\ &= -2 \\ \поэтому & (-3;-2) \end{align*}
параллельно линии \(y=4x-2\).
 {2} \\
& = 1
\конец{выравнивание*}
{2} \\
& = 1
\конец{выравнивание*}Следовательно, касательная параллельна данной прямой в точке точка \((1;1)\).
перпендикулярно прямой \(2y+x-4=0\).
\начать{выравнивать*} \text{Перпендикулярно } 2y + x — 4 &= 0 \\ y&= -\frac{1}{2}x+2\\ \поэтому \text{ градиент } \perp \text{ линия } & = 2 \quad (m_1 \times m_2 = -1) \\ \поэтому f'(x) &= 8x-4 \\ \поэтому 8x-4 &=2\\ 8x&=6\\ х&=\фракция{3}{4} \\ \поэтому y&=\left[2\left(\frac{3}{4}\right)-1\right]^{2} \\ &=\фракция{1}{4} \\ \поэтому \влево(\frac{3}{4};\frac{1}{4}\right) \конец{выравнивание*}
Следовательно, касательная перпендикулярна данной прямой в точке точка \(\left(\frac{3}{4};\frac{1}{4}\right)\).
 {2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)
{2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)Найдите уравнения касательных к \(f\) в точке:
- \(y\)-пересечение \(f\).
- поворотный момент \(f\).
- точка, где \(x = \text{4,25}\).
- \begin{выравнивание*} у _ {\ текст {целое}}: (0; -3) \\ m _ {\ text {тангенс}} = f ‘(x) &= -2x + 4 \\ f'(0) &=-2(0) + 4 \\ \поэтому m &=4\\ \text{Касательная}y&=4x+c\\ \text{Через }(0;-3) \поэтому y&=4x-3 \end{выравнивание*}
- \begin{выравнивание*} \text{Поворотный момент: } (2;1) \\ m _ {\ text {тангенс}} = f ‘(2) &= -2 (2) + 4 \\ &=0\\ \text{Касательное уравнение } y &= 1 \end{выравнивание*} 9{2}+4(\текст{4,25})-3 \\ &= -\текст{4,0625} \\ m _ {\ text {тангенс}} \ text { в } x & = \текст{4,25} \\ m&=-2(\text{4,25})+4\\ &=-\текст{4,5} \\ \text{Касательная}y&=-\text{4,5}x+c\\ \text{Через}(\text{4,25};-\text{4,0625}) \\ -\text{4,0625}&=-\text{4,5}(\text{4,25})+c\\ \поэтому c&= \text{15,0625} \\ у&=-\текст{4,5}х+\текст{15,0625} \end{выравнивание*}
Начертите три касательные выше на графике \(ф\).

Запишите все наблюдения о трех касательные к \(f\).
Тангенс в точке \(y_{\text{int}}\) (синяя линия): градиент равен положительна, функция в этой точке возрастает.
Касательная в точке поворота (зеленая линия): уклон равен нулю, касательная — это горизонтальная линия, параллельная оси \(x\).
Касательная в точке \(x=\text{4,25}\) (фиолетовая линия): градиент отрицательно, функция в этой точке убывает.
Предыдущий
6.3 Правила дифференциации
Оглавление Следующий
6,5 Вторая производная
Производные полиномиальных функций.
 Задача 2
Задача 2Напомним, что наклон касательной к точке равен производной функции в этой точке. Итак, чтобы найти уравнение касательной в определенной точке, вычислите производную функции в этой точке, чтобы найти ее наклон. Затем, используя точку, в которой вы намотали касательную, вы можете использовать форму точка-наклон, чтобы найти точку пересечения по оси y. Помните, что форма точки-наклона y-y 1 = m(x-x 1 ), где (x 1 ,y 1 ) — точка, в которой вы находите касательную, а m — наклон, рассчитанный с использованием производной.
постоянное кратное правило правило сумм производных полиномиальные функции касательная линия формула наклона точки производная
Итак, одна проблема, которую вы можете увидеть в своем домашнем задании: найти уравнение прямой, касательной к кривой в некоторой точке.
 Это то, что вы можете сделать с производной, потому что наклон касательной в данной точке зависит от производной. Но просто помните, что если вы хотите найти уравнение прямой, вам нужны две вещи. Вам нужна точка, через которую проходит линия, и наклон.
Это то, что вы можете сделать с производной, потому что наклон касательной в данной точке зависит от производной. Но просто помните, что если вы хотите найти уравнение прямой, вам нужны две вещи. Вам нужна точка, через которую проходит линия, и наклон.Итак, давайте рассмотрим этот пример проблемы здесь. В нем говорится, напишите уравнение касательной к графику. Тогда у меня есть эта большая полиномиальная функция f(x), равная 2x³ минус 5x² плюс 3x минус 5. Точка касания будет в точке x, равной 1. Итак, сначала я хочу найти координаты x и y точки касание. Итак, это координата x. Координата y будет f(1). Итак, 2 раза 1³, 2 раза 1минус 5 раз 1², 5 раз 1 плюс 3 раза 1 минус 5. Итак, у меня есть 2 минус 5, -3, плюс 3, 0, -5. Это означает, что точка касания будет 1,-5.
Итак, все, что мне нужно сделать, это найти наклон. Наклон получается из производной.
Производной этой вещи будет производная по x всего этого 2x³ минус 5x² плюс 3x минус 5. Итак, сначала я хочу разбить эту часть, используя правило сумм.

- Определить уравнение нормали к кривой \(xy = -4\) в точке
\(\влево(-1;4\вправо)\).

 05.16
05.16

 {2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\).
{2} \\
&=1-3 \влево( \frac{25}{36} \вправо) \\
&=1 — \фракция{25}{12} \\
&= — \фракция{13}{12} \\
\поэтому & \left( — \frac{5}{6};- \frac{13}{12} \right)
\end{выравнивание*} 9{2}+2x+1\) равно \(\text{0}\). {2} \\
& = 1
\конец{выравнивание*}
{2} \\
& = 1
\конец{выравнивание*} {2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)
{2} — 4х + 3 = 0 \\
(х-3)(х-1) = 0 \\
х=3 \текст{ или } х=1 \\
\text{Форма: «хмурый» } (a < 0) \\\)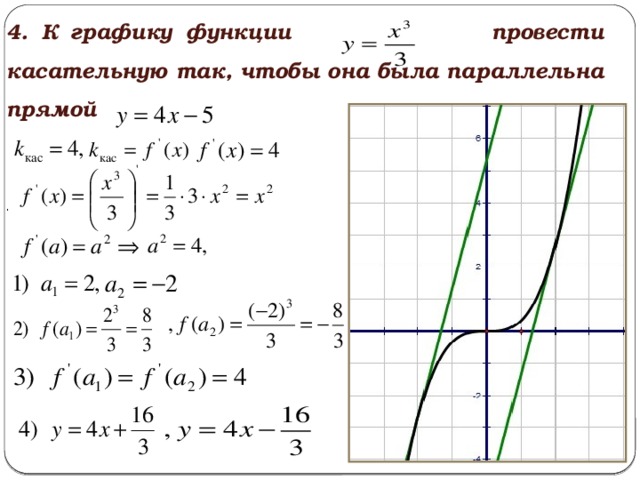
 Задача 2
Задача 2 Это то, что вы можете сделать с производной, потому что наклон касательной в данной точке зависит от производной. Но просто помните, что если вы хотите найти уравнение прямой, вам нужны две вещи. Вам нужна точка, через которую проходит линия, и наклон.
Это то, что вы можете сделать с производной, потому что наклон касательной в данной точке зависит от производной. Но просто помните, что если вы хотите найти уравнение прямой, вам нужны две вещи. Вам нужна точка, через которую проходит линия, и наклон.