Основные теоремы о пределах. Способы вычисления пределов функций. (Семинар 5) презентация, доклад
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
- 1. Основные теоремы о пределах. Способы вычисления пределов функций. (Семинар 5)
- 2. Теорема 4 Если делимое f(x) и делитель g(x)
-
3.
2. Найти Решение. Числитель и знаменатель
- 5. Решение. Положим
-
6.
Решение. Имеет место неопределенность вида
- 7. Скачать презентацию
2. Найти Решение. Числитель и знаменатель
Решение. Имеет место неопределенность вида
Теорема 4 Если делимое f(x) и делитель g(x) имеют пределы при и предел делителя отличен от нуля, то предел их частного при
Слайды и текст этой презентации
Слайд 1Семинар 5. Основные теоремы о пределах. Основные способы вычисления пределов функций
Предполагается,
что функции, рассматриваемые в следующих теоремах определены на некотором общем множестве Х, для которого точка а является предельной точкой.
Теорема 1 Если каждое слагаемое алгебраической суммы конечного числа функций имеет предел при , то предел этой алгебраической суммы при существует и равен такой же алгебраической сумме пределов слагаемых.
Теорема 2 Если каждый из сомножителей конечного числа функций имеет предел при
, то предел произведения при существует и равен произведению пределов сомножителей.
Следствие 1 Постоянный множитель можно выносить за знак предела.
Пусть С – постоянная, тогда
Следствие 2 Если функция f(x) имеет предел при , то предел при целой положительной степени ее равен такой же степени предела этой функции, то есть
Пример
Теорема 3 Если функция f(x) имеет предел при , отличный от нуля, то предел
обратной ей по величине функции равен обратной величине предела данной
функции, то есть
Слайд 2Теорема 4 Если делимое f(x) и делитель g(x) имеют пределы при
и предел делителя отличен от нуля, то предел их частного при равен частному пределов делимого и делителя, то есть
Теорема 5 Если функция f(x) имеет предел при и (n – натуральное) существует в точке а и в некоторой ее окрестности , то
Теорема о промежуточной функции
Пусть в некоторой окрестности точки а функции f(x) заключена между двумя функциями и , имеющими одинаковый предел А при , то есть
(1) и (2), тогда функция f(x) имеет тот же предел, то есть (3).
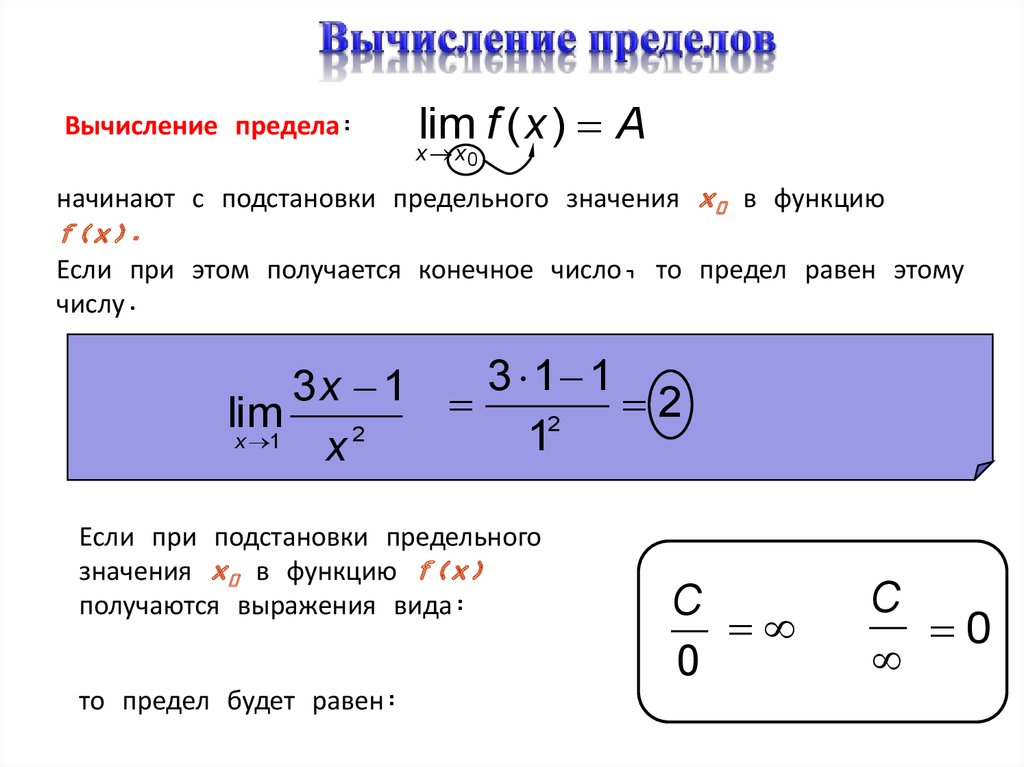
Вычисление пределов основано на применении основных теорем о пределах, признаков существования пределов, а также теорем о бесконечно малых и бесконечно больших функциях.
Рассмотрим вычисление пределов на различных примерах.
1. Найти
Решение. Так как , то числитель стремится к числу 4*4+2=22, а знаменатель к числу 2*4+3=11. Следовательно
Решение. Числитель и знаменатель неограниченно возрастают при
. В таком случае говорят, что имеет неопределенность вида . Разделив на х числитель и знаменатель дроби, получим
3. Найти
Решение. Числитель и знаменатель при стремятся к нулю. Принято говорить,
что получается неопределенность . Имеем .
Если , то . Но при дробь . Итак
4. Найти
Решение.
Здесь имеет место неопределенность вида . Разложим на множители
числитель и знаменатель дроби.
Решение. Имеет место неопределенность вида .
Имеем
, так как
числитель дроби стремится к числу 300, а знаменатель стремится к нулю, то есть является бесконечно малой величиной, следовательно рассматриваемая дробь – бесконечно большая величина.
6. Найти
Решение умножим числитель и знаменатель на сопряженное к числителю, то есть сумму .Получим
7. Найти
Слайд 5Решение. Положим
,
тогда
8. Найти
Решение. Числитель и знаменатель неограниченно возрастают при . В таком случае говорят, что имеет неопределенность вида . Разделив числитель и
знаменатель дроби на старшую степень х, то есть получим
9.
Решение. Разделив числитель и знаменатель дроби на старшую степень х, то есть получим
10. Найти
Слайд 6Решение. Имеет место неопределенность вида
. Умножим и разделим данное выражение на сопряженное
Примеры для самостоятельного решения.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Математический анализ. Дифференциальное исчисление
Математический анализ. Дифференциальное исчисление
ОглавлениеПРЕДИСЛОВИЕГЛАВА 1. ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ.  ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ2. Определение непрерывности функции в точке «на языке приращений». § 2. ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ В ТОЧКЕ 2. Связь между непрерывностью и дифференцируемостью функции в точке. 3. Производная и дифференциал. 4. Односторонние и бесконечные производные. § 3. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ И ДИФФЕРЕНЦИАЛА ДЛЯ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ И ФИЗИЧЕСКИХ ЗАДАЧ 3. Применения производной в физических задачах. Механический смысл производной. § 4. ДИФФЕРЕНЦИРОВАНИЕ ОПЕРАЦИЙ 2. Дифференцирование произведения. 3. Дифференцирование частного. § 5. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ 2. Инвариантность формы записи дифференциала. § 6. ДИФФЕРЕНЦИРОВАНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 2. Дифференцирование обратной функции. 3. Дифференцирование обратных тригонометрических функций. 4. Дифференцирование показательной и логарифмической функций. 5. Дифференцирование гиперболических функций. 6.  Сводка правил и формул дифференцирования.7. Логарифмическое дифференцирование. § 7. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. Механический смысл второй производной. 3. Натуральная степень бинома (формула Ньютона). 4. Свойства производной n-го порядка. 5. Дифференциалы высшего порядка. ГЛАВА 2. ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ 1. СВЯЗЬ МЕЖДУ ХОДОМ ИЗМЕНЕНИЯ ФУНКЦИИ И ЕЕ ПРОИЗВОДНОЙ 2. Экстремумы функции. § 2. ТЕОРЕМА ЛАГРАНЖА И ЕЕ СЛЕДСТВИЯ 2. Теорема 2 (теорема Ролля). 3. Теорема Лагранжа. 4. Условие постоянства функции. § 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ 2. Исследование функций на экстремум с помощью первой производной. 3. Использование второй производной для исследования функций на экстремум. 4. Нахождение наибольшего и наименьшего значений функции на данном отрезке. § 4. ВЫПУКЛЫЕ ФУНКЦИИ 2. Достаточные условия выпуклости. 3. Точки перегиба. § 5. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ДОКАЗАТЕЛЬСТВУ НЕРАВЕНСТВ И РЕШЕНИЮ УРАВНЕНИЙ 2.  Приближенное решение уравнений.§ 6. ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ ДЛЯ ВЫЧИСЛЕНИЯ ПРЕДЕЛОВ ФУНКЦИЙ 2. Правило Лопиталя. § 7. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ § 8. КРИВЫЕ НА ПЛОСКОСТИ 2. Жордановы кривые. 3. Связь между различными видами уравнений линий. 4. Дифференцирование параметрически заданных функций. 5. Полярное уравнение кривой. 6. Производная второго порядка для параметрически заданной функции. 7. Построение кривых, заданных параметрическими уравнениями. 8. Построение кривых, заданных полярными уравнениями. ОТВЕТЫ |
Как найти пределы в вычислениях
В этой статье
Что такое предел?
Как найти пределы
Практические упражнения и решения
Что такое предел?
Прежде чем перейти к тому, как найти предел, давайте сначала определим предел. Для функции fff предел — это слово, используемое для описания значения, к которому стремится f(x)f(x)f(x), когда xxx стремится к некоторому значению.
Обозначение предела функции fff при приближении xxx к некоторому числу ccc выглядит так:
limx→cf(x)=L\lim_{x\to c}f(x) = Llimx→cf(x)=L
Приведенное выше обозначение можно прочитать как «Предел f (x)f(x)f(x) при приближении xxx к ccc равно LLL».
Другими словами, f(x)f(x)f(x) стремится к LLL, как xxx стремится к ccc.
Как найти пределы
При нахождении пределов мы можем использовать несколько методов. Мы рассмотрим шесть возможных методов:
Прямая замена
Факторизация
Рационализация
Теорема сжатия
Тригонометрические тождества
Правило Лопиталя
Однако метод, который мы используем для нахождения предела, будет зависеть от типа функции.
Прямая замена
Термин «прямая замена» звучит именно так; вы напрямую подставляете заданное значение в предел. Теперь, когда нам нужен этот метод? Если ваша функция fff непрерывна, значение fff в ccc и предел f(x)f(x)f(x) при приближении xxx к ccc совпадают.
Другими словами, limx→cf(x)=f(c)\lim_{x\to c}f(x) = f(c)limx→cf(x)=f(c). 92 + 0 + 10 = 10limx→0(x2+x+10)=02+0+10=10
Стоит отметить, что значение fff при ccc и предел f(x)f(x)f (x) по мере приближения xxx к ccc не всегда совпадают. Мы часто можем оценить предел f(x)f(x)f(x), когда xxx приближается к ccc, даже если f(c)f(c)f(c) не определено.
Пример 2
В качестве другого примера рассмотрим рациональную функцию f(x)=1x−2f(x) = \frac{1}{x-2}f(x)=x−21. У нас не может быть нулевого знаменателя, поэтому f(2)=12−2=10f(2)=\frac{1}{2-2}=\frac{1}{0}f(2)=2 −21=01 не определено. 9+ }f(x)limx→c+f(x). Это предел, поскольку xxx приближается к некоторому значению ccc справа.
Взгляните на график f(x)=1x−2f(x) = \frac{1}{x-2}f(x)=x−21 ниже.
Посмотрите внимательно на поведение функции вблизи x=2x = 2x=2. Переменная xxx бесконечно приближается к 2 с обеих сторон, но никогда не достигает 2.
Когда xxx приближается к 2 слева, yyy становится бесконечно меньше.
Когда xxx приближается к 2 справа, yyy становится бесконечно больше. Тогда верны следующие односторонние пределы: 9-}f(x)limx→a+f(x)=limx→a−f(x). Чтобы предел существовал, односторонние пределы всегда должны быть равны друг другу. Если предел существует на вертикальной асимптоте, значение этого предела всегда будет +∞+ \infty+∞ или -∞- \infty-∞. Обычно, если вы подставите x=ax=ax=a в f(x)f(x)f(x) и получите, что знаменатель равен нулю, а числитель отличен от нуля, это хороший признак того, что в точке есть вертикальная асимптота. х=ах = ах=а.
Чтобы дать более точное определение, у нас есть это правило: 92+2-6}{2-2} = \frac{6-6}{0} = \frac{0}{0}f(2)=2−222+2−6=06−6= 00.
При оценке пределов мы говорим, что 00\frac{0}{0}00 является неопределенным. Это означает, что 00\frac{0}{0}00 не дает нам достаточно точного представления о том, как ведет себя f(x)f(x)f(x) при приближении xxx к 2.
Поскольку мы определяем деление просто как обратное умножению, мы можем сказать, что n=00n = \frac{0}{0}n=00 подразумевает, что 0=n⋅00 = n \cdot 00=n⋅0 для любого действительного числа nnn.
Поскольку любое число, умноженное на 0, равно просто 0, существует бесконечное количество ответов. Таким образом, 00\frac{0}{0}00 является неопределенным и указывает на то, что нам нужно использовать другой метод, указанный ниже.
Факторизация
Когда прямая подстановка дает нам неопределенную форму, такую как 00\frac{0}{0}00, мы можем попробовать разложить на множители. Факторинг позволяет нам отменить факторы, которые являются общими как для числителя, так и для знаменателя, а затем применить правило частного.
Правило частного гласит, что limx→af(x)g(x)=limx→af(x)limx→ag(x)\lim_{x\to a}\frac{f(x)} {g(x)} = \frac{ \lim_{x\to a}f(x)}{ \lim_{x\to a}g(x)}limx→ag(x)f(x) =limx→ag(x)limx→af(x), учитывая, что limx→ag(x)≠0\lim_{x\to a}g(x) \neq 0limx→ag (х)=0. Проще говоря, предел частного есть частное пределов при условии, что знаменатель не равен нулю. 92+x-6}{x-2} = 5limx→2x−2×2+x−6=5.
Рационализация
При работе с пределами, которые имеют радикалы, полезно переместить радикал из числителя в знаменатель или наоборот.
Для этого используем рационализацию. Этот метод включает умножение на сопряженное. Мы можем найти сопряженное выражение, поменяв знак в середине выражения.
Например, давайте оценим limx→0x+1−1x\lim_{x\to 0}\frac{\sqrt{x+1}-1}{x}limx→0xx+1−1 . Поскольку подстановка x=0x = 0x=0 дает нам 00\frac{0}{0}00, попробуем умножить на сопряженное число числителя.
limx→0x+1−1x=limx→0x+1−1x⋅x+1+1x+1+1\lim_{x\to 0}\frac{\sqrt{x+1}- 1}{x} = \lim_{x\to 0}\frac{\sqrt{x+1}-1}{x} \cdot \frac{\sqrt{x+1}+1}{\sqrt{x +1}+1} limx→0xx+1
−1=limx→0xx+1
−1⋅x+1
+1x+1
+1
=limx →0x+1−1x(x+1+1)= \lim_{x\to 0}\frac{x+1-1}{x(\sqrt{x+1}+1)} =limx→0x(x+1
+1)x+1−1
=limx→0xx(x+1+1)= \lim_{x\to 0}\frac{x {х(\sqrt{х+1}+1)} =limx→0x(x+1
+1)x
=limx→01x+1+1) = \lim_{x\to 0}\frac{1}{\sqrt{x+1}+1)} =limx→0x+1
+1)1
=10+1+1) = \frac{1}{\sqrt{0+1}+1)} =0+1
+1)1
=12 = \frac{1}{2} =21
Таким образом, limx→0x+1−1x=12\lim_{x\to 0 }\frac{\sqrt{x+1}-1}{x} = \frac{1}{2}limx→0xx+1−1=21.
Теорема сжатия
Теорема сжатия — это метод, в котором мы «помещаем» функцию между двумя более простыми, чтобы оценить ее предел. Этот метод утверждает, что если мы можем найти две функции f(x)f(x)f(x) и h(x)h(x)h(x), которые «сжимают» или захватывают g(x)g(x)g (x) между ними на некотором интервале [a,b][a, b][a,b], и если f(x)f(x)f(x) и h(x)h(x)h(x ) имеют одинаковый предел LLL в точке ccc, то g(x)g(x)g(x) также должен иметь такой же предел LLL в точке ccc.
Точнее, если f(x)≤h(x)≤g(x)f(x) \leq h(x) \leq g(x)f(x)≤h(x)≤g(x) для всех xxx на [a,b][a, b][a,b] (за исключением, возможно, x=cx = cx=c) и limx→cf(x)=limx→cg(x) =L\lim_{x\to c}f(x) = \lim_{x\to c}g(x) = Llimx→cf(x)=limx→cg(x)=L, тогда lim x→ch(x)=L\lim_{x\to c}h(x) = Llimx→ch(x)=L
Опять же, теорема о сжатии заключает одну сложную функцию в ловушку между двумя более простыми функциями.
Используя теорему сжатия, оценим h(x)=limx→0sin(x)xh(x) = \lim_{x\to 0}\frac{\sin (x)}{x}h( х)=limx→0xsin(x).
Нам нужно заключить h(x)h(x)h(x) между двумя более простыми функциями. Чтобы найти эти функции, посмотрите на график ниже, где графики f(x)=cos(x)f(x) = \cos (x)f(x)=cos(x), g(x)=1g( х) = 1g(x)=1, и h(x)=sin(x)xh(x) = \frac{\sin(x)}{x}h(x)=xsin(x).
Используя этот график, мы можем сказать, что cos(x)≤sin(x)x≤1\cos (x) \leq \frac{\sin (x)}{x} \leq 1cos(x)≤ xsin(x)≤1.
Теперь обратите внимание, что:
limx→0cos(x)=1\lim_{x\to 0}\cos (x) = 1limx→0cos(x)=1
andand и
lim x→01=1\lim_{x\to 0}1 = 1limx→01=1
Так как h(x)=sin(x)xh(x) = \frac{\sin (x)} {x}h(x)=xsin(x) зажато между f(x)=cos(x)f(x) = \cos (x)f(x)=cos(x) и g(x) =1g(x) = 1g(x)=1, и поскольку limx→0f(x)=limx→0g(x)=1\lim_{x\to 0}f(x) = \lim_{ x\to 0}g(x) = 1limx→0f(x)=limx→0g(x)=1, теорема о сжатии утверждает, что limx→0sin(x)x=1\lim_{ x\to 0}\frac{\sin (x)}{x} = 1limx→0xsin(x)=1.
Тригонометрические тождества
Использование тригонометрических тождеств — еще один умный способ манипулировать функциями, чтобы нам было легче вычислять предел.
Тригонометрические тождества — это правила, включающие тригонометрические функции, которые всегда истинны. Эти уравнения можно заменить тригонометрическими функциями, чтобы упростить задачу.
Хотя существует множество различных тригонометрических тождеств, знакомство с ними всеми стоит того.
Некоторые тождества для оценки тригонометрических функций:
Пифагорейские тождества
Взаимные тождества
Тождества с двойным углом
Частные тождества
В этом примере мы рассмотрим пифагорейское тождество.
Пусть f(x)=1−cos(x)xf(x) = \frac{1-\cos{(x)}}{x}f(x)=x1−cos(x). Оценим limx→0f(x)\lim_{x\to 0 }f(x)limx→0f(x).
Подстановка x=0x=0x=0 дает нам f(x)=00f(x) = \frac{0}{0}f(x)=00, поэтому нам придется найти другой способ.
Сначала умножим на сопряженное числителю. Мы можем найти сопряжение числителя, просто поменяв знак в середине выражения. Умножение на сопряженное — очень удобный инструмент, позволяющий находить тригонометрические тождества, которые не очевидны в исходной форме заданной функции.
2(x) = 1sin2(x) +cos2(x)=1. Итак, у нас есть:
92 (х)}{х(1+ \cos (х)}
=limx→0x(1+cos(x)sin2(x)
=limx→0sin(x)x⋅sin(x)1+cos(x)= \lim_{ x\to 0}\frac{\sin (x)}{x} \cdot \frac{\sin (x)}{1 + \cos (x)}=limx→0xsin(x)⋅1+ cos(x)sin(x)
По правилу произведения мы знаем, что:
limx→0sin(x)x⋅sin(x)1+cos(x)=limx→ 0sin(x)x⋅limx→0sin(x)1+cos(x)\lim_{x\to 0}\frac{\sin (x)}{x} \cdot \frac{\sin (x)}{1 + \cos (x)} = \lim_{x\to 0}\frac{\sin (x)}{x} \cdot \lim_{x\to 0}\frac{\sin ( x)}{1 + \cos (x)}limx→0xsin(x)⋅1+cos(x)sin(x)=limx→0xsin(x)⋅limx→01+ cos(x)sin(x)
И, используя наш ответ из примера Теоремы сжатия, мы знаем, что limx→0sin(x)x=1\lim_{x\to 0}\frac{\sin (x)}{x} = 1limx →0xsin(x)=1. Тогда у нас есть:
limx→01−cos(x)x=limx→0sin(x)x⋅limx→0sin(x)1+cos(x)\lim_{x\to 0} \frac{1-\cos{(x)}}{x} = \lim_{x\to 0}\frac{\sin (x)}{x} \cdot \lim_{x\to 0}\frac{ \sin(x)}{1 + \cos(x)} limx→0x1−cos(x)=limx→0xsin(x)⋅limx→01+cos(x)sin(x)
=1⋅limx→0sin(x ) 1 + cos (x) = 1 \ cdot \ lim_ {x \ to 0} \ frac {\ sin (x)} {1 + \ cos (x)} =1⋅limx→01+cos(x)sin(x)
= 1 ⋅ sin (0) 1 + cos (0) = 1 \ cdot \ frac {\ sin (0)} {1+ \ cos (0)} =1⋅1+cos(0)sin(0)
=1⋅02= 1 \cdot \frac{0}{2} =1⋅20
=0 = 0=0
Таким образом, limx→01−cos(x)x=0\lim_{x\to 0}\frac{1-\cos{(x) }}{x} = 0limx→0x1−cos(x)=0.
Правило Лопиталя
Правило Лопиталя утверждает, что limx→∞f(x)g(x)=limx→∞f'(x)g'(x)\lim_{x\to\ infty}\frac{f(x)}{g(x)} = \lim_{x\to\infty}\frac{f'(x)}{g'(x)}limx→∞g(x) f(x)=limx→∞g'(x)f'(x), если первый предел limx→af(x)g(x)\lim_{x\to a}\frac{f( x)}{g(x)}limx→ag(x)f(x) неопределенно. Это означает, что когда прямая подстановка дает нам неопределенную форму, мы можем дифференцировать числитель и знаменатель, а затем снова взять тот же предел. 92-5x-6}{x+1} = \lim_{x\to -1}\frac{(x-6)(x+1)}{x+1} limx→−1x+1×2−5x−6=limx→−1x+1(x−6)(x+1)
=limx→−1(x−6) = \lim_ {х\до -1}(х-6) =limx→−1(x−6)
=−1−6 = -1 -6 =−1−6
=−7 = -7=−7
Упражнение 3
Вычислить limx→4x−2x−4\lim_{x\to 4}\frac{\sqrt{x}-2 {x-4}limx→4x−4x−2.
Решение:
Прямая замена дает нам 00\frac{0}{0}00, поэтому для решения этой задачи воспользуемся рационализацией. Чтобы рационализировать радикал в
числитель, умножим на сопряженный.
limx→4x−2x−4=limx→4x−2x−4⋅x+2x+2\lim_{x\to 4}\frac{\sqrt{x}-2}{x-4 } = \lim_{x\to 4}\frac{\sqrt{x}-2}{x-4} \ cdot \ frac {\ sqrt {x} +2} {\ sqrt {x} +2} limx→4x−4x
−2=limx→4x−4x
−2⋅x
+2x
+2
=limx→4x−4 (x−4)(x+2=\lim_{x\to 4}\frac{x-4}{(x-4)(\sqrt{x}+2} =limx→4(x−4)(x
+2x−4
=limx→41x+2= \lim_{x\to 4}\frac{1}{\sqrt{x} +2}=limx→4x
+21
=14 = \frac{1}{4}=41 92 \cos (\frac{1}{x}) = 0limx→0x2cos(x1)=0.
Упражнение 5
Вычислить limx→0sin(x)sin(2x)\lim_{x\to 0} \frac{\sin (x)}{\sin (2x)}limx→0sin(2x)sin(x ).
Решение:
Прямая замена дает нам 00\frac{0}{0}00, поэтому мы будем использовать триггерные тождества для решения этой задачи.
В частности, будет полезно использовать тождество двойного угла, которое утверждает, что sin(2x)=2sin(x)cos(x)\sin(2x) = 2\sin(x)\cos(x)sin (2x)=2sin(x)cos(x).
92
=3(3)2
=27= 27=27
Ознакомьтесь с отмеченными наградами курсами For-Credit от OutlierКомпания Outlier (от соучредителя MasterClass) собрала лучших в мире инструкторов по игре дизайнеров и кинематографистов, чтобы создать будущее онлайн-колледжа.
Ознакомьтесь с этими родственными курсами:
Исчисление I
Изучите курс
Исчисление I
Математика изменений.
Изучить курс
Введение в статистику
Изучить курс
Введение в статистику
Как данные описывают наш мир.
Изучить курс
Введение в микроэкономику
Изучить курс
Введение в микроэкономику
Почему маленькие решения имеют большое влияние.
Изучить курс
Ограничения по факторингу | Brilliant Math & Science Wiki
Адитья Вирани,
Махиндра Джейн,
Джейди Лусеро,
и
92+4x}+x}\\\\
&=\lim_{x \rightarrow \infty}\frac{4}{\sqrt{1+\frac{4}{x}}+1}\\\\
&=\фракция{4}{2}\\\\
&=2.
\ _\квадрат
\end{выровнено}x→∞lim(x2+4x−x)=x→∞limx2+4x+x(x2+4x−x)(x2+4x+x)=x →∞limx2+4x+xx2+4x−x2=x→∞limx2+4x+x4x=x→∞lim1+x4+14=24=2. □
Что такое limx→04+3x−2x?{\displaystyle\lim_{x \rightarrow 0}}\frac{\sqrt{4+3x}-2}{x}?x→0limx4+3x− 2?
На этот раз с помощью правила подстановки получается 00\frac{0}{0}00. Снова умножаем числитель и знаменатель на сопряженное 4+3x+2\sqrt{4+3x}+24+3x+2 и получаем
limx→04+3x−2x=limx→0(4+3x−2)(4+3x+2)x⋅(4+3x+2)=limx→0(4+3x) −4x⋅(4+3x+2)=limx→03xx⋅(4+3x+2)=limx→034+3x+2=34. □\begin{выровнено} \lim_{x \rightarrow 0}\frac{\sqrt{4+3x}-2}{x} &=\lim_{x \rightarrow 0}\frac{\left(\sqrt{4+3x}-2\right)\left(\sqrt{4+3x}+2\right)}{x\cdot \left (\sqrt{4+3x}+2\справа)}\\\\ &=\lim_{x \rightarrow 0}\frac{(4+3x)-4}{x\cdot \left(\sqrt{4+3x}+2\right)}\\\\ &=\lim_{x \rightarrow 0}\frac{3x}{x\cdot \left(\sqrt{4+3x}+2\right)}\\\\ &=\lim_{x \стрелка вправо 0}\frac{3}{\sqrt{4+3x}+2}\\\\ &=\фракция{3}{4}.
