§ Сравнение десятичных дробей
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Площадь кругаАлгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Правильная постановка вопроса свидетельствует о некотором знакомстве с предметом.
на главную
Введите тему
Поддержать сайт
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
Запомните!
Удобно сравнивать десятичные дроби с одинаковым количеством цифр (знаков) справа от запятой.
Чтобы сравнить десятичные дроби нужно:
- Убедиться, что у обеих десятичных дробей одинаковое количество знаков (цифр) справа от запятой. Если нет, то дописываем (убираем) нужное количество нулей в одной из десятичных дробей.
- Сравниваем десятичные дроби слева направо. Целую часть с целой, десятые с десятыми, сотые с сотыми и т.д.
- Когда одна из частей десятичной дроби (целая часть, десятые, сотые и т. д.) окажется больше чем в другой дроби, эта дробь и больше.
д.) окажется больше чем в другой дроби, эта дробь и больше.Пример. Сравним десятичные дроби:
- Сперва дописываем в первой десятичной дроби нужное количество нулей,
чтобы уравнять количество знаков справа от запятой.
39,700 и 39,719
- Начинаем сравнивать десятичные дроби слева направо.
Целую часть с целой частью:
39 = 39
Целые части равны. Переходим к десятым.
Десятые с десятыми:
7 = 7
Десятые также равны. Переходим к сотым.
Сотые с сотыми:
0 < 1
Так как сотые второй десятичной дроби оказались больше, значит и сама дробь больше.
39,700 < 39,719
39,7 < 39,719
Другой способ сравнения десятичных дробей
Так же как и в предыдущем методе сравнения
необходимо вначале уравнять количество знаков
справа от запятой в обеих десятичных дробях.
Затем, отбросив запятую в обеих дробях, сравнить полученные результаты.
Пример:
3,656 и 3,48
Уравняем количество знаков справа у десятичных дробей.
3,656 и 3,480
Теперь отбросим запятые и сравним полученные числа.
3 656 > 3 480
3,656 > 3,48
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
Задание 6 ОГЭ по математике. Числа и вычисления.
Задача 6 ОГЭ по математике называется «Числа и вычисления». Это действия с обыкновенными и с десятичными дробями. Действия со степенями. Сравнение чисел.
Приступим к решению задач.
Пример 1. Найдите значение выражения
Решение. Вспоминаем, что при вычитании дробей нужно их привести к общему знаменателю, а при делении дробей первую из них умножаем на перевёрнутую вторую.
Посчитаем, чему равен знаменатель.
Получим:
Ответ: 0,9.
Пример 2. Соотнесите обыкновенные дроби с равными им десятичными дробями.
| А. | Б. | В. | Г. |
| 1) 0,5 | 2) 0,02 | 3) 0,12 | 4) 0,625 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | |
Решение. Каждую из данных обыкновенных дробей можно представить в виде десятичной, например, используя деление в столбик.
Итак, деление выполнено. Сопоставим полученные результаты:
| А | Б | В | Г |
| 4 | 3 | 1 | 2 |
Ответ: 4312.
Замечание 1. Преобразование обыкновенных дробей в десятичные можно произвести и без деления в столбик. Т. к. любая десятичная дробь записывается как обыкновенная со знаменателем 10, 100, 1000 и т. д., то данные обыкновенные дроби можно «доделать» до десятичных. Для этого используем основное свойство дроби: дробь не изменится, если её числитель и знаменатель домножить на одно и тоже число.
Замечание 2. В этой задаче можно было, наоборот, преобразовывать заданные десятичные дроби в обыкновенные путём упрощения, т. е. сокращения числителя и знаменателя.
Выбирайте любой способ. Здесь важен правильный результат!
Для выполнения следующих заданий нам потребуются свойства степеней. Напомним основные из них.
Степенью называется выражение вида
Здесь a — основание степени, c — показатель степени.
По определению,
Возвести число в квадрат — значит умножить его само на себя:
Возвести число в куб — значит умножить его само на себя три раза:
Возвести число в натуральную степень n — значит умножить его само на себя n раз:
По определению,
Это верно для Выражение не определено.
Определим, что такое степень с целым отрицательным показателем.
Конечно, все это верно для поскольку на ноль делить нельзя.
Соберем свойства степеней и основные формулы в одной таблице.
| При перемножении степеней с одинаковыми основаниями показатели степеней складываются. | |
| При делении степеней с одинаковыми основаниями показатели степеней вычитаются. | |
| При возведении степени в степень показатели степеней перемножаются. | |
| При возведении в отрицательную степень получаем дробь, где единица делится на степень с положительным показателем. | |
| При возведении произведения двух множителей в степень каждый из этих множителей возводится в заданную степень. | |
При возведении дроби в степень получается дробь, числитель и знаменатель которой возведены в заданную степень. | |
| При возведении дроби в отрицательную степень дробь переворачивается, а показатель степени становится положительным. |
Пример 3. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 3328.
Пример 4. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 0,5604.
Пример 5. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 81.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ОГЭ по математике. Числа и вычисления.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Публикация обновлена: 06.01.2023
теория чисел — работа с большими показателями
Задать вопрос
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 7к раз
$\begingroup$ 9b$ имеет миллионы цифр. Очевидно, вычислить число невозможно, но я все же хотел бы определить некоторые вещи о них.
Меня особенно интересуют идеи или правила оценки того, какое из двух больших чисел больше. Я считаю, что хочу каким-то образом использовать логарифмы, но они всегда меня немного смущали, поэтому я не совсем понимаю, куда идти дальше.
{d_2}) \\
b_1\log(a_1) + b_2\log(a_2) &> d_1\log(c_1) + d_2\log(c_2) \\
\end{выравнивание} 9б $
$\endgroup$
Как найти закономерности в показателях степени
Все математические ресурсы GRE
13 диагностических тестов 452 практических теста Вопрос дня Карточки Learn by Concept
GRE Math Help » Алгебра » Экспоненты » Поведение шаблонов в экспонентах » Как найти закономерности в показателях
Количественное сравнение
Количество A: x 2
Количество B: x 3
Возможные ответы:
Количество A больше.
Обе величины равны.
Связь не может быть определена на основании предоставленной информации.
Количество B больше.
Правильный ответ:
Связь не может быть определена на основе предоставленной информации.
Пояснение:
Давайте выберем числа. Для количественных сравнений с показателями хорошо попробовать 0, отрицательное число и дробь.
0: 0 2 = 0, 0 3 = 0, поэтому две величины равны.
–1: (–1) 2 = 1, (–1) 3 = –1, поэтому количество А больше.
У нас уже есть противоречие, поэтому ответ не может быть определен.
Сообщить об ошибке
Если , то что из следующего также должно быть верным?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы знаем, что выражение должно быть отрицательным. Следовательно, один или все члены x 7 , y 8 и z 10 должны быть отрицательными; однако четные степени всегда дают положительные числа, поэтому y 8 и z 10 оба будут положительными.
Нечетные степени могут давать как отрицательные, так и положительные числа, в зависимости от того, является ли основной член отрицательным или положительным. В этом случае x 7 должно быть отрицательным, поэтому x должно быть отрицательным. Таким образом, ответ x < 0,
Сообщить об ошибке
Какое количество больше?
Количество A
Количество B
Возможные ответы:
Количество B больше.
Реальность не может быть определена на основании предоставленной информации.
Количество A больше.
Обе величины равны.
Правильный ответ:
Количество A больше.
Объяснение:
Сначала перепишите количество B так, чтобы оно имело то же основание, что и количество A.
можно переписать как , что эквивалентно .
Теперь мы можем сравнить две величины.
больше .
Сообщить об ошибке
Упростите следующее:
Возможные ответы:
Правильный ответ:
Объяснение:
При подобных проблемах всегда лучше разбить ваши ценности на основные факторы. Давайте посмотрим на числитель и знаменатель отдельно:
Числитель
Продолжая упрощение:
Теперь у этих множителей есть общее a . Разложите это в множители:
Знаменатель
Это намного проще:
Теперь вернитесь к вашей дроби:
Отменить общие множители :
Сообщить об ошибке
Какая цифра появляется на месте единиц при умножении?
Возможные ответы:
Правильный ответ:
Объяснение:
Эта задача довольно проста, если вспомнить, что разряд единиц степени двойки следует простой последовательности из 4 шагов.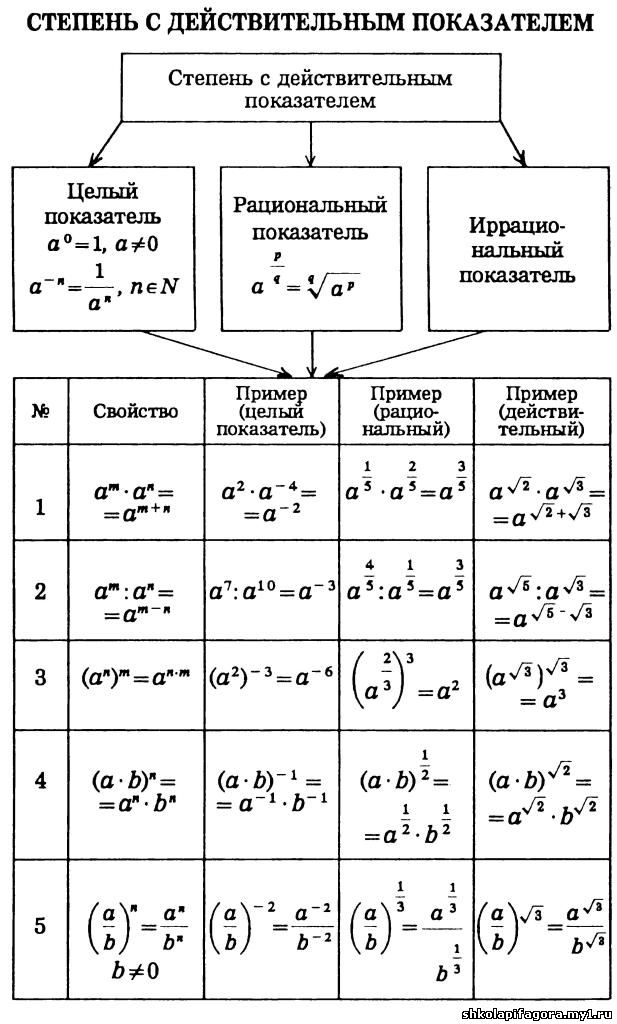
Соблюдайте первые несколько степеней 2:
2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16, 2 5 = 32, 2 6 = 64, 2 7 = 128. , 2 8 = 256 . . .
Разряд единиц следует за последовательностью 2, 4, 8, 6, 2, 4, 8, 6 и т. д. Таким образом, разделите 102 на 4. Это даст остаток 2.
Второе число в последовательности 4, поэтому ответ равен 4.
Сообщить об ошибке
Какое из следующих чисел кратно ?
Возможные ответы:
Правильный ответ:
Объяснение:
Для подобных задач с экспонентами проще всего разбить все числа, которые у вас есть, на их простые множители. Начните с числа, которое вам дали:
Теперь, чтобы получить число, кратное этому, вам нужно иметь хотя бы простую факторизацию данного числа.