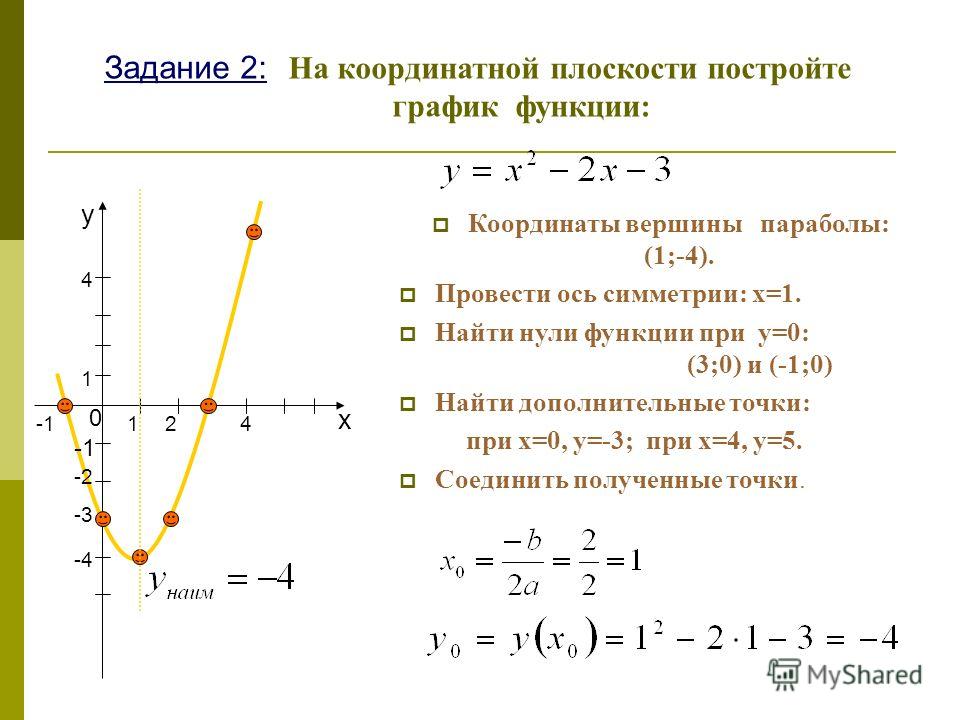
Графики квадратных уравнений — Концепция
Упрощение рациональных выражений объединяет все знания о разложении на множители общих множителей и многочленов. Когда упрощают рациональные функции , разложите числитель и знаменатель в члены, умножающие друг друга, и найдите эквиваленты единицы (чего-то, что делится само на себя). Включите круглые скобки вокруг любого выражения с «+» или «-», и если все термины в числителе сокращаются, там все еще есть один.
x пересечений у перехватывает вершина ось симметрии дискриминант заменить
Когда приходит время рисовать параболы, вы всегда можете составить таблицу значений и подставить точки x одну за другой, чтобы найти их точки y.
Первое, что вам нужно найти, это точку пересечения по оси y. Помните, что точка пересечения по оси y находится, если x=0. Обычно это очень быстрый и отличный способ найти хотя бы одну точку на вашей параболе.
Пересечение x связано со всеми теми вещами, которые вы изучали при изучении квадратичных уравнений, о которых мы говорим, чтобы найти пересечения x, которые вы могли бы использовать для определения количества пересечений x, а затем найти фактическое x перехватов, у вас есть выбор, какой метод использовать; разложение на множители, квадратичная формула, извлечение квадратных корней или завершение квадрата — все это варианты для вас.
 Все они занимают разное количество времени, некоторые из них более просты для решения одних задач, чем для других, поэтому вы захотите попрактиковаться в том, чтобы уметь определять, какой метод использовать в каких обстоятельствах, и ваши учителя, надеюсь, помогут вам с этим в классе. .
Все они занимают разное количество времени, некоторые из них более просты для решения одних задач, чем для других, поэтому вы захотите попрактиковаться в том, чтобы уметь определять, какой метод использовать в каких обстоятельствах, и ваши учителя, надеюсь, помогут вам с этим в классе. . Еще одна вещь, на которую вам следует обратить внимание, это то, открывается ли парабола вверх или вниз. Некоторые люди думают об этом как о смайлике, похожем на положительное значение, или грустном лице, отрицательном значении, по которому вы определяете, открывается ли парабола вверх или вниз. Это часто проявляется в тестах с множественным выбором. Много раз учителя давали вам правильные точки пересечения x и y, и они давали вам, например, один график, на котором парабола открывается один график, на котором парабола открывается так, как вы сможете. чтобы сказать, посмотрев на ваш опережающий коэффициент, если положительное значение параболы открывается, я напишу, что здесь, если положительное значение, оно открывается вниз, если отрицательное значение.

Хорошо, узкая или широкая парабола. Если ваше значение представляет собой целое число, например 2, 3, 4 или что-то в этом роде, или это может быть -2, -3, -4, тогда это будет узкая парабола. Если у вас есть дробь a, это будет широкая парабола, дробь a, помните, что a означает опережающий коэффициент, это коэффициент перед x в квадрате.
Последнее, на что вам, возможно, захочется обратить внимание, — это вершина, и напомню, что способ найти вершину — сначала найти значение x, где x равно –b больше 2a. Как только вы найдете свой номер x, подставьте это значение обратно в функцию, чтобы найти значение y. Вершина — это точка, в которой ваша парабола либо достигает своего основания, либо вершины, это действительно важная точка, она также помогает вам найти ось симметрии, помните, что ось симметрии — это уравнение x равно отрицательному b над 2a, и оно идет, это вертикальная линия, которая проходит прямо через вашу вершину. Это также поможет вам, когда вы рисуете график.
И последнее, но не менее важное: если вы все еще чувствуете, что испробовали все эти вещи, и у вас все еще нет хорошего представления о том, как выглядит ваша парабола, попробуйте составить таблицу значений, вы всегда можете использовать этот метод, и до тех пор, пока вы будьте осторожны с порядком операций, эти точки помогут вам нарисовать параболу, но эти вещи являются наиболее важными элементами квадратичной функции, поэтому важно, чтобы вы, ребята, знали, как использовать все эти навыки.

Решение квадратных уравнений с помощью графиков
Приступим к работеВведениеИспользование графиков для описания решенийИспользование графиков для определения решенийСводка Словарь ActivityJournal Activity
Давайте изучим, как решать квадратные уравнения, глядя на их графики.
Стандарты TEKS и ожидания учащихся
A(1) Стандарты математических процессов. Студент использует математические процессы, чтобы приобрести и продемонстрировать математическое понимание. Студент должен:
A(1)(C) выбрать инструменты, включая реальные объекты, манипуляции, бумагу и карандаш, а также соответствующие технологии, а также методы, включая ментальную арифметику, оценку и чувство чисел, для решения задач
A(1)(D) сообщать математические идеи, рассуждения и их последствия, используя различные представления, включая символы, диаграммы, графики и соответствующий язык
A(8) Квадратичные функции и уравнения. Учащийся применяет стандарты математического процесса для решения квадратных уравнений с помощью технологий и без них и оценивает обоснованность их решений. Студент формулирует статистические зависимости и оценивает их обоснованность на основе реальных данных. Студент должен:
Учащийся применяет стандарты математического процесса для решения квадратных уравнений с помощью технологий и без них и оценивает обоснованность их решений. Студент формулирует статистические зависимости и оценивает их обоснованность на основе реальных данных. Студент должен:
A(8)(A) решать квадратные уравнения, имеющие действительные решения, путем разложения на множители, извлечения квадратных корней, завершения квадрата и применения квадратной формулы учащийся будет использовать графические методы для решения уравнения.
Основные вопросы
Как решить квадратное уравнение, глядя на график?
Как узнать, сколько решений имеет квадратное уравнение?
Словарь
- Коэффициент
- y -Перехват
- Квадратное уравнение
- Функция
- x -Перехват
- Нули
- Корень
- Константа
Давайте рассмотрим способы использования графика для представления и определения решения квадратного уравнения.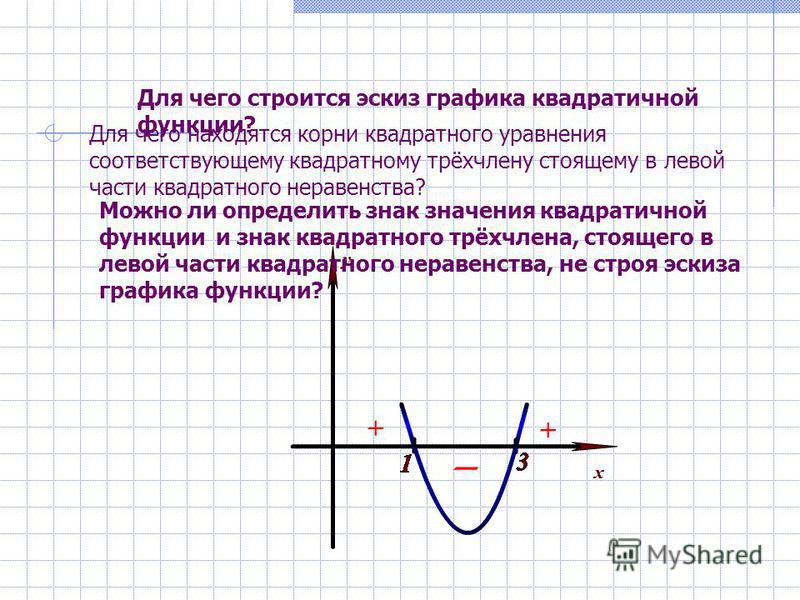
График и таблица ниже показывают точки для квадратичной функции y = х ² − х − 6.
Как график, так и таблицу значений можно использовать для решения уравнения x ² − x – 6 = 0, которое связано с функцией y = x ² – x − 6. Вы можете найти, когда y = 0 в таблице, и значение x в этой точке решит функцию. Значение x , где график пересекает ось x , также можно использовать для решения квадратного уравнения. Вы будете использовать аналогичный подход для поиска точек на графиках, удовлетворяющих определенным условиям.
Хотя все квадратичные функции имеют решение, оно не всегда может быть действительным числом. Следовательно, квадратичная функция может иметь два действительных корня, один действительный корень или ноль действительных корней.
Изучите три графика ниже. Нажмите на знак «плюс» у кнопки «Пуск», чтобы узнать больше об их решениях.
График — это изображение точек, которые делают функцию истинной. Например, на графике и в таблице ниже показаны точки для квадратичной функции y = x 9.0071 ² – х – 6.
Как график, так и таблицу значений можно использовать для решения уравнения x ² – x – 6 = 0, что связано с функцией y = x ² – x – 6 Нажимайте на каждый вопрос, чтобы проверить свой ответ.
Interactive
y = x ² – x – 6. Красная линия представляет график г = к. Сопоставьте каждый график с уравнением, перетащив график в соответствующий слот. Затем укажите правильные решения, представленные на графике, перетащив правильные упорядоченные пары в поле решения.
Видео
Посмотрите следующее видео, чтобы узнать больше о решении квадратного уравнения.
Источник
Оценка функций с помощью графического калькулятора, Gdawy Enterprises, You Tube
Практика
Найдите решение каждого квадратного уравнения с помощью графика. Нажмите на проблему, чтобы увидеть ответ.
График представляет собой полезное представление для определения решения квадратного уравнения. Чтобы лучше использовать график, представьте, что квадратное уравнение состоит из двух частей: a x ² + b x + c = k
Нарисуйте каждую часть квадратного уравнения: a x ² + b x + с = к и y = k
Найдите пересечение двух графиков. Координаты точек пересечения x сообщат вам значения x , которые являются решениями исходного уравнения.