Диаметр в радиус: Онлайн калькулятор диаметра круга. Как узнать диаметр круга, окружности.

Содержание

Калькулятор диаметра

Рассчитайте диаметр круга по длине окружности, радиусу или площади круга.

Что известно

Длина окружностиРадиусПлощадь круга

Известное равно

см

Размерность

СантиметрыМетрыМиллиметрыКилометры

Раcсчитать

Скопировать:

ссылку link

код code

Что такое диаметр круга?

Диаметр круга – это отрезок, соединяющий две точки на окружности и проходящий через центр круга.

Если же говорить, про другие фигуры, то диаметром называется максимальное расстояние между точками этой фигуры. Диаметр круга – не исключение, так как это самый длинный отрезок, который можно провести в границах окружности.

Если нарисовать диаметр, то он будет выглядеть следующим образом (выделен красным на рисунке ниже).

Теперь давайте рассмотрим, как можно найти диаметр и какие для этого существуют формулы.

Формулы определения диаметра круга

Для определения диаметра существует несколько разных способов в зависимости от известных частей круга.

По радиусу

Самая простая формула определения диаметра может быть использована, если известен радиус круга. Радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности. Диаметр равен двум радиусам.

d = r × 2

Где d – это диаметр, а r – радиус.

По длине окружности

Второй способ нахождения диаметра можно использовать тогда, когда известна длина окружности. Окружность — это замкнутая плоская кривая, все точки которой равноудалены от центра. Тако вот, диаметр равен длине окружности, делённой на число Пи.

d = L / π

Где d – это диаметр, а L – длина окружности, а π – константа, равная 3,14.

Эта формула, основывает на том, что отношение длины окружности к её диаметру всегда является постоянным числом, которое равняется примерно 3,14 и называется π (пи).

Через площадь круга

Чуть более изощренной и сложной является формула вычисления диаметра через площадь круга. Чаще всего требуется, наоборот, посчитать площадь круга, если известен диметр.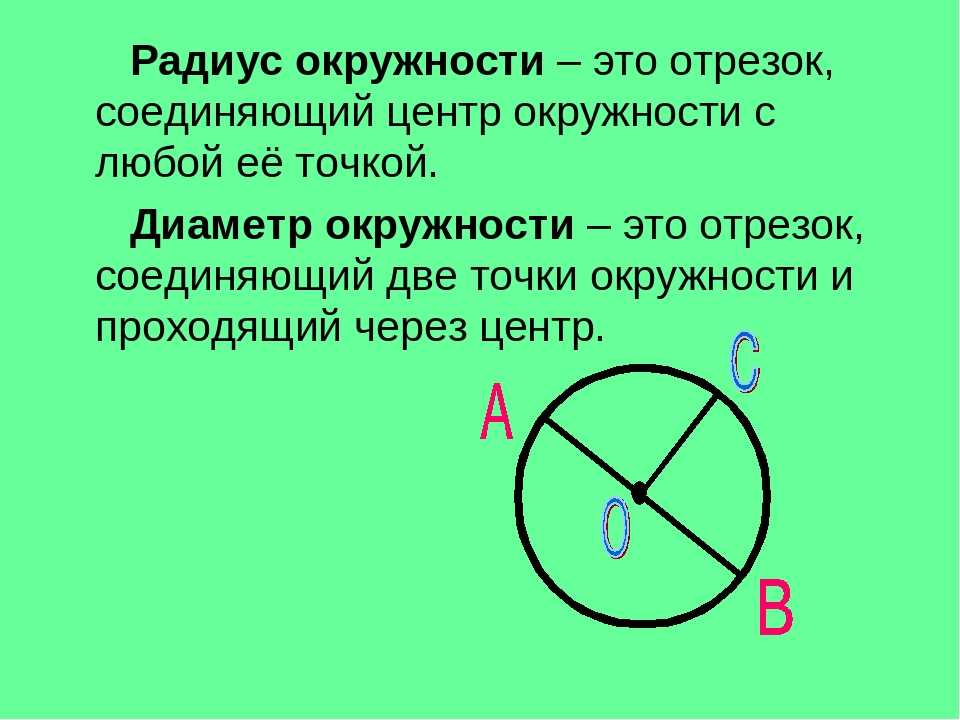 Но если задача стоит обратная, то формула расчёта будет выглядеть следующим образом:

d = 2 × (S/π)^1/2

Где d — диаметр, S — площадь круга, а π — константа, которая примерно равна 3,14.

То есть диаметр равен удвоенному корню частного площади круга к числу пи. Стоит отметить, что корень и степень ½ – это одно и то же.

Примеры вычисления диаметра

Давайте для закрепления рассмотрим несколько примеров.

Пример 1. Диаметр по длине окружности трубы 🚿

Предположим, у вас под рукой не оказалось штангенциркуля (устройства для измерения ширины изделий).

А вам требуется рассчитать диаметр действующей трубы, конца которой не видно. Для этого с помощью рулетки или сантиметра, вы можете измерить длину окружности, просто обернув рулетку вокруг трубы. А потом эту длину нужно будет разделить на 3,14. Если длина окружности трубы оказалась 31,4 сантиметра, тогда диаметр будет равен частному этой длинны к числу Пи, то есть:

d = 31,4 / 3,14 = 10 см.

Это и есть правильный ответ – 10 сантиметров.

Пример 2. Диаметр по колеса радиусу 🚲

Тут всё гораздо проще. Предположим, что вы знаете радиус колеса велосипеда – 10 дюймов. Какой будет диаметр?

Диаметру будет равен двум радиусам, то есть 20 дюймов.

Кстати, для справки, 1 дюйм = 2,54 сантиметра. То есть 10 дюймов = 25,4 сантиметра. В итоге диаметр колеса равен: 2 × 25,4 = 50,8 см.

❓Вопросы и ответы

И конечно же обратите внимание на ответы на часто задаваемые вопросы относительно расчёта длины диаметра круга.

Как работает ваш онлайн-калькулятор?

Просто. Вы выбираете, что известно: радиус, длина окружности или площадь круга (1), затем вписываете известное значение (2), выбираете размерность из мм, см, м, км (3) и нажимаете кнопку «рассчитать»?

Какие есть ещё калькуляторы для круга у вас на сайте?

org/Answer»>У нас есть различные калькуляторы, в частности калькуляторы: площади круга, длины окружности и диаметра. Для последнего калькулятор находится на данной странице.

Достаточно ли у меня данных для расчёта?

Для вычисления диаметра круга нужно что-то одно: радиус, длина окружности или площадь круга. Остальное вычислит наш калькулятор по специальным формулам, которые описаны выше.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим.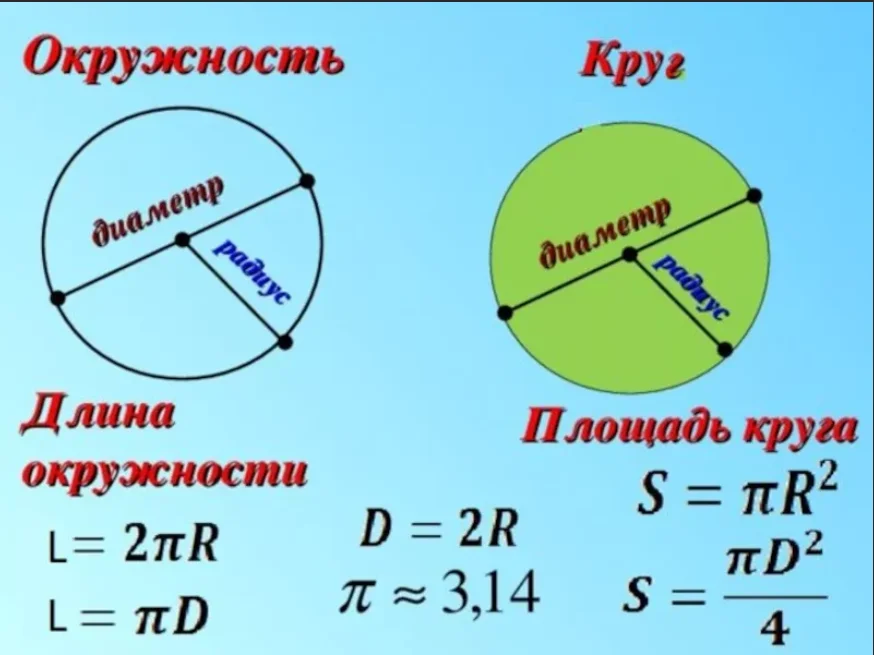 На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Если у автомобильного колеса параметр R16, то какой у него диаметр?

16 дюймов, а радиус 8 дюймов. Как ни странно, диаметр такого колеса (точнее диска колеса) составляет 16 дюймов, то есть 40,64 см. Очень часто люди называют радиус в качестве единицы измерения: мол, радиус 16 дюймов. Но тогда представьте, для какого трактора диаметр диска будет более 80 сантиметров.

Поделитесь в соцсетях

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.

Диаметр круга с учетом окружности Калькулятор

✖Окружность круга — это расстояние вокруг круга. ⓘ Окружность круга [C]

створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр

+10%

-10%

✖Диаметр окружности – это длина хорды, проходящей через центр окружности. ⓘ Диаметр круга с учетом окружности [D]

⎘ копия

👎

Формула

сбросить

👍

Диаметр круга с учетом окружности Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Окружность круга: 30 метр —> 30 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

9.54929658551372 метр —> Конверсия не требуется

< 4 Диаметр круга Калькуляторы

Диаметр круга с учетом окружности формула

Диаметр круга = Окружность круга/pi
D = C/pi

Что такое Круг?

Окружность — это базовая двумерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки. Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга. То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.

Copied!

Радиус, диаметр и длина окружности

Автор:

Malcolm McKinsey

16 января 2023 г.

В математике окружность — это множество всех компланарных точек, равноудаленных от данной точки. Эта заданная точка является центром круга и не лежит на круге. Окружность — это всего лишь набор точек (образующих изогнутую линию, возвращающуюся обратно на себя), которые находятся в одной плоскости и на одном и том же расстоянии от центральная точка , центр окружности.

Сам круг не является внутренним пространством, центральной точкой или пространством вне круга. Окружность — это линия, которая замыкается на себя.

Что такое круг

Без определяющей центральной точки круг безымянный. Центр круга — это то, как называется круг, поэтому возьмите круг и поместите Точка I в середину, и теперь у нас есть Окружность I.

Радиус круга

Чтобы добраться от центральной точки до фактический круг, мы движемся по прямой линии, называемой радиус . Радиус является мерой этого расстояния. Радиус круга является одним из способов измерения размера круга. Радиус всегда обозначается маленькой буквой r .

Вот отрезок IE с конечной точкой II в центре окружности и конечной точкой E на самой окружности:

Радиус окружности

Формула радиуса

Радиус равен 12\frac{1}{2} 21 диаметр. Вот формула радиуса:

Диаметр круга

Если у нас есть два радиуса вместе, они могут образовывать центральные углы или прямую линию, пересекающую окружность. Прямая линия, начинающаяся на окружности, проходящая через центр и снова достигающая окружности, имеет диаметр .

Вот диаметр Окружности 2 , построенный путем удлинения радиуса IE в другом направлении до точки P :

Диаметр окружности

Вместо того, чтобы идентифицировать это как два отдельных радиуса (множественное число от радиуса) , мы можем просто вызвать PE диаметр круга. Это расстояние по всей окружности. Диаметр круга всегда обозначается строчной буквой d .

Формула диаметра

Это означает, что диаметр в 2 раз больше радиуса окружности. Вот формула диаметра:

Круги появляются повсюду, как пицца на обеде!

Окружность круга

Для многоугольников периметр равен сумме длин их сторон. У кругов тоже есть периметр, но мы даем ему специальное слово: окружность (от латинского носить с собой) . Длина окружности – это расстояние по окружности.

Давайте посмотрим на отношение длины окружности к диаметру в этих кругах ниже. Вот Окружность 1 диаметром 1 метр и Окружность 2 диаметром 2 метра :

Окружность и отношение диаметра

Расстояние по всей окружности Окружность 1, длина окружности 1 , это 3,1415926 метров .

Длина окружности Окружность 2 равна 6,2831852 метра .

Установите длину окружности каждого круга на его диаметр. Эти формы соотношений. Вижу ничего?

Отношение длины окружности C к диаметру dd обоих кругов упростить до одинакового значения, 3,1415926 !

Отношение длины окружности, C , любого круга к его диаметру dd всегда равно одному и тому же значению, 3,1415926 , названный с использованием греческой буквы pi (как в яблочном пироге), который выглядит так: π .

При использовании пи допускается округление до двух знаков после запятой.

Формула окружности

Теперь мы можем подставить π вместо этого длинного числа и вывести формулу длины окружности ( C ) и диаметра ( d ). Когда мы умножаем обе части формулы на ( d ), мы получаем:

Теперь мы можем найти длину окружности ( C) любого круга, если мы знаем диаметр ( d) . Если у вас есть радиус, вы все равно можете найти длину окружности, так как радиус равен половине диаметра:

Как найти длину окружности

Давайте попробуем решить практическую задачу и найти длину окружности диаметром 20 .

Начните с подключения 20 для нашего диаметра ( d ) в нашей формуле:

Вы сделали это! Мы можем оставить наш ответ в виде ππ, поэтому длина окружности равна 20π единиц.

Детали окружности

Осталось покрыть еще части круга. Представьте, вы садитесь за вкусную, горячую пиццу, а она не разрезана! Вы отрезаете один срез, например:

Малая и большая дуги

Часть корки в отрезанном куске намного меньше, чем остальная часть корки. Эта меньшая часть является малой дугой окружности. Большая часть, оставшаяся окружность, является большой дугой.

Малая дуга это часть окружности, центральный угол которой меньше 180° . Большая дуга является частью окружности, центральный угол которой больше 180° .

Радиус, диаметр, длина окружности и площадь кругов0204 Тригонометрия для чайников

Исследуйте книгу Купить на Amazon

Круг — это геометрическая фигура, для идентификации и классификации которой нужны только две части: ее центр (или середина) и ее радиус (расстояние от центр в любую точку окружности).

После того, как вы выбрали точку в качестве центра круга и знаете, как далеко эта точка находится от всех точек, лежащих на окружности, вы можете нарисовать довольно приличную картину.

Измерив радиус, можно многое сказать о круге: его диаметр (расстояние от одной стороны до другой, проходящее через центр), его окружность (насколько далеко вокруг него) и его площадь (сколько квадратных дюймов, футов, ярдов, метров — что имеют ты — вписываешься в него).

Древние математики выяснили, что длина окружности всегда чуть более чем в три раза превышает диаметр окружности. С тех пор они сузили это «немногим более чем в три раза» до значения, называемого

пи (произносится как «пирог»), обозначаемого греческой буквой 9.0208 № .

Десятичное значение π не является точным — оно продолжается вечно, но в большинстве случаев люди называют его примерно равным 3,14 или 22/7, в зависимости от того, какая форма лучше подходит для конкретных вычислений.

Формула для вычисления длины окружности связана с π и диаметром:

Длина окружности: C = πd = 2 πr

d представляет меру диаметра, а r представляет меру радиуса. Диаметр всегда в два раза больше радиуса, поэтому работает любая форма уравнения.

Точно так же формула площади круга связана с π и радиусом:

Площадь круга: A = πr ²

Эта формула гласит: «Площадь равна пи в квадрате».

Найдите радиус, длину окружности и площадь круга, если его диаметр равен 10 футам в длину.

Если диаметр ( d ) равно 10, вы записываете это значение как d = 10 . Радиус равен половине диаметра, поэтому радиус равен 5 футам, или r = 5 . Вы можете найти длину окружности, используя формулу

Итак, длина окружности составляет около 31,5 фута. Вы находите площадь, используя формулу

, поэтому площадь составляет около 78,5 квадратных футов.