Как строить график квадратичной функции: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

Построение графика квадратичной функции – Документ 1 – УчМет

Конспект урока по алгебре в 8 классе

Бояринова Татьяна Вячеславовна,

учитель математики

первой категории

МБОУ Берендеевская СОШ
Лысковского района Нижегородской области

Тема урока: «Построение графиков квадратичных функций».

Тема урока: «Построение графиков квадратичных функций»

Тип урока: урок систематизации знаний.

Цель урока: повторить, систематизировать, обобщить изученный материал

Задачи урока:

Образовательные:

• отработать умение строить графики функций у = ах ², у=а(х–x₀)², у=ах²+y₀, у=а(х–x₀)²+ y₀, применяя правила преобразования графиков.

• проверить степень усвоения учащимися изученного материала;

Развивающие:

• развитие математической культуры, логического мышления, внимания, памяти, речи учащихся;

• развитие самостоятельности, способности к самоконтролю, самооценке.

Воспитательные:

• воспитание стремления достигать поставленную цель;

• воспитание чувства ответственности, уверенности в себе, умения работать в коллективе;

• воспитание интереса к предмету.

План урока.

1. Оргмомент.

2. Проверка домашнего задания.

3. Выступления учащихся.

4. Элементарные преобразования графиков квадратичной функции. Работа с программой «Математика 5-11кл.

   Практикум»

5. Решение тестовых заданий.

6. Подведение итогов урока.

7. Сообщение домашнего задания

Ход урока.

1. Приветствие учащихся, проверка готовности к уроку.

2. Консультанты (дежурные) докладывают о готовности учащихся к уроку.

3. При работе используется мультимедийный проектор и презентация, выполненная в программе Microsoft PowerPoint.

Тема сегодняшнего урока «Построение графика квадратичной функции». Слайд№1. Тема для вас не новая, но на прошлых уроках мы учились строить графики по пяти характеристическим точкам, а ещё раньше говорили о том, что график квадратичной функции можно строить с помощью преобразований растяжения, сжатия, сдвига (параллельного переноса) и симметрии. Сегодня мы должны всё вспомнить, привести полученные знания в систему.

Вначале мы послушаем ребят, которые выполняли индивидуальные задания. Слушая их, вы проверите правильность выполнения своей домашней работы. Затем потренируемся в преобразовании графиков. В конце урока разберём тестовые задания.

Сейчас я предоставляю слово Алексейчук Ксении, она напомнит нам, как построить график квадратичной функции по пяти характеристическим точкам.

Выступление 1 ученика.

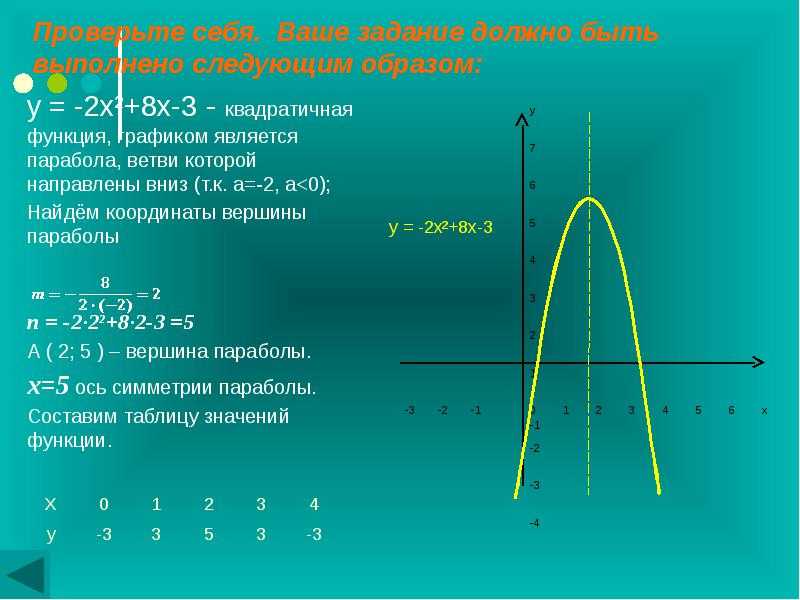
Задание. Построить график функции (Приложение 1). Слайд №2




Следующий выступающий Бойчук Юрий расскажет о построении графика квадратичной функции сжатием и растяжением вдоль оси ординат.

Слайд №3

Выступление 2 ученика.

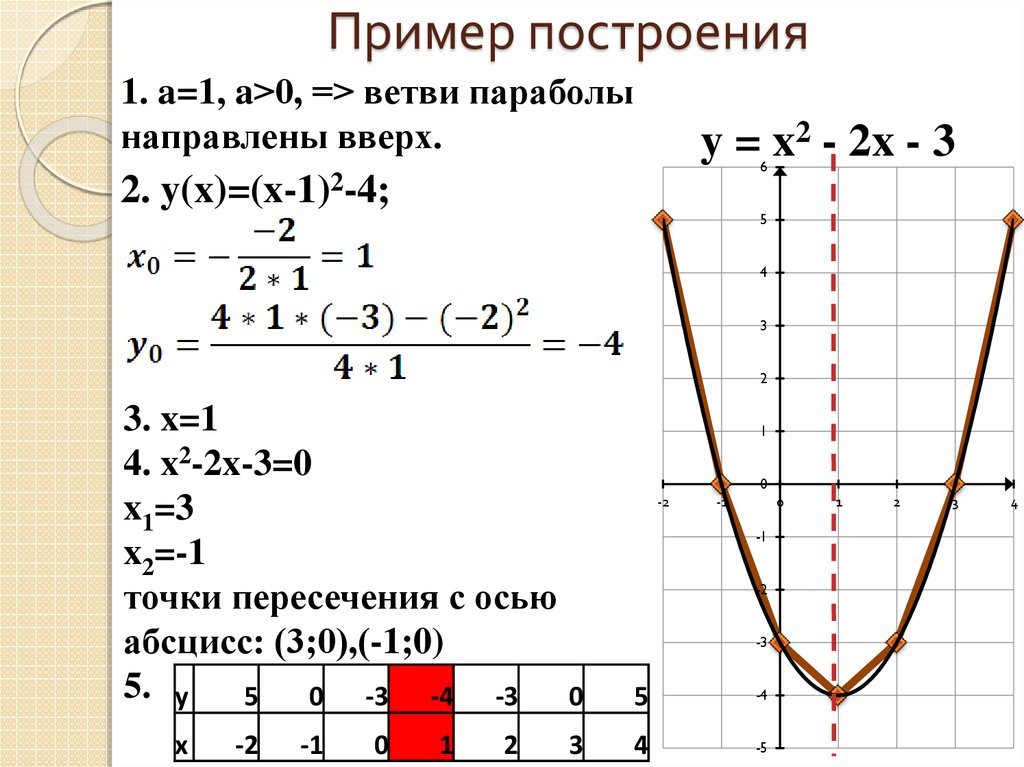
Задание. В одной координатной плоскости построить графики функций . (Приложение 2)

Теперь послушаем Бученкову Юлю, она расскажет, как построить график функции . Слайд №4

Выступление 3 ученика.

Задание. Построить график функции у=3(х+2)² –4 (Приложение 3)




слайд № 3 слайд № 4

Орлова Влада расскажет, как построить график функции сдвигом вдоль оси абсцисс

Выступление 4 ученика. Слайд №5

Задание. В одной координатной плоскости построить графики функций ; . (Приложение 4)

Андреева Надя расскажет, как построить график функции сдвигом вдоль оси ординат. Слайд № 6

Выступление 5 ученика.

Задание. В одной координатной плоскости построить графики функций ; . (Приложение 5)

слайд № 5 слайд № 6

Ребята рассказали о построении графика квадратичной функции с помощью преобразований сжатия, растяжения, сдвига (параллельного переноса) и симметрии.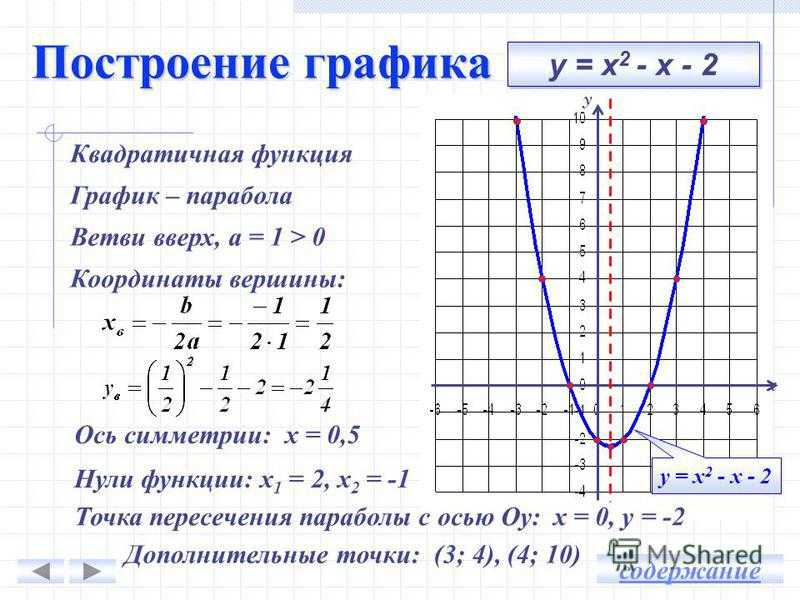 Все преобразования можно оформить в виде таблицы, которую желательно записать в тетрадь и запомнить, потому что этот материал пригодится вам при изучении алгебры в старших классах и построении более сложных графиков.

Слайд №7.

Преобразования графика квадратичной функции

у = ах2, а > 1	Растяжение графика функции у = х2вдоль оси ординат в а раз
у = ах2, 0<а<1	Сжатие графика функции у = х2вдоль оси ординат в а раз
у = –ах2	Симметрия графика функции у = ах2относительно оси абсцисс
у = а(х – х0)2	Сдвиг (параллельный перенос) графика функции у=ах2 вправо (если х0>0) или влево (еслих0 <0) вдоль оси абсцисс на |а| единиц
у = ах2 + у0	Сдвиг (параллельный перенос) графика функции у = ах2 вверх (если у0>0) или вниз (если у0 <0) вдоль оси ординат на |а| единиц
у = а(х – х0)2+ у0	Сдвиг (параллельный перенос) графика функции у=ах2 вдоль координатных осей

4. Далее учащимся предлагается поработать с программой «Математика 5-11кл. Практикум». Работая с этой программой ребята отрабатывают навыки преобразований графиков и написания формул квадратичной функции.

Ребята, сейчас мы с вами потренируемся выполнять преобразования графиков квадратичной функции. Вам необходимо совместить синюю параболу с красной, выполняя указанные действия. Синяя парабола задаётся формулой у = х². Следуя тем преобразованиям которые вы выполняете нужно записать формулу, которой задаётся красная парабола. Помните, что вы должны выполнить наименьшее количество действий.

Выполнение заданий.

5. Подошло время проверить ваши умения.

   Слайд №8.

слайд №7 слайд №8

ТЕСТ Слайды 9 — 16

1) Какая линия является графиком функции у =(х+2)² – 4

1. Прямая, проходящая через начало координат.

2. Прямая, не проходящая через начало координат.

3. Парабола.

4. Гипербола

2) В каких координатных четвертях расположен график функции у = -3,2 х² -1,8

1. 1 и 2

2. 3 и 4

3. 1,2,3,4

3) Парабола получена их графика функции у = 2,5х² с помощью двух параллельных переносов: сдвига на 3 единицы влево вдоль оси х и сдвига на 6 единиц вверх вдоль оси у. Графиком какой функции является парабола?

1. у = 2,5 (х -3)² +6

2. у = 2,5 (х +3)² — 6

3. у = 2,5 (х +3)² +6

4. у = 2,5 (х -3)² — 6

4) На рисунке построены графики функций: а) у = 1,6х² +2, б) у = — 1,6х² +2, в)у=1,6(х-2)², г) у = 1,6(х+2)² . Каждый график соотнесите с соответствующей ему формулой.

5) На рисунке изображен график одной из указанных функций. Выберите соответствующую формулу.

1. у = (х-2)² – 4

2. у = 0,5(х-2)² – 2

3. у = 0,5(х+2)² – 2

6) График функции у = 3х² – 2 получается из графика функции у = 3х² сдвигом на 2 единицы масштаба:

1. Вправо

2. Влево

3. Вверх

4. Вниз

7) Какая из перечисленных функций является ограниченной снизу?

1. у = 3х² – 1

2. у = 2х +2

3. у = –0,5(х–1)²

4. у = 5–2(х+1)²

8) Уравнение оси симметрии параболы у=2(х+1)²-8 имеет вид:

1. х = -8

2. х = -1

3. х = 2

4. х = 1

слайд № 9 слайд № 10

слайд № 11 слайд № 12

слайд № 13 слайд № 14

слайд № 15 слайд № 16

Все задания теста разбираются с классом.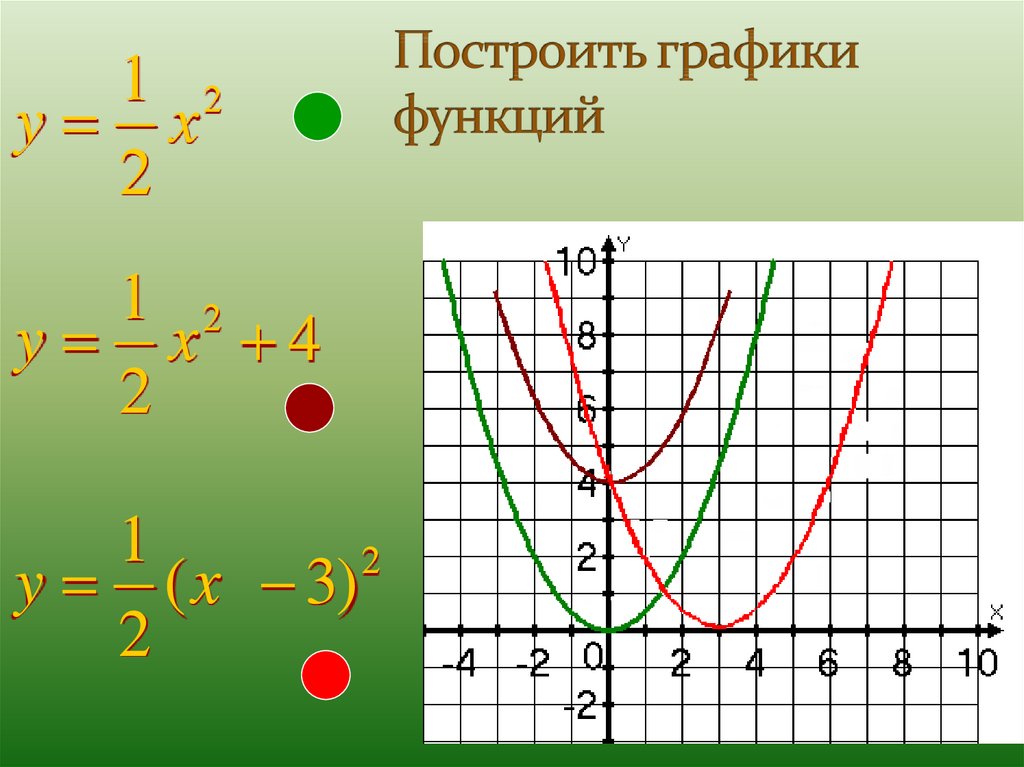 Наиболее активным учащимся можно поставит оценки.

6. На этом наш урок подходит к концу. Вы не должны забывать о том, что не всегда удобно использовать построение графика квадратичной функции по пяти характеристическим свойствам. Графики функций вида у = –ах², у = а(х – х₀)² , у = ах² + у₀ , у = а(х – х₀)²+ у₀ удобно строить с помощью преобразований сжатия, растяжения, сдвига (параллельного переноса) и симметрии. На следующем уроке мы готовимся к контрольной работе, которая покажет на сколько хорошо вы поработали в течении месяца. А сегодня на уроке хотелось бы отметить следующих учащихся …

7. Домашнее задание. Слайд № 17.

Постройте графики, применяя правила преобразования графиков функций:

у = 3х² – 2;

у = (х+2)² – 4;

у= –0,5(х–1)² ;

у=5–(х+1)²

слайд № 17

Приложение 1.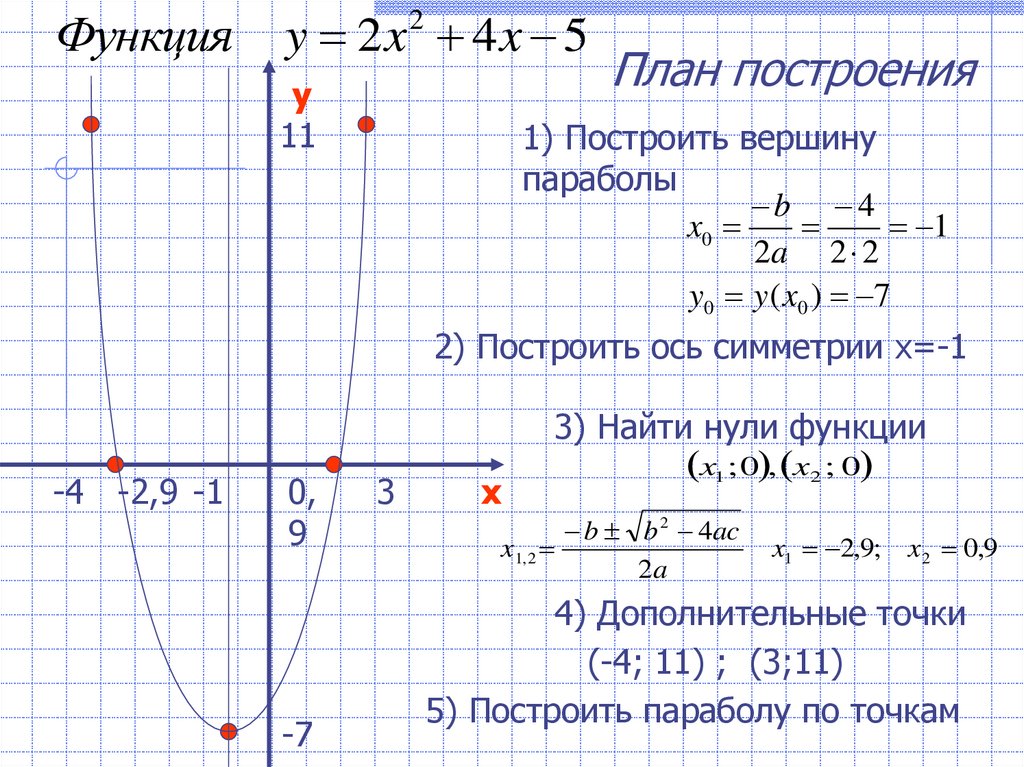

Приложение 2.

Приложение 3.




Приложение 4.

Приложение 5.

Список использованной литературы


1. Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров, М.В.Ткачёва, Н.Е.Фёдорова, М.И.Шабунин Алгебра. 8класс.-М.: Просвещение, 2007

2. Ю.М.Колягин, Ю.В.Сидоров, М.В.Ткачёва, Н.Е.Фёдорова, М.И.Шабунин

Изучение алгебры в 7-9 классах. -М.: Просвещение, 2002


Использованные материалы и Интернет-ресурсы

1. festival.1september.ru

2. http://konsaltmaster.ru/images/stories/sovi/22.jpg

3. http://www.123rf.com/photo_7554190_pile-of-four-old-books.html

Рекомендуемая литература

ax2 bx c график функции

Вы искали ax2 bx c график функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y x 2 bx c, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «ax2 bx c график функции».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как ax2 bx c график функции,y x 2 bx c,y x 2 c x,y x в квадрате парабола,y x2 bx c,ветвь параболы,ветвь параболы функция,ветвь параболы функция ее свойства и график,график квадратичная функция,график квадратичной,график квадратичной функции,график квадратичной функции y ax2 bx c,график квадратичной функции как строить,график квадратичной функции примеры,график парабола,график парабола функция,график параболы,график параболы как построить,график параболы как строить,график параболы формула,график параболы функции,график функции 2 y x bx c,график функции ax2 bx c,график функции y x 2 bx c,график функции y x2 bx c,график функции график параболы,график функции квадратного уравнения,график функции парабола,график функции парабола как строить,график функции парабола построить,график функции парабола примеры,график функции парабола формула,график функции параболы,графики квадратичной функции,графики квадратичных функций,графики параболы,графики параболы и их формулы,графики функций парабола,как называется график квадратичной функции,как найти вершину параболы графика функции y ax2 bx c,как найти нули функции по графику параболы,как построить график квадратичной функции,как построить график квадратного уравнения,как построить график параболы,как построить график параболы по уравнению,как построить график функции y ax2 bx c,как построить график функции квадратичной функции,как построить график функции квадратного уравнения,как построить график функции парабола,как построить квадратичную функцию,как построить параболу по квадратному уравнению,как построить функцию квадратичную,как решать квадратичная функция,как решать квадратичные функции,как решать функции квадратные,как решить квадратичную функцию,как составить таблицу значений функции параболы,как строить график квадратичной функции,как строить график параболы,как строить график параболы по уравнению,как строить график по уравнению параболы,как строить график функции парабола,как строить графики квадратичной функции,как строить квадратичную функцию,как строить квадратичную функцию график парабола,как строить параболу по квадратному уравнению,квадратичная парабола,квадратичная функция график,квадратичная функция как построить,квадратичная функция как решать,квадратичные функции и их графики,квадратичные функции как решать,квадратная функция и ее график,квадратные функции и ее график,нули функции параболы,парабола x в квадрате,парабола y x в квадрате,парабола график,парабола график как строить,парабола график функции,парабола график функции y ax2 bx c,парабола график функции примеры,парабола график функции формула,парабола графики функций,парабола квадратичная,парабола формула график функции,парабола функции,парабола функция,парабола функция ее свойства и график,параболы графики,параболы графики функций,параболы и их формулы,параболы построить график,построение графика параболы,построение параболы по квадратному уравнению,построение параболы по уравнению,построение параболы по уравнению квадратному,построить график квадратичной функции,построить график квадратичной функции примеры,построить график параболы,построить график функции квадратичной,построить параболу,постройте график квадратичной функции,приведите пример квадратичной функции график которой касается прямой y 4 в точке с абсциссой 2,пример квадратичной функции,решение квадратичной функции,с 3 график квадратичной функции,формула график парабола,формула графика параболы,формула квадратичной функции,формула параболы графика,функции парабола,функции параболы,функция ветвь параболы,функция квадратного уравнения,функция парабола,функция парабола ее свойства и график,функция параболы,функция параболы формула. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и ax2 bx c график функции. Просто введите задачу в окошко и нажмите «решить» здесь (например, y x 2 c x).

Решить задачу ax2 bx c график функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Графики квадратных уравнений

Квадратное уравнение это многочлен уравнение степень 2 . Стандартная форма квадратного уравнения:

0 знак равно а Икс 2 + б Икс + с

куда а , б и с все действительные числа и а ≠ 0 .

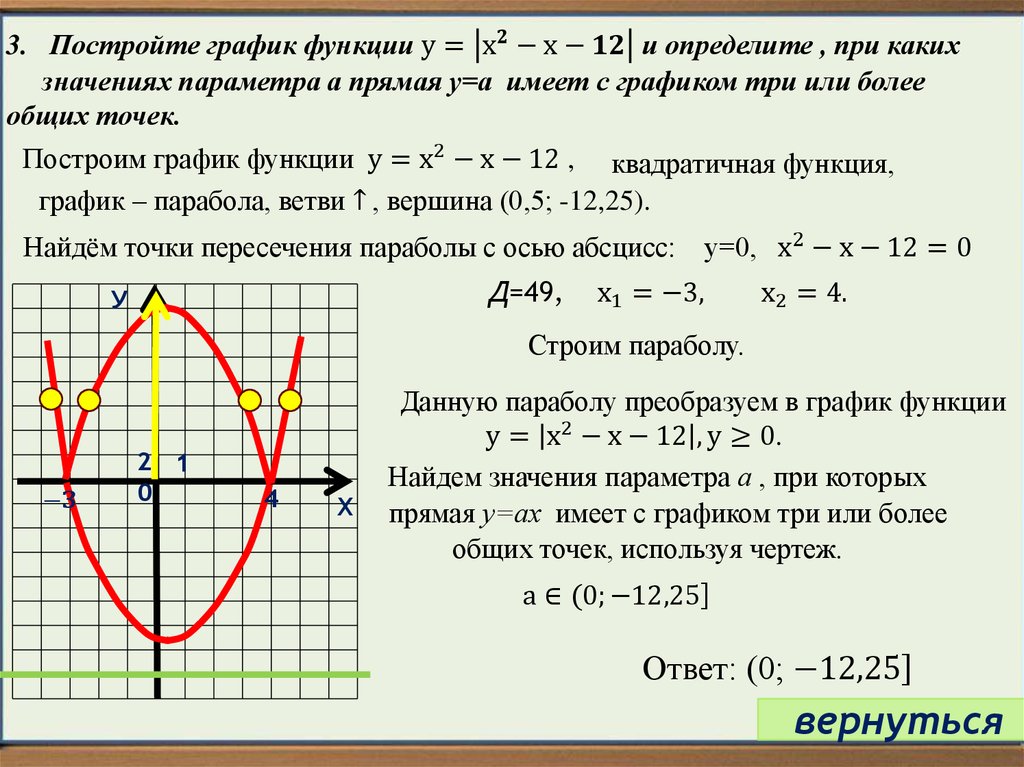
В этом уравнении ( 0 , с ) это у -пересечение параболы.

Знак а определяет, открывается ли парабола вверх или вниз: если а положительна, парабола раскрывается, и если а отрицательный, он открывается вниз.

Если а имеет высокое абсолютное значение, парабола «тощая»; если она имеет низкое абсолютное значение, парабола широкая.

Обратите внимание, что уравнение синей параболы имеет а знак равно 3 , положительное число больше 1 ; поэтому он тощий и открывается вверх. Он также имеет с знак равно − 2 , Итак у -перехват − 2 .

Уравнение красной параболы имеет а знак равно − 1 8 , отрицательное число близко к 0 ; поэтому он широкий и открывается вниз.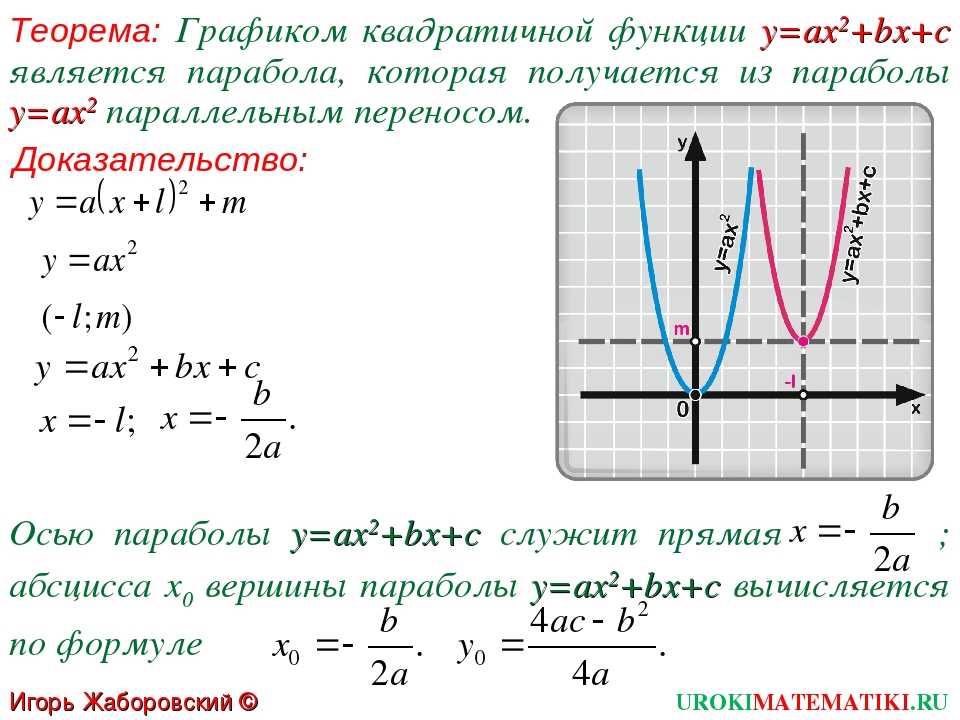 Он также имеет с знак равно − 6 , Итак у -перехват − 6 .

Даже если вы знаете, у -перехват, не всегда легко начертить график параболы, записанный в стандартной форме. Вы можете использовать таблицу значений ИЛИ преобразовать уравнение в другую форму, например:

Форма вершины : у знак равно а ( Икс − час ) 2 + к

Эта форма уравнения для квадратичной функции называется вершинная форма , потому что мы можем легко прочитать вершину параболы: точка ( час , к ) . Значение а такое же, как и в стандартной форме, и оказывает такое же влияние на график.

Пример 1:

График функции ф ( Икс ) знак равно − 1 2 ( Икс − 1 ) 2 + 2

Здесь уравнение имеет вершинную форму.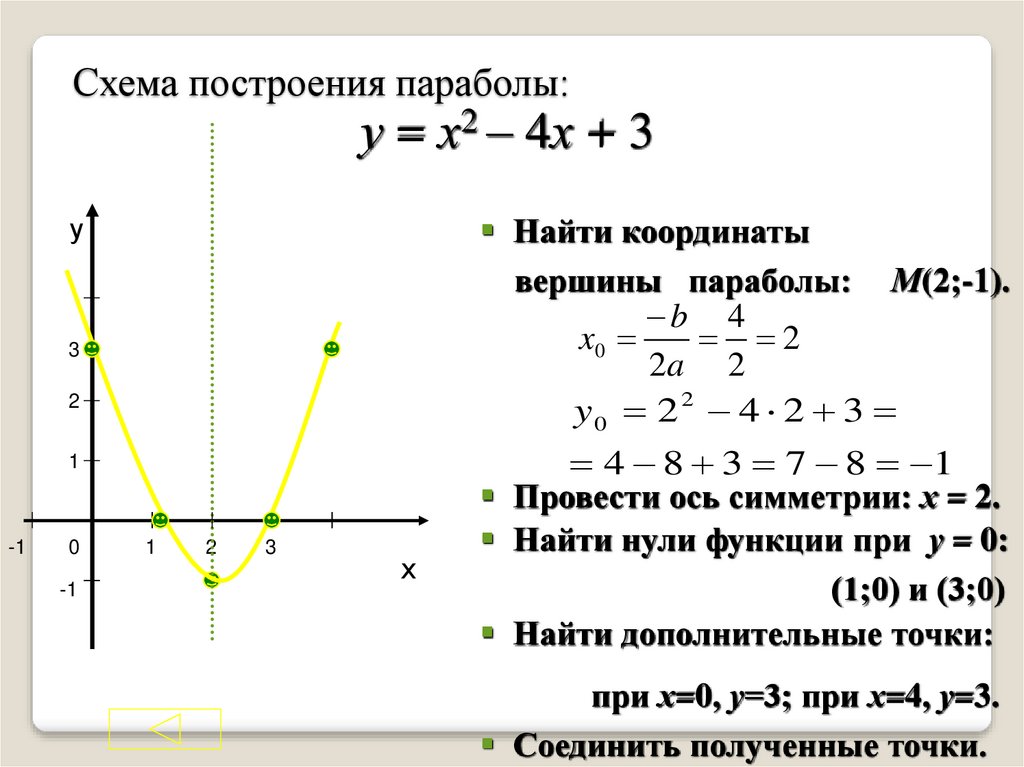 Вершина параболы ( 1 , 2 ) . С а знак равно − 1 2 , парабола открывается вниз и немного широка.

Если квадратное уравнение легко записать в факторизованная форма , вы можете использовать это, чтобы быстро нарисовать график.

Пример 2:

График функции у знак равно Икс 2 + Икс − 6 .

Это уравнение может быть факторизованный и написано как

у знак равно ( Икс + 3 ) ( Икс − 2 )

Здесь сразу видно, что когда Икс равно − 3 или же 2 , у равно 0 . Так ( − 3 , 0 ) и ( 2 , 0 ) являются Икс -перехватывает. С а в этом случае положителен (коэффициент Икс 2 является 1 ), график открывается вверх.

Математика и естественные науки: построение графика квадратичных функций в форме вершин

Мой замечательный муж подарил мне доску на Рождество, чтобы я могла начать снимать обучающие видео по математике. Потратив несколько дней на то, чтобы все настроить, все время размышляя, с чего начать, я решил проработать свои математические шпаргалки и сделать сопутствующие видео, начиная с Алгебры 2.

В этом посте видео-пример графическое изображение квадратичных функций в вершинной форме, ссылка на бесплатный справочный лист по математике, который можно использовать вместе с видео, и ссылка на квадратичную задачу в виде свободной вершинной формы.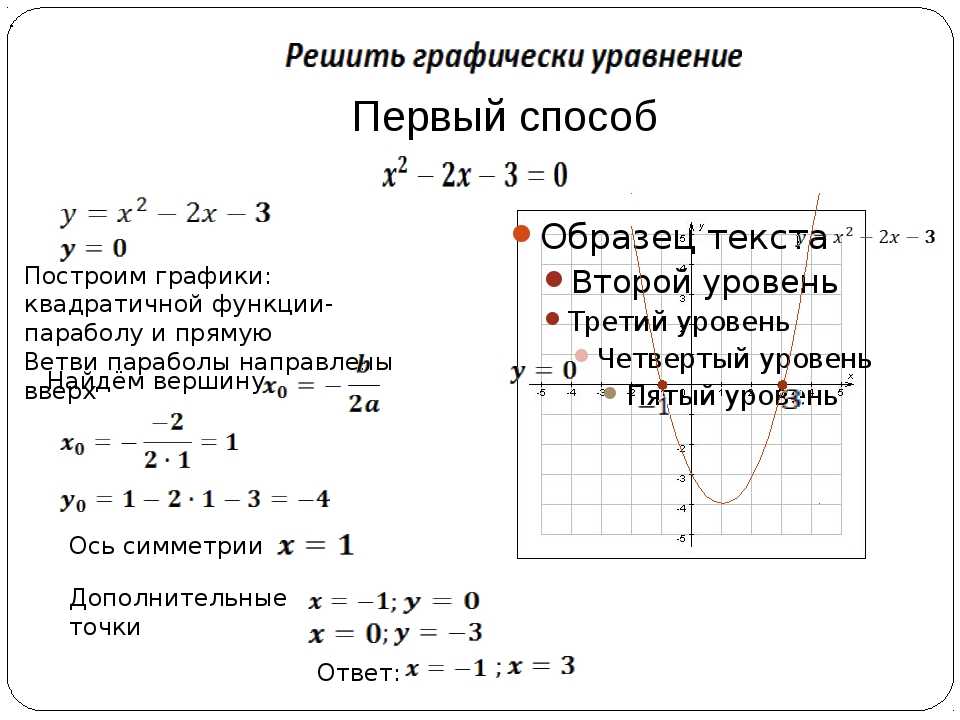

Ближе к концу видео находится ярлык для графического построения квадратичных форм вершин с шаблоном вместо таблицы.

Краткая история: Когда я переключился с офисной работы на преподавательскую, я подрабатывал в государственных школах Бостона, а также стажировался в компании по производству видео. Стажировка была неоплачиваемой, поэтому я согласился устроиться на первую попавшуюся работу — преподавать полный рабочий день или оплачивать монтаж видео. Преподавание открылось первым, а остальное уже история. Это порадовало и моих родителей. Тем не менее, мне всегда не хватало креативности, связанной с редактированием видео. Математика тоже творческая вещь, но вы понимаете, о чем я. Так что я рад объединить эти два аспекта, редактируя математические видеоролики. Прошло немного, так что я ржавый! Но я взволнован для вызова.

Если вы читали мой блог раньше, вы, вероятно, уже читали, как сильно я люблю алгебру. Мне нравится рост студентов в предмете и модели, которые формируются.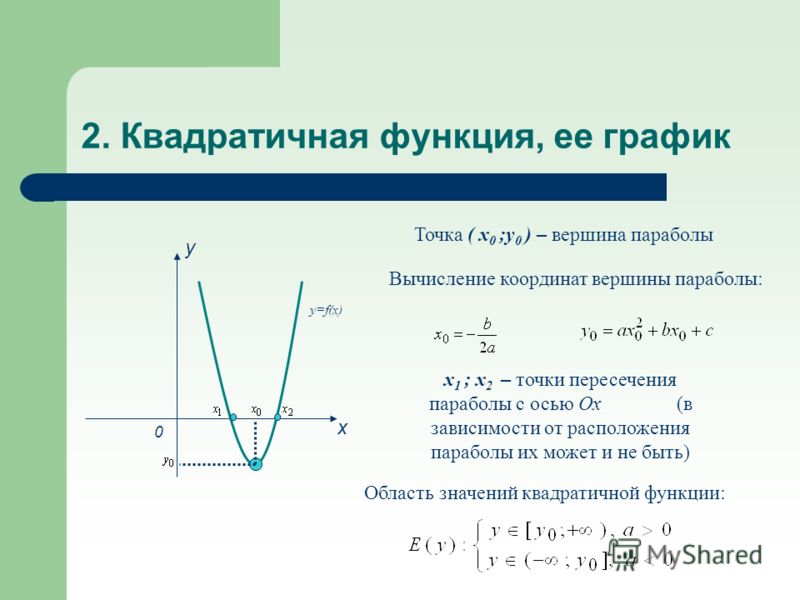 Мне нравится, как нервничают дети в начале учебного года, а потом в них появляется уверенность, что они могут справиться с трудными задачами.

Я надеюсь, что вы сможете использовать мои видео в качестве дополнения в своем классе в дополнительный день, в перевернутом классе для просмотра детьми дома или как способ принести алгебру 2 в свой класс домашней школы.

Ниже вы найдете ссылки на видео, бесплатную математическую шпаргалка по построению графиков квадратичных функций в вершинной форме и бесплатные карточки с заданиями в формате pdf.

Видео: 

Вот очень короткое видео, показывающее, как построить график квадратичного уравнения в вершинной форме:


А вот более длинное видео с дополнительными пояснениями, которое я добавил к исходному сообщению еще в 2020 году.

No related posts.