Как строится интервальный вариационный ряд: Интервальный вариационный ряд – просто и кратко

Интервальный вариационный ряд – просто и кратко



Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина  принимает слишком много различных значений . Зачастую ИВР появляется в результате изучения непрерывной характеристики объектов. Типично – это время, масса, размеры и другие физические величины. Вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.

В таких ситуациях затруднительно либо невозможно применить тот же подход, что для дискретного ряда. Это связано с тем, что ВСЕ варианты  различны (во многих случаях). И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, а фактически значения всё равно отличаются хоть какими-то микрограммами.

Поэтому здесь используется другой подход, а именно определяется интервал,

в пределах которого варьируются значения , затем этот интервал делится на частичные интервалы (обычно равной длины ) и по каждому частичному интервалу подсчитываются частоты  (либо ) – количество вариант, которые в него попали.
Если варианта попала на «стык» интервалов, то её относят к старшему интервалу.

Интервальный вариационный ряд  (ИВР) статистической совокупности  – это упорядоченное множество смежных интервалов и соответствующие им частоты, в сумме равные объёму совокупности. Дабы не плодить лишних букв и индексов, я никак не обозначил эти интервалы. Придирчивый читатель, к слову, наверняка заметил, что через  я обозначаю как исходные варианты, так и значения сгруппированного ряда.

Следует отметить, что исследуемая характеристика не обязана быть непрерывной, и мы как раз начнём с такой задачи:

Пример 6

По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в денежных единицах):

Составить вариационный ряд, построить гистограмму частот, гистограмму и полигон относительных частот + бонус: эмпирическую функцию распределения.

Решение: очевидно, что перед нами выборочная совокупность объема , и вопрос номер один: какой ряд составлять – дискретный или интервальный? Заметьте, что в вопросе задачи ничего не сказано о характере ряда. Строго говоря, цены дискретны и среди них даже есть одинаковые. Однако они могут быть округлены, да и разброс цен довольно велик. Поэтому здесь целесообразно провести интервальное разбиение.

Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.

Тактика действий похожа на работу с дискретным вариационным рядом. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:

Теперь начинаем вычёркивать числа из исходного списка и записываем их в соответствующие колонки нашей импровизированной таблицы:

После этого находим самое маленькое число в левой колонке (минимальное значение) и самое большое число – в правой (максимальное значение). Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
  ден. ед. – не забываем указывать размерность!

Вычислим размах вариации:
 ден. ед. – длина общего интервала, в пределах которого варьируется цена.

Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса: 

, где  – десятичный логарифм* от объёма выборки и
 – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

* есть на любом более или менее приличном калькуляторе.

В нашем случае получаем:  интервалов.

Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов следует проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
 – длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

И коль скоро мы прибавили 0,04, то по пяти частичным интервалам получается «перебор»: . Посему от самой малой варианты  отмеряем влево 0,1 влево

(половину «перебора») и к значению 5,7 начинаем прибавлять по , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины  (например, ) – они требуются почти во всех тематических задачах:

– убеждаемся в том, что самая большая варианта  вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой таблице обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем:

Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее. Варианта  попала на «стык» интервалов и, согласно озвученному выше правилу, её следует отнести к последующему интервалу .

В результате получаем интервальный вариационный ряд:

при этом обязательно убеждаемся в том, что ничего не потеряно:
, ОК.

…Да, кстати, все ли представили свой любимый товар, чтобы было интереснее разбирать это длинное решение? J

Точно также как и в дискретном случае, интервальный вариационный ряд можно
(и нужно) изобразить графически. И здесь у нас весьма большое разнообразие. Но сначала добавим в таблицу дополнительные столбцы и продолжим расчёты:

По каждому интервалу рассчитываем (не тушуемся): плотность частот , относительные частоты  (округляем их до 2 знаков после запятой), а также плотность относительных частот . Поскольку длина

частичного интервала , то вычисления заметно упрощаются:

Если интервалы имеют разные длины , то при нахождении плотностей каждую частоту нужно разделить на длину своего интервала: . Но у нас группировка равноинтервальная, да не абы какая, а с единичным частичным интервалом. Дело за чертежами. Один за другим:

2.2.1. Гистограммы

2.1.2. Эмпирическая функция распределения

| Оглавление |



построение, гистограмма, выборочная дисперсия и СКО

1. Построение интервального вариационного ряда по данным эксперимента
2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
3. Выборочная средняя, мода и медиана. Симметрия ряда
4. Выборочная дисперсия и СКО
5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
6. Алгоритм исследования интервального вариационного ряда
7. Примеры

п.1. Построение интервального вариационного ряда по данным эксперимента

Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.

Общий вид интервального вариационного ряда

Интервалы, \(\left.\left[a_{i-1},a_i\right.\right)\)	\(\left.\left[a_{0},a_1\right.\right)\)	\(\left.\left[a_{1},a_2\right.\right)\)	…	\(\left.\left[a_{k-1},a_k\right.\right)\)
Частоты, \(f_i\)	\(f_1\)	\(f_2\)	…	\(f_k\)

Здесь k — число интервалов, на которые разбивается ряд.

Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$

Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+\lfloor\log_2 N\rfloor $$ или, через десятичный логарифм: $$ k=1+\lfloor 3,322\cdot\lg N\rfloor $$

Скобка \(\lfloor\ \rfloor\) означает целую часть (округление вниз до целого числа).

Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=\left\lceil\frac Rk\right\rceil $$

Скобка \(\lceil\ \rceil\) означает округление вверх, в данном случае не обязательно до целого числа.

Алгоритм построения интервального ряда
На входе: все значения признака \(\left\{x_j\right\},\ j=\overline{1,N}\)

Шаг 1. Найти размах вариации \(R=x_{max}-x_{min}\)
Шаг 2. Найти оптимальное количество интервалов \(k=1+\lfloor\log_2 N\rfloor\)
Шаг 3. Найти шаг интервального ряда \(h=\left\lceil\frac{R}{k}\right\rceil\)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min},\ \ a_i=1_0+ih,\ \ i=\overline{1,k} $$ Шаг 5. Найти частоты \(f_i\) – число попаданий значений признака в каждый из интервалов \(\left.\left[a_{i-1},a_i\right.\right)\).
На выходе: интервальный ряд с интервалами \(\left.\left[a_{i-1},a_i\right.\right)\) и частотами \(f_i,\ i=\overline{1,k}\)

Заметим, что поскольку шаг h находится с округлением вверх, последний узел \(a_k\geq x_{max}\).

Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: \(N=100,\ x_{min}=142\ см,\ x_{max}=197\ см\).
Размах вариации: \(R=197-142=55\) (см)
Оптимальное число интервалов: \(k=1+\lfloor 3,322\cdot\lg ⁡100\rfloor=1+\lfloor 6,644\rfloor=1+6=7\)
Шаг интервального ряда: \(h=\lceil\frac{55}{5}\rceil=\lceil 7,85\rceil=8\) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142,\ a_i=142+i\cdot 8,\ i=\overline{1,7} $$

\(\left.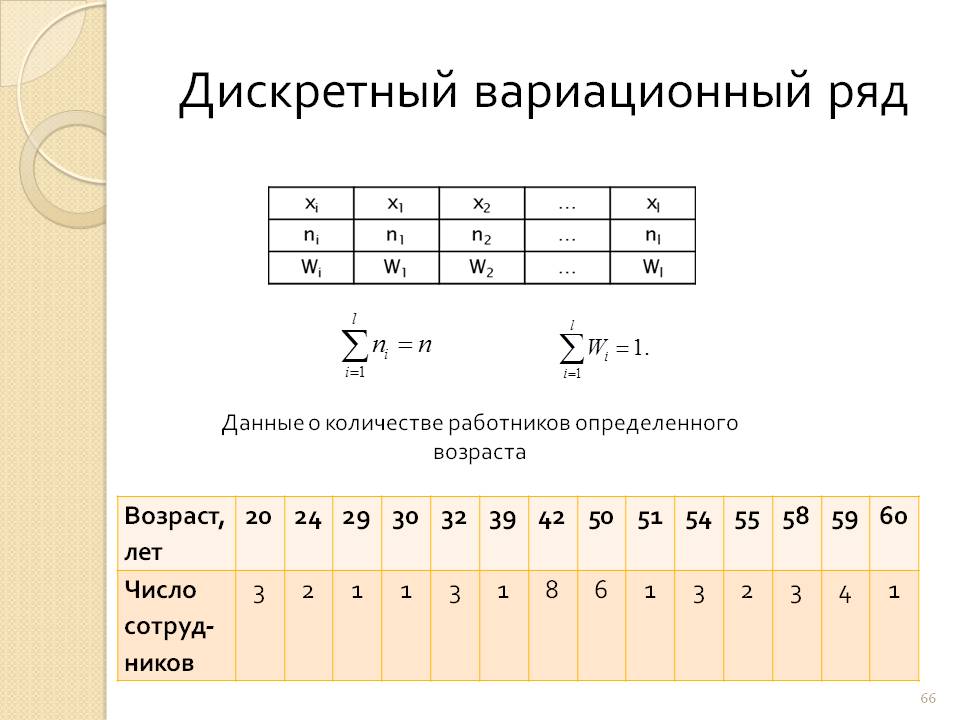 \left[a_{i-1},a_i\right.\right)\) cм

\(\left.\left[142;150\right.\right)\)

\(\left.\left[150;158\right.\right)\)

\(\left.\left[158;166\right.\right)\)

\(\left.\left[166;174\right.\right)\)

\(\left.\left[174;182\right.\right)\)

\(\left.\left[182;190\right.\right)\)

\(\left[190;198\right]\)

п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения

Относительная частота интервала \(\left.\left[a_{i-1},a_i\right.\right)\) — это отношение частоты \(f_i\) к общему количеству исходов: $$ w_i=\frac{f_i}{N},\ i=\overline{1,k} $$

Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.

Полигон относительных частот интервального ряда – это ломаная, соединяющая точки \((x_i,w_i)\), где \(x_i\) — середины интервалов: \(x_i=\frac{a_{i-1}+a_i}{2},\ i=\overline{1,k}\).

Накопленные относительные частоты – это суммы: $$ S_1=w_1,\ S_i=S_{i-1}+w_i,\ i=\overline{2,k} $$ Ступенчатая кривая \(F(x)\), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки \((x_i,S_i)\), где \(x_i\) — середины интервалов.

Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:

i	1	2	3	4	5	6	7
\(\left.\left[a_{i-1},a_i\right.\right)\) cм	\(\left.\left[142;150\right.\right)\)	\(\left.\left[150;158\right.\right)\)	\(\left.\left[158;166\right.\right)\)	\(\left. \left[166;174\right.\right)\)	\(\left.\left[174;182\right.\right)\)	\(\left.\left[182;190\right.\right)\)	\(\left[190;198\right]\)
\(f_i\)	4	7	11	34	33	8	3

Найдем середины интервалов, относительные частоты и накопленные относительные частоты:

\(x_i\)	146	154	162	170	178	186	194
\(w_i\)	0,04	0,07	0,11	0,34	0,33	0,08	0,03
\(S_i\)	0,04	0,11	0,22	0,56	0,89	0,97	1

Построим гистограмму и полигон:


Построим кумуляту и эмпирическую функцию распределения:


Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= \begin{cases} 0,\ x\leq 146\\ 0,04,\ 146\lt x\leq 154\\ 0,11,\ 154\lt x\leq 162\\ 0,22,\ 162\lt x\leq 170\\ 0,56,\ 170\lt x\leq 178\\ 0,89,\ 178\lt x\leq 186\\ 0,97,\ 186\lt x\leq 194\\ 1,\ x\gt 194 \end{cases} $$

п.

k x_iw_i $$

Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+\frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
\(h\) – шаг интервального ряда;
\(x_o\) — нижняя граница модального интервала;
\(f_m,f_{m-1},f_{m+1}\) — соответственно, частоты модального интервала, интервала слева от модального и интервала справа.

Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+\frac{0,5-S_{me-1}}{w_{me}}h $$ где
\(h\) – шаг интервального ряда;
\(x_o\) — нижняя граница медианного интервала;
\(S_{me-1}\) накопленная относительная частота для интервала слева от медианного;
\(w_{me}\) относительная частота медианного интервала.

Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. k x_iw_i=171,68\approx 171,7\ \text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: \begin{gather*} x_o=166,\ f_m=34,\ f_{m-1}=11,\ f_{m+1}=33,\ h=8\\ M_o=x_o+\frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\\ =166+\frac{34-11}{(34-11)+(34-33)}\cdot 8\approx 173,7\ \text{(см)} \end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: \begin{gather*} x_o=166,\ w_m=0,34,\ S_{me-1}=0,22,\ h=8\\ \\ M_e=x_o+\frac{0,5-S_{me-1}}{w_me}h=166+\frac{0,5-0,22}{0,34}\cdot 8\approx 172,6\ \text{(см)} \end{gather*} \begin{gather*} \\ X_{cp}=171,7;\ M_o=173,7;\ M_e=172,6\\ X_{cp}\lt M_e\lt M_o \end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом \(\frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=\frac{2,0}{0,9}\approx 2,2\lt 3\), т.е. распределение умеренно асимметрично.

п.4. Выборочная дисперсия и СКО

Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: \begin{gather*} D=\frac1N\sum_{i=1}^k(x_i-X_{cp})^2 f_i=\frac1N\sum_{i=1}^k x_i^2 f_i-X_{cp}^2 \end{gather*} где \(x_i\) — середины интервалов: \(x_i=\frac{a_{i-1}+a_i}{2},\ i=\overline{1,k}\). 2w_i\)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.

п.7. Примеры

Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.

1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18,\ \ x_{max}=38,\ \ N=30 $$ Размах вариации: \(R=38-18=20\)
Оптимальное число интервалов: \(k=1+\lfloor\log_2⁡ 30\rfloor=1+4=5\)
Шаг интервального ряда: \(h=\lceil\frac{20}{5}\rceil=4\)
Получаем узлы ряда: $$ a_0=x_{min}=18,\ \ a_i=18+i\cdot 4,\ \ i=\overline{1,5} $$

\(\left. \left[a_{i-1},a_i\right.\right)\) лет

\(\left.\left[18;22\right.\right)\)

\(\left.\left[22;26\right.\right)\)

\(\left.\left[26;30\right.\right)\)

\(\left.\left[30;34\right.\right)\)

\(\left.\left[34;38\right.\right)\)

Считаем частоты для каждого интервала. Получаем интервальный ряд:

\(\left.\left[a_{i-1},a_i\right.\right)\) лет	\(\left.\left[18;22\right.\right)\)	\(\left.\left[22;26\right.\right)\)	\(\left.\left[26;30\right.\right)\)	\(\left.\left[30;34\right.\right)\)	\(\left.\left[34;38\right.\right)\)
\(f_i\)	1	7	12	6	4

2) Составляем расчетную таблицу:

\(x_i\)	20	24	28	32	36	∑
\(f_i\)	1	7	12	6	4	30
\(w_i\)	0,033	0,233	0,4	0,2	0,133	1
\(S_i\)	0,033	0,267	0,667	0,867	1	—
\(x_iw_i\)	0,667	5,6	11,2	6,4	4,8	28,67
\(x_i^2w_i\)	13,333	134,4	313,6	204,8	172,8	838,93

3) Строим полигон и кумуляту


Эмпирическая функция распределения: $$ F(x)= \begin{cases} 0,\ x\leq 20\\ 0,033,\ 20\lt x\leq 24\\ 0,267,\ 24\lt x\leq 28\\ 0,667,\ 28\lt x\leq 32\\ 0,867,\ 32\lt x\leq 36\\ 1,\ x\gt 36 \end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=\sum_{i=1}^k x_iw_i\approx 28,7\ \text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка). 2}\approx 4,2\)
Коэффициент вариации: \(V=\frac{4,2}{28,7}\cdot 100\text{%}\approx 14,7\text{%}\lt 33\text{%}\)
Выборка однородна. Найденное значение среднего возраста \(X_{cp}=28,7\) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).

4.5.2 Визуализация графика прямоугольников и усов

Содержание

Текст начинается

Навигация по теме

• 4 Исследование данных
  • 4.5 Меры рассеивания
    • 4.5.1 Расчет диапазона и межквартильный диапазон
    • 4.5.2 Визуализация графика прямоугольников и усов
    • 4.5.3 Расчет дисперсии и стандартного отклонения

Диаграмма с ячейками и усами, иногда называемая просто диаграммой с ячейками, представляет собой тип диаграммы, которая помогает визуализировать сводку из пяти чисел. Он не показывает распределение так подробно, как гистограмма, но особенно полезен для определения того, является ли распределение асимметричным и есть ли в наборе данных потенциальные необычные наблюдения (выбросы). Коробчатая диаграмма идеальна для сравнения распределений, потому что сразу видны центр, разброс и общий диапазон.

На рис. 4.5.2.1 показано, как построить диаграмму с прямоугольниками и усами на основе пятизначной сводки.

Описание к рисунку 4.5.2.1

На рисунке показана форма прямоугольника и графика «усов», а также положение минимума, нижнего квартиля, медианы, верхнего квартиля и максимума.

На графике в виде прямоугольника и усов:

• Левая и правая стороны прямоугольника представляют собой нижний и верхний квартили. Коробка охватывает межквартильный интервал, где находится 50% данных.
• Вертикальная линия, разделяющая прямоугольник пополам, является медианой. Иногда среднее значение также обозначается точкой или крестиком на диаграмме.
• Усы — это две линии вне прямоугольника, идущие от минимума к нижнему квартилю (начало прямоугольника), а затем от верхнего квартиля (конец прямоугольника) к максимуму.
• График обычно представлен с осью, указывающей значения (не показаны на рисунке 4.5.2.1).
• График с прямоугольниками и усами может быть представлен горизонтально, как на рисунке 4.5.2.1, или вертикально.

Разновидность графика прямоугольников и усов ограничивает длину усов максимум 1,5-кратным межквартильным диапазоном. То есть ус достигает значения, которое находится дальше всего от центра, но все еще находится в пределах расстояния, в 1,5 раза превышающего межквартильный диапазон от нижнего или верхнего квартиля. Точки данных, которые находятся за пределами этого интервала, представлены точками на графике и считаются потенциальными выбросами.

Пример 1. Сравнение трех диаграмм «ящик и ус»

Три графика с ячейками и усами на диаграмме 4. 5.2.1 были созданы с использованием программного обеспечения R. Что вы можете сказать о трех дистрибутивах?

Таблица данных для диаграммы 4.5.2.1 

Таблица данных для схемы 4.5.2.1
Сводка таблицы
В этой таблице отображаются результаты таблицы данных для диаграммы 4.5.2.1. Информация сгруппирована по измерениям (появляются в виде заголовков строк), распределению A, распределению B и распределению C (появляются в виде заголовков столбцов).

Измерение	Распределение А	Распределение B	Распределение C
Минимум	0,00	0,11	0,14
Нижний квартиль (Q1)	0,02	0,37	0,69
Медиана (Q2)	0,11	0,48	0,88
Верхний квартиль (Q3)	0,32	0,58	0,95
Максимум	0,86	0,93	1,00

• Центр распределения А является самым низким из трех распределений (медиана 0,11). Распределение имеет положительную асимметрию, поскольку ус и полубокс длиннее справа от медианы, чем слева.
• Распределение B приблизительно симметрично, так как оба полубокса имеют почти одинаковую длину (0,11 слева и 0,10 справа). Это наиболее концентрированное распределение, поскольку межквартильный размах составляет 0,21 по сравнению с 0,30 для распределения А и 0,26 для распределения С.
• Центр распределения C является самым высоким из трех распределений (медиана 0,88). Распределение C имеет отрицательную асимметрию, поскольку ус и полубокс длиннее слева от медианы, чем справа.

Все три распределения содержат потенциальные выбросы. Возьмем, к примеру, распределение А. Межквартильный диапазон составляет Q3 — Q1 = 0,32 — 0,02 = 0,30. Согласно определению, используемому функцией в программном обеспечении R, все значения, превышающие Q3 + 1,5 x (Q3 — Q1) = 0,32 + 1,5 x 0,30 = 0,77, находятся за пределами правого уса и обозначены кружком. В распределении A есть два потенциальных выброса.



• Статистика: сила данных! — Главная страница
• 1 Данные, статистическая информация и статистика
• 2 Источники данных
• 3 Сбор и обработка данных
• 4 Исследование данных
• 5 Визуализация данных
• Библиография
• Глоссарий

Сообщить о проблеме на этой странице

Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?

Пожалуйста, свяжитесь с нами и дайте нам знать, как мы можем вам помочь.

Уведомление о конфиденциальности

Дата изменения:

2021-09-02

Интервальные данные и как их анализировать

Опубликован в 28 августа 2020 г. к Прита Бхандари. Отредактировано 17 ноября 2022 г.

Интервальные данные измеряются по числовой шкале, которая имеет равные расстояния между соседними значениями. Эти расстояния называются «интервалами».

На интервальной шкале нет истинного нуля, что отличает ее от шкалы отношений. На интервальной шкале ноль — это произвольная точка, а не полное отсутствие переменной.

Общие примеры интервальных шкал включают стандартные тесты, такие как SAT, и психологические опросники.

Содержание

1. Уровни измерения
2. Интервальные шкалы соотношений
3. Примеры интервальных данных
4. Интервальный анализ данных
5. Часто задаваемые вопросы об интервальных данных

Уровни измерения

Интервал — это один из четырех иерархических уровней измерения. Уровни измерения указывают, насколько точно записываются данные. Чем выше уровень, тем сложнее измерение.

В то время как номинальные и порядковые переменные являются категориальными, интервальные и относительные переменные являются количественными. На количественных данных может быть выполнено гораздо больше статистических тестов, чем на категориальных.

Интервальные и относительные шкалы

Шкалы интервалов и отношений имеют одинаковые интервалы между значениями. Однако только шкалы отношений имеют истинный нуль, который представляет собой полное отсутствие переменной.

шкалы Цельсия и Фаренгейта являются примерами интервальных шкал . Каждая точка на этих шкалах отличается от соседних точек интервалом ровно в один градус. Разница между 20 и 21 градусами идентична разнице между 225 и 226 градусами.

Однако эти шкалы имеют произвольные нулевые точки — ноль градусов — это не самая низкая возможная температура.

Поскольку истинного нуля не существует, вы не можете умножать или делить баллы на интервальных шкалах. 30°С не в два раза горячее 15°С. Аналогично, -5°F не вполовину холоднее, чем -10°F.

Напротив, шкала температуры Кельвина представляет собой шкалу отношения . По шкале Кельвина ничего не может быть холоднее 0 К. Поэтому соотношения температур в Кельвинах имеют смысл: 20 К в два раза горячее, чем 10 К9.0003

Примеры интервальных данных

Психологические понятия, такие как интеллект, часто количественно оцениваются посредством операционализации в тестах или инвентаризациях. Эти тесты имеют равные интервалы между оценками, но в них нет истинных нулей, потому что они не могут измерить «нулевой интеллект» или «нулевую личность».

Тип	Примеры
Стандартные тесты	IQ СБ ГРЭ GMAT
Психологические опросники	Опросник депрессии Бека Прогрессивные матрицы Raven Тесты личностных качеств Большой пятерки

Чтобы определить, является ли шкала интервальной или порядковой, рассмотрите, используются ли в ней значения с фиксированными единицами измерения, где расстояния между любыми двумя точками имеют известный размер. Например:

• Шкала оценки боли от 0 (нет боли) до 10 (сильнейшая возможная боль) является интервальной.
• Шкала оценки боли, которая идет от отсутствия боли, легкой боли, умеренной боли, сильной боли до самой сильной боли, является порядковой.

Обработка ваших данных как интервальных данных позволяет выполнять более мощные статистические тесты.

Интервальный анализ данных

Чтобы получить обзор ваших данных, вы можете сначала собрать следующую описательную статистику:

• частотное распределение в числах или процентах,
• мода, медиана или среднее значение для нахождения центральной тенденции,
• диапазон, стандартное отклонение и дисперсия для обозначения изменчивости.

Пример интервальных данныхВы собираете результаты SAT группы из 59 выпускников из города А. Участники теста могут набрать от 400 до 1600 баллов по SAT.

Распределение

Таблицы и графики можно использовать для организации данных и визуализации их распределения.

Чтобы упорядочить данные, введите их в сгруппированную таблицу частотного распределения.

Оценка SAT	Частота
401 – 600	0
601 – 800	4
801 – 1000	15
1001 – 1200	19
1201 – 1400	16
1401 – 1600	5

Чтобы визуализировать данные, нанесите их на многоугольник частотного распределения. Постройте группы по оси x и частоты по оси y и соедините среднюю точку каждого интервала с помощью линий.

Центральная тенденция

Из вашего графика видно, что ваши данные распределены довольно нормально. Поскольку перекоса нет, чтобы найти, где находится большинство ваших значений, вы можете использовать все 3 общих показателя центральной тенденции: моду, медиану и среднее значение.

Режим является наиболее часто повторяющимся значением в вашем наборе данных. В этом случае режим отсутствует, поскольку каждое значение появляется только один раз.

Медиана — это значение, находящееся точно в середине набора данных. Чтобы найти среднее положение, возьмите значение в ( n +1)/2, где n — общее количество значений.

( n +1)/2 = (59+1)/2 = 30

Медиана находится на 30-й позиции и имеет значение 1120 .

Среднее использует все значения, чтобы дать вам единое число для центральной тенденции ваших данных. Чтобы найти среднее значение, используйте формулу ⅀x/ n . Суммируйте все значения (⅀x) и разделите сумму на n.

⅀x = 65850
n = 59
⅀x/ n = 65850/59 = 1116,1

 

Среднее обычно считается лучшей мерой центральной тенденции, когда у вас есть нормально распределенные количественные данные. Это потому, что он использует каждое значение в вашем наборе данных для вычисления, в отличие от моды или медианы.

Изменчивость

Диапазон, стандартное отклонение и дисперсия описывают, насколько разбросаны ваши данные. Диапазон вычислить проще всего, в то время как стандартное отклонение и дисперсия более сложны, но и более информативны.

Чтобы найти диапазон, вычтите наименьшее из самого высокого значения в вашем наборе данных. Наше максимальное значение — 1500, а минимальное — 620.

Диапазон = 1500 – 620 = 880

Стандартное отклонение ( s ) — это средняя величина изменчивости в вашем наборе данных. Он говорит вам, в среднем, насколько далеко каждая оценка находится от среднего значения. Большинство компьютерных программ легко вычислят для вас стандартное отклонение. Если вы хотите сделать это вручную, выполните следующие действия.

с = 210,42

Дисперсия ( с ² ) представляет собой среднеквадратичное отклонение от среднего значения. Отклонение от среднего — это разница между значением в вашем наборе данных и средним значением. Чтобы найти дисперсию, возведите стандартное отклонение в квадрат.

с ² = 44279,36

Статистические тесты

Теперь, когда у вас есть обзор ваших данных, вы можете выбрать подходящие тесты для создания статистических выводов. При нормальном распределении интервальных данных возможны как параметрические, так и непараметрические критерии.

Параметрические тесты обладают большей статистической мощностью, чем непараметрические тесты, и позволяют делать более обоснованные выводы относительно ваших данных. Однако для применения параметрических тестов ваши данные должны соответствовать нескольким требованиям.

Следующие параметрические тесты являются одними из наиболее распространенных, применяемых для проверки гипотез об интервальных данных.

Цель	Образцы или переменные	Тест	Пример
Сравнение средств	2 образца	Т-тест	Какова разница в средних баллах SAT учащихся двух разных средних школ?
Сравнение средств	3 или более образцов	Анализ	В чем разница в средних баллах SAT учащихся трех программ подготовки к экзаменам?
Корреляция	2 переменные	Пирсон р	Как связаны результаты SAT и средний балл?
Регрессия	2 переменные	Простая линейная регрессия	Как влияет доход родителей на результаты SAT?

Часто задаваемые вопросы об интервальных данных

org/FAQPage»>

Каковы четыре уровня измерения?

Уровни измерения сообщают вам, насколько точно записываются переменные. Существует 4 уровня измерения, которые можно ранжировать от низкого к высокому:

• Номинальный: данные можно только классифицировать.
• Порядковый номер: данные можно классифицировать и ранжировать.
• Интервал: данные могут быть классифицированы и ранжированы, а также равномерно распределены.
• Соотношение: данные могут быть классифицированы, ранжированы, равномерно распределены и имеют натуральный нуль.

В чем разница между интервальными и относительными данными?

org/Answer»>

Хотя данные интервалов и отношений могут быть классифицированы, ранжированы и иметь одинаковые интервалы между соседними значениями, только шкалы отношений имеют истинный нуль.

Например, температура в градусах Цельсия или Фаренгейта находится на интервальной шкале, поскольку ноль не является самой низкой возможной температурой. В шкале Кельвина, шкале отношений, ноль представляет собой полное отсутствие тепловой энергии.

Являются ли шкалы Лайкерта порядковыми или интервальными?

Индивидуальные вопросы типа Лайкерта обычно считаются порядковыми данными, потому что элементы имеют четкий порядок ранжирования, но не имеют равномерного распределения.

Общие баллы по шкале Лайкерта иногда рассматриваются как интервальные данные. Считается, что эти оценки имеют направленность и равномерный интервал между ними.

Тип данных определяет, какие статистические тесты следует использовать для анализа данных.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Бхандари, П. (2022, 17 ноября). Интервальные данные и способы их анализа | Определения и примеры. Скриббр. Проверено 8 мая 2023 г., с https://www.scribbr.com/statistics/interval-data/

Процитировать эту статью

Полезна ли эта статья?

Вы уже проголосовали.