Как медианы делят треугольник: Медиана делит треугольник

Медиана прямоугольного треугольника

Примечание. В данном уроке изложены теоретические материалы и решение задач по геометрии на тему «медиана в прямоугольном треугольнике». Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Почти наверняка курс будет дополнен.

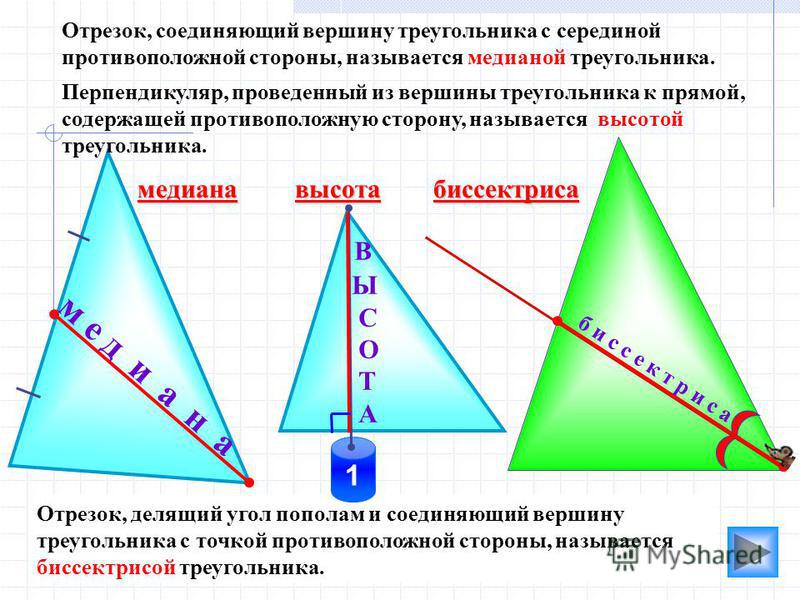
Определение медианы

Медианой треугольника называется отрезок, соединяющий один из углов треугольника с серединой противолежащей ему стороны. (медианой также называют прямую, содержащую данный отрезок)

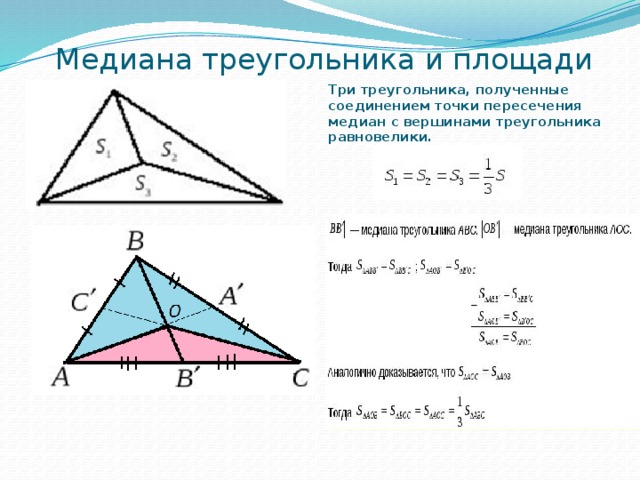
• Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины угла. Точка их пересечения называется центром тяжести треугольника (относительно редко в задачах для обозначения этой точки используется термин «центроид»), 
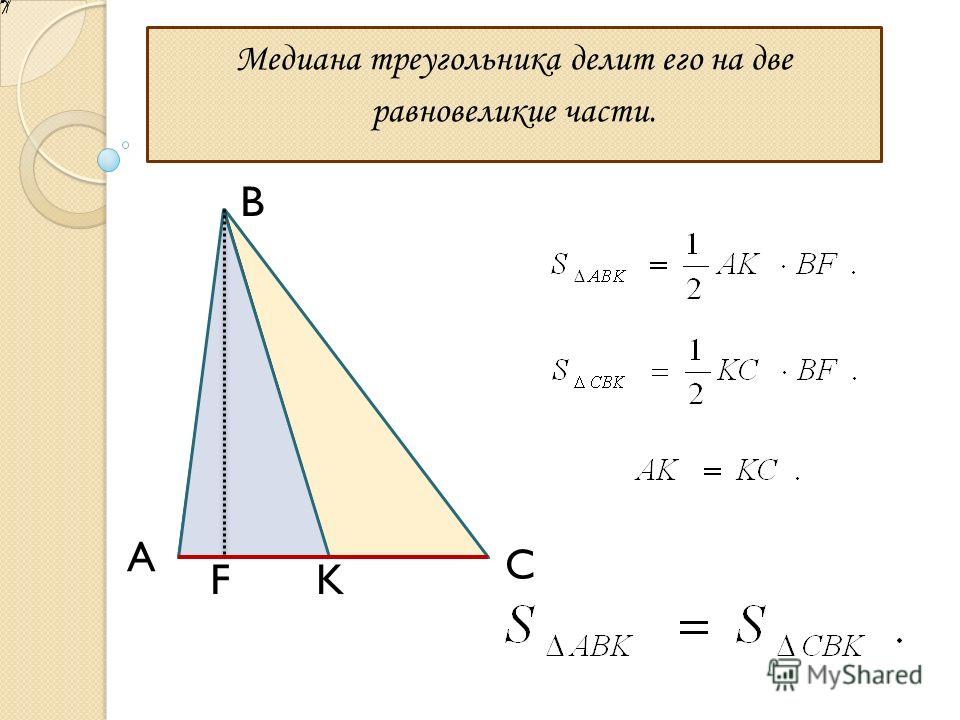
• Медиана разбивает треугольник на два равновеликих треугольника.
• Треугольник делится тремя медианами на шесть равновеликих треугольников.
• Большей стороне треугольника соответствует меньшая медиана.

Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.

• Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
• Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
• Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
• Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов
   (Формула 3)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
• Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
• Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)

Обозначения в формулах:

a, b — катеты прямоугольного треугольника

c — гипотенуза прямоугольного треугольника

Если обозначить треугольник, как ABC, то 

ВС = а

AC = b

AB = c

(то есть стороны a,b,c — являются противолежащими соответствующим углам)

m_a — медиана, проведенная к катету а 

m_b — медиана, проведенная к катету b

m_c — медиана прямоугольного треугольника, проведенная к гипотенузе с

α (альфа) — угол CAB, противолежащий стороне а

Задача про медиану в прямоугольном треугольнике

Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно,  3 см и 4 см. Найдите гипотенузу треугольника

Решение

Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике. В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y). 

Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC — общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора   

AC² + CD² = AD²

Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4x² + y² = 9 

Одновременно, рассмотрим прямоугольный треугольник EBC.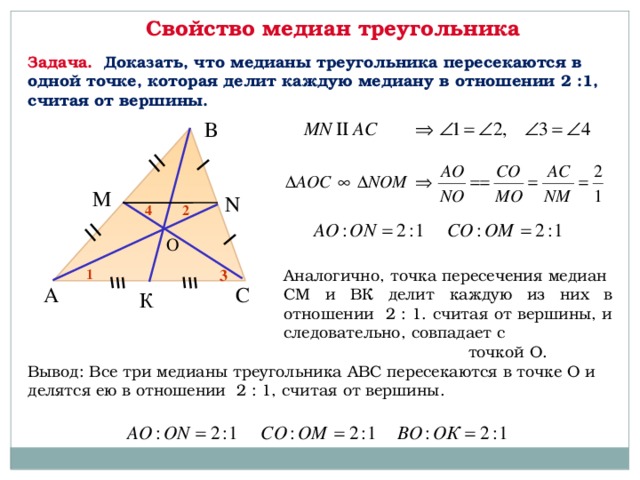 У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.

По теореме Пифагора:
EC² + BC²  = BE²

Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x² + 4y²  = 16

Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений. 
4x² + y² = 9
x² + 4y²  = 16 

Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5x² + 5y² = 25  
5( x² + y² ) = 25
x² + y² = 5 

Обратимся к исходному треугольнику ABC.

По теореме Пифагора  
AC² + BC²  = AB²

Так как длина каждого из катетов нам «известна», мы приняли, что их длина равна 2x и 2y, то есть
4x² + 4y² = AB²
Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки      
4 ( x² + y² ) = AB²  
Чему равно  x² + y² мы уже знаем (см. выше x² + y² = 5), поэтому просто подставим значения вместо  x² + y² 

AB² = 4 х 5
AB² = 20
AB = √20 = 2√5  

Ответ: длина гипотенузы равна 2√5     

0  

 Угол между высотой и медианой треугольника | Описание курса | Медіана прямокутного трикутника 

   

ее определение, свойства, функции, формула нахождения

Что такое медиана

В геометрии понятие «медианы» рассматривается с позиции линии, разделяющей треугольник на две части.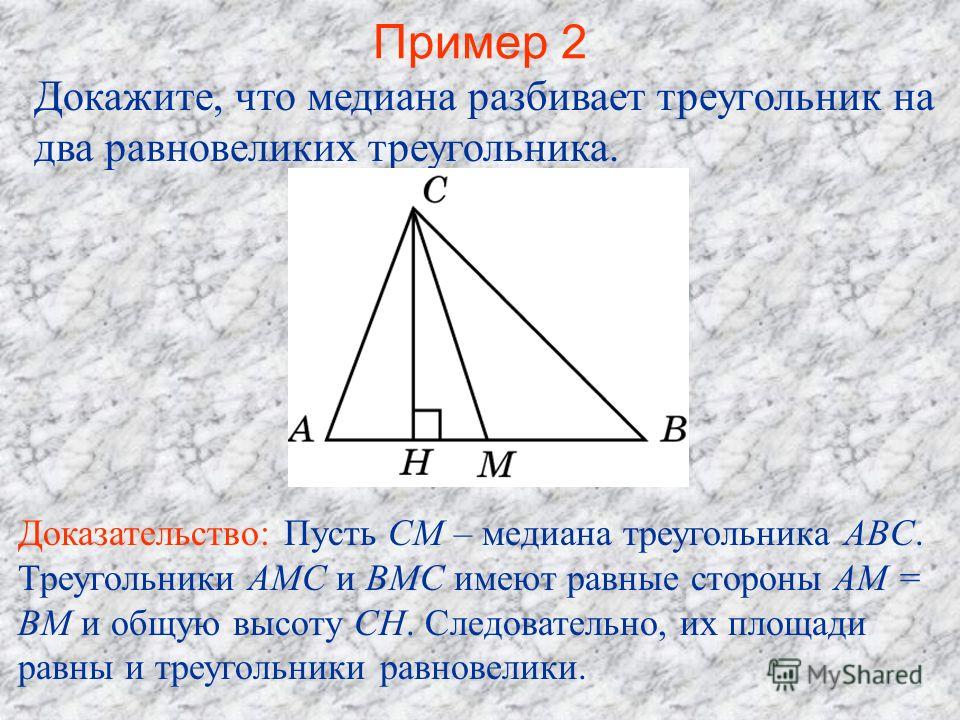 Многие задачи опираются на ее свойство и требуют знаний профильных теорем.

Определение 1

Медианой называется отрезок, который берет свое начало в вершине треугольника, а заканчивается на середине противоположной стороны.

Для равнобедренного треугольника медиана совпадает с его биссектрисой и высотой.   

Определение 2

Равнобедренным называется треугольник, у которого две стороны одинаковой длины. Эти две стороны считаются боковыми, а третья — основанием.

Определение 3

Равносторонним (правильным) называется треугольник, который имеет три стороны одинаковой длины.

Определение 4

Прямоугольным называется треугольник, имеющий угол 90°. В таком треугольнике сторона, противоположная прямому углу, называется гипотенузой, а две другие — катетами.

Определение 5

Треугольник с тремя острыми углами называется остроугольным, а тот, у которого один угол тупой — тупоугольным.

Определение 6

Биссектрисой угла называется луч, начинающийся в вершине угла и делящий его пополам. Биссектриса треугольника — часть (отрезок) биссектрисы угла, который соединяет вершину и точку, расположенную на стороне, противоположной стороне.

Определение 7

Высотой в треугольнике принято называть отрезок, соединяющий вершину треугольника и его противоположную сторону, таким образом, что является к ней перпендикуляром.

Определение 8

Отрезок, который соединяет середины сторон в треугольнике, носит название средней линии.

Определение 9

Прямая, которая проходит через середину выбранного отрезка, образуя с ним прямой угол, — серединный перпендикуляр.

Функции медианы в треугольниках

Существует несколько теорем, дающих характеристику функций медианы.

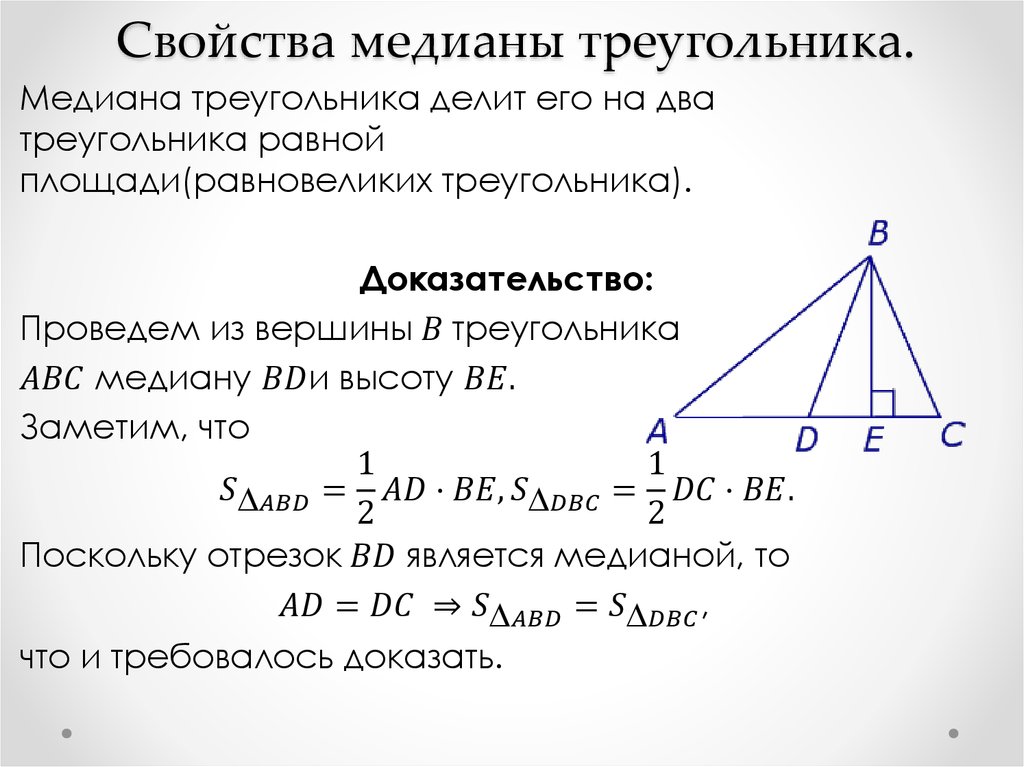
Теорема 1

Правильно построенная медиана делит треугольник на два, равных по площади.

Источник: fmclass.ru

Теорема 2

Центроид — точка, в которой пересекаются медианы треугольника. Центроид делит медианы на две части 2:1, считая от вершины.

Источник: fmclass.ru

Теорема 3

Отрезками медиан, заключенными между вершинами и центроидом, треугольник делится на три одинаковых.

Источник: fmclass.ru   

Теорема 4

Когда медианы пересекаются, они делят треугольник на шесть одинаковых по площади.

Источник: fmclass.ru

Теорема 5

Для вычисления длины медианы, которую провели из угла к стороне с (рисунок), пользуются формулой:

Источник: fmclass.ru

Схематически выглядит так:

Источник: fmclass.ru

Примеры заданий с объяснениями

Приведенные функции медианы находят свое применение при решении геометрических и прочих заданий.

Задача 1

Дан равнобедренный треугольник. Его характеристики: длина боковой стороны — 5 см, проведенная медиана имеет длину 4 см. Необходимо посчитать площадь этого треугольника.

Решение

Для нахождения искомой величины рассмотрим чертеж:

Источник: ru.solverbook.com

Зная правило медианы, делить треугольник на два одинаковых, получаем следующее равенство: 

Значит нужно определить 

По условию следует, что для равнобедренного треугольника медиана является высотой.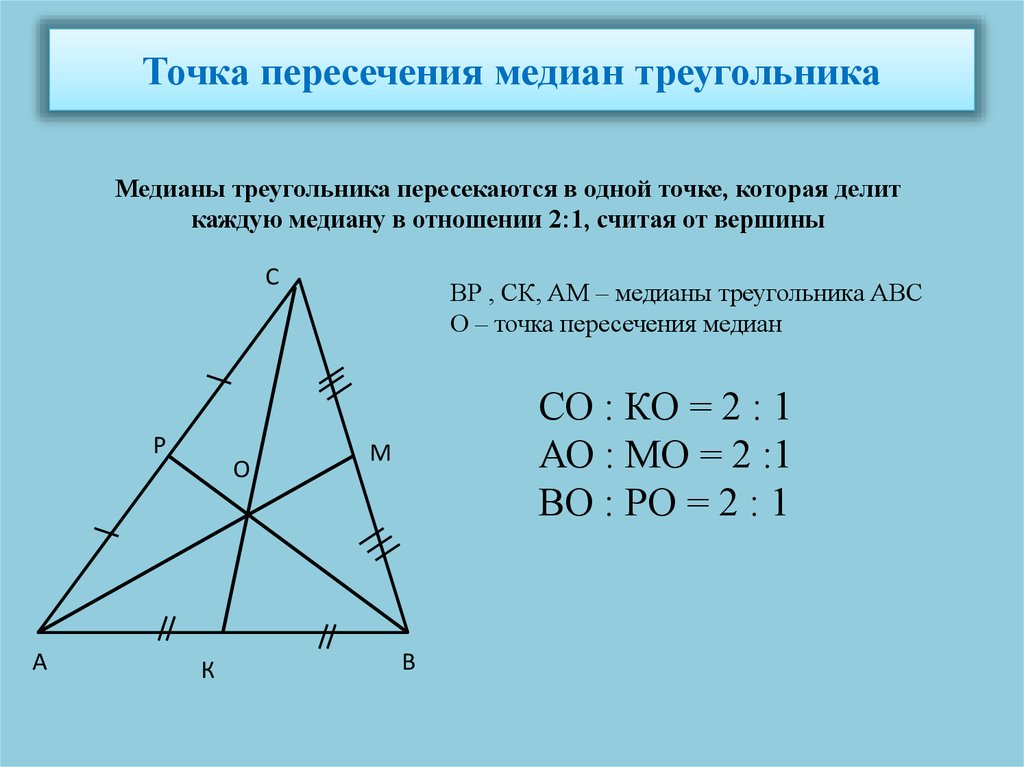 Поэтому справедлива формула: 

Катет AL по теореме Пифагора равен:

Источник: ru.solverbook.com

Теперь подставляем в формулу значения:  .

Настало время определить площадь .

Рассмотрим другой пример.

Задача 2

Дан треугольник со сторонами:  и углом .

В примере проведено две медианы:

Источник: ru.solverbook.com

Рассматривая треугольник ABL, используем теорему косинусов и получаем уравнение:

Источник: ru.solverbook.com

Дальнейшее объяснение опирается на свойство двух пересекающихся медиан, которые в этой точке делятся на отрезки с соотношением 2:1. Тогда:

Источник: ru.solverbook.com

Задачи для самостоятельной работы

Задача 3

Источник: shkolkovo.net

Решение

Источник: shkolkovo.net

Задача 4

Источник: shkolkovo.net

Решение:

Источник: shkolkovo.net

Задача 5

Источник: https://shkolkovo.net/catalog/planimetriya_chast_i/treugolnik_fakty_o_vysote_bissektrise_i_mediane

Решение

Рисунком к задаче является треугольник:

Источник: shkolkovo.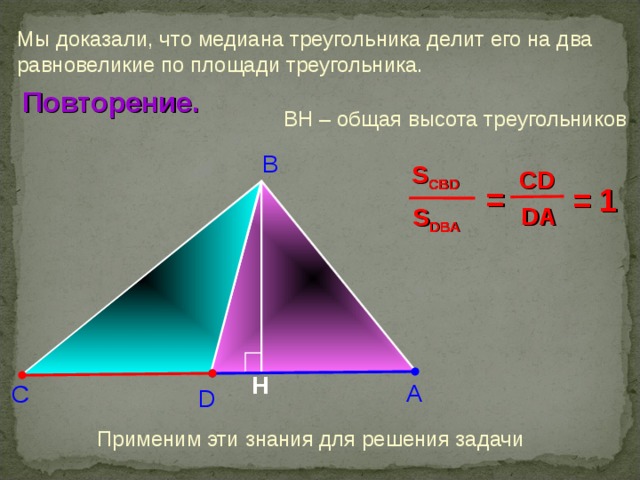 net

Источник: shkolkovo.net

Центроид делит площадь треугольника на 3 или 6 равных частей

Как три медианы, сходящиеся в центре тела, делят площадь треугольника на 3 и 6 равных частей и свойства чевиан

Центроид делит площадь треугольника на 3 равные части, образованные более длинными срединными сегментами в центре тяжести и 6 равных частей всеми шестью срединными сегментами в центре тяжести.

Также точка на чевиане делит площадь треугольника в соотношении его сегментов в этой точке.

Медианы, встречающиеся в центре тяжести, создают богатый набор из отношения, включающие фрагментированные области и сегментированные линии, включая стороны треугольника.

Содержание:

1. Как каждая медиана делит площадь треугольника на две равные части.
2. Как три медианы, сегментированные в центре тяжести, делят площадь треугольника на 6 равных частей.
3. Как три медианы, сходящиеся в центре тяжести , делят площадь треугольника на 3 равные части своими более длинными сегментами.
4. Отношение между площадями треугольников, образованных медианами в центре тяжести и линией, параллельной основанию и проходящей через середины двух других сторон.
5. Концепция отношения площади к чевианскому сегменту: Площадь треугольника делится в том же отношении, что и чевианское сегментное отношение, в точке, которая действует как вершина второго треугольника.
6. Площадь треугольника из длин медиан.

Медиана делит треугольник на 2 части равной площади

На следующем рисунке AD — это медиана $\треугольника ABC$, делящая пополам противоположную сторону BC в точке D. Центроид — это точка G, через которую проходят две другие медианы. , если нарисовано, пройдет. AH — высота треугольника с основанием BC; PAQ — прямая, параллельная основанию BC.

При основании BC и высоте AH площадь $\треугольника ABC$ равна,

$A=\frac{1}{2}BC\times{AH}$.

AS $BD=CD=\frac{1}{2}BC$, площадь $\треугольника ABD$ равна,

$A_{ABD}=\frac{1}{2}BD\times{AH} =\frac{1}{4}BC\times{AH}=\frac{1}{2}A$.

Для $\triangle ADC$ также высота равна AH, как и для любого треугольника с основанием BC и вершиной, лежащей на параллельной ему прямой PAQ. Таким образом, площадь $\треугольника ADC$ равна

$A_{ADC}=\frac{1}{2}DC\times{AH}=\frac{1}{4}BC\times{AH}=\frac {1}{2}А$.

Таким образом, медиана AD делит площадь треугольника на две равные части.

Прежде чем мы покажем вам, как три медианы делят площадь треугольника на шесть равных частей, мы обобщим первый результат в мощную концепцию Отношение площади к основанию и покажем его механизм.

Концепция соотношения площади к основанию

На следующем рисунке показано решение проблемы.

В $\треугольнике ABC$, поскольку отрезок AD от вершины A до основания BC делит BC в отношении, $CD:BD=x:y$, отношения площадей $\треугольника ACD$ и $ \треугольник ABD$ также будет равен $x:y$. Чтобы формально сформулировать этот важный общий результат,

Отрезок от вершины треугольника до противоположной стороны, являющейся основанием, делит основание и площадь треугольника в одинаковом отношении.

Доказательство концепции отношения площади к основанию

В $\треугольнике ABC$ отрезок AD делит основание BC в точке D так, что

$CD:BD=x:y$.

Поскольку оба треугольника, $\triangle ACD$ и $\triangle ABD$, имеют одинаковую высоту AP, которая также является высотой родительского $\triangle ABC$,

$\text{Площадь }\triangle ABD=A_{ ABD}=\frac{1}{2}BD\times{AP}$.

Аналогично,

$\text{Площадь }\треугольника ACD=A_{ACD}=\frac{1}{2}CD\times{AP}$.

Взяв отношение последнего к первому,

$A_{ACD}:A_{ABD}=CD:BD=x:y$.

Результат очень простой, но общий.

Особый случай, когда AD является медианой и $CD=BD$. В этом случае медиана делит треугольник на две равные по площади части.

В качестве другого примера, если $BD=2CD$,

$A_{ABD}=2A_{ACD}$.

Мы будем использовать этот последний результат, чтобы объяснить, как три медианы делят треугольник на шесть частей одинаковой площади.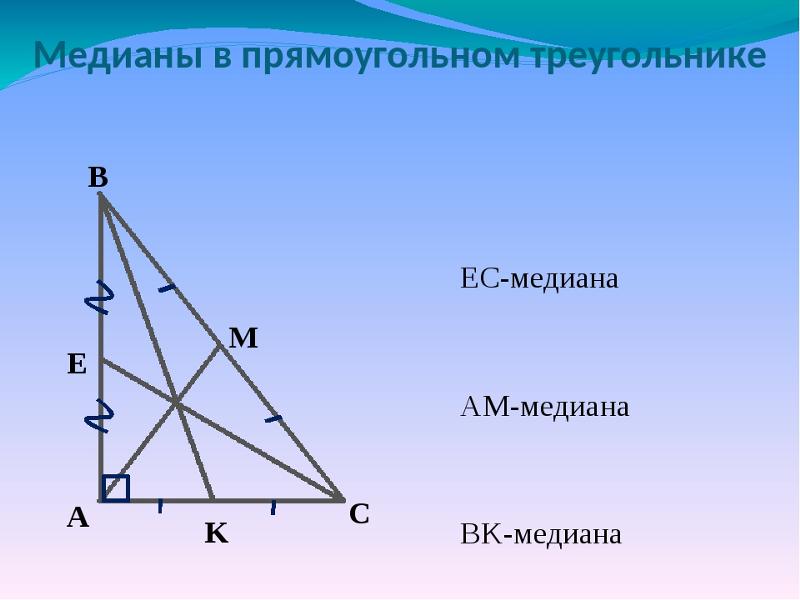

Все три медианы вместе делят треугольник на 6 равных частей, доказательство

Следующий рисунок поможет объяснить механизм этой связи. AD, BE и CF — три медианы, делящие $\треугольник ABC$ на шесть неполных треугольников, точкой пересечения которых является центр тяжести G. AP — перпендикуляр к медиане BE и высота всех трех треугольников $\треугольника ABG$, $\треугольник AEG$ и $\треугольник ABE$.

Медианы делят треугольник на шесть непересекающихся треугольных областей с вершинами, встречающимися в центре тяжести G. Эти шесть треугольников на самом деле состоят из трех пар равных треугольников, образованных путем деления трех треугольников, образованных из центра тяжести и трех пар вершин. , частью медианы от вершины G до основания. Например, площади одной такой пары равновеликих треугольников имеют отношение

$A_{BGD}=A_{CGD}$.

Наша цель — показать площадь одной соседней пары из трех пар треугольников как равную. Например, мы покажем,

$A_{AFG}=A_{AEG}$.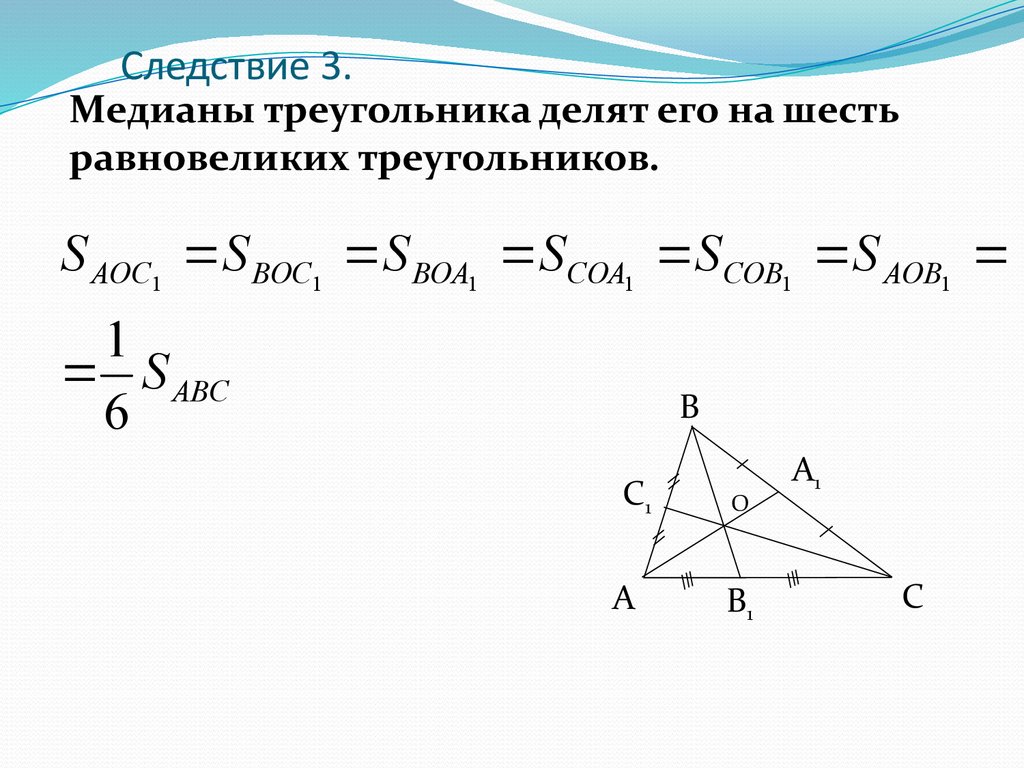

$\треугольник ABE$ делится на два треугольника $\треугольник ABG$ и $\треугольник AEG$ медианным сечением $AG$, падающим на основание BE в точке G. Соотношение сечения по центроиду концепции , оно разделено на две секции BG и EG с соотношением $BG:EG=2:1$ .

Итак, согласно концепции отношения площади к основанию ,

$A_{ABG}=2A_{AEG}$.

Снова в $\треугольнике ABG$

$A_{ABG}=2A_{AFG}$.

Таким образом,

$A_{AEG}=A_{AFG}$, то есть пара смежных треугольников равны по площади.

Это делает площади всех шести треугольников с совпадающими вершинами в точке G равными.

Три отрезка от вершины к центроиду делят треугольник на 3 равные части

Согласно этой концепции, G является центроидом, на рисунке ниже GA, GB и GC делят треугольник на 3 равные части.

Это можно легко сделать, сложив соседние равные пары шести равных треугольников, образованных тремя медианами, как в предыдущем разделе.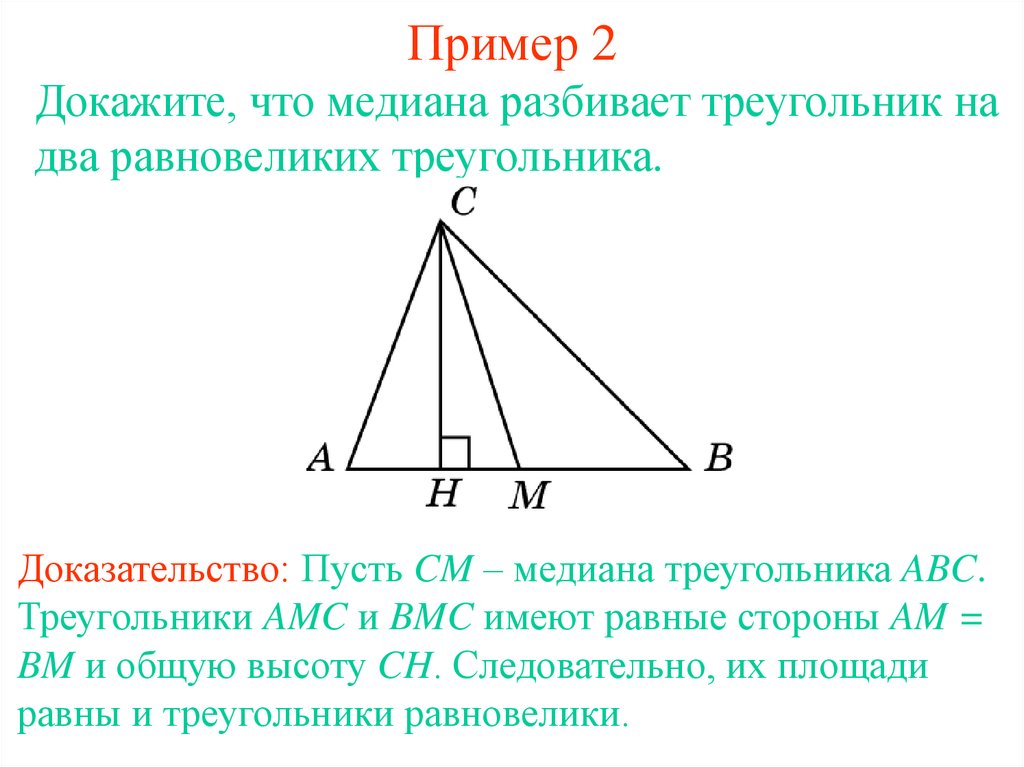

Прежде чем мы перейдем к следующим разделам, нам нужно объяснить часто используемую концепцию Треугольника с богатым сходством.

Подобие треугольника, богатая концепция, механизм

Следующий рисунок поможет объяснить концепцию.

Мы официально заявляем сходство треугольника богатое понятие as,

Отношение всех пар соответствующих сторон соответствующих пар треугольников, образованных прямой линией, параллельной основанию, будет равным.

В качестве альтернативы этот результат приводит к

Прямая линия, параллельная основанию треугольника, разделит все участки прямой линии, опущенные от вершины к основанию, в равном отношении.

Эта мощная богатая концепция часто используется в обеих формах.

Точнее, по отношению к рисунку выше, прямая $PQ||BC$, основание, пересекает четыре прямые $AB$, $AM$, $AN$ и $AC$, опущенные из вершины A в вершину основания ВС в точках D, E, F и G соответственно в равном соотношении.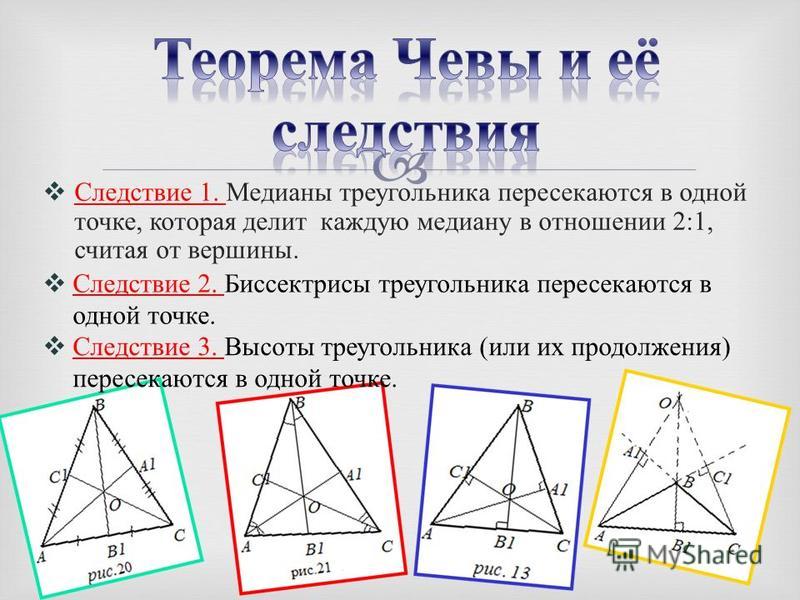

То есть

$AD:BD=AE:EM=AF:FN=AG:GC$.

Это вторая форма богатого понятия и следует из более широкой первой формы определения понятия.

Первичная форма концепции, богатой сходством треугольника

Прямая PQ||BC образует шесть пар соответствующих треугольников, пересекая четыре прямые, опущенные из вершины в основание,

$\треугольник ADE$ и $\треугольник ABM$,

$\треугольник AEF$ и $\triangle AMN$,

$\triangle AFG$ и $\triangle ANC$,

$\triangle ADF$ и $\triangle ABN$,

$\triangle AEG$ и $\triangle AMC$, и, наконец, ,

$\треугольник ADG$ и $\треугольник ABC$.

В каждой такой паре треугольников отношения соответствующих сторон будут равны, так что отношения всех пар соответствующих сторон будут равны.

Частично это составляет

$\displaystyle\frac{AD}{AB}=\frac{AE}{AM}=\frac{AF}{AN}=\frac{AG}{AC}=\frac {DG}{BC}$.

Таких равных соотношений будет больше.

Это происходит прежде всего потому, что, скажем, в паре треугольников $\треугольник ADG$ и $\треугольник ABC$,

• угол при вершине $\угол A$ общий, а
• остальные две пары углов, $\угол ADG=\угол ABC$ и $\угол AGD =\угол ACB$, поскольку каждый из AB и AC пересекает пару параллельных прямых DG и BC.

При равенстве трех пар соответствующих углов $\треугольник ADG$ и $\треугольник ABC$ подобны, так что отношение всех трех пар соответствующих сторон становится равным.

Один и тот же механизм работает в каждой паре соответствующих треугольников.

Тривиально показать, что этот результат приводит ко второй форме определения этого важного богатого понятия.

Нам нужно объяснить еще одну богатую концепцию, отношение площади к чевианскому сегменту , прежде чем переходить к следующим разделам.

A cevian is,

Линия, идущая от вершины к противоположной стороне треугольника или пересекающая ее.

Концепция отношения площади к сегменту Cevian, доказательство

Следующий рисунок поможет определить и подтвердить концепцию.

A чевиан определяется как,

Линия от вершины, достигающая или пересекающая противоположную сторону треугольника.

На рисунке выше AD является таким чевианом. Частными случаями чевиан являются медиана и высота треугольника.

Концепция отношения площади к чевианскому сегменту формально утверждает,

Любая точка на чевианской линии, делящая прямую в отношении $x:y$, также разделит всю площадь треугольника на две области в том же самом отношение, выступая в качестве вершины второго треугольника внутри основного треугольника.

В качестве альтернативы,

Отношение двух отрезков линии, образованных точкой на чевиане, будет таким же, как отношение двух площадей, образованных точкой как вершиной треугольника с основанием, таким же, как у исходного треугольника.

Конкретно по рисунку:

$AF:FD=\text{Площадь области }ABFCA:\text{Площадь }\треугольника BFC$.

Здесь точка F делит чевиан AD на два участка FD и AF в отношении $x:y$.

Из этого результата следует,

$FD:AD=A_{AFD}:A_{ABC}=x:(x+y)$.

Мы получаем этот результат просто инвертированием дроби, добавлением 1 и затем инвертированием обратно.

Давайте посмотрим, почему эта концепция работает.

В $\треугольнике ABD$ с AD в качестве основания, применяя концепцию отношения площади к основанию деления ,

$A_{DBF}:A_{ABF}=FD:FA=x:y$.

Аналогично в $\треугольнике ACD$ с AD в качестве основания и применяя ту же концепцию, мы получаем

$A_{DCF}:A_{ACF}=FD:FA=x:y$.

Таким образом, по понятиям соотношения,

$A_{BFC}:A_{ABFC}=x:y$,

Или, $A_{BFC}:A_{ABC}=x:(x+y)$.

Частный случай центроида как чевианской точки на медиане, в данном случае чевиана

В качестве особого случая, если F является центроидом, AD является медианой, так что F делит медиану в отношении,

$FD :AF=1:2$, поэтому в этом особом случае

$A_{BFC}:A_{ABC}=1:3$.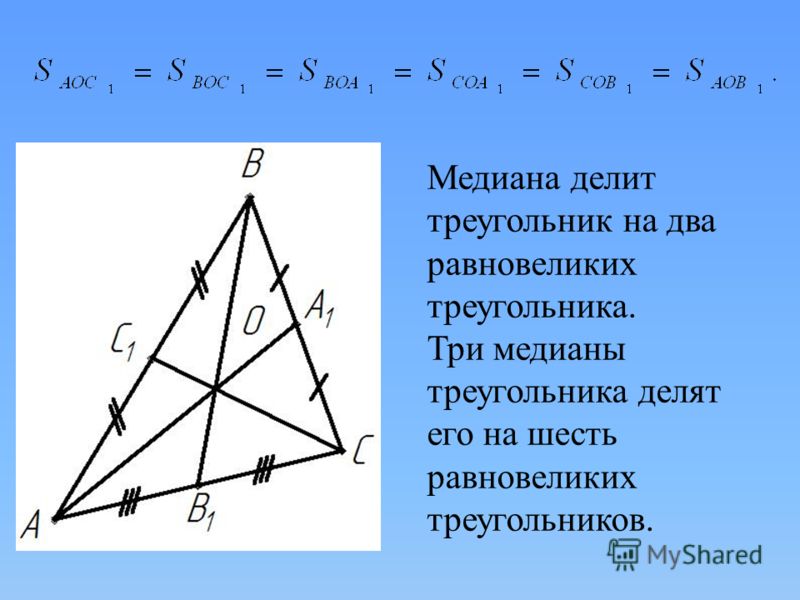

Другими словами, площадь $\треугольника BFC$ будет равна одной трети площади основного $\треугольника ABC$.

Имея эти богатые концепции, мы теперь готовы приступить к элегантной работе с остальными концепциями.

Дополнительные полезные отношения между площадями треугольников, образованных медианами в центроиде

Мы будем использовать следующий рисунок для пояснения концепции в этом разделе. В частности, мы увидим, как площади треугольников $\triangle GFP$, $\triangle GEP$ или $\triangle BGC$ связаны друг с другом и с площадью основного $\треугольника ABC$.

В этом разделе мы рассмотрим отношения площадей треугольников $\triangle GFP$, $\triangle GFE$ и $\triangle BGC$ к площади родительского треугольника.

Площадь $\треугольника GFP$ относительно площади $\треугольника GFE$

Поскольку медиана AD – это прямая из вершины к основанию последнего треугольника BC, проходящая через основания треугольников, $\треугольник AFE$ и $ \triangle AGE$, где эти два треугольника имеют общее основание FE, медиана AD делит FE пополам также в точке P.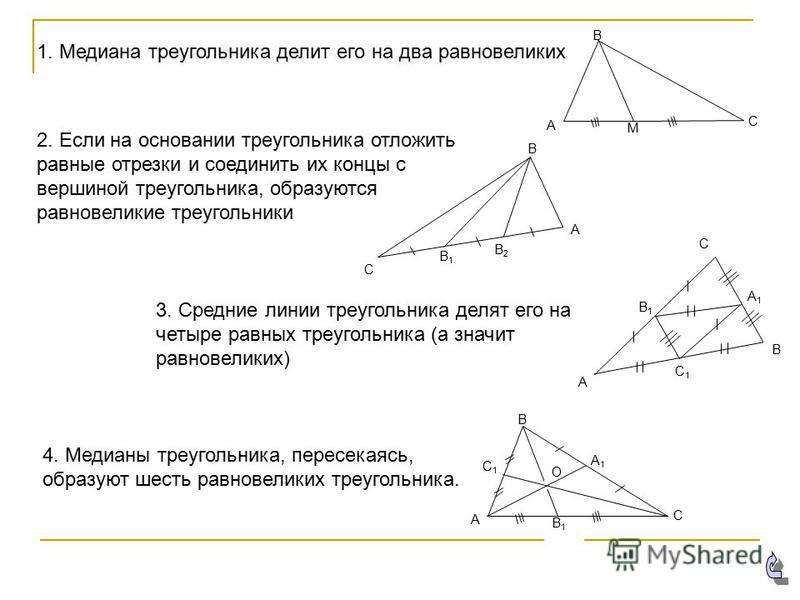 Мы заключаем этот результат, применяя концепцию большого подобия треугольника.

Итак,

$FP=EP$.

Таким образом, GP делит $\треугольник GFE$ на две равные части. Мы заключаем это из понятия медианы, делящей пополам площадь треугольника.

Тогда этот результат говорит:

$A_{GFP}=\frac{1}{2}A_{GFE}$.

Площадь $\треугольника GFE$ относительно площади $\треугольника ABC$

Для решения этой задачи определим протяженность GP.

By богатая концепция подобия треугольника ,

$AP=DP=DG+PG$.

Добавление PG к уравнению,

$AP+PG=AG=DG+2PG$.

Снова по отношение медианного сечения при концепции центроида ,

$AG=2DG=DG+2PG$.

Итак,

$DG=2PG$, что мы подозревали, но теперь знаем.

As $DG=\frac{1}{3}AD$,

$PG=\frac{1}{6}AD$, где $AD$ – медиана.

Вертикальное отражение $\треугольника GFP$ с перемещением вершины вдоль медианы

При этом мы образуем прямоугольник GEHF, диагонали которого делятся пополам в точке P, а его площадь делится пополам общим основанием FE.

Кроме того,

$PH=PG=\frac{1}{6}AD=\frac{1}{3}AP$.

By Концепция отношения площади к чевианскому сегменту then,

$A_{GFE}=A_{FHE}=\frac{1}{3}A_{AFE}=2A_{GFP}$,

Также ,

$A_{AFE}=\frac{1}{4}A_{ABC}$, так как основание и высота меньшего треугольника вдвое меньше, чем у большего треугольника.

Отношение площадей всех этих треугольников,

$A_{GFP}=\frac{1}{2}A_{GFE}=\frac{1}{6}A_{AFE}=\frac{1}{ 24}A_{ABC}=\frac{1}{8}A_{BGC}$.

Последний результат, который мы получаем из более раннего результата,

$A_{BGC}=\frac{1}{3}A_{ABC}$, поскольку GD составляет одну треть от AD.

Обратите внимание , что мы не использовали высоту или длину основания. Мы могли бы избежать этого из-за симметричных отношений между медианой и основаниями и, следовательно, площадями за счет использования мощных богатых понятий.

Площадь треугольника, полученная из длин его медиан, доказательство

Рисунок ниже поможет объяснить.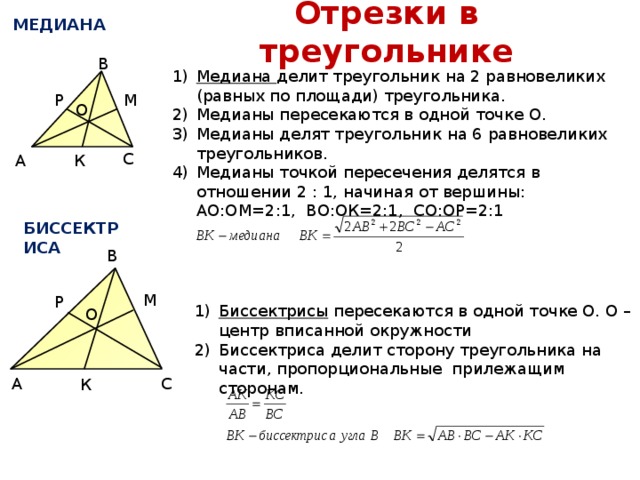

Как обычно, AD, BE и CF являются тремя медианами $\треугольника ABC$, пересекающимися в центре тяжести G.

Значения $AD=m_1$, $BE=m_2$ и $CF=m_3$ даны . Нам нужно найти площадь $\треугольника ABC$.

Как мы знаем, для трех сторон треугольника a, b и c, его полупериметра,

$s=\frac{1}{2}(a+b+c)$ и площади,

$A=\sqrt{s(s-a)(sb)(s-c)}$.

Затем нам нужно построить треугольник с тремя сторонами в качестве медиан, вывести соотношение между площадью медианного треугольника и площадью исходного треугольника, а затем получить площадь исходного треугольника, вычислив площадь медианного треугольника с помощью концепция полупериметра.

Построение медианного треугольника

Для построения медианного треугольника сначала зафиксировали сторону медианы AD, а переместили сторону медианы BE в направлении, параллельном ВС, на расстояние BD, чтобы достичь положения DQ . Этот параллельный перевод привел к $BE||DQ$ и $BE=DQ$, а также к $EQ||BD||BC$ и $EQ=BD=DC$.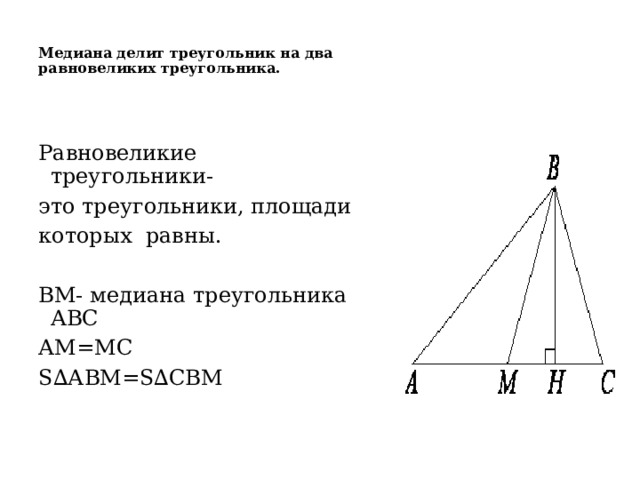 Это сформировало вторую сторону треугольника медиан.

Для формирования третьей стороны третья медиана CF была перемещена в направлении, параллельном AB, в сторону AQ, так что $CF||AQ$ и $CF=AQ$, а также $CQ||AF||AB ||DE$ и $CQ=AF=FB=DE$.

В результирующем параллелограмме DEQC две диагонали делят друг друга пополам, так что $ER=CR$ и $DR=QR$, так что AR является медианой $\треугольника ADQ$, состоящей из медиан исходный $\треугольник ABC$.

Таким образом, AR делит площадь $\треугольника ADQ$ на две равные части, каждая из которых, скажем, равна $x$.

AS $AE=EC=2ER$, $AR=AE+ER=3ER$, то есть

$ER=\frac{1}{3}AR$, что дает

$A_{DER}=A_ {DCR}=\frac{1}{3}A_{ADR}=z$, скажем.

Теперь мы будем использовать следующий рисунок, упрощенный из приведенного выше, чтобы изложить заключительную часть рассуждений.

Мы удалили медианы BE и CF в качестве меры очистки.

Обозначим,

Площадь $\треугольника ABD=A_{ABD}=y$,

Площадь $\треугольника ADR=A_{ADR}=x$ и

Площадь $\треугольника DCR= A_{DCR}=z$.

И площадь $\треугольника ABC$ равна $A_{ABC}=2y$, а площадь $\треугольника ADQ$ равна $A_{ADQ}=A_m=2x$.

Теперь

$A_{ACD}=y=x+z=x+\frac{1}{3}x=\frac{4}{3}x$.

Итак,

$A_{ABC}=\frac{4}{3}A_m$.

Другими словами, площадь любого треугольника составляет четыре трети площади треугольника, образованного его медианами.

Поскольку мы знаем, как найти площадь треугольника по заданным длинам его сторон, это еще один простой шаг, чтобы найти площадь $\треугольника ABC$ по заданной длине его медиан.

Наконец, мы просто пробежимся по вопросу о нахождении площади равностороннего треугольника с точки зрения его сторон или медиан.

Площадь равностороннего треугольника по его сторонам и медианам 92$, где $a$ — длина стороны равностороннего $\треугольника ABC$, а $m$ — длина всех трех его медиан.

Примечание: Будучи ПОЛЬЗОВАТЕЛЯМИ знаний для наилучшего решения проблем, мы должны как можно более ясно знать механизм, стоящий за концепцией. Ясность понимания понятия имеет большое значение для укрепления нашей веры в понятие и, следовательно, нашей способности использовать понятие, когда оно действительно необходимо.

---

Пошаговая помощь по геометрии в Suresolv

Чтобы получить наилучшие результаты из обширного ассортимента статей учебников , вопросов и решений по Геометрия в Suresolv, следуйте инструкциям,

9 0002 Suresolv Geometry Reading and Practice Руководство по сдаче экзаменов SSC CHSL, SSC CGL, SSC CGL Tier II и других конкурсных экзаменов.

Список статей включает ВСЕ статьи по геометрии и соответствующие темы в Suresolv и актуален.

---

←   →

Покажите, что медиана треугольника делит его на два равновеликих треугольника.

Ответить

Проверено

215. 2k+ просмотров

Подсказка: Для доказательства проведем медиану к заданному треугольнику. Мы используем определение медианы. Тогда у нас будет два треугольника с общей вершиной и основаниями одинаковой длины. Найдите площадь одного треугольника и докажите, что он равен площади другого.

Полное пошаговое решение:

Пусть ABC — треугольник.
Пусть AD — одна из ее медиан.

∆ABD и ∆ADC имеют общую вершину A.

Следовательно, основания BD и DC равны (поскольку AD — медиана).

Теперь проведите линию AE перпендикулярно BC, AE ⊥ BC.

Мы знаем, что площадь треугольника с основанием b и высотой h равна = $\dfrac{1}{2} \times {\text{b}} \times {\text{h}}$

Теперь площадь треугольник ∆ABD = $\dfrac{1}{2} \times {\text{base}}$× высота ∆ABD
                                                      = $\dfrac{1}{2} \times {\text{BD}} \times {\text{AE}}$
                                = $\dfrac{1}{2} \times {\text{DC}} \times {\text{AE}}$ — (Поскольку BD = DC)

Но DC и AE являются основанием и высотой ∆ACD соответственно.