Как умножать числа с разными степенями и основаниями: Свойства степеней, действия со степенями

Открытый урок по теме «Умножение и деление степеней»

Урок алгебры по теме «Умножение и деление степеней»

Цель урока: ввести правила умножения и деления степеней с одинаковым основанием.

— ученик научится различать свойства умножения и деления степеней с натуральным показателем; применять эти свойства в случае с одинаковыми основаниями;

— ученик получит возможность уметь выполнять преобразования степеней с разными основаниями и уметь выполнять преобразования в комбинированных заданиях.

Задачи:

— вывести и сформулировать свойства умножения и деления степеней, диагностика усвоения знаний и умений, применение знаний на практике;

— совершенствование вычислительных навыков;

— форми­рование способности к самооценке выполненной деятельности;

— развитие индивидуальных способностей обучающихся;

— развитие памяти, внимания, познавательной активности и сообразительности;

— воспитание чувства ответственности за качество и результат выполняемой работы.

Ход урока

1. Организационный момент (слайд 1)

Начинаем наш урок.

Должен он пойти вам впрок.

Постарайтесь все понять,

Не лениться, не зевать,

Ответы полные давать!

2. Актуализация знаний

Давайте вспомним теоретический материал, для каждого начала из левого столбца, найдите продолжение из правого так, чтобы высказывания были верными (слайд 2)

Степенью числа а с натуральным показателем n большим 1 называется произведение n множителей каждый из которых равен а.

Степень отрицательного числа с четным показателем — положительное число.

Степень отрицательного числа с нечетным показателем — отрицательное число.

(Слайд 3) Выполните задания, используя полученные знания.

1.Представьте в виде степени:

а) 5 ∙ 5 ∙ 5 ∙ 5 ∙ 5 = …; б) x ∙ x ∙ x ∙ x ∙ x ∙ x ∙ x = . .. ; в) (xy) ∙ (xy) ∙ (xy) = …

2. Верно ли, что:

aⁿ =a•a•a•a•…•а (n раз)

b^k=b•b•b•b•a…•b (k раз)

Ответ поясните.

3.Вычислите:

а) 2³ = …; б) (−1)⁹ = …; в) 3² = …; г) 2³ ∙ 2² = …; д)3⁵ : 3³ = …

3. Постановка учебной задачи:

— Какие действия нам необходимо научиться выполнять со степенями, чтобы решить два последних примера (умножение и деление степеней).

— Сформулируем тему урока. (Умножение и деление степеней)

— Попробуйте сформулировать свою цель на урок.

Ученики: — научиться умножать и делить степени.

4. Открытие нового знания:

Вернемся к выражению: 2³ ∙ 2² = (распишем, используя определение степени) = 2 ∙ 2 ∙ 2∙ 2 ∙ 2 = (Чем необходимо воспользоваться для дальнейшего преобразования (определением степени)) = 2⁵.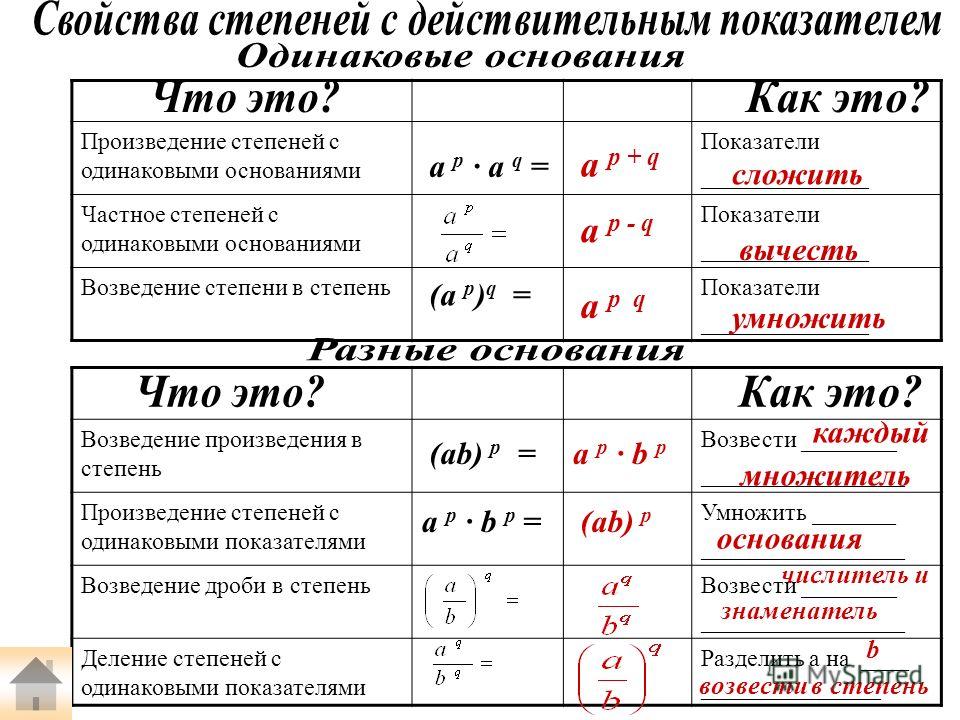

Что вы заметили?

Чему равно основание? Везде 2 и было 2 и осталось 2

А что стало с показателем?

Как мы его получили? З + 2 = 5 — Мы их сложили.

— Давайте попробуем сформулировать правила (при умножении степеней с одинаковым основанием основание остается прежним, а показатели складываются)

— Как это правило можно записать в виде формулы (Слайд 4):

аⁿ ∙ а^m = а^n + m

Вернемся к выражению: 3⁵ : 3² = (распишем, используя определение степени) = = (Чем необходимо воспользоваться для дальнейшего преобразования (определением степени)) = 3².

— Что можно заметить, сравнивая начало и конец в нашей записи? (основание осталось, показатели вычитаются).

— Давайте попробуем сформулировать правила (при делении степеней с одинаковым основанием основание остается прежним, а показатели вычитаются).

— Как это правило можно записать в виде формулы (Слайд 5):

аⁿ : а^m = а^n — m  при условии, что а ≠ 0 m  n

Если m=n, то можно записать: а^m : а^m = а^m – m = а⁰ = 1 при а ≠ 0 (т.к. 0⁰ не имеет смысла)

При каком значении m справедливо равенство? (Слайд 6)

а¹⁶•а^m = а³² ; х^m•х¹⁴ = х²⁸; х⁸•(m) = х¹⁴

Верно ли: х³• хⁿ= х³ⁿ ; 3⁴•3² = 9⁶; а¹⁶: а⁸ = а² ; a⁰ = a?

Теперь попробуем выполнить задания на доске:

№ 403 (а, в, д, ж) а) ; в) ; д) ж) .

№ 414 (а, в, д, ж) а) ; в) ; д) ; ж)

5. Первичное закрепление:

— Сейчас мы с вами постараемся объединить несколько правил в одном примере.

№ 418 (а, в)

а)

в)

Зарядка для глаз.

(По классу развешены геометрические фигуры разного цвета). Посмотрите по сторонам и найдите все треугольники, найдите все четырехугольники.

6. Проверка усвоения материала:

(Слайд 7) Самостоятельная работа с самопроверкой. (Проверку задания 7 из варианта 2 контролирует учитель)

Вариант 1

Вариант 2 7)* № 418 (б), 419 (а, е)

Обучающиеся сами выбирают себе подходящий вариант. Задание 7 и варианта 2 оценивается отдельно

«5» − 0 ошибок

«4» − 1 ошибка

«3» − 2 ошибки

7. Рефлексия:

Поделитесь своими мыслями по данному уроку. Выскажите свое мнение одним предложением, взяв за начало следующие фразы: (Слайд 8)

1. Сегодня я узнал…

2. Было трудно…

3. Я понял, что…

4. Теперь я умею…

5. Я научился…

6. У меня получилось …

7. Урок дал мне…

8. Мне захотелось…

8. Домашнее задание индивидуальное в зависимости от уровня математической подготовки (Слайд 9)

«3» П.19, №408, №409

«4», «5» П.19, №410, №417

Открытый урок по теме «Умножение и деление степеней»

Тип урока: объяснение нового материала.

Цели урока:

• образовательные: научить умножать и делить степени;
• развивающие: научить наблюдать, выводить закономерности, проводить рассуждения по аналогии;
• воспитательные: воспитать интерес к математике, работать в парах.

Оборудование: интерактивная доска, компьютер.

Задачи урока: сформировать навыки сложения чисел с разными знаками.

Образовательные задачи урока (формирование познавательных УУД):

• познакомить учащихся со степенью с натуральным показателем;
• тренировать способность к использованию выведенного алгоритма;
• организовать деятельность учащихся по приобретению необходимых умений и навыков;
• повторить и закрепить;

Воспитательные задачи урока (формирование коммуникативных и личностных УУД):

• содействовать развитию познавательного интереса учащихся к предмету;
• прививать учащимся навыки организации самостоятельной работы;
• умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

Развивающие задачи урока: (формирование регулятивных УУД)

• развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей.

Структура урока:

1. Организационный момент
2. Актуализация
3. Историческая справка
4. Формирование новых способов и действий
5. Физкультминутка
6. Закрепление ЗУН
7. Самостоятельная работа
8. Домашнее задание

Ход урока

1. Организационный момент

Учитель: Здравствуйте, учащиеся! (проверка наличия учеников и выполнение домашнего задания). Сегодня мы с вами продолжим работать со степенями. Внимательно посмотрели на интерактивную доску. Файл (index.ppt).

2. Актуализация

Учитель: Проведём небольшую разминку. Известно, что степени изучали многие учёные и один из них сказал следующую фразу

«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»

Ваша задача назвать фамилию учёного. Для этого нам помогут наши примеры на вычисления. Необходимо под каждым найденным ответом приписать соответствующую букву и расшифровать слово.

№	Примеры	Ответы	буквы
1	25	32	м
2	33	27	о
3	(-10)3	-1000	н
4	(-4)2	16	л
5	23+32	17	с
6	(-3)3-(-2)2	-31	в

Бланк расположения ответов задач:

32	27	-1000	27	16	27	-31	27	17
м	о	н	о	л	о	в	о	с

Расшифровка слова:

16	27	32	27	-1000	27	17	27	-31
л	о	м	о	н	о	с	о	в

Учитель: Какое ключевое слово мы разгадали?

Ученик: Ломоносов.

Учитель: Верно.

3. Историческая справка

Учитель: Рассмотрим историческую справку про степень и узнаем какие ещё учёные вложили свой интерес в развитие степени.

История возникновения степени числа

У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней.

Немецкие математики Средневековья стремились ввести единое обозначение и сократить число символов. Книга Михеля Штифеля «Полная арифметика» (1544 г.) сыграла в этом значительную роль.

Француз, бакалавр медицины Никола Шюке (около 1500 г.) смело ввёл в свою символику не только нулевой, но и отрицательный показатель степени. Он писал его мелким шрифтом сверху и справа от коэффициента.

У Рене Декарта в его «Геометрии» (1637) мы находим современное обозначение степеней а², а³,… Немецкий ученый Лейбниц считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и применял знак а

2.

4. Формирование новых способов и действий

Учитель: Тема нашего урока «Умножение и деление степеней».

Цели урока.

Рассмотрим следующие правила:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются

a^m ·aⁿ = a^m+n

например:

а) а⁵ · а⁶ = а⁵⁺⁶ = а¹¹

б)2³ · 2² = 2⁵⁺² = 2⁵ = 32

в) (-2)³ · 2² = (-2)³⁺² = (-2)⁵ = -32

1.

При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются

a^m : aⁿ= a^m-n,
где, m n, a ≠ 0

например:

а) х⁶ : х⁴ = х^6-4 = х⁴

б) 3⁴ : 3² = 3^4-2 = 3² = 9

в) (-3)⁴ : (-3)² = (-3)^4-2 = (-3)² = 9

Степень с нулевым показателем не была определена и считают, что при а≠0

а⁰ = 1

например: 13⁴ : 3⁴ =13^4-4 = 13⁰ =1

а¹ = а

например:

50¹ = 50,

3∙3⁴ = 31¹⁺⁴ = 3⁵

5. Физкультминутка

Учитель: Проведём небольшую разминку. Выполняем гимнастику для глаз и рук.

Закрепление ЗУН

Учитель: Для закрепления новой темы решим задачи. Каждый ученик решает свой уровень трудности (ученики распределены по трём уровням: слабый, средний и повышенный).

Задачи	Отметки
№	«3»	«4»	«5»
403	+	+	+
414	+	+	+
416(а,б)			+

6. Самостоятельная работа

I вариант	II вариант
1) а5 · а8 (а13)	1) у9 : у5 (у4)
2) 57 : 55 (52)	2) 42 · 4 (64)
3) 219 : 214 (32)	3) 52 : 50 (25)
4) 33 · 30 (27)	4) 86 · 812 (818)
5) 65 · 69 (614)	5) 711 : 79 (49)

7. Домашнее задание

Задачи	Уровень учащихся
№	«I»	«II»	«III»
404	+	+	+
415		+	+
419			+

8. Дополнительное задание

1. В комнате находятся 2 собаки, 4 птички и 3 мухи.

Сколько лап у всех животных вместе? (34)

2. У Маши 3 брата и 2 сестры. Сколько братьев и сестёр у её брата Миши?

Решите пример, соотнесите результат с порядковым номером буквы в алфавите

№	Примеры	Ответы	буквы
1	25
2	(-3)3 — (-2)2

Решите пример, соотнесите результат с порядковым номером буквы в алфавите

№	Примеры	Ответы	буквы
1	33
2	23 + 32

Решите пример, соотнесите результат с порядковым номером буквы в алфавите

№	Примеры	Ответы	буквы
1	(-10)3
2	(-4)2

Предварительное исчисление по алгебре — Умножение чисел с разными основаниями с одинаковым показателем степени

спросил 1 год, 6 месяцев назад

Изменено 1 год, 6 месяцев назад

Просмотрено 202 раза

$\begingroup$

Решая задачу на упрощение («simplify $(2^n-2^{n-1})(3^n-3^{n-1})»)$, я получил это: $$ 2^n\cdot 3^n $$ 9н$.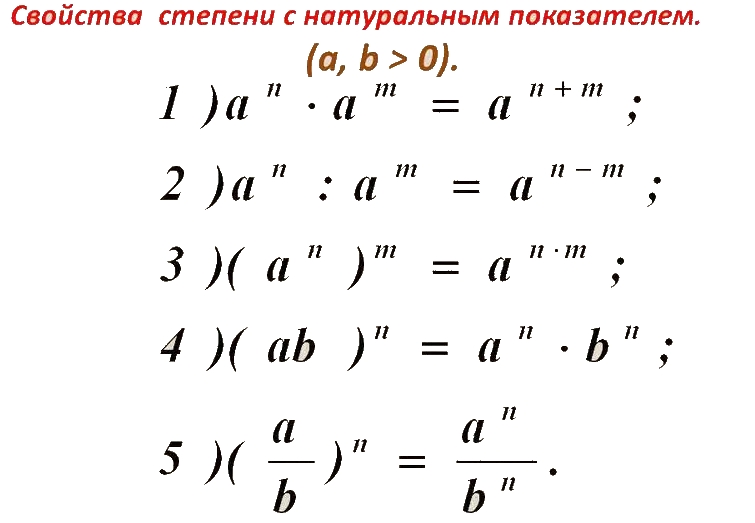

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Что такое экспонента? Определение, свойства, примеры, факты

Показатель степени числа указывает общее время использования этого числа при умножении. Например, 8 × 8 × 8 можно представить как 8 ³ , потому что 8 умножается само на себя 3 раза. Здесь 3 — это «показатель степени» или «степень», указывающая, сколько раз 8 умножается само на себя, а 8 — это «основание», которое представляет умножаемое число. Короче говоря, степень или показатель степени указывает, сколько раз число должно быть умножено само на себя. Здесь основанием может быть любое целое число, дробь или десятичная дробь. Показатель степени также может принимать любое значение, будь то положительное или отрицательное. 9{n}}$ = a ^{m – n} , где m и n — действительные числа, а a — ненулевой член.

Правило отрицательного показателя степени гласит, что когда показатель степени отрицательный, мы можем преобразовать его в положительный, изменив его. Оно представляется как:

Согласно этому закону, если показатель степени действительного числа равен 0, то его значение равно 1, как

Согласно этому закону, умножение двух различных оснований с одинаковой степенью равно произведение базы на мощность. Например, 

9{6}$ = $\frac{729}{64}$

1 Каково значение (–3) 3 ? 27 -27 24 -24 Правильный ответ: -27 $ −3 × −3 × −3 = −27$ 2 9 0 0 – 2 0 ? 1 -1 2 Правильный ответ: 0 4 0 – 2 0 = 1 – 1 = 0 5 3 {2}}$ = 0,0625

Каково реальное применение экспоненты?

Экспоненты имеют различные применения. Ниже перечислены некоторые из них:

• Научные шкалы, такие как шкала Рихтера и шкала Ph, основаны на показателях степени.

  No related posts.