Умножение двоичных чисел онлайн
Примеры решенийПеревод дробных чисел Формат с плавающей точкой Перевести в 2 систему Перевод в 8 систему Перевод в 10 систему Дополнительный код Сложение двоичных чиселУмножение двоичных чисел
- Решение онлайн
- Видеоинструкция
Число №1
Число №2
Пример №1. Умножить двоичные числа
111 и 101.
Решение.
| 1 | 1 | 1 | ||
| 1 | 0 | 1 | ||
| = | = | = | = | = |
| 1 | 1 | 1 | ||
| 0 | 0 | 0 | ||
| 1 | 1 | 1 | ||
| = | = | = | = | = |
| 0 | 0 | 0 | 1 | 1 |
При суммировании в разрядах 2, 3, 4 возникло переполнение.
 Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100011
Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100011
В десятичной системе счисления данное число имеет следующий вид:
Для перевода необходимо умножить разряд числа на соответствующую ему степень разряда.
100011 = 25*1 + 24*0 + 23*0 + 22*0 + 21*1 + 20*1 = 32 + 0 + 0 + 0 + 2 + 1 = 35
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 111 и 101 в десятичное представление.
1112 = 22*1 + 21*1 + 20*1 = 4 + 2 + 1 = 7
1012 = 22*1 + 21*0 + 20*1 = 4 + 0 + 1 = 5
7 x 5 = 35
Пример №2. Найти двоичное произведение 11011*1100. Перевести ответ в десятичную систему.
Решение. Умножение начинаем с младших разрядов: если текущий разряд второго числа равен 0, то везде записываем нули, если 1 — то переписываем первое число.
| 1 | 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 0 | ||||
| = | = | = | = | = | = | = | = |
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | |||
| 1 | 1 | 0 | 1 | 1 | |||
| 1 | 1 | 0 | 1 | 1 | |||
| = | = | = | = | = | = | = | = |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
При суммировании в разрядах 3, 4, 5, 6, 7 возникло переполнение.
 Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 101000100
Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 101000100В десятичной системе счисления данное число имеет следующий вид:
101000100 = 28*1 + 27*0 + 26*1 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*0 = 256 + 0 + 64 + 0 + 0 + 0 + 4 + 0 + 0 = 324
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 11011 и 1100 в десятичное представление.
11011 = 24*1 + 23*1 + 22*0 + 21*1 + 20*1 = 16 + 8 + 0 + 2 + 1 = 27
1100 = 23 *1 + 22*1 + 21*0 + 20*0 = 8 + 4 + 0 + 0 = 12
27 x 12 = 324
Пример №3. 1101.11*101
Будем умножать числа без учета плавающей точки: 110111 x 101
Умножение начинаем с младших разрядов: если текущий разряд второго числа равен 0, то везде записываем нули, если 1 — то переписываем первое число.
| 1 | 1 | 0 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | |||||
| = | = | = | = | = | = | = | = |
| 1 | 1 | 0 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 0 | 1 | 1 | 1 | ||
| = | = | = | = | = | = | = | = |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
При суммировании в разрядах 2, 3, 4, 5, 6, 7 возникло переполнение.
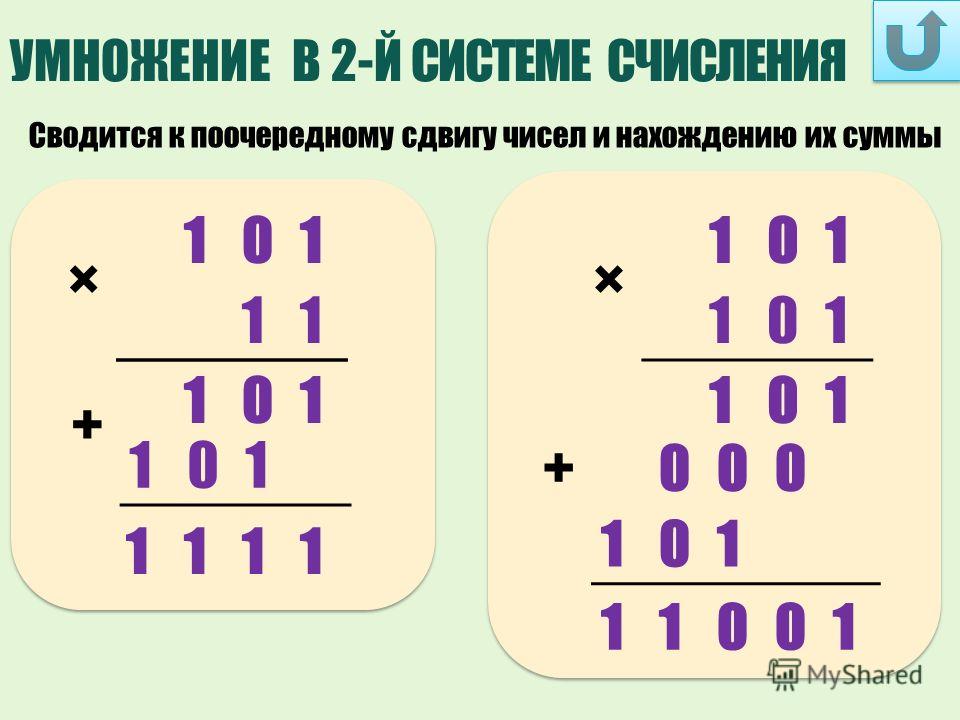 Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100010011
Причем переполнение возникло и в старшем разряде, поэтому записываем 1 впереди полученного числа, и получаем: 100010011Поскольку умножали без учета плавающей запятой, то окончательный результат запишем как: 1000100.11
В десятичной системе счисления данное число имеет следующий вид:
1000100 = 26*1 + 25*0 + 24*0 + 23*0 + 22*1 + 21*0 + 20*0 = 64 + 0 + 0 + 0 + 4 + 0 + 0 = 68
Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда.
В итоге получаем число 68.75
Проверим результат умножения в десятичной системе счисления. Для этого переводим числа 1101.11 и 101 в десятичное представление.
1101 = 23*1 + 22*1 + 21*0 + 20*1 = 8 + 4 + 0 + 1 = 13
11 = 2-1*1 + 2-2*1 = 0.75
В итоге получаем число 13.75
Переводим число: 1012 = 22*1 + 21*0 + 20*1 = 4 + 0 + 1 = 5
13. 75 x 5 = 68.75
75 x 5 = 68.75
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Умножение в двоичной системе счисления
Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика которой мы пользуемся также называется десятичной. Это потому, что каждое число можно составить из набора цифр содержащего 10 символов – цифр – “0123456789”.
Так шло развитие математики, что именно этот набор стал главным, но десятичная арифметика не единственная. Если мы возьмём только пять цифр, то на их основе можно построить пятиричную арифметику, из семи цифр – семиричную. В областях знаний связанных с компьютерной техникой часто используют арифметику в которой числа составляются из шестнадцати цифр, соответственно эта арифметика называется шестнадцатиричной.
Арифметические действия в двоичной системе производится по тем же правилам что и в десятичной системе счисления. Однако так как в двоичной системе счисления используются только две цифры 0 и 1, то арифметические действия выполняются проще, чем десятичной системе.
Однако так как в двоичной системе счисления используются только две цифры 0 и 1, то арифметические действия выполняются проще, чем десятичной системе.
В этой работе рассмотрим умножение в двоичной системе счисления.
- Основная часть
Для понимания умножения в двоичной системе счисления, необходимо знать правила при сложении в двоичной системе счисления. Разберем все по порядку.
Сложение двоичных чисел.
Способ сложения столбиком в общем-то такой же как и для десятичного числа. То есть, сложение выполняется поразрядно, начиная с младшей цифры. Если при сложении двух цифр получается СУММА больше девяти, то записывается цифра=СУММА- 10, а ЦЕЛАЯ ЧАСТЬ (СУММА 10), добавляется в старшему разряду.
Так и с двоичным числом. Складываем поразрядно, начиная с младшей цифры столбиком, начиная с младшего разряда и используя таблицы двоичного сложения:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10.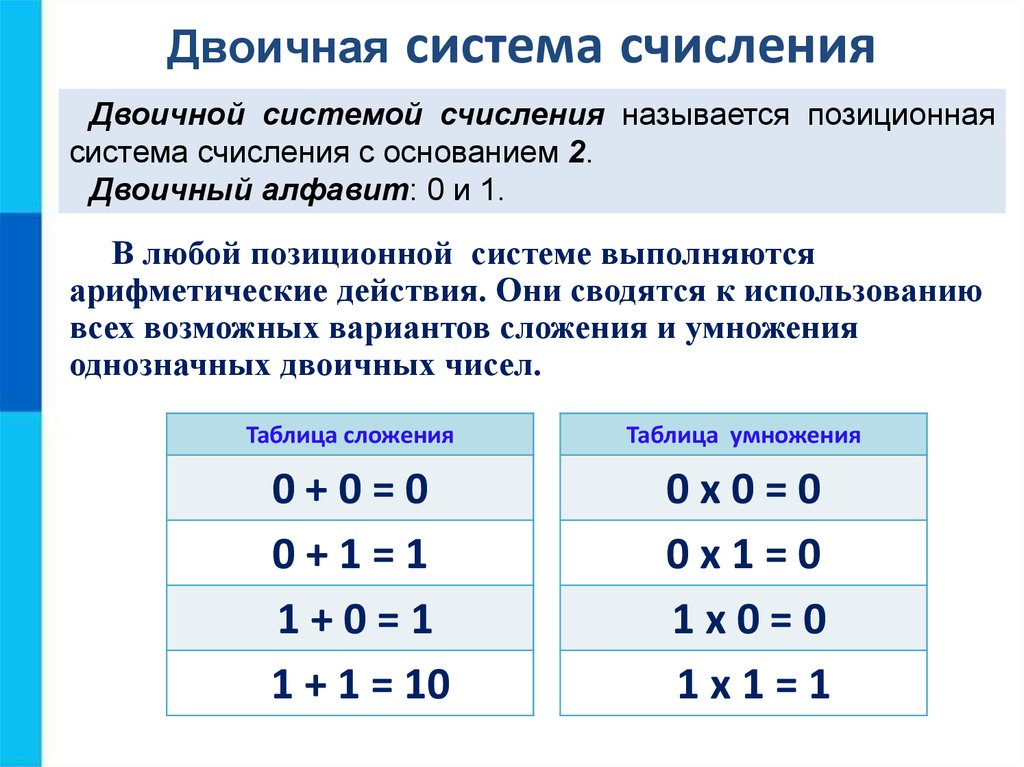
При сложении необходимо помнить, что 1+1 дают нуль в данном разряде и единицу переноса в старший («на ум пошло»)
Выполним пример: 10011 + 10001.
| 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 0 |
Первый разряд: 1+1 = 2. Записываем 0 и 1 на ум пошло.
Второй разряд: 1+0+1(запомненная единица) =2. Записываем 0 и 1 на ум пошло.
Третий разряд: 0+0+1(запомненная единица) = 1. Записываем 1.
Четвертый разряд 0+0=0. Записываем 0.
Пятый разряд 1+1=2. Записываем 0 и добавляем к шестым разрядом 1.
Переведём все три числа в десятичную систему и проверим правильность сложения.
Для проверки и перевода в десятичную систему счисления очень просто. Метод такого перевода даёт наш способ записи чисел. Возьмём, к примеру, следующее двоичное число 1011. Разложим его по степеням двойки. Получим следующее:
Разложим его по степеням двойки. Получим следующее:
1011 = 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20
Выполним все записанные действия и получим:
1 * 23 + 0 * 22 + 1 * 21 + 1 * 20 = 8 + 0+ 2 + 1 = 11. Таким образом, получаем, что 1011 (двоичное) = 11 (десятичное). Сразу видно и небольшое неудобство двоичной системы. То же самое число, которое, в десятичной системе записано одним знаком в двоичной системе, для своей записи требует четыре знака. Итак, проверяем:
10011 = 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 16 + 2 + 1 =19
10001 = 1*24 + 0*23 + 0*22 + 0*21 + 1*20 = 16 + 1 = 17
100100 = 1*25 + 0*24 + 0*23 + 1*22 + 0*21 + 0*20 =32+4=36
17 + 19 = 36 верное равенство
Теперь приступим к нашей основной части – умножение в двоичной системе счисления.
Умножение в двоичной системе счисления.
Для начала рассмотрим следующий любопытный факт. Для того, чтобы умножить двоичное число на 2 (десятичная двойка это 10 в двоичной системе) достаточно к умножаемому числу слева приписать один ноль.
Пример. 10101 * 10 = 101010
Проверка.
10101 = 1*24 + 0*23 + 1*22 + 0*21 +1*20 = 16 + 4 + 1 = 21
101010 =1*25 + 0*24 + 1*23 + 0*22 +1*21 +0*20 = 32 + 8 + 2 = 42
21 * 2 = 42
Если мы вспомним, что любое двоичное число разлагается по степеням двойки, то становится ясно, что умножение в двоичной системе счисления сводится к умножению на 10 (то есть на десятичную 2), а стало быть, умножение это ряд последовательных сдвигов. Общее правило таково: как и для десятичных чисел, умножение двоичных выполняется поразрядно. И для каждого разряда второго множителя к первому множителю добавляется один ноль справа.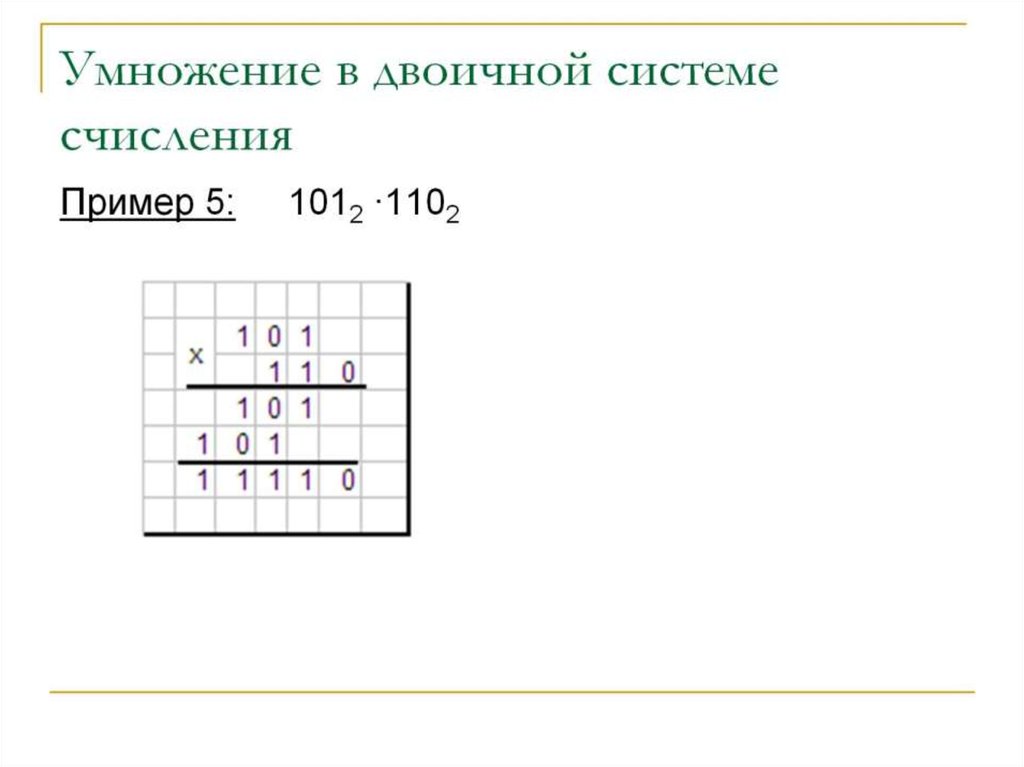 Пример (пока не столбиком):
Пример (пока не столбиком):
1011 * 101 Это умножение можно свести к сумме трёх поразрядных умножений:
1011 * 1 + 1011 * 0 + 1011 * 100 = 1011 +101100 = 110111
В столбик это же самое можно производить по тому же принципу что и в десятичной системе счисления, при этом используется таблица двоичного умножения:
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1.
| 1 | 0 | 1 | 1 | ||
| * | 1 | 0 | 1 | ||
| 1 | 0 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | 1 |
Проверка:
101 = 5 (десятичное)
1011 = 11 (десятичное)
110111 = 55 (десятичное)
5*11 = 55 верное равенство.
- Заключение
Внутри компьютера арифметические операции в основном выполняются над двоичными числами. Порядок выполнения операции над двоичными числами проходит как и в десятичной системе счисления.
Порядок выполнения операции над двоичными числами проходит как и в десятичной системе счисления.
Умножение в двоичной системе счисления требует для начала понимания сложения в двоичной системе счисления.
Умножение в двоичной системе выполняется довольно просто. Умножение заменяется сдвигом столько раз, сколько разрядов в множителе. В тех разрядах, где значение рано нулю, соответствующая строка в столбике обнуляется. Затем все значения складываются. При расчете используется таблица двоичного умножения:
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1.
Как делать умножение в двоичной системе
Для начала рассмотрим следующий любопытный факт. Для того, чтобы умножить двоичное число на 2 (десятичная двойка это 10 в двоичной системе) достаточно к умножаемому числу слева приписать один ноль.
Пример. 10101 * 10 = 101010
10101 = 1*2 4 + 0*2 3 + 1*2 2 + 0*2 1 +1*2 0 = 16 + 4 + 1 = 21
101010 =1*2 5 + 0*2 4 + 1*2 3 + 0*2 2 +1*2 1 +0*2 0 = 32 + 8 + 2 = 42
Если мы вспомним, что любое двоичное число разлагается по степеням двойки, то становится ясно, что умножение в двоичной системе счисления сводится к умножению на 10 (то есть на десятичную 2), а стало быть, умножение это ряд последовательных сдвигов. Общее правило таково: как и для десятичных чисел, умножение двоичных выполняется поразрядно. И для каждого разряда второго множителя к первому множителю добавляется один ноль справа. Пример (пока не столбиком):
Общее правило таково: как и для десятичных чисел, умножение двоичных выполняется поразрядно. И для каждого разряда второго множителя к первому множителю добавляется один ноль справа. Пример (пока не столбиком):
1011 * 101 Это умножение можно свести к сумме трёх порязрядных умножений:
1011 * 1 + 1011 * 0 + 1011 * 100 = 1011 +101100 = 110111 В столбик это же самое можно записать так:
Примечание: Кстати таблица умножения в двоичной системе состоит только из одного пункта 1 * 1 = 1
101 = 5 (десятичное) 1011 = 11 (десятичное)
110111 = 55 (десятичное) 5*11 = 55 верное равенство
а) 1101 * 1110 = _________________ б) 1010 * 110 = __________________
в) 1011 * 11 = _______________ г) 101011 * 1101 = _______________
д) 10010 * 1001 = __________________
Деление в двоичной системе счисления
Мы уже рассмотрели три действия и думаю уже понятно, что в общем-то действия над двоичными числами мало отличаются от действий над десятичными числами. Разница появляется только в том, что цифр две а не десять, но это только упрощает арифметические операции. Так же обстоит дело и с делением, но для лучшего понимания алгоритм деления разберём более подробно. Пусть нам необходимо разделить два десятичных числа, например 234 разделить на 7. Как мы это делаем.
Разница появляется только в том, что цифр две а не десять, но это только упрощает арифметические операции. Так же обстоит дело и с делением, но для лучшего понимания алгоритм деления разберём более подробно. Пусть нам необходимо разделить два десятичных числа, например 234 разделить на 7. Как мы это делаем.
Мы выделяем справа (от старшего разряда) такое количество цифр, чтобы получившееся число было как можно меньше и в то же время больше делителя. 2 — меньше делителя, следовательно, необходимое нам число 23. Затем делим полученное число на делитель с остатком. Получаем следующий результат:
Описанную операцию повторяем до тех пор, пока полученный остаток не окажется меньше делителя. Когда это случится, число полученное под чертой, это частное, а последний остаток — это остаток операции. Так вот операция деления двоичного числа выполняется точно также. Попробуем
Пример: 10010111 / 101
Ищем число, от старшего разряда которое первое было бы больше чем делитель. Это четырехразрядное число 1001. Оно выделено жирным шрифтом. Теперь необходимо подобрать делитель выделенному числу. И здесь мы опять выигрываем в сравнении в десятичной системой. Дело в том, что подбираемый делитель это обязательно цифра, а цифры у нас только две. Так как 1001 явно больше 101, то с делителем всё понятно это 1.
Это четырехразрядное число 1001. Оно выделено жирным шрифтом. Теперь необходимо подобрать делитель выделенному числу. И здесь мы опять выигрываем в сравнении в десятичной системой. Дело в том, что подбираемый делитель это обязательно цифра, а цифры у нас только две. Так как 1001 явно больше 101, то с делителем всё понятно это 1.
Итак, остаток от выполненной операции 100. Это меньше чем 101, поэтому чтобы выполнить второй шаг деления, необходимо добавить к 100 следующую цифру, это цифра 0. Теперь имеем следующее число:
1000 больше 101 поэтому на втором шаге мы опять допишем в частное цифру 1 и получим следующий результат (для экономии места сразу опустим следующую цифру).
Полученное число 110 больше 101, поэтому и на этом шаге мы запишем в частное 1. Получиться так:
Полученное число 11 меньше 101, поэтому записываем в частное цифру 0 и опускаем вниз следующую цифру. Получается так:
Полученное число больше 101, поэтому в частное записываем цифру 1 и опять выполняем действия.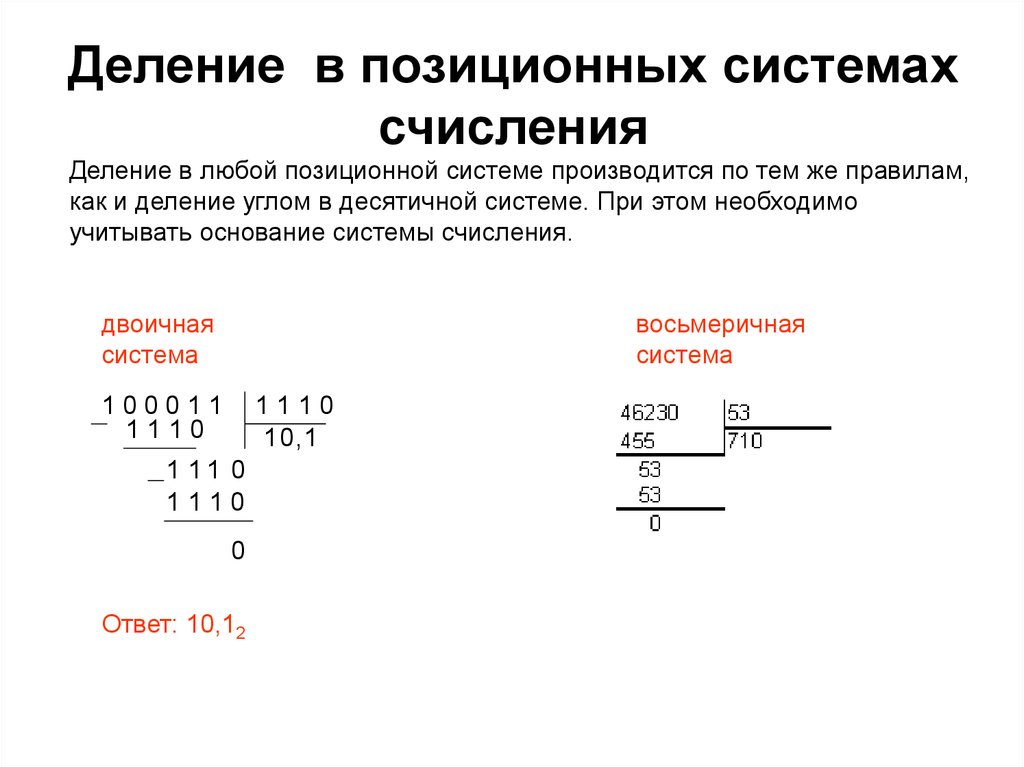 Получается такая картина:
Получается такая картина:
Полученный остаток 10 меньше 101, но у нас закончились цифры в делимом, поэтому 10 это окончательный остаток, а 1110 это искомое частное.
Проверим в десятичных числах
10010011 = 147 101 = 5
10 = 2 11101 = 29
На этом мы заканчиваем описание простейших арифметических операций, которые необходимо знать, для того, чтобы пользоваться двоичной арифметикой, и теперь попробуем ответить на вопрос «Зачем нужна двоичная арифметика». Конечно, выше уже было показано, что запись числа в двоичной системе существенно упрощает арифметические операции, но в то же время сама запись становится значительно длиннее, что уменьшает ценность полученного упрощения, поэтому необходимо поискать такие задачи, решение которых существенно проще в двоичных числах.
Самостоятельная работа № 4
1. Выполните сложение, вычитание, умножение в двоичной системе счисления:
| 1.1111 и 1011; |
| 2.1001 и 110; |
3. 11001 и 10111; 11001 и 10111; |
| 4.111 и 101; |
| 5.10011 и 1101; |
| 6.10011 и 1001; |
| 7.110110 и 11111; |
| 8.10011001 и 1101; |
| 9.10101 и 1101; |
| 10. 10111и 111; |
| 11.11001и 111; |
| 12.10111 и 111100; |
| 13.11000 и 1101; |
| 14.1011и 111. |
| 15.1100100 и 100011; |
| 16.101101 и 1101; |
2. Выполните деление в двоичной системе счисления:
- 10100101: 1011=
- 10100101:1111=
- 110110:110=
- 110110:1001=
- 1000111111:11001=
- 1000111111:10111=
- 11110111:10011=
- 11110111:1101=
- 10101011: 10011=
- 10101011: 1001=
- 10100001:111=
- 10100001:10111=
- 10101111:111=
- 10101111:11001=
- 1001101:1011=
- 1001101:111=
Контрольная работа по теме «Системы счисления»
В-1.
Представьте в развернутой форме:
а) 4563 ; б) 100101 ;
Переведите число 75 из десятичной системы счисления в двоичную.
а) 11001101011 + 1110000101 ; б) 101011 – 10011 ; в) 1011 · 101 .
В-2.
Представьте в развернутой форме:
а) 1563 ; б) 100111 ;
Переведите число 67 из десятичной системы счисления в двоичную.
а) 11001101111 + 1110000101 ; б) 10111 – 10011 ; в) 1111 · 101 .
В-3.
Представьте в развернутой форме:
а) 2563 ; б) 110101 ;
Переведите число 59 из десятичной системы счисления в двоичную.
а) 11111101011 + 1110000111 ; б) 11111 – 10011 ; в) 10011 · 101 .
В-4.
Представьте в развернутой форме:
а) 2573 ; б) 1010101 ;
Переведите число 95 из десятичной системы счисления в двоичную.
а) 11111101001 + 1110000111 ; б) 11101 – 10011 ; в) 10111 · 101 . Дополнительный раздел: «Занимательно и интересно!»
А) Рисуем по точкам.
В таблице 1 приведены номер точки и ее координаты, записанные в двоичной системе счисления.
Для каждой точки выполните перевод ее координат в десятичную систему счисления и отметьте точку на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, вы получите некоторый рисунок. Рисунок изобразите в рабочей тетради.
| № точки | Координаты точки | (X;Y) |
| X | Y | |
| 1002 | 102 | |
| 1012 | 1012 | |
| 12 | 1012 | |
| 112 | 10102 | |
| 1002 | 10102 | |
| 112 | 1102 | |
| 1012 | 1102 | |
| 1102 | 1012 + 1002 | |
| 1112 | 10012 | |
| 1102 | 1102 | |
| 1002 * 102 | 1102 | |
| 10002 | 1012 | |
| 1102 | 1012 | |
| 1012 | 102 |
Б) Рождение цветка.
Понаблюдаем за рождением цветка: сначала появился один листочек, затем второй … и вот распустился бутон. Постепенно подрастая, цветок показывает нам некоторое двоичное число. Если вы до конца проследите за ростом цветка, то узнаете, сколько дней ему понадобилось, чтобы вырасти.
В) Русская поговорка.
Здесь зашифрована известная русская поговорка. Прочитайте ее, двигаясь с помощью двоичных цифр в определенной последовательности.
Для любознательных
Ещё два способа преобразования чисел 10-й в 2-ую систему счисления:
I. Метод вычитания
С детства мы считать учились – раз, два, три, четыре, пять
Десятичной ту систему мы привыкли называть.
Были палочки и счеты, калькулятор, Пифагор,
А теперь перед глазами – серебристый монитор.
Эта умная машина сможет все нам сосчитать
Ну, а как она считает – предстоит нам разобрать.
Мы считаем в десятичной – два, двенадцать, сто один,
А компьютер лишь в двоичной – либо ноль, либо один.
Разберемся на примере: число будет – сорок пять
Наибольшую здесь степень нам придется сосчитать
Раз считаем мы в двоичной основанье всегда два
Показатель мы находим от начального числа.
И поскольку изначально наша цифра сорок пять,
| 32=2 5 |
Мы подумаем и скажем показатель будет пять.
В показателе пятерка в основанье цифра два
Возведем мы двойку в степень и получим 32.
Возвращаемся мы снова к нашей цифре 45
Нам теперь от этой цифры 32 нужно отнять.
Разность сосчитать нам просто мы уже не первый класс
Видим: циферка 13 получается у нас.
Теперь циферку 13 также как и 45
Вместе с вами нам придется разложить и посчитать
Снова в основанье двойка показатель будет три
Двойка в третьей будет восемь ну, а дальше сам смотри.
У 45-ти два в пятой умножаем на один
У 13 два в третьей тоже множим на один
Два в четвертой не встречалась, тут и нечего гадать
Значит, будем два в четвертой мы на нолик умножать.
Запись: 4510 = 1*2 5 +0*2 4 +1*2 3 +1*2 2 +0*2 1 +1*2 0 =1011012
Подводим итог: Необходимо разложить данное нам число по степеням «2». В том случае, если полная степень «2» присутствует при разложении, сомножителем будет единица, если степени «2» нет – сомножитель ноль. Важно! При записи числа в «2»-ой системе счисления нельзя пропускать ни одну степень.
II. Метод степеней
Разберем еще один пример: Перевести из «10»-ой системы счисления в «2»-ю число 23. Какие степени «2» представлены в этом числе?
1) Ищем максимальную степень «2» – это 2 4 =16. Итак: 23-16=7
2) Для числа 7 подбираем максимальную степень это 2 2 =4. Вычитаем 7-4=3.
3) Для числа 3 подбираем максимальную степень это 2 1 =2. Вычитаем 3-2=1.
4) Для числа 1 остался единственный вариант это степень 2 0 =1.
Теперь можем записать разложение числа 23 по степеням «2»:
Запись: 2310 =1*2 4 +0*2 3 +1*2 2 +1*2 1 +1*2 0
Этот калькулятор умеет осуществлять простейшие арифметические операции над числами. Причем числа могут быть введены в разных системах счисления.
Причем числа могут быть введены в разных системах счисления.
Вам необходимо определиться сколько чисел вам необходимо посчитать и выбрать это количество в графе количество чисел.
Далее Вам необходимо ввести каждое число и выбрать его систему счисления. Если в указанном списке Вы не нашли нужной СС, то выберите пункт другая и введите числом основание вашей системы счисления.
После ввода всех чисел и выбора арифметических операций нажмите кнопку рассчитать.
| Поставить LIKE | и поделиться ссылкой |
Дата и время данного расчета 12.09.2019 0:12 МСК Вы ввели выражение:111101.1112*110111.112 Все числа находятся в двоичной системе счисления. Поэтому все расчеты будем выполнять в ней. 1) Выполним умножение 111101. |
| x | 1 | 1 | 1 | 1 | 1 | . | 1 | 1 | 1 | ||||||||
| 1 | 1 | 1 | 1 | 1 | . | 1 | 1 | ||||||||||
| + | |||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1. | 1 | 1 |
Получилось: 111101.1112*110111.112 = 110101111001.1000102
Вы пожелали видеть ответ в двоичной системе счисления
Результат расчета уже находится в нужной СС.
Постоянная ссылка на результат этого расчета
Вы можете отблагодарить нас:
Этот калькулятор умеет осуществлять простейшие арифметические операции над числами. Причем числа могут быть введены в разных системах счисления.
Пример решения: 5436 7 — 1101 2
Пример состоит из двух чисел 5436 7 и 1101 2 где в первом 7 и втором 2 — это основания системы счисления.
Введем сначала 5436 7 в поле «число 1» без основания СС (то есть без 7) и укажем его систему в соответствующем поле — выбираем пункт другая и вводим 7. Результат на скришоте:
Теперь также введем число 11011 в двоичной системе счисления:
Далее выбираем в поле «операция» вычитание и указываем что расчет должен быть выполнен в десятичной СС. Если мы хотим чтобы результат расчета был в двоичной СС, то указываем это как на скриншоте:
Если мы хотим чтобы результат расчета был в двоичной СС, то указываем это как на скриншоте:
Теперь нажимаем копку «Рассчитать» и смотрим результат:
Если хотите посмотреть ход решения, то нажмите ссылку «Показать как оно получилось»
Если Вам необходимо рассчитать более двух чисел то выберите нужное количество в пункте «Количество чисел» Максимум 7 чисел.
При расчете сначала выполняются операции деления и умножения затем сложения и вычитания.
Вы можете выполнять операции расчета деления столбиком.
Умножение в двоичной системе счисления требует знания таблицы умножения двоичных чисел.
Таблица умножения двоичных чисел:
Здесь все числа двоичные.
Умножение в двоичной системе счисления.
Умножать будем «столбиком», как и в десятичной системе счисления:
Умножая двоичные числа, мы используем таблицу умножения двоичных чисел. Принцип точно такой же, как и при умножении десятичных чисел.
Умножение в двоичной системе счисления. Рассмотрим ещё один очень простой пример.
Рассмотрим ещё один очень простой пример.
Как умножать в двоичной системе
Двоичный калькулятор онлайн
Данный калькулятор может производить следующие действия над двоичными числами:
- сложение +
- вычитание −
- умножение ×
- деление ÷
- логическое И (AND)
- логическое ИЛИ (OR)
- исключающее ИЛИ (XOR)
Сложение двоичных чисел
Сложение двух двоичных чисел производится столбиком поразрядно. Начиная с младшего разряда (справа на лево), как и при сложении столбиком десятичных чисел. Но так как цифр всего две (0 и 1), их сложение происходит по следующим правилам:
Пример
Для примера сложим 1011 и 101:
| + | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 0 | 0 | 0 | 0 |
Вычитание двоичных чисел
Вычитание двоичных чисел производится аналогично сложению – столбиком, но по следующим правилам:
Пример
Для примера вычтем из числа 1011 число 101:
| − | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 1 | 0 |
Умножение двоичных чисел
Умножение двоичных чисел производится в столбик аналогично умножению в десятичной системе, но по следующим правилам:
Пример
Для примера перемножим числа 1011 и 101:
| × | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | |||
| + | 1 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | 1 |
Деление двоичных чисел
Внешне деление двоичных чисел похоже на деление десятичных чисел, но тут есть свои нюансы: такое деление производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Чтобы понять этот процесс рассмотрим пример:
Чтобы понять этот процесс рассмотрим пример:
Арифметические операции в двоичной системе счисления
В двоичной системе счисления арифметические операции выполняются по тем же правилам, что в десятичной системе счисления, так как они обе являются позиционными. Это же касается восьмеричной и шестнадцатеричной систем.
Сложение
Сложение одноразрядных двоичных чисел выполняется по следующим правилам:
В последнем случае, при сложении двух единиц происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления (в данном случае это число 2) или больше его (для двоичной системы счисления это не актуально).
Пример сложения многоразрядных двоичных чисел:
Вычитание
Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:
В случае вычитания в текущем разряде из нуля единицы происходит заем из старшего разряда. По-сути мы вычитаем не из единицы, а из двоичного числа 10.
Умножение
Умножение одноразрядных двоичных чисел выполняется по следующим правилам:
Двоичная арифметика
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.
Таблица сложения, вычитания и умножения для двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 — 0 = 0 | 0 ∙ 0 = 0 |
| 0 + 1= 1 | 1 — 0 = 1 | 0 ∙ 1 = 0 |
| 1 + 0 = 1 | 1 — 1 = 0 | 1 ∙ 0 = 0 |
| 1 + 1 = 10 | 10 — 1 = 1 | 1 ∙ 1 = 1 |
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Пример : 1011,12 + 1010,112
Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример : 111,12 + 1112 + 101,12
При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 1002. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 1012. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Вычитание двоичных чисел
В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример : 10110,012 — 1001,12
Умножение и деление двоичных чисел
Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 1011110112 в десятичную систему счисления.
Поскольку 1010 = 10102, запишем
Полученные остатки, 10012 = 910, =1112 = 710, 112 = 310. Искомое число 1011110112 = 37910.
Двоичная система счисления
Однажды в Риме
Древних римлян часто поминают дурным словом за их громоздкую систему записи чисел. Люди не любят римские числа, так как они обременяют вычисления. Никто не обрадуется перспективе перемножать XLVII и DCDXXIV. А вот задача умножить 47 на 924 не выглядит настолько угрожающей (хотя большинство из нас все равно побежит за калькулятором). Впрочем, прежде чем сбрасывать римские числа со счетов как причудливый анахронизм, нам необходимо признать, что их основополагающий принцип – буквы вместо цифр – используется до сих пор. Этот ключевой аспект римских чисел обрел новое воплощение. Что легче прочесть?
Люди не любят римские числа, так как они обременяют вычисления. Никто не обрадуется перспективе перемножать XLVII и DCDXXIV. А вот задача умножить 47 на 924 не выглядит настолько угрожающей (хотя большинство из нас все равно побежит за калькулятором). Впрочем, прежде чем сбрасывать римские числа со счетов как причудливый анахронизм, нам необходимо признать, что их основополагающий принцип – буквы вместо цифр – используется до сих пор. Этот ключевой аспект римских чисел обрел новое воплощение. Что легче прочесть?
• Реновация школ в нашем округе обойдется в 23000000 долларов
• Реновация школ в нашем округе обойдется в 23 млн долларов
Разумеется, я не стал разделять разряды в первом случае, чтобы число было сложнее прочесть (и я попал в точку, не правда ли?). Но, даже если проставить пробелы, фраза «Пентагон требует дополнительные 19 000 000 000 долларов» сложнее для восприятия, чем «Пентагон требует дополнительные 19 млрд долларов». Иногда удобнее использовать слова вместо чисел.
Мнимое преимущество позиционной системы счисления (это такая система счисления, в которой значение каждого символа в записи числа зависит от его позиции/разряда) – это то, что в ней проще производить вычисления. Но давайте задумаемся о том, сколько сил уходит на перемножение двух чисел. Во-первых, нам необходимо запоминать дополнительные математические данные. К тому же мы обязаны помнить таблицу умножения. Во-вторых, мы проделываем многоуровневую процедуру: сортируем числа по разрядам, умножаем по соответствующему правилу, получаем промежуточные данные, складываем.
Да, десятичные числа легче перемножать, чем их римские аналоги, однако это по-прежнему утомительно. Возникает вопрос, есть ли способ записывать числа, который бы облегчал вычисления. Мы выяснили, что да, есть, но для этого придется пожертвовать наглядностью.
Единичная система счисления
Простейший способ записи чисел – единичная система счисления: мы просто записываем столько же символов (будем использовать цифру 1), сколько единиц в интересующем нас числе. Например, число 3 окажется трехзначным: 111. Сложение и умножение становятся исключительно простыми. Чтобы сложить 3 и 5, мы просто запишем два числа, 111 и 11111, друг за другом (без пробела) – и вот он, ответ: 11111111. Умножать тоже просто. Мы запишем одно число вертикально, а другое горизонтально и получим следующую таблицу:
Например, число 3 окажется трехзначным: 111. Сложение и умножение становятся исключительно простыми. Чтобы сложить 3 и 5, мы просто запишем два числа, 111 и 11111, друг за другом (без пробела) – и вот он, ответ: 11111111. Умножать тоже просто. Мы запишем одно число вертикально, а другое горизонтально и получим следующую таблицу:
Затем мы заполним таблицу, поставив единичку в каждом столбце и в каждой колонке:
Наконец, мы выпишем все единички в ряд и получим ответ: 111111111111111. Складывать и перемножать числа в единичной системе счисления существенно проще, чем десятичные или римские числа. Разумеется, такая простота вычислений дается ценой титанических затрат внимания и времени. Никому не захочется прибегать к этому методу, чтобы перемножить 47 и 924.
Компромисс
Числа, записанные в двоичной системе счисления (система счисления с основанием 2), не так привычны нам, как десятичные или римские, но с ними проще делать вычисления. Вот почему в компьютерах используется именно двоичная система. Чтобы разобраться, как она устроена, нам нужно припомнить особенности десятичной системы.
Вот почему в компьютерах используется именно двоичная система. Чтобы разобраться, как она устроена, нам нужно припомнить особенности десятичной системы.
Для записи чисел в десятичной системе счисления используют десять символов, располагаемых в разных комбинациях в ряд по горизонтали. Значение символа зависит от его места в ряду. 29 и 92 означают разные числа, потому что 2 и 9 занимают разные позиции. 29 означает «два десятка и девять единиц». 5804 означает «пять тысяч, восемь сотен, ни одного десятка и четыре единицы». Позиция цифры в десятичном числе означает, на какую степень десяти мы ее умножаем. Напомним, что показатель степени означает, сколько раз мы перемножаем основание: например, 10³ = 10 × 10 × 10. Естественно, 101 = 10. По договоренности, 100 = 1. Это логично, так как каждая следующая степень десяти в десять раз больше предыдущей. Разряды растут справа налево: единицы, десятки, сотни, тысячи, десятки тысяч и т. д. Иными словами, запись 5804 означает:
5 × 10³ + 8 × 10² + 0 × 101 + 4 × 100
Чем больше символов в десятичном числе, тем труднее его прочесть. Обычно каждый четвертый разряд отделяют пробелом или запятой. В англоязычных странах в качестве разделителя разрядов используется запятая, в России – неразрывный пробел, который ставится только в числах с пятью и более разрядами. Двоичная система устроена схожим образом, просто позиция в записи означает, на какую степень двух (а не десяти) мы должны умножить эту конкретную цифру. В двоичной системе счисления используются всего два символа: 0 и 1. Разряды здесь тоже растут справа налево, обозначая количество единиц, двоек, четверок, восьмерок и т. д. Например, в двоичной записи 10110 означает:
Обычно каждый четвертый разряд отделяют пробелом или запятой. В англоязычных странах в качестве разделителя разрядов используется запятая, в России – неразрывный пробел, который ставится только в числах с пятью и более разрядами. Двоичная система устроена схожим образом, просто позиция в записи означает, на какую степень двух (а не десяти) мы должны умножить эту конкретную цифру. В двоичной системе счисления используются всего два символа: 0 и 1. Разряды здесь тоже растут справа налево, обозначая количество единиц, двоек, четверок, восьмерок и т. д. Например, в двоичной записи 10110 означает:
1 × 2⁴ + 0 × 2³ + 1 × 2² + 1 × 21 + 0 × 20 = 16 + 4 + 2 = 22
Проверьте, насколько вы ориентируетесь в новой теме: чему равно число 42 в двоичной системе и чему равно число 110112 в десятичной? (чтобы отличить запись в двоичной системе от записи в десятичной, мы будем ставить нижний индекс: 11012 или 110110).
Вычисления
Двоичные числа труднее для чтения, чем десятичные. Двоичная запись 1011001 кажется менее привычной, чем десятичная запись того же числа: 89. Преимущество двоичных чисел в том, что их использование облегчает вычисления. Вместо огромного количества математических данных нам необходимы всего две таблицы:
Двоичная запись 1011001 кажется менее привычной, чем десятичная запись того же числа: 89. Преимущество двоичных чисел в том, что их использование облегчает вычисления. Вместо огромного количества математических данных нам необходимы всего две таблицы:
Заметьте, что в таблице умножения 10 означает число два. Сложение двоичных чисел устроено так же, как в десятичной системе. Например, нам нужно найти сумму 101002 и 11102. Расположим эти числа друг над другом:
Дальше нужно двигаться справа налево, складывая цифры в каждом столбце и при необходимости перемещая единицу на столбец влево. В нашем случае мы сложим два нуля и получим ноль:
Дальше идет столбец двоек. Мы складываем 1 и 0 (переносить ничего не требуется):
Дальше – столбец четверок. Мы складываем 1 и 1, получаем 10, пишем 0, держим 1 в уме и переносим на столбец влево:
Следующий столбец – восьмерки. Складываем 1 и 0 и 1, получаем 10, пишем 0 и держим 1 в уме:
Складываем 1 и 0 и 1, получаем 10, пишем 0 и держим 1 в уме:
Заканчиваем на столбце, означающем, сколько раз в числе встречается 16. Сложение дает 10, мы пишем 0 в текущем столбце и 1 в столбце с разрядом 32:
Мы обнаружили, что 10100 + 1110 = 100010.
Переведем это на язык десятичных чисел:
101002 = 20, 11102 = 14, 1000102 = 34.
Разумеется, 20 + 14 = 34.
Умножение в двоичной системе проще, чем в десятичной. Достаточно усвоить два принципа: сложение двоичных чисел (мы в нем только что разобрались) и умножение на степени двойки.
Умножение числа на 10 в десятичной системе не представляет сложности: мы просто добавляем цифру 0 справа: 23 × 10 = 230. Точно так же выглядит умножение на 2 в двоичной системе: 1101 × 10 = 11010. В случае десятичных чисел это очевидно, в случае двоичных 1101 означает:
1 × 8 + 1 × 4 + 0 × 2 + 1 × 1.
Умножение на 2:
1 × 16 + 1 × 8 + 0 × 4 + 1 × 2 + 0 × 1
Лишний ноль на конце дает 11010.
Умножение на 4, 8 и другие степени двойки тоже просто: например, умножение на 810 (10002) равнозначно приращению трех нулей с правой стороны числа. Итак, умножение превращается в игру «перемести-и-добавь-цифры». Проиллюстрируем это на примере умножения 11010 на 1011. Для начала запишем второе число так:
1011 = 1000 + 10 + 1.
Умножение на 11010 можно представить так:
11010 × 1011 = 11010 × (1000 + 10 + 1) = 11010 × 1000 + 11010 × 10 + 11010 × 1 = 11010000 + 110100 + 11010.
Удобнее умножать в столбик:
А вот и ответ:
Давайте переведем числа в десятичные, чтобы удостовериться, что все правильно:
110102 = 16 + 8 + 2 = 26;
10112 = 8 + 2 + 1 = 11;
1000111102 = 256 + 16 + 8 + 4 + 2 = 286.
Мы не ошиблись: 26 × 11 = 286.
В десятичной системе мы можем записывать не только целые числа. Если поставить в конце запятую, мы получим новые места для цифр: по мере движения вправо степени десяти будут все меньше. Например, 34,27 – это компактный способ записи такого выражения:
Например, 34,27 – это компактный способ записи такого выражения:
Двоичная система тоже позволяет записывать дробные значения. Каждую следующую цифру после запятой (в случае с двоичной системой неправильно говорить «десятичная запятая», лучше называть ее двоичной запятой, или запятой в позиционном представлении числа) мы умножаем на предыдущую степень двойки. Например, 101,0112 означает:
Непривычный способ записать одну вторую: 0,12! Есть и другие системы счисления, помимо десятичной, единичной и двоичной. Программисты нередко пользуются шестнадцатеричной системой счисления. В десятичной системе 10 цифр (от 0 до 9), в шестнадцатеричной нам нужно 16 разных символов, поэтому числа от 10 до 15 обозначают с помощью букв от A до F. В третичной системе мы пользуемся цифрами 0, 1 и 2, здесь все строится на степенях тройки. Скажем, 11023 означает:
1 × 27 + 1 × 9 + 0 × 3 + 2 × 1 = 38
В дробях первая позиция справа от запятой означает умножение на одну третью, вторая позиция – на одну девятую и т. д.:
д.:
Ответ на задачу
Если представить 42 в виде суммы степеней двойки, мы увидим, что это 1010102. А число 110112 можно представить как 16 + 8 + 2 + 1 = 27.
Отрывок из книги Эдварда Шейнермана «Путеводитель для влюбленных в математику»
11 умножить на 11 в двоичной системе счисления
Вы искали 11 умножить на 11 в двоичной системе счисления? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выполните умножение в двоичной системе счисления, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «11 умножить на 11 в двоичной системе счисления».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 11 умножить на 11 в двоичной системе счисления,выполните умножение в двоичной системе счисления,выполните умножение в двоичной системе счисления 10010 10001,выполните умножение в двоичной системе счисления 10011 11000,выполните умножение в двоичной системе счисления 1101 1110,выполнить умножение в двоичной системе счисления,двоичная система счисления умножение,двоичное умножение,деление в двоичной системе калькулятор,деление двоичных чисел онлайн,деление двоичных чисел онлайн калькулятор,деление двоичных чисел онлайн калькулятор с решением,деление двоичных чисел онлайн калькулятор с решением столбиком,деление чисел в двоичной системе счисления онлайн,как умножать в двоичной системе,как умножать в двоичной системе счисления,как умножать двоичную систему счисления,как умножать двоичные числа,как умножать двоичные числа столбиком,как умножать числа в двоичной системе счисления,калькулятор двоичной системы счисления онлайн умножение,калькулятор двоичных чисел умножение,калькулятор систем счисления онлайн с решением умножение,калькулятор систем счисления онлайн умножение,калькулятор систем счисления с решением онлайн умножение,калькулятор систем счисления умножение,калькулятор систем счисления умножение онлайн,калькулятор умножение в двоичной системе,калькулятор умножение в двоичной системе счисления онлайн,калькулятор умножение двоичных чисел,калькулятор умножение систем счисления,калькулятор умножение систем счисления онлайн,калькулятор умножения двоичных чисел,онлайн деление в двоичной системе,онлайн калькулятор деление двоичных чисел,онлайн калькулятор деление двоичных чисел с решением,онлайн калькулятор систем счисления с решением умножение,онлайн калькулятор систем счисления умножение,онлайн калькулятор умножение в двоичной системе счисления,онлайн калькулятор умножение двоичных чисел с решением,онлайн калькулятор умножение систем счисления,онлайн калькулятор умножение систем счисления с решением,онлайн умножение в двоичной системе счисления,онлайн умножение восьмеричных чисел,онлайн умножение двоичных чисел,онлайн умножение чисел в двоичной системе счисления,онлайн умножить двоичные числа,примеры умножение двоичных чисел,система счисления онлайн умножение,система счисления умножение онлайн,умножение в 2 системе счисления,умножение в двоичной,умножение в двоичной системе,умножение в двоичной системе калькулятор,умножение в двоичной системе счисления,умножение в двоичной системе счисления онлайн,умножение в двоичной системе счисления онлайн калькулятор,умножение в системах счисления онлайн,умножение двоичная система счисления,умножение двоичной системы,умножение двоичной системы счисления,умножение двоичной системы счисления онлайн калькулятор,умножение двоичных чисел,умножение двоичных чисел калькулятор,умножение двоичных чисел калькулятор онлайн,умножение двоичных чисел онлайн,умножение двоичных чисел онлайн калькулятор,умножение двоичных чисел онлайн калькулятор с решением,умножение двоичных чисел примеры,умножение над двоичными числами,умножение онлайн в двоичной системе счисления,умножение систем счисления калькулятор,умножение систем счисления онлайн калькулятор,умножение систем счисления онлайн калькулятор с решением,умножение системы счисления,умножение чисел в двоичной системе,умножение чисел в двоичной системе счисления,умножение чисел в двоичной системе счисления онлайн,умножения двоичных чисел калькулятор,умножить двоичные числа онлайн,умножьте два числа в двоичной системе счисления 110112 1012. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 11 умножить на 11 в двоичной системе счисления. Просто введите задачу в окошко и нажмите
«решить» здесь (например, выполните умножение в двоичной системе счисления 10010 10001).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 11 умножить на 11 в двоичной системе счисления. Просто введите задачу в окошко и нажмите
«решить» здесь (например, выполните умножение в двоичной системе счисления 10010 10001).
Где можно решить любую задачу по математике, а так же 11 умножить на 11 в двоичной системе счисления Онлайн?
Решить задачу 11 умножить на 11 в двоичной системе счисления вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Двоичное умножение — правила, метод умножения двоичных чисел, примеры.

LearnPracticeDownload
Двоичное умножение — это процесс умножения двоичных чисел. Процесс умножения двоичных чисел такой же, как и при арифметическом умножении десятичных чисел. Единственное отличие состоит в том, что при двоичном умножении используются числа, состоящие из нулей и единиц, тогда как при десятичном умножении используются числа, состоящие из цифр от 0 до 9. Давайте шаг за шагом изучим процесс двоичного умножения.
| 1. | Двоичные правила умножения |
| 2. | Как умножать двоичные числа? |
| 3. | Примеры двоичного умножения |
| 4. | Практические вопросы по двоичному умножению |
| 5. | Часто задаваемые вопросы о двоичном умножении |
Правила двоичного умножения
Двоичное умножение похоже на умножение десятичных чисел. У нас есть множитель и множимое. В результате умножения получается произведение. Поскольку в двоичном умножении участвуют только двоичные цифры, мы можем умножать только 0 и 1. Правила двоичного умножения следующие.
У нас есть множитель и множимое. В результате умножения получается произведение. Поскольку в двоичном умножении участвуют только двоичные цифры, мы можем умножать только 0 и 1. Правила двоичного умножения следующие.
| Множимое | Множитель | Продукт |
|---|---|---|
| 0 | 0 | 0 × 0 = 0 |
| 0 | 1 | 0 × 1 = 0 |
| 1 | 0 | 1 × 0 = 0 |
| 1 | 1 | 1 × 1 = 1 |
Как умножать двоичные числа?
Процесс умножения двоичных чисел аналогичен и более прост в выполнении, чем десятичное умножение, поскольку двоичные числа состоят только из двух цифр: 0 и 1. Метод умножения двоичных чисел приведен ниже. Тот же набор правил применим и к двоичным числам с десятичной точкой. Возьмем пример умножения (\(11101)_{2}\) и (\(1001)_{2}\). Десятичный эквивалент (\(11101)_{2}\) равен 29, а десятичный эквивалент (\(1001)_{2}\) равен 9. Теперь давайте перемножим эти числа.
Десятичный эквивалент (\(11101)_{2}\) равен 29, а десятичный эквивалент (\(1001)_{2}\) равен 9. Теперь давайте перемножим эти числа.
Шаг 1: Запишите множимое (\(11101)_{2}\) и множитель (\(1001)_{2}\) один под другим на соответствующих позициях.
Шаг 2: Умножьте самую правую цифру или младший значащий бит (LSB) множителя (1) на все цифры множимого (\(11101)_{2}\).
Шаг 3: Добавьте заполнитель «0» или «X» перед умножением следующего старшего разряда множителя& на множимое.
Шаг 4: Повторите тот же процесс для всех следующих цифр более высокого порядка, пока мы не достигнем самого старшего бита (MSB), который является самой левой цифрой множимого с множителем.
Шаг 5: Произведение, полученное в каждой строке, называется частичным произведением. Наконец, добавьте все частичные продукты. Чтобы сложить все двоичные числа, используйте правила двоичного сложения.
(Правила двоичного сложения перечислены ниже: 0 + 0 = 0, 0 + 1 = 1 и 1 + 1 = 0 с переносом 1. Таким образом, 1 + 1 = 10 и 1 + 1 + 1 = 11 в двоичной системе счисления)
Таким образом, 1 + 1 = 10 и 1 + 1 + 1 = 11 в двоичной системе счисления)
Давайте рассмотрим следующий процесс двоичного умножения, описанный выше.
Следовательно, произведение (\(11101)_{2}\) и (\(1001)_{2}\) равно (\(100000101)_{2}\). Проверим наш ответ. Десятичный эквивалент (\(100000101)_{2}\) равен 261. Чтобы узнать, как преобразовать двоичное число в десятичное, нажмите здесь. Десятичный эквивалент & (\(11101)_{2}\) равен 29, а десятичный эквивалент (\(1001)_{2}\) равен 9. Когда мы умножаем 29 на 9, произведение равно 261. Десятичный эквивалент of (\(100000101)_{2}\) равно 261. Следовательно, произведение правильное.
Темы, относящиеся к двоичному умножению
Ознакомьтесь с некоторыми интересными темами, связанными с двоичным умножением.
- Двоичная система счисления
- Двоичное вычитание
- Двоичный раздел
- Двоичный код в десятичный
- Системы счисления
Примеры двоичного умножения
Пример 1.
 Используя правила двоичного умножения, умножьте ( \(110)_{2}\) и ( \(11)_{2}\).
Используя правила двоичного умножения, умножьте ( \(110)_{2}\) и ( \(11)_{2}\). Решение:
Правила двоичного умножения:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Давайте воспользуемся приведенными выше правилами для умножения двоичных чисел.GIven, множимое = \(110_{2}\), множитель = \(11_{2}\). Мы умножаем два числа, как показано ниже.
Следовательно, произведение (\(110)_{2}\) и (\(11)_{2}\) равно (\(10010)_{2}\).Пример 2. Используя правила двоичного умножения, найдите произведение (\(11011)_{2}\) и (\(101)_{2}\).
Решение:Множитель GIven = (\(11011)_{2}\) и множитель = (\(101)_{2}\)
При умножении получаемСледовательно, произведение (\(11011)_{2}\) и (\(101)_{2}\) равно (\(10000111)_{2}\).
Пример 3. Используя правила двоичного умножения, умножьте двоичные числа (\(1011.
 1)_{2}\) и (\(10.1)_{2}\).
1)_{2}\) и (\(10.1)_{2}\). Решение:
Учитывая множимое = (\(1011.1)_{2}\) и множитель = (\(10.1)_{2}\).
Следовательно, произведение (\(1011.1)_{2}\) и (\(10.1)_{2}\) равно (\(11100.11)_{2}\)
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по двоичному умножению
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о двоичном умножении
Что такое двоичное умножение?
Двоичное умножение — это процесс умножения двоичных чисел. Двоичные числа образуют систему счисления с основанием 2. Данные хранятся в компьютере в виде нулей и единиц. Процесс умножения двоичных чисел такой же, как и арифметическая операция умножения, которая выполняется над десятичными числами или числами с основанием 10. Единственное отличие состоит в том, что двоичные числа состоят из нулей и единиц.
Процесс умножения двоичных чисел такой же, как и арифметическая операция умножения, которая выполняется над десятичными числами или числами с основанием 10. Единственное отличие состоит в том, что двоичные числа состоят из нулей и единиц.
Каковы правила двоичного умножения?
Двоичное умножение также похоже на умножение десятичных чисел (от 0 до 9). Двоичные числа состоят только из 0 и 1. Следовательно, нам нужно знать произведение, когда 0 умножается на 0 и 1, а 1 умножается на 0 и 1. Правила двоичного умножения следующие.
- 0 × 0 = 0
- 0 × 1 = 0
- 1 × 0 = 0
- 1 × 1 = 1
Каков результат двоичного умножения (\(111)_{2}\) и (\(111)_{2}\)?
Произведение (\(111)_{2}\) и (\(111)_{2}\) равно (\(110001)_{2}\).
Как выполнить двоичное умножение?
Двоичное умножение двух чисел можно выполнить, выполнив шаги, указанные ниже.
Шаг 1: Расположите множитель и множимое в нужных местах. Например, мы можем перемножить трехзначное число и двузначное число. В этом случае 2-значное число должно быть правильно размещено под 3-значным числом, например,
Например, мы можем перемножить трехзначное число и двузначное число. В этом случае 2-значное число должно быть правильно размещено под 3-значным числом, например,
110
× 10
———
_____
Шаг 2: Следующим шагом является умножение каждой цифры множимого на каждую цифру множителя, начиная с самой правой цифры или младшего значащего бита (LSB). Произведение, полученное после умножения каждой цифры множимого на множитель, называется частичным произведением. Наконец, мы складываем частичные продукты, полученные на каждом шаге, используя правило бинарного сложения.
Чему равно произведение (\(1111)_{2}\) и (\(1111)_{2}\) с помощью двоичного умножения?
Произведение (\(1111)_{2}\) и (\(1111)_{2}\) с использованием двоичного умножения равно (\(11100001)_{2}\). В этом двоичном умножении множитель и множимое являются одними и теми же двоичными числами. Мы используем правила двоичного умножения, а именно «0 × 0 = 0, 1 × 0 = 0, 0 × 1 = 0& и 1 × 1 = 1», и умножаем числа в соответствии с обычным методом арифметического умножения.
Что такое двоичное умножение отрицательных чисел?
В десятичной системе счисления или системе счисления с основанием 10 есть отрицательные числа, такие как -1, -2, -3 и так далее. Также можно умножать отрицательное число на положительное число или отрицательное число на отрицательное число в двоичном формате. Для этого мы представляем каждое число с помощью 8 бит. Здесь мы используем 4 бита для представления числа в дополнении до 2 и 4 бита для представления знака. Если знак числа положительный, то мы используем четыре нуля, а если число отрицательное, мы используем четыре единицы. Дополнение до 2 двоичного числа получается путем добавления 1 к дополнению до единицы двоичного числа. Дополнение до 1 означает замену каждого 0 на 1 и каждой 1 на 0.
Каков результат двоичного умножения чисел (\(10100)_{2}\) и (\(01011)_{2}\)?
Произведение (\(10100)_{2}\) и (\(01011)_{2}\) равно (\(011011100)_{2}\).
Скачать бесплатные материалы для исследования
Связанный рабочий лист
Математические листы и
Визуальная учебная программа
Двоирный мультипликационный калькулятор
Создан Филиппом Маусом
Обзор Стивена Вудинг
Последний0131
Калькулятор двоичного умножения описывает как умножать двоичные числа . В этой статье вы также узнаете сходства и различия двоичной и десятичной системы счисления и увидите пошаговые инструкции по умножению двоичных чисел .
В этой статье вы также узнаете сходства и различия двоичной и десятичной системы счисления и увидите пошаговые инструкции по умножению двоичных чисел .
Как умножать двоичные числа?
В то время как десятичная система счисления, с которой мы все знакомы, основана на степенях 10, двоичная система имеет основание 2 . Это означает, что каждая цифра двоичного числа, так называемый бит, может представлять только два логических значения: 0 или 1 . Поэтому двоичные числа обычно используются в цифровой электронике и связи, представляя два состояния «включено» и «выключено». Двоичные числа можно преобразовать в десятичную систему. Они также позволяют применять арифметические операции, такие как сложение, вычитание, деление и, как мы увидим в калькуляторе двоичного умножения, умножение. Кроме того, двоичные числа позволяют выполнять операции, уникальные для двоичной системы, такие как сдвиг битов и побитовые операции AND, OR и XOR.
Эти операции также можно выполнять с отрицательными двоичными числами. Они показаны в так называемом дополнении до двух со знаком , в котором первая цифра указывает на знак числа . Этот калькулятор двоичного деления использует представление со знаком, что означает, что первый бит ваших входных чисел будет считаться битом со знаком. Будьте осторожны, чтобы не получить ложные результаты из-за этого , и при необходимости увеличьте битовое представление.
Каковы правила двоичного умножения?
Двоичное умножение имеет 4 основных правила :
-
0×0=0 -
0×1=0 -
1×0=0 -
1×1=1
На основе этих правил двоичное умножение очень похоже на десятичное длинное умножение . Это даже можно считать немного проще, поскольку нам нужно иметь дело только с цифрами
Это даже можно считать немного проще, поскольку нам нужно иметь дело только с цифрами 0 и 1 .
Умножение — это коммутативная операция , что означает, что произведение не зависит от порядка множителей. Тем не менее, рекомендуется для длинного деления устанавливать более длинное число в качестве множителя (множитель 1), а более короткое число — в качестве множимого (множитель 2), чтобы уменьшить количество шагов. Умножьте множитель на каждую цифру множимого, чтобы получить промежуточные произведения, последняя цифра которых находится на позиции соответствующей цифры множимого. Конечный продукт представляет собой сумму этих промежуточных продуктов.
В качестве примера рассмотрим умножение 1011 и 0101 (13 и 5 в десятичной системе):
Пошаговая процедура умножения этих двоичных чисел выглядит следующим образом: :
- Установите большее число в качестве множителя .

1011имеет четыре значащих бита и поэтому имеет коэффициент 1. - Умножить множитель на последнюю цифру множимого :
- Следуя основным правилам, указанным выше,
1011×1=1011. Это первый промежуточный продукт, начиная с позиции последней цифры множимого.
- Умножить множитель на предпоследнюю цифру множимого :
1011×0=0000. Это второй промежуточный продукт, начиная со второй до последней цифры множимого.
- Умножить множитель на третью до последней цифры множимого :
1011×1=1011. Это третий промежуточный продукт, начиная с позиции третьей до последней цифры множимого.
- Умножьте множитель на предпоследнюю (первую) цифру множимого :
1011×0=0000.Это четвертый промежуточный продукт, начиная с позиции четвертой и заканчивая последней цифрой множимого.
- Конечный продукт представляет собой сумму промежуточных продуктов :
1011+00000+101100+0000000=0110111
Как пользоваться калькулятором двоичного умножения?
Теперь вы знаете, как выполнять умножение двоичных чисел, так что давайте научиться пользоваться калькулятором двоичного умножения . В качестве примера, давайте проверим правильность нашей пошаговой процедуры выше и умножим 1011 и 101 :
- . представлен в.
- Как мы уже знаем, максимальное число битов произведения равно 6, поэтому 8 битов вполне достаточно.
- Введите коэффициенты.
 Поскольку операция умножения коммутативна, порядок не имеет значения.
Поскольку операция умножения коммутативна, порядок не имеет значения.
1011и101
- Калькулятор двоичного умножения представляет произведение в двоичной и десятичной системе . Это результат вашего умножения двоичных чисел: .
- Двоичный:
0011 0111- Десятичный:
13
Если ваш двоичный результат имеет значение 1 в старшем разряде и может быть понят как положительный результат в нотации без знака или отрицательный результат в нотации со знаком, будут отображаться оба результата .
Часто задаваемые вопросы
Как умножать двоичные числа?
Для умножения двоичных чисел выполните следующие действия:
- Установите более длинное число в качестве множителя и более короткое число как множимое .

- Умножьте множитель на каждую цифру множимого , чтобы получить промежуточные произведения, последняя цифра которых находится на позиции соответствующей цифры множимого.
- Суммируйте промежуточные продукты , чтобы получить конечный продукт.
Как умножать двоичные числа с помощью битового сдвига?
Двоичное умножение, особенно с коэффициентами, равными степени двойки, можно выполнить с помощью сдвига битов влево . Умножение на 2 — это сдвиг на один бит, 4 — 2 бита, 8 — 3-битный сдвиг и т. д. Благодаря своей математической эффективности этот метод обычно используется в цифровых приложениях.
Как умножить двоичные числа 101 и 11?
на Умножьте двоичные номера 101 и 11 , выполните следующие шаги:
- SET
101как увеличение и11как увеличение и11как увеличение и11.
- Умножить
101на последнюю цифру11:101×1=101. Это первый промежуточный продукт . - Умножьте
101на первую цифру11:101×1=101. Добавьте0в конце, чтобы представить позицию цифры множимого:1010. Это второй промежуточный продукт . - Суммируйте промежуточные продукты , чтобы получить конечный продукт:
101+1010=1111.
Филип Маус
Двоичное представление
Вы можете записывать двоичные числа, содержащие не более 8 цифр. Вам не нужно вводить лидирующие нули.
Фактор 1
Фактор 2
Посмотреть 10 похожих бинарных калькуляторов 1️0️
Двоичное сложениеДвоичное делениеДвоичная дробь… 7 еще
арифметика — Двоичное умножение отрицательных чисел
Задавать вопрос
Спросил
Изменено 3 года назад
Просмотрено 15 тысяч раз
$\begingroup$
Вопрос касается двоичного умножения отрицательных чисел. Предположим, мы хотим умножить
Предположим, мы хотим умножить -5 * -3 , чтобы в результате получилось +15 .
1) На первом шаге мы должны использовать дополнение до 2 для входных данных.
+5 = 0101 -> -5 = 1011 +3 = 0011 -> -3 = 1101
2) Мы следуем простому методу карандаша и бумаги, и мы должны отметить расширение знака. Для ясности я поставил расширения знаков в []
1011
* 1101
----------------
[1] [1] [1] 1 0 1 1
[0] [0] 0 0 0 0
[1] 1 0 1 1
1 0 1 1 +
------------------------------
с7 с6 с5 с4 с3 с2 с1
3) суммирование столбцов показывает, что
c1 = 1 + 0 + 0 + 0 = 1 с2 = 1 + 0 + 0 + 0 = 1 с3 = 0 + 0 + 1 + 0 = 1 c4 = 1 + 0 + 1 + 1 = 1 (перенести 1 в c5) c5 = 1 (перенос) + 1 (знак) + 0 + 0 + 1 = 1 (перенос 1 в c6) c6 = 1 (перенос) + 1 (знак) + 0 (знак) + 1 + 0 = 1 (перенос 1 в c7) c7 = 1 (перенос) + 1 (знак) + 0 (знак) + 1 (знак) + 1 = ???
На самом деле c7 = 100 , но мы должны представить только одну цифру в c7. Значит ли это, что
Значит ли это, что
c7 = 0 (перенести 10)
?? Обычно последний бит переноса состоит только из одной цифры. Более того, итоговое число не равно +15 . Где я сделал ошибку?
- арифметика
- бинарные операции
$\endgroup$
2
$\begingroup$
Я считаю, что ответ, данный «Подстановочным знаком», не полностью отвечает на этот вопрос. Он не продлевает знак перед умножением, что может вызвать путаницу у новых зрителей. Кроме того, вы не «умножаете навсегда, чтобы получить бесконечные биты», знаки просто расширяются заранее. Так что это должно выглядеть лучше:
1 1 1 1 1 0 1 1 = -5
* 1 1 1 1 1 1 0 1 = -3
--------------------------------------------
1 1 1 1 1 0 1 1
0 0 0 0 0 0 0 0 |
1 1 1 1 1 0 1 1 |
1 1 1 1 1 0 1 1 |
1 1 1 1 1 0 1 1 | |
1 1 1 1 1 0 1 1 | |
1 1 1 1 1 0 1 1 | |
1 1 1 1 1 0 1 1 | |
--------------------------------------------
отброшено| 0 0 0 0 1 1 1 1 = +15
Биты в конце отбрасываются, поскольку число 8-битное.
Справочник и дополнительная литература: https://en.wikipedia.org/wiki/Two%27s_complement
$\endgroup$
2
$\begingroup$
1011
* 1101
----------------
[1][1] [1] [1] 1 0 1 1
[0] [0] 0 0 0 0
[1][1] 1 0 1 1
[1] 1 0 1 1 +
1 0 1 1
... 1 1
------------------------------
с7 с6 с5 с4 с3 с2 с1
Это проясняет?
Если вы продолжите двигаться влево, вы получите бесконечное количество битов. Но так и должно быть. Фактический ответ справа заканчивается как … 01111, если вы включаете запись 1011, заканчивающуюся в столбце 5. Чем больше 1011 записей вы включаете (оканчивающихся на c6, c7 и т. д.), тем больше нулей у вас будет в начале вашего ответа.
Я не знаю ответа из учебника о том, где остановиться, чтобы двигаться влево, но вы можете, по крайней мере, концептуально увидеть это из вышеприведенного.
$\endgroup$
$\begingroup$
Когда вы умножаете два отрицательных числа, в последнем члене вы должны написать дополнение до 2 первого числа. В этом случае дополнение до 2 числа 1011 равно 0101. Я поставил дополнение до 2 в ().
1011
* 1101
----------------------------------
[1] [1] [1] [1] 1 0 1 1
[0] [0] [0] 0 0 0 0 х
[1] [1] 1 0 1 1 х х
[0] (0 1 0 1) х х х +
----------------------------------
0 0 0 0 1 1 1 1
Отбросить оставшийся бит, так как нам нужен ответ в 8-битном формате, если мы продолжим двигаться влево, мы получим только больше 0 слева от числа.
$\endgroup$
$\begingroup$
Как упомянул @Hamza Bhati,
Когда вы умножаете два отрицательных числа, в последнем члене вы должны написать дополнение до 2 первого числа.
Объясню причину: на вашем примере 1011x1101=1011x(1000+0101)=1011x1000+1011x0101 , вы должны использовать обычное умножение для части 0101 , а для части 1011x1000 вы должны использовать дополнение до 2 и сложить их вместе.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Двоичное умножение: объяснение, правила и примеры решений
Апурва Бали
Старший специалист по контенту | Обновлено 5 апреля 2022 г.
Двоичное умножение — это операция, выполняемая над двоичными цифрами. Двоичная система — это система обозначения числовых обозначений, которая имеет основание 2, а не обычное обозначение, которое имеет основание 10. Оно содержит нули и единицы, а не числа обозначения основания 10, которые включают от 0 до 9цифры. Двоичные операции при выполнении имеют процедуру, аналогичную обычным операциям. Единственная разница заключается в включенных цифрах. Двоичное сложение, вычитание , умножение и деление включает только 1 и 0, остальные шаги такие же.
Содержание
| 1010139
ДВУРНАЯ НОМЕР | Значение 0051 |
0 x 0 | 0 |
1 x 0 | 0 |
0 x 1 | 0 |
1 x 1 | 1 |
Что следует помнить
[Нажмите здесь, чтобы просмотреть примеры вопросов]
- Двоичное умножение выполняется для двоичных цифр.

- Двоичные цифры включают 0 и 1.
- Процедура операций остается такой же, как и при обычных методах.
- Запишите множимое и множитель один под другим.
- Умножить младший бит на все цифры множимого.
- Повторяйте процесс, пока не будет достигнут старший бит.
- Добавьте все частичные ответы, чтобы получить полный ответ.
Примеры вопросов
Вопросы.
10111 по 1101
Ответ.
1 0 1 1 1
1 1 0 1
1 0 1 1 1 ← Первый неполный продукт 1 1
1 0 0 1 0 1 0 1 1 ← Итоговая сумма.
Следовательно, требуемый продукт 100101011.
Ques. Верно ли, что все бинарные операции завершены?
Ответ. Некоторые бинарные операторы могут закрывать некоторые наборы, с которыми вы, возможно, знакомы, но многие другие — нет. Как следствие, количество нечетных целых частей было закрыто. Например, число странных целых чисел не замкнуто, потому что сумма двух странных чисел не всегда является странной и никогда не бывает странной.
Например, число странных целых чисел не замкнуто, потому что сумма двух странных чисел не всегда является странной и никогда не бывает странной.
Вопрос.
11011.101 по 101.111
Ответ.
1 1 0 1 1 . 1 0 1
1 0 1 . 1 1 1
1 1 0 1 1 . 1 0 1
1 1 0 1 1 1 . 0 1 ← Первый частичный продукт
1 0 1 0 0 1 0 1 1 1 ← Первая промежуточная сумма
1 1 0 1 1 1 0 1
1 1 0 0 0 0 0 1 0 1 1 ← Вторая промежуточная сумма
1 1 0 1 1 1 0 1
1 1 0 0 1 1 1 1 0 0 1 1 ← Третья промежуточная сумма
1 1 0 1 1 1 0 1
1 0 1 0 0 0 1 0 0 1 0 0 1 1
Следовательно, требуемый результат равен 10100010,010011.
Вопрос 3. Вычислить (10) 2 * (11) 2
Ответ. Мы можем получить вывод, преобразовав двоичные числа в соответствующие числа с основанием 10 и умножив их, чтобы получить окончательный вывод.
Здесь (10) 2 = (2) 10 , (11) 2 = (3) 10 и (110) 2 = (6) 10 .
Когда мы умножаем 2 и 3 , мы получим произведение как 6 , которое мы получаем путем умножения двоичных чисел. Следовательно, наше решение верно.
Вопрос. Является ли квадратный корень бинарной операцией?
Ответ. Недвоичная транзакция — это процесс, которому для выполнения задачи требуется только одно число. Сложение, вычитание, умножение и деление являются примерами бинарных операций. Квадратные корни, факториалы и абсолютные значения являются типичными недвоичными операциями.
Вопрос. Вычислить (111) 2 * (101) 2
Ответ. Следовательно, результат — (111) 2 * (101) 2 = (100011) 2
Следовательно, результат — (111) 2 * (101) 2 = (100011) 2
. Вычислить (1010.01) 2 * (1.01) 2
Ответ. Таким образом, результат равен (1010.01) 2 * (1.01) 2 = (1100,1101) 2
2 Воп. Умножьте 11101 * 1001
Ответ. Следовательно, произведение (11101) 2 и (1001) 2 равно (100000101) 2 .
Проверка
Десятичный эквивалент (100000101)2 равен 261. Десятичный эквивалент (11101)2 равен 29, а десятичный эквивалент (1001)2 равен 9. При умножении 29 на 9 получается 261. Десятичный эквивалент (100000101)2 равен 261. Следовательно, произведение верное.
Следовательно, произведение верное.
Вопрос. Что является элементом идентичности бинарной операции?
Ответ. Двоичный элемент, также известный как нейтральный элемент, — это тип элемента в наборе, который не влияет на элемент набора при его сочетании с бинарной функцией. Это описание используется в алгебраических структурах, таких как группы и кольца.
Вопрос. Что такое бинарное переполнение?
Ответ. Переполнение происходит, когда размер битового поля превышает размер числа. В этой ситуации возможно переполнение, потому что битовые поля двух чисел, помеченных одной и той же сигнатурой, сильно различаются.
Вопрос. Умножить 1101 * 1110
Ответ.
Вопрос. 1010 * 0110
Отв.
Читайте также:
Площадь треугольника: формулы, виды и примеры
Операции над матрицами: сложение, вычитание, умножение и примеры решения
Плоскость: уравнение плоскости в трехмерном линейном пространстве
3
Программирование: определение, методы и примерыВероятность: определение, формула, типы и проблемы
Непрерывность и дифференцируемость функции с решенными примерами
Применение производных: касательные, максимумы-минимумы и объяснение
Транспонирование матрицы: определение, свойства и примеры
Треугольники
Вещественные числа: определение, свойства и примеры
Окружности Примечания к пересмотру: Теоремы касательной к окружности
Статистика Важные вопросы
Типы и графическое представлениеФормула действительных чисел: некоторые основные свойства вещественных чисел
Пара линейных уравнений с двумя переменными: примечания к редакции
Советы по подготовке к математике
Тригонометрические тождества: формулы, соотношения и примеры
Пара линейных уравнений с двумя переменными Формула: пересекающиеся и совпадающие прямые Уравнение, эксцентрик, формула, свойства, примеры вопросов
Типы отношений: определение, классификация и примеры
Определенный интеграл: определение, свойства, применение и примеры
Интегрирование неполными дробями: определение, различные формы и примеры решения
Векторы: введение, типы, операции и свойства
Окружность круга: радиус, вывод, периметр и решенные вопросы Примеры вопросов
Логарифм: определение, как пользоваться таблицей логарифмов, примеры
Sin Cos Tan: формула, таблица, значения и примеры
Значение Cos 180 градусов: расчет и примеры решения
Формула угла: определение, различные типы, решенный пример
Двоичное умножение
Двоичное умножение — это процесс умножения двоичных чисел. Процесс умножения двоичных чисел такой же, как и арифметическое умножение десятичных чисел. Единственная разница, которую вы видите, заключается в том, что двоичное умножение включает в себя числа, состоящие из нулей и единиц. Но десятичное умножение содержит числа, состоящие из цифр от 0 до 9. Давайте шаг за шагом узнаем больше о методе двоичного умножения.
Процесс умножения двоичных чисел такой же, как и арифметическое умножение десятичных чисел. Единственная разница, которую вы видите, заключается в том, что двоичное умножение включает в себя числа, состоящие из нулей и единиц. Но десятичное умножение содержит числа, состоящие из цифр от 0 до 9. Давайте шаг за шагом узнаем больше о методе двоичного умножения.
В двоичной системе число выражается двумя цифрами, 0 и 1. Таким образом, основание двоичной системы равно двум. В этой системе отдельные цифры 0 и 1 представляют собой коэффициенты при степенях числа 2 (два). Например, десятичное число 6 записывается так:
6=4+2=1×2 2 +1×2 1 +0×2 0 . Таким образом, двоичное представление десятичного числа 6 равно 110 (читается как один-один-ноль, а не сто десять).
Аналогично, двоичным эквивалентом десятичного числа 17 является 10001 (читается как единица — нуль — ноль — ноль — единица). Чтобы избежать возможной путаницы с десятичными числами, двоичные числа иногда заключают в скобки, а основание 2 записывают в виде нижнего индекса. Таким образом, двоичное число 10101 записывается как (10101) 2 . Скобки необязательны: номер также может быть записан как 10101 2 .
Чтобы избежать возможной путаницы с десятичными числами, двоичные числа иногда заключают в скобки, а основание 2 записывают в виде нижнего индекса. Таким образом, двоичное число 10101 записывается как (10101) 2 . Скобки необязательны: номер также может быть записан как 10101 2 .
Двоичная цифра (1 или 0) также известна как бит. Группа битов со значением называется битом (или байтом), словом или кодом. Обычно «байт» представляет собой группу из восьми битов: слово «байт» происходит от «по восемь». Например, двоичное число 10010101 состоит из восьми цифр или восьми битов. Само число является байтом. Группа из четырех битов составляет откусывание. Таким образом, 1101 — это откусывание.
Преобразование десятичного числа в двоичное
Чтобы преобразовать десятичное число в его двоичный эквивалент, десятичное число выражается как сумма возрастающих степеней 2. Последовательные коэффициенты степени 2 представляют число в двоичной системе. Таким образом, чтобы преобразовать число 7 в его двоичную форму, мы напишем
Таким образом, чтобы преобразовать число 7 в его двоичную форму, мы напишем
7=4+2+1=1×2 2 +1×2 1 +1×2 0 .
Коэффициенты 2 2 , 2 1 и 2 0 равны 1, 1 и 1 соответственно. Следовательно, двоичное представление числа 7 равно 111 (один-один-один). Альтернативный метод преобразования десятичной системы в двоичную состоит в том, чтобы постепенно делить десятичное число на 2, пока частное не станет равным нулю. Остатки последовательных делений, записанные в обратном порядке, дают двоичное число.
Десятичная система счисления — это число, которое мы используем в наших повседневных операциях. Десятичная система состоит из 10 цифр 0, 1, 2,3,4,5,6,7,8,9.и двоичное число, упомянутое как число с основанием 2, как обсуждалось выше.
Шаги по преобразованию
Теперь, когда вы просто понимаете представление нижней части числа по основанию 2, вы можете преобразовать десятичную систему в двоичную, используя последовательное деление на 2. Должен быть остаток от 0 и 1, и запишите его сбоку от проблема деления.
Должен быть остаток от 0 и 1, и запишите его сбоку от проблема деления.
Возьмите результат первой задачи деления и снова разделите его на 2. Как и прежде должен быть остаток 0 или 1, который вы должны написать в сторону задачи.
Продолжайте этот метод, пока результат не станет 0.
Напоминанием, которое вы написали в сторону задач на деление, является полученное двоичное число. Число будет читаться снизу вверх. Наименее важная цифра должна быть вверху, а самая важная внизу.
Например, преобразуйте 25 из 10 по основанию в 2.
25 ÷ 2 = 12 R1322 0
6 ÷ 2 = 3 r 0
3 ÷ 2 = 1 R 1
1 ÷ 2 = 0 R
131313
13131313131313131313131313131313131313131313131313131313131 снизу вверх 11001.

Преобразование двоично-десятичного числа
Преобразование двоичного числа в десятичное выполняется для представления числа, заданного в двоичной системе счисления, в его эквивалент в десятичной системе счисления. Система счисления чрезвычайно важна для представления чисел.
Двоичное число может быть преобразовано в его десятичный эквивалент с помощью последовательных цифр с крайнего правого края двоичного числа, являющихся коэффициентами возрастающих степеней 2, начиная с нулевой степени 2 в крайнем правом углу. Например, двоичное число 10110 записывается как
10110=1×2 4 +0×2 3 +1×2 2 +1×2 1 +0×2 0
= 16 + 0 + 4 + 2 + 0 = 22 (двадцать два)
Таким образом, десятичный эквивалент двоичного числа 10110 равен 22,9.0003
Преобразование двоичных чисел в десятичные может быть выполнено простым суммированием процесса двоичных цифр с их соответствующим весом в форме
— двоичная цифра × 2, возведенная в степень положения цифры, начинающейся с крайней правой цифра.
Преобразование двоичного числа в десятичное число.
Решение:
Данное двоичное число =
Давайте умножим каждую цифру из (старшего бита на младший бит), уменьшив степень основания числа 2.
1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0
= 8 + 4 + 0 + 1
= 13
Таким образом, равное десятичное число для данного двоичного числа равно
Как выполнять двоичное умножение
Умножение двоичных чисел подчиняется следующим четырем правилам двоичного умножения:
1. 0 × 0 = 0;
2. 1 × 0 = 0;
3. 0 × 0 = 0; и
4. 1 × 1 = 1.
Умножение двоичных чисел (двух больших чисел), состоящих из нескольких разрядов (т. е. цифр), выполняется аналогично десятичному умножению. Согласно правилам двоичного умножения числа в скобках представляют собой десятичные эквиваленты двоичных чисел.
е. цифр), выполняется аналогично десятичному умножению. Согласно правилам двоичного умножения числа в скобках представляют собой десятичные эквиваленты двоичных чисел.
Действия по умножению двоичных чисел
Процесс умножения двоичных чисел проще, чем умножение десятичных, поскольку двоичные числа содержат две цифры, равные либо 0, либо 1. Здесь описан метод умножения двоичных чисел. Эти правила также применимы для двоичных чисел с процентной точкой.
Теперь рассмотрим пример умножения и. Здесь десятичный эквивалент первого числа будет 29, а десятичный эквивалент — 9. Теперь давайте перемножим эти числа.
Шаг 1: Запишите множимое и, следовательно, множитель в позиции один под другим.
Шаг 2. Теперь умножьте крайнюю правую цифру, которая также называется младшим значащим битом (LSB) множителя (1), на все цифры множимого, которое здесь равно 9.0003
Шаг 3. Теперь добавьте заполнитель «X» перед умножением цифры следующего порядка множителя на множимое.
Теперь добавьте заполнитель «X» перед умножением цифры следующего порядка множителя на множимое.
Шаг 4. Повторите аналогичный процесс для всех цифр следующего порядка, пока не дойдете до самой левой цифры множимого, которая также называется старшим битом (MSB).
Шаг 5: Произведение, полученное в каждой из строк, будет называться частичным произведением. Теперь, наконец, добавьте все частичные произведения. Для их сложения используйте основные принципы бинарного сложения
Given below are the binary multiplication examples:
1001.11
× 100.1
————
100111
000000
000000
100111
—- ————
101011.111
Интересные факты
● В Индии бинарная система была разработана индийским ученым Пингалой (ок. 2 века до н.э.) для описания просодии.
2 века до н.э.) для описания просодии.
● Двоичная система была фактически открыта человеком по имени Готфрид Лейбниц и используется в большинстве современных компьютеров для простоты использования.
● Обычно это единицы, десятки, сотни и тысячи, но в двоичной системе это не одно и то же. Он состоит из 1, 2, 4, 8. Столбец единиц удваивается независимо от того, насколько велико число.
● Если последняя цифра двоичного числа равна 1, то число нечетное, а если 0, то число четное.
Binary Урок 11 – Двоичное умножение
⌚ 25 сентября 2014 г.
Двоичное умножение выполняется так же, как десятичное умножение. Числа, которые мы перемножаем вместе, называются множителями, а результат умножения называется произведением.
Единственная проблема связана с многорядным сложением, которое упрощается, если мы выполняем сложение по две строки за раз.
Умножение целых двоичных чисел
11 х 11 ------ 11 + 11 ------ 1001b
Иногда полезно заполнить строки нулями, чтобы сделать выравнивание столбцов более очевидным и избежать ошибок при сложении.
11 х 11 ------ 011 + 110 ------ 1001b
Часть умножения до смешного проста, потому что мы умножаем на 1 или 0. Фактически, при умножении на 1 просто скопируйте строку. При умножении на ноль заполните строку всеми нулями и сделайте правильный отступ в нулевой строке. Не пропускайте нулевые строки, так как они помогают нам получить правильный ответ.
101 х 101 ------- 101 <--- Скопируйте верхнюю строку 000 <--- Все нули 101 <--- Скопируйте верхнюю строку -------
Если опустить вторую строку, содержащую все нули, то легко забыть сделать отступ третьей строки на два знака.
Умножить 111b x 111b
111 х 111 --------- 111 111 + 111 ------------
Здесь мы видим три строки, которые нужно добавить после завершения умножения. Хотя можно сложить несколько строк вместе, двоичное сложение проще всего выполнять по две строки за раз. Суммируйте две строки за раз, начиная с верхней строки. Сохраняйте выравнивание, заполняя каждую строку нулями, чтобы каждая строка содержала одинаковое количество битов и значения на своих местах. Если бит смещен, продукт будет неправильным. Форма столбиков должна быть квадратной или прямоугольной.
Если бит смещен, продукт будет неправильным. Форма столбиков должна быть квадратной или прямоугольной.
111 00111 111 ---> 01110 + 111 + 11100 ----------- --------
Выполнить двухрядное прибавление в сторону, а пройденные ряды вычеркнуть.
Сложение трех рядов по два за раз. Хотя можно добавить несколько строк в двоичном формате, разделение сложения на два этапа помогает уменьшить количество ошибок двоичного сложения.
111б х 111б = 110001б. Проверьте путем преобразования в десятичную и умножения.
111b = 7d. 7 х 7 = 49д. Преобразовать 49d в двоичный код: 110001b. Следовательно, продукт правильный.
Умножение двоичных дробей
Выровняйте обе строки по младшему значащему биту и умножьте так же, как при десятичном умножении. Конечная позиция точки счисления представляет собой сумму количества позиций точек счисления от обоих факторов.
10.10b 2.5d х 1.01b 1.25d ----------- 1010 0000 1010 ---------------- 11,0010b (3 1/8 = 3,125d) 9| +---- Точка счисления ставится через три позиции от младшего значащего бита.Верхний фактор имеет точку счисления в одном месте справа, а нижний фактор имеет точку счисления в трех местах справа. 1 место + 2 места = 3 места, поэтому мы вставляем точку счисления в трех местах.
Что касается добавления,
101,1 х 1,01 ---------- 1011 0000 1011 ----------
Мы дополняем нулями, чтобы избежать ошибок выравнивания.
101.1 х 1,01 ---------- 001011 000000 101100 ----------
Можно было бы добавить две строки за раз, но в данном случае в этом нет необходимости. Строку, состоящую из всех нулей, можно игнорировать, поэтому мы добавляем верхнюю и нижнюю строки за один шаг. Используйте бинарное сложение.
101.1 х 1,01 ---------- 1 <------ Бит переноса из суммы столбца 4. 1 + 1 = 10b, помните? 001011 000000 101100 ---------- 110111
Теперь мы включаем точку счисления в произведение в трех местах справа.
101.1 х 1,01 ---------- 001011 000000 101100 ---------- 110.111 <--- Точки счисления добавлены в трех местах, потому что 1 место + 2 места = 3 места.
Мы можем проверить правильность произведения путем преобразования в десятичное число, умножения в десятичном виде, а затем обратного преобразования в двоичное число. Если полученное двоичное число совпадает с исходным двоичным произведением, то ответ правильный.
101.1б = 5.5д 1,01б = 1,25д 1,25 х 5,5 --------- 6.875 6,875d = 110,111b Верно
Мы еще не рассмотрели преобразование десятичной дроби в двоичную, поэтому в этом примере использовался шаблон, который мы видели раньше: 0,111 = 0,875. Всегда. (0,5 + 0,25 + 0,125 = 0,875d)
Практика
Удивительно, но двоичное умножение займет больше всего времени со сложением, так что это отличная практика сложения. Попробуйте решить эти практические задачи, используя карандаш и бумагу. Вы можете использовать калькулятор только для проверки двоичных/десятичных преобразований.

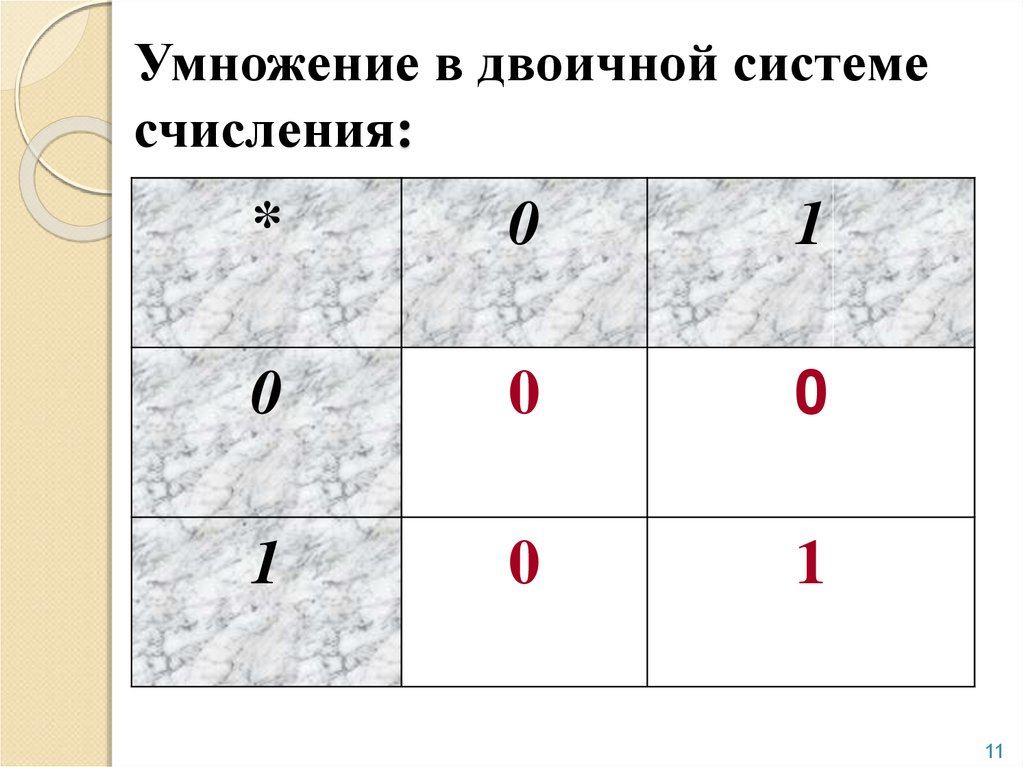 75 x 5 = 68.75
75 x 5 = 68.75