Числовые и буквенные выражения и их значения. Упрощение выражений.
Работа учащихся в группе.
При делении класса на группы применяется
стратегия «Пазл».
Учитель разбивает класс на 4 группы. В каждую группу он определяет ученика с сильными математическими знаниями – он является координатором. Остальным раздаёт кусочки пазла,
(4 разрезанные фотографии), учащиеся собрав фотографии объединяются в группы.
Повторили правила работы в группах.
«Пазл» — фото учёного – математика Рене Декарта, который стал обозначать неизвестные величины буквами х, у и z
Физкультминутка
Я буду зачитывать выражения, если выражение числовое, то хлопаете в ладоши один раз, если буквенное выражение — топаете.(учащиеся выполняют физзарядку стоя)
2х +3; 15 + 4; 44 : у; 32 – 12; 16 + а; 7с; 45 · 2 + 6; 100 – 55.
Каждая группа получает одинаковые задания дифференцированного характера.
Координатор распределяет задания в группе по уровню подготовленности учащихся.
После выполнения всех заданий, координатор получает шаблоны решённых заданий. И происходит обсуждение учащимися, решённых заданий. Самооценивание по шаблону выполненных заданий.
Уровень — А —
Задание 1. Найдите значение выражения
1) 10000 – b , если b = 8276;
2) а + 8729, если а =1271;
3) 5566 : с, если с = 506.
Критерии оценивания | Дескриптор |
Находят значения буквенного выражения по заданным значениям букв | 1) подставляют значение буквы в буквенное выражение; 2) находят значение разности: 3) находят значение суммы; 4) находят значение частного. |
Уровень – В —
Задание 2.
Ученики 5 класса посадили на пришкольном участке а берез, а кленов на 4 дерева больше. Сколько всего деревьев посадили ученики? Найдите количество деревьев если а = 10.
Сколько всего деревьев посадили ученики? Найдите количество деревьев если а = 10.
Критерии оценивания | Дескриптор |
Находят значение буквенного выражения по заданным значениям букв |
4) подстановка значения буквы в буквенное выражение; 5) нахождение значения числового выражения; 6) правильная запись ответа. |
Уровень – С —
Задание 3.
Подсчитайте прибыль за ноябрь, если затраты на аренду территории под автостоянку в месяц составили 150000 тг, на автостоянке ежедневно стояло а машин и плата была 200тг/сут. Вычислите прибыль при а = 30.
Критерии оценивания | Дескриптор |
Находят значение буквенного выражения по заданным значениям букв |
3) подстановка значения буквы в буквенное выражение; 4) нахождение значения числового выражения; 5) правильная запись ответа. |
Индивидуальная работа.
Выполнение теста.
1 вариант.
Выберите из данных выражений буквенное:
А. 2 · 5 + 4; В. 7х – 6;
С. 36 : 4 – 5; D. (81 + 15) · 2.
2) При каком значении а верно равенство 3а = 18.
А. 15; В. 54; С. 6; D. 21.
3) Составьте выражение по условию задачи:
У Асхата 7 смайликов, а у Серика х смайликов. Сколько смайликов у Асхата и Серика вместе?
А. 7х; В. 7 : х; С. 7 – х; D. 7 + х.
4) Найдите значение выражения 6х, при х = 21.
А. 116; В. 27; С. 126; D. 24
5) Найдите значение выражения b : 5 + 12,
при b = 20.
А. 16; В. 24; С. 20; D. 24.
2 вариант.
Выберите из данных выражений числовое:
А. 2у + 4; В. 7х – 6;
С. 36 : 4х – 5; D. (81 + 15) · 2.
2) При каком значении d верно равенство 3 + d = 18.
А. 15; В. 21; С. 6; D. 5 .
21; С. 6; D. 5 .
3) Составьте выражение по условию задачи:
У Сауле в корзине 18 белых грибов а подберёзовиков в х раз больше. Сколько подберёзовиков в корзине Сауле?
А. 18х; В. 18 : х; С. 18 – х; D. 18 + х.
4) Найдите значение выражения 9х, при х = 12.
А. 98; В. 21; С. 108; D. 28
5) Найдите значение выражения 36 – 𝑚 : 4,
при 𝑚 = 20.
А. 4; В. 31; С. 41; D. 64.
Взаимопроверка по готовому шаблону.
№1 | №2 | №3 | №4 | №5 | |
1 вариант | В | С | С | А | |
2 вариант | D | А | А | С | В |
Работа учащихся оценивается формативно (взаимооценивание в виде словесной похвалы).
Критерии оценивания:
5 правильных ответов – молодец
4 правильных ответа – хорошо
1 – 3 правильных ответа – надо подумать
Конспект урока «Упрощение выражений» по математике для 5 класса
Тема урока: «Упрощение выражений»
Тип урока: урок обобщения и систематизации знаний, закрепления способов деятельности.
Формы организации деятельности учащихся на уроке: групповая, индивидуальная работа.
Цели урока:
образовательные:
научить читать и записывать числовые и буквенные выражения;
сформировать умение составлять числовые и буквенные выражения по условию задачи, находить значение буквенного выражения.
развивающие:
способствовать развитию памяти, логического мышление, математически грамотной речи (устной и письменной).

организовать деятельность учащихся по обобщению знаний и способов деятельности по изучению темы.
воспитательные:
способствовать развитию интереса к математике и математическим наукам;
содействовать развитию умения общаться между собой и вести совместную работу;
развивать усидчивость, самостоятельность, самоконтроль, наблюдательность;
Оборудование для демонстраций: иллюстрации на доске, раздаточный материал по теме «Упрощение выражений», мультимедийный проектор.
Требования к уровню подготовки обучающихся:
знать:
уметь:
упрощать выражения, зная распределительное и сочетательное свойства умножения;
решать уравнения, предварительно упростив их с помощью свойств умножения;
составлять числовые и буквенные выражения по условию задачи;
- находить значение буквенного выражения.

Дополнительные знания и умения: научить наблюдать, анализировать, делать выводы, осмысливать и обобщать учебный материал; объективно оценивать свою деятельность и деятельность других.
Дидактические цели элементов урока | Содержание урока, формы взаимодействия с учащимися | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Мотивационная беседа с учащимися (1 мин.) | Обратить внимание учащихся на актуальность темы, необходимость полного усвоения темы для дальнейшего обучения, прикладной значимости. Сообщить цель урока. | Рассказ учителя. Компьютерная презентация. Сообщаю тему урока, эпиграф урока. «Математика является фундаментом, на котором строятся способность правильно воспринимать действительность и создают основу для развития ума и сообразительности в отношении практических вопросов» И. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Актуализация опорных знаний (5 мин.) | Входной контроль. Диагностика усвоения темы, выявление пробелов, работа над ними, подготовка к работе на уроке. | Устный счет. Великая отечественная война началась 22 июня 1941 года. Узнать, сколько дней продолжалась война, поможет нам удивительный квадрат.
Фламинго из песка строят гнезда в форме усеченного конуса, в верхнем основании делают углубления, в которые откладывают яйца. Если лето ожидается дождливым, то гнезда строятся высокими, чтобы их не могла затопить вода, если засушливым, — то более низкими. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Усвоение содержания учебного материала (20 мин.) | Игровой замысел способствует развитию познавательного интереса к математике, формированию у учащихся положительного мотива учения. | Далее учащимся предлагается вспомнить, какие законы сложения и умножения они знают. (Переместительный и сочетательный) Сформулируйте распределительный закон умножения относительно сложения. (Для того чтобы умножить сумму на число, надо умножить сумму на число, надо умножить на это число каждое слагаемое и сложить получившиеся произведения) Сформулируйте распределительное свойство вычитания. (Для того, чтобы умножить разность на число, надо умножить на это число уменьшаемое и вычитаемое, и из первого произведения вычесть второе). 2. Укажите, какой способ решения проще. или или
а) б) в) г) 4. Как используется распределительное свойство при решении уравнений.
а) б) в)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Физкультминутка (2 мин.) | Снять утомление учащихся, повысить умственную работоспособность учащихся. | Читается стихотворение, а дети выполняют действия.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обеспечение осознанности формируемых знаний (8 мин.) | Диагностика усвоения темы, учет пробелов в знаниях, коррекция знаний. | «Математическое лото». Учащиеся делятся на 3 группы, каждая из которых получает конверт с заданием. Необходимо задания на упрощение буквенных выражений, закрыть карточки с заданиями карточками с правильными ответами. (Приложение 1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рефлексия (2 мин.) | Надеюсь, что вы этот материал не забудете, и мы в дальнейшем будем часто его использовать. А теперь пусть каждый из вас оценит свою работу. (Учащимся предлагается выбрать геометрическую фигуру, которая, по его мнению, соответствует оценке за работу на уроке) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выставление отметок (1 мин.) | Сообщить учащимся отметки, полученные во время урока. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашнее задание (1 мин.) | Проанализировать результат взаимоконтроля. Работа над ликвидацией выявленного пробела. | Составить две задачи и решить их с помощью уравнения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Здесь представлен конспект к уроку на тему «Упрощение выражений», который Вы можете бесплатно скачать на нашем сайте. Предмет конспекта: Математика (5 класс). Также здесь Вы можете найти дополнительные учебные материалы и презентации по данной теме, используя которые, Вы сможете еще больше заинтересовать аудиторию и преподнести еще больше полезной информации.
Узнайте, что такое алгебраическое выражение и как его использовать
Алгебра — это математическая дисциплина, которая помогает нам понимать и решать уравнения. Алгебраическое выражение — это уравнение, содержащее одну или несколько переменных. Эти переменные могут быть представлены буквами, цифрами или другими символами.
Решая алгебраическое выражение, мы можем найти значение переменной (переменных) в уравнении.
В этом сообщении блога мы более подробно рассмотрим значение и использование алгебраических выражений и ответим на вопрос «Что такое алгебраическое выражение?» Время для быстрого обновления алгебры!
Что такое алгебра?
Алгебра — увлекательная часть математики, помогающая понимать числа и работать с ними более абстрактно.
Он работает, беря отношения между двумя или более переменными и используя эти отношения для решения уравнений, описания закономерностей и установления связей между различными частями информации.
Алгебраические формулы позволяют нам брать сложные задачи из реального мира и превращать их в вопросы, на которые можно дать логические ответы, что дает нам удовлетворительные ответы как в классе, так и в реальном мире.
Алгебру можно использовать для моделирования реальных проблем и анализа данных, например для прогнозирования будущих тенденций. Он также используется в таких областях, как физика и инженерия, для понимания поведения систем в различных условиях.
Изучая алгебру, мы учимся понимать, как можно использовать математику для объяснения сложных идей и решения сложных задач. Это также помогает нам придумывать новые способы решения проблем и улучшает нашу способность мыслить логически и абстрактно — навыки, полезные во многих областях.
Алгебраические уравнения позволяют разбивать сложные задачи на части, которые легче решать с помощью основных математических операций, таких как сложение, вычитание, умножение, деление и возведение в степень. Это позволяет легко решать задачи быстро, точно и без калькулятора. Алгебра учит нас, как читать графики и другие наборы визуальных данных, что помогает нам понять тенденции во многих различных областях исследования.
Это позволяет легко решать задачи быстро, точно и без калькулятора. Алгебра учит нас, как читать графики и другие наборы визуальных данных, что помогает нам понять тенденции во многих различных областях исследования.
При правильном использовании алгебра может открыть совершенно новый взгляд на проблемы и помочь найти решения, выходящие далеко за рамки того, что было возможно ранее.
Четыре основных операции
Алгебра — это раздел математики, который фокусируется на изучении переменных и констант и их взаимосвязей.
В основе алгебры лежат четыре основных операции: сложение, вычитание, умножение и деление. Сложение стремится найти сумму двух или более чисел; вычитание ищет разницу между двумя или более числами; умножение умножает два или более чисел вместе; и деление делит одно число на другое, чтобы узнать частное.
Когда дело доходит до понимания алгебраических уравнений и основ, необходимы эти четыре операции.
Числа, переменные и операции
Алгебраические выражения часто используются в математике, потому что они позволяют нам кратко показать математические уравнения и отношения.
Выражение может быть чем угодно: от одного числа или переменной до группы терминов, объединенных с помощью таких операторов, как сложение или умножение.
При составлении алгебраических выражений важно помнить порядок операций. Чтобы решить выражение, вы должны работать в определенном порядке, обычно начиная со круглых скобок, затем степеней, затем умножения или деления и, наконец, сложения или вычитания.
Придерживаясь этого правила, можно легко решать сложные уравнения, не запутавшись. Таким образом, алгебраические выражения чрезвычайно полезны для быстрого представления и вычисления математических значений.
Давайте рассмотрим пример. Рассмотрим уравнение 5x + 7. Здесь x известен как переменная и может представлять любое целочисленное значение; таким образом, это уравнение также может быть записано как 5(1) + 7 = 12 или 5(-3) + 7 = -8 и так далее. В этом случае скобки показывают, что 5 нужно умножить на 1 (или -3), а затем добавить 7, что даст в сумме 12 (или -8).
Если вы знаете, как решать алгебраические выражения, легко изменить уравнения, чтобы получить то, что вы хотите. Примером может быть нахождение x в выражении 5x + 7 = 12. Отняв 7 от обеих частей уравнения, мы можем легко выяснить, что такое x, что даст нам ответ 5x = 5. Разделив обе части на 5, мы получим х = 1; таким образом, решение этого выражения равно x = 1.
Как видите, алгебраические выражения — это сокращенный способ представления уравнений и вычислений. Они могут сэкономить вам много времени, потому что вы можете написать кучу вычислений в одном выражении. Используя порядок действий, мы можем решить эти выражения, не запутавшись, и быстро получить правильный ответ.
Как читать алгебраические выражения
Понимание алгебраических выражений и уравнений является жизненно важной частью математики. Каждое выражение состоит из терминов, разделенных знаками сложения (+) или вычитания (-).
Первый шаг в решении более сложных задач по алгебре — научиться распознавать и записывать основные выражения. От, казалось бы, простых операций, таких как «2x + 5y», до алгебраических формул, определяющих длину окружности, знание того, как комбинировать термины с комбинацией этих операторов, является важной частью математических знаний.
От, казалось бы, простых операций, таких как «2x + 5y», до алгебраических формул, определяющих длину окружности, знание того, как комбинировать термины с комбинацией этих операторов, является важной частью математических знаний.
Умение работать с выражениями может помочь вам понять более сложную математику, что может открыть новые способы изучения геометрии и других предметов.
Хорошим примером алгебраического выражения является уравнение для вычисления площади прямоугольника. Формула A=LxW, что означает «площадь равна длине, умноженной на ширину». В этом выражении буква L представляет длину прямоугольника, а W — его ширину. Перемножая эти два термина вместе, можно получить ответ на задачу: площадь прямоугольника.
Одним из наиболее важных аспектов алгебраических выражений является умение их упрощать. Это требует знания различных алгебраических операций, таких как сложение, вычитание, умножение и деление. Манипулируя этими операторами в определенном порядке (известном как «порядок операций»), можно привести уравнения к их простейшей форме.
Это может быть очень полезно при работе со сложными выражениями с несколькими переменными, потому что упрощение выражения может помочь вам увидеть, как разные термины связаны друг с другом. Кроме того, это часто может значительно упростить поиск конкретной переменной.
Каков порядок действий?
Порядок операций, также известный как стандартный порядок операций, является важным понятием для понимания в математике. Он указывает порядок, в котором выполняются операции при оценке выражений, чтобы можно было найти другой ответ, если выражение вычислено неправильно.
Как правило, большинство математиков используют аббревиатуру PEMDAS (скобки, экспоненты, умножение и деление слева направо только в круглых скобках, сложение и вычитание слева направо) при соблюдении правил для этого порядка.
Например, если бы вы вычисляли выражение 2 + 3 x 7 =, согласно PEMDAS, вы должны начать с умножения (3 x 7), затем сложения (2 + 21), в результате чего в результате получится 23. Понимание этой системы дает нам надежный метод правильного решения сложных математических уравнений с точностью и уверенностью.
Понимание этой системы дает нам надежный метод правильного решения сложных математических уравнений с точностью и уверенностью.
Использование порядка операций также может помочь вам решать уравнения, состоящие более чем из одного шага, не запутываясь и не допуская ошибок. Если порядок не соблюдается, это может привести к другому ответу, чем предполагалось. Эта концепция важна как для студентов, изучающих математику, так и для профессиональных математиков, поскольку она обеспечивает точность при выполнении расчетов.
Важно помнить, что все операции следует выполнять слева направо. Это включает в себя сложение, вычитание, умножение, деление, возведение в степень и группировку символов, таких как круглые скобки.
Кроме того, при работе с дробями и десятичными числами следует строго соблюдать порядок операций, поскольку их решение может оказаться более сложным, чем целые числа.
Использование скобок
Важно знать, как правильно использовать скобки в математических уравнениях, если вы хотите понимать и выполнять математические операции. При правильном использовании круглых скобок их можно использовать для группировки терминов, стоящих до, после или одновременно до и после других терминов в уравнении.
При правильном использовании круглых скобок их можно использовать для группировки терминов, стоящих до, после или одновременно до и после других терминов в уравнении.
Позволяет изменить порядок выполнения операций. Операции, заключенные в круглые скобки, должны выполняться первыми.
При выполнении математических операций неправильное использование скобок может сильно повлиять на результат уравнения, поэтому важно привыкнуть к ним.
Получите квалифицированную помощь по алгебре сегодня
Алгебра может быть сложным предметом, и ее часто упускают из виду, когда речь идет об основах математики. Потратив время на изучение алгебраических принципов, вы сможете лучше понять, как применять их в повседневной жизни.
Ваш ребенок может освоить математические навыки, необходимые ему в будущем, с помощью опытного репетитора. В Learner работает большое количество опытных математиков, которые хотят помочь учащимся изучить алгебру и другие математические темы.
С их помощью легко лучше понять основы и опробовать более продвинутые идеи.
Свяжитесь с нами сегодня, чтобы начать улучшать свои математические навыки!
Видео-урок: Упрощение выражений: Объединение похожих терминов
Стенограмма видео
В этом видео мы будем глядя на то, как упростить алгебраические выражения, комбинируя подобные термины. Мы будем рассматривать выражения которые содержат цифры и буквы и комбинации букв и думать о Влияние скобок на некоторые выражения.
Мы можем упростить алгебраические выражения, комбинируя или собирая подобные термины. Например, все числа на свои, все 𝑥, все 𝑦 и так далее.
Так упрости два плюс три 𝑥 плюс
два 𝑦 минус 𝑥 плюс пять 𝑦 плюс четыре 𝑥 минус три 𝑦 плюс семь. Итак, думая о чистом
сначала числовые термины, у нас есть два и у нас есть плюс семь. А затем, глядя на термины 𝑥,
у нас есть плюс три 𝑥, убираем 𝑥, добавляем четыре 𝑥. И это оставляет нас с нашим 𝑦
слагаемых, плюс два 𝑦, плюс пять 𝑦, отнять три 𝑦. Некоторым людям полезно использовать
либо система цветового кода, либо система различных символов, чтобы отслеживать, какие
как термины, с которыми они столкнулись и которые они использовали до сих пор, и какие из них они
нет.
Некоторым людям полезно использовать
либо система цветового кода, либо система различных символов, чтобы отслеживать, какие
как термины, с которыми они столкнулись и которые они использовали до сих пор, и какие из них они
нет.
Таким образом, имея дело с чисто численные термины сначала, два плюс семь равно девять. Теперь у нас есть условия 𝑥. У нас есть не- три 𝑥 забрать 𝑥 два 𝑥, прибавьте четыре 𝑥, получится шесть 𝑥, так что это плюс шесть 𝑥. Тогда 𝑦 условия, у нас есть два 𝑦 плюс пять 𝑦 будет семь 𝑦, отнимем три 𝑦 получится плюс четыре 𝑦. И большинство людей склонны ставить буквенные термины сначала и чисто числовые термины в конце этого выражения. Итак, мы скажем, что это шесть 𝑥 плюс четыре 𝑦 плюс девять.
Но иногда термины включают в себя больше
сложные термины, такие как 𝑥𝑦 или 𝑦 в кубе. И нам нужно уметь идентифицировать
как термины в этих выражениях тоже.
Например, упростите три 𝑥 плюс четыре 𝑥 в квадрате минус два 𝑥𝑦 плюс семь 𝑦 в квадрате минус два 𝑥 плюс пять 𝑦𝑥 минус 𝑦 в кубе минус два 𝑥 в квадрате.
В этом выражении есть два слагаемых, три 𝑥 и убрать два 𝑥, которые являются просто числами, умноженными на 𝑥. Итак, давайте поставим их первыми. И тогда, если мы ищем 𝑥 в квадрате, мы получили плюс четыре 𝑥 в квадрате и минус два 𝑥 в квадрате. Теперь давайте искать термины 𝑥𝑦. Ну и минус два 𝑥𝑦. Но есть и плюс пять 𝑦𝑥. А поскольку умножение коммутативный, это означает, что 𝑦𝑥 совпадает с 𝑥𝑦. Так что я просто напишу пять 𝑦𝑥 как пять 𝑥𝑦.
Далее у нас есть 𝑦 в квадрате
условия. Ну, есть только один из них,
семь 𝑦 в квадрате. И мы разобрались с остальными,
кроме 𝑦 в кубе. Так что у нас только минус 𝑦
в кубе. Таким образом, подобные термины — это термины, которые
просто кратные одной и той же букве, или одной и той же букве в той же степени или
показатель степени или одна и та же комбинация букв, умноженная вместе, поэтому 𝑥𝑦, 𝑦𝑥. И три 𝑥 убери два 𝑥 это
только один 𝑥 или только 𝑥. Четыре 𝑥 в квадрате убирают два 𝑥
Squareds просто оставляет нас с двумя 𝑥 в квадрате.
И три 𝑥 убери два 𝑥 это
только один 𝑥 или только 𝑥. Четыре 𝑥 в квадрате убирают два 𝑥
Squareds просто оставляет нас с двумя 𝑥 в квадрате.
Теперь, если мы начнем с отрицательного две 𝑥𝑦, а затем мы добавим к этому еще пять 𝑥𝑦, мы получим положительные три 𝑥𝑦с. Тогда мы только что получили положительную семерку 𝑦 в квадрате и минус 𝑦 в кубе. Теперь ни один из них не похож на термины, таков наш ответ. Так что это почти как если бы 𝑥 лечили как другую букву 𝑥 в квадрате. И это трактуется как другое буква 𝑥𝑦 и 𝑦 в квадрате и 𝑦 в кубе и так далее.
Давайте посмотрим на это визуально и увидим
почему мы определили термин «подобные термины» именно таким образом. Представьте, что у нас есть один за другим
прямоугольники и некоторые прямоугольники один за 𝑦. Итак, прямоугольник один за 𝑥, один раз
𝑥, имеет площадь 𝑥. Так что мы назовем их 𝑥. И один за 𝑦, один раз 𝑦, имеет
площадь 𝑦. Итак, это 𝑦 прямоугольники.
Так что мы назовем их 𝑥. И один за 𝑦, один раз 𝑦, имеет
площадь 𝑦. Итак, это 𝑦 прямоугольники.
Итак, у меня три 𝑥 прямоугольники и два из 𝑦 прямоугольников. Таким образом, мы можем записать это как три 𝑥 плюс два 𝑦. Теперь 𝑥 прямоугольники — это другое размер до 𝑦 прямоугольников. Так что мы не можем совместить их. Это просто констатация факта что у нас есть три стиля 𝑥 и два стиля 𝑦.
Теперь добавим 𝑥-by-𝑦
прямоугольник. Так что это- площадь этого будет 𝑥
раз 𝑦, поэтому мы будем называть это 𝑥𝑦. Теперь у нас есть три 𝑥
прямоугольников, два из 𝑦 прямоугольников и один из 𝑥𝑦 прямоугольников. Поэтому мы должны написать это как
этот. Мы не можем упростить это
дальше. Это просто заявление наших трех
различные варианты прямоугольников, 𝑥s, 𝑦s и 𝑥𝑦s. И это говорит нам, сколько из каждого
мы получили.
Теперь мы добавили три 𝑦 на 𝑦 прямоугольников, 𝑦 квадратных прямоугольников и один 𝑥 на 𝑥 прямоугольник, поэтому 𝑥 квадратный прямоугольник. Итак, теперь у нас есть три 𝑥 плюс два 𝑦 плюс 𝑥𝑦 плюс 𝑥 в квадрате и три прямоугольника в квадрате 𝑦. Надеюсь, мы увидим, что 𝑥 сильно отличается от 𝑥 в квадрате. И 𝑦 сильно отличается от 𝑦 в квадрате. А 𝑥𝑦 это что-то совершенно снова разные. Вот почему мы должны выразить их отдельно в нашем алгебраическом выражении здесь.
Теперь давайте взглянем на некоторые выражения, содержащие скобки.
Например, упростите в пять раз 𝑥
плюс два плюс семь раз 𝑥 плюс два. И это действительно означает, что у нас есть
пять лотов 𝑥 плюс два. Представьте себе 𝑥 плюс два размера акций
прямоугольник. И у нас есть семь лотов 𝑥 плюс
два. Итак, у нас есть пять таких 𝑥 плюс
два прямоугольника, и у нас есть еще семь таких 𝑥 плюс два прямоугольника. Итак, 𝑥 плюс два в скобках
как термины. И пять чего-то плюс семь
больше чего-то сделать 12 чего-то. Итак, у нас есть 12 лотов 𝑥 плюс
два.
Итак, 𝑥 плюс два в скобках
как термины. И пять чего-то плюс семь
больше чего-то сделать 12 чего-то. Итак, у нас есть 12 лотов 𝑥 плюс
два.
Теперь мы можем использовать дистрибутив свойство умножения, чтобы сказать, что это означает 12 умножить на 𝑥 плюс 12 умножить на два. И мы можем написать это алгебраически как 12𝑥, сокращенно 12 раз 𝑥. И 12 умножить на два будет 24, значит 12𝑥 плюс 24.
Теперь мы могли применить
распределительная собственность ранее в этом вопросе. Так что это означало бы пять раз
𝑥 и пять раз два и семь раз 𝑥 и семь раз два. Так что будет пять 𝑥 плюс 10
плюс семь 𝑥 плюс 14, что означает, что теперь мы можем собрать подобные термины. Пять 𝑥 и семь 𝑥 похожи
условия. А дальше цифры сами по себе,
10 плюс 14, что дает нам 12𝑥 плюс 24. Таким образом, мы получаем тот же ответ.
Но заметив тот факт, что мы здесь был такой термин, 𝑥 плюс два. Это означало, что нам нужно было сделать только один много раздачи здесь, а не две партии раздачи здесь. Так что этот метод здесь немного больше заниматься. Мы сэкономили себе немного работы, заметив этот подобный термин здесь, в первую очередь, в скобках.
Теперь некоторые выражения содержат круглые скобки, которые при внимательном рассмотрении могут быть удалены.
Например, упростите пять плюс
скобки 11𝑥 плюс 12, закрыть скобки. Теперь, поскольку это выражение использует
сложение в двух местах, а сложение ассоциативно, мы получим тот же результат, если
мы прибавляем результат 11𝑥 плюс 12 к пяти, как если бы мы прибавляли 12 к результату пять плюс
11𝑥. Итак, скобки говорят нам
сделать расчет в одну сторону. Но это не имеет никакого значения
если мы поступим иначе. Они просто лишние. Так что мы можем стереть их.
Они просто лишние. Так что мы можем стереть их.
И теперь у нас есть два подобных числовых условия. А пять и 12 дают нам 17. Итак, наш ответ: 17 плюс 11𝑥, или поскольку некоторые люди предпочитают писать это с буквенным термином сначала 11𝑥 плюс 17.
Теперь последнее, прежде чем мы идти. Мы разобрались с положительными и отрицательными количественные термины, такие как три 𝑥, минус пять 𝑦, минус 12 𝑦 в квадрате и так далее. Но мы также можем иметь дело с дробное количество терминов точно так же. Например, половина 𝑥 плюс еще половина 𝑥, две половинки одного и того же дают нам одно и то же вещь. Итак, половина 𝑥 плюс половина 𝑥 — это один 𝑥, или просто 𝑥, как сейчас принято писать.
Например, если нам нужно
упростить минус треть 𝑥 плюс две трети 𝑥 плюс четверть плюс две трети 𝑥 плюс
половина, мы можем идентифицировать наши подобные термины. Итак, мы приведем все термины 𝑥
вместе. И мы приведем числовые термины
также вместе. Итак, у нас есть отрицательная треть 𝑥
плюс две трети 𝑥 плюс еще две трети 𝑥 плюс четверть плюс половина.
Итак, мы приведем все термины 𝑥
вместе. И мы приведем числовые термины
также вместе. Итак, у нас есть отрицательная треть 𝑥
плюс две трети 𝑥 плюс еще две трети 𝑥 плюс четверть плюс половина.
Давайте подумаем об этих терминах 𝑥
затем. Мы начинаем с негатива
одна треть 𝑥. И мы добавляем две трети
𝑥. Итак, одна треть, две трети 𝑥
приводит нас сюда. И тогда мы добавляем еще один
две трети 𝑥. Итак, мы пойдем на одну, две трети
𝑥 приведет нас сюда, в час. Так что это один 𝑥 или просто 𝑥. И тогда у нас есть одна четверть плюс
одна половина. Ну половина это две четверти. Итак, у нас есть одна четверть плюс
две четверти, то есть три четверти. Таким образом, применяются те же правила. Даже если у вас есть дроби, вы
может по-прежнему собирать или комбинировать одинаковые термины в алгебраических выражениях для упрощения
их.
Итак, наконец, подведем итоги того, что мы узнали тогда, мы можем упростить алгебраические выражения, комбинируя или собирая как термины. Например, три 𝑥 минус 12𝑦 плюс семь 𝑥 плюс два 𝑦. Мы можем рассматривать термины 𝑥 как термины и термины 𝑦 как похожие термины. И три 𝑥 плюс семь 𝑥 дает нам 10𝑥, а минус 12𝑦 плюс два 𝑦 дают минус 10𝑦.
Но помните, термины с разными
показатели или степени не похожи на термины. Например, пять 𝑥 плюс семь 𝑥
в квадрате минус два 𝑥 минус три 𝑥 в квадрате пять 𝑥 и минус два 𝑥 как бы
слагаемых и семь 𝑥 в квадрате минус три 𝑥 в квадрате как одинаковые слагаемые. Так что, когда я объединяю их, пять 𝑥
минус два 𝑥 дает нам три 𝑥. И семь 𝑥 в квадрате минус три 𝑥
в квадрате дает нам четыре 𝑥 в квадрате. Как будто 𝑥 в квадрате
другое письмо к 𝑥. Просто подумайте о тех разных
прямоугольники размера, которые мы показывали вам ранее, когда у нас было визуальное представление
этот.

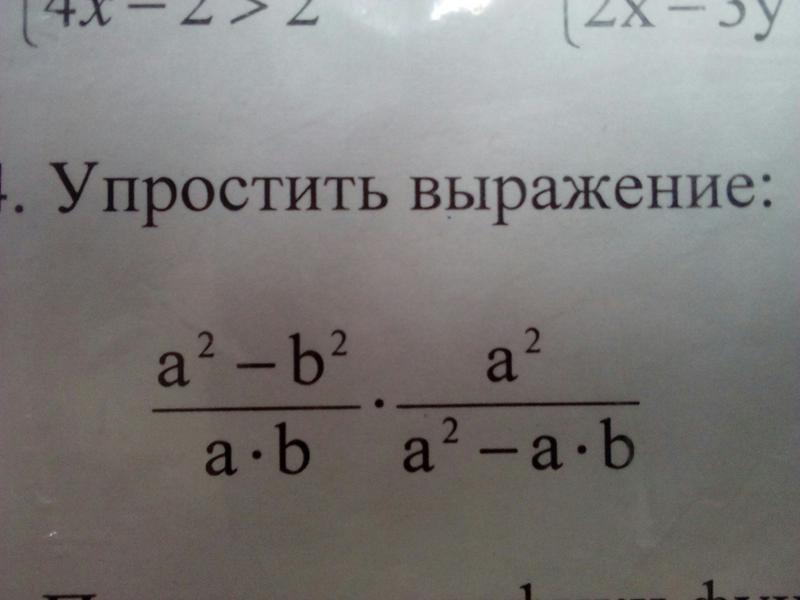


 Г.Песталоцци
Г.Песталоцци
 Название одной из них зашифровано примерами. Применяя прием последовательного деления, найдите частные: 125:5; 84:4; 90:6; 180:4; 420:3; 72:3; 68:4; 350:10. Замените частные буквами и узнайте название птицы.
Название одной из них зашифровано примерами. Применяя прием последовательного деления, найдите частные: 125:5; 84:4; 90:6; 180:4; 420:3; 72:3; 68:4; 350:10. Замените частные буквами и узнайте название птицы.


