2+n-72)=1/(n+9)7.3.1. Определитель квадратной матрицы MathCAD 12 руководство
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- MathCAD 12
org/Breadcrumb»>CAD / CAM /- Линейная алгебра
- 7.1. Простейшие матричные операции
- 7.1.1. Транспонирование
- 7.1.2. Сложение и вычитание
- 7.1.3. Умножение
- 7.2. Векторная алгебра
- 7.2.1. Модуль вектора
- 7.2.2. Скалярное произведение
- 7.2.3. Векторное произведение
- 7.2.4. Векторизация массива
- 7.3. Вычисление определителей и обращение квадратных матриц
- 7.3.1. Определитель квадратной матрицы
- 7.3.2. Ранг матрицы
- 7.3.3. Обращение квадратной матрицы
- 7.3.4. Возведение квадратной матрицы в степень
- 7.3.5. Матричные нормы
- 7.3.6. Число обусловленности квадратной матрицы
- 7.4. Вспомогательные матричные функции
- 7.
4.1. Автоматическая генерация матриц - 7.4.2. Разбиение и слияние матриц
- 7.4.3. Сортировка элементов матриц
- 7.4.4. Вывод размера матрицы
- 7.
4.1. Автоматическая генерация матрицОпределитель (Determinant) матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinant (Определитель) на панели инструментов Matrix (Матрица) (листинг 7.14) или набрать на клавиатуре <|> (нажав клавиши <Shift>+<\>). В результате любого из этих действий появляется местозаполнитель, в который следует поместить матрицу. Чтобы вычислить определитель уже введенной матрицы:
1. Переместите курсор в документе таким образом, чтобы поместить матрицу между линиями ввода (напоминаем, что линии ввода — это вертикальный и горизонтальный отрезки синего цвета, образующие уголок, указывающий на текущую область редактирования).
2. Введите оператор нахождения определителя матрицы.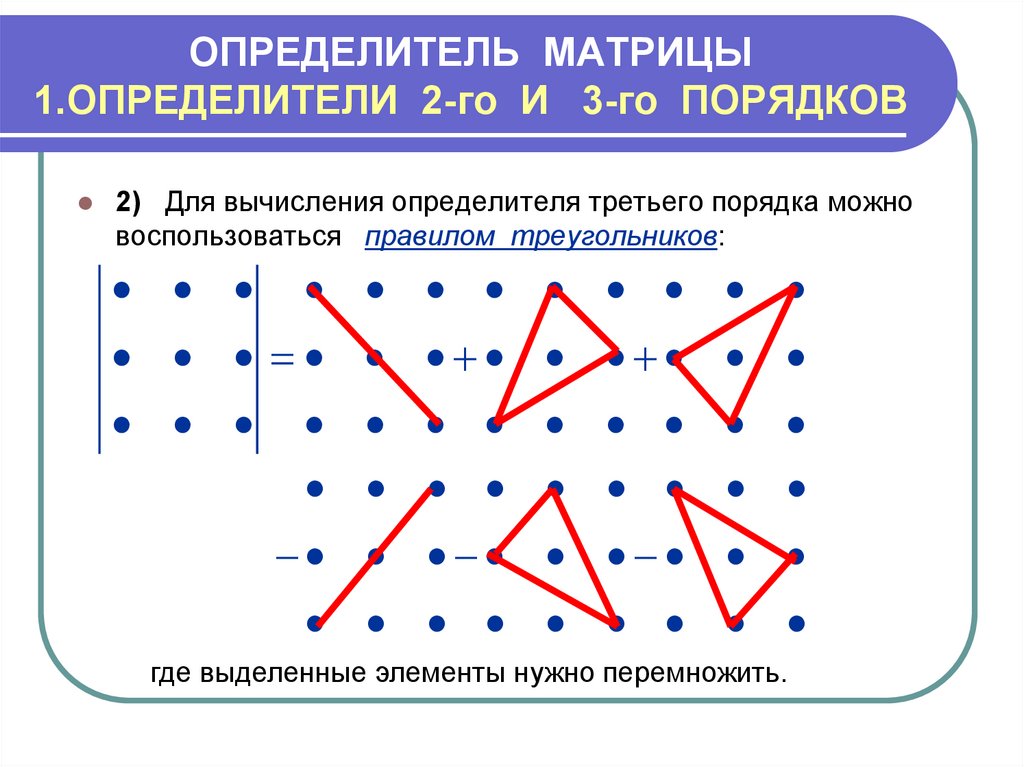
3. Введите знак равенства (либо символьного вывода), чтобы вычислить определитель (численно или аналитически соответственно, как это показано в листинге 7.14).
ВНИМАНИЕ!
Не путайте операторы вычисления определителя квадратной матрицы и длины вектора. В Matncad 12 введен принудительный контроль действий пользователя при вводе этих операторов во избежание путаницы (т. к. один и тот же символ используется для этих двух операций). При попытке вычислить определитель матрицы с помощью оператора |А|, введенного с панели Calculator (Калькулятор), а не Matrix (Матрица), будет выдано сообщение об ошибке, а результат вычисления детерминанта появится только после того, как пользователь вызовет контекстное меню и подтвердит в нем, что он собирается вычислить именно определитель матрицы. То же самое касается и длины вектора, если попытаться ввести его не с панели Calculator (Калькулятор), а с панели Matrix (Матрица).
Листинг 7.14. Вычисление определителя квадратной матрицы
Нравится
Твитнуть
Теги MathCad САПР
Сюжеты MathCad
Глава 1 Основы работы с системой Mathcad 11
9893 0
Глава 10 Работа с информационными ресурсами Mathcad 11
6924 0
Глава 2 Работа с файлами Mathcad 11
12340 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2461 s
Как найти определитель матрицы?
В математике матрица представляет собой массив чисел или символов прямоугольной или квадратной формы, сгруппированных в строки и столбцы для представления математического объекта или одного из его качеств. Например, это квадратная матрица. С другой стороны, это прямоугольная матрица.
Определитель матрицы Определитель матрицы представляет собой произведение компонентов любой строки или столбца и их соответствующих кофакторов. Они существуют только для квадратных матриц, т.е. таких, которые имеют одинаковое количество строк и столбцов. Определитель любой квадратной матрицы A представлен detA (или) |A|. Иногда его обозначают знаком . Вычисление определителей матриц 1 × 1 и 2 × 2 очень просто, но процедура усложняется по мере роста ранга матрицы.
Миноры и кофакторы участвуют в процессе определения определителя матрицы.
Свойства определителя
- Определитель матрицы и ее транспонированная всегда равны, т. е.
- Перестановка любых двух строк или столбцов матрицы меняет знак ее определителя, т. е., .
- Определитель матрицы с любыми двумя одинаковыми строками или столбцами равен нулю, т. е. .
- Определитель матрицы с нулями в качестве элементов любой из ее строк или столбцов равен нулю, т. е.
- Умножение каждой строки определителя на константу m также увеличит значение определителя в m раз, т. е. .
- Определитель матрицы 1 × 1
Матрица 1 × 1 — это строка, состоящая только из одной строки и одного столбца и, следовательно, только из одного элемента. Определитель каждой матрицы 1 × 1 всегда равен матричному элементу.
Пример: Если матрица A = [69] 1 × 1 , то det A или |A| = 69.
- Определитель матрицы 2 × 2
Если матрица A = , то ее определитель определяется как ad – bc. Он просто рассчитывается путем перекрестного умножения компонентов слева направо и сверху вниз, а затем находит разницу между ними.
Пример: Вычислить,
Здесь a = 4, b = 7, c = 5 и d = 8.
Следовательно, |A| = 4(8) – 5(7)
|А| = −3
- Определитель матрицы 3 × 3
Чтобы найти определитель матрицы 3 × 3, нам нужно понять термин минор элемента,
Минор элемента
Определитель квадратной матрицы любого порядка, полученный удалением строки и столбца, содержащего элемент, является минором элемента.
Пример: Найдите меньшую часть числа 6 в матрице
Решение:
Поскольку число 6 лежит во второй строке и третьем столбце данной матрицы, ее матрица будет равна определителю полученной матрицы удалив вторую строку и третий столбец.
Младший из 6 =
= 8 × 1 – 2 × 7
= 8 – 14
= -6
Необходимо выполнить следующие шаги:
Выберите любую строку или столбец 900. Чтобы найти определитель, мы обычно начинаем с первой строки. Определите сопутствующие факторы каждого элемента строки/столбца, которые мы выбрали на шаге 1. Умножьте элементы строки/столбца из шага 1 на соответствующие сопутствующие факторы из шага 2. Сложите все продукты из шага 3, чтобы получить определитель матрицы.
В качестве альтернативы для этой цели можно использовать следующую формулу:
|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
Примеры задач
Вопрос 1. Найдите минор числа 9в матрице .
Решение:
Поскольку 9 лежит в третьей строке и третьем столбце данной матрицы, ее матрица будет равна определителю матрицы, полученной удалением третьей строки и третьего столбца.
Минор 9 =
= 1 × 5 – 2 × 4
= 5 – 8
= -3
Вопрос 2. Найдите значение |4A| если А = .
Решение:
A =
Таким образом, 4A =
Теперь |4A| = 4 (128 – 96) – 4 (64 – 0) – 4 (48 – 0)
= 4(32) – 4(64) – 4(48)
|4A| = -320
Вопрос 3. Найдите x, если определитель матрицы равен 0. = 4(x) – 8(2)
= 4x – 16
Так как |A| = 0,
⇒ 4x – 16 = 0
или, 4x = 16
⇒ x = 4,
Вопрос 4: Оценка: . Используйте свойства определителей.
Решение:
Ясно, что элементы третьей строки имеют общий делитель 3. Это можно изобразить как:
Так как первая и третья строки данной матрицы теперь равны, используя третье свойство, значение матрицы было бы равно нулю.
|А| = 3 × 0
|А| = 0
Вопрос 5: Найдите значение (a 2 + б 2 – в 2 )|А| если А = .
Решение:
|A| = 0(0(0) – a(a)) – c(0(-c) – a(b)) + (-b)((-c)(-a) – 0(b))
= 0 × (a 2 ) − c(0 − ab) − b(ac – 0)
= 0
Следовательно, (a 2 + b 2 – c 2 )|A| = (a 2 + b 2 – c 2 )(0)
⇒ (a 2 + b 2 – c 2 )|А| = 0
Вопрос 6. Найдите t, если определитель матрицы равен 10. = 3(0) – 5(x)
= 0 – 5x
= -5x
Так как |A| = 10.
⇒ -5x = 10
⇒ x = -2
0006
Дано: A =
|A| = 5(x) – 3(1)
= 5x – 3
Так как |A| = 12
⇒ 5x — 3 = 12
⇒ 5x = 15
⇒ x = 3
Вопрос 8: Оценка:
Решение:
здесь, A = 1, B, b Решение:
.
Таким образом, |A| = 1(5(9) – 6(8)) – 2(4(9) – 6(7)) + 3(4(8) – 5(7))
= 1(45 – 42) – 2 (36 – 42) + 3(32 – 35)
= 1(3) – 2(-6) + 3(-3)
= 3 + 12 – 9
⇒ |A| = 0
Определитель больших матриц
В определении 4.1.1 определитель матриц размера \(n \le 3\) был определен с помощью простых формул. Для больших матриц, к сожалению, простой формулы нет, поэтому мы используем другой подход. Сведем задачу нахождения определителя одной матрицы порядка \(n\) к задаче нахождения \(n\) определителей матриц порядка \(n-1\text{.}\) Так, например, мы находим определитель матрицы порядка \(4\), вычисляя определители \(4\) матриц порядка \(3\text{.}\) У нас есть формула для матриц порядка \(3\text {,}\) так что, в принципе, можно будет вычислить определитель любой матрицы порядка \(4\text{.}\) Мы можем использовать эту возможность для нахождения определителя любой матрицы порядка \(5 \text{:}\) сведем ее к задаче о \(5\) матрицах порядка \(4\text{,}\), решение которой мы уже знаем.
Продолжая линию рассуждений, мы можем оценивать детерминанты любого размера.Хотя это дает теоретическую возможность вычислять определители, количество вычислений быстро становится невыполнимым. Нам необходимо улучшить наши математические методы, чтобы сделать возможными практические вычисления. Материал, развитый в этом разделе, позволяет легко оценить многие большие матрицы.
Подраздел 4.3.1 Мотивирующее вычисление
Этот подраздел содержит дополнительные материалы. Цель состоит в том, чтобы мотивировать теорему 4.3.4. При желании его можно пропустить при первом чтении.
Определение 4.3.1. Произведение Адамара двух матриц.
Если \(A=[a_{i,j}]\) и \(B=[b_{i,j}]\) являются матрицами \(m\x n\), то
произведение Адамара \ (A\circ B\) — матрица \(m\times n\), определяемая как\begin{уравнение*} (A\circ B)_{i,j}= a_{i,j}b_{i,j} \end{уравнение*}
Другими словами, умножение выполняется поэлементно.
Лемма 4.
Если \(М\) — матрица миноров, а \(С\) — матрица кофакторов, то
\begin{уравнение*} C = P \ круг М \end{уравнение*}
Доказательство.
Это просто переформулировка наблюдения 4.2.7
Сравните результаты примера 4.2.5 и примера 4.2.6.
Начиная с заданной квадратной матрицы \(A\text{,}\), мы определили матрицу миноров \(M\) и матрицу кофакторов \(C\), используя определение 4.2.1 и определение 4.2.2. Мы также использовали умножение матриц Адамара. Определение 4.3.1, чтобы увидеть, что \(C=P\circ M\text{.}\) Теперь мы хотим выполнить дальнейшее вычисление \(A\circ P\circ M=A \circ C\text{.}\)
Пример 4.3.3. \(A\circ C\) имеет постоянные суммы строк и столбцов.
Пусть
\begin{уравнение*} А= \begin{bmatrix} 1\amp0\amp-1\amp2\\ 1\amp-1\amp1\amp0\\ 0\amp1\amp-2\amp1\\ -1\amp1\amp0\amp1 \end{bmatrix} \end{уравнение*}
Тогда матрица миноров \(M\text{,}\) равна
\begin{уравнение*} М= \begin{bmatrix} 2 \ампер -3 \ампер 1 \ампер 1\\ 4\амп -5\амп 2\амп 1\\ -3\амп 4\амп -1\амп -1\\ 1\ампер -2\ампер 1\ампер 0 \end{bmatrix} \end{уравнение*}
, а матрица кофакторов \(C\) равна
\begin{уравнение*} С= \begin{bmatrix} 2 \amp 3 \amp 1 \amp -1\\ -4\амп -5\амп -2\амп 1\\ -3\амп -4\амп -1\амп 1\\ -1\ампер -2\ампер -1\ампер 0 \end{bmatrix} \end{уравнение*}
Как отмечалось ранее, \(C=P\circ M\), где
\begin{уравнение*} Р= \begin{bmatrix} 1 \амп -1 \ампер 1\ампер -1\\ -1 \ампер 1 \ампер -1\ампер 1\\ 1 \амп -1 \ампер 1\ампер -1\\ -1 \ ампер 1 \ ампер -1 \ ампер 1 \end{bmatrix} \end{уравнение*}
Продолжаем вычислять \(A\circ C=A\circ P\circ M\text{.
\начать{выровнять*} А \ круг С \амп = \begin{bmatrix} 1\amp0\amp-1\amp2\\ 1\amp-1\amp1\amp0\\ 0\amp1\amp-2\amp1\\ -1\amp1\amp0\amp1 \end{bmatrix} \циркуляр \begin{bmatrix} 2 \amp 3 \amp 1 \amp -1\\ -4\амп -5\амп -2\амп 1\\ -3\амп -4\амп -1\амп 1\\ -1\ампер -2\ампер -1\ампер 0 \end{bmatrix}\\ \амп = \begin{bmatrix} 2 \ампер 0 \ампер -1 \ампер -2 \\ -4 \ампер 5 \ампер -2 \ампер 0 \\ 0 \ампер -4 \ампер 2 \ампер 1 \\ 1 амп -2 амп 0 амп 0 \end{bmatrix} \end{выравнивание*}
Наконец, мы компотируем суммы записей в каждой строке и каждом столбце.
\begin{уравнение*} \begin{матрица} \amp \textrm{Суммы строк} \\ \begin{bmatrix} 2 \ампер 0 \ампер -1 \ампер -2 \\ -4 \ампер 5 \ампер -2 \ампер 0 \\ 0 \ампер -4 \ампер 2 \ампер 1 \\ 1 амп -2 амп 0 амп 0 \end{bmatrix} \усилитель \begin{матрица} -1\\-1\\-1\\-1 \end{матрица} \\ \begin{матрица} \llap{\textrm{Суммы по столбцам: }}-1\amp-1\amp-1\amp-1 \end{матрица} \end{матрица} \end{equation*}
В этом примере виден поразительный результат.
Доказательство.
Эквивалентная теорема 4.3.8 будет доказана позже.
Теперь воспользуемся теоремой 4.3.4, чтобы определить определитель для больших матриц.
Определение 4.3.5. Определитель квадратной матрицы.
Пусть \(A\) — квадратная матрица с \(M\) в качестве матрицы миноров и \(C\) в качестве кофакторной матрицы. Тогда определитель для \(A\) является общей суммой строк и столбцов \(A\circ P\circ M= A\circ C\text{.}\)
Подраздел 4.3.2 Определение определителя
Мы можем сделать определение более точным, сосредоточившись на конкретной строке. Для любой квадратной матрицы \(A\) порядка \(n\text{,}\) элементами первой строки матрицы кофакторов являются \(C_{1,1}, C_{1,2},\ldots ,C_{1,n}\text{.}\) Записи первой строки \(A\) равны \(a_{1,1},a_{1,2},a_{1,3}, \ldots,a_{1,n}\text{.
Теперь мы переформулируем теорему 4.3.4.
Теорема 4.3.8. Теорема разложения Лапласа.
Для любой квадратной матрицы \(A\text{,}\) \(i\)-я строка и \(j\)-й столбец равны.
Доказательство.
Доказательство сложное и требует дополнительных математических инструментов. Чтобы сохранить последовательность нашей презентации, мы отложили ее до Раздела 4.6.
Теорема разложения Лапласа допускает альтернативное (и более обычное) определение определителя.
Определение 4.3.9. Определитель матрицы.
Для любой квадратной матрицы \(A\text{,}\) определитель \(A\) есть общее значение разложений \(i\)-й строки и \(j\)-го столбца матрицы \ (А\текст{.}\)
Пример 4.3.10. Пример расширения кофактора с \(n=4\).
Пусть \(A= \begin{bmatrix} 1\усилитель 2\усилитель 2\усилитель 3\\ -1\амп 4\амп 5\амп 3\3\амп 4\амп 8\амп -1\\ 1\амп 2\амп 2\амп 1 \end{bmatrix}\text{.
= 2, c = 3, d = 4, e = 5, f = 6, g = 7, h = 8, i = 9.
3.2. \(C=P\circ M\).
}\)
Добавление записей в любую заданную строку или в любой заданный столбец дает идентичные суммы строк и столбцов. 9{i+j}\text{.}\) Тогда суммы строк и суммы столбцов \(A\circ P\circ M\) идентичны.
n a_{1,j}C_{1,j}
\end{уравнение*} 9n a_{i,j}C_{i,j}.
\end{equation*}